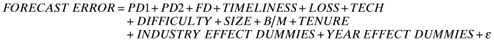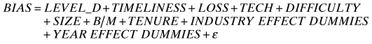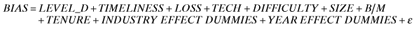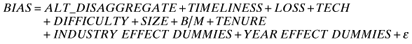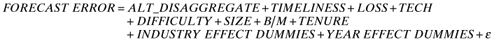Additional Evidence on Analysts’ Decision to Issue Disaggregated Earnings Forecasts: Strategic Biasing
The authors gratefully acknowledge the thoughtful comments and suggestions of the anonymous reviewer. The authors also gratefully acknowledge financial support for this research from the College of Business Administration at California State University, Long Beach.
Abstract
This study examines why analysts issue disaggregated earnings forecasts to I/B/E/S. Some recent studies suggest that analysts with superior forecasting ability issue disaggregated earnings forecasts to build reputation in the marketplace and stop forecast disaggregation once their reputation has been established. Based on an analysis of I/B/E/S forecast data for U.S. firms from 1998 to 2008, we find that, in a given year, about 20%–34% of analysts disaggregate for some, but not for all the firms that they follow. This evidence of selective disaggregation by analysts suggests that reputation building alone does not fully explain the decision to disaggregate forecasts. We hypothesize that the decision to disaggregate earnings forecasts is at the firm-level as well and is systematically related to the analysts’ bias in the issued forecasts. Our findings are that (a) analysts’ overall optimistic bias and forecast errors decrease monotonically with the level of forecast disaggregation, and (b) analysts that selectively disaggregate their forecasts for some firms or who do not persistently disaggregate a given firm's forecasts exhibit more positive bias and larger forecast errors. Our findings are consistent with the notion that the analysts who issue biased forecasts, for example, to curry favour with the management, are less likely to provide disaggregated information as part of the forecast.
Sell-side financial analysts issue research reports for the firms they follow as part of the service they provide to their clients. These research reports contain stock recommendations and insights into the future outlook on the firm and may include analysts’ forecast of firms’ financial statement elements, such as sales, expenses, gross profits, book value, net earnings and earnings per share. Subsequent to the issuance of these research reports to their clients, analysts may submit their forecasts to the Institutional Broker Estimate System (henceforth I/B/E/S)—a repository of forecast information for dissemination to the wider investing public (Henry, 2001). I/B/E/S (now merged with FirstCall) combines these individual analysts’ forecasts into a consensus forecast of earnings and makes these data available to a much larger pool of I/B/E/S subscribers. I/B/E/S subscribers also receive estimates of the individual contributing analysts, enabling them to develop customized consensus estimates by assigning different weights to the earnings estimates of individual analysts. Beginning in the mid-1990s, I/B/E/S started collecting and disseminating information on analysts’ sales estimates in addition to earnings estimates. Since then, there has been a significant increase in the number of analysts who issue both earnings and sales (henceforth, disaggregated) forecasts to I/B/E/S.
The issue of what incentives financial analysts face and what drives the bias in their forecasts is an important one for markets and academics alike. If analysts that disaggregate their forecasts are more biased than those who do not, this should be useful information to all market participants. If markets understand analysts’ reporting incentives, they will construct firms’ consensus earnings expectations by appropriately discounting biased forecasts. This is especially important in the current post-Internet bubble period because it is now clear that during that time period the prices of many stocks were inflated. The inflated stock valuations were based partly on overly optimistic earnings forecasts and strong, but misleading, buy recommendations of some of the best-known ‘all-star’ analysts (Feldman and Caplin, 2002). Accounting and finance studies that use individual analysts’ forecasts to construct estimates of market earnings expectations (e.g., Stickel, 1992) may find this additional source of bias useful in improving their estimates.
Marks (2008) and Ertimur et al. (2011) examined incentives for providing disaggregated forecasts to I/B/E/S. Both of these studies identify reputation building as one such incentive and show that new analysts provide disaggregated forecasts to signal to the market their superior forecasting ability and to build their reputation, whereas analysts with more established reputations (such as those ranked as ‘all-star’ analysts by Institutional Investor magazine) protect their earned reputation by refraining from issuing disaggregated forecasts. These studies explicitly assume that the decision to issue disaggregated forecasts is at the analyst level, regardless of the firms followed by the analysts. However, it has been well established in the literature that analysts are strategic at the firm-level because of conflicts of interests that they face. For instance, their forecasts and stock recommendations for a firm are biased and/or overly optimistic because of conflicts of interests arising from investment banking relationships (Lin and McNichols, 1998; Michaely and Womack, 1999), access to private management information (Francis and Philbrick, 1993), analysts’ desire to boost their brokerage houses’ short-term trading volume (Jackson, 2005), and to curry favour with the management when earnings are harder to predict (Das et al., 1998). The current study introduces strategic biasing at the firm-level as an additional explanatory variable for the observed earnings disaggregation documented by Marks (2008) and Ertimur et al. (2011). We argue that strategic biasing may be more readily discernible when forecasts are disaggregated due to potential inconsistencies that can arise between the sales forecasts and the earnings forecasts. Analysts who intentionally or strategically bias their forecasts may be reluctant to issue disaggregated forecasts in order to avoid revealing their bias in the earnings forecast.
We provide evidence that the issuance of disaggregated forecasts is driven by an analyst's decision to strategically bias the forecast for some, but not for all the firms that the analyst covers. Indeed, our findings provide an explanation for why not all analysts disaggregated their forecasts for all the firms in a given time period, corroborating the conjecture that the decision to disaggregate forecasts is made at the firm level, in addition to the analyst level as identified in prior studies. We develop matrices that classify analysts into four ordinal forecast disaggregation categories—No disaggregation (ND), Partial disaggregation-1 (PD1), Partial disaggregation-2 (PD2), and Full disaggregation (FD)—based on the proportion of firms for which an analyst's forecasts are disaggregated. This is the first study to analyse the data in this fashion. We hypothesize and find that analysts belonging to the ND category were more optimistically biased and less accurate than those belonging to other categories. Furthermore, this relationship of optimistic bias and accuracy of forecasts with the level of analyst forecast disaggregation is monotonic and significant across all categories. To better understand if the forecast disaggregation is driven by strategic considerations, we focus on a subsample of analysts who disaggregated their forecasts for some, but not all, of the firms they followed in a given year (in contrast to those analysts who, in a given year, disaggregated for all the firms or did not disaggregate for any firm that they followed). We refer to these analysts as selective disaggregators and find evidence that they were more optimistically biased and less accurate for firms for which their forecasts were not disaggregated. Alternatively, selective disaggregators were less biased and more accurate for firms for which their forecasts were disaggregated. As an alternative test of strategic biasing, we conduct a temporal examination of the analyst-level data over years after the issuance of their first disaggregated forecast, and identify two distinct categories of analysts. First, the ones who disaggregated the forecasts of a specific firm in some years but not others, and second, those who disaggregated their forecasts of the firm over all the years of coverage, after issuing the first disaggregated forecast. We refer to these analysts as non-persistent disaggregators and persistent disaggregators, respectively. The results show that the non-persistent disaggregators provided significantly more optimistically biased and less accurate forecasts than the persistent disaggregators. Thus, while analyst reputation building provides one explanation of the differences in the incidence of disaggregated earnings forecasts, our findings suggest that strategic biasing at the firm-level provides an additional explanation for the observed patterns of behaviour among analysts who voluntarily submit their earnings forecasts to I/B/E/S.
RESEARCH QUESTION AND HYPOTHESES
In the mid-1990s, I/B/E/S started to include sales forecasts along with earnings forecasts in its monthly and real-time reports provided to subscribers. This was also the beginning of the stock market boom fuelled in part by the proliferation of Internet firms going public in the early 1990s. Because many of these Internet firms were reporting losses, conventional price-to-earnings ratio-based valuation approaches could not be applied to value these companies. Consequently, sales estimates became increasingly important as an input into valuation models because investors started using the price-to-sales multiple instead of the price-to-earnings multiple to value Internet companies that had no profits to report in the forecast horizon (e.g., see Bagnoli et al., 2001; Davis, 2002). This increased demand for sales forecasts was met by I/B/E/S when the firm started disseminating sales forecasts along with earnings forecasts. Although more pronounced in the technology sector, analysts across all industries responded by issuing disaggregated forecasts to I/B/E/S. Even after the crash of the stock market bubble in the technology sector in early 2000s, the trend towards issuing disaggregated sales and earnings forecasts has continued to grow over all sectors of the economy. The decision to contribute earnings forecast to I/B/E/S, whether the forecast is aggregated or disaggregated, is a voluntary one on the part of analysts. In the I/B/E/S database used in the current study, approximately 4,000 analysts contributed earnings forecasts to the database in 1998, of which only 1,142 (29%) included sales estimates (see Table 1). By 2008, the percentage of analysts that included sales forecasts with their earnings estimates had grown to 81% (3,417 analysts), more than a 250% increase. As the number of analysts who issue disaggregated forecasts has grown over the years, so has the interest among researchers in trying to understand this change in voluntary analyst reporting behaviour.
| Presented below is the count and proportion of analysts who (a) did not disaggregate, (b) disaggregated for some, but not all, firms followed, and (c) disaggregated their forecasts for all firms followed in each year over the sample period 1998–2008. Disaggregation refers to issuing a sales forecast along with the earnings forecast. | |||||||
|---|---|---|---|---|---|---|---|
| Year | Number of analysts | Number and percentage of analysts who did not disaggregate their forecasts for any firm | Number and percentage of analysts who disaggregate their forecasts for only some firms | Number and percentage of analysts who disaggregate their forecasts for all firms | |||
| 1998 | 3,966 | 2,824 | 71% | 875 | 22% | 267 | 7% |
| 1999 | 4,215 | 2,828 | 67% | 901 | 21% | 486 | 12% |
| 2000 | 4,211 | 2,476 | 59% | 1,086 | 26% | 649 | 15% |
| 2001 | 4,090 | 1,870 | 46% | 1,397 | 34% | 823 | 20% |
| 2002 | 4,298 | 1,534 | 36% | 1,299 | 30% | 1,465 | 34% |
| 2003 | 4,312 | 1,062 | 25% | 1,040 | 24% | 2,210 | 51% |
| 2004 | 4,209 | 851 | 20% | 818 | 20% | 2,540 | 60% |
| 2005 | 4,269 | 759 | 18% | 827 | 19% | 2,683 | 63% |
| 2006 | 4,334 | 768 | 18% | 791 | 18% | 2,775 | 64% |
| 2007 | 4,437 | 762 | 17% | 832 | 19% | 2,843 | 64% |
| 2008 | 4,197 | 780 | 19% | 625 | 15% | 2,792 | 66% |
One naïve explanation for this change in behaviour is that it is simply a trend that an increasing number of analysts have felt compelled to adopt over time. However, Ertimur et al. (2011) and Marks (2008) argue and document that the decision to issue disaggregated forecasts over an analyst's career is driven by reputation considerations. These studies show that analysts issue disaggregated forecasts during the early stages of their careers as a means to showcase their superior forecasting ability and to build their reputation. They also find that the established ‘all-star’ analysts discontinue issuing disaggregated forecasts in order to (a) protect their established reputation which can be tarnished if their sales forecasts decrease in accuracy in the future, and (b) protect the market that is willing to pay for this information.
Despite the evidence that disaggregation is motivated by reputation building, in 2008 (the most recent year for which the data are analysed in this study) 66% of analysts disaggregated their forecasts for all of the firms that they followed and 19% did not disaggregate their forecasts for any firm that they followed. This leaves 15% of analysts who disaggregated their forecasts for some, but not all, of the firms that they followed at the same point in time. If reputation building was the only determinant of the decision to disaggregate earnings, we would not expect analysts to exhibit this selective disaggregation in a given year. The evidence suggests that forecast disaggregation may be driven by considerations other than reputation building. In particular, we propose that analysts’ intent to strategically bias their forecasts is one possible determinant of their decision to disclose disaggregated or non-disaggregated earnings forecasts. We present the argument for this possibility in the Hypotheses Development section.
Hypotheses Development
It has been well established in the literature that analysts strategically bias their forecasts to curry favour with management and to establish and maintain investment banking relationships with clients. Francis and Philbrick (1993) suggest that Value Line analysts issue overly optimistic earnings forecasts in an effort to gain access to management's private information. Lin and McNichols (1998) and Michaely and Womack (1999) show that affiliated analysts (analysts whose employers provide underwriting services to their clients) issue more optimistically biased stock recommendations than unaffiliated analysts. In a recent study, Jackson (2005) suggests that analysts also issue overly optimistic forecasts to increase the trading volume and therefore, commissions, for their brokerage houses. Understandably, analysts who engage in the type of strategic biasing described above are not likely to make public the details of their biased forecasts. For instance, an overly optimistic bias in disaggregated earnings forecasts is more likely to be detected by those who follow the sales projections through examining expected changes in economic and industry conditions, and the firm's market share, backlog and strategy, etc. In this case, the aggregated forecasts may delay the identification of this bias because outside observers cannot readily determine whether the optimistic earnings forecast resulted from intentional bias by the analyst or good faith estimates of lower expenses. Furthermore, some evidence (Ertimur et al., 2003) suggests that investors can use sales forecasts to assess the quality of earnings forecasts. Absent a sales forecast, this quality of earnings forecast assessment is not immediately obvious. In short, these strategic analysts are less likely to disaggregate their forecasts submitted to I/B/E/S. Other analysts, who may not have easy access to management or are more concerned with their professional reputation, may choose to focus on and showcase their forecast accuracy. These analysts are more likely to issue disaggregated forecasts (Ertimur et al., 2011; Marks, 2008). Because higher bias also translates into higher forecast error, ceteris paribus, our first hypothesis (stated in alternative form) is as follows:
-
H1: Forecasts of non-disaggregators will be more optimistically biased and less accurate than those of disaggregator analysts.
As pointed out above, in the most recent year examined in the current study, 85% of the sample analysts either always, or never, disaggregated their forecasts when submitting them to I/B/E/S. Despite the significant upward trend over time towards disaggregation, a sizable number of analysts disaggregated for some firms, but not others, in the same year. These analysts are identified in the middle columns of Table 1 and we refer to them as selective disaggregators. If these analysts are attempting to balance reputation building (by being more accurate) with developing a closer relationship with management and investment banking clients (by strategically biasing their forecasts), we can test our predictions with respect to strategic disaggregation by focusing exclusively on this group. These analysts, when providing less biased and more accurate forecasts, will be able to justify their positions by providing additional corroborating evidence such as forecasts of sales and expenses. Alternatively, when they strategically bias their forecasts, they may find it difficult to justify their forecasted numbers when accompanied by the disclosure of additional data (sales forecasts) that make the bias more obvious. Consequently, these strategic analysts are less likely to disaggregate their biased forecasts. Furthermore, their disaggregated forecasts are likely to be less optimistically biased when compared to their own non-disaggregated forecasts. Because higher bias also translates into higher forecast error, ceteris paribus, our second hypothesis (stated in alternative form) is as follows:
-
H2: Forecasts of selective disaggregators will be more optimistically biased and less accurate when they do not disaggregate their forecasts.
The decision to disaggregate, if driven by strategic biasing, may also be reflected at the firm-level in a given year. For example, the analyst may strategically choose to not disaggregate a forecast for a particular firm in a given year when there is a need to bias the forecast to promote a security issuance of an investment banking client. For instance, defamed and banned ‘all-star’ telecom analyst Jack Grubman issued more optimistic forecasts and changed his recommendation to ‘buy’ for AT&T in order to attract underwriting business for his employer, Solomon Smith Barney-Citi Group, in the initial public offering of ATT Wireless tracking stock (AWE). Though this strategic biasing received considerable media coverage and public attention because of its blatancy and the stature of the analyst, other similar occurrences by lesser known analysts in other contexts may be less obvious. Therefore, we analyse an additional measure of the degree of analyst disaggregation at the analyst-firm level by examining the persistence of an analyst's disaggregation for a firm over the years of his/her coverage. If an analyst disaggregated forecasts for a given firm for all future years after initially issuing a disaggregated forecast for that firm, we refer to that analyst as a persistent disaggregator. Alternatively, an analyst who does not disaggregate all future forecasts after initially issuing a disaggregated forecast for a particular firm is referred to as non-persistent disaggregator. Because the actions of non-persistent disaggregator analysts are more likely to be strategic and optimistically biased, our third hypothesis (stated in alternative form) is as follows:
-
H3: Forecasts of non-persistent disaggregators will be more optimistically biased and less accurate than those of persistent disaggregator analysts.
DATA AND RESULTS
We obtained analyst-level detailed forecast data from I/B/E/S for all U.S. firms covered during the period 1998–2008. We used one-year-ahead annual earnings per share forecasts of individual analysts and the actual earnings per share data (from I/B/E/S). In instances where analysts issued multiple earnings forecasts during the fiscal year, we used the most recent forecast. If an analyst issued at least one sales forecast for a given firm during any year, we label that firm's earnings forecast to be disaggregated for that year. Following prior literature (e.g., Sinha et al., 1997), we computed an analyst's earnings forecast error as the absolute value of the difference between analyst one-year-ahead earnings per share forecast and the reported actual earnings per share, scaled by the absolute value of the actual earnings per share, as follows:

where EPSf represents the analyst's one-year-ahead earnings per share forecast and EPSa represents the corresponding actual earnings per share. The higher the value of FORECAST ERROR, the lower the analyst's forecast accuracy. We measured an analyst's forecast bias, BIAS, using the following formula:
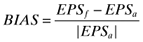
Thus, BIAS is a signed and scaled forecast error, with a positive sign indicative of optimistic bias; the higher the magnitude of the measure, the more optimistically biased is the analyst's forecast. Because these measures are subject to extreme values when EPS is near zero, we mitigated the influence of potential outliers by deleting 1% of the observations on both the lowest and the highest ends of BIAS and FORECAST ERROR distributions.
To better understand the pervasiveness of disaggregation practice for each year examined, we classified analysts into one of the following three categories: (a) analysts who did not disaggregate forecasts for any of the firms that they covered, (b) analysts who disaggregated forecasts for only some of the firms that they covered, and (c) analysts who disaggregated forecasts for all the firms that they covered. Table 1 presents the number and percentage of the total analysts in each of the three categories. For instance, the first row presents data for 1998 and shows that of the 3,966 total analysts, 2,824 (71%) did not disaggregate forecasts for any of the firms they covered, 875 (22%) issued disaggregated forecasts for some of the firms they followed, and only 267 (7%) issued disaggregated forecasts for all the firms that they followed. An examination of the data over the entire 11-year period confirms the increasing trend in the provision of disaggregated earnings forecasts identified in previous studies (e.g., Ertimur et al., 2011; Marks, 2008). The percentage of analysts that issued sales forecasts for all of the firms they covered increased monotonically from 7% in 1998 to 66% in 2008 while the percentage of analysts that did not include sales forecasts for any of the firms covered over the same period decreased steadily from 71% to 19%. Interestingly, the proportion of analysts that provided disaggregated forecasts for some, but not all, of the firms that they followed did not change in any consistent fashion. Over the time period examined (1998–2008), it ranges from a low of 15% (in 2008) to a high of 34% (in 2001). A test of the hypothesis that the observed proportion of selective disaggregators is equal to zero would be rejected at conventional levels of significance (0.05 or better), suggesting that a non-trivial number of analysts belong to this category. Furthermore, if data are pooled over all 11 years, the mean and standard deviation are 23% and 6%, respectively. In only two of the 11 years examined (2001 and 2002), the annual percentage is one standard deviation beyond the mean. These results suggest that a non-trivial and stable percentage of analysts selectively disaggregated their earnings forecasts during the sample period.
Test of Hypothesis 1
Hypothesis 1 predicts that analysts who do not disaggregate their forecasts are expected to be more optimistically biased and less accurate than analysts who disaggregate. To test this hypothesis, it is necessary to construct a measure of analysts’ level of disaggregation. Because analysts can disaggregate for a firm in one year and not in other years, or they can disaggregate for one firm and not for other firms in the same year, and because the proportions disaggregated can vary across analysts, the data are analysed by developing a categorical classification scheme based on analysts’ overall disaggregation behaviour. Another consideration is that the number of years that a given analyst's earnings forecasts appear in the I/B/E/S database can vary significantly from a few years to a relatively long tenure. We initially examined a sample that required analysts to have provided forecasts in at least three of the 11 years covered by the data and then we incrementally ratcheted the minimum requirement up to at least six years in the 11 years examined. In the Sensitivity Tests section of the paper, we test the robustness of our findings to these additional (more restrictive) analyst inclusion criteria. Because the largest sample size is achieved when the least restrictive analyst inclusion criterion is applied, we present results here for the sample that includes all analysts that had a minimum of three years of forecasts in I/B/E/S. We classify selected analysts into one of the following four categories:
- 1
ND (non-disaggregators): analysts who never issued disaggregated forecasts for any firm they followed during the entire sample period.
- 2
PD1 (partial disaggregators 1): analysts who issued disaggregated forecasts for some, but not all, of the firms they followed each year and analysts who provided no sales forecast for some of the sample years but did issue sales forecasts for some of their firms in the other sample years. In other words, PD1 analysts issued disaggregated forecasts for some firms in some years but the scope of their disaggregation was never expanded to include all the firms that they followed in any given year.
- 3
PD2 (partial disaggregators 2): all other analysts whose disaggregation levels were higher than the limited disaggregation levels of PD1. For instance, PD2 includes analysts who issued disaggregated forecasts for all the firms that they followed in at least one year but not in all the years in which their forecasts appeared in I/B/E/S.
- 4
FD (full disaggregators): analysts who issued disaggregated forecasts for all the firms they followed for all the sample years.
Because we are examining differences in bias and accuracy of analysts’ forecasts based on the extent of disaggregation of issued forecasts, the four categories of analysts are constructed such that the level of disaggregation increases monotonically when moving from category 1 to category 4. Categories 1 and 4 represent two extremes of the disaggregation categorization because they include analysts who either never disaggregated their forecasts (category 1) or always disaggregated their forecasts (category 4) over the sample years. Because partial disaggregators are non-homogeneous in terms of the pattern of their disaggregation behaviour, some judgment was required to classify them into meaningful categories for analysis. PD1 includes analysts who we judged to be less prevalent disaggregators than those included in the PD2 group. To test Hypothesis 1, we employ both univariate and multivariate (regression-based) tests to arrive at our conclusions.
Univariate tests We use Duncan's multiple-range test in our univariate examination of differences of the mean BIAS and mean FORECAST ERROR of the analysts in the four categories, based on the ranking of the four categories. Hypothesis 1 predicts that forecast bias will be highest for analysts belonging to the ND category and then decrease as we move to the PD1, PD2 and FD categories, respectively, because there is an ordinal increase in the level of disaggregation over the four categories. These predicted rankings are presented in Panel A of Table 2 along with the actual rankings obtained from Duncan's multiple range test. The actual BIAS rankings of the four categories correspond with the predicted BIAS rankings, and the mean BIAS for each category is significantly smaller than the adjacent preceding category across all four categories. The mean forecast BIAS for ND, PD1, PD2 and FD category analysts decreases monotonically from 0.070 to 0.056 to 0.042 to 0.034, suggesting that mean BIAS decreases with the level of disaggregation. The results of Duncan's multiple range test confirms that the differences in BIAS across all analyst categories are significantly different from zero at conventional levels of significance (0.05 or better). These results support the hypothesis that analysts who are optimistic about firms’ expected earnings are unlikely to issue disaggregated forecasts.
| Presented below are the average BIAS and FORECAST ERROR of an analyst belonging to the four forecast disaggregation categories—ND, PD1, PD2, and FD. BIAS is defined as (forecasted one-year ahead EPS – actual EPS) ÷|actual EPS| and the FORECAST ERROR is defined as |forecasted one-year ahead EPS – actual EPS|÷|actual EPS|. Panel A presents the predicted and the actual rankings of BIAS and FORECAST ERROR across disaggregation categories based on our hypothesis and the Duncan's multiple range test respectively. Panel B presents the same results using yearly mean-adjusted BIAS and FORECAST ERROR measures. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Panel A: BIAS and FORECAST ERROR | |||||||||
| Analyst category | Number of | BIAS | FORECAST ERROR | ||||||
| Analysts | Firm-years | Mean | Predicted ranking | Actual ranking | Mean | Predicted ranking | Actual ranking | ||
| 1 | ND | 1,306 | 41,435 | 0.070 | 1 | 1 | 0.169 | 1 | 1 |
| 2 | PD1 | 1,077 | 67,673 | 0.056 | 2 | 2 | 0.155 | 2 | 2 |
| 3 | PD2 | 3,309 | 212,242 | 0.042 | 3 | 3 | 0.150 | 3 | 3* |
| 4 | FD | 1,166 | 28,817 | 0.034 | 4 | 4 | 0.150 | 4 | 3 |
| Panel B: Yearly Mean-adjusted BIAS and FORECAST ERROR | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Analyst category | Number of | Yearly mean-adjusted BIAS | Yearly mean-adjusted FORECAST ERROR | ||||||
| Analysts | Firm-years | Mean | Predicted ranking | Actual ranking | Mean | Predicted ranking | Actual ranking | ||
| 1 | ND | 1,306 | 41,435 | 0.009 | 1 | 1 | 0.200 | 1 | 1 |
| 2 | PD1 | 1,077 | 67,673 | 0.001 | 2 | 2 | 0.190 | 2 | 2 |
| 3 | PD2 | 3,309 | 212,242 | −0.007 | 3 | 3 | 0.180 | 3 | 3 |
| 4 | FD | 1,166 | 28,817 | −0.007 | 4 | 3* | 0.170 | 4 | 4 |
- Analyst disaggregation categories are (1) ND representing analysts who never issued disaggregated forecasts for any firm they followed during the entire sample period, (2) PD1 representing analysts who issued disaggregated forecasts for some, but not all, of the firms they followed each year and analysts who provided no sales forecast for some of the sample years but did issue sales forecasts for some of their firms in the other sample years, (3) PD2 representing analysts who issued disaggregated forecasts for all of the firms they followed for some, but not all, of the sample years, and (4) FD representing analysts who issued disaggregated forecasts for all the firms they followed for all the sample years.
- * Analyst categories with mean BIAS/FORECAST ERROR that are not significantly different receive the same ranking.
Panel A of Table 2 shows that the mean FORECAST ERROR of analysts who did not disaggregate their forecasts (ND) is 0.169, whereas the corresponding measure for the analysts who disaggregated all their forecasts (FD) is 0.150. The mean FORECAST ERROR of analysts belonging to the PD1 and PD2 categories is 0.155 and 0.150, respectively. Duncan's multiple range test indicates that the differences in means for the first three categories (ND, PD1 and PD2) are significantly different at conventional levels of significance (0.05 or better). This is consistent with the accuracy expectations of Hypothesis 1 that the forecast errors are monotonically decreasing with the level of disaggregation. The only exception is that there is no detectable difference in the mean FORECAST ERROR of analysts belonging to the PD2 and FD categories.
As pointed out earlier, the number of analysts who issue disaggregated forecasts to I/B/E/S has grown significantly over the sample period. At the same time, after the burst of the Internet bubble, the level of analysts’ optimism and bias may have declined. To ensure that our findings are not simply driven by a potential link between these two factors, we analysed mean BIAS and FORECAST ERROR of analyst disaggregation categories after controlling for year effects. To this end, we computed the mean BIAS and mean FORECAST ERROR of all forecasts issued by all I/B/E/S analysts for each sample year. We then subtracted this mean from our original measures of BIAS and FORECAST ERROR to obtain yearly mean-adjusted BIAS and FORECAST ERROR measures. Results presented in Panel B of Table 2 show that, after controlling for possible year effects, the mean BIAS of NP analysts (0.009) remains statistically higher than that of PD1 analysts (−0.001), which in turn remains statistically higher than the average BIAS of both PD2 analysts (-0.007) and FD analysts (-0.007) at the 95% confidence level. Similar to the results in Panel A, the results in Panel B show that after controlling for potential year effects, the mean FORECAST ERROR of the four analyst categories decrease monotonically (from a high of 0.20 to a low of 0.17) with increases in the level of disaggregation. These results provide strong evidence in support of our hypotheses. Furthermore, the finding that FD category analysts have the most accurate and the least biased forecasts also suggests that these analysts have both better skills and a higher level of professional integrity. These findings are also consistent with the arguments advanced by Ertimur et al. (2011) and Marks (2008) that these analysts may be using sales forecasts as a means to showcase their superior forecasting ability.
Multivariate tests In addition to the univariate tests described above, we also performed multivariate regression analyses to control for other factors identified in the prior literature that have an effect on analyst forecast bias and accuracy. Das et al. (1998) find that bias is positively associated with the level of difficulty in predicting the firm's future earnings. As a proxy for the information environment of the firm, size has been shown to be negatively associated with the level of bias (e.g., Brown, 1997, 2001; Das et al., 1998). Brown (2001) finds that firms reporting losses receive more optimistically biased earnings forecasts. Richardson et al. (2004) show that analysts issue optimistic earnings forecasts at the beginning of the year and then gradually revise down their estimates to a level that the firms can beat later in the year. Consequently, there appears to be a negative relation between the timeliness of earnings forecasts and measures of forecast bias. The same study also shows that high book-to-market (low growth) firms receive more optimistically biased earnings forecasts. In addition, previous studies have found that the level of investment in technology (e.g., the ratio of research and development expenditures to total assets) is positively associated with pessimistic earnings forecasts (Matsumoto, 2002; Richardson et al., 2004). At the analyst level, analysts with longer tenure should be better forecasters because of their experience, although they may be indifferent with respect to the decision to bias their forecasts. Lastly, regardless of other factors, some forecasts may be less accurate simply because they are less timely (Sinha et al., 1997). To control for these factors, we included the following variables in our multivariate regression models:
- 1
TIMELINESS is a measure of closeness of the forecast to the earnings announcement date, measured as the number of months prior to the actual earnings announcement date that the earnings forecast is issued. As a result, this variable takes on a negative value with higher values associated with more timely forecasts.
- 2
LOSS is a dummy variable equal to 1 if actual EPS as reported on I/B/E/S for the fiscal year is negative, and 0 otherwise.
- 3
Because some firm-years may be harder to forecast than others, we define DIFFICULTY as the standard deviation of the most recent forecasts made by all analysts for that firm in a given year, normalized by the mean of these forecasts, as a control for differences in difficulty in predicting a firm's earnings.
- 4
Because large firms face less information asymmetry than small firms, we use SIZE, measured by the log of the market value of owners’ equity at the start of the current fiscal year, as a proxy to control for this effect.
- 5
We use B/M, the ratio of book value to market value, computed as the book value of common equity at the start of the fiscal year divided by market capitalization at the start of the fiscal year, to control for differences in errors and biases induced by firms with different future growth opportunities.
- 6
Difference in forecasting accuracy induced by experience in the industry is controlled by the TENURE variable, measured by the number of years an analyst has appeared in the I/B/E/S database on the forecast date (Clement, 1999).
- 7
To control for the potential biasing effects of the level of investment in technology, we include a dummy variable TECH, which takes a value of 1 if the firm belongs to the Information Technology and Health Care sectors (including 15 high tech industries) of the Global Industry Classification Standard (GICS) industry classification, and 0 otherwise.
- 8
We control for differences in forecasting earnings for the remaining (non-Tech) industries and across the 11 years that cover various stages of economic expansion and contraction, by adding dummy variables for industry effects and year effects.
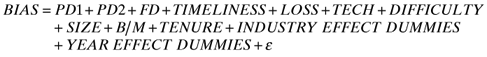 ()
()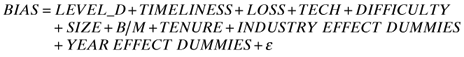 ()
()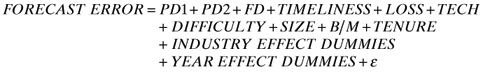 ()
() ()
()In models (1a) and (2a), we use PD1, PD2 and FD as dummy variables corresponding to the analyst disaggregation categories described earlier. A directional test of the significance of the difference in the coefficients of these dummy variables provides a test of the relationship between the level of disaggregation and BIAS and FORECAST ERROR while controlling for the variables discussed above. In models (1b) and (2b), we construct a single ordinal disaggregation variable, LEVEL_D, which takes a value of 1, 2, 3 or 4 for analysts classified into ND, PD1, PD2 or FD categories, respectively. A test of significance of the coefficient for this variable provides a basis for testing the hypothesis.
Tests of BIAS Panel A and Panel B of Table 3 present results of the estimation of models (1a) and (1b), respectively. The F-statistics for the two models and the t-statistics for the significance of coefficients for all the control variables (except TENURE) are significant at conventional levels of significance (0.05 or better). In both models, all the control variables, except for DIFFICULTY, have the expected signs. For model (1a), the estimated coefficients for PD1, PD2, and FD are significantly different from zero at the conventional levels of significance (0.05 or better) and monotonically decreasing from −0.006 to −0.010 to −0.016, respectively. The F-statistics for the tests that PD1=PD2 is 4.85 (p= 0.028), that PD2=FD is 9.38 (p < 0.001), and that PD1=PD2=FD is 8.5 (p < 0.001), all statistically significant at conventional levels of significance (0.05 or better). For model (1b), disaggregation is measured using an ordinal variable, LEVEL_D. The estimated coefficient for this variable is -0.005, which is negative and statistically significant (p= 0.010). These results corroborate our univariate analysis findings that the level of disaggregation is negatively associated with the level of FORECAST BIAS. Collectively, these multivariate results, along with the univariate results presented earlier, provide strong support for Hypothesis 1.
| Presented below are the results from the regression of BIAS and FORECAST ERROR on analysts, firm and industry control variables and levels of analyst forecast disaggregation. BIAS is defined as (forecasted one-year ahead EPS – actual EPS) ÷|actual EPS| and the FORECAST ERROR is defined as |forecasted one-year ahead EPS – actual EPS|÷|actual EPS|. Panel A presents results when forecast disaggregation is measured using PD1, PD2 and FD categorical dummy variables. Panel B presents regression results when forecast disaggregation is measured using LEVEL_D, an ordinal variable that takes values of 1, 2, 3, and 4 for analysts belonging to categories ND, PD1, PD2, and FD, respectively. | |||||
|---|---|---|---|---|---|
| Panel A: Categorical measurement of forecast disaggregation categories | |||||
| Predicted sign | Dependent variable | ||||
| BIAS | FORECAST ERROR | ||||
| Coefficient | p-value | Coefficient | p-value | ||
| Intercept | 0.045 | (0.01) | 0.240 | (0.01) | |
| PD1 | − | −0.006 | (0.01) | −0.010 | (0.01) |
| PD2 | − | −0.010 | (0.01) | −0.011 | (0.01) |
| FD | − | −0.016 | (0.01) | −0.020 | (0.01) |
| TIMELINESS | − | −0.010 | (0.01) | −0.015 | (0.01) |
| LOSS | + | 1.430 | (0.01) | 1.330 | (0.01) |
| TECH | − | −0.017 | (0.01) | −0.010 | (0.01) |
| DIFFICULTY | + | −0.000 | (0.01) | 0.000 | (0.77) |
| SIZE | − | −0.007 | (0.01) | −0.019 | (0.01) |
| B/M | + | 0.008 | (0.01) | 0.004 | (0.01) |
| TENURE | ? | −0.0004 | (0.11) | −0.002 | (0.01) |
| INDUSTRY EFFECT | Yes | Yes | |||
| YEAR EFFECT | Yes | Yes | |||
| Adj R2 | 23.10% | 27.22% | |||
| N | 242,334 | 242,334 | |||
| Test | F-statistic | p-value | F-statistic | p-value | |
| PD1= PD2 | 4.85 | 0.028 | 0.68 | 0.41 | |
| PD1= FD | 16.94 | <0.0001 | 28.50 | <0.0001 | |
| PD2= FD | 9.38 | <0.0001 | 29.16 | <0.0001 | |
| PD1=PD2= FD | 8.50 | <0.0001 | 16.15 | <0.0001 | |
| Panel B: Ordinal measurement of forecast disaggregation categories | |||||
|---|---|---|---|---|---|
| Predicted sign | Dependent variable | ||||
| BIAS | FORECAST ERROR | ||||
| Coefficient | p-value | Coefficient | p-value | ||
| Intercept | 0.0508 | (0.01) | 0.2400 | (0.01) | |
| LEVEL_D | − | −0.0050 | (0.01) | −0.0070 | (0.01) |
| TIMELINESS | − | 0.0000 | (0.01) | 0.0005 | (0.01) |
| LOSS | + | 1.4300 | (0.01) | 1.3300 | (0.01) |
| TECH | − | −0.0170 | (0.01) | −0.0090 | (0.01) |
| DIFFICULTY | + | −0.0000 | (0.01) | 0.0000 | (0.77) |
| SIZE | − | −0.0070 | (0.01) | −0.0190 | (0.01) |
| B/M | + | 0.0080 | (0.01) | 0.0040 | (0.01) |
| TENURE | ? | −0.0003 | (0.16) | −0.0020 | (0.01) |
| INDUSTRY EFFECT | Yes | Yes | |||
| YEAR EFFECT | Yes | Yes | |||
| Adj R2 | 23.10% | 27.25% | |||
| N | 242,334 | 242,334 | |||
- PD1, PD2 and FD are dummy variables corresponding to analyst disaggregation categories, PD1, PD2 and FD, respectively. LEVEL_D is an ordinal disaggregation variable, which takes a value of 1, 2, 3 or 4 for analysts belonging to ND, PD1, PD2 or FD categories, respectively. Analyst disaggregation categories are (1) ND representing analysts who never issued disaggregated forecasts for any firm they followed during the entire sample period, (2) PD1 representing analysts who issued disaggregated forecasts for some, but not all, of the firms they followed each year and analysts who provided no sales forecast for some of the sample years but did issue sales forecasts for some of their firms in the other sample years, (3) PD2 representing analysts who issued disaggregated forecasts for all of the firms they followed for some, but not all, of the sample years, and (4) FD representing analysts who issued disaggregated forecasts for all the firms they followed for all the sample years. TIMELINESS is measured by the number of months prior to the actual earnings announcement date that the earnings forecast is issued. LOSS is a dummy variable equal to 1 if actual EPS as reported on I/B/E/S for the fiscal year is negative, and 0 otherwise. DIFFICULTY is the standard deviation of the most recent EPS1 forecasts made by all analysts for that firm in a given year, normalized by the mean of these forecasts. SIZE is measured by the log of market value of the firm equity at the start of the current fiscal year. B/M is the book value of common equity at the start of the fiscal year divided by market capitalization at the start of the fiscal year. TENURE is measured by the number of years an analyst has appeared in the I/B/E/S database. TECH is a dummy variable, which takes a value of 1 if the firm belongs to Information Technology and Health Care sectors (including 15 high tech industries) of the GICS industry classification, and 0 otherwise. INDUSTRY EFFECT represents results from the test of the hypothesis of the equality of coefficients for the dummy variables constructed on the basis of the second level of GICS industry classification. YEAR EFFECT represents results from the test of the hypothesis of the equality of coefficients for the year dummy variables.
Tests of FORECAST ERROR Panel A and Panel B of Table 3 present the results of models (2a) and (2b) with FORECAST ERROR as the dependent variable. Both models have significant F-statistics and adjusted R2s around 0.27. All the control variables have the expected signs and are statistically significant at conventional levels of significance (0.05 or better). The disaggregation variables, PD1, PD2, and FD in model (2a) and LEVEL_D in model (2b), are all negative and statistically significant indicating that higher levels of disaggregation are associated with lower levels of FORECAST ERROR. For specification (2a), an additional test of the comparison of coefficients for PD1, PD2 and FD shows that the coefficients are monotonically non-decreasing taking a value of -0.010, to -0.011 to -0.020, respectively. These results, along with those from the univariate tests, provide strong support for Hypothesis 1.
Test of Hypothesis 2
Hypothesis 2 makes predictions about the BIAS and FORECAST ERROR of selective disaggregators who disaggregate earnings forecasts for some, but not all, firms in a given year. As per this hypothesis, selective disaggregators are likely to be less biased and more accurate in their disaggregated forecasts when compared to their aggregated forecasts. These analysts are identified in the middle columns of Table 1. The number of analysts falling into this group ranges from a low of 625 (15%) in 2008 to a high of 1,397 (34%) in 2001. In order to provide a strong test for differences in bias and accuracy of these analysts on the disaggregation dimension, we compared the BIAS and FORECAST ERROR of selective disaggregators for the set of firms for which they issued aggregate forecasts versus the set of firms for which they issued disaggregated forecasts. We first computed the mean BIAS and mean FORECAST ERROR for each analyst for the two sets of firms in a given year and then pooled these data across all years. Table 4 presents the results of a matched-pair t-test of the differences in BIAS and FORECAST ERROR between the two sets of firms. By analysing the data in this fashion, each analyst is essentially serving as his/her own control for differences that may exist amongst analysts with respect to factors affecting forecasting ability. As the results in Table 4 show, the difference in mean BIAS and the difference in mean FORECAST ERROR of aggregated and disaggregated forecast of an average selective disaggregator is 0.059 and 0.085, respectively. Both of these differences are positive and significantly different from zero at the 5% level of significance (p= 0.030 and 0.010, respectively). Consistent with the predictions of Hypothesis 2, these results provide evidence that the selective disaggregators are more optimistically biased and less accurate when they do not disaggregate their forecasts than when they do disaggregate.
| Presented below are results from the matched-pair t-test of the difference in the BIAS and FORECAST ERROR of analysts classified as selective disaggregators. BIAS is defined as (forecasted one-year ahead EPS – actual EPS) ÷|actual EPS| and the FORECAST ERROR is defined as |forecasted one-year ahead EPS – actual EPS|÷|actual EPS|. Selective disaggregators are analysts who disaggregated their forecasts for some, but not all, of the firms that they followed in a given year. The pairing involves the forecasts of the same analyst for the same year but for two sets of firms–one for which they did not disaggregate versus those for which they did disaggregate their forecasts. | ||||
|---|---|---|---|---|
| Difference | Mean difference | t-statistic | p-value | Number of analyst-years |
| Mean BIAS of aggregated forecasts − Mean BIAS of disaggregated forecasts | 0.059 | 2.21 | 0.03 | 9,108 |
| Mean FORECAST ERROR of aggregated forecasts − Mean FORECAST ERROR of disaggregated forecasts | 0.085 | 3.18 | 0.01 | 9,108 |
- Mean BIAS of aggregated (disaggregated) forecasts is computed using the set of firms for which the analyst issued only aggregated (disaggregated) earnings forecasts in a given year. Mean FORECAST ERROR of aggregated (disaggregated) forecasts is computed using the set of firms for which the analyst issued only aggregated (disaggregated) earnings forecasts in a given year.
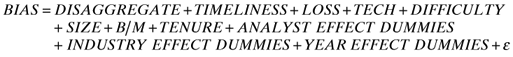 ()
()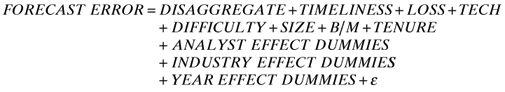 ()
()The results presented in Table 5 from the estimation of model (3a) with BIAS as the dependent variable show that the adjusted R2 is 0.238 and the model is significant at conventional levels (0.05 or better). All the control variables, except DIFFICULTY, have the predicted signs and are statistically significant at conventional levels of significance (0.05 or better). The coefficient for DISAGGREGATE is -0.006, which is negative and significant (p < 0.01).
| Presented below are the results from the regression of BIAS and FORECAST ERROR on analysts, firm and industry control variables and analysts’ decision to disaggregate the issued forecast. BIAS is defined as (forecasted one-year ahead EPS – actual EPS) ÷|actual EPS| and the FORECAST ERROR is defined as |forecasted one-year ahead EPS – actual EPS|÷|actual EPS|. Analysis is confined to the sample of selective disaggregators who disaggregated for some, but not all, of the firms that they followed in a given year. | |||||
|---|---|---|---|---|---|
| Predicted sign | Dependent variable | ||||
| BIAS | FORECAST ERROR | ||||
| Coefficient | p-value | Coefficient | p-value | ||
| Intercept | 0.085 | (0.01) | 0.250 | (0.01) | |
| DISAGGREGATE | − | −0.006 | (0.01) | −0.005 | (0.01) |
| TIMELINESS | − | −0.010 | (0.01) | −0.016 | (0.01) |
| LOSS | + | 1.499 | (0.01) | 1.325 | (0.01) |
| TECH | − | −0.032 | (0.01) | −0.005 | (0.20) |
| DIFFICULTY | + | −0.020 | (0.01) | −0.002 | (0.02) |
| SIZE | − | −0.008 | (0.01) | −0.019 | (0.01) |
| B/M | + | 0.006 | (0.01) | 0.003 | (0.01) |
| TENURE | ? | −0.001 | (0.05) | −0.002 | (0.01) |
| ANALYST EFFECT | Yes | Yes | |||
| INDUSTRY EFFECT | Yes | Yes | |||
| YEAR EFFECT | Yes | Yes | |||
| Adj R2 | 23.84% | 27.90% | |||
| N | 81,760 | 81,760 | |||
- DISAGGREGATE is a dummy variable that takes the value of 1 if the analyst issues disaggregated forecasts for a firm in a given year, and 0 otherwise. TIMELINESS is the number of months prior to the actual earnings announcement date that the earnings forecast is issued. LOSS is a dummy variable equal to 1 if actual EPS as reported on I/B/E/S for the fiscal year is negative and 0 otherwise. DIFFICULTY is the standard deviation of the most recent EPS1 forecasts made by all analysts for that firm in a given year, normalized by the mean of these forecasts. SIZE is the log of market value of the firm equity at the start of the current fiscal year. B/M is the book value of common equity at the start of the fiscal year divided by market capitalization at the start of the fiscal year. TENURE is measured by the number of years an analyst has appeared in the I/B/E/S database. TECH is a dummy variable, which takes a value of 1 if the firm belongs to Information Technology and Health Care sectors (including 15 high tech industries) of the GICS, and 0 otherwise. INDUSTRY EFFECT represents results from the test of the hypothesis on the equality of coefficients for the dummy variables constructed on the basis of the second level of GICS industry classification. YEAR EFFECT represents results from the test of the hypothesis on the equality of coefficients for the year dummy variables.
Table 5 also presents results from the estimation of model (3b) with FORECAST ERROR as the dependent variable. The adjusted R2 is 0.279 and the model F-statistic (not reported) is significant at conventional levels of significance (0.05 or better). All the control variables have the expected signs and are statistically significant at conventional levels of significance (0.05 or better). The coefficient for the test variable, DISAGGREGATE, is -0.005, which is negative and significant (p < 0.01). Overall, both sets of regression results are consistent with the univariate results reported above and support the predictions of Hypothesis 2 that selective disaggregators’ disaggregated forecasts will be associated with lower levels of forecast errors and less optimistic bias than their non-disaggregated forecasts.
Test of Hypothesis 3
To test Hypothesis 3, we developed definitions of persistent and non-persistent disaggregators. This posed somewhat of a challenge because the data are not balanced, and the number of analysts and the number of firms covered by each analyst often change from year to year. For purposes of this analysis, we defined a persistent disaggregator (P) at the analyst-firm level as an analyst who meets the following two criteria. First, the analyst must have continued to issue sales forecasts for a particular firm every year subsequent to the year the first sales forecast was generated for that firm. This condition was imposed to ensure that an analyst was committed to issuing disaggregated forecasts once he/she started that practice. Second, we also required that the analyst followed the firm for a minimum of three years subsequent to the year of the initial sales forecast generated for that firm. This is done to minimize the possibility that this group included those analysts who may have begun issuing disaggregated forecasts for a firm toward the end of the period examined in this study and then stopped doing so in the later years for which data were unavailable. This effectively limited persistent disaggregators to those analysts who had issued disaggregated forecasts for their firms for a minimum of four consecutive years.
Because non-persistent disaggregators can vary with respect to the extent of non-disaggregation, we developed three mutually exclusive sub-categories at the analyst-firm level as follows: (a) analysts who never disaggregated the forecasts of the firm (NP0), (b) analysts who never disaggregated a forecast of the firm after issuing just one sales forecast (NP1), and (c) analysts who disaggregated the forecasts of the firm more than once but did not meet the strict definition of a persistent disaggregator (NP2). Thus, NP0, NP1, NP2 and P are categories that include analysts who are progressively increasing in the degree of their forecast disaggregation persistence.
Table 6 presents the mean BIAS and the mean FORECAST ERROR of analyst-firm forecasts pooled over the years for which the forecasts were made by each of the four forecast persistence categories defined above. The table is arranged starting with the least persistent group of disaggregators (NP0) and ending with the most persistent group (P). Our predictions, based on Hypothesis 3, are that the mean BIAS (FORECAST ERROR) of the analyst-firm categories will monotonically decrease (increase) from the least persistent disaggregators (NP0) to the most persistent disaggregators (P). The results presented in Table 6 show that the mean BIAS for NP0, NP1, NP2, and P are 0.080, 0.058, 0.036 and 0.007 respectively. The magnitude of BIAS decreases monotonically as the level of persistence increases. The results of Duncan's multiple range test confirms that the differences in BIAS are statistically significant across all disaggregation categories at conventional levels of significance (0.05 or better). We obtain similar results for FORECAST ERROR. As predicted, the mean FORECAST ERROR decreases from 0.186 to 0.163 to 0.146 to 0.095 (and thus, the mean forecast accuracy increases) monotonically as the level of disaggregation increases from NP0 to NP1 to NP2 to P, respectively. Duncan's multiple range test confirms that the differences in FORECAST ERROR are significantly different across all categories at conventional levels of significance (0.05 or better). To summarize, the results presented in Table 6 suggest that analysts who provide disaggregated forecasts for a firm in some years, but not others, are more biased and less accurate than analysts who issue disaggregated forecasts on a more consistent basis. This finding provides support for Hypothesis 3, and the argument that strategic biasing is an important determinant of analysts’ disaggregation decision.
| Presented below are results of Duncan's multiple range test that ranks and tests differences in the mean BIAS and FORECAST ERROR of analysts belonging to the Persistent and Non-persistent analyst categories. BIAS is defined as (forecasted one-year ahead EPS – actual EPS) ÷|actual EPS| and the FORECAST ERROR is defined as |forecasted one-year ahead EPS – actual EPS|÷|actual EPS|. The rankings of mean BIAS and FORECAST ERROR as per our hypotheses and as determined by Duncan's multiple range test are shown under ‘Predicted ranking’ and ‘Actual ranking’, respectively. | |||||||
|---|---|---|---|---|---|---|---|
| Analyst category | Number of analyst-firm-years | BIAS | FORECAST ERROR | ||||
| Mean | Predicted ranking | Actual ranking | Mean | Predicted ranking | Actual ranking | ||
| NP0 | 125,753 | 0.080 | 1 | 1 | 0.186 | 1 | 1 |
| NP1 | 16,539 | 0.058 | 2 | 2 | 0.163 | 2 | 2 |
| NP2 | 140,758 | 0.036 | 3 | 3 | 0.146 | 3 | 3 |
| P | 62,336 | 0.007 | 4 | 4 | 0.095 | 4 | 4 |
- Definitions of Persistent (P) and Non-Persistent (NP) analyst categories are as follows:
- P: analyst-firm combinations that satisfy the following conditions:
- 1. The analyst continued to issue sales forecasts for the firm every year after the first sales forecast was generated for that firm.
- 2. The analyst continued to issue sales forecasts for the firm for at least three years after the first sales forecast was generated for that firm.
- NP0: analyst-firm combinations in which the analyst never issued a sales forecast for the firm during the sample period.
- NP1: analyst-firm combinations in which the analyst issued one sales forecast for one firm and then never issued any sales forecasts for the firm during the sample period.
- NP2: analyst-firm combinations in which the analyst issued a sales forecast for the firm in some years after the first sales forecast was issued or in which the analyst issued sales forecasts for the firm every year subsequent to the first sales forecast, but that did not satisfy the second and the third conditions of the P category.
SENSITIVITY TESTS
The results presented in the previous section provide strong support for the three hypotheses proposed in this study. The purpose of this section is to test the sensitivity of these findings to the sample selection criteria utilized, the controls employed and the variable definitions used. By using alternative sample selection criteria, controls and definitions of variables, we try to rule out the possibility that the results presented earlier are driven by these factors. A discussion of the additional tests employed is presented next.
Sensitivity Test 1
Tests of Hypothesis 1, using the univariate and multivariate analyses presented in Panel A of Tables 2 and 3, show that the level of forecast bias decreases monotonically as the degree of disaggregation increases from Non-disaggregators (ND) to Full disaggregators (FD). However, if the decision to disaggregate earnings forecasts is tied to specific industries such as the high tech industry where losses are frequently reported and the demand for sales forecasts is higher, the documented relationship between forecast bias and the degree of disaggregation may also be driven by analyst industry coverage. To this end, we examined analyst disaggregation behaviour across industry groupings. Panel A of Table 7 presents a breakdown of Technology, Non-technology and Unclassifiable industry groupings by disaggregation categories. The proportions of analysts belonging to ND, PD1, PD2, and FD categories for technology firms are 13%, 16%, 36%, and 48%, respectively. This evidence of the largest (smallest) concentration of FD (ND) analysts for the technology firms is consistent with the expected source of bias. To ensure that the reported results are robust and not driven by this potential underlying industry effect, we partitioned the original sample of analysts into two subsamples—a technology subsample and a non-technology subsample. Regression models (1a) and (1b) were estimated separately for each subsample and the results and inferences were qualitatively similar for both the estimations. For brevity, only the results from the estimation of model (1b) are presented in Panel B of Table 7. The results show that for both of the subsamples, the coefficient of the disaggregation variable, LEVEL_D, is negative and significantly different from zero at conventional levels of significance (0.05 or better). Although not reported here, we also estimated a regression model with an ordinal measure of the degree of disaggregation as the dependent variable. We find that the analyst forecast bias is negatively associated with the degree of disaggregation after controlling for analysts’ industry coverage using a high-tech dummy variable. In short, these tests suggest that although the decision to disaggregate is related to industry coverage, our finding that analysts avoid issuing disaggregated forecasts when their forecasts are optimistically biased is robust.
| Presented below are the results of analyst disaggregation behaviour across Technology and Non-technology industry groupings. Panel A presents percent of analysts belonging to each industry grouping, by analyst category. Panel B presents results from the regression of BIAS on analysts, firm and industry control variables and levels of analyst forecast disaggregation, for the two industry groupings. BIAS is defined as (forecasted one-year ahead EPS—actual EPS) ÷|actual EPS|. | ||||
|---|---|---|---|---|
| Panel A: Industry compostion of firms by analyst disaggregation categories | ||||
| Analyst category | Percent technology | Percent non-technology | % of firms with no GICS code | Number of analyst-firms |
| ND | 13% | 61% | 27% | 30,409 |
| PD1 | 16% | 64% | 21% | 53,593 |
| PD2 | 36% | 47% | 17% | 184,247 |
| FD | 48% | 41% | 11% | 22,651 |
| Panel B: Regression results for the technology and the non-technology industry groupings | |||||
|---|---|---|---|---|---|
| Predicted sign | Dependent variable: BIAS | ||||
| Technology firms | Non-technology firms | ||||
| Coefficient | p-value | Coefficient | p-value | ||
| Intercept | 0.0030 | (0.01) | 0.050 | (0.01) | |
| LEVEL_D | − | −0.0060 | (0.01) | −0.004 | (0.01) |
| TIMELINESS | − | −0.0004 | (0.01) | −0.000 | (0.01) |
| LOSS | + | 1.4300 | (0.01) | 1.460 | (0.01) |
| IFFICULTY | + | −0.0240 | (0.01) | −0.000 | (0.77) |
| SIZE | − | −0.0040 | (0.01) | −0.007 | (0.01) |
| B/M | + | 0.0070 | (0.01) | 0.007 | (0.01) |
| TENURE | ? | −0.0007 | (0.07) | −0.002 | (0.42) |
| INDUSTRY EFFECT | Yes | Yes | |||
| YEAR EFFECT | Yes | Yes | |||
| Adj R2 | 19.91% | 25.09% | |||
| N | 79,387 | 162,947 | |||
- LEVEL_D is a single level of disaggregation variable, which takes a value of 1, 2, 3 or 4 for analysts belonging to ND, PD1, PD2 or FD categories, respectively. Analyst disaggregation categories are (1) ND representing analysts who never issued disaggregated forecasts for any firm they followed during the entire sample period, (2) PD1 representing analysts who issued disaggregated forecasts for some, but not all, of the firms they followed each year and analysts who provided no sales forecast for some of the sample years but did issue sales forecasts for some of their firms in the other sample years, (3) PD2 representing analysts who issued disaggregated forecasts for all of the firms they followed for some, but not all, of the sample years, and (4) FD representing analysts who issued disaggregated forecasts for all the firms they followed for all the sample years. TIMELINESS is the number of months prior to the actual earnings announcement date that the earnings forecast is issued. LOSS is a dummy variable equal to 1 if actual EPS as reported on I/B/E/S for the fiscal year is negative. DIFFICULTY is the standard deviation of the most recent EPS1 forecasts made by all analysts for that firm in a given year, normalized by the mean of these forecasts. SIZE is measured by the log of market value of the firm equity at the start of the current fiscal year. B/M is the book value of common equity at the start of the fiscal year divided by market capitalization at the start of the fiscal year. TENURE is measured by the number of years an analyst has appeared in the I/B/E/S database. TECH is a dummy variable, which takes a value of 1 if the firm belongs to Information Technology and Health Care sectors (including 15 high tech industries) of the GICS, and 0 otherwise. INDUSTRY EFFECT represents results from the test of the hypothesis on the equality of coefficients for the dummy variables constructed on the basis of the second level of GICS industry classification. YEAR EFFECT represents results from the test of the hypothesis on the equality of coefficients for the year dummy variables.
Sensitivity Test 2
The number of years that an individual analyst contributes earnings forecasts to the I/B/E/S database in our sample varies from one year to a longer tenure. When we classified analysts into four groups of disaggregation behaviour (ND, PD1, PD2, and FD), we included only those analysts in the sample who had contributed forecasts to I/B/E/S for at least three of the 11 years examined. To ensure that the inclusion of short tenure (transitory) analysts in our sample does not create any systematic bias, we re-examined BIAS and FORECAST ERROR by re-defining the four disaggregation categories (ND, PD1, PD2, and FD) using more restrictive criteria of including only those analysts who had provided at least (a) four, (b) five or (c) six years of earnings forecasts. The univariate results under these three alternative definitions are presented in Panels A–C of Table 8. As we move from the most relaxed to the most restrictive criterion of analyst inclusion, the number of analysts decreases from 4,959 (Panel A), to 3,622 (Panel B) to 2,638 (Panel C). Because drastic reductions in sample sizes can make it difficult to reliably estimate multivariate models, we tested each set in an essentially identical manner to those reported in Panel A of Table 2 for the BIAS and FORECAST ERROR variables. For the BIAS variable, the predicted and the actual ranking based on Duncan's multiple range test are identical for the samples with four and five years of analysts’ forecasts as the inclusion criterion. For the six year analysts’ forecast inclusion criterion, the rankings of BIAS of the PD1 and PD2 analysts are statistically lower than the BIAS of the ND analysts, but are not significantly different from one another. However, the relative ranking of the two extreme categories (ND and PD) is the same as in the prior tests.
| Presented below are average BIAS and FORECAST ERROR for the four analyst disaggregation categories. Panels A (B, C) present disaggregation categories constructed using four (five, six) years of analyst presence in I/B/E/S as the analyst inclusion criterion. BIAS= (forecasted one-year-ahead EPS – actual EPS) ÷|actual EPS| and FORECAST ERROR=|forecasted one-year-ahead EPS – actual EPS|÷|actual EPS|. Also presented are the results of Duncan's multiple-range test that ranks and tests the differences in average BIAS and FORECAST ERROR across the analyst categories. The rankings of mean BIAS and FORECAST ERROR as per our hypotheses and as determined by Duncan's multiple range test are shown under ‘Predicted rankings’ and ‘Actual ranking’, respectively. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Analyst category | Number of | BIAS | FPRECAST ERROR | ||||||
| Analyst | Firm-years | Mean | Predicted ranking | Actual ranking | Mean | Predicted ranking | Actual ranking | ||
| Panel A: Sample of analysts who provided at least four years of forecasts to I/B/E/S DURING 1998–2008 | |||||||||
| 1 | ND | 711 | 30,837 | 0.067 | 1 | 1 | 0.160 | 1 | 1 |
| 2 | PD1 | 813 | 61,064 | 0.053 | 2 | 2 | 0.151 | 2 | 2 |
| 3 | PD2 | 2,776 | 203,512 | 0.042 | 3 | 3 | 0.149 | 3 | 2* |
| 4 | FD | 659 | 22,168 | 0.031 | 4 | 4 | 0.144 | 4 | 3 |
| 4,959 | 317,581 | ||||||||
| Panel B: Sample of analysts who provided at least five years of forecasts to I/B/E/S during 1998–2008 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | ND | 363 | 18,353 | 0.054 | 1 | 1 | 0.147 | 1 | 1 |
| 2 | PD1 | 562 | 50,999 | 0.047 | 2 | 2 | 0.146 | 2 | 1* |
| 3 | PD2 | 2,316 | 191,408 | 0.040 | 3 | 3 | 0.142 | 3 | 1 &2* |
| 4 | FD | 381 | 16,150 | 0.026 | 4 | 4 | 0.138 | 4 | 2* |
| 3,622 | 276,910 | ||||||||
| Panel C: Sample of analysts who provided at least six years of forecasts to I/B/E/S during 1998–2008 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | ND | 210 | 12,335 | 0.053 | 1 | 1 | 0.146 | 1 | 1 |
| 2 | PD1 | 380 | 40,570 | 0.044 | 2 | 2 | 0.142 | 2 | 1&2* |
| 3 | PD2 | 1,869 | 172,367 | 0.039 | 3 | 2 | 0.138 | 3 | 2&3* |
| 4 | FD | 179 | 9,339 | 0.025 | 4 | 3 | 0.135 | 4 | 3 |
| 2,638 | 234,611 | ||||||||
- Analyst disaggregation categories are (1) ND representing analysts who never issued disaggregated forecasts for any firm they followed during the entire sample period, (2) PD1 representing analysts who issued disaggregated forecasts for some, but not all, of the firms they followed each year and analysts who provided no sales forecast for some of the sample years but did issue sales forecasts for some of their firms in the other sample years, (3) PD2 representing analysts who issued disaggregated forecasts for all of the firms they followed for some, but not all, of the sample years, and (4) FD representing analysts who issued disaggregated forecasts for all the firms they followed for all the sample years.
- * Analyst categories with mean BIAS/FORECAST ERROR that are not significantly different receive the same ranking.
With respect to FORECAST ERROR, results presented in Panel A of Table 8 show that for the samples with four years of analysts’ forecasts as the inclusion criterion, ND category analysts issued the least accurate forecasts. PD1 and PD2 category analysts were more accurate than ND category analysts but were indistinguishable from each other in forecast accuracy, and the FD category analysts were significantly more accurate than the analysts belonging to the other three categories. When we examined the samples that include only those analysts who provided at least five (Panel B) or six (Panel C) years of forecasts, differences in FORECAST ERROR remain only for the analysts belonging to the two extreme categories (ND and FD). The difference in forecast accuracy across all four analyst categories is no longer detectable. This is possibly because of decreased variance in the forecasting experience of the smaller number of remaining analysts.
Sensitivity Test 3
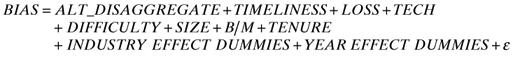 ()
()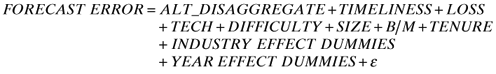 ()
()The results from the estimation of (4a) and (4b) are presented in Table 9. In both of the estimations, the results are qualitatively similar to those reported earlier. Specifically, the signs of all the variables are as expected and significant at conventional levels of significance (0.05 or better). The only exception is DIFFICULTY in model (4b) with FORECAST ERROR as the dependent variable. However this control variable was not significant in our earlier estimation (reported in Table 3) either. The estimated coefficient of ALT_DISAGGREGATE is negative and significant in both of the regression models, consistent with our hypothesis. These results provide corroborating evidence to our earlier finding that the act of issuing disaggregated forecasts is associated with less biased and more accurate earnings forecasts. We considered even more restricted definitions of disaggregation in which the analyst was considered to have issued a disaggregated forecast for the firm in a particular year only if the ratio of sales forecasts to EPS forecasts was greater than 0.5. The results (not reported here) were qualitatively similar.
| Presented below are the results from the regression of BIAS and FORECAST ERROR on analysts, firm and industry control variables and the alternative definition of analyst forecast disaggregation. BIAS is defined as (forecasted one-year ahead EPS – actual EPS) ÷|actual EPS| and the FORECAST ERROR is defined as |forecasted one-year ahead EPS – actual EPS|÷|actual EPS|. ALT_DISAGGREGATE is a dummy variable that takes on a value of 1 if the ratio of number of sales forecasts to the total number of EPS forecasts of an analyst exceeds 50% in a given firm-year. | |||||
|---|---|---|---|---|---|
| Predicted sign | Dependent variable | ||||
| BIAS | FORECAST ERROR | ||||
| Coefficient | p-value | Coefficient | p-value | ||
| Intercept | 0.056 | (0.01) | 0.253 | (0.01) | |
| ALT_DISAGGREGATE | − | −0.010 | (0.01) | −0.009 | (0.01) |
| TIMELINESS | − | −0.010 | (0.01) | −0.015 | (0.01) |
| LOSS | + | 1.440 | (0.01) | 1.339 | (0.01) |
| TECH | − | −0.017 | (0.01) | −0.013 | (0.01) |
| DIFFICULTY | + | −0.000 | (0.01) | 0.000 | (0.91) |
| SIZE | − | −0.007 | (0.01) | −0.019 | (0.01) |
| B/M | + | 0.008 | (0.01) | 0.005 | (0.01) |
| TENURE | ? | −0.001 | (0.01) | −0.008 | (0.01) |
| INDUSTRY EFECT | Yes | Yes | |||
| YEAR EFFECT | Yes | Yes | |||
| Adj R2 | 22.99% | 27.36% | |||
| N | 244,645 | 244,645 | |||
- TIMELINESS is the number of months prior to the actual earnings announcement date that the earnings forecast is issued. LOSS is a dummy variable that equals 1 if the actual EPS for the fiscal year is negative, and 0 otherwise. DIFFICULTY is the standard deviation of the most recent EPS forecasts made by all analysts for that firm in a given year, normalized by the mean of these forecasts. SIZE is the log of market value of the firm equity at the start of the current fiscal year. B/M is the book value of common equity at the start of the fiscal year divided by market capitalization at the start of the fiscal year. TENURE is the number of years an analyst has appeared in the I/B/E/S database. TECH is a dummy variable, which takes on a value of 1 if the firm belongs to Information Technology and Health Care sectors (including 15 high tech industries) of the GICS industry classification, and 0 otherwise. INDUSTRY EFFECT represents results from the test of the hypothesis on the equality of coefficients for the dummy variables constructed on the basis of the second level of GICS industry classification. YEAR EFFECT represents results from the test of the hypothesis on the equality of coefficients for the year dummy variables.
SUMMARY AND CONCLUSIONS
Recent studies suggest that financial analysts disaggregate earnings forecasts when submitting them to I/B/E/S in order to build their reputation in the marketplace. This study introduces strategic biasing as an additional explanatory variable, and shows that the decision to disaggregate is also at the analyst-firm level in addition to the analyst level as documented in the prior literature. Using I/B/E/S forecast data for U.S. firms from 1998–2008, we categorize analysts according to the level and persistence of their disaggregation behaviour and use these groupings to test three hypotheses: (H1) optimistic forecast bias will decrease, and forecast accuracy (as measured by forecast error) will increase, as the prevalence of earnings disaggregation increases, (H2) when a particular analyst issues both disaggregated and non-disaggregated forecasts in a given year, that analyst's optimistic forecast bias (accuracy) will be lower (greater) for the disaggregated forecasts than for the non-disaggregated forecasts, and (H3) optimistic forecast bias (accuracy) will be lower (higher) for those analysts classified as persistent disaggregators compared to analysts who are less persistent in issuing disaggregated forecasts. All three hypotheses are strongly supported by our empirical results.
There are several features of this study that are important to note. First, this is the only study to identify a group of analysts, whom we refer to as selective disaggregators, who disaggregate earnings forecasts for some, but not all, of the firms they follow in any given year. By definition, these analysts are distinct from the ones examined in previous studies. These analysts are found to be strategic in their behaviour and tend to exhibit larger forecast bias than the analysts who fully disaggregate. Second, we show that this larger bias is manifested in the disaggregation decision because these analysts are far more accurate and less biased when they disaggregate their forecasts than when they do not. It is this strategic bias that makes these analysts less accurate. The results also show that analysts who do not issue sales forecasts have the most optimistically biased and least accurate earnings forecasts. Finally, we show that analysts who issue sales forecasts for their firms persistently over the period examined in this study are less biased and more accurate than analysts who are not persistent in their disaggregation behaviour.
The main objective of this study was to determine whether analysts’ decision to bias earnings forecasts is systematically associated with the decision not to disaggregate those forecasts. While the decision to issue a disaggregated earnings forecast to I/B/E/S is clearly observable, we are unable to observe directly whether an analyst is purposely biasing the forecast. Thus, our conclusions are based on an observed bias which may or may not reflect an intentional decision on the part of the analyst to bias the forecast.