CASINOS, HOTELS, AND CRIME
Abstract
This paper examines the links among casinos, hotels, and crime using Indiana's counties for 1994-2004. In estimating casinos' impacts, I introduce a measure of casino activity in addition to variables related to the timing of casino opening. I test whether or not the number of hotel rooms affects crime rates. Increased casino activity reduces crime rates except for burglary, where crime rates rise after a lag. Leaving out a measure of casino activity appears to create a serious specification error. Finally, including problem crime data plagued by incomplete reporting affects the estimated impact of casinos on crime. (JEL R11, L83)
ABBREVIATIONS
-
- E&T
-
- Evans and Topoleski
-
- FBI
-
- Federal Bureau of Investigation
-
- G&M
-
- Grinols and Mustard
-
- ICPSR
-
- Interuniversity Consortium for Political and Social Research
-
- IGC
-
- Indiana Gaming Commission
-
- UCR
-
- Uniform Crime Reporting
I. INTRODUCTION
In recent decades, casinos have spread to many states in which they had previously been illegal. Nevada legalized casino gambling in 1931. In having legal casinos, it remained alone among the states until New Jersey legalized Atlantic City casinos in 1976. Recently, a total of 12 states have allowed commercial casinos (American Gaming Association, 2009). Other states have allowed gaming devices at racetracks. Following action by the U.S. Supreme Court in 1987 and the Congress in 1988, Native American casinos have opened in 28 states (American Gaming Association, 2009). This spread of casino gaming has been very controversial. The public, regulators, and researchers in health and social sciences have been interested, among other things, in the effects of casino gambling on crime.
A few researchers have empirically investigated the connection between the opening of new casinos and local area crime rates. Two of the most important of these are Evans and Topoleski (2002) (E&T) and Grinols and Mustard (2006) (G&M).1 Using a large panel of U.S. county data on casino openings and crime rates, G&M test the hypothesis that casinos cause crime. They estimate the parameters of a fixed-effects panel model using all 3,165 U.S. counties for the period 1977 through 1996. Their dependent variables are numbers of reported offenses in each of the following seven categories: aggravated assault, rape, robbery, murder, larceny, burglary, and motor vehicle theft. The source for these crime rates is the Federal Bureau of Investigation's (FBI) Uniform Crime Reporting (UCR) program, which the Interuniversity Consortium for Political and Social Research (ICPSR) makes available to researchers.2 G&M find that casino openings cause county crime rates in all categories except murder to rise after a lag of a few years. E&T also use UCR data to estimate a similar model to test the effects of opening Native American casinos on county crime rates. They find statistically significant positive lagged effects of new Native American casinos on crime.
In this paper, I reexamine the link between new casinos and crime rates. Here, I use the 92 counties of Indiana over the period 1994 through 2004. During this period, Indiana opened its first commercial casinos, including 10 casinos in seven counties. (Indiana has no Native American casinos.) Also, Indiana's casinos have a readily available measure of casino activity, the turnstile count of patrons, which we can use in addition to the often used dates of casino opening. Finally, I have created a database of the number of hotel rooms for each Indiana county for each of these years. I add this variable to the crime equations. The annual series of data on hotel rooms by county allows a test of whether or not the opening of other public accommodations besides casinos, specifically hotels, affects crime rates.
II. THEORY OF CASINOS AND CRIME
The economic model of crime proposed by Becker (1968), and investigated by Ehrlich (1973), Sjoquist (1973), Cornwell and Trumbull (1994), Raphael and Winter-Ebmer (2001), Gould, Weinberg, and Mustard (2002), Levitt (1998, 2004a, 2004b), Ihlanfeldt (2006), and many others asserts that potential criminals are utility maximizing agents who allocate time between legal work and crime based on the potential benefits and costs of each.3 To the extent that this is true, increasing the opportunity cost of criminal behavior would reduce crime. Increasing the probability of arrest and conviction along with more severe penalties would increase the opportunity cost of crime. Also, increasing legitimate work opportunities for potential criminals or the wages for that work would increase the opportunity cost of crime. As explained below, this theory has testable implications for the link between new casinos and crime.
Following the economic model of crime, new casinos could either increase or decrease local crime rates. If introducing new casinos increases job opportunities in the area, new casinos could, by increasing the opportunity cost of crime, reduce crime rates. Also, increasing activity within existing casinos could have the same effect. Many studies have supported the idea that better local labor market conditions reduce local crime rates and have found this result using various levels of aggregation. Raphael and Winter-Ebmer (2001) find that higher state unemployment rates lead to higher property crime rates. Gould, Weinberg, and Mustard (2002) find that movements of wages of unskilled men explain a large fraction of the movements in county crime rates. Ihlanfeldt (2006) finds that greater neighborhood employment opportunities for young males lower neighborhood crime rates. Levitt (2004a, pp. 170–171), however, questions the importance of the direct link between wages or unemployment rates and property crime rates.
The economic model of crime suggests that closer proximity of potential criminals and potential victims would increase local crime rates. Bowes and Ihlanfeldt (2001) investigate the impact of location and transportation costs on census tract crime rates and find that lowering transportation costs between potential criminals and victims (by the presence of a nearby rapid transit rail station) increases crime rates. This locational effect suggests that new casinos could reduce local crime rates by displacing crime-ridden locations with new construction. Alternatively, new casinos could lower the opportunity cost of crime by bringing new criminal opportunities to the local area. If this effect were important, new casinos would increase crime rates.
Another consideration that may be important in investigating the link between casinos and crime is that casino openings are typically followed, often with a lag, by the opening of hotels, entertainment venues, retail shops, and other public accommodations. These new public accommodations could raise or lower the opportunity cost of crime in the same ways discussed above for new casinos. Thus, because new casinos and other new public accommodations are linked, leaving these other new public accommodations out of the model explaining crime rates could lead to a specification error. Then finding that new casinos increase local crime rates after a lag of a few years could actually be the finding that casinos cause hotels and other public accommodations with a lag and the increased presence of these public accommodations causes a contemporaneous increase in crime rates.4
As with new casinos, the activities associated with new hotels and other public accommodations could reduce crime rates by providing increased legal employment opportunities, by displacing crime-ridden locations, or through some other mechanism. Or, they might increase crime by bringing together potential victims and potential criminals. Tourists visiting casinos or other sites may be particularly vulnerable to crime because they often carry large amounts of cash and other valuables and because they are outside their normal home territory.5
Thus, the economic model of crime suggests that the opening of new casinos, the level of activity at existing casinos, and the extent of other public accommodations may help explain local crime rates. Here, I use dates of opening of new casinos, leads and lags around these opening dates, a measure of the level of casino activity, and the number of hotel rooms in the specification explaining each county's crime rates. Previous studies of casinos and crime have accounted only for the introduction of casinos—they have not examined the impact of the level of casino activity or the extent of other public accommodations. In some cases, local areas have seen substantial new activity including multiple large casinos, new hotels, new restaurants, new entertainment venues, and new shopping areas. In other areas, introduction of casinos may mean that the area has a single relatively small casino. This study is the first to empirically examine the impacts of the level of casino activity and the level of related activity, in this case the number of hotel rooms, on local crime rates.
It is possible that opening a new casino in Indiana increases crimes rates in bordering states. I do not investigate that possibility here for two reasons. First, some of the Indiana casinos are in the Chicago area, and explaining crime rates in Chicago is beyond the scope of this paper. Second, most Illinois counties did not report crime rates during the period covered here, making investigation of spillovers infeasible.
III. DATA
The UCR crime data used to examine links between casinos and crime have severe and well known defects, discussed below. Furthermore, researchers have lacked useful, broadly applicable measures of casino activity.6 Here, I test the hypothesis that new casinos caused increases in crime rates in the counties of Indiana over the years 1994 to 2004 using the standard data sources previous investigators have used plus a measure of casino activity and a unique annual panel data set on hotel accommodations. The counties of Indiana are particularly well suited for a study of the links among casinos, hotels, and crime. In 1993, the Indiana legislature created the Indiana Gaming Commission (IGC) and authorized it to issue up to 11 riverboat casino licenses (IGC, 1994). This Riverboat Gaming Act specified that the city of Gary would receive the first one or two licenses. The IGC set up local referendums on the desirability of casinos in the city or county. In the 1993 elections, four counties rejected casino referendums and five counties and two cities passed casino referendums. The IGC then established a sequence of locations for consideration for riverboat casino licenses. These included four Lake Michigan cities or counties, four Ohio River counties, and Patoka Lake in the southern interior of Indiana. The Army Corps of Engineers, owner of Patoka Lake, subsequently denied permission for a riverboat casino. In 2003, the legislature approved a replacement land-based casino north of the lake in Orange County near French Lick. At the same time, the legislature created a Historic Hotel Preservation Commission to work with the IGC to develop the historic resort hotels in the area (IGC, 2003).
As a result of this and subsequent activity, Indiana, which had no casinos before 1995, opened 10 casinos in seven counties over the period 1995–2000. Four of the riverboat casinos are in Lake County in the extreme northwest of Indiana near Chicago. Six other counties have one riverboat casino each. Indiana also opened an 11th casino in an 8th county in 2006, which is outside the period for which crime rate data are currently available. (This 11th casino does, however, enter the data through the variable indicating a 2-yr lead in casino opening.)
Indiana's casinos also have a readily available measure of casino activity that we can use in addition to the dummy variables related to dates of casino opening that other researchers have used. The IGC's monthly revenue reports show “turnstile” counts of casino admissions for the entire period covered here7 (IGC, 1996–2004). As each riverboat casino owes $3 in admissions taxes for each patron admitted to the casino, it must accurately count admissions. In the early years of Indiana's riverboat casino operations, patrons had to be readmitted for a new “excursion” every 2 h even if they had not left the casino. In 2002, the state allowed dockside operations and amended the admissions tax scheme to eliminate the readmission process. This change did not affect the definition of the turnstile count because throughout the period each casino had reported turnstile admissions, which is a count of the number of patrons actually entering the casino. That is, before the 2002 change, patrons who were readmitted for a new excursion had not passed through the turnstile again (Klacik et al., 2003, pp. 5–6).
Two of the Lake County casinos share dockside facilities. With the 2002 admissions tax changes, these casinos got IGC permission to operate a single turnstile granting admission to both casinos and to evenly split the admissions tax liabilities between them.8 Thus, before this change, these casinos operated two turnstiles and all patrons went through one or the other. (In a minority of cases, patrons would go through both [Klacik, Littlepage, and Payton 2001].) After the change, all patrons for the two casinos would pass through a single turnstile, and one-half of the total admissions were assigned to each casino. Beginning with September 2002, the monthly reports of turnstile admissions and admissions taxes for these two casinos show the totals evenly split between them. With both casinos in the same county, this change had no effect on county turnstile admission totals. This 2002 change seems to have had little effect on the turnstile count, as the average turnstile count for these two casinos for the preceding years 2000 and 2001 was 1,753,209 and for the following years 2003 and 2004 was 1,738,138.
Indiana is also a good choice for studying the link between casinos and crime because there are adequate offense data for Indiana counties in the annual FBI UCR program data.9 While researchers have often used the UCR as the source for crime rate data, these crime reports have some very important limitations:10
- •
the reported data are voluntary self reports of state or local law enforcement agencies, which may not report at all in some years or may report incompletely, with errors, or nonuniformly across jurisdictions;
- •
the UCR only records the most serious crime in incidents in which multiple crimes are committed;
- •
some agencies only report state totals; to get county offense numbers, the ICPSR allocates offenses reported by these agencies to the counties in proportion to each county's share of the state's population.
- •
Most interesting for our purposes, the UCR includes imputations of some incompletely reported offense data. That is, in adjusting for incomplete reports the ICPSR replaces some incompletely reported data with values not actually from the reporting agencies.
It is important to examine the imputation of incompletely reported data more closely. Some agencies report offenses for only part of the year. For agencies reporting 3–11 mo of data, the ICPSR inflates the reported data up to a 12-mo equivalent. For example, if an agency reported 6 mo of data, the ICPSR doubles the number of reported offenses to get a 12-mo number. For agencies reporting 0, 1, or 2 mo of data, the ICPSR discards the reported data and replaces the number of offenses with an estimate based on reports of agencies reporting 12 mo of data within the same state and in cities or counties of the same type based on urbanization and population. If there are no cities or counties of that type having agencies reporting 12 mo of data, the ICPSR does not estimate the missing values; instead it shows the number of offenses as 0.
Thus, in some cases, the idea that the UCR provides offense data is an illusion, as the coded value is a number but it is not a reported number of offenses. Recall that the ICPSR has coded some incompletely reported values as 0. This listing of the number of crimes as “0” can be particularly important for research relating new casinos to local crime rates. For example, Iowa reported no offense data for 1991. Thus for 1991, the year in which Iowa's first casinos opened,11 all Iowa counties show UCR crime totals of 0 for all crimes. Tunica County, Mississippi, which had its first casino open in 1992,12 reported no crime data for 1990–1998; so that, its offense totals for those years are coded as 0. Illinois has casinos, but few Illinois counties reported offense data over the period 1993–2004; so that, the UCR shows most Illinois county offense totals as “0.” Thus, 0s in the UCR are often not actual offense totals. It is important to recall that not all imputed values are 0s, however; so that, some nonzero values are also not actual reported offense totals for the county. Finally, the ICPSR's imputation method for UCR data changed beginning with 1994, causing an important break in the continuity of the crime data. The ICPSR cautions that researchers should not compare UCR county-level crime data from 1993 and earlier with UCR data from 1994 and later.13
Both E&T and G&M used UCR offense data in constructing their dependent variables and used data from before and after the 1994 break in continuity. E&T, however, dealt with the ICPSR's changing imputation methods to try to get consistent crime data over time. E&T (p. 38) deleted post-1993 county-year observations having inadequate data based on the coverage variable, discussed below, and pre-1994 observations based on the proportion of the county's Census Bureau population for which crimes were reported. G&M used every county in every year 1977 through 1996, including the counties and years in Mississippi, Iowa, and Illinois where many crime rates resulting from incomplete reporting are inaccurate. Furthermore, G&M treated the offense rates uniformly across the 1994 break in continuity. Problems with these crime rate data suggest that the results reported in G&M should be treated with caution.
Here, unlike previous studies, I avoid the worst of these problems. I use data from Indiana counties for 1994 through 2004. Beginning my analysis with 1994 data, I avoid the break in the data at 1993–1994. I examine the statistical relationships among crime, casinos, and hotels after deleting some observations with crime rate data having problems created by incomplete reporting, as explained below.
As part of the change in imputations, beginning with 1994 the ICPSR reports a variable called “coverage,” which is the percentage of the crime rate data for each county that is not imputed. This percentage is 0, showing 100% imputation, for only 14 instances of Indiana's counties over the period 1994 through 2004. I delete those 14 observations with coverage equaling 0. Also, beginning with 1994, the ICPSR reports the county population of jurisdictions reporting crime data. For example, a county may include an incorporated city with a municipal police force and a county police force for the remainder of the county. If only the city agency reports crime data, the ICPSR data show the population of the city as the county population of jurisdictions reporting crime data. (The meaning of this population variable and the coverage variable, which depends on the population figure, is complicated by the fact that some jurisdictions, such as parks or toll roads, have 0 population. Thus, in some cases, there will be reported crimes for jurisdictions with 0 population, and these crime reports will not affect the coverage number.) To deal with this varying population coverage, I also delete those observations for which the UCR's county population of jurisdictions reporting crime data is less than 60% of the county's population as reported by the Census Bureau. For Indiana's counties for 1994 through 2004, there were 503 county-year observations having nonzero values for the coverage variable and having ratios of county population of jurisdictions reporting crime data to total county population of at least 0.6. Note that I am truncating the sample based on coverage and population reporting ratios, not the crime rate dependent variable—some of the remaining crime rates are 0 and some of the deleted observations have nonzero crime rates. I also deleted six observations in county panels having only one observation, as these observations have no effect on parameter estimates in a fixed-effects model. This leaves a data set of 497 observations. This smaller data set with adequate crime rate data has information on 69 Indiana counties, including five counties having casinos.
Data on hotel rooms by county over a long time period have not previously been available. I have constructed this data set for Indiana using a historical series of publications including AAA TourBook (AAA Publishing, 1995–2005), Mobil Travel Guide, Great Lakes, and other sources. I began by listing, for each year, all Indiana lodging establishments (with their addresses and number of rooms) included in the AAA TourBook (Illinois, Indiana, Ohio edition), assuming that the guide covers lodging available for the year preceding the Guide's copyright date. (This is clearly the case, as in a few cases the guide for one year states that a hotel was scheduled to open on a date from the previous year.) I then added any establishments that were in the appropriate Mobil Travel Guide but had not been included in the AAA guide. I then filled in any intervening years for establishments that moved in and out of the guides. I then checked Internet sources (including websites of the Association of Indiana Convention and Visitors Bureaus, Hotel-Guides.us (2007), triprewards.com, ChoiceHotels.com, and DaysInn.com) to see if any listed establishment was still operating in early 2007. For those that were, I filled in up through 2004 from the most recent year having a guide listing. I also added any casino hotels listed in IGC (various years) riverboat casino evaluation reports but not included in the AAA or Mobil guides. Finally, in some cases, I was able to fill backwards in time using Internet travel sites, including TravelPost.com, that show the establishment's date of opening. I then used each property's town or street address to assign it to a county, using State of Indiana (2007) or, for properties near county borders, Mapquest.com. The result is a database of lodging properties by Indiana county for the years 1994 through 2004. I found 7,526 property-year observations in 78 of Indiana's 92 counties.14 For each county and year, I added the rooms of all establishments to get the county's total rooms for that year. The 14 counties for which I found no lodging establishments have 0 rooms for all years.
IV. HOTEL ROOMS FOLLOW CASINOS
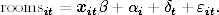
Here roomsit is the number of hotel rooms in county i in year t. The row vector xit contains the values of the independent variables for county i at time t, and β is a vector of parameters to be estimated. I use a dummy variable for the year of casino opening, 5 yr of lag dummy variables indicating year after casino opening, population, population squared, population density, and real per capita income, and various other demographic variables as independent variables to explain the number of hotel rooms in each county. (See below for data sources.) The constants αi capture unobserved influences of county i on hotel rooms that do not vary over the time period of the sample. The constants δt capture unobserved effects of year t on hotel rooms that are the same for all counties. The term εit is the unobserved random error.
The direction of causality between casinos and hotels raises an econometric issue here if the State of Indiana granted casino licenses to localities because they had a large number of hotel rooms. The recent French Lick Resort Casino, seems to illustrate such an occurrence. It was constructed in French Lick, which for many years has been the site of two large resort hotels. This casino, however, opened in 2006, which is outside the range of this study. As for the remaining counties, the Riverboat Gaming Act originally envisioned all of the Indiana casinos to be on riverboats, so that all of Indiana's counties bordering Lake Michigan or the Ohio River (or Patoka Lake, discussed above) were eligible for casinos and no other counties were eligible (IGC, 1994). Waterside location had little to do with the number of hotel rooms, and indeed the counties in the Indianapolis area with the state's largest number of hotel rooms were not eligible for casinos. Other relatively large hotel markets (including South Bend, Fort Wayne, Lafayette, Richmond, and Terre Haute) were also not eligible. Thus, the state did not generally locate casinos in areas having the most hotel rooms.
Table 1 shows the results of estimating the parameters of the lodging rooms equation using all 92 counties for all 11 yr. Table A1 shows the average values of the dependent and independent variables. The figures in parentheses are ratios of estimated coefficients to estimated standard errors. The results confirm the conjecture that hotel rooms follow casinos with a lag. Lags 3, 4, and 5 have statistically significant, positive coefficients. The values peak 4 yr after the casino's opening, indicating an increase of 241 rooms in the new casino's county. Other variables are also positive and highly statistically significant, including population and its square, population density, and real per capita income. The “within”R2 goodness-of-fit measure used here, and throughout the paper, shows that variation over time in the explanatory variables within each county explains almost 75% of the variation in rooms.
| Rooms | |
|---|---|
| Casino open | –148.0* (3.76) |
| LAG1 | –110.3* (2.80) |
| LAG2 | 49.0 (1.24) |
| LAG3 | 179.6* (4.56) |
| LAG4 | 241.4* (6.14) |
| LAG5 | 187.0* (4.43) |
| Population | –37.3* (7.23) |
| Pop squared | 0.0612* (22.01) |
| Density | 9.78* (5.00) |
| Real income | 42.1* (5.42) |
| Male | –71.4* (3.40) |
| White | 51.0* (2.01) |
| Black | 189.1* (7.52) |
| Pop 10–19 | –53.9* (2.97) |
| Pop 20–29 | –45.0* (2.88) |
| Pop 30–39 | –92.3* (3.85) |
| Pop 40–49 | –28.0 (1.60) |
| Pop 50–64 | –89.5* (5.19) |
| Pop over 64 | –58.4* (3.12) |
| Constant | 3176.3 (0.95) |
| R 2 | .7356 |
| Num obs | 1012 |
- Note: t-values are given in parentheses.
- *Statistically significant in a two-tailed test at the .95 level.
We turn now to our main concern, casinos and crime.
V. RESULTS FOR CASINOS AND CRIME
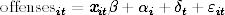
I include the same independent variables used by G&M, except that they also used a variable measuring the extent to which the county issued permits to carry concealed handguns under “shall issue” requirements. I exclude this variable here because Indiana had a statewide shall-issue requirement over the entire period examined here. (Maltz and Targonski, 2002, p. 314) The explanatory variables in the vector xit include dummy variables for the year in which the first casino opened in the county, dummy variables for 1-yr and 2-yr leads before casino opening and 1-yr through 5-yr lags after casino opening. It also includes control variables that vary across counties and year, including population density, real per capita income, real per capita receipts of income maintenance payments and unemployment compensation, real retirement payments per person over 64yr of age, and percentages of population in various age and race categories. My source for casino opening dates is IGC (various years). My sources for the remaining data are U.S. Census Bureau and U.S. Department of Commerce sources.16 I augment the model with three additional variables. First, I add two variables to the G&M specification: the number of hotel rooms in the county and the turnstile measure of casino activity. Later, I will add a deterrence variable, which will also require changing to instrumental variables estimation.
A. An Aside on the Impacts of the Defective Data
We will spend little time looking at the crime equations for the full sample because as discussed above, the dependent variable is defective for about one-half of the sample. We can, however, examine the impact of the defective crime rate data on some of the results. Table 2 shows the estimated parameters for the hotel room and casino variables from Equation (2) for each category of crimes for both the full and reduced samples. For each crime category, the first column shows results using the reduced sample of 497 observations, and the second column shows the results for the same specification using the full sample of 1,012 observations. In all cases, the estimated equations include county and year fixed effects. Many of the results are qualitatively similar in the full and reduced samples. (The crime data for Indiana are not especially low in quality, as they are for Illinois, for example.) There are, however, some important differences, especially for the burglary equation. For burglary, we see that eliminating the bad data reduces the coefficients of rooms and turnstile by half and eliminates their statistical significance. It has the opposite effect on the 3-yr and 4-yr lag variables, doubling the coefficients and making them statistically significant. Thus, moving from the complete sample to the reduced sample changes some of the results. We now turn to analysis of the results and some additional specifications using the reduced sample.
| Sample | Larceny | Burglary | Motor Vehicle Theft | Assault | Robbery | Rape | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reduced | Full | Reduced | Full | Reduced | Full | Reduced | Full | Reduced | Full | Reduced | Full | |
| Rooms | −0.245*(2.02) | −0.283*(2.03) | −0.046(0.97) | −0.098*(2.12) | −0.049*(2.33) | −0.053*(2.91) | −0.063(1.58) | −0.024(0.83) | −0.0063(0.71) | −0.0087(1.32) | −0.0067*(1.96) | −0.0062*(2.07) |
| Turnstile | −0.0845*(2.61) | −0.0888*(2.15) | −0.0146(1.14) | −0.0287*(2.12) | −0.0444*(7.87) | −0.0432*(7.99) | −0.0436*(4.10) | −0.0460*(5.41) | −0.0110*(4.63) | −0.0113*(5.83) | −0.0017(1.91) | −0.0019*(2.12) |
| LEAD2 | −303.9(1.48) | −421.5(1.91) | 30.21(0.37) | −66.4(0.91) | −78.4*(2.19) | −70.7*(2.44) | −156.0*(2.31) | −106.5*(2.34) | −8.65(0.57) | −8.21(0.79) | −4.48(0.78) | −7.04(1.48) |
| LEAD1 | −141.7(0.69) | −277.8(1.23) | −10.2(0.13) | −92.9(1.25) | −49.4(1.39) | −56.2(1.89) | −194.8*(2.90) | −135.4*(2.90) | −2.45(0.16) | −5.16(0.48) | 0.421(0.07) | −2.44(0.50) |
| Casino open | −248.1(1.27) | −337.9(1.56) | −42.1(0.55) | −112.6(1.58) | −71.4*(2.11) | −63.0*(2.22) | −128.9*(2.01) | −59.0(1.32) | −28.3*(1.99) | −19.8(1.94) | 1.23(0.23) | −2.84(0.61) |
| LAG1 | 136.7(0.76) | 76.7(0.38) | −9.21(0.13) | −44.2(0.66) | 45.2(1.45) | 41.9(1.58) | −162.0*(2.74) | −65.9(1.58) | 9.98(0.76) | 13.3(1.39) | 2.87(0.57) | −1.99(0.46) |
| LAG2 | 102.4(0.59) | 98.7(0.49) | −70.5(1.02) | −60.9(0.92) | −6.0(0.20) | 7.2(0.27) | −165.0*(2.87) | −68.6(1.65) | −2.34(0.18) | 0.76(0.08) | 1.55(0.31) | 0.63(0.14) |
| LAG3 | 216.9(1.26) | 157.4(0.78) | 131.8(1.94) | 71.6(1.08) | 4.3(0.14) | 16.2(0.61) | −152.6*(2.69) | −89.3*(2.15) | −2.03(0.16) | 2.86(0.30) | −1.70(0.35) | 1.30(0.30) |
| LAG4 | 141.1(0.82) | 85.1(0.42) | 146.3*(2.16) | 74.1(1.12) | −11.6(0.39) | −3.81(0.14) | −147.5*(2.61) | −102.0*(2.46) | −6.05(0.48) | −3.10(0.33) | 5.31(1.10) | 1.61(0.37) |
| LAG5 | 58.2(0.34) | 52.3(0.25) | 84.0(1.26) | 61.7(0.88) | −6.8(0.23) | 2.22(0.08) | −79.9(1.44) | −57.5(1.31) | −6.78(0.55) | −2.57(0.26) | 6.50(1.37) | 7.76(1.69) |
| R 2 | .164 | .094 | .118 | .071 | .286 | .143 | .319 | .182 | .182 | .104 | .139 | .064 |
| Num obs | 497 | 1012 | 497 | 1012 | 497 | 1012 | 497 | 1012 | 497 | 1012 | 497 | 1012 |
- Note: t-values are given in parentheses.
- *Statistically significant in a two-tailed test at the .95 level
B. Results and Analysis Using the Reduced Sample
The results for the reduced sample in Table 2 show that increased casino activity (turnstile) reduces all crime rates, although the negative coefficient is not statistically significant for burglary or rape. The coefficients on the casino lead and lag variables are generally insignificant, except for aggravated assault where they are large and negative, burglary where they are positive and at the borderline of significance at Lag 3 and positive and significant at Lag 4, motor vehicle theft where they are negative at the casino opening and at the 2-yr lead, and robbery where the coefficient on casino opening is negative. The coefficient on the hotel rooms variable is also always negative, but it is statistically significant only for larceny, motor vehicle theft, and at the borderline of significance for rape. Before interpreting these results further, we examine one more important issue—allowing for deterrence in determining crime rates.
The economic model of crime suggests that increasing the opportunity cost of crime reduces the crime rate. The specification used up to this point leaves out components of the opportunity cost of crime associated with the probability of arrest and conviction, often known as deterrence. Many of the papers cited above that apply the economic model of crime try to measure the impact of deterrence variables on crime rates. Some researchers (e.g., Gould, Weinberg, and Mustard, 2002; Levitt, 1998) use arrest rates, while others use measures of enforcement effort such as the number of police (e.g., Levitt, 2002). While the results in the deterrence literature are mixed, researchers have found that deterrence variables can be important in crime equations.
Introducing deterrence variables to the crime equation leads to important potential sources of bias in estimating the crime equation's parameters. There are two main issues. The first is spurious correlation resulting from measurement error in the number of offenses (Gould, Weinberg, and Mustard, 2002; Levitt, 1998). If the dependent variable is the crime rate (offenses/population) and we use the arrest rate (arrests/offenses) as an explanatory variable, then the number of offenses is both the numerator of the dependent variable and the denominator of this right-hand-side variable. Any measurement error in the number of offenses will appear on both sides of the equation, creating a negative bias in the estimated coefficient of the arrest rate. Gould, Weinberg, and Mustard (2002, p. 51) call this “division bias.” As we have seen, in this data set, measurement error in the number of offenses is an important problem.
The second source of bias arises from the fact that that we can expect that measures of deterrence will be jointly determined with crime rates. That is, a rise in local crime rates will almost certainly cause local officials to increase crime deterrence efforts, such as hiring more police. This creates a simultaneous equations bias in OLS estimates of the effects of deterrence variables in the crime equation.
One could potentially deal with measurement error biases and simultaneous equations bias using instrumental variables (IV). This requires having at least one instrumental variable that is correlated with the arrest rate or other deterrence variable but is uncorrelated with the error in the crime equation, εit in Equation (2). Levitt (1997) used local election cycles for a wide range of U.S. cities as instruments, arguing that the timing of local elections may affect the hiring of new police but the timing of local elections is not related to local crime. Using local election cycles as instruments will not work when we, unlike Levitt, are dealing with only one state. Indiana has most municipal elections on the same 4-yr cycle, so that there will be no variation in timing of elections across counties. With no cross-section variation in election timing, we cannot use election cycles as an instrumental variable in a panel equation.
Here we will use the aggregate arrest rate for the four categories of violent crime (aggravated assault, robbery, rape, and murder) as the measure of deterrence in the property crime equations. Using the violent crime arrest rate to measure deterrence in the property crime equations avoids the division bias. Furthermore, for the property crime equations, we have a variable having the properties we seek in an instrument for the violent crime arrest rate: the percentage of local government employment in total county employment.17 First, we would expect that local government employment would be higher where local deterrence effort is higher. Second, this variable is statistically significant is explaining the violent crime arrest rate.18 Third, this variable is not significant in explaining any of the property crime rates.19
Unfortunately, we cannot make the analogous argument for using the property crime arrest rate as the measure of deterrence in the violent crime equations. The problem here is that the percentage of local government employment in total county employment is significant in explaining violent crime rates. This correlation of the proposed instrument with the dependent variable rules it out as an instrument for the deterrence variable. Therefore, we proceed below with estimates including the deterrence variable for the property crimes only.
Table 3 shows the estimated parameters for the deterrence, hotel room, and casino variables from Equation (2) with various specifications of the right-hand side variables xit. (Table A2 shows the estimated parameter values for the other independent variables.) In all cases, the estimated equations include county and year fixed effects. For each category of offense, the first column shows results using OLS, reproduced from Table 2. The second column shows the same equation estimated using OLS with the violent crime arrest rate added. The third column for each crime category shows the equation including the deterrence variable and estimated using instrumental variables with the percentage of local government employment in total county employment as the instrument.
| OLS | Larceny | Burglary | Motor Vehicle Theft | ||||||
|---|---|---|---|---|---|---|---|---|---|
| OLS | IV | OLS | OLS | IV | OLS | OLS | IV | ||
| Violent arrest rate | − 14.53 ( 0.59) | − 48.52 ( 0.23) | − 14.76 ( 1.51) | 38.87 ( 0.45) | − 6.98 ( 1.62) | − 13.04 ( 0.36) | |||
| Rooms | − 0.245* ( 2.02) | − 0.244* ( 2.01) | − 0.242* ( 1.98) | − 0.046 ( 0.97) | − 0.045 ( 0.95) | − 0.048 ( 0.97) | − 0.049* ( 2.33) | − 0.049* ( 2.31) | − 0.048* ( 2.28) |
| Turnstile | − 0.0845* ( 2.61) | − 0.0846* ( 2.61) | − 0.0849* ( 2.61) | − 0.0146 ( 1.14) | − 0.0147 ( 1.15) | − 0.0144 ( 1.08) | − 0.0444* ( 7.87) | − 0.0444* ( 7.90) | − 0.0445* ( 7.88) |
| LEAD2 | − 303.9 ( 1.48) | − 303.0 ( 1.47) | − 301.0 ( 1.45) | 30.2 ( 0.37) | 31.1 ( 0.38) | 27.9 ( 0.33) | − 78.4* ( 2.19) | − 78.0* ( 2.18) | − 77.7* ( 2.16) |
| LEAD1 | − 141.7 ( 0.69) | − 140.3 ( 0.68) | − 137.0 ( 0.66) | − 10.2 ( 0.13) | − 8.81 ( 0.11) | − 14.0 ( 0.17) | − 49.4 ( 1.39) | − 48.7 ( 1.37) | − 48.1 ( 1.34) |
| Casino open | − 248.1 ( 1.27) | − 247.4 ( 1.27) | − 245.6 ( 1.25) | − 42.1 ( 0.55) | − 41.4 ( 0.54) | − 44.1 ( 0.55) | − 71.4* ( 2.11) | − 71.1* ( 2.10) | − 70.8* ( 2.08) |
| LAG1 | 136.7 ( 0.76) | 145.8 ( 0.81) | 167.0 ( 0.75) | − 9.21 ( 0.13) | − 0.011 ( 0.00) | − 33.4 ( 0.37) | 45.2 ( 1.45) | 49.6 ( 1.58) | 53.4 ( 1.38) |
| LAG2 | 102.4 ( 0.59) | 105.7 ( 0.60) | 113.3 ( 0.62) | − 70.5 ( 1.02) | − 67.2 ( 0.97) | − 79.2 ( 1.07) | − 6.02 ( 0.20) | − 4.46 ( 0.15) | − 3.10 ( 0.10) |
| LAG3 | 216.9 ( 1.26) | 215.3 ( 1.25) | 211.7 ( 1.21) | 131.8 ( 1.94) | 130.2 ( 1.92) | 136.0 ( 1.91) | 4.27 ( 0.14) | 3.52 ( 0.12) | 2.86 ( 0.09) |
| LAG4 | 141.1 ( 0.82) | 140.6 ( 0.82) | 139.5 ( 0.81) | 146.3* ( 2.16) | 145.8* ( 2.15) | 147.6* ( 2.10) | − 11.6 ( 0.39) | − 11.8 ( 0.40) | − 12.0 ( 0.40) |
| LAG5 | 58.2 ( 0.34) | 56.5 ( 0.33) | 52.6 ( 0.31) | 84.0 ( 1.26) | 82.3 ( 1.24) | 88.5 ( 1.27) | − 6.80 ( 0.23) | − 7.62 ( 0.26) | − 8.33 ( 0.28) |
| R 2 | .164 | .164 | .160 | .118 | .123 | .056 | .286 | .291 | .287 |
| Num obs | 497 | 497 | 497 | 497 | 497 | 497 | 497 | 497 | 497 |
- Note: t-values are given in parentheses.
- *Statistically significant in a two-tailed test at the .95 level
Looking at the center columns, for each category of property crime (OLS) the deterrence variable has a negative coefficient; but it is only at the borderline of statistical significance in a one-tailed test for burglary and motor vehicle theft. The statistical significance of deterrence disappears in the instrumental variable estimation, shown for each category of property crime in the columns on the right. Adding the deterrence variable has little effect on the estimated parameters and ratios of parameters to standard errors of the casino timing, turnstile, and rooms variables.
We can examine the patterns of coefficients on lead, casino opening, lag variables, and turnstile in Table 3 to look for impacts of new casinos on crime. The patterns are the same in all three specifications. There are no significant effects of the timing of casino openings on rates of larceny, although the coefficients on all of the lag variables are positive. (The five lag variables are not jointly significantly different from 0 in any of the three specifications.) The coefficient on the turnstile variable shows a large and significant negative effect of casino activity on larceny. The coefficient on the turnstile variable shows a significant and negative effect of casino activity on motor vehicle thefts. The casino opening and 2-yr lead variables are negative and statistically significant in explaining motor vehicle thefts, while the lag coefficients are small, insignificant, and vary in sign. (Again, the five lag variables are not jointly significantly different from 0 in any of the three specifications.) The burglary equations show a different result. For burglary, the coefficient on the turnstile variable is small and not statistically significant. The coefficients for the 3-yr lag are positive and near the borderline for significance and for the 4-yr lag are positive and significant, suggesting that increased burglary rates follow new casinos. The lags at years 3 and 4 are jointly significant at the .95 level for all three specifications. For the first OLS burglary specification, all five lag variables are also jointly significant at the .95 level (F = 2.32; critical value 2.21), while the five lag variables are at the borderline of significance in the second and third specifications.
VI. IMPLICATIONS OF THE RESULTS
These results suggest that introducing a new casino increases local burglary rates after a lag of a few years. Otherwise, contrary to the results in G&M and E&T, these results do not show that introducing new casinos increases local crime rates. The results suggest, moreover, that increasing casino activity, in this case the turnstile count of casino patrons, leads to reductions in local crime rates. (This effect of casino activity is, however, small and statistically insignificant for burglary.) These results suggest that for some crime categories, new casinos may actually reduce local crime rates. Furthermore, new casinos lead to new hotel room construction, which may lead to additional reductions in some crime rates.
We can use the estimated parameter values and the average of the turnstile variable to calculate an estimate of the quantitative effect on crime rates of the opening of a new casino in an Indiana county. Table 4 shows the averages of the turnstile variable (in thousands) by county, for counties having casinos in the reduced sample, by years since the opening of the county's first casino. In calculating the effects of new casinos, I use only the results for the first column for each crime category from Table 3. I begin with the average crime rate for the counties and years included in the reduced sample and then add the lead or lag coefficient plus the product of the turnstile coefficient and the average turnstile count for the appropriate lag from Table 4. The results show approximate average effects of new casinos on crime rates over time. (I do not attribute to casinos any of the effects of hotel rooms on crime rates.) 1-3 show these net effects of the lead, casino open, lag, and turnstile variables on the predicted crime rates for larceny, burglary, and motor vehicle theft, respectively. The figures also show the 95% confidence bounds above and below the estimated values. The net effect of a new casino on larceny rates is small, as the large and significant turnstile effect roughly cancels out the large (but insignificant) lag effects. We can see that county burglary rates rise a few years after opening a new casino because the turnstile effect is too small to cancel out the large effects increasing burglary rates 3 and 4 yr after the casino's opening. The large negative turnstile effect substantially reduces the rate of motor vehicle thefts.
| Year Casino Opens | Lag 1 | Lag 2 | Lag 3 | Lag 4 | Lag 5 |
|---|---|---|---|---|---|
| 899.6 | 2887.1 | 3447.9 | 3519.4 | 3591.2 | 3542.9 |
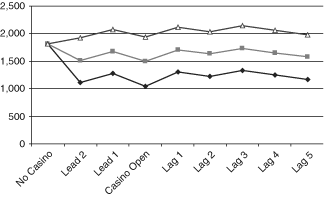
Net Effects of Opening a New Casino on Larceny Rates
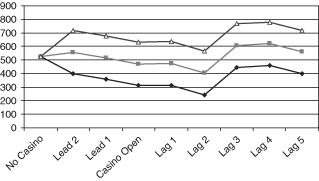
Net Effects of Opening a New Casino on Burglary Rates
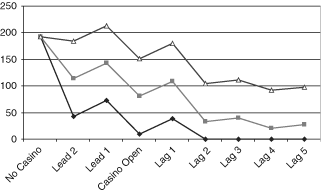
Net Effects of Opening a New Casino on Motor Vehicle Theft Rates
VII. CONCLUSION
This paper examines the link between casinos and crime using Indiana's counties for the years 1994 through 2004. This paper uses a specification of the equations explaining crime rates which includes the number of hotel rooms in the county and a count of casino patrons as a measure of casino activity. I have also deleted defective crime rate data that have plagued earlier studies. As a first result, I find that construction of new hotel rooms follows the introduction of casinos into the county. These new hotel rooms seem to reduce the levels of larceny and motor vehicle theft. Turning to casinos and crime, I find very limited support for the proposition that new casinos increase local crime rates. Opening new casinos appears to increase the number of burglaries in the county after a lag of a few years. Opening new casinos appears, however, to reduce the number of motor vehicle thefts and aggravated assaults. Increased casino activity, measured using turnstile count of casino patrons, seems to reduce rates of larceny, motor vehicle theft, aggravated assault, and robbery. These results do not match those of earlier studies that show large increases in a broad range of local crime rates after opening new casinos. The results presented here, however, are based on only a small segment of the nation's experience with the casino industry, and this narrow focus limits the applicability of the results. Expanding investigations like this to other states will be limited by the availability of adequate crime data, annual data by county on hotels or other establishments, and consistent measures of casino activity.
Nevertheless, the new results presented here provide guidance for future work on casinos and crime. I introduce a measure of casino activity in addition to variables related to the timing of casino opening. The measure of casino activity, turnstile count of patrons entering the casinos, is often statistically significant and its effect is negative, suggesting that increased casino activity reduces crime rates. It may also suggest that casinos aimed at attracting large numbers of patrons are more likely than small casinos to reduce local crime rates. I also test whether or not the number of hotel rooms affects crime rates. The estimated effect of the number of hotel rooms in the county on crime rates is always negative, but when restricting the sample to observations with relatively complete data, this variable is only significant in the equations for larcenies and motor vehicle theft. The statistical significance of the turnstile variable suggests that leaving out a measure of casino activity when estimating the effect of casinos on crime is a serious specification error. The significance of the hotel room variable in equations for some crime rates suggests that a measure of the level of other public accommodations in addition to casinos may be necessary to avoid specification error.
These results provide some support for the economic model of crime—the statistically significant negative effect of the turnstile measure of casino activity may suggest that increasing casino activity increases the opportunity cost of crime by providing increased legitimate employment opportunities.
Finally, researchers need to exercise care in using county-level Uniform Crime Reports data to study links between casinos and crime. In all cases, the UCR's coded number of crimes at the county level is a number, but in many cases it is not a reported number of crimes.
APPENDIX
| Crime Rate Equations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Reduced Sample | Full Sample | |||||||||
| Variable | Observations | Average | SD | Minimum | Maximum | Observations | Average | SD | Minimum | Maximum |
| Turnstile | 497 | 295.00 | 1324.5 | 0.00 | 11429 | 1012 | 164.42 | 952.9 | 0.00 | 11429 |
| Rooms | 497 | 942.63 | 2232.6 | 0.00 | 16202 | 1012 | 569.99 | 1616.9 | 0.00 | 16202 |
| Larceny | 497 | 1817.07 | 1073.8 | 24.23 | 4685.7 | 1012 | 1211.68 | 1102.8 | 0.00 | 4685.7 |
| Burglary | 497 | 527.02 | 298.6 | 3.01 | 1417.3 | 1012 | 341.53 | 311.8 | 0.00 | 1639.9 |
| MV theft | 497 | 191.93 | 185.9 | 0.00 | 1225.5 | 1012 | 122.53 | 156.0 | 0.00 | 1225.5 |
| Assault | 497 | 176.84 | 158.4 | 5.83 | 1021.4 | 1012 | 125.54 | 136.9 | 0.00 | 1021.4 |
| Robbery | 497 | 46.63 | 70.8 | 0.00 | 403.7 | 1012 | 27.68 | 55.2 | 0.00 | 403.7 |
| Rape | 497 | 18.90 | 15.2 | 0.00 | 118.3 | 1012 | 13.36 | 14.5 | 0.00 | 177.5 |
| Density | 497 | 254.89 | 385.7 | 23.31 | 2178.6 | 1012 | 173.19 | 287.7 | 22.34 | 2178.6 |
| Male | 497 | 49.28 | 0.96 | 47.24 | 52.4 | 1012 | 49.40 | 0.92 | 47.24 | 54.0 |
| White | 497 | 95.57 | 5.99 | 72.35 | 99.9 | 1012 | 97.05 | 4.64 | 72.35 | 99.9 |
| Black | 497 | 3.66 | 5.73 | 0.02 | 26.7 | 1012 | 2.33 | 4.39 | 0.00 | 26.7 |
| Pop 10–19 | 497 | 14.82 | 0.89 | 12.71 | 18.4 | 1012 | 14.84 | 0.86 | 12.71 | 18.4 |
| Pop 20–29 | 497 | 13.24 | 3.06 | 9.00 | 29.6 | 1012 | 12.80 | 2.56 | 9.00 | 29.6 |
| Pop 30–39 | 497 | 14.50 | 1.41 | 11.10 | 19.7 | 1012 | 14.63 | 1.33 | 11.10 | 19.9 |
| Pop 40–49 | 497 | 14.99 | 1.16 | 11.17 | 17.6 | 1012 | 15.03 | 1.08 | 11.17 | 17.9 |
| Pop 50–64 | 497 | 15.54 | 1.83 | 10.45 | 22.7 | 1012 | 15.58 | 1.69 | 10.41 | 22.7 |
| Pop over 64 | 497 | 13.13 | 1.96 | 7.38 | 16.9 | 1012 | 13.35 | 1.80 | 7.38 | 16.9 |
| Real income | 497 | 14.61 | 2.18 | 10.84 | 25.7 | 1012 | 14.18 | 2.17 | 9.73 | 25.7 |
| Retirement | 497 | 7.67 | 0.63 | 5.32 | 9.4 | 1012 | 7.55 | 0.63 | 5.30 | 9.4 |
| Maintenance | 497 | 149.38 | 54.77 | 41.08 | 324.3 | 1012 | 142.16 | 50.96 | 41.08 | 324.3 |
| Unemployment | 497 | 46.19 | 26.91 | 9.41 | 129.1 | 1012 | 45.27 | 26.98 | 9.41 | 159.4 |
| Viol arrest rate | 497 | 0.75 | 0.97 | 0.00 | 9.50 | 1012 | 1.80 | 3.69 | 0.00 | 58.0 |
| Local government | 497 | 0.085 | 0.026 | 0.043 | 0.149 | 1012 | 0.091 | 0.026 | 0.043 | 0.187 |
| Rooms Equation | |||||
|---|---|---|---|---|---|
| Variable | Observations | Average | SD | Minimum | Maximum |
| Rooms | 1012 | 569.99 | 1616.9 | 0.00 | 16202 |
| Population | 1012 | 65.56 | 108.7 | 5.49 | 863.29 |
| Popsq | 1012 | 16098 | 79949 | 30.2 | 745268 |
| Density | 1012 | 173.19 | 287.7 | 22.34 | 2178.65 |
| Male | 1012 | 49.40 | 0.92 | 47.24 | 53.95 |
| White | 1012 | 97.05 | 4.64 | 72.35 | 99.91 |
| Black | 1012 | 2.33 | 4.39 | 0.00 | 26.71 |
| Pop 10–19 | 1012 | 14.84 | 0.86 | 12.71 | 18.44 |
| Pop 20–29 | 1012 | 12.80 | 2.56 | 9.00 | 29.59 |
| Pop 30–39 | 1012 | 14.63 | 1.33 | 11.10 | 19.95 |
| Pop 40–49 | 1012 | 15.03 | 1.08 | 11.17 | 17.91 |
| Pop 50–64 | 1012 | 15.58 | 1.69 | 10.41 | 22.69 |
| Pop over 64 | 1012 | 13.35 | 1.80 | 7.38 | 16.87 |
| Real income | 1012 | 14.18 | 2.17 | 9.73 | 25.70 |
| Larceny | Burglary | Motor Vehicle Theft | |||||||
|---|---|---|---|---|---|---|---|---|---|
| OLS | OLS | IV | OLS | OLS | IV | OLS | OLS | IV | |
| Density | − 0.155 ( 0.06) | − 0.144 ( 0.06) | − 0.119 ( 0.05) | 0.840 ( 0.84) | 0.851 ( 0.86) | 0.811 ( 0.78) | 0.065 ( 0.15) | 0.070 ( 0.16) | 0.075 ( 0.17) |
| Male | − 465.2* ( 2.89) | − 468.5* ( 2.91) | − 476.2* ( 2.83) | 107.4 ( 1.69) | 104.0 ( 1.64) | 116.2 ( 1.69) | 26.2 ( 0.94) | 24.6 ( 0.88) | 23.3 ( 0.80) |
| White | − 370.3* ( 2.62) | − 372.5* ( 2.63) | − 377.5* ( 2.60) | 6.77 ( 0.12) | 4.60 ( 0.08) | 12.5 ( 0.21) | 31.6 ( 1.28) | 30.6 ( 1.24) | 29.7 ( 1.18) |
| Black | − 285.2* ( 2.04) | − 285.8* ( 2.04) | − 287.2* ( 2.04) | 13.4 ( 0.24) | 12.8 ( 0.23) | 15.0 ( 0.26) | 37.4 ( 1.53) | 37.1 ( 1.52) | 36.8 ( 1.51) |
| Real income | − 1.18 ( 0.03) | − 0.805 ( 0.02) | 0.080 ( 0.00) | − 0.693 ( 0.04) | − 0.309 ( 0.02) | − 1.704 ( 0.10) | 19.16* ( 2.71) | 19.34* ( 2.74) | 19.50* ( 2.73) |
| Retirement | − 9.51 ( 0.08) | − 8.72 ( 0.07) | − 6.87 ( 0.06) | 68.9 ( 1.41) | 69.7 ( 1.43) | 66.8 ( 1.31) | 21.4 ( 0.99) | 21.8 ( 1.01) | 22.1 ( 1.02) |
| Maintenance | 1.40 ( 0.54) | 1.45 ( 0.56) | 1.55 ( 0.58) | − 0.602 ( 0.59) | − 0.559 ( 0.55) | − 0.715 ( 0.66) | − 0.591 ( 1.31) | − 0.571 ( 1.27) | − 0.553 ( 1.19) |
| Unemployment | 1.761 ( 0.80) | 1.862 ( 0.85) | 2.099 ( 0.79) | 0.485 ( 0.56) | 0.588 ( 0.68) | 0.214 ( 0.20) | 0.119 ( 0.31) | 0.168 ( 0.44) | 0.210 ( 0.46) |
| Pop 10–19 | − 354.7* ( 3.27) | − 354.6* ( 3.27) | − 354.5* ( 3.26) | − 88.0* ( 2.06) | − 87.9* ( 2.06) | − 88.1* ( 1.99) | − 10.88 ( 0.58) | − 10.85 ( 0.58) | − 10.83 ( 0.57) |
| Pop 20–19 | − 356.9* ( 3.63) | − 355.5* ( 3.61) | − 352.3* ( 3.50) | − 24.9 ( 0.64) | − 23.5 ( 0.61) | − 28.6 ( 0.70) | 8.62 ( 0.50) | 9.28 ( 0.54) | 9.86 ( 0.56) |
| Pop 30–19 | − 250.0 ( 1.59) | − 247.5 ( 1.57) | − 241.6 ( 1.49) | − 52.8 ( 0.85) | − 50.2 ( 0.81) | − 59.5 ( 0.90) | 18.40 ( 0.67) | 19.61 ( 0.72) | 20.66 ( 0.73) |
| Pop 40–19 | − 115.5 ( 1.08) | − 112.6 ( 1.05) | − 105.6 ( 0.92) | 12.5 ( 0.30) | 15.6 ( 0.37) | 4.59 ( 0.10) | 37.44* ( 2.02) | 38.86* ( 2.10) | − 40.10* ( 2.00) |
| Pop 50–64 | − 179.8 ( 1.64) | − 179.5 ( 1.64) | − 179.0 ( 1.63) | − 4.53 ( 0.10) | − 4.29 ( 0.10) | − 5.15 ( 0.11) | 10.93 ( 0.57) | 11.05 ( 0.58) | 11.14 ( 0.58) |
| Pop over 64 | − 209.0 ( 1.81) | − 209.2 ( 1.81) | − 209.8 ( 1.81) | 29.1 ( 0.64) | 28.79 ( 0.63) | 29.8 ( 0.63) | 24.79 ( 1.23) | 24.67 ( 1.23) | 24.56 ( 1.22) |
| Constant | 82231 ( 3.98) | 82484 ( 3.99) | 83078 ( 3.95) | − 3997 ( 0.49) | − 3740 ( 0.46) | − 4676 ( 0.54) | − 5823 ( 1.62) | − 5701 ( 1.59) | − 5595 ( 1.53) |
| Num obs | 497 | 497 | 497 | 497 | 497 | 497 | 497 | 497 | 497 |
- Note: t-values are given in parentheses.
- *Statistically significant in a two-tailed test at the .95 level




