Rate maintenance and resonance in the entorhinal cortex
Present address: Center for Brain Science, Harvard University, Cambridge, MA 02138, USA.
Abstract
Throughout the brain, neurons encode information in fundamental units of spikes. Each spike represents the combined thresholding of synaptic inputs and intrinsic neuronal dynamics. Here, we address a basic question of spike train formation: how do perithreshold synaptic inputs perturb the output of a spiking neuron? We recorded from single entorhinal principal cells in vitro and drove them to spike steadily at ∼5 Hz (theta range) with direct current injection, then used a dynamic-clamp to superimpose strong excitatory conductance inputs at varying rates. Neurons spiked most reliably when the input rate matched the intrinsic neuronal firing rate. We also found a striking tendency of neurons to preserve their rates and coefficients of variation, independently of input rates. As mechanisms for this rate maintenance, we show that the efficacy of the conductance inputs varied with the relationship of input rate to neuronal firing rate, and with the arrival time of the input within the natural period. Using a novel method of spike classification, we developed a minimal Markov model that reproduced the measured statistics of the output spike trains and thus allowed us to identify and compare contributions to the rate maintenance and resonance. We suggest that the strength of rate maintenance may be used as a new categorization scheme for neuronal response and note that individual intrinsic spiking mechanisms may play a significant role in forming the rhythmic spike trains of activated neurons; in the entorhinal cortex, individual pacemakers may dominate production of the regional theta rhythm.
Introduction
A basic question of neuroscience concerns the procedure of neural coding: what does a spike train represent? While neural responses are assumed to represent inputs in some sense, the precise details of that coding procedure are unknown. Rate, temporal or synchrony codes have been suggested (Theunissen & Miller, 1995; Eggermont, 1998; Shadlen & Movshon, 1999; Tiesinga et al., 2008) in which spiking rate, detailed timing or coordination between action potentials act to encode aspects of inputs, including stimulus intensity (Oswald et al., 2007), timing (Chase & Young, 2006), texture (Wolfe et al., 2008) or pitch (Tramo et al., 2005).
Individual spike times represent integration of hundreds to thousands of synaptic inputs combined in space and time, which are modulated by intrinsic neuronal dynamics, transformed by an unpredictable spike threshold, and integrated differently in various populations of neurons. In many cortical neurons, maintained spiking requires a maintained drive (Cowan & Wilson, 1994), while in other cells, such as cerebellar Purkinje cells, output is driven primarily by an intrinsic pacemaker within the neuron itself (Hausser & Clark, 1997). In principle, a spike train could result from only the input, only a cell’s intrinsic mechanisms or anything between. Understanding the balance between synaptic and intrinsic mechanisms in forming the output of a neuron is critical for understanding how a neural circuit functions.
It is also unclear how integration affects encoding within an active network. Many studies demonstrate the effects of specific membrane conductances on neuronal firing characteristics (Klink & Alonso, 1993; White et al., 1998; Brumberg et al., 2000; Dorval & White, 2005; Gu et al., 2005; Haas et al., 2006). Studies using single neurons driven with time-varying inputs (Mainen & Sejnowski, 1995; Tateno & Robinson, 2006) and studies varying parameters of computational models (Schreiber et al., 2009) have demonstrated a link between intrinsic properties – including subthreshold resonance and suprathreshold frequency preference – and spiking reliability (Haas & White, 2002; Hunter & Milton, 2003; Schreiber et al., 2004a). However, some reliability studies found that in order to elicit a highly reproducible response, inputs need to be overwhelmingly large, driving membrane fluctuations up to 25 mV in amplitude. Phase–response curves and similar approaches have been used to quantify the effects of temporally sparse inputs on spike times (Reyes & Fetz, 1993b; Netoff et al., 2005; Ermentrout & Saunders, 2006).
In this study, we address the question of whether intrinsic mechanisms or input timings dominate the formation of a rhythmic spike train – in essence, whether a neuron’s internal pacemaker can be hijacked by faster or slower input. With experimental data, we show that cortical neurons employ several mechanisms to maintain their average firing rates in the face of strong drive, indicating that intrinsic dynamics, rather than inputs, prevail on the formation of a spike train. While rate is preserved, neurons respond differently to input trains of varying speeds, resonating to some inputs but ignoring others. Our results imply that for a steadily spiking neuron, the malleability of its responses to input is an essential component of neuronal coding.
To provide explanations of experimental observations, it is often useful to develop models. This is typically implemented by matching suitable sets of differential equations to biophysical mechanisms. However, it is not always possible to ensure extrapolations from such models, especially if one wishes to keep the number of variables small. Therefore, we instead developed a data-driven minimal Markov model, which reproduces the relevant observed correlations and provides insight on how rate is maintained. This type of simple stochastic model can be fruitfully extrapolated as a testing ground for many neuronal types.
Materials and methods
Electrophysiological recordings
All experiments were conducted as approved by the UCSD Institutional Animal Care and Use Committee. Young (14- to 21-day-old) Long–Evans rats were anesthetized by overexposure to CO2 and decapitated. The brain was quickly removed and immersed in cold (0 °C) oxygenated artificial cerebral spinal fluid (ACSF; in mm: NaCl 126; KCl 3; NaH2PO4 1.25; MgSO4 2; NaHCO3 26; glucose 10; CaCl2 2; buffered to pH 7.4 with 95/5% O2/CO2). Horizontal slices were prepared using a Vibratome cutter (TPI). Slices were allowed to recover for 1 h prior to recording in a holding chamber at room temperature, continuously bathed in oxygenated ACSF. Slices were transferred to an immersion chamber (RC-27L; Warner Instruments) and visualized with IR-DIC optics (Zeiss Axioskop 2FS Plus, Dage CCD100), maintained at 34 °C (TC-344B; Warner). Electrodes of resistance 4 – 6 MΩ were pulled on a horizontal puller (Sutter Instruments) and filled with a recording solution (in mm: KGluconate 135; KCl 4; NaCl 2; HEPES 10; EGTA 0.2; MgATP 4; GTP-tris 0.3; phosphocreatine-tris 10). Excitatory synaptic transmission was blocked by 6-cyano-2,3-dihydroxy-7-nitroquinoxaline acid (CNQX; 10 μm) and d-2-Amino-5-phosphonovaleric acid (d(-)-APV) (50 μm), produced by Sigma (St Louis, MO, USA).
We obtained whole-cell recordings from superficial entorhinal cortical (EC) layer II neurons, selected by their oblong cell bodies, as well as particular characteristics of their electrophysiological responses to long current steps – a prominent (> 30%) sag in response to both depolarizing and hyperpolarizing current injections (Alonso & Klink, 1993), as well as an early first spike in response to suprathreshold stimuli (Haas & White, 2002). Recordings were made in current-clamp mode. Intracellular signals were amplified (Axoclamp 2B; Molecular Devices), low-pass filtered (eight-pole Butterworth at 5 kHz) and digitized at 10 kHz with a DAQ card (NI PCI-6035E) controlled by lab-made software created in LabView (National Instruments). Series and input resistances, and resting potentials, were monitored throughout each experiment; data from cells with variations > 25% in those parameters were discarded. We compensated for series and access resistance, which was typically 20 – 40 MΩ.
In parallel, we recorded from and stimulated neurons with a real-time Linux-based dynamic clamp (Dorval et al., 2001). In dynamic-clamp mode, a current was injected that varied with cellular voltage and time and was recalculated at each acquisition time step (0.1 ms). In this manner it was possible to mimic a synaptic conductance input, rather than command a voltage or current input, to the cell. We delivered excitatory synaptic inputs as double exponential waveforms S(t) governed by an ordinary differential equation of the form 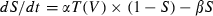 , with
, with  = 0.2ms and
= 0.2ms and 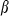 = 5ms. T represents neurotransmitter in the synapse as a function of Vpre, the presynaptic voltage train (to simplify, we used square pulses rising from −100 to +10 mV for 2 ms at the input times, as presynaptic spikes):
= 5ms. T represents neurotransmitter in the synapse as a function of Vpre, the presynaptic voltage train (to simplify, we used square pulses rising from −100 to +10 mV for 2 ms at the input times, as presynaptic spikes): 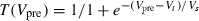 (Vt = 0 mV, Vs = 5 mV). The total injected synaptic current was then
(Vt = 0 mV, Vs = 5 mV). The total injected synaptic current was then 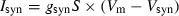 , with synaptic conductance gsyn = 2 nS, membrane potential Vm and synaptic reversal potential Vsyn = 0 mV. Synaptic inputs were added to the current injected through the amplifier; the DC amplitude of the injected current was chosen to elicit steady spiking at ∼5 Hz.
, with synaptic conductance gsyn = 2 nS, membrane potential Vm and synaptic reversal potential Vsyn = 0 mV. Synaptic inputs were added to the current injected through the amplifier; the DC amplitude of the injected current was chosen to elicit steady spiking at ∼5 Hz.
Data were discarded from any cells in which the cell health or recording degraded or failed before having recorded the full set of time-rescaled stimulations for all six inputs (roughly 1 h); this yielded a dataset of six neurons. From the six neurons, the average rest potential was −63.7 ± 4.6 mV, without correction for junction potential. The times of the conductance inputs were taken from six sets of inputs – one regular input with coefficient of variation (standard deviation divided by the mean) CV = 0, and five different sets of spike times as previously recorded from a cell depolarized with current injection only. To mimic the range of natural variability of cellular spiking, the CV values of these ‘quasi-regular’ sets covered the range from 0.05 to 0.45, with mean CV = 0.16. Each train of inputs was delivered repeatedly with temporal scalings chosen such that the input intervals would range between one-third and three times the unperturbed interspike interval (ISI) of the recorded neuron. The baseline current injected to the cell was maintained through all input sets. For a total of six neurons, with six input trains and five to nine (mean 7.19) compressions of each input for each neuron, we delivered a total of 259 inputs, each of 1 min duration. Inputs with different compressions were delivered in random order, to minimize any effects of rate accommodation. Offline analysis was performed in Matlab (Mathworks). Errors are reported as standard deviations (SD) or standard errors of the mean (SEM) where indicated.
ISI-distance
To assess the reliability or similarity between input and output for different input firing rates, we employed a slightly modified version of the ISI-distance, a novel method that has the advantage of being parameter free and time scale independent (Kreuz et al., 2007, 2009).
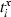 . At each moment in time, the ISI is taken as
. At each moment in time, the ISI is taken as
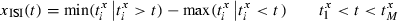
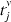 .;]> The ISI-ratio between xISI and yISI is then formed and normalized:
.;]> The ISI-ratio between xISI and yISI is then formed and normalized:
This measure becomes zero at moments when both cells are firing at the same rate, and approaches −1 or 1, respectively, if the firing rate of the first (or second) train is infinitely high and the other infinitely low.

 ;;]> the measures are equal when the ISI-ratios are always positive or always negative (e.g. for periodic spike trains with CV = 0). This usage also allows us to compute the expected values of
;;]> the measures are equal when the ISI-ratios are always positive or always negative (e.g. for periodic spike trains with CV = 0). This usage also allows us to compute the expected values of 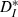 ;;]> for periodic spike trains differing only by a constant frequency mismatch, and thus to assess the extent to which differences between input and output cannot be explained as a consequence of pure frequency mismatch.
;;]> for periodic spike trains differing only by a constant frequency mismatch, and thus to assess the extent to which differences between input and output cannot be explained as a consequence of pure frequency mismatch.Spike classification
Spike times were determined as the time when the voltage crossed a fixed threshold value (defined as the minimum value plus half the data range) from below. We classified output spikes into categories of natural, perturbed and forced according to whether they were not preceded, not immediately preceded, or immediately preceded, respectively, by an input. Interestingly, we were able to perform this classification using information from the output voltage trace only (cf. Fig. 4A), a strategy that may be very useful for recordings in which only the output, but not the input, is accessible. To start with, the output voltage trace within each ISI was low-pass filtered by a moving average of 10 time steps (1 ms). Within each ISI, the voltage signal was scanned for a transition from concavity to convexity (i.e. a change of sign from positive to negative of the second derivative), which marked the occurrence of a synaptic input (e.g. at 0.33 s and at 0.61 s in Fig. 4A). If there was no such transition within an ISI (i.e. membrane voltage was concave up for the entire interval), the spike terminating the interval was classified as natural (e.g. the second spike in Fig. 4A). To distinguish between perturbed and forced spikes, the voltage signal between the last transition and the following output spike was examined. In case of a voltage decrease, the following spike was categorized as perturbed (e.g. the third spike in Fig. 4A); otherwise, it was considered to be a forced spike (e.g. the first and the fourth spikes in Fig. 4A). Inputs were subsequently classified as forcing when they preceded a forced spike, perturbing if they were the last input within an ISI but did not trigger an immediate response, or as neutral if they were not the last input within an ISI.
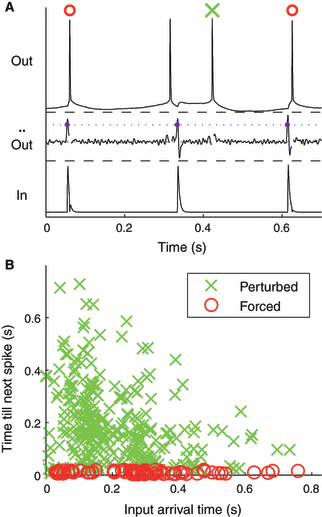
(A) Spikes were classified according to signatures of membrane voltage response in the previous ISI (see Materials and methods). In this example, the first and fourth spikes (top trace) immediately followed inputs (bottom trace); our algorithm classified them as forced. The second spike had no input preceding it, and was classified as natural. The third spike was classified as perturbed. (B) Spike classification was verified by incorporating the input. Elapsed time from an input to the next spike is plotted against the arrival time of the input since the preceding spike. Forced spikes (red symbols) resulted in uniformly small latencies from their inputs (latency ≤ 0.02 s), while perturbed spikes (green symbols) had a scattered distribution of larger input-to-spike latencies.
Results
Overall statistics: rate, coefficient of variation and resonance
First, we carefully determined a reasonable dynamic range for our experiments, performed on single cortical neurons in vitro. To parameterize this range, we drove spiking with long injections of varying amplitudes of direct current injection, as a proxy for the activation of internal dynamics and ionic currents underlying regular spiking, in current-clamp recordings. We found that we could easily drive these neurons to fire at 20+ Hz (Fig. 1; further data not shown). The CV of the ISI distribution was overall inverse to firing rate; for rates of 1–2 Hz, CV of firing approached 1, while for rates closer to 20 Hz, CV was ∼0.2.

Firing characteristics of entorhinal stellate cells. (A) When depolarized to spike by long (> 1 s) injections of direct current of various amplitudes (x-axis), cortical cells spike with mean rates up to tens of Hz. (B) Corresponding coefficients of variation (standard deviation/mean) of spiking are higher for low spiking rates. In both panels, data shown were collected from n = 6 neurons. We performed subsequent experiments on cells driven by DC input to spike at ∼5 Hz, the rate at which firing was fairly regular and neurons were sensitive to input.
We chose 5 Hz as a target rate for further experiments for several reasons: first, 5 Hz is within the physiologically and behaviorally relevant theta range of frequencies (Fyhn et al., 2004; Buzsaki, 2005; Hasselmo & Brandon, 2008). Second, it is the lowest rate at which firing is still fairly regular; frequencies below 5 Hz were too irregular to quantify a meaningful value of ISI. At higher frequencies, sensitivity to input is inverse to firing rate (Reyes & Fetz, 1993a). Thus, 5 Hz is a range in which neurons are maximally sensitive to input while firing regularly – enough above spiking threshold to fire, but not so far that sensitivity to input is reduced. To elicit spikes near 5 Hz, we used inputs of 229 ± 28 pA (mean ± SEM, n = 6). The average CV of unperturbed firing in the cells to which we later delivered conductance inputs was 0.28 ± 0.03 (mean ± SEM, n = 36). Thus, we drove neurons with direct current to a weakly active range, firing near 5 Hz, with plenty of interspike time and dynamic range remaining to respond to synaptic inputs.
Once we stimulated each neuron to fire near 5 Hz, we added strong synaptic inputs via a dynamic clamp on top of the depolarizing current, with input rates varying from one-third to three times the firing rate of the stimulated neuron. These inputs differed from those used in previous studies of reliability in that they were temporally discrete instead of continuous; also, we did not zero-mean them, in order to not constrain neural spike rates (i.e. artificially lower rates for our faster inputs by subtracting DC current). A similar paradigm was used in earlier experiments (Reyes & Fetz, 1993a; Gutkin et al., 2005) to predict modulation of firing times and rates in response to varied sizes of temporally sparse inputs, but these studies sought to avoid entrainment. In contrast, we used only one input strength but varied input rate, seeking to test entrainment specifically. We aimed to test the assumption that strong inputs can more strongly modulate, or ‘hijack’, neuronal firing.
We initially tested several conductances for our synaptic inputs and settled on a final strength of 2 nS, which drove spikes about half of the time. To broadly test the overall efficacy of the synaptic inputs (which will be addressed in a more detailed manner below), we totaled the percentage of spikes preceded by an input within 20 ms and found that this was about 51%. As a null hypothesis test, we computed the percentage of spikes preceded by inputs within 20 ms in shuffled spike trains; this fraction was close to 10%. For the inputs that failed to immediately elicit a spike, the average evoked excitatory postsynaptic potential (EPSP) was 4.9 ± 1.7 mV (mean ± SD, n = 804, measured from baseline to peak). Because these ∼5 mV inputs were delivered to neurons that were already supra-threshold and firing steadily, and often drove spikes directly, we qualify them as strong (Destexhe et al., 2003); our inputs were twice as large as the perturbations used to test phase–response curves, without directly driving spikes, in a similar paradigm (Netoff et al., 2005), and correspond to the largest of inputs used in other similar studies (Reyes & Fetz, 1993b). These results confirm that we provided a strong (but not overwhelming) synaptic input to the spiking neurons.
These choices of firing rate and input size were critical – our intent was to allow inputs to interact with intrinsic dynamics, rather than overpower or overdrive neurons with either the direct current injection or the synaptic conductance inputs.
Subsequently, we delivered six different trains of conductance inputs to each of the six neurons and repeated each of those input trains using different temporal compressions (Fig. 2; see Materials and methods), resulting in 259 input presentations in total. One of these trains was periodic, and the rest had coefficients of variation varying from 0.05 to 0.45, which spans the natural variability in spike times as discussed above.
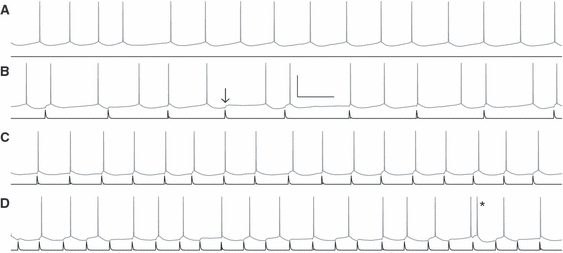
Mean firing rate is preserved over varying rates of strong inputs. (A) Driven with a current input (black), neurons fire quasi-regularly (gray); in this example, the mean ISI was 187 ± 12 ms (mean ± SEM). Conductance inputs (black) were superimposed on the same current input with rates slower (B, mean input interval of 346 ms), approximately matched (C, mean input interval of 169 ms), or faster (D, mean input interval of 124 ms) than the unperturbed neuronal rate (A). Most inputs elicited a spike within 20 ms; when the input did not immediately elicit a spike, the average response (arrow) was 4.9 mV. Inputs arriving quickly after a spike sometimes elicited a quick second spike or doublet (asterisk). Despite these strong inputs, neurons maintained their average intrinsic spiking intervals (B: 206 ms; C: 170 ms; D: 160 ms when including the doublet, 168 ms excluding its interval). Scale bar is 40 mV, 200 ms.
We plotted the mean output interspike intervals (ISIs) of the driven neurons against the mean input interconductance intervals (ICIs; Fig. 3A). For each stimulus presentation, we normalized both input ICIs and output ISIs to the ISIs of the unperturbed neuron (driven with only direct current injection and no synaptic input; cf. the top trace in Fig. 2). Over the six neurons used, the mean unperturbed ISI was 189 ± 41 ms (mean ± SEM). We found that despite the strong synaptic inputs, neurons generally maintained their natural firing rates for both slower and faster inputs (Fig. 3A). To quantify the effect of input rate on the neuronal firing rate, we measured the slope of a linear fit to the normalized response rates for each of the temporally scaled repetitions of one input, for each neuron. For quasi-regular inputs, the average slope was 0.14 ± 0.06 (P > 0.1, mean ± SEM, n = 6 neurons), over a range of input rates varying from about one-third of each neuron’s unperturbed rate to three times the neuronal rate. For perfectly regular inputs, the slope was 0.11 ± 0.05 (P > 0.1, mean ± SEM, n = 6 neurons). Differences in slopes between responses to periodic and quasi-regular inputs were not statistically significant (P > 0.1, Student’s t-test). Responses to perfectly regular inputs were slightly faster overall than responses to quasi-regular inputs: the ratio of each cell’s overall mean rate in response to periodic stimuli to its mean rate for quasi-regular stimuli was 0.82 ± 0.04 (mean ± SEM, n = 6, P < 0.01, Student’s t-test).
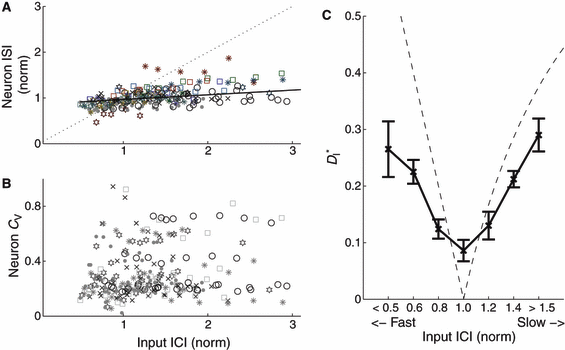
Mean interspike interval (ISI) and individual CV for each cell remained constant when driven by strong inputs of varying speeds, while simultaneously resonating to inputs of matched speed. (A) Neuronal ISI plotted against input interconductance interval (ICI); for each cell, both ISI and ICI are normalized to the ISI of the unperturbed neuron (cf. Fig. 2A). Different inputs are coded by symbols, with the responses to perfectly periodic inputs marked by filled circles. The black line is a linear fit (slope 0.11) to the lumped data over all neurons and inputs. (B) Coefficient of variation of the ISIs for each cell, plotted against input ICI. Responses to perfectly periodic inputs (dots) are overall less variable than responses to quasi-regular inputs. The ratio of the average neuronal CV for perfectly periodic inputs to the average CV for quasi-regular inputs was 0.87 ± 0.02 (mean ± SEM, n = 6). (C) Modified ISI-distance 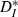 (see Materials and methods) between input and output spike trains (mean and SEM) plotted against binned input ICIs. A resonance effect was seen: neurons followed the input most reliably (smallest
(see Materials and methods) between input and output spike trains (mean and SEM) plotted against binned input ICIs. A resonance effect was seen: neurons followed the input most reliably (smallest 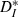 ) when the firing rates matched more closely. The dashed line shows the theoretical values that would be expected for strictly periodic spike trains with a constant frequency mismatch. Deviations demonstrate the effectiveness of the forcing inputs. Except for the resonant value, neuronal responses were less distant from the input than the expected values for a pure frequency mismatch.
) when the firing rates matched more closely. The dashed line shows the theoretical values that would be expected for strictly periodic spike trains with a constant frequency mismatch. Deviations demonstrate the effectiveness of the forcing inputs. Except for the resonant value, neuronal responses were less distant from the input than the expected values for a pure frequency mismatch.
Similar to the rate maintenance, despite the strong and varied inputs, cells maintained their individual CV (Fig. 3B); while individual cells fired with different coefficients of variation, each cell tended to maintain its own CV when driven with varying rates of input (cf. horizontal strata of various symbols in Fig. 3B). Input CV had little overall effect on output CV : responses to any given input (in Fig. 3B each input is represented by a different symbol) spanned almost the whole range of output CV. Responses to perfectly regular inputs were slightly less variable than responses to quasi-regular inputs: the ratio of each cell’s CV, in response to periodic stimuli, to its CV for quasi-regular stimuli was 0.87 ± 0.02 (mean ± SEM, n = 6, P < 0.05, F distribution). Responses to periodic stimuli were, of course, still much more variable than the input itself.
As an additional means of testing the overall effects of our input on the output trains, we assessed the correspondence between input and output spike trains by the ISI-distance 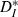 (Kreuz et al., 2007), which measures the ratio of input ICIs to output ISIs and is inverse to synchrony. Over the input speeds used,
(Kreuz et al., 2007), which measures the ratio of input ICIs to output ISIs and is inverse to synchrony. Over the input speeds used, 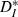 was minimal (synchrony was maximal) when input firing rates most closely matched the unperturbed firing rate of the neurons (Fig. 3C), in a form of spiking resonance. To measure the effectiveness of our stimuli in modulating spike times, we compared the value of
was minimal (synchrony was maximal) when input firing rates most closely matched the unperturbed firing rate of the neurons (Fig. 3C), in a form of spiking resonance. To measure the effectiveness of our stimuli in modulating spike times, we compared the value of 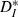 to theoretical values computed for pairs of strictly periodic spike trains with a frequency mismatch (see Materials and methods). For very slow or fast inputs (normalized ICIs furthest from 1), the value of
to theoretical values computed for pairs of strictly periodic spike trains with a frequency mismatch (see Materials and methods). For very slow or fast inputs (normalized ICIs furthest from 1), the value of 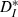 for our driven cells was smaller than 0.3, corresponding to more-similar trains. In comparison, mismatched periodic trains were less similar to each other and reached values of
for our driven cells was smaller than 0.3, corresponding to more-similar trains. In comparison, mismatched periodic trains were less similar to each other and reached values of 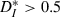 . We also noted that even for well-matched input rates (normalized ICI close to 1),
. We also noted that even for well-matched input rates (normalized ICI close to 1), 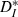 reaches a minimum of ∼0.09 but does not reach zero, as pairs of periodic trains do; this indicates a residual effect of intrinsic variability in spike times despite the resonance to strong inputs. We also observed a resonance in reliability as a function of input CV, though due to their construction and compression, our inputs did not sample the range of coefficients of variation sufficiently to quantify this effect.
reaches a minimum of ∼0.09 but does not reach zero, as pairs of periodic trains do; this indicates a residual effect of intrinsic variability in spike times despite the resonance to strong inputs. We also observed a resonance in reliability as a function of input CV, though due to their construction and compression, our inputs did not sample the range of coefficients of variation sufficiently to quantify this effect.
Time-dependent effects
To investigate possible mechanisms for the maintenance of intrinsic firing rate, simultaneous with the resonance to input rate, we classified spikes according to their response signatures to the input (see Materials and methods) into categories of forced, perturbed and natural spikes. Spike classification used solely the response voltage traces to allow us to differentiate between spikes that were immediately forced by an input, spikes that followed an input with some latency, and naturally occurring spikes (Fig. 4A). To confirm the performance of our spike-classification algorithm, we then used the input to plot the latency of the classified spikes against the relative arrival time of inputs; indeed, spikes our algorithm classified as forced had uniformly small (< 0.1 periods) latencies (Fig. 4B), while the input-to-spike latencies of spikes we classified as perturbed were widely distributed in both their input-to-spike latency and their arrival time within the ISI.
Next we determined the effects of our input compressions on spike type by binning the classified output spikes in their respective categories, separated according to relative input rate (from fast to slow, relative to the unperturbed ISI of the neuron). From this separation, we saw one marked trend: the occurrence of natural spikes increased monotonically as input rate decreased (Fig. 5A). In this case, neurons spiked naturally in between input arrivals. Conversely, for fast inputs neurons spiked naturally much less often.
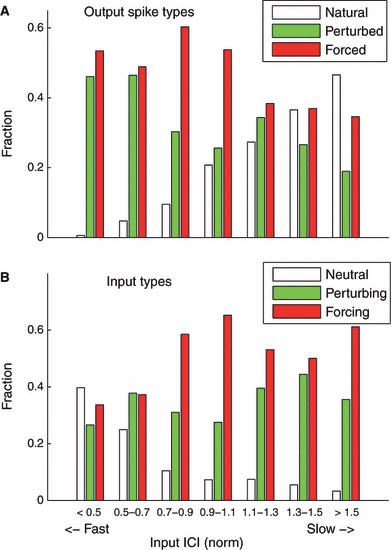
(A) Percentage of forced, perturbed and natural spikes plotted against binned relative input interconductance interval (ICI). Input ICIs were normalized to the unperturbed ISI for each cell; normalized ICIs < 1 represent faster inputs, and normalized ICIs > 1 represent slower inputs. For the slowest inputs (input ICI > 1.5), spike trains contained more natural spikes than forced or perturbed spikes. For the fastest inputs (input ICI < 0.5), few natural spikes occurred. (B) Percentage of immediately spike-eliciting inputs (forcing, red), perturbing inputs (green) and inputs that failed to force a spike (neutral, white), plotted against normalized input rate. Faster inputs were least likely to elicit immediate spikes, and inputs were most likely to force a spike at the resonant speed (input rate matched to neuronal rate, or norm ICI = 1).
We also classified the inputs according to their success in eliciting an immediate spike into the categories of forcing, perturbing and neutral (see Materials and methods), and binned them similarly by relative input rate. Two effects from this separation emerged (Fig. 5B). We found the highest fraction of forcing inputs for the resonance case, where the rate of the input matched the rate of the unperturbed neurons; this is again largely intuitive. For the fastest inputs the fraction of neutral inputs is highest and, correspondingly, the percentage of inputs that successfully forced an immediate spike is decreased. This result indicates that neurons were overall less responsive to faster inputs, even while the neurons maintained their intrinsic rates of ∼5 Hz. For very slow inputs, the percentage of forcing inputs is enhanced by episodes of 1:2 synchrony.
One potential mechanism for rate maintenance despite strong input is via short-term memory, i.e. a dependence of any given ISI on the previous spike type (forced, perturbed or natural). In order to isolate the effect of single inputs from additional effects of subsequent inputs, we looked at the length of natural ISIs (which are undisturbed by input, and thus reflect intrinsic dynamics) following either a forced or a perturbed spike. Natural ISIs following a forced spike (e.g. Fig. 2B, second and second-to-last ISIs) were significantly longer (mean normalized ISI = 1.02, corresponding to an increase of ∼4 ms for a 200-ms theta cycle; P < 0.001) than following a perturbed spike (mean normalized ISI = 0.98), indicating a memory effect and a potential contributor to rate maintenance. Here we have corrected for the differences in arrival times of perturbed spikes, which arrive later after the previous input than forced spikes, as this could also affect the occurrence of natural spikes.
To visualize the temporal dependence of input influence during rate maintenance, we computed the probability of forcing inputs over input arrival times within the ISI (Fig. 6A; we will indicate this distribution in our model as the probability Q). As expected, inputs arriving very quickly after a spike are least likely to force another spike, and inputs arriving latest within the ISI are more likely to force immediate spikes, with a maximal probability at the natural ISI. In between these two extremes we observed a very pronounced peak in the probability of an input forcing a quick second spike, or doublet, centered at a normalized input arrival time of ∼0.07 of the natural ISI following a spike (this is 10 - 20 ms for a cell spiking at ∼5 Hz). Correspondingly, the probability of an input eliciting a perturbed spike was lower during this ‘doublet window’. Neutral inputs, which failed to elicit either a forced or perturbed spike, decreased in probability with elapsed time, except for a similar small dip corresponding to the doublet peak. We also looked at the latency distributions of perturbed spikes over different input arrival times [Fig. 6B; in our modeling, this will be the latency distribution R(Δp)]. The mean latency for perturbing inputs generally decreased with input arrival time, to a plateau latency of 0.3 (normalized); latency peaked during the doublet window.
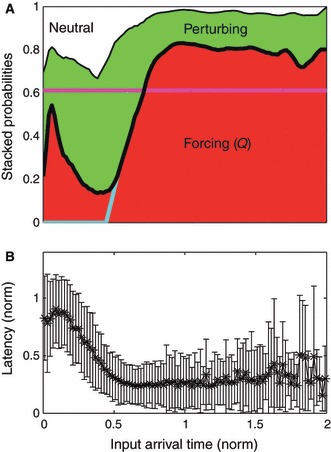
(A) Stacked input response probabilities vs. the elapsed input arrival times normalized (for each input individually) to the natural firing rate of each neuron. For each input arrival time the sum of these three input probabilities adds up to 1. In our model, the red area represents the probability Q of forcing inputs, and together the combined green and white areas represent 1 − Q. We note a strong probability of forcing a second spike, or a doublet peak, in the time window immediately following a spike, followed by a refractory period of markedly reduced probability. Colored lines describe modified models of response (see text). (B) Distribution of input-to-spike latencies for perturbing inputs (represented by mean and standard deviation) vs. input arrival time. In the model this set of probabilities is defined as R.
Modeling
In order to test whether we could reproduce the neuron’s behavior using only these basic probabilities (cf. Fig. 6) as ingredients, we built a simple stochastic model that is schematically described in Fig. 7. We used two streams taken from our experiments: the input (ICIs), in exactly the same order as delivered during the experimental recordings (Fig. 8A); and neuronal ISIs, drawn randomly from the distribution P(t) of intervals recorded from unperturbed neurons (Fig. 8B). The model proceeded as follows:
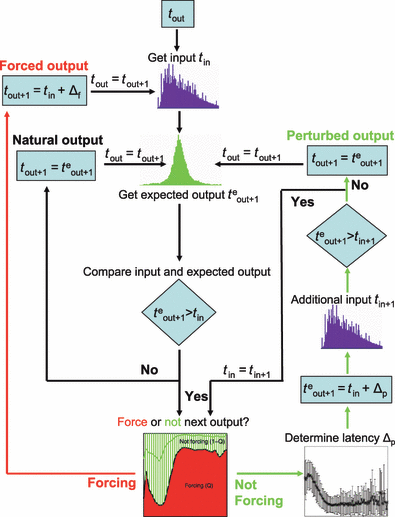
Flowchart of the minimal Markov model that determines the time of the next output spike using only the previous output spike, the actual sequence of inputs and experimentally estimated probabilities. For each spike time tout, a next natural spike teout + 1 is chosen from the experimental distribution of natural ISIs, and an input time is determined from the stream of input intervals used in experiments. The next spike time tout + 1 is then determined according to the distributions and probabilities derived from the experimental results. There are three possible output loops – one for the forced spikes, one for natural spikes and one for perturbed spikes. The last loop incorporates the next input; if an additional input occurs before the perturbed spike, the spike type is reconsidered with the new input time. The whole procedure is iterated until the sequence of inputs has ended.
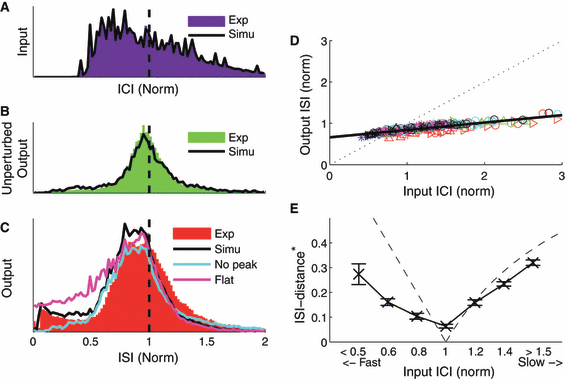
Inputs, the spiking model and the output of the simulated data. In all plots, colored histograms represent experimental data, and black lines represent the simulation. (A) Distributions of input intervals; in the simulations the same inputs were delivered exactly as in experiments. (B) Distribution of intervals recorded from unperturbed neurons (i.e. natural spiking). In the model simulations, ISIs were drawn at random from this interval distribution (defined as P). (C) Distributions of output ISIs. Using only the response probabilities and the latency distributions from Fig. 6, the streaming model reproduces the observed ISI-distribution quite well. A modified model lacking the doublet peak observed in the data (Fig. 6) produced fewer short ISIs (cyan line), whereas a modified model with flat response probabilities produced a larger number of short ISIs than seen in the experimental data (magenta line). (D and E) The simultaneous effects of rate maintenance and resonance were reproduced by the original model.
We start with an output spike, at time tout, and seek to determine the next output spike time tout+1. Let teout+1 denote the expected time of a possible next natural output spike, drawn from the distribution P(t). First we consider the next input, arriving at time tin. If tin > teout+1, the input is too late; the next output spike, tout+1 is taken as emitted at time teout+1, and is considered of natural type. Alternatively, if tin < teout+1, an input arrives before a natural spike would have arrived; then the next output spike is taken as forced with probability Q(tin − tout) or as perturbed with probability 1 − Q(tin − tout) (Fig. 6A). In the former case, the forced spike tout+1 is elicited at time tin + Δf, where Δf is the measured latency of forced spikes (cf. Fig. 4B). In the latter case, the latency of a potential output spike Δp is chosen from the probability distribution R(Δp|tin − tout) (Fig. 6B, the latencies of perturbed spikes); the expected spike time teout+1 = tin + Δp is also compared with the time of the next input tin+1, and forced or further delayed in a similar manner if tin+1 arrives before the perturbed spike at tin + Δp. Having thus determined the next spike time tout+1, we then proceed from one output spike to the next until the experimental input stream has ended.
We compared the ISI distributions from the simulation and the experimental data. As shown in Fig. 8C, the distribution of simulated outputs reproduces the measured ISI distribution (black lines) reasonably well. Quantifying the overlap of the two distributions using Receiver-Operator-Characteristics (Hanley & McNeil, 1982) yields a value of 0.99, a highly significant similarity (P-value < 0.001). Our simulations reproduced the simultaneous rate maintenance (Fig. 8D) and the resonance effects of the experiments (Fig. 8E).
In the experimental data we distinguished three different input types (cf. 5, 6), while in the streaming model we can only distinguish a priori whether an input forces an immediate spike or not (Fig. 7, dashed green lines). The reason is causality: whether a not-forcing input subsequently becomes a neutral or a perturbing input depends on whether the next randomly drawn input appears before or after the next randomly selected output spike. However, for the simulation we can evaluate post hoc the relative fractions of perturbed and neutral spikes. In the simulation, the fraction of perturbing inputs was overestimated by only 12%, which, given the simplifying assumptions, serves as another indication that the model captures the essential features of the data very well.
In the temporal probabilities of input types (Fig. 6A) we noted a distinct peak in probability of forcing a spike near normalized t = 0.07 of the natural ISI. We hypothesized that this doublet peak would likely account for the slightly elevated probability of short ISIs in our simulations, and might account in part for the rate maintenance in output. To test this hypothesis, we reran our simulations after altering the probabilities of Fig. 6A: first, we artificially removed the doublet peak, by sending the probability of forcing a spike smoothly to zero for smaller elapsed arrival times (Fig. 6A, cyan line). As expected, this had the effect of diminishing the elevated probability of short ISIs in the output stream (Fig. 8C, cyan line). Second, we ran another simulation with temporally flattened response probabilities, where the response probabilities were set to their average over input arrival time (Fig. 6A, magenta). This model produced a larger number of short ISIs than found in the original data (Fig. 8C, magenta). Both altered models produced fewer long ISIs than were present in the original data. These are two simple examples of how such a model can be used to explore contributions of specific response attributes; many others are conceivable.
Removing the doublet peak also diminished or eliminated the rate maintenance and resonance effects. For both the experimental data and the output stream formed by simulating the experimental response properties, strong quasi-regular inputs varying in speed from one-third to three times the unperturbed neuronal rate had a slope of 0.14 (Fig. 8D). However, after smoothing away the doublet peak as above, the slope between input rate and output rate in our simulations was increased by 72%, to 0.24. In contrast, using flattened response probabilities resulted in a small decrease in slope, to 0.12. Moreover, the original streaming simulation matched the resonance feature of the experiments (Fig. 8E; the minimum in 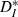 was 0.06 for the simulations), while both altered simulations failed to resonate to a single input speed. Thus, we conclude that the temporal response profiles of cortical cells (Fig. 6A) are finely tuned and shaped by the doublet window and by other contributing intrinsic effects (e.g. ionic and post-spike currents) to preserve the overall rate, while varying timings of individual spikes within a train in response to inputs.
was 0.06 for the simulations), while both altered simulations failed to resonate to a single input speed. Thus, we conclude that the temporal response profiles of cortical cells (Fig. 6A) are finely tuned and shaped by the doublet window and by other contributing intrinsic effects (e.g. ionic and post-spike currents) to preserve the overall rate, while varying timings of individual spikes within a train in response to inputs.
Discussion
To investigate the interplay between intrinsic mechanisms and synaptic input in the formation of a neural spike train, and to address how two neurons each firing quasi-regularly at theta rates might coordinate their firing, we delivered sets of sparsely timed, strong excitatory synaptic conductance inputs to spiking neurons in vitro. We varied the relative rate of the inputs, from roughly one-third to three times the ISI of the unperturbed neurons. We found that although these inputs were strong and elicited spikes on average 51% of the time (or ∼5 mV PSPs when they failed to elicit a spike), the average ISI of the output remained fairly constant, while input varied over orders of magnitude. Simultaneously, neurons resonated only to inputs with matched arrival rate. By classifying spikes into three categories according to their response to the input, we showed that overall neuronal responsiveness varies with input speed, to preserve the mean intrinsic rates in the presence of strong inputs. We also showed, and verified with a minimal model, that response probability is finely tuned within the natural ISI, and showed how this tuning helps the neuron to maintain its rate as it modulates the timings of individual spikes within a train.
The question of what a neural code represents is an open and evolving field of study (Eggermont, 1998; Shadlen & Movshon, 1999; Hong et al., 2008; Wang et al., 2008). Our results suggest the internal pacemaker of a neuron has a dominant effect in the formation of its spike train. Intrinsic conductances within the cell, which shape its response to the average intensity of an input, thus potentially exert considerable influence on spike timing and the neural code it represents (Schreiber et al., 2004b). In this manner, the unique set of ionic conductances, such as Ih, IA, IT, or various forms of after-hyperpolarizing or after-depolarizing currents, within each neuron or class of neurons endow each individual neuron with unique coding properties (Fig. 6); after-hyperpolarizing currents in particular can shape the doublet window we observed. Further, the maintenance of rate (Fig. 3A), simultaneous with resonance to input rate (Fig. 3C), implies that while a neuron works to preserve its output rate, the type and timing of its responses to its inputs is the crucial information-bearing component of the neural code.
As a neuron works to maintain its mean firing rate, we found that it shifts its coding properties: input–output reliability, overall probability of response and response type (forced or perturbed) in time, and the proportions of natural spikes amid the forced spikes (Fig. 5). In particular, even as a neuron maintains spiking at a non-saturated rate, it exhibits short-term fatigue when inputs drive it too often, and becomes less responsive to that input. This shift in spiking response further suggests an input-dependent difference in coding properties (Haas et al., 2006); in this case, even as it responds unreliably to too-fast or too-slow input, a neuron applies different rules (Fig. 6) to when, how and to which inputs it responds. Our results suggest an ability of activated principal cells to differentially pass along information while maintaining their firing rate within a network rhythm, in a form of nested encoding.
We found a period of elevated probability to force a second spike immediately, in the 10–20-ms time window following a spike, and our modeling showed that this doublet peak is a crucial component of rate maintenance. We saw a doublet window both for forced spikes, and for perturbed spikes. Further, perturbed latencies were longest just after a spike (Fig. 6B) – thus, following a spike or a doublet, another spike was highly unlikely. A doublet spike, in combination with the observed refractoriness to spiking following the doublet peak, may serve as a temporal ‘reset button’ for subsequent inputs and spike times. The doublet may arise from after-depolarizations following spikes; subsequent after-hyperpolarization currents following a set of doublet spikes may then be summed or enhanced, preventing a triplet spike, and contributing to rate maintenance by prolonging the next ISI. Removing this effect would correspond to diminished rate maintenance, as seen in our modeling. For neurons spiking around theta frequency, this lends an error tolerance for input arrival times – even if an informationally important input arrived just a bit too late (i.e. after a spike) at a cycle peak, it can still evoke a second spike within a window much smaller than the theta cycle time, while keeping overall spiking within the theta range. This effect also spreads out the expected spiking times and synchrony of neurons spiking in a theta rhythm. Furthermore, a doublet peak is likely to have pronounced effects for a postsynaptic neuron, either by simple summation or by various forms of synaptic plasticity associated with short time intervals.
We observed a resonance in reliability for matched firing rates (Fig. 3C), whereby neurons most reliably pass on the inputs with which they are already most synchronized. In this case, neurons firing at a common rate of theta are more likely to pass on a more faithful representation of each other’s inputs, and more likely to form a coherent group rhythm. These results are complementary to other studies in which neurons responded with resonance to various forms of frequency content of input (Mainen & Sejnowski, 1995; Hunter et al., 1998; Haas & White, 2002; Hunter & Milton, 2003; Schreiber et al., 2004a).
Many studies of network behavior or synchrony employ relatively weak inputs or coupling strengths, in part for simplicity and in part with the assumption that stronger inputs will result in a simple scenario of output simply following or relaying input (Ermentrout & Kleinfeld, 2001). Other studies indicated that stronger inputs exert larger influences on individual spike times (Reyes & Fetz, 1993b). However, our results suggest that this may not be the case over longer timescales of inputs and spikes, whether rate-matched or rate-mismatched. Instead, we find that even for relatively strong synaptic input, a cell that is depolarized or excited to the level of quasi-regular spiking will produce a spike train formed largely according to its intrinsic conductances and dynamics, rather than simply following a strong input, even in the resonant case – our ISI-distance never fell to zero. In the EC, these results imply that the intrinsic pacemakers of individual neurons may be a dominating factor in the regional theta rhythm.
We do not expect this to be uniformly true across the brain; thus, various cell types could be classified by this characteristic, the strength of the internal pacemaker. Indeed, the allegiance of a neuron to either its intrinsic rate or an input rhythm may serve as a novel way to assess rhythmogenesis in different areas of the brain.
Moreover, it is also important to construct models to mimic the neuronal response, as they allow testing and understanding of the role of each ingredient in neural dynamics. We have shown that all of the above response features are reproduced by a simple stochastic Markov-type model, which we constructed by incorporating minimal probabilistic information extracted from the experimental data. Although it is highly desirable to put this heuristic model on a more firm ground by establishing connections with the underlying biophysical processes, the model proved useful for identifying relevant response properties that are involved in the neural spiking activity; its simplicity is one of its merits. Indeed, the model reproduces the observed resonance and simultaneous rate maintenance while using only one set of probabilities, and without taking into account neuronal, input or speed variability. In Fig. 8C, we note that the major inaccuracy of the stochastic model is a shift towards slightly smaller ISIs of the simulations with respect to the experimental data. This can be presumably attributed to the absence, in the model, of any explicit mechanism accounting for the fatigue of the neuron; indeed, our experimental results point towards a longer-term memory effect, of longer natural ISIs following forced spikes. We are confident that incorporating this mechanism into the stochastic model would improve it; however, this would also lead to a more complex and specific model, whereas here we mainly aimed for generality. In particular, we would like to stress once more that our approach based on the construction of a data-driven Markov model can be used to test the responses predicted by first-principle models within a very broad range of applications.
Acknowledgements
The authors wish to thank Daniel Chicharro and Carole Landisman for helpful comments on the manuscript. This work was supported by a grant from The San Diego Foundation to J.S.H. T.K. has been supported by the Marie Curie Individual Outgoing Fellowship ‘STDP’, project no. 040576. A.T. gratefully acknowledges the support received within the CNR short-term mobility program 2006 for his visit to the INLS at UCSD.
Abbreviations
-
- ACSF
-
- artificial cerebrospinal fluid
-
- EC
-
- entorhinal cortex
-
- EPSP
-
- excitatory postsynaptic potential
-
- ICI
-
- interconductance interval
-
- ISI
-
- interspike interval




