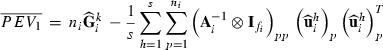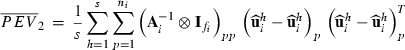Employing a Monte Carlo algorithm in expectation maximization restricted maximum likelihood estimation of the linear mixed model
Summary
Multiple-trait and random regression models have multiplied the number of equations needed for the estimation of variance components. To avoid inversion or decomposition of a large coefficient matrix, we propose estimation of variance components by Monte Carlo expectation maximization restricted maximum likelihood (MC EM REML) for multiple-trait linear mixed models. Implementation is based on full-model sampling for calculating the prediction error variances required for EM REML. Performance of the analytical and the MC EM REML algorithm was compared using a simulated and a field data set. For field data, results from both algorithms corresponded well even with one MC sample within an MC EM REML round. The magnitude of the standard errors of estimated prediction error variances depended on the formula used to calculate them and on the MC sample size within an MC EM REML round. Sampling variation in MC EM REML did not impair the convergence behaviour of the solutions compared with analytical EM REML analysis. A convergence criterion that takes into account the sampling variation was developed to monitor convergence for the MC EM REML algorithm. For the field data set, MC EM REML proved far superior to analytical EM REML both in computing time and in memory need.
Introduction
Use of multiple-trait and random regression test day (TD) models has increased the number of equations needed to estimate breeding values and variance–covariance components (VC) by orders of magnitude compared with simple single-trait analyses. VC estimation using restricted maximum likelihood (REML) algorithms based on analytical calculation of the likelihood may need enormous computing time and huge memory requirement for inversion or decomposition of the mixed model coefficient matrix (Misztal 2008). Therefore, many VC estimation studies have chosen Bayesian approaches where computation can be effectively made via Markov chain Monte Carlo (MCMC) methods even for quite large data sets and models. MCMC methods, however, require careful examination of the MCMC chain, for example sufficient chain length and burn-in period. The implementation and optimization of MCMC methods demand close attention to achieve correct estimates and fast computing time, especially when analysing highly hierarchical and complex models (Misztal 2008).
Wei & Tanner (1990) introduced the Monte Carlo expectation maximization (MC EM) algorithm for cases where maximization for complete data is simple and the expectation can be approximated by Monte Carlo simulations. This has mainly been used within the classical likelihood framework in the analysis of complex models, like nonlinear or generalized linear mixed models, for which expectations cannot be calculated analytically (e.g. McCulloch 1997; Booth & Hobert 1999; Jaffrézic et al. 2006). It can also be utilized in VC estimation of linear mixed models via Gibbs sampling to avoid insurmountable computations in the analysis of large data sets and models by the analytical EM REML algorithm (e.g. Guo & Thompson 1991; Thompson 1994; García-Cortés & Sorensen 2001; Harville 2004). García-Cortés et al. (1992) applied MCEM to the VC estimation in a different way. To estimate prediction error variances (PEV) within each REML round, independent data sets are generated to resemble the original data, and location parameters (fixed and random effect) are then estimated from the simulated data sets. This enables the calculation of PEV without inversion or decomposition of the coefficient matrix and leads to memory requirements equal to solving the mixed model equations (MME). In addition, VC estimation for large models and data sets using MC EM REML is expected to have lower computational requirements than analytical EM REML. The MC sample size needed to obtain PEV and the time required to solve MME are the most critical points with respect to computing time, whereas the time required for generating samples and computing quadratics is negligible. Issues such as MC sample size per iteration, whether to change the MC sample size for later iterations and how to detect convergence have been discussed extensively in the MCEM literature (e.g. McCulloch 1997; Booth & Hobert 1999; Levine & Casella 2001; Ripatti et al. 2002; Levine & Fan 2004; Meza et al. 2009).
The aim of this study is to show the feasibility of the MC EM REML algorithm proposed in García-Cortés et al. (1992) for large data sets and complex linear mixed models. We present the algorithm for a general model and test and compare it with analytical EM REML using simulated and field data. We further study alternative ways to calculate PEV, required MC sample size, convergence characteristics and a new convergence criterion. The efficiency of the algorithm is tested with a multiple-trait random regression TD model applied to Finnish Ayrshire TD data with missing observations.
Material and methods
Model
Consider a data set with observations in q records, a record containing observations on t traits measured at the same time for a given subject. The traits of a particular record form a set of observations with correlated residuals, although observations from some traits can be missing. There can be multiple records on any subject. For example, a dairy cattle TD record of a cow (subject) may comprise observations on daily milk, protein and fat yields (traits) measured at the same date. Further, the cow may have several TD records along lactation.
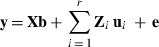
Assume that the random effects ui are normally distributed with mean zero and variance 
. The size of Gi is 
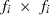, where fi is the number of traits or the number of traits times the order of the regression function of a random effect i, i.e. 
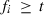. Matrix Ai has size 
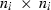representing the covariance structure among subjects in ui, where ni is the number of subjects in the random effect i. For example, when ui is a vector of breeding values in an animal model, then Ai is the numerator relationship matrix and Gi is the matrix of genetic VC.
Furthermore, assume that the residual vector e is normally distributed with mean zero and variance R. Because residuals can have non-zero correlations only between traits in the same record, it is convenient to order the observations in y by traits within records. Then,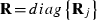 
, j = 1,...,q, where Rj is the sub-matrix of 
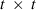-matrix R0 corresponding to the subset of traits observed for record j.
EM REML
where 
is a constant, 
contains the estimated residuals and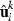 
contains the solutions to the MME with current 
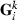and Rk, 
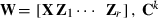is the inverse of the full MME coefficient matrix with the current VC, and 
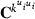is a submatrix of 
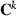corresponding to random effect i. The iteration number k will be omitted hereafter in the right hand side of the equations for clarity of presentation.
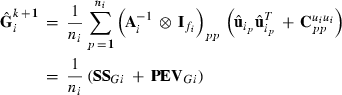(1)
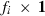subvector and 
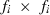submatrix pertaining to subject p, respectively. Part SSGi in equation (1) consists of the sum of squares of solutions 
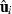, whereas part PEVGi is comprised of the PEV of random effects ui. Estimation of residual VC is less straightforward than estimation of VC for random effects if missing traits occur. With t traits, there are up to 2t-1 possible combinations of missing traits, and the records can be divided into classes according to these missing data patterns. Then, obtaining VC at iteration round k + 1 requires, for each missing data pattern c, computing
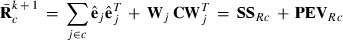(2)
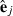is a subvector of estimated residuals for record j using VC from round k and Wj is a submatrix of W collecting rows pertaining to record j. Similar to random effects, part SSRc in equation (2) relates to the sum of squares of estimated residuals 
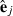, whereas part PEVRc contains the PEV of the residuals. Without missing observations, there is only one class and 
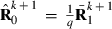where q is the number of records. Calculation of 
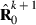for missing trait patterns is presented in Appendix 1.MC EM REML
The sums of squares SSGi and SSRc in equations (1) and (2) are easy to calculate, whereas PEVGi and PEVRc require inversion of a coefficient matrix which may be large. The idea in García-Cortés et al. (1992) is to estimate the elements of inverse coefficient matrix C by generating samples from the same distribution as the original data and then solving the MME using the sampled data as observations. By generating the samples, we know the true random effect and residual values, and we can calculate the mean of prediction error variances over the samples. After setting the starting values (k = 0), each EM iteration round consists of a data generating step, summing of quadratics and computing of new VC estimates as explained below.
Data generation involves simulating s replicates of the observation vector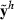 
, h = 1,…,s. First, draw a random sample 
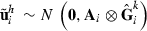for each random effect i = 1,…,r. Then, loop through the data by records. For each record j = 1,…,q, draw a sample 
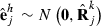and calculate 
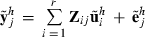. Fixed effects can be set to zero (b = 0), because 
and 
are not affected by them.
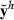are attained by a suitable MME solver. Define the real data as a replicate h = 0, i.e. 
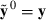. Furthermore, define 
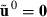and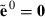 
. Obtain estimates 
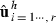from the MME using 
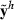as observations, and calculate 
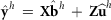for each data replicate h = 0,…,s. The sum of squares for random effect i is then calculated as
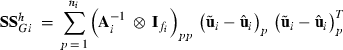(3)
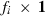subvector and 
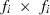the submatrix pertaining to pth level of random effect i, respectively. After calculating the sum of squares for all replicates h = 0,…,s within each REML round k + 1, the new MC approximation for 
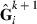in (1) is
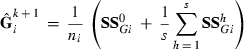
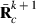in (2) is calculated as
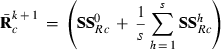
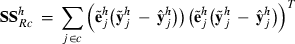(4)Implementation of MC EM REML
MC sample size
The stochastic nature of the MC EM REML algorithm leads to sampling variation. Increasing the MC sample size (s) will improve the accuracy of the calculated PEV within an MC EM REML round, but at the cost of increased computing time. To minimize the computing time, an extreme alternative would be to use only one sample within an MC EM REML round (Celeux & Diebolt 198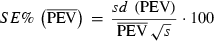5).
(5)The mean of the SE% over the last 10% of MC EM REML rounds was studied for different s (5, 10, 20, 50, 100, 500 and 1000) to illustrate the approximate level of error in the calculation of PEV. We further examined the s required to achieve an SE% of <0.1, 0.5 and 1.0.
Calculation of PEV
The method used for the calculation of PEV has an effect on sampling variance. The efficiency of the PEV calculation method depends on the relative size of PEV with respect to VC, especially when s is small (Hickey et al. 2009). Methods 1 and 2 presented in García-Cortés et al. (1995) are practical for multiple-trait analysis because they avoid possible divisions by zero covariances (see Appendix 2). Although pooling of the methods 1 and 2, named method 3, in García-Cortés et al. (1995) proved to be one of the most appropriate for single-trait analysis also in the study by Hickey et al. (2009), the estimate is more complicated for multiple-trait or random regression models. The weights for method 3 could be calculated elementwise (Appendix 2), but there is no guarantee that the estimated VC matrix will be positive-definite. Furthermore, calculation of the empirical variance of the PEV estimate within a REML round is questionable when s is small and impossible when s is equal to one.
To illustrate the effect of the choice of method 1 or 2 on sampling variation, examples are given about the approximate level of error in the calculation of PEV using equation (5).
Assessment of convergence
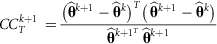
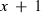rounds of estimates, that is, estimates from the rounds (k + 1–x) to (k + 1). Define 
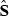(x + 1) as a vector of predictions of VC estimates θ for the REML round k + 1 and 
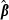as a vector of linear regression coefficients. These were used to form a new convergence criterion where the change in consecutive VC estimates was replaced by the change in linear predictions:
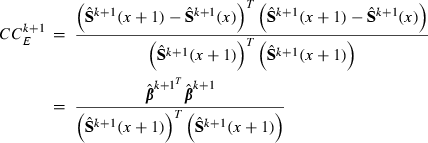((6)The larger the x, the smaller the effect of MC noise on the convergence criterion. However, if poor starting values are used, estimates at the early rounds of analysis may increase the bias of the linear predictor at the latest REML rounds. To reduce the effect of MC noise and to take into account possible poor starting values, we used the latest half of the REML rounds, that is,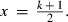 
Computation
An efficient scheme for solving the MME is vitally important for the presented MC EM REML algorithm because it requires solutions for the location parameters from the data and from s samples in each MC EM REML round. We used preconditioned conjugate gradient (PCG) iteration with a block diagonal preconditioner matrix approximating the MME (Strandén & Lidauer 1999). The MC EM REML algorithm was implemented into the MiX99 software (Lidauer et al. 2011). To obtain solutions within short computing times with large data sets and complex models, the preconditioner matrix has to be periodically updated owing to changes in the MME via VC estimates. This is especially important when poor starting values are used. Hence, we updated the preconditioner matrix every 10th REML round during the first 100 rounds and every 100th round thereafter.
Examples
Two data sets were used to illustrate the MC EM REML algorithm. The data sets were analysed with a different maximum number of REML rounds and different MC sample sizes to study the performance of the algorithm. Random effects other than the residual were assumed to have high PEV with respect to VC and method 1 in García-Cortés et al. (1995) was used to calculate the PEV estimate for them. For the residual variance, a relatively low PEV was presumed, and therefore method 2 was used to calculate the PEV estimates. Identity matrices were used as initial values for VC matrices in all analyses, although better starting values may be needed in practice. For comparison, analytical EM REML estimates were obtained by DMU (Madsen & Jensen 2000).
Simulated data
Records resembling 305-day milk and fat yields were simulated for 3000 animals assigned to 100 herds. Thus, there were 30 animals per herd on average, with a minimum of 13 animals and a maximum of 46 animals in a herd. The base generation comprised 150 unrelated sires without observation records. Each base generation sire had 20 daughters, whose dams were assumed to be unknown and unrelated.
| Parameter | Simulation value | Analytical EM REML | MC EM REML | ||
|---|---|---|---|---|---|
| 20 | 100 | 1000 | |||
 |
500 000 | 605 923 | 614 715 | 611 875 | 606 540 |
 |
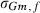14 000 | 18 393 | 18 675 | 18 524 | 18 408 |
 |
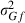800 | 916 | 922 | 917 | 916 |
 |
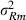750 000 | 681 799 | 676 628 | 677 600 | 681 594 |
 |
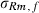29 000 | 25 597 | 25 395 | 25 493 | 25 596 |
 |
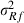1400 | 1294 | 1289 | 1291 | 1294 |
For the analytical EM REML, the convergence criterion value was defined at 10−9 for relative change in VC estimates of consecutive rounds (ccT). The MC EM REML runs were terminated when they had completed the number of REML rounds required by the analytical algorithm. We studied three alternatives for MC sample size within an MC EM REML round: 1000, 100 and 20.
Field data
The computing efficiency of the MC EM REML algorithm was tested with dairy cattle data. A subset from a large data set was taken to enable calculation of analytical EM REML estimates. The milk, protein and fat test day (TD) data comprised 5399 animals with records and 10822 animals in the pedigree. There were 51004 TD records for milk, approximately half of which were associated with observations for protein and fat.
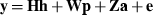
where h is a vector of fixed herd and TD interaction and lactation curve regression effects, p is a vector of non-genetic animal random regression effects, a is a vector of genetic animal random regression effects, and e is a vector of random residuals. The fixed lactation curves were modelled with third-order Legendre polynomials (intercept, slope, quadratic and cubic terms) plus an exponential term (e−0.04*days in milk), and W and Z had the appropriate coefficients for second-order Legendre polynomials (intercept, slope and quadratic terms). Variances for random effects were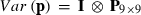 
, 
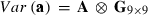and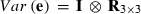 
. The total number of estimated variance parameters was 96.
The analytical and MC EM REML algorithms were iterated 1000 rounds. We studied three alternatives for MC sample size within an MC EM REML round: 20, 5 and 1.
Results
Simulated data
VC estimates by the analytical and the MC EM REML method converged similarly, considering the sampling variance. Figure 1 illustrates the genetic covariance between milk and fat by EM REML round, estimated by both algorithms. In general, the MC EM REML estimates followed well those obtained by analytical EM REML. During iteration, the more the variation around the analytical EM REML estimates, the lower the MC sample size within an MC EM REML round. Estimates from the last EM REML round are shown in Table 1. Despite differences in the parameter estimates, the heritability estimates for milk and fat were 0.47 and 0.41, respectively, in all analyses.
Estimates of the genetic covariance component between milk and fat for simulated data in the REML rounds 50–304 by analytical EM (aEM) and MC EM with 1000, 100 and 20 MC samples (MCEM1000, MCEM100 and MCEM20, respectively).
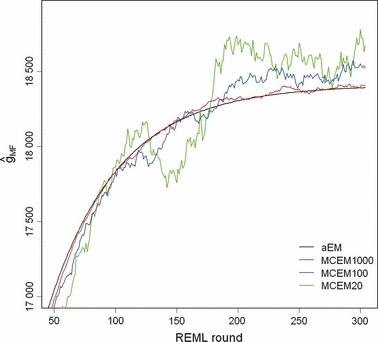
Solving VC by the analytical EM REML algorithm required 304 iterations to reach the convergence criterion value of ccT = 10−9, which took less than half a minute. In contrast, the CPU times needed for 304 EM REML iterations with the MC EM REML algorithm were 278, 28 and 6 min with 1000, 100 and 20 MC samples, respectively. Figure 2 illustrates the behaviour of the convergence criteria for the analytical and MC EM REML algorithms. As seen for the analytical EM REML estimates, values based on the convergence criterion in (6) stayed above those of the traditional criterion. The values of the convergence criterion for MC EM REML with 1000 MC samples followed the corresponding values for analytical EM REML. Decreasing the number of MC samples within MC EM REML rounds increased the fluctuation in the convergence criterion.
Convergence criteria for the analysis of the simulated data by analytical EM REML (aEM_T based on relative round-to-round changes and aEM_E based on relative deviations of regression coefficients from zero) and MC EM REML with 1000, 100 and 20 MC samples (MCEM1000, MCEM100 and MCEM20, respectively, based on relative deviations of regression coefficients from zero).
Field data
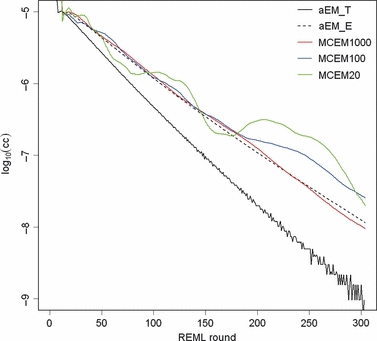
Estimates from the field data analysis converged similarly by analytical and MC EM REML. Figure 3 illustrates the convergence of the covariance estimate between the genetic intercept terms of milk and fat yield by both methods with different MC sample sizes. When 20 samples were generated within an MC EM REML round, estimates followed closely those from the analytical EM REML analysis. Estimates using only one sample within an MC EM REML round were associated with a larger MC error, although this did not hamper convergence, giving estimates that followed those from the analytical EM REML analysis.
Estimates of the genetic covariance component between the intercept terms of milk and fat for field data in REML rounds 200–1000 by analytical EM REML (aEM) and MC EM REML with 20, 5 and 1 MC samples (MCEM20, MCEM5 and MCEM1, respectively).
With only one MC sample within an MC EM REML round, the means of relative differences between VC estimates by the analytical and MC EM REML algorithms at the final iteration were 2.8%, 6.7% and 0.3% for permanent environment, genetic and residual (co)variances, respectively. Similarly, the mean differences with five MC samples were 2.8%, 3.9% and 0.1%, respectively, and with 20 MC samples 0.8%, 1.5% and 0.1%, respectively, within an EM REML round. In general, the smallest relative differences were found for residual (co)variance parameter estimates and the largest differences for genetic (co)variance parameter estimates. Relative differences decreased when the MC sample size increased.
305-day based VC estimates were derived from the estimated random regression variance components to combine the information over the time span into one value. Table 2 shows the 305-day VC estimates from analytical EM REML analysis and the differences between VC estimates from the analytical and MC EM REML analyses. Despite the differences in the estimates on the VC of random regression model, the algorithms arrived at the same composite 305-day VC estimates. Even with just one MC sample within an MC EM REML round, the results were very similar.
| Parameter | MC EM REML | Analytical EM REML | ||
|---|---|---|---|---|
| 1 | 5 | 20 | ||
 |
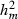0.004 | 0.001 | 0.000 | 0.339 |
 |
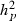−0.001 | 0.001 | 0.000 | 0.261 |
 |
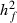0.000 | 0.002 | 0.001 | 0.263 |
 |
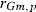−0.001 | 0.000 | 0.000 | 0.876 |
 |
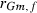−0.004 | 0.002 | 0.000 | 0.678 |
 |
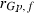−0.003 | 0.001 | 0.001 | 0.774 |
 |
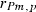−0.001 | 0.000 | 0.000 | 0.938 |
 |
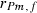−0.004 | 0.000 | 0.000 | 0.814 |
 |
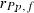−0.003 | 0.000 | 0.000 | 0.847 |
Calculation of 1000 EM REML rounds using the analytical EM REML algorithm took 56 days. The MC EM REML algorithm required 65, 20 or 7 h with 20, 5 or 1 MC samples per MC EM REML round, respectively. The large differences in computing times for 1000 EM REML rounds are attributable to computation of the inverse of the coefficient matrix of size 160,221 that was required in analytical EM REML analysis.
The convergence criterion for MC EM REML followed well that for analytical EM REML (Figure 4) and was smooth when 20 MC samples were used in each MC EM REML round. However, with only one MC sample within an MC EM REML round, the MC noise was not entirely removed from the convergence criterion. The analytical EM REML algorithm reached a convergence criterion value of ccT = 10−9 after 565 iterations. At round 565, the convergence criterion for the MC EM REML algorithm with five MC samples per MC EM REML round was ccE = 4.6 10−9. At this convergence, heritability and both the genetic and phenotypic correlations were equal to the solutions reported at round 1000 of analytical and MC EM REML. The computing time for 565 iterations would have been approximately 31 days by the analytical EM REML algorithm and 12 h by the MC EM REML algorithm with five MC samples.
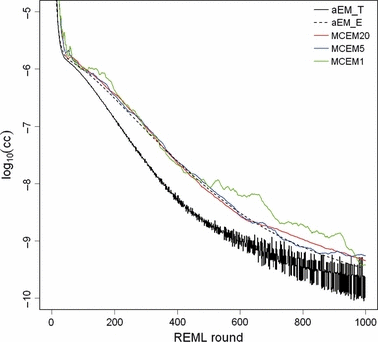
Convergence criteria for the analysis of a Finnish Ayrshire first lactation data set by analytical EM REML (aEM_T based on relative round-to-round changes and aEM_E based on relative deviations of regression coefficients from zero) and MC EM REML with 20, 5 and 1 MC samples (MCEM20, MCEM5 and MCEM1, respectively, based on relative deviations of regression coefficients from zero).
MC sample size
The relative standard error of PEV (SE%) defined in equation (5) was estimated for genetic covariance between milk and fat with simulated data and for genetic covariance between the intercept terms of milk and fat with field data. In all cases, the SE% decreased when MC sample size s increased (Table 3), and both in simulated and field data, SE% was smaller when method 1 was used for PEV calculation of genetic random effects rather than method 2 (of García-Cortés et al. (1995)). The field data also had a smaller SE% than simulated data with the same s, although it should be noted that these are for different models and the field data had more records. The MC EM REML algorithm with five samples within each round showed very variable results for the small simulated data set, whereas relatively steady results were obtained for the larger data set.
| Number of MC samples | Simulated data | Field data | ||
|---|---|---|---|---|
| SE%(PEV1) | SE%(PEV2) | SE%(PEV1) | SE%(PEV2) | |
| 5 | 0.61 | 1.33 | 0.15 | 0.73 |
| 10 | 0.53 | 0.85 | 0.11 | 0.50 |
| 20 | 0.38 | 0.65 | 0.08 | 0.35 |
| 50 | 0.24 | 0.40 | – | – |
| 100 | 0.17 | 0.29 | – | – |
| 500 | 0.08 | 0.13 | – | – |
| 1000 | 0.05 | 0.09 | – | |
Equation (5) was used to derive the s needed to reach a relative standard error of less than 0.1% in the calculation of PEV. Based on the last 10% of MC EM REML rounds, a genetic covariance between milk and fat in the simulated data example would require on average (standard deviation) 216 (171), 285 (107), 295 (98), 282 (66), 287 (46), 292 (21) and 292 (12) MC samples based on analyses with 5, 10, 20, 50, 100, 500 and 1000 MC samples in each MC EM REML round, respectively. Similarly, in the field data, to reach 0.1% error level for the genetic covariance between the intercept terms of milk and fat yield would require on average (standard deviation) 13 (8), 14 (6) and 14 (4) MC samples based on 5, 10 and 20 MC samples per MC EM REML round.
The ranges of values of s required to achieve a specified level of accuracy of PEV for all VC in both analyses are given in Table 4. For simulated data, analyses with 1000 MC samples, and for field data, analyses with 20 MC samples were used. Based on the last 10% of MC EM REML rounds, on average 939 (38 and 10) MC samples per MC EM REML round would be needed for the simulated data analyses to achieve a relative standard error of less than 0.1% (0.5% and 1.0%) in the calculation of PEV for all parameters. In the case of field data, problems occurred owing to the small VC estimates obtained by the random regression model. Division by near-zero values of PEV gave estimates of s to be millions for some parameters. However, the distributions of the estimated s within an MC EM REML round were strongly positively skewed. The estimate of s decreased remarkably when it was based on the variance components only, although distribution of s within an MC EM REML round was still positively skewed (Table 4).
| Relative standard error (%) | Simulated data | Field data | |||||
|---|---|---|---|---|---|---|---|
| Min | Med | Max | Min | Med | Max | ||
| All | 0.1 | 197 | 532 | 939 | 3 | 510 | a |
| 0.5 | 8 | 21 | 38 | 1 | 20 | a | |
| 1.0 | 2 | 5 | 10 | 1 | 5 | a | |
| Var | 0.1 | 197 | 532 | 768 | 3 | 150 | 1669 |
| 0.5 | 8 | 21 | 31 | 1 | 6 | 67 | |
| 1.0 | 2 | 5 | 8 | 1 | 2 | 17 | |
- aValues were estimated to be larger than 10 000.
Discussion
The VC estimates from analysis of the simulated and field data sets by analytical EM REML and MC EM REML converged similarly and to the same solutions, as was expected. The MC sample size required for estimates with an acceptably low MC error depended on the method for calculating PEV and on the size of the problem. The MC EM REML algorithm gave reliable estimates for field data with five MC samples per round and reasonable results with just one MC sample within a round. Thus, the solving times for the MC EM REML analysis were favourable compared with analytical EM REML for the large field data. Decisions regarding the choice of the stopping rule and MC sample size are crucial in analyses by the MC EM REML algorithm, and an automated procedure would help to avoid postprocessing of the chain of estimates.
We introduced a stopping rule that can be calculated during the analysis. This alternative convergence criterion for MC EM REML was based on relative differences in the linear regression coefficients from zero. Although linear regression is easy to implement, the choice needs to be made on how many EM REML rounds to use for the prediction of the linear regression coefficients. The more rounds we used, the less the convergence criterion was affected by the MC noise. It also worked reasonably well with low MC sample sizes – a property that may be useful for analysing complex models with many VC to be estimated. The EM REML round at which the commonly used convergence criterion reached a value of 10−9, the alternative criterion gave values of 1.2 × 10−8 and 4.2 × 10−9 for analytical EM REML estimates with simulated and field data, respectively. Hence, the size of the data and type of the model fitted influence the critical value of the convergence criterion. Applying the same value (10−9) for MC EM REML as for analytical EM REML analysis will ensure convergence. While this may unnecessarily increase the number of MC EM REML rounds, it will protect against uncertainty from sampling variation.
The automated procedure for choice of MC sample size during the analysis can be based on the relative standard error of the PEV estimates. It is sufficient to specify the largest acceptable standard error in PEV estimation, because that also gives an upper limit of the MC noise in estimates of the variance components. The limit depends on the accuracy required. A limit of 0.5% may be sufficient for genetic studies, because in our results the heritabilities and genetic correlations were estimated more accurately than individual VC. However, the SE% of the PEV may suggest unnecessarily high MC sample sizes when a low error is desired for near-zero PEV. Results from this study would suggest that using the median instead of the maximum value is preferable. This issue requires further investigation, as all VC are correlated and affect each other during analysis.
From a computational point of view, the most efficient alternative would be to use only one MC sample in MC EM REML round at the beginning of the iteration process and then increase the MC sample size towards convergence. Booth & Hobert (1999) suggested increasing the MC sample size by half, if the solutions from the previous round fall within the confidence interval, which is calculated by an approximated sandwich estimator based on the central limit theorem for independent samples. Furthermore, Levine & Fan (2004) defined the confidence interval for dependent samples and went on to define a method for MC sample size estimation. However, the calculation of confidence intervals requires computationally demanding estimates of variance. Ripatti et al. (2002) suggested a simpler criterion for indicating the need to increase MC sample size, based on the coefficient of variation for maximum relative difference in parameter estimates calculated over the last three rounds. This criterion is applicable also when only one MC sample is generated within an MC EM REML round, whereas the SE% criterion, which is based on variation between samples within a round, is infeasible when there is only one MC sample per round.
Recommendations for increasing the MC sample size presented in the MC EM literature tend to propose numbers that are too high for our purposes in the context of large data sets and many VC. Delyon et al. (1999) used a stochastic approximation EM (SAEM) algorithm where approximation in the E-step was made by weighting the estimated Q-function of the previous and the current EM REML round with a decreasing weight on the current round. Although this eliminates the need of increasing the MC sample size as the simulations from previous iterations are ‘recycled’, the choice of the smoothing parameter is crucial. The commonly used recommendation (e.g. Jaffrézic et al. 2006) results in a fast reduction in the MC error, but also in a slow convergence rate. The estimates therefore need to be close to the true values when the SAEM algorithm is started – a situation that may not necessarily be viable with only one MC sample within an MC EM REML round. Alternatively, the required MC sample size could be approximated by the SE% of the estimated PEV. After convergence is achieved using the approximated MC sample size, the SAEM algorithm is applied to eliminate the MC noise. Despite the additional MC EM REML rounds needed for SAEM, this combined algorithm is expected to be faster than the analytical EM REML algorithm when large data sets and complex models are analysed.
Analysis of the field data demonstrated the potential of MC EM REML for large and complex models. VC estimates were obtained with relatively fast computing times compared with analytical EM REML and also with low memory requirements corresponding to those for breeding value estimation. However, the convergence rate of the MC EM REML algorithm, like that of the EM algorithm in general, is very slow. Improvements for the unfavourable properties of EM REML, such as slow convergence and poor stability with complex models, have been offered, for example, by the AI REML (Gilmour et al. 1995) and PX-EM (Foulley & van Dyk 2000) algorithms. Also, second-order algorithms have been proposed with the sampling scheme, for example Fisher’s method of scoring via simulation in Klassen & Smith (1990) and approximation of observed Fisher’s information in Wei & Tanner (1990).
Conclusions
In this study, we implemented the MC EM REML algorithm for complex multivariate linear mixed models with missing traits. MC EM REML converged to the same solutions as analytical EM REML, and a small MC sample size did not introduce bias to the estimates of genetic parameters. The applied convergence criterion monitored the progress of convergence and was little influenced by MC noise. Nevertheless, the method for PEV calculation in the case of multivariate models needs to be developed to diminish the amount of MC noise. Finally, MC EM REML was found superior to analytical EM REML in analysis of large data, but studies on accelerating the convergence are recommended.
Acknowledgements
The authors thank Faba co-op, Hollola, Finland, and the Nordic Cattle Genetic Evaluation NAV, Aarhus, Denmark, for providing the field data for this study. The authors are grateful to anonymous reviewers for their suggestions and help.
Appendices
Appendix 1
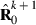at iteration k + 1 of the EM REML algorithm can be made by an iterative method. According to equation (12) in Mäntysaari & Van Vleck’s (1989) study, for each residual (co)variance matrix element (m,o), m = 1,…,t and o = 1,…,t, the following equality has to be fulfilled:
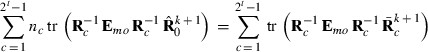
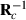is the inverse of round k residual (co)variance matrix for missing pattern class c with zero rows and columns added to missing data traits, and 
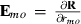, that is, Emo has ones in positions (m,o) and (o,m) but zero elsewhere. The estimate for 
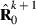can be calculated by repeatedly solving the equation
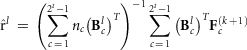
where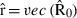 
, the row of 
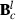pertaining to element (m,o) in 
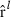is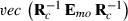 
, 
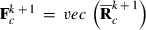, and vec() is the vectorized form of a matrix. At first round 
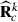, can be used to form 
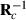needed in calculation of 
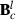. Later on, 
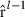can be used to form new 
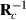and in that way new 
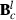. Finally, at the convergence,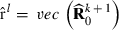 
Appendix 2
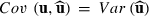. Then, 
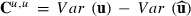and the PEV estimator for random effect i can be written as
