Evaluation of a multi-line broiler chicken population using a single-step genomic evaluation procedure
Summary
Effects on prediction of analysing a multi-line chicken population as one line were evaluated. Body weight records were provided by Cobb-Vantress for two lines of broiler chickens. Phenotypic records for 183 695 and 164 149 broilers and genotypic records for 3195 and 3001 broilers were available for each line. Lines were combined to create a multi-line population and analysed using a single-step procedure combining the additive relationship matrix and the genomic relationship matrix (G). G was scaled using allele frequencies from each line, the multi-line population, or 0.5. When allele frequencies were calculated from each line, distributions of diagonal elements were bimodal. When allele frequencies were calculated from the multi-line population, the distribution of diagonal elements had one peak. When allele frequency 0.5 was used, the distribution was bimodal. Genomic estimated breeding values (GEBVs) were predicted using each allele frequency. GEBVs differed with allele frequency but had ≥0.99 correlations with GEBVs predicted with correct allele frequencies. Means of each line and differences in mean between the lines differed based on allele frequencies. Assumed allele frequencies have little impact on ranking within line but larger impact on ranking across lines. G may be used to evaluate multiple populations simultaneously but must be adjusted to obtain properly scaled estimates when population structure is unknown.
Introduction
Genomic selection in dairy cattle generally follows the multi-step procedures by VanRaden (2008). Traditional pedigree-based genetic evaluation is combined with genotypic information of a subset of animals. Typically, a traditional best linear unbiased prediction (BLUP) evaluation is completed; pseudo observations such as daughter yield deviations (DYD) or deregressed evaluations are obtained for each sire (Guillaume et al. 2008). Next, genomic effects for each genotyped animal are estimated and can be combined with traditional parent averages and estimated breeding values (EBV). Increases in reliability using this method can be large (VanRaden et al. 2009). Inclusion of parent average is important for increasing the accuracy of predictions (Vazquez et al. 2010). The success of genomic selection in dairy with such an implementation is because of a large number of high-accuracy bulls.
An alternate strategy is to only use phenotypes of genotyped animals directly for the genomic prediction step (Dekkers et al. 2009). The increased accuracy using genomic information could compensate for reduction in the number of phenotypes. Latest results, however, indicate that maintaining a large population size that maximizes phenotypic observations, while also using genomic information, is superior to only using genotyped animals and pedigree-only methods (Chen et al. 2011a; Wolc et al. 2011). The number of phenotypes necessary for a given accuracy increases drastically as heritability becomes lower (Hayes et al. 2009b), which was evidenced in the study by Chen et al. (2011a).
One way to retain all phenotypes while simplifying the computing procedure is to use BLUP with a relationship matrix that combines the genomic and pedigree relationships (Legarra et al. 2009; Misztal et al. 2009). This procedure can be called single-step genomic BLUP (ssGBLUP) because only one evaluation combining information from genotyped and phenotyped as well as phenotyped-only animals is needed. The inverse of the combined relationship matrix is simple (Aguilar et al. 2010; Christensen & Lund 2010), and ssGBLUP is easy to apply without modelling restrictions. The ssGBLUP method was successfully applied in dairy (Aguilar et al. 2010), in pigs (Forni et al. 2010) and in chicken (Chen et al. 2011a).
An important issue in the implementation of ssGBLUP is the construction and scale of the genomic relationship matrix (G). Allele frequencies are used to construct G and can be assumed to have a constant value at all loci (such as 0.5) or can be estimated based on the allele frequencies in the population of interest (VanRaden et al. 2008; Aguilar et al. 2010; Forni et al. 2010) In US Holsteins, the highest accuracy EBVs were obtained using G assuming equal gene frequencies (Aguilar et al. 2010) despite the theory favouring the base population frequencies (Gengler et al. 2007). Simianer reported that genomic predictions in dairy obtained with different G matrices are nearly identical (personal communication, 2010). Forni et al. (2010) used several G matrices with ssGBLUP for litter size in pigs. The estimates of variance components were unbiased only when elements of G were scaled to be similar to pedigree relationships; however, EBVs obtained with different G were highly correlated. In a study by Chen et al. (2011b), EBVs of genotyped animals could be biased upward or downward depending on assumed allele frequencies. The bias was eliminated by scaling G to be compatible with pedigree-based relationship matrix A. Vitezica et al. (2011) compared two-step genomic evaluation using DYD and ssGBLUP with simulated data under light and strong selection and with genotyping for 10 generations. With G constructed using the base allele frequencies, the accuracy with ssGBLUP was 0.06 higher under light selection but 0.05 lower under strong selection. After calibration of G, ssGBLUP was always more accurate, by 0.07 and 0.08, respectively. Thus, the scaling of G seems important with limited phenotypic information and strong selection, but less important or unimportant otherwise.
Simeone et al. (2011) examined distributions of diagonal elements of G of one chicken line described as in Chen et al. (2011a). After scaling G, most of the diagonal elements were centred around 1.0; however, a small fraction was centred around 2.0. That fraction corresponded to genotypes from a different line that was included unintentionally. In simulation, the distribution of the diagonal elements of G was narrow unimodal with a single breed, bimodal with two breeds of unequal size, and broad unimodal with breeds of equal size. Thus, such a distribution is useful in identifying animals from different lines, but not in every instance.
Many populations contain multiple lines or even multiple breeds, e.g. in beef (Legarra et al. 2007). In genetic evaluations using BLUP, using a single relationship matrix for all animals seems to be a satisfactory solution to analysing multi-breed populations (Lutaaya et al. 2002; Sanchez et al. 2008). A special way to model different subpopulations in BLUP is by unknown parent groups (Quaas 1988). However, in ssGBLUP, the issue is complicated because of the scaling of G; different breeds or lines are likely to have alleles segregating at different frequencies. When the breed composition is known, G may be scaled as proposed by Harris & Johnson (2010). However, such composition may not be known or could be inaccurate. In populations where breed composition is unknown and subsets of multiple breeds may exist, it is unclear how EBVs will be affected using different allele frequency calculations.
The general purpose of this paper is to examine whether adjusting the scaling of G for different lines or breeds influences ranking of animals within lines or breeds. The specific purpose was to examine changes of EBVs in analysis of two lines when G was constructed with allele frequencies of either line, the average allele frequencies of both lines, and a constant 0.5.
Materials and methods
Data
Body weight at 6 weeks (100 g) was provided by Cobb-Vantress (Siloam Springs, AR, USA) for two lines of broiler chickens: A and B, each with three generations. Phenotypic records were available for 183 695 and 164 149 broilers for lines A and B, respectively. Subsets of these populations were genotyped and genotypic records were available for 3195 and 3001 broilers for lines A and B, respectively; animals of both sexes were genotyped. Genotyped animals were available for all three generations for each line; the third generation consisted only of genotyped animals. Animals from lines A and B were genotyped for the same 57 636 SNPs, and all SNPs were used in the analysis. Frequencies of the second allele at each locus were calculated for each line and ranged from 0 to 1 at each locus. Second-allele frequencies at each locus between lines A and B were moderately correlated (r = 0.57), indicating that differences in frequencies at loci existed. Of 57 636 SNP, 480 (0.83%) had a second-allele frequency of <0.2 in line A and >0.8 in line B; 468 (0.81%) had a second allele frequency of <0.2 in line B and >0.8 in line A.
The data sets for Lines A and B were concatenated to create a multi-line data set. Descriptions of the phenotypic data for all animals and genotyped animals in lines A and B, and the multi-line population are provided in Table 1. Lines A and B were analysed separately with and without genomic data to establish GEBVs and EBVs using the correct population structure and allele frequencies. G for the multi-line population was scaled using allele frequencies computed from line A or line B, estimated from the multi-line population, or using the constant 0.5. The multi-line population was split into a training data set, consisting of all animals from the first two generations, and a validation data set, consisting of all animals with phenotypes and genotypes from the third generation. Animals in the validation data set included offspring from the training data set. The training data set included 290 632 animals (155 811 from line A and 134 821 from line B), and the validation data set included 1597 animals (798 animals from line A and 799 animals from line B).
| Line | No. of records | Mean (SD) |
|---|---|---|
| A | ||
| All animals | 183 695 | 24.50 (3.22) |
| Genotyped animals2 | 3195 | 25.12 (2.97) |
| B | ||
| All animals | 164 149 | 23.53 (3.17) |
| Genotyped animals | 3001 | 23.39 (2.63) |
| Multi-Line3 | ||
| All animals | 347 844 | 24.04 (3.24) |
| Genotyped animals | 6196 | 24.28 (2.94) |
- 1Phenotypic data for body weight (100 g) at 6 weeks existed for two lines of broiler chickens, A and B, over three generations.
- 2Genotyped animals represent subsets of lines A and B with both phenotypes and genotypes.
- 3Multi-line represents both lines A and B treated as one data set.
Model and analysis
A single-trait model was used for the analysis:
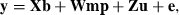
in which y was a vector of BW observations; X, W and Z were the appropriate incidence matrices relating observations to animals; b was a vector of fixed effects for hatch and sex, mp was a vector of random maternal permanent environmental effects, u was a vector of random additive genetic effects that integrated polygenic and genomic breeding values (Aguilar et al. 2010) and e was a vector of residuals. Line was not included in the model in order to analyse the combined data set as if no knowledge of two different lines existed. Variance components for the multi-line population were estimated using REML as 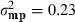 ,
,  , and
, and 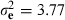 , with h2 = 0.17. These estimates were comparable to those within line estimates from Chen et al. (2011a), with h2 = 0.20and h2 = 0.17, for lines A and B, respectively. Analysis was carried out as in Chen et al. (2011a) and used the combined genomic and pedigree relationship matrix, H.
, with h2 = 0.17. These estimates were comparable to those within line estimates from Chen et al. (2011a), with h2 = 0.20and h2 = 0.17, for lines A and B, respectively. Analysis was carried out as in Chen et al. (2011a) and used the combined genomic and pedigree relationship matrix, H.
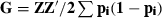 , where Z is equal to M-P, M is a matrix of marker alleles
, where Z is equal to M-P, M is a matrix of marker alleles
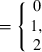
GEBVs were predicted for all animals in the validation data set from the multi-line population using second-allele frequencies from line A, line B, the multi-line population and constant 0.5. GEBVs from the multi-line population analysis were separated into GEBVs for line A and B and were correlated with the GEBVs obtained when line A and line B were analysed alone as well as EBVs obtained with no genomic information.
Results and discussion
To examine how the construction of G changed as a result of differences among the second-allele frequencies, the distributions of the diagonal elements of G were plotted after each analysis (Figure 1). When the second-allele frequencies from either line A or line B were used, two distinct peaks appeared in the distributions. When the second-allele frequency from line A was used, the mean of the diagonal elements for line A animals was 1.00 (0.04) and ranged from 0.56 to 1.40, while the mean of the diagonal elements for line B animals was 2.04 (0.09) and ranged from 1.61 to 2.17. Similarly, when the second-allele frequency from line B was used, the mean of the diagonal elements for line A animals was 2.16 (0.05) and ranged from 1.65 to 2.34, while the mean of the diagonal elements for line B animals was 1.00 (0.04) and ranged from 0.62 to 1.17. When the second-allele frequency calculated from the multi-line population or the constant 0.5 were used, the distribution of the diagonal elements did not behave the same way. Using multi-line second allele frequencies, lines A and B were indistinguishable from each other. Line A animals had a mean diagonal element of 1.14 (0.03) and ranged from 0.72 to 1.42, while line B animals had a mean diagonal element of 1.13 (0.04) and ranged from 0.77 to 1.53. The overall mean of the diagonal distribution using multi-line allele frequencies was 1.15 (0.05). The single peak in the distribution indicates that it may be possible to use multi-line populations by estimating a combined allele frequency. The expected mean of the diagonal elements is 1.0 when the founder population is unrelated; in this population, the founder population included the first generation of genotyped and ungenotyped animals. Use of genotypes detects relationships not present when using pedigree alone, and thus, the larger value of diagonals may better represent animal inbreeding. Using the constant second-allele frequency of 0.5, diagonal elements of lines A and B overlapped but the distribution was bimodal. Line A animals had a mean diagonal element of 1.42 (0.03) and ranged from 0.89 to 1.52, while line B animals had a mean diagonal element of 1.39 (0.03) and ranged from 1.06 to 1.79.
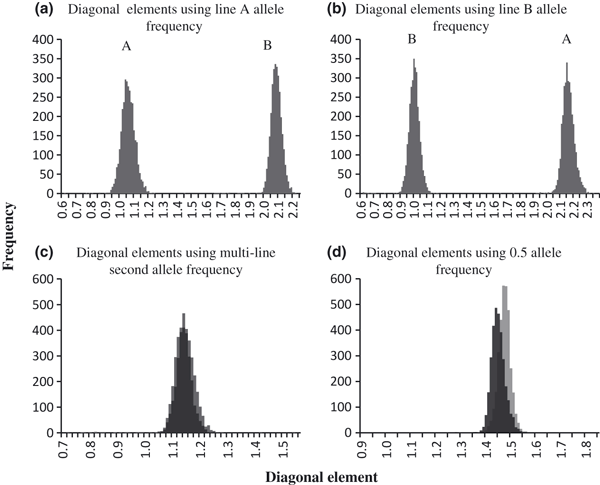
Distributions of the diagonal elements of G constructed with second-allele frequencies from line A (a), line B (b), the multi-line population of A (c) and B, and 0.5 (d). Distributions are shown on different scales.
When the second-allele frequencies of line A were used, the off-diagonals of G ranged from −0.18 to 2.15 and had a mean of 0.25 (0.49). When the second-allele frequencies of line B were used, the off-diagonals of G ranged from −0.16 to 2.29 and had a mean of 0.29 (0.53). When the second-allele frequencies of the multi-line population were used, the off-diagonals of G ranged from −0.36 to 1.21 and had a mean of 0.00 (0.27). When the constant 0.5 was used, the off-diagonals of G ranged from −0.11 to 1.45 and had a mean of 0.5 (0.19). Negative off-diagonal elements represent individuals sharing fewer alleles than would be expected, given the allele frequencies used to scale G (Astle & Balding 2009). Combining lines A and B likely created relationships among animals that did not exist because of SNP markers that were identical by state rather than identical by descent.
After the evaluation of the multi-line population, GEBVs for animals in the validation data set were separated into those for animals from line A or line B and then correlated with GEBVs or EBVs obtained from prior analysis using either line A or line B and the correct second-allele frequency for each (GEBVA and GEBVB, EBVA and EBVB). This was completed for each of the four second-allele frequencies used. Statistics for GEBVs estimated for the validation data set from the multi-line population are presented in Table 2, and correlations between GEBVs and EBVs are provided in Table 3.
| Population | Mean (G)EBV (SD) | Minimum | Maximum |
|---|---|---|---|
| Line A, traditional | −0.14 (0.47) | −1.32 | 1.01 |
| Line A, SSP2 (A) | 0.07 (0.59) | −1.71 | 1.70 |
| Multi (A) | 0.07 (0.60) | −1.75 | 1.76 |
| Multi (B) | −0.12 (0.60) | −1.96 | 1.54 |
| Multi (AB)3 | 0.13 (0.58) | −1.64 | 1.70 |
| Multi (0.5) | −0.18 (0.53) | −1.81 | 1.29 |
| Line B, traditional | −0.28 (0.34) | −1.31 | 0.69 |
| Line B, SSP (B) | 0.00 (0.47) | −1.51 | 1.31 |
| Multi (A) | −0.25 (0.47) | −1.74 | 0.93 |
| Multi (B) | 0.02 (0.49) | −1.54 | 1.25 |
| Multi (AB) | −0.06 (0.47) | −1.49 | 1.11 |
| Multi (0.5) | −0.34 (0.42) | −1.64 | 0.76 |
- 1The combined population consisted of animals from lines A and B. After genomic evaluation, GEBVs obtained for animals in the third generation were separated into those belonging to A or B. Frequencies used to scale G are in parentheses. This frequency was used to scale the genomic relationship matrix.
- 2Single-step procedure.
- 3AB refers to the second-allele frequency calculated from the multi-line population.
| Line A (G)EBVs | ||||||
|---|---|---|---|---|---|---|
| Line A, traditional | Line A, SSP (A) | Multi (A) | Multi (B) | Multi (AB) | Multi (0.5) | |
| Line A, traditional | 1.00 | 0.74 | 0.72 | 0.72 | 0.72 | 0.75 |
| Line A, SSP (A) | 1.00 | 0.97 | 0.97 | 0.97 | 0.97 | |
| Multi (A) | 1.00 | 1.00 | 1.00 | 0.99 | ||
| Multi (B) | 1.00 | 1.00 | 0.99 | |||
| Multi (AB) | 1.00 | 0.99 | ||||
| Multi (0.5) | 1.00 | |||||
| Line B (G)EBVs | ||||||
|---|---|---|---|---|---|---|
| Line B, traditional | Line B, SSP (B) | Multi (A) | Multi (B) | Multi (AB) | Multi (0.5) | |
| Line B, traditional | 1.00 | 0.61 | 0.55 | 0.55 | 0.56 | 0.59 |
| Line B, SSP (B) | 1.00 | 0.96 | 0.96 | 0.96 | 0.96 | |
| Multi (A) | 1.00 | 1.00 | 1.00 | 0.99 | ||
| Multi (B) | 1.00 | 1.00 | 0.99 | |||
| Multi (AB) | 1.00 | 0.99 | ||||
| Multi (0.5) | 1.00 | |||||
- 1Allele frequency used to scale G is in parentheses.
GEBVs and EBVs estimated for the single populations were obtained. EBVs predicted with traditional BLUP evaluation had a mean of −0.14 (0.47) for Line A and −0.28 (0.34) for Line B, while GEBVs predicted using the correct allele frequencies for each line had a mean of 0.07 (0.59) for Line A and 0.00 (0.47) for Line B. GEBVs were slightly larger compared with EBVs when genomic information was included in the evaluation; moreover, the ranges of GEBVs were larger than those of EBVs for both Line A and B. Forni et al. (2010) also found that means of GEBVs change with different G. The mean differences between GEBVs of line A and B varied from −0.52 to 0.07. Thus, ranking across line may change with different G. The closest mean difference to that of BLUP (traditional; −0.42) was obtained by G using 0.5 allele frequencies (0.52). This allele frequency resulted in highest accuracy and minimum bias in the study by Aguilar et al. (2010). Mean GEBVs for Lines A and B varied based on second-allele frequency used. Mean GEBVs for animals in either line were closest or equal to GEBVA or GEBVB when the correct second-allele frequency for Line A or B was used but the ranges of GEBVs changed. Use of second-allele frequencies that did not correspond to a line resulted in decreased estimates of GEBVs compared with GEBVA or GEBVB, but means were similar to those estimated without genomic information. Use of the multi-line second-allele frequency resulted in inflated (Line A) or deflated (Line B) GEBVs compared with GEBVA and GEBVB, respectively. Use of 0.5 second-allele frequency resulted in deflated GEBVs for both Line A and Line B compared with GEBVs and EBVs. While mean values indicate differences in GEBV predictions, the correlations between GEBVs from Line A animals and GEBVA were all 0.97, and correlations between GEBVs from Line B and GEBVB were all 0.96, indicating that despite differences in predictions, animals were ranked appropriately and the combined population could be used if differences in lines were unknown.
Forni et al. (2010) also observed that although the mean and the SD of GEBVs changed with different G, GEBVs were highly correlated. Chen et al. (2011b) found that mean GEBVs of genotyped animals compared with GEBVs of all animals changed with scale of G. Thus, an incorrect scale of G can bias GEBVs of genotyped animals relative to GEBVs of ungenotyped ones. Incorrect G can affect comparisons across generations and between genotyped and ungenotyped animals. In this study, we looked at GEBVs of genotyped animals only and incorrect scaling of GEBVs did not change rankings. Vitezica et al. (2010) observed less accurate GEBVs with incorrectly scaled G but only under strong selection and when genotyping was across 10 generations.
Slight differences were observed between GEBVs from the multi-line population and EBVA and EBVB. Correlations between line A GEBVs and line A EBVs were 0.72 using second-allele frequencies from line A, line B, and the multi-line population, and 0.75 using 0.5. Correlations between line B GEBVs and line B EBVs were 0.55 for line A and line B, 0.56 for the multi-line population and 0.59 for 0.5. These correlations were slightly less than those between correctly estimated single-line GEBVs and EBVs. The values of correlations between GEBVs and EBVs are hard to assess, especially because the correlations among GEBVs were all 0.99 or higher. Therefore, the type of G is not critical when selecting within lines but is critical when ranking across lines as the mean difference of GEBVs would differ based on the scaling of G. The prediction of GEBVs is of primary interest to animal breeders. Inclusion of genomic relationship information allows for more accurate predictions by constructing relationships based on shared alleles instead of expected relationships (VanRaden 2008; Hayes et al. 2009b). Rather than using prediction equations to estimate SNP effects, as in Meuwissen et al. (2001), G utilizes information by more accurately reconstructing family relationships and also can be combined with a pedigree relationship matrix (Aguilar et al. 2010; Christensen & Lund 2010). Use of multiple populations in one evaluation has proven difficult because differences in allele frequencies between breeds should be taken into account (Harris & Johnson 2010). In this case, GEBV estimates were inflated or deflated depending on the second-allele frequency used to scale G. Animals do, however, appear to be ranked the same regardless of the allele frequency used to scale G, though this ranking is different from that using traditional BLUP. This indicates that it may be possible to use combined allele frequencies to analyse multiple populations. It is possible to scale the difference between G and A in the construction of the combined genomic-pedigree relationship matrix in order to reduce differences in GEBVs, and this could prove to be a valuable tool in multi-line evaluations (Vitezica et al., 2011). If the populations are clearly identified, sections of G need to be scaled separately for each populations and possibly crossbreds (Harris & Johnson 2010).
Allele frequencies for the same loci vary from population to population. Harris & Johnson (2010) indicated that diagonal elements of G are distorted when animals of different breeds are analysed together, even if G is constructed by regression methods without using second-allele frequencies. It may be possible to use G as a diagnostic tool to identify population substructure (Simeone et al. 2011); however, this does not occur in the multi-line population because of the large number of shared SNP. Separation of populations will occur only when allele frequencies between populations are very different. If the two populations have similar allele frequencies or similar numbers of animals exist in each, it may be almost impossible to differentiate between the two using diagonal elements if G is scaled using the combined population second-allele frequencies. If some other allele frequency is used in place of the current allele frequency, it may be possible to separate two, equally sized, similar populations. When the constant 0.5 was used to scale G, the distribution of diagonal elements overlapped but showed two distinct peaks, indicating that multiple populations may be detectable but not necessarily separable prior to analysis.
Use of G avoids the problem of population substructure by estimating relationships rather than SNP effects (Hayes & Goddard 2008); with a dense enough marker map it may not be necessary to worry about population structure (Toosi et al. 2010). Alternatively, clustering methods can be used to assign individuals to sub-populations (Pritchard et al. 2000) or principal component analysis can be used to determine significant variation between populations of individuals (Patterson et al. 2006). This analysis indicates that even without taking population structure into consideration, ranking of animals is unchanged within line.
The use of correct allele frequencies, however, is crucial to the construction of G because G is scaled to be analogous to A using allele frequencies (VanRaden 2008). Animals that are homozygous for rare alleles will tend to have a higher genomic inbreeding coefficient than those who are not (VanRaden 2007); moreover, allele frequency estimation has more of an effect on genomic inbreeding than on genomic predictions (VanRaden et al. 2008). Differences in allele frequencies between populations indicate that animals from one population will be homozygous for alleles that a second population is not. Use of incorrect allele frequencies can cause apparent high inbreeding; additionally, increased false relationships among animals that are also incorrectly scaled can inflate or deflate GEBV predictions or cause incorrect ranking of animals in a population.
Conclusions
Evaluation of two populations changed with the allele frequency used to scale the genomic relationship matrix. Using allele frequencies from line A, line B, the multi-line population, or the constant, 0.5, resulted in inflated or deflated genomic breeding values but showed strong correlations with GEBVs or estimated breeding values obtained from single lines. It may be possible to use G to evaluate multiple populations simultaneously by using the average allele frequency of the mixed population or by using different approaches to separate subpopulations and then scaling appropriately. This will be of great value when presented with a data set of unknown population structure.
Acknowledgements
The authors thank Cobb-Vantress for access to data for this study. This study was partially funded by AFRI grants 2009-65205-05665 and 2010-65205-20366 from the USDA NIFA Animal Genome Program. The assistance of Dr Ching-Yi Chen and Dr Shogo Tsuruta for computational and theoretical support is greatly appreciated.




