Use of the uncertain relationship matrix to compute effective population size
Abstract
Summary
The rules for computing the relationship matrix with uncertain parentage can be used to obtain effective population size. Given a population structure, e.g. the number of males and females, generation interval, and a prior probability of parentage, the expected inbreeding coefficient in any generation can be computed using the rules of the tabular method. Increase in inbreeding can then be related to effective population size. Examples are given for monoecious and dioecious species: overlapping and discrete generations, and closed or open populations. This approach allows the retrieval of well-known results in simple cases. A disadvantage is that it is not obvious how to take into account selection.
Résumé
L'utilisation de la matrice de rélations avec incertitude sur les apparentements pour calculer la taille efficace de population
Le présent travail a pour but montrer la rélation entre la matrice de rélations avec incertitude sur les apparentements et la taille efficace de population. Sachant une structure de population donnée, e.g. le nombre des reproducteurs de chaque sexe, l'intervalle de génération et une probabiltié a priori de parenté, on peut calculer le coefficient de consanguinité attendu dans une génération quelquonque. Par conséquent, on peut dériver la taille efficace de la population. On présent plusieurs exemples sur populations monoïques et dioïques, fermées et ouvertes, et générations discretes ou chevauchantes. On montre aussi, dans les cas les plus simples, que cette approche est equivalente a l'utilisation des formules classiques. C'est ne pas évident, par contre, comment prendre en compte l'effect de la sélection.
Resumen
Utilización de la matriz de relaciones aditivas con parentesco incierto para calcular censos efectivos
Mostramos la relación entre las reglas para calcular la matriz de relaciones aditivas en el caso de parentesco incierto y el concepto de censo efectivo. Una de las ventajas del método propuesto es su flexibilidad. Dado una estructura poblacional cualquiera, y conociendo el número de reproductores, el intervalo generacional medio y una probabilidad, a priori, de parentesco, la aplicación de unas mismas reglas nos permite predecir el incremento en consanguinidad y, por tanto, estimar el censo efectivo. La principal desventaja de este método es que no es obvio cómo considerar la existencia de selección.
Zusammenfassung
Verwendung ungewisser Verwandtschaftsmatrix zur Berechnung wirksamer Populationsgrößen
Die Regeln zur Berechnung der Verwandtschaftsmatrix bei ungewisser Abstammung kann zur Schätzung der wirksamen Populationsgröße verwendet werden. Bei einer gegebenen Populationsstruktur, z.B. Zahl männlicher und weiblicher Zuchttiere, Generationsintervall und apriori Wahrscheinlichkeit der Abstammung, kann der erwartete Inzuchtkoeffizient in jeder Generation unter Verwendung der Regeln der Tabellenmethode berechnet werden. Steigerung der Inzucht kann mit der wirksamen Populationsgröße verbunden werden. Beispiele werden für monözische und diözische Spezies gegeben, für überlappende und diskrete Generationen, für geschlossene und offene Populationen. Der Ansatz erlaubt für einfache Verhältnisse die bekannten Resultate zu gewinnen. Als Nachteil muß betrachtet werden, daß sich die Auswirkung der Selektion nicht offensichtlich erkennen läßt.
Introduction
The term ‘uncertain parentage’ is used to refer to the situation in which one or both parents for a number of animals in a population are unknown, but a subset of animals within the pedigree can be identified as potential parents and assigned a probability of being the true parent. Each combination of potential parents for animals with unknown parents can be represented by a different pedigree (Poivey and Elsen 1984). Once information about a given experience is collected, uncertain parentage may be due to errors in recording animal identifications or due to management practices that make it impossible to record precisely the parents of the animals. In this case, uncertain parentage is seen retrospectively. Alternatively, uncertain parentage also occurs when relationship coefficients in the next generations are being predicted. Here uncertainty about the future pedigree is complete, because the actual matings have not been realized yet.
Effective population size is a key parameter in the design of breeding schemes, as it enables the prediction of inbreeding coefficients (for a recent review see Caballero (1994)). Unfortunately, there are no unique formulas for calculating effective population sizes, and these depend on, for example, whether there is a different number of males and females, a constant number of animals, or whether generations overlap. The purpose of this report is to show the connection between uncertain parentage methods and the concept of effective population size.
Theory
Suppose that the ith individual has a number s of males, coded m1, … mj, … ms, as potential sires with probabilities of being the true sire
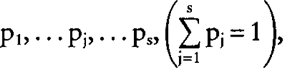
respectively, and a number d of females, f1,… fk, … fd, as potential dams with corresponding probabilities q1, … qk, … qd. Then the (n,i) element of the uncertain numerator relationship matrix (NRM) is:

and the diagonal element is:
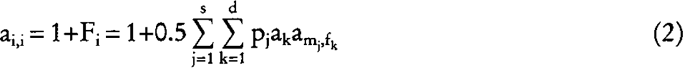
(Pérez-Enciso and Fernando 1992), where Fi is the inbreeding coefficient of ith individual. Equation (1) and (2) reduce to the usual rules to compute the NRM when parentage is known with certainty, i.e. pj = qk = 1 for some mj and fk. The following examples illustrate how formulas (1) and (2) can be used in a wide variety of instances to predict inbreeding coefficients.
Application 1: non-overlapping generations, monoecious diploid population
First consider a monoecious diploid population with discrete generations and N breeding animals per generation. It is assumed that any ith individual of generation t has 1/N probability of being the true sire and 1/N probability of being the true dam of any individual of the next generation (self-mating allowed). Thus it is assumed that uncertainty about parentage is total, and that nothing is known about the identity of the parents of any individual in generation t+1 except that they were born in generation t. Then from equation (1) and (2), it follows:
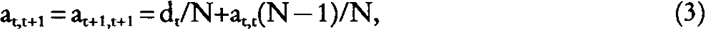
where at,t is the generic element of the NRM matrix between individuals from generations t and t (All off-diagonals elements of the NRM between individuals born in the same generation are identical). The generic diagonal element is:
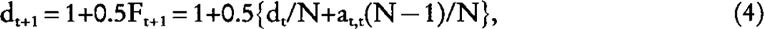
where Ft is the expected inbreeding coefficient of individuals of generation t. From equation (3) and (4), it follows that dt = 1+0.5 at,t, and substituting this in equation (4), we obtain:
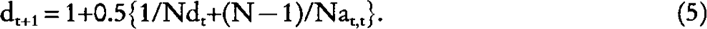
Applying equation (3) and (5) into the well-known formula (e.g. Crow and Kimura 1970)

where Ne is the effective population size, it is found that:
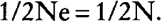
Thus, when self-fertilization is allowed and equiprobability of parentage is assumed, the effective size is equal to the number of breeding individuals as is well known.
Application 2: non-overlapping generations, dioecious population
Let us consider now a dioecious population where any of the Nm males per generation has a probability 1/Nm of being the true sire of any individual in the next generation, and that any of the Nf females has a probability 1/Nf of being the true dam of any individual in the next generation. Using equation (1) and (2):
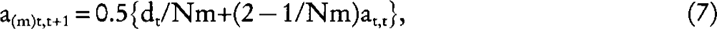
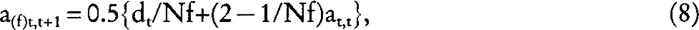
and
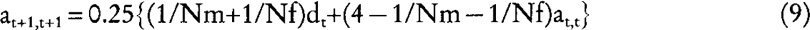
where the subscript m (f) refers to the covariance between male (female) parents and their offspring. Substituting equation (7), (8), and (9) into:
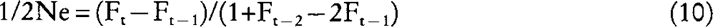
which relates effective size with inbreeding coefficient in dioecious populations (e.g. Crow and Kimura 1970), and having in mind that:
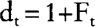
and
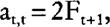
we obtain:

which is the well-known result for unequal numbers of animals of each sex.
Application 3 overlapping generations
Because rules (1) and (2) are general, prediction of inbreeding coefficients will be possible in any situation, provided that a priori probabilities of parentage can be specified. Nonetheless, a known relationship between F and Ne may not exist, such as those in equation (6) and (10). Effective size can be estimated instead from a log regression of (1—F) on generation number, using the formula:

As an example, inbreeding coefficients were predicted for a population with overlapping generations. A nucleus of five sires and 20 dams born each year was considered. (In the following, breeding season and year are used indistinctly). Four cases were considered: a. Sires and dams were kept for one breeding season only (i.e. discrete generations); b. Sires were allowed to mate for three consecutive years, whereas dams were kept for one season; c. Sires mated for one year and dams, for 3 consecutive years; and d. Both sires and dams bred for three seasons. Equiprobability of parentage was assumed again. For instance, in case b, the 15 sires born in the last three years had the same probability of being the true parent, whereas only the 20 dams born in the last year were potential dams. Figure 1 shows the expected increase in inbreeding, together with estimated effective sizes, from equation (12) (in parentheses). Case a is the same as discrete generations. In this case the estimated Ne was 16.5, which was close to the exact figure obtained from (11) (Ne = 16). Effective size increases as animals are allowed to breed in more breeding seasons, because there are more potential parents. Note that the effective size with overlapping generations is approximately equal to Ne with discrete generations times average generation interval, e.g. Ne in case d is 16 × 2 approximately, in agreement with Hill (1979). The small discrepancy can be due to the fact that the estimate of Ne from equation (12), as well as Hill's (1979) results, are exact only asymptotically.
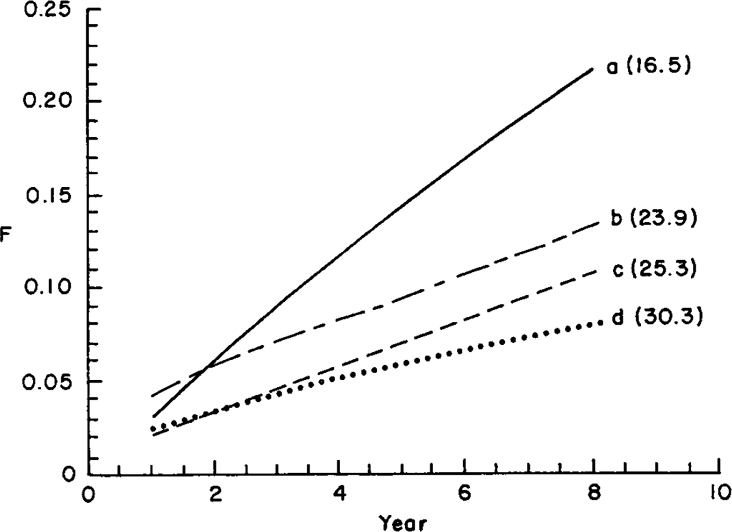
. Expected inbreeding coefficients and estimated effective sizes (in parentheses) for a closed population: a. discrete generations; b. sires were kept for 3 years and dams only 1 year; c. sires were kept for 1 year and dams for 3 years; d. both sires and dams were kept for 3 years
An open population can be conceptualized as one in which all base animals do not enter into breeding at the same time but sequentially. In practice, most real breeding schemes are open. In this case, however, Ne is not well defined because F may even decrease in successive generations. Nonetheless, inbreeding coefficients can always be computed. Consider a nucleus of five sires and 20 dams. Four cases were examined: either zero (case a), one (case b), two (case c), or three (case d) sires out of five were imported each year.
In order to calculate probabilities of parentage, it was assumed that animals born in the nucleus and imported had equal probabilities of leaving offspring and that generations were discrete.
Expected inbreeding coefficients are given in Figure 2. With only one sire of foreign origin, opening the population was a very effective way of controlling increase in inbreeding. In this example, importing two sires per season (case c) caused inbreeding to remain below 2%.
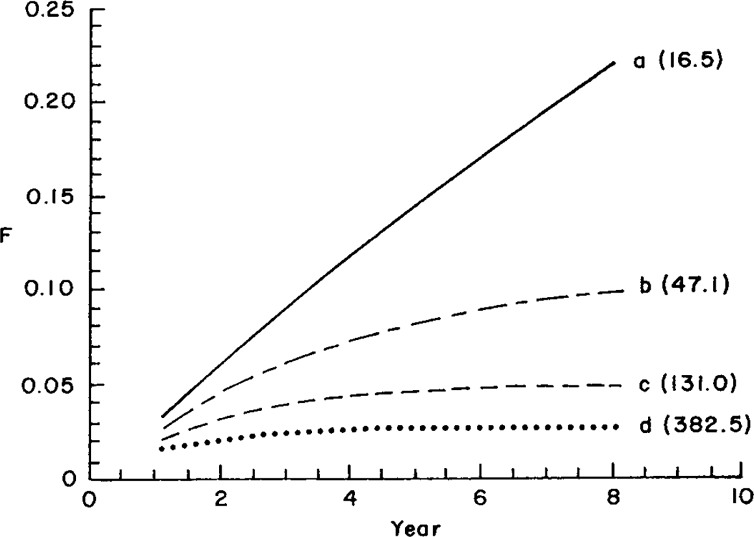
. Expected inbreeding coefficients and estimated effective sizes (in parentheses) for a population with discrete generations: a. no males imported (closed population); b. one sire imported per year; c. two sires imported per year; d. three sires imported per year
The interaction between generation interval and number of males imported was studied further, in a nucleus of 100 dams. In this application five or 10 sires born per year were considered, and either none or one male was imported per year. The annual renewal rate, r, was 50% for dams and 100% or 50% for sires. With a renewal rate r, the probability of being the true parent decreases in every generation by a factor of (1—r). The results are given in Table 1. When all sires were renewed each year, a closed population of 10 sires behaved similarly to one of five sires where one sire was imported annually. However, when the renewal rate was 50%, doubling the number of sires was a better strategy for restricting inbreeding than importing. Importation of animals was more relevant as the size of the nucleus and generation interval decreased.
| Sire renewal rate | Sires imported | Number of sires | |
|---|---|---|---|
| (%) | (no.) | 5 | 10 |
| 100 | 0 | 5.86 | 3.24 |
| 100 | 1 | 3.44 | 2.48 |
| 50 | 0 | 4.91 | 2.60 |
| 50 | 1 | 3.36 | 2.14 |
Discussion and conclusions
In summary, the rules of the tabular method with uncertain parentage allow the retrieval of some well-known formulas for effective population size, with the advantage that this approach can accommodate any population structure, i.e. overlapping generations, open populations, etc. In a real breeding scheme, the actual pedigree would replace the uncertain pedigree as the experiment progresses, so more accurate predictions of inbreeding can be made. Results such as those in Table 1 can be used to make approximate predictions of genetic gain with different schemes and optimize response over a given time-scale. This method should also be useful in the analysis of wild populations and in experiments with laboratory animals where pedigrees have not been recorded. The main drawback to this approach is that it does not take into account selection. Under selection, the probability of sharing identical alleles by descent among offspring increases, because part of the selective advantage of individuals remains in successive generations. Thus a way of incorporating selection would be to include a term in equation (1) and (2) that reflected the increase in relationship among relatives. Santiago and Caballero (1995) have given expressions for the fraction of the covariance between selective advantage and gene frequency that is passed to the next generation as a consequence of selection, and a similar approach might be followed here. An alternative viewpoint would be to consider the long-term genetic contributions of individuals, as suggested by Wray and Thompson (1990).




