Quantifying reciprocity in distylous and tristylous plant populations
Abstract
Reciprocal herkogamy (heterostyly) is an example of extreme relevance of accuracy of the location of the sexual organs within some floral systems. It involves the reciprocal positioning of anthers and stigmas in flowers of different plants within the same population, and the accuracy of this positioning is important to promote out-cross pollination, prevent self-interference, or both. Hence, several indices have been proposed to quantify reciprocity, most of them for populations with two different morphs (distylous). Here, we propose an extension of our index of reciprocity for distylous populations to be applied also to populations with three morphs (tristylous), allowing effective comparisons of reciprocity between tristylous, but also distylous populations. As for the distylous version, the index is based on comparison of the position of every single sexual organ in the sample with each and every organ of the opposite sex, for each of the three possible organ levels. Due to the massive amount of calculations required, a macro was developed that is available as Supplementary Information and at the website of the authors. The index and macro were tested on several hypothetical tristylous and distylous populations with predetermined mean and dispersion of sexual organs at each level, as well as on several actual tristylous and distylous populations. The index proposed is a solid tool for the study of reciprocity in distylous and tristylous populations. Comparisons between distylous and tristylous populations are easily performed and can be readily interpreted. The applicability of the index is facilitated through the software provided.
Introduction
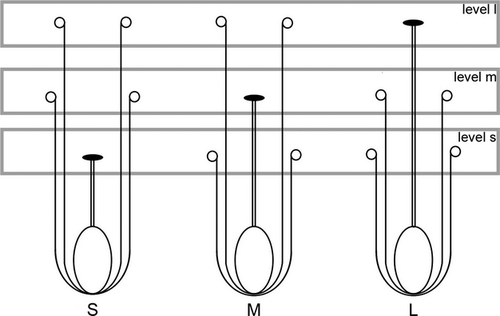
The accuracy of interactions affecting sexual function within flowers is assumed to have a critical adaptive importance (Armbruster et al. 2009). As an instance of the evolutionary result of such interactions, reciprocal herkogamous (heterostylous) systems have evolved to promote cross-pollination, prevent self-interference, or both (e.g., Baena-Díaz et al. 2012) by placing the pollen in a precise spot on the pollinator's body; thus pollen grains will be transferred to complementary stigmas of the opposite morph(s). Such systems have long intrigued scientists, both as an example of accuracy and as an ideal framework for testing ecological and evolutionary hypotheses. A particular form of those floral polymorphisms, tristyly, may be the less common but is the most complex. Tristyly is characterised by the presence of plants with one of three different floral morphs that differ reciprocally in the position of their sexual organs within the same plant population. There are three sexual whorls in the flowers of tristylous species, one corresponding to the style and the others to two levels of anthers. In the Long (L) morph the stigma is placed above the two whorls of anthers, in the Mid (M) morph the stigma is placed between them, and in the Short (S) morph the stigma is below the two anthers whorls (Fig. 1).
Tristyly was known to occur in several genera of three unrelated families of angiosperms: Lythraceae (e.g., Lythrum, Decodon, Nesaea, Pemphis, Adenaria, Rotala), Oxalidaceae (Averrhoa, Biophytum, Oxalis) and Pontederiaceae (Eichhornia, Pontederia). Recently, additional taxa in three other angiosperm families have been identified as tristylous: Agelaea, Jollydora and Manotes in Connaraceae, Hugonia and Roucheria in Linaceae and Narcissus in Amaryllidaceae (see Dulberger 1970; Ganders 1979; Lemmens 1989; Lloyd et al. 1990; Eckert & Barrett 1992; Weller 1992; Barrett 1993; Thompson et al. 1996).
Precise reciprocity among the plants in a population is achieved when the height of the stigmas of one morph corresponds exactly to the same position (height) of the anthers of the other morphs for that level, and for all morphs and levels in the population (Fig. 1). The evolutionary pathways to heterostyly may include transitions among different degrees of reciprocity; e.g., the main hypotheses on the evolution of distyly assume successive steps from monomorphism to reciprocal herkogamy involving increasing reciprocity (Charlesworth & Charlesworth 1979; Lloyd & Webb 1992). The final form at the end of the evolutionary pathway is the most reciprocal (but see Ferrero et al. 2009a).
In spite of the fact that distyly and tristyly seem to derive from one another (e.g., Lewis & Rao 1971; Ornduff 1972; Weller & Denton 1976; Charlesworth 1979; Pérez et al. 2004; Weller et al. 2007; Sosenski et al. 2010), few studies have considered the relationship between them in terms of reciprocity. For example, the shift from tristyly to distyly in Oxalis alpina is related to different degrees of reciprocity at the population level due to the loss of mid-stigmas (i.e. the M morph) and subsequent re-allocation of the corresponding anthers of the other morph's flowers in the remaining levels (Weller 1992). Such a pattern has also been observed several times in other angiosperm families and is especially frequent in Lythraceae (Weller 1992; Eckert & Mavraganis 1996).
Although the consideration of reciprocity as a continuous character is recognised (Lloyd et al. 1990), to the best of our knowledge only four attempts have been made to quantify reciprocity for heterostylous populations: the studies of Richards & Koptur (1993), Eckert & Barrett (1994), Sánchez et al. (2008) and Sosenski et al. (2010). Among these studies, only the index proposed in Eckert & Barrett (1994) comprises two different terms, one being related to the reciprocity itself and the other being related to the precision, but those terms are separated, making it difficult to make comparisons between species or populations. The proposal of Sánchez et al. (2008) for distylous systems attempts to overcome this drawback by unifying reciprocity and precision within the same term in order to facilitate comparisons among populations, species or even genera, although this comparison is only applicable to distylous populations. That index comprises both stigma–stamen height distance at each level (reciprocity) and precision (i.e. dispersion of the data). Based on Richards & Koptur (1993), the first term is calculated as the Euclidean distance from zero (maximum reciprocity) to the population's point in the bivariate space defined by the relative reciprocity indices, as one per each level (Fig. 2). To calculate these relative values, all possible combinations between each stigma and every anther of all other flowers in the population are considered, and the absolute value of each comparison (difference) is related to the mean value of all sexual organs in the population. The second term considers the dispersion of the data (standard deviation – SD values) in the final calculation: for higher SD values, reciprocity is lower (see Sánchez et al. 2008). This index captures critical characteristics of both optimality and precision (Armbruster et al. 2009). In this context, we propose a new index to quantify the reciprocity in tristylous plants that is an extension of the index of Sánchez et al. (2008). Such an index would be useful to characterise reciprocity in these systems and, in addition, would be useful for comparing distylous and tristylous taxa. Thus, this new reciprocity index can be used for tracing the evolutionary steps leading to heterostyly along phylogenetic pathways in cases in which distylous and tristylous taxa are present within the same group (e.g., Narcissus, Pérez et al. 2004; Oxalis, Weller & Denton 1976). The index can also be used to correlate reciprocity with indicators of population fitness, e.g., as the pollinator efficiency in Ferrero et al. (2011a) for distylous populations.

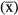 , and all the resultant values of each level are averaged to obtain a mean value that is the relative reciprocity for that level (e.g., for the s level, relative reciprocity
, and all the resultant values of each level are averaged to obtain a mean value that is the relative reciprocity for that level (e.g., for the s level, relative reciprocity 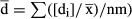 . B: Graphic representation of the distance (r) from zero (maximum reciprocity) to the point defined by the relative reciprocity values. Once that distance is calculated, the index of reciprocity is completed by multiplying by the values of dispersion (see Sánchez et al. 2008).
. B: Graphic representation of the distance (r) from zero (maximum reciprocity) to the point defined by the relative reciprocity values. Once that distance is calculated, the index of reciprocity is completed by multiplying by the values of dispersion (see Sánchez et al. 2008).The index here proposed also corrects a problem associated with the previous version for distylous populations, namely that the highest reciprocity was counter-intuitively represented by a minimum value of zero. After repeated use and testing (e.g., Ferrero et al. ,b, 2011a,b; Sánchez et al. 2010; Wu et al. 2010; Valois-Cuesta et al. 2011; Rodrigues Faria et al. 2012), we believe that the index could be improved and become more comprehensive by matching its highest values with the highest reciprocity.
Material and Methods
Modification of the index for distylous populations
 (1)
(1)Reciprocity index for tristylous populations
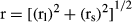 (2)
(2)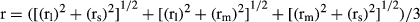 (3)
(3) (4)
(4)Since our index considers all possible stigma–anther distances for all levels, the amount of calculations required is massive. Therefore a Microsoft Excel macro was programmed to facilitate calculation of the index. This macro is available as Supplementary Information at our website: (http://webs.uvigo.es/plantecology/software.es.html).
Results and Discussion
Testing the index
We compared the performance of the new index between distylous and tristylous populations with different reciprocity among stigmas and anthers, and with different dispersions of the data. To this end, distylous and tristylous populations were randomly constructed with the Microsoft Excel data generator tool, which allowed us to select the mean and standard deviation values of the sexual organ heights (stigmas and anthers) for each level within the population. Since the main objective of this work was to obtain an index that can be reliably compared between distylous and tristylous populations, hypothetical populations were constructed in such a way that distylous and tristylous populations share the same data in levels l and s; therefore, similar index values were to be expected for those distylous and tristylous populations with the same l and s data. All populations were isopletic (i.e. with the same proportion of each of morph, 33 individuals per morph). The following two cases were tested:
- Comparison between distylous and tristylous populations with approximately the same mean values for stigmas and stamens at each level with increasing dispersion of the data (SD) (Fig. 3).
- Comparison between distylous and tristylous populations with approximately the same dispersion of the data for stigmas and stamens at each level and an increasing difference between the mean values of stigmas and stamens at each level (Fig. 4).
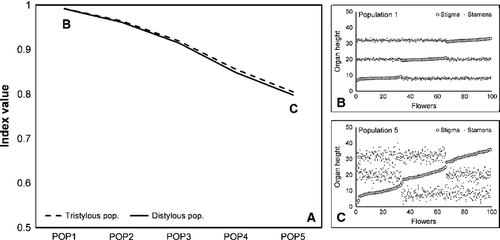
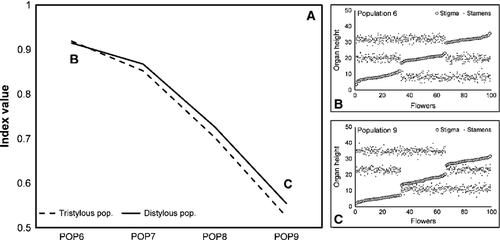
The primary results of these comparisons were that (i) the indices for distylous and tristylous populations are comparable, being almost coincident for all cases (paired t-test t = −1.51, df = 13, P = 0.15), and (ii) similar to the previous version of the index, the difference between the values of the organ heights is the main factor determining the final value of the index (see results and Fig. 4 in Sánchez et al. 2008), which is also modulated by dispersion of the data. Modification of the previous (distylous) index makes the new one more intuitive and easier to comprehend; the maximum values of the index now correspond to situations of high reciprocity, whereas lower values reflect lower reciprocity.
The values of the index here proposed for distylous and tristylous populations are completely comparable because they are practically coincident in all the simulations. Slight differences can be attributed to minimal stochastic differences among generations of the hypothetical populations, but are statistically irrelevant. The index measures reciprocity correctly and responds well to differences in mean values (reciprocity sensu stricto) and to increments in dispersion.
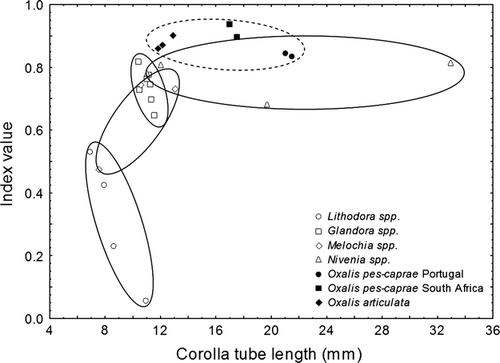
The new index is a modification of the index proposed in Sánchez et al. (2008) for application in tristylous and distylous populations, and can be used for the same purposes. As an example of this index's applicability, several preliminary results are shown in Fig. 5, where reciprocity values are related to corolla tube length for several species of five genera (see Fig. 5 legend for data sources and taxa). Some interesting observations are readily noticeable, for example: the index values are comparable between species and genera, both distylous as well as tristylous; in this case, the distylous species seem to be less reciprocal than tristylous species; moreover, these results also seem to validate segregation of the Glandora and Lithodora genera, which until recently were considered a single genus (Thomas et al. 2008; Ferrero et al. 2009a). Another promising possible comparison could be studies of the relationship between reciprocity and the degree of incompatibility. The index presented here and the macro developed to calculate it can be beneficial for future studies of the evolution of heterostyly, as well as investigations of the factors driving its evolution.
Acknowledgements
This research was supported by the Spanish Dirección General de Investigación, Ciencia y Tecnología (grant CGL2009-10466), FEDER funds from the European Union, the CYTED project (409AC0369) and the Xunta de Galicia (grant INCITE09-3103009PR). The Fundación Ramón Areces supported Victoria Ferrero through a postdoctoral fellowship. The authors thank Dr. F. Botana for contributing his mathematical expertise, and S. Troncoso for revision of the language.




