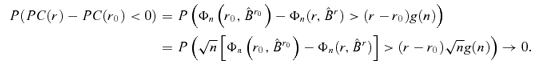Determining the number of factors in a multivariate error correction–volatility factor model
Abstract
Summary In order to describe the co-movements in both conditional mean and conditional variance of high dimensional non-stationary time series by dimension reduction, we introduce the conditional heteroscedasticity with factor structure to the error correction model (ECM). The new model is called the error correction–volatility factor model (EC–VF). Some specification and estimation approaches are developed. In particular, the determination of the number of factors is discussed. Our setting is general in the sense that we impose neither i.i.d. assumption on idiosyncratic components in the factor structure nor independence between factors and idiosyncratic errors. We illustrate the proposed approach with a Monte Carlo simulation and a real data example.
1. INTRODUCTION
The concept of co-integration (Granger, 1981, Granger and Weiss, 1983, and Engle and Granger, 1987) has been successfully applied to modelling multivariate non-stationary time series. The literature on co-integration is extensive. The most frequently used representations for a cointegrated system are the ECM of Engle and Granger (1987), the common trends form of Stock and Watson (1998) and the triangular model of Phillips (1991). The error correction model has been applied in various practical problems, such as determining exchange rates, capturing the relationship between expenditure and income, modelling and forecasting inflation, etc. From the equilibrium point of view, the term ‘error correction’ reflects the correction on the long-run relationship by the short-run dynamics.
However, the ECM ignores the characteristics of time-varying volatility, which plays an important role in various financial areas such as portfolio selection, option evaluation and risk management. Kroner and Sultan (1993) argued that the neglect of either co-integration or time-varying volatility would affect the hedging performance of existing models in the literature for the futures market. Similar conclusion has been given by Ghost (1993) and Lien (1996) through empirical calculation and theoretical analysis, respectively. Therefore, the traditional ECM needs to be generalized to have conditional heteroscedasticity for capturing both co-integration and time-varying volatility.
Univariate volatility models have been extended to multivariate cases. Extensions of the generalized autoregressive heteroscedastic (GARCH) model (Bollerslev, 1986) include, e.g. vectorized GARCH (VEC-GARCH) model of Bollerslev et al. (1988), the BEKK model of Engle and Kroner (1995), a dynamic conditional correlation (DCC) model of Engle (2002) and Engle and Sheppard (2001), a generalized orthogonal GARCH model of van der Weide (2002); see a survey of multivariate GARCH models by Bauwens et al. (2006).1 These models assume that a vector transformation of the covariance matrix can be written as a linear combination of its lagged values and the innovations. Andersen et al. (1999) showed that these models perform well relatively to competing alternatives. But the curse of dimensionality becomes a major obstacle in application. A useful approach to simplifying the dynamic structure of a multivariate volatility process is to use factor models. As is well known, factor models have been used for performance evaluation and risk measurement in finance. Moreover, it is now widely accepted that the financial volatilities move together over time across assets and markets (Anderson et al., 2006). These make it reasonable that we impose a factor structure on the residual term of a multivariate error correction model. In this sense, an error correction–volatility factor (EC–VF) model can capture the features of co-movements in both conditional mean (co-integration) and conditional variance (volatility factors) of a high dimensional time series.
The contribution of this paper is to estimate the EC–VF model. The set of parameters is divided into three subsets: structural parameter set including lag order and all autoregressive coefficient vector and matrices, co-integration parameter set including the co-integration vectors and the rank, and factor parameter set including the factor loading matrix and the number of factors. We conduct a two-step procedure to estimate relevant parameters. First, assuming that the structural and co-integration parameters are known, we give the estimation of factor loading matrix in the volatility factor model, and then give a method to determine the number of factors consistently. Our model specification and estimation approaches are general, because we impose neither i.i.d. assumption on the idiosyncratic components in the factor structure nor independence between factors and idiosyncratic errors. In contrast to the innovation expansion method in Pan and Yao (2008) and Pan et al. (2007), where they can not prove that their algorithm for the number of factors is consistent, our method in this paper is based on a penalized goodness-of-fit criterion. We prove our estimator of the number of factors is consistent. Secondly, the structural and co-integration parameters will be consistently estimated without knowing the true factor structure. The main distinction between Bai and Ng (2002) and this paper is that their factor model concerned the unconditional mean of economic variables while our factor structure is imposed on the conditional variance to reduce the dimension of volatilities.
The rest of the paper is organized as follows. Section 2 defines the EC–VF model and mentions some practical backgrounds of the model. Section 3 presents an information criterion for determining the number of factors and the consistency of our estimator. In Section 4, a simple Monte Carlo simulation is conducted to check the accuracy of the proposed estimation for the factor loading matrix and the number of factors. In Section 5, an application to financial risk management is discussed to show the advantages of the EC–VF model to other traditional alternatives. All theoretical proofs are given in the Appendix.
2. MODEL
2.1. Definition
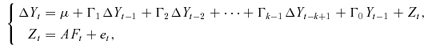 ((2.1))
((2.1))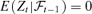 and
and 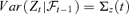 , where
, where 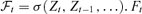 is a r × 1 time series, r < d is unknown, A is a d ×r unknown constant matrix. Ft and et are assumed to satisfy
is a r × 1 time series, r < d is unknown, A is a d ×r unknown constant matrix. Ft and et are assumed to satisfy
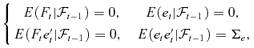 ((2.2))
((2.2))Remark 2.1. The error term {Zt} in an EC–VF model is conditionally heteroscedastic and follows a factor structure, while the error term in the traditional ECM developed by Engle and Granger (1987) is covariance stationary with mean 0. Here, the factor structure is not the classical one because we assume neither that the idiosyncratic components et are i.i.d. with a diagonal covariance matrix nor that the factor components Ft is independent of et.
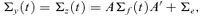 ((2.3))
((2.3))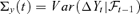 and
and 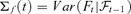 . Without loss of generality, we assume rank (A) =r. The lower dimensional volatility dynamics Σf(t) can be fitted by, e.g. the dynamic conditional correlation model of Engle (2002) or the conditionally uncorrelated components model of Fan et al. (2008).
. Without loss of generality, we assume rank (A) =r. The lower dimensional volatility dynamics Σf(t) can be fitted by, e.g. the dynamic conditional correlation model of Engle (2002) or the conditionally uncorrelated components model of Fan et al. (2008).2.2. Practical background
Factor analysis is an effective way for dimension reduction, and then it is a useful statistical tool for modelling multivariate volatility. Because there might exist co-integration relationship among financial asset prices, the framework given by equation (2.1) applies to many cases of financial analysis.
2.2.1. Value-at-risk Value-at-risk (VaR) defines the maximum expected loss on an investment over a specified horizon at a given confidence level, and is used by many financial institutions as a key measurement of market risk. The VaR of a portfolio of multiple assets can be obtained when the prices are described by an EC–VF model. The EC–VF model can be also used to determine an optimal portfolio based on maximizing expected returns subject to a downside risk constraint measured by VaR.
2.2.2. Hedge ratio The importance of incorporating the co-integration relationship into statistical modelling of spot and futures prices is well documented in the literature for futures market. It has been shown in Lien and Luo (1994) that although GARCH model may characterize the price behaviour, the co-integration relationship is the only indispensable component when comparing ex post performance of various hedge strategies. A hedger who omits the co-integration relationship will adopt a smaller than optimal futures position, which results in a relatively poor hedge performance; see Lien and Tse (2002) for a survey on hedging and references there.
2.2.3. Multi-factor option A multi-factor option (or multi-asset option) is an option whose payoff depends upon the performance of two or more underlying assets. Basket and rainbow options belong to this category. Duan and Pliska (2004) investigated theoretical and practical aspects of such options when the multiple underlying assets are co-integrated. In particular, they proposed an ECM with stochastic volatilities that follow a multivariate GARCH process. To avoid introducing too many parameters, they give a parsimonious diagonal model for the volatilities, but it is rather restrictive for the cross-dynamics. In contrast, volatility factor models can be used for reducing dimension as well as for representing the dynamics of both variances and covariances. The EC–VF model, with some modification, is more suitable for valuating the multi-factor options.
3. ESTIMATION OF THE NUMBER OF FACTORS
The parameter set of the EC–VF model (2.1) is {Θ; Γ0; A}, in which Θ={μ, Γ1, …, Γk−1} is called the structural parameter, Γ0 the co-integration parameter and A the factor parameter. In first two subsections, {Θ, Γ0} is assumed known and its determination will be discussed later in subsection 3.3.
3.1. Determining A
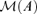 be the linear subspace of Rd spanned by the columns of A, which is called the factor loading space. Then, we need to estimate
be the linear subspace of Rd spanned by the columns of A, which is called the factor loading space. Then, we need to estimate 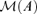 or its orthogonal complement
or its orthogonal complement 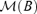 , where B is a d × (d −r) matrix for which (A, B) forms a d ×d orthogonal matrix, i.e. B′A = 0 and B′B =Id−r. Now it follows from equation (2.1) that
, where B is a d × (d −r) matrix for which (A, B) forms a d ×d orthogonal matrix, i.e. B′A = 0 and B′B =Id−r. Now it follows from equation (2.1) that
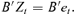 ((3.1))
((3.1))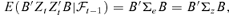
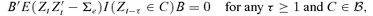 ((3.2))
((3.2))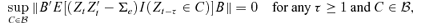 ((3.3))
((3.3))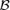 consists of some subsets in Rd, and ∥M∥=[tr(M′M)]1/2 denotes the norm of matrix M. Hence, we may estimate B by minimizing
consists of some subsets in Rd, and ∥M∥=[tr(M′M)]1/2 denotes the norm of matrix M. Hence, we may estimate B by minimizing
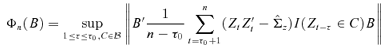 ((3.4))
((3.4))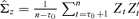 . This is a high-dimensional optimization problem, but it does not explicitly address the issue how to determine the number of factors r consistently. We first assume r is known and introduce some properties of the estimator of B derived by Pan et al. (2007) before we present a consistent estimator of r.
. This is a high-dimensional optimization problem, but it does not explicitly address the issue how to determine the number of factors r consistently. We first assume r is known and introduce some properties of the estimator of B derived by Pan et al. (2007) before we present a consistent estimator of r.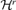 be the set of all d × (d −r) (d ≥r) matrix B satisfying B′B =Id−r. We partition
be the set of all d × (d −r) (d ≥r) matrix B satisfying B′B =Id−r. We partition 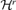 into equivalent classes such that
into equivalent classes such that 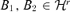 belong to the same class if and only if
belong to the same class if and only if 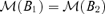 , which is equivalent to
, which is equivalent to
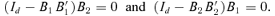 ((3.5))
((3.5))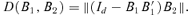
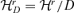 defined by D-distance. It can be shown that D is a well-defined metric distance on the space
defined by D-distance. It can be shown that D is a well-defined metric distance on the space 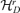 , and thus
, and thus 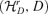 , which is our parametric space, is a metric space; see Pan and Yao (2008).
, which is our parametric space, is a metric space; see Pan and Yao (2008).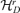 , i.e.
, i.e.
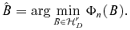
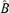 is consistent with a convergence rate
is consistent with a convergence rate 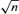 .
.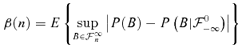
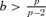 , where
, where 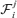 is the σ-algebra generated by {Zt, i ≤t ≤j}.
is the σ-algebra generated by {Zt, i ≤t ≤j}.Assumption 3.2 Denote 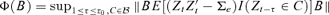 . There exists a matrix
. There exists a matrix 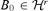 which minimizes Φ(B), and Φ(B) reaches its minimum value at a matrix
which minimizes Φ(B), and Φ(B) reaches its minimum value at a matrix 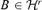 if and only if D(B, B0) = 0.
if and only if D(B, B0) = 0.
Assumption 3.3 There exists a positive constant a such that Φ(B) −Φ(B0) ≥aD(B, B0) for any matrix 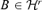 .
.
By the similar way to that in proof of Theorem 2 in Pan et al. (2007), we can prove the following result, which is useful in deriving a consistent estimator for the number of factors in next subsection.
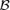 of subsets in Rd is a VC-class, and Assumptions 3.1 and 3.2 hold, then
of subsets in Rd is a VC-class, and Assumptions 3.1 and 3.2 hold, then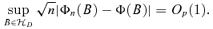 ((3.6))
((3.6))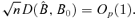 ((3.7))
((3.7))Remark 3.1 The definition of Vapnik-C̆ervonenkis (VC) class can be found in van der Vaart and Wellner (1996).
3.2. Determining r
Let r0 be the true number of factors and A0 the true factor loading matrix with rank r0. We discuss how to estimate r0 based on the estimated factor loading matrix 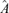 (or its counterpart
(or its counterpart 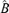 ) derived in the previous subsection. The basic idea is to treat the number of factors as the ‘order’ of model (2.1) and to determine the order in terms of an appropriate information criterion.
) derived in the previous subsection. The basic idea is to treat the number of factors as the ‘order’ of model (2.1) and to determine the order in terms of an appropriate information criterion.
In the following, we always assume that Assumptions 3.1–3.3 hold. Let Ml denote a matrix with rank d −l. In particular, B 0 and
0 and 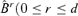 ) denote the matrices B0 and
) denote the matrices B0 and 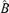 with ranks d −r0 and d −r, respectively.
with ranks d −r0 and d −r, respectively.
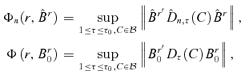 ((3.8))
((3.8))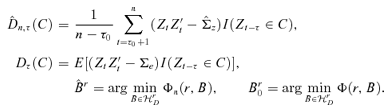
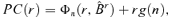 ((3.9))
((3.9))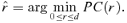
Remark 3.2 Φn(·) can be regarded as fitting error, because a model with r + 1 factors can fit no worse than a model with r factors, while Lemma A.1 shows that Φn(·) is a non-increasing function of r. But the efficiency is lost as more factors are estimated. For example, there is neither error nor efficiency in the extreme case when 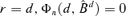 with
with 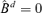 .
.
The following theorem shows that  is a consistent estimator of r0 provided that the penalty function g(n) satisfies some mild conditions.
is a consistent estimator of r0 provided that the penalty function g(n) satisfies some mild conditions.
Theorem 3.2 Under Assumptions 3.1–3.3, as 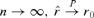 provided that g(n) → 0 and
provided that g(n) → 0 and 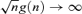 .
.
3.3. Determining {Θ, Γ0}
In this subsection, we give an estimation of the structural and co-integration parameter sets without knowledge of the true factor structure for Zt. By the Grange representation theorem, if there are exactly m co-integration relations among the components of Yt, and Γ0 admits the decomposition Γ0=γα′, then α is a d ×m matrix with linearly independent columns and α′Yt is stationary. In this sense, α consists of m co-integration vectors. As α and γ are not separately identifiable, our goal is to determine the rank of α, i.e. the dimension of the space spanned by the columns of α. Besides Assumptions 3.1–3.3 on {Zt}, we need an additional assumption on {Yt} as follows.
Assumption 3.4 The process Yt satisfies the basic assumptions of the Granger representation theorem given by Engle and Granger (1987), and E∥α′Yt−1∥4 < ∞.
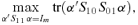 ((3.10))
((3.10)) . The solution of equation (3.10) is
. The solution of equation (3.10) is 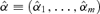 , where
, where  are the m generalized eigenvectors of S10S01 with respect to S11 corresponding to the m largest generalized eigenvalues.
are the m generalized eigenvectors of S10S01 with respect to S11 corresponding to the m largest generalized eigenvalues.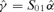 of the co-integration loading matrix and the estimator
of the co-integration loading matrix and the estimator 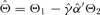 of the structural parameter are also consistent. These conclusions are obtained by Li et al. (2006), who also give a joint estimation for the co-integration rank and the lag order of the error correction model by a penalized goodness-of-fit measure
of the structural parameter are also consistent. These conclusions are obtained by Li et al. (2006), who also give a joint estimation for the co-integration rank and the lag order of the error correction model by a penalized goodness-of-fit measure
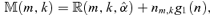 ((3.11))
((3.11))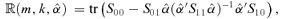 ((3.12))
((3.12))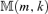 , i.e.
, i.e.
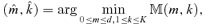
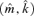 is a consistent estimator for (m0, k0).
is a consistent estimator for (m0, k0).Theorem 3.3 Under Assumptions 3.1–3.4, as 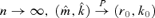 provided that g1(n) → 0 and ng1(n) →∞.
provided that g1(n) → 0 and ng1(n) →∞.
In practice, the choice of penalty function g(·) is flexible, e.g. 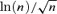 or
or 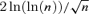 .
.
4. MONTE CARLO SIMULATION
We present a simple Monte Carlo experiment to illustrate the proposed approach in this section. Particularly, we check the accuracy of our estimation for the factor loading matrix A and the number of factors r.
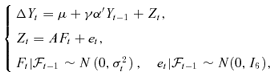 ((4.1))
((4.1))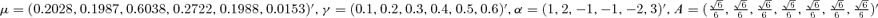 and β= (β0, β1, β2)′= (0.02, 0.10, 0.76)′.
and β= (β0, β1, β2)′= (0.02, 0.10, 0.76)′.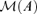 by
by
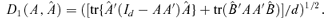
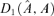 |
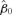 |
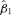 |
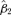 |
||
| n = 500 | Mean | 0.0563 | 0.0179 | 0.0894 | 0.7414 |
| Median | 0.0438 | 0.0183 | 0.0827 | 0.7521 | |
| STD | 0.0601 | 0.0022 | 0.0403 | 0.0935 | |
| Bias | – | −0.0021 | −0.0106 | −0.0186 | |
| RMSE | – | 0.0029 | 0.0454 | 0.0958 | |
| n = 1000 | Mean | 0.0477 | 0.0193 | 0.0922 | 0.7481 |
| Median | 0.0390 | 0.0199 | 0.0897 | 0.7543 | |
| STD | 0.0426 | 0.0010 | 0.0276 | 0.0724 | |
| Bias | – | −0.0007 | −0.0078 | −0.0119 | |
| RMSE | – | 0.0013 | 0.0295 | 0.0766 | |
The mean of estimation errors 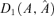 is less than 0.06, while it decreases over 15% as the sample size increases from 500 to 1000. The negative biases indicate a slight underestimation for the heteroscedastic coefficients. The relative frequencies for
is less than 0.06, while it decreases over 15% as the sample size increases from 500 to 1000. The negative biases indicate a slight underestimation for the heteroscedastic coefficients. The relative frequencies for  taking different values are listed in Table 2. It shows that when the sample size n increases, the estimation of r becomes more accurate.
taking different values are listed in Table 2. It shows that when the sample size n increases, the estimation of r becomes more accurate.
 taking different values, when r = 1.
taking different values, when r = 1.  |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| n = 500 | 0.0120 | 0.8425 | 0.1310 | 0.0105 | 0.0040 | 0 | 0 |
| n = 1000 | 0.0090 | 0.9765 | 0.0100 | 0.0045 | 0 | 0 | 0 |
5. APPLICATION TO REAL DATA
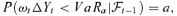 ((5.1))
((5.1))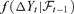 is normal, equation (5.1) reduces to the well-known formula
is normal, equation (5.1) reduces to the well-known formula
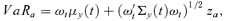 ((5.2))
((5.2))In this section, we attempt to compare the VaR forecasting results by assuming three different models: AR-DCC, EC-DCC, EC-VF-DCC for the asset price series {Yt}. The DCC refers to dynamic conditional correlation, a volatility model proposed by Engle (2002). Focusing on the methodology, we only consider the case when the conditional multivariate density 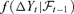 is normal, while the impact of other distributions (like Student-t and some non-parametric densities) on VaR computation is beyond our scope here.
is normal, while the impact of other distributions (like Student-t and some non-parametric densities) on VaR computation is beyond our scope here.
5.1. Data set and estimation of the EC-VF-DCC model
Our data set consists of 2263 daily log prices of CSCO, DELL, INTC, MSFT and ORCL, the five most active stocks in US market, from 19 June 1997 to 16 June 2006. The plots of log returns (in percentage) are presented in Figure 1 which shows significant time-varying volatilities. Descriptive statistics are listed in Table 3. All unconditional distributions of these series exhibit excessive kurtosis and non-zero skewness, indicating significant departure from the normal distribution.
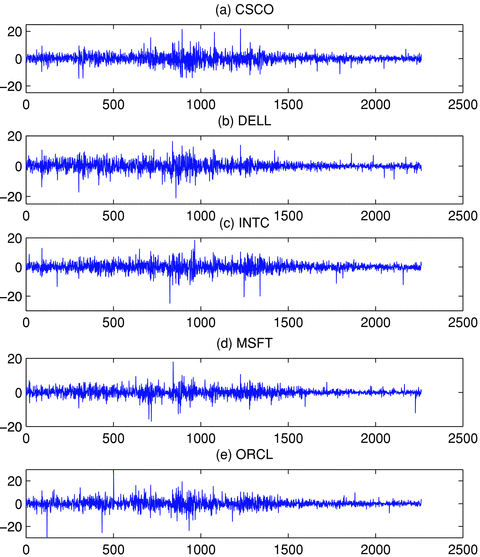
Plots of daily log-returns in percentage.
| n = 2263 | CSCO | DELL | INTC | MSFT | ORCL |
|---|---|---|---|---|---|
| Mean | 0.000423 | 0.000523 | 1.95 × 10−5 | 0.000200 | 0.000418 |
| Stdev | 0.031847 | 0.030270 | 0.030313 | 0.023074 | 0.036400 |
| Min | −0.145000 | −0.20984 | −0.248680 | −0.169760 | −0.346150 |
| Max | 0.218239 | 0.163532 | 0.183319 | 0.178983 | 0.270416 |
| Skewness | 0.149215 | −0.118260 | −0.391560 | −0.173470 | −0.226370 |
| Kurtosis | 4.558020 | 3.690575 | 5.631860 | 5.955046 | 8.519630 |
The estimation procedure for the EC-VF-DCC model is given step by step as follows.
-
Step 1. Fit an ECM for Yt to determine the structural and co-integration parameters. Compute the estimate of conditional mean vector
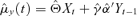 .
. -
Step 2. Conduct a multivariate portmanteau test for the squared residuals obtained from the previous step to detect conditional heteroscedasticity. If there exists serial dependence, fit a volatility factor model for the residual series {Zt} to determine the factor loading matrix
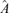 , otherwise switch to Step 3 with
, otherwise switch to Step 3 with 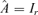 and r =d.
and r =d.Denote B = (b1, b2, …, bd−r), the objective function (3.4) can be modified to
where w(C) ≥ 0 are weights which ensure that the sum over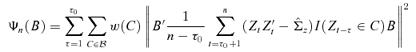
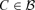 converges. In numerical implementation, we simply take
converges. In numerical implementation, we simply take 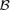 as the collection of all the balls centred at the origin in Rd and
as the collection of all the balls centred at the origin in Rd and 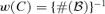 .
.
An algorithm for estimating B and r is given as follows. Put
Compute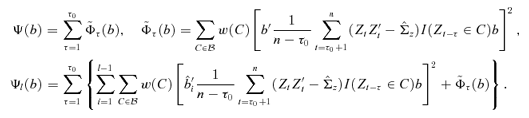
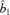 by minimizing Ψ (b) subject to the constraint b′b = 1. For l = 2, …, d, compute
by minimizing Ψ (b) subject to the constraint b′b = 1. For l = 2, …, d, compute 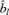 which minimizes Ψl(b) subject to the constraint
which minimizes Ψl(b) subject to the constraint 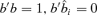 for i = 1, 2, …, l − 1.
for i = 1, 2, …, l − 1.
Let
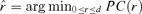 with
with 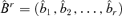 , where PC(r) is defined by equation (3.9). Note that
, where PC(r) is defined by equation (3.9). Note that 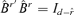 . Let
. Let 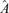 consist of the
consist of the  (orthogonal) unit eigenvectors, corresponding to the common eigenvalue 1, of matrix
(orthogonal) unit eigenvectors, corresponding to the common eigenvalue 1, of matrix 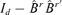 .
. -
Step 3. Fit a DCC volatility model (Engle, 2002) for
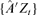 and compute its conditional covariance
and compute its conditional covariance 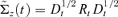 .
.To this end, we first fit each element of Dt with a univariate GARCH(1,1) model using the ith component of
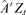 only, and then model the conditional correlation matrix Rt by
where ɛt is a
only, and then model the conditional correlation matrix Rt by
where ɛt is a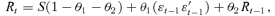
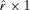 vector of the standardized residuals obtained from the separate GARCH(1,1) fittings for the
vector of the standardized residuals obtained from the separate GARCH(1,1) fittings for the  components of
components of 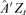 , and S is the sample correlation matrix of
, and S is the sample correlation matrix of 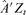 .
.
If
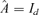 , the estimate of conditional covariance matrix
, the estimate of conditional covariance matrix 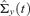 of ΔYt is equal to
of ΔYt is equal to 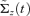 and terminate the algorithm. Otherwise, proceed to Step 4.
and terminate the algorithm. Otherwise, proceed to Step 4. - (5.3)
Step 4. The factor structure in equation (2.1) and the facts B′A = 0, B′et=B′Zt, AA′+BB′=Id lead to a dynamics for Σy(t) ≡Σz(t) as follows
where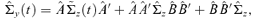 ((5.3))
((5.3))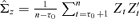 .
.
We determine the co-integration rank by minimizing 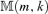 defined by equation (3.11). The surface of
defined by equation (3.11). The surface of 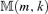 is plotted against m and k in Figure 2. The minimum point of the surface is attained at (m, k) = (1, 1), leading to an error correction model for this data set with lag order 1 and co-integration rank 1. Applying the Ljung-Box statistics to the squared residuals, we have Q5(1) = 63.2724, Q5(5) = 305.7613 and Q5(10) = 633.7103. Based on asymptotic χ2 distributions with degrees of freedom 11, 111 and 236, the p-values of these Q statistics are all close to zero.2 Consequently, the portmanteau test confirms the existence of conditional heteroscedasticity. The algorithm stated in Step 2 leads to an estimator for the number of factors, and PC(r) is plotted against r in Figure 3. Clearly, a two-factor structure (i.e.
is plotted against m and k in Figure 2. The minimum point of the surface is attained at (m, k) = (1, 1), leading to an error correction model for this data set with lag order 1 and co-integration rank 1. Applying the Ljung-Box statistics to the squared residuals, we have Q5(1) = 63.2724, Q5(5) = 305.7613 and Q5(10) = 633.7103. Based on asymptotic χ2 distributions with degrees of freedom 11, 111 and 236, the p-values of these Q statistics are all close to zero.2 Consequently, the portmanteau test confirms the existence of conditional heteroscedasticity. The algorithm stated in Step 2 leads to an estimator for the number of factors, and PC(r) is plotted against r in Figure 3. Clearly, a two-factor structure (i.e.  ) is determined for the residual series {Zt}.
) is determined for the residual series {Zt}.
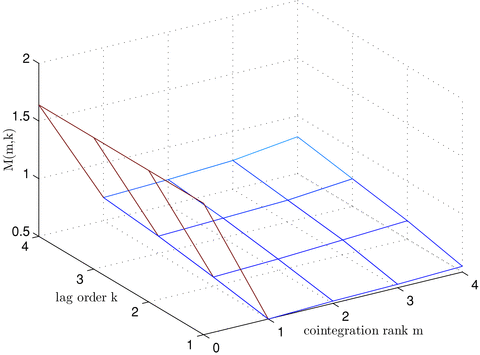
Plot of 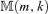 against the co-integration rank m and the lag order k.
against the co-integration rank m and the lag order k.
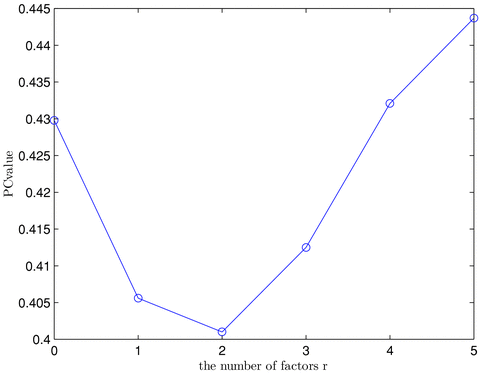
Plot of PC(r) against the number of factors r.
5.2. Comparison of value-at-risk forecasting results
The VaRs are computed at level 0.05 (denoted by VaR0.05) for the last 1000 trading days of data span. We assume three models: AR-DCC, EC-DCC, EC-VF-DCC for the asset prices {Yt}, and four time invariant portfolios with weights ω1= (1, 1, 1, 1, 1)′/5, ω2= (1, 2, 3, 4, 5)′/15, ω3= (5, 4, 3, 2, 1)′/15, ω4= (1, 3, 5, 4, 2)′/15. To compare the VaR forecasting performances, we calculate failure rates for the different specifications. The failure rate is defined as the proportion of rt=ω′tΔYt smaller than the VaRs. For a correctly specified model, the empirical failure rate is supposed to be close to the true level a. Table 4 displays the results for the 5% level.
| ω1 | ω2 | ω3 | ω4 | t (Min) | |
|---|---|---|---|---|---|
| AR-DCC | 0.067 (0.001) | 0.071 (0.000) | 0.065 (0.005) | 0.062 (0.032) | 287.3 |
| EC-DCC | 0.052 (0.659) | 0.059 (0.061) | 0.051 (0.713) | 0.053 (0.268) | 294.7 |
| EC-VF-DCC | 0.049 (0.713) | 0.056 (0.308) | 0.053 (0.268) | 0.055 (0.312) | 41.5 |
- Note: Figures in parentheses are p-values for the Kupiec likelihood ratio test used to compare the empirical failure rate with its theoretical value, see Kupiec (1995). The average computing time in minute for each model is recorded in the last column.
We observe from Table 4 that the EC-VF-DCC performs reasonably well, while AR-DCC has a difficulty in providing failure rates close to 0.05. The empirical failure rates for AR-DCC are high, which means that it underestimates the risk. The results for the EC-DCC and EC-VF-DCC model are comparable, but the average computing time for EC-DCC is much longer, see the last column of Table 4. This shows that the factor structure imposed on the residual term of an ECM can improve the computational velocity in high-dimensional problems.
The above results show that the EC-VF model proposed in this paper is a promising tool for risk analysis. First, it incorporates the impact of co-integration which makes the VaR computation more accurate. Second, it deduces a high-dimensional optimization problem into a much lower-dimensional problem, thus accelerates the VaR computation to a great extent.
Footnotes
ACKNOWLEDGMENTS
The authors are grateful to an anonymous referee and the co-editor for their insightful comments and valuable suggestions. Qiaoling Li was partially supported by the National Natural Science Foundation of China (grant no. 10571003). Jiazhu Pan was partially supported by the starter grant from University of Strathclyde (UK) and the National Basic Research Program of China (grant no. 2007CB814902).
Appendix
APPENDIX: PROOFS OF RESULTS
The first lemma shows the  defined in subsection 3.2 is a non-increasing function of the number of factors r.
defined in subsection 3.2 is a non-increasing function of the number of factors r.
Lemma A.1 If 0 ≤r1 < r2≤d, then  .
.
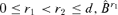 can be written as
can be written as 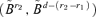 where
where 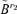 consists of the first d −r2 columns of the matrix
consists of the first d −r2 columns of the matrix 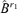 . We have
. We have
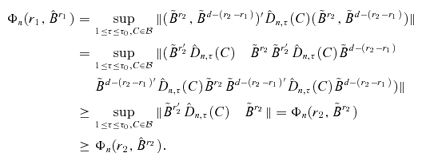
 is the minimizer of Φn(B) in the metric space
is the minimizer of Φn(B) in the metric space  . □
. □The proof of Theorem 3.2 needs the following two lemmas.
Lemma A.2 For any fixed r with r0≤r ≤d, there exists a  such that Φ(r, B) = 0. For 0 ≤r < r0, Φ(r, B) > 0 holds for all
such that Φ(r, B) = 0. For 0 ≤r < r0, Φ(r, B) > 0 holds for all 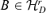 .
.
Proof: It is clear that B′A0= 0 implies Φ(r, B) = 0 from the relation between Φ(r, B) and the factor model with true loading matrix A0.
For r =r0, there must be a matrix in 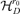 , denoted by B
, denoted by B , such that
, such that 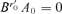 , thus
, thus 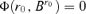 and it reaches the minimum value. We have
and it reaches the minimum value. We have 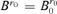 in
in 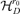 by Assumption 3.2.
by Assumption 3.2.
For r0 < r ≤d, let 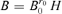 , where H is an arbitrary (d −r0) × (d −r) matrix such that H′H =Id−r. Then,
, where H is an arbitrary (d −r0) × (d −r) matrix such that H′H =Id−r. Then, 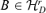 and B′A0= 0. In the other words,
and B′A0= 0. In the other words, 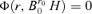 .
.
For any 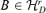 with r < r0, B′A0≠ 0. If Φ(r, B) = 0, which means that for any 1 ≤τ≤τ0 and any
with r < r0, B′A0≠ 0. If Φ(r, B) = 0, which means that for any 1 ≤τ≤τ0 and any 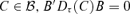 , by choosing
, by choosing 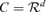 , we have B′A0E(FtFt′)A0′B = 0. This is impossible because E(FtFt′) is a positive definite matrix. □
, we have B′A0E(FtFt′)A0′B = 0. This is impossible because E(FtFt′) is a positive definite matrix. □
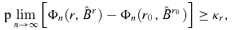
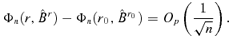
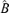 that
that
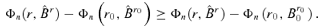
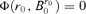 by Lemma A.2. Hence,
by Lemma A.2. Hence,
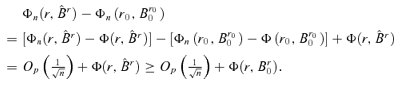 ((A.1))
((A.1))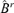 is related to n. The last inequality is from the definition of B0. These imply that, for any 0 ≤r < r0,
is related to n. The last inequality is from the definition of B0. These imply that, for any 0 ≤r < r0,
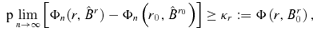
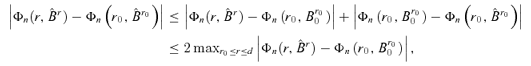
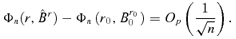
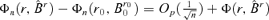 . Thus, we need to prove
. Thus, we need to prove 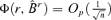 for any r0≤r ≤d, where
for any r0≤r ≤d, where
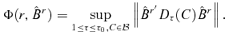
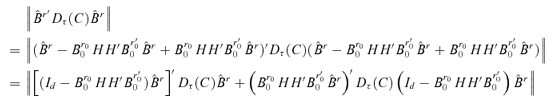
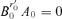 implies that
implies that 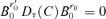 for any τ≥ 1 and
for any τ≥ 1 and 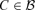 . Hence,
. Hence,
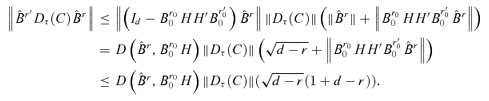
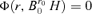 by Lemma A.2, i.e.
by Lemma A.2, i.e. 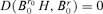 . Thus,
. Thus, 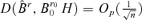 . It is easy to see that
. It is easy to see that 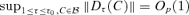 . Therefore,
. Therefore, 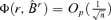 . □
. □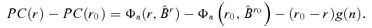
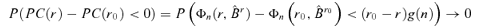
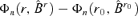 has a positive limit in probability.
has a positive limit in probability.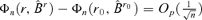 . Thus, if
. Thus, if 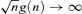 as n →∞, we have
as n →∞, we have