Evidence for a large-scale population structure among accessions of Arabidopsis thaliana: possible causes and consequences for the distribution of linkage disequilibrium
Abstract
The existence of a large-scale population structure was investigated in Arabidopsis thaliana by studying patterns of polymorphism in a set of 71 European accessions. We used sequence polymorphism surveyed in 10 fragments of ∼600 nucleotides and a set of nine microsatellite markers. Population structure was investigated using a model-based inference framework. Among the accessions studied, the presence of four groups was inferred using genetic data, without using prior information on the geographical origin of the accessions. Significant genetic isolation by geographical distance was detected at the group level, together with a geographical gradient in allelic richness across groups. These results are discussed with respect to the previously proposed scenario of postglacial colonization of Europe from putative glacial refugia. Finally, the contribution of the inferred structure to linkage disequilibrium among 171 pairs of essentially unlinked markers was also investigated. Linkage disequilibrium analysis revealed that significant associations detected in the whole sample were mainly due to genetic differentiation among the inferred groups. We discuss the implication of this finding for future association studies in A. thaliana.
Introduction
Arabidopsis thaliana is an important model species to ask a variety of questions in ecological and evolutionary genetics (Pigliucci 2002). Its utility may depend though on the assessment of the structure of genetic diversity of this species in nature. Indeed, characterization of population structure can be useful for understanding population dynamics, historical events, or testing whether genomic areas harbour the footprint of selection. Furthermore, on a practical level, not taking into account the presence of population structure can lead to the detection of spurious associations in association studies (e.g. Helgason et al. 2005).
Some essential factors contributing to the distribution of the genetic diversity of this plant species in nature are already well known. A. thaliana is considered a highly selfing species (selfing rate > 95%, Abbott & Gomes 1989). Its weedy lifestyle and population dynamics are characterized by colonization/extinction events. So, as for many selfing plant species, the distribution of the genetic variability in A. thaliana is usually highly structured among pairs of sampling locations (e.g. Todokoro et al. 1995; Kuittinen et al. 2002). However, recent studies (Nordborg et al. 2005) have shown that linkage disequilibrium decays within a range of 25–50 kb in this species, which is similar to what can be observed in several outcrossing species. This species is also believed to have undergone some exponential growth phase associated with a postglaciation history of colonization (e.g. Mitchell-Olds 2001). In empirical studies, the requirement for a large amount of diversity generally leads to the utilization of worldwide samples of A. thaliana accessions (e.g. Kuittinen & Aguadé 2000; Aguadé 2001; Haubold et al. 2002). So far, few studies have attempted to account for these characteristics in the modelling of nucleotidic diversity of A. thaliana (but see Innan & Stephan 2000; Schmid et al. 2005).
Here, we use a model-based approach to investigate the existence of a population structure (also referred to as genetic stratification) among accessions of A. thaliana. We analyse patterns of diversity and isolation by distance among the groups we found and discuss those in the light of previous studies and phylogeographical scenarios. Finally, we evaluate the impact of the stratification we found on the detection of linkage disequilibrium among markers and discuss how this will affect future association studies in this species.
Materials and methods
Plant material
The sample studied includes 71 mainly European accessions obtained from the collection of Versailles, France. These accessions were chosen among a larger set of accessions obtained from the Arabidopsis Biological Research Center and Nottingham stock centres or derived from collections carried out by French groups (Lavigne et al. 2001; Le Corre et al. 2002). The accessions used and their geographical origin are listed in Table 1. More details on this collection are available at http://dbsgap.versailles.inra.fr/vnat/. Note that each accession is maintained by controlled self-fertilization and is therefore expected to be highly homozygous. Genomic DNA was extracted from leaves or from seedlings using a CTAB (cetyltrimethyl ammonium bromide) protocol in microtitre plates (Loudet et al. 2002). For a given accession, all sequences were obtained using the DNA of the same inbred line. In some cases however, microsatellite alleles were genotyped using the DNA from another inbred line representing the same accession.
| Gr-3 | Austria | RAN | France | Lip-0 | Poland | N17 | Russia |
| In-0 | Austria | PYL-1 | France | Ler-1 | Poland | N13 | Russia |
| Ka-0 | Austria | Sp-0 | Germany | Mh-0 | Poland | N14 | Russia |
| Pi-0 | Austria | No-0 | Germany | Col-0 | Poland | N6 | Russia |
| Can-0 | Canary Islands | Bay-0 | Germany | N7 | Russia | Stw-0 | Russia |
| Cvi-0 | Cape Verde Islands | Db-1 | Germany | Chi-0 | Russia | Sah-0 | Spain |
| Sap-0 | Czech Rep. | Enkheim-T | Germany | Est-0 | Russia | Alc-0 | Spain |
| Sav-0 | Czech Rep. | Kas-1 | India | Rsch-4 | Russia | Bla-1 | Spain |
| Jl-3 | Czech Rep. | Pa-1 | Italy | Ws | Russia | Ost-0 | Sweden |
| Blh-1 | Czech Rep. | Bl-1 | Italy | Rld-2 | Russia | St-0 | Sweden |
| Dra-0 | Czech Rep. | Mir-0 | Italy | Petergof | Russia | Ge-0 | Switzerland |
| Br-0 | Czech Rep. | Ct-1 | Italy | N4 | Russia | Shakdara | Tadjikistan |
| Ta-0 | Czech Rep. | Mt-0 | Libya | 9481B | Russia | Hodja | Tadjikistan |
| Bur-0 | Eire | Kn-0 | Lituania | Ms-0 | Russia | Kondara | Tadjikistan |
| Fl-1 | Finland | Wil-1 | Lituania | N8 | Russia | Rubezhnoe-1 | Ukraine |
| Te-0 | Finland | Ita-0 | Morocco | N11 | Russia | Edi-0 | United Kingdom |
| LDV-5 | France | Nok-1 | Netherlands | N15 | Russia | Abd-0 | United Kingdom |
| JEA | France | Oy-0 | Norway | N10 | Russia |
DNA sequences
Ten fragments of approximately 600 bp distributed among the five chromosomes of A. thaliana (two fragments per chromosome) were sequenced for each of the 71 accessions in a previous study (McKhann et al. 2004). Sequence information and patterns of sequence diversity detected in the whole sample are given in Table 2. Each fragment comprises at least one intron and two exons. Details on polymerase chain reactions (PCR) and sequence alignment are available in McKhann et al. (2004). The polymorphic sites (hereafter SNPs) were used to define the set of alleles (haplotypes) at each of the 10 loci (fragments) in the sample. All SNPs were used in this study.
| Marker name | Chr. | Mb | cM | No. of SNPs | No. of haplotypes | H E |
|---|---|---|---|---|---|---|
| 125 CF | 1 | 7.1 | 30 | 7 | 7 | 0.37 |
| 133 CR | 1 | 27.6 | 116 | 24 | 9 | 0.74 |
| 49 AR | 2 | 2.9 | 18 | 43 | 12 | 0.62 |
| 67 DR | 2 | 19.5 | 87 | 9 | 9 | 0.76 |
| 92 BR | 3 | 5.4 | 24 | 13 | 12 | 0.77 |
| 100 DF | 3 | 11.1 | 100 | 10 | 10 | 0.51 |
| 76 DF | 4 | 6.9 | 48 | 20 | 17 | 0.84 |
| 82 AF | 4 | 14.3 | 80 | 5 | 7 | 0.50 |
| 115 AR | 5 | 9.4 | 59 | 19 | 9 | 0.68 |
| DFR | 5 | 16.8 | 91 | 29 | 19 | 0.81 |
Microsatellite loci
Microsatellite information and patterns of genetic diversity detected in the whole sample are given in Table 3. PCR was carried out in a reaction mixture (20 µL) containing 30 ng of template DNA, 0.125 mm dNTP, 0.125 µm each primer, 50 mm KCl, 1.5 mm MgCl2, 10 mm Tris-HCl (pH 9) and 1 U of Taq polymerase (Sigma). The forward primer was 5′-labelled with one of the three fluorophores (6FAM, NED or HEX). The PCR conditions were as follows: an initial denaturation step of 2 min at 94 °C, followed by 30 cycles of 30 s at 94 °C, 30 s at 55 °C, 30 s at 72 °C and a final extension step at 72 °C for 10 min. Amplified products were detected on an ABI PRISM 3100 Genetic Analyser. Samples were prepared by adding 3 µL of diluted PCR products to 6.875 µL formamide and 0.125 µL GenSize 500 Rox. Analyses were performed using genescan 3.1 and genotyper 2.5 software (Applied Biosystems). The proportion of missing data in the microsatellite data set was 10%. Fifty-eight per cent of the accessions had no missing data and all microsatellite data were missing for two accessions. In the subset of incompletely genotyped accessions, a mean of two loci were missing.
| Marker name | Chr. | Mb | cM | No. of alleles | HE |
|---|---|---|---|---|---|
| nga 8 | 4 | 5.6 | 3 | 34 | 0.96 |
| nga 128 | 1 | 20.6 | 22 | 21 | 0.93 |
| nga 129 | 5 | 20.1 | 70 | 16 | 0.79 |
| nga 139 | 5 | 48.4 | 4 | 27 | 0.92 |
| nga 162 | 3 | 4.6 | 35 | 12 | 0.86 |
| nga 168 | 2 | 16.3 | 4 | 12 | 0.84 |
| msat1–10 | 1 | 7.3 | n.a. | 19 | 0.94 |
| msat1–13 | 1 | 25.8 | n.a. | 21 | 0.90 |
| msat3–19 | 3 | 8.8 | n.a. | 22 | 0.94 |
Inference of population structure
The detection of a genetic stratification was performed with the structure program (version 2.0; Pritchard et al. 2000a) using the admixture model. This model assumes that the genome of individuals is a mixture of genes originating from K unknown ‘ancestral’ populations that may have undergone introgression events. Under this model, the structure algorithm estimates the proportion of membership (genome ancestry) of each individual in each of the K ancestral populations (hereafter p̂jk refers to the estimated proportion of membership of individual j in population k). This model assumes that the unknown K ancestral populations are at Hardy–Weinberg equilibrium and at linkage equilibrium. Because A. thaliana is a highly selfing species, the Hardy–Weinberg equi- librium assumption is clearly inappropriate. Therefore, the data were treated as haploid to relax the modelling assumption regarding the statistical independence of the two alleles present at a given locus within an individual, as recommended in Falush et al. (2003). Because microsatellite markers typically mutate at a faster rate than DNA sequences, inferences were carried out on the complete data set and on the two types of markers separately. Because free recombination is much more likely to occur between fragments than within them, alleles (haplotypes) were defined for each sequenced fragment instead of using all SNPs independently. For the rest of this paper, a SNP marker will refer to the set of haplotypes (alleles) that was defined for a particular sequenced fragment (locus). The parameter α that modulates the degree of admixture was constrained to be the same for all ancestral populations (see Pritchard et al. 2000a). This corresponds to making the prior assumption that the unknown ancestral populations contribute roughly equal amounts of genetic material to the sample (Falush et al. 2003). α was explored within the range [0, 10], an estimated α value smaller than one indicating that each individual mainly originates from a single ancestral population. We also investigated population structure under the no-admixture model. This model differs from the one we used only in that it assumes that all the genes of a given individual originate from one single discrete population at linkage equilibrium. This model yielded almost identical results to the ones obtained under the admixture model (not shown).
The length of the burn-in period and the number of iterations chosen was 200 000 and 2 000 000, respectively. The number of iterations was fixed to make sure that the obtained likelihood estimates were as accurate as possible and less variable across different runs. Ten independent runs were performed at each K value, from K = 2 to K = 6, with K referring to the number of groups to be inferred. The choice of the appropriate K value was conducted as recommended in Pritchard & Wen (2003). The K value at which a maximum log likelihood of data was reached was retained. However, genuine genetic stratification was inferred only when most individual p̂jk values were different from 1/K and were stable among the different runs. The stability of these estimates at a given K value was evaluated using the similarity coefficient (hereafter SC) between run pairs, as described in Rosenberg et al. (2002). An SC greater than 0.85 indicates stable clustering solutions (completely identical estimates among runs would yield an SC of 1). Computation of this coefficient from the output of structure was performed using a mathematica program (Wolfram 1991).
Analysis of the inferred structure
To quantify the between-groups component of genetic variation, FST's (Weir & Cockerham 1984) were estimated and significance levels were determined through permutation tests (genetix software, Belkhir et al. 2004; available at http://www.Univ-montp2.fr/~genetix/genetix/intro.htm). The expected heterozygozity, HE, the mean number of alleles per locus, Na, and the mean of allelic richness after rarefaction, Rs, were calculated within each inferred group. For a given locus, Rs is defined as the expected number of different alleles in a sample of s individuals and was calculated using contrib software (by R. J. Petit, available at http://www.pierroton.inra.fr/genetics/labo/Softwares/). We tested the existence of a geographical gradient in allelic richness among groups. Briefly, the allelic richness (after rarefaction) at locus j within group i, was modelled as Rsij = Gi + Lj, where a group at a geographical position i (Gi) was an explicative variable and locus (Lj) was used as a cofactor. Because we used population as a continuous variable in this model and distances between groups were not equal, we also performed a Spearman correlation rank test on standardized allelic richness. For locus j within group i, the allelic richness Rsij, was standardized as (Rsij–Rs.j)/Rs.j, where Rs.j is the allelic richness of locus j averaged over the n groups. Isolation by distance at the group level was tested by computing the correlation between matrices of genetic and geographical distances. We used the natural logarithm of geographical distance among all pairs of the inferred groups. The pairwise measure FST/(1 − FST) (Rousset 1997) was used as a measure of genetic distance between groups and we used Spearman rank correlation coefficient as a test statistic. Geographical distances between group pairs were calculated as Euclidian distances using the mean longitude and latitude of accessions in each inferred group. The coordinates of accessions are available at http://dbsgap.versailles.inra.fr/vnat/. The three accessions for which geographical coordinates were missing were assigned the mean coordinates of the accessions sampled in the same country.
The contribution of the inferred population structure to linkage disequilibrium (hereafter LD) was investigated. LD between each pair of loci was estimated in the complete data set of accessions as the mean correlation coefficient r̂ij, defined as the correlation coefficient averaged over all possible pairs of alleles carried at loci i and j. Significance of each r̂ij value was assessed using a null empirical distribution obtained by permuting alleles among all accessions. However, r̂ij may be significant either because of nonrandom association of alleles within the inferred groups and/or because allele frequencies differ among groups. To quantify the number of pairs that reached significance because of population structure only, significance of the r̂ij values was also tested against another null hypothesis. This second null hypothesis assumed no LD within the inferred groups and the corresponding null empirical distribution for the test statistic was obtained by permuting alleles among individuals within the inferred groups. Because this latter distribution reflects the correlation values that would be obtained only because of population structure, the pairs where r̂ij was no longer significant under this latter hypothesis were considered as ‘spurious’ LD due to population structure. LD analysis was performed using genetix (Belkhir et al. 2004).
Results
Clustering results
Using the complete data set of markers allowed clustering of our sample into groups that were not defined a priori. For the sake of clarity, hereafter we have labelled the groups using the geographical location of the majority of accessions comprising each group. Note that this by no means implies that the clusters uncovered here were defined a priori on the basis of geography. Results of the structure we uncovered are summarized in Table 4 and in 1, 2. Group composition is given in the Appendix. For the rest of this paper, a ‘clustering solution’ refers to the particular partition of the whole set of accessions into K distinct groups. Under the framework of structure's admixture model, this corresponds to the partition obtained when individual accessions were assigned according to their highest estimated proportion of membership (hereafter, p̂max) into a group.
| K | Ln P(D|K) | N |
|---|---|---|
| 3 | − 2760.2 (0.22; 0.37) | 8 (0.37); 36 (0.40); 27 (0.40) |
| 4 | − 2688.5 (0.14; 0.99) | 8 (0.75); 17 (0.71); 29 (0.72); 17 (0.80) |
| 5 | − 2733.4 (0.15; 0.03) | 7 (0.37); 20 (0.25); 32 (0.44); 6 (0.23); 6 (0.30) |

Barplot of the proportional membership of individual accessions within each of the four inferred groups. Each accession is represented as a vertical bar comprising different grey levels on the X-axis. Each group is represented with a different grey level. From left to right, black, white, medium grey and light grey correspond to Western Europe, Eastern Europe, Eurasia and West Mediterranean group, respectively.

Geographical distribution of accessions assigned to each group. A corresponds to K = 2, B to K = 3 and C to K = 4. D corresponds to K = 4, but includes only accessions characterized with p̂max > 0.70. In C and D, green, red, blue and black correspond to West Mediterranean, Western Europe, Eastern Europe and Eurasia, respectively. The coordinates of a few accessions were slightly shifted, for better visualization.
Individual proportions of membership in each group estimated using the whole data set (microsatellites + SNPs) are in good agreement with the existence of a genetic stratification (population structure) in the sample. A maximum in log likelihood was reached at K = 4 (Table 4). At this stage, most accessions (49/71) were assigned with p̂max > 70%. The small estimated value of the α parameter (α = 0.14) is consistent with the distribution of p̂max, indicating that ancestry of most accessions originated from mainly one population, with a few fairly admixed individuals (see Fig. 1).
It is informative to examine the clustering solutions sequentially obtained from K = 2 to K = 4. Typically, structure splits the most divergent groups first although sample sizes and within-group diversity levels also affect splitting order (Rosenberg et al. 2002). At K = 2, the algorithm mainly puts together accessions from both edges of the geographical range of the sample, that is eastern accessions together with southwestern accessions (black circles in Fig. 2A). At K = 3, southwestern accessions were discriminated from the others (green circles in Fig. 2B). At K = 4, the previous cluster located at the centre of the geographical range of the sample (blue circles in Fig. 2B) was split longitudinally, defining two groups characterized by a highly mixed suture zone between them (red and blue circles in Fig. 2C). This last split went together with an important reduction of the previous Eastern cluster (black circles in Fig. 2B, C). At this maximum log likelihood K value, the four inferred groups were geographically delineated, on a SW to NE axis. For the remainder of this paper, these groups will therefore be referred to as the West Mediterranean, Western Europe, Eastern Europe and Eurasian groups (respectively green, red, blue and black circles in Fig. 2C, D). As illustrated in Fig. 2(D), such geographical consistency in the location of groups is obvious when accessions characterized with p̂max > 70% are placed on the map.
No robust genetic stratification was detected when using either the microsatellite or the SNP markers separately. When using the microsatellite markers alone, no maximum log likelihood K value was obtained. When using the SNP markers alone, although a maximum in log likelihood was obtained at K = 4, individual estimated proportions of membership were all very close to 1/K and one cluster was ‘empty’ in the sense that no accession was assigned to this cluster according to the p̂max rule.
Genetic differentiation between the inferred groups
Results are summarized in Tables 5 and 6 and in Fig. 3. In the following, FST values refer to overall FST values if not otherwise stated. For both the SNP and the microsatellite markers, single locus FST values were highly significant (P < 0.001), as were all pairwise multilocus FST values (P < 0.01). Pairwise multilocus SNP FST values were always higher than multilocus microsatellite FST values (Table 5). On the whole, multilocus SNP FST was almost twofold greater than multilocus microsatellite FST(0.12 and 0.07, respectively). However, single locus FST estimates were not significantly different among the two types of markers (exact Wilcoxon rank sum test, P = 0.06). For both types of markers, the mean of allelic richness after rarefaction (Rs.) was ordered and decreasing across groups, that is from the West Mediterranean to the Eurasian region (see Table 6). This gradient was significant (F1;56 = 10.24, P < 0.01; Spearman correlation rank test, rho = −0.31, P < 0.01).
| E | EE | WE | WM | |
|---|---|---|---|---|
| E | — | 0.14 | 0.15 | 0.13 |
| EE | 0.06 | — | 0.11 | 0.11 |
| WE | 0.07 | 0.05 | — | 0.12 |
| WM | 0.09 | 0.08 | 0.07 | — |
| Group | SNP | Microsatellite | ||||
|---|---|---|---|---|---|---|
| H E | N a | R s | H E | Na | R s | |
| E | 0.57 (0.16) | 4.1 | 2.2 | 0.82 (0.08) | 7.1 | 4.0 |
| EE | 0.56 (0.20) | 6.1 | 2.3 | 0.83 (0.09) | 11 | 4.2 |
| WE | 0.62 (0.18) | 5.2 | 2.7 | 0.85 (0.06) | 8.4 | 4.5 |
| WM | 0.64 (0.20) | 4.2 | 3.2 | 0.82 (0.08) | 5.7 | 4.7 |
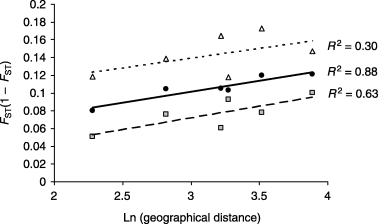
Regressions of pairwise FST/(1 − FST) on Ln of linear geographical distance among the inferred groups. ▵---, □--- and •–– correspond to FST estimated using SNP markers only, microsatellite markers only and both sets of markers, respectively.
Significant genetic isolation by geographical distance was detected at the group level, confirming the visual impression that the groups inferred were a posteriori consistent with geography. The Spearman rank correlation coefficient was found significant when using FST estimated on either the 19 markers (rho = 0.83; P < 0.05, R2 = 0.88, see Fig. 3), or the microsatellite markers alone (rho = 0.88, P < 0.05, R2 = 0.63, see Fig. 3). However, the correlation was no longer significant when using FST estimated on the SNP markers alone (rho = 0.43, P = 0.77, R2 = 0.3, see Fig. 3). No relationship was found between genetic distance and geographical distance among all pairs of individual accessions (R2 around 1%, not shown).
Linkage disequilibrium
When considering the whole sample, an excess in the number of pairs of loci in significant LD was found: 23 out of 171 pairs were in significant LD when ∼8 pairs were expected by chance alone when testing at the 5% level (binomial two-tailed test, P < 0.0001). When significance was assessed using a null hypothesis obtained by assuming no LD within groups (using permutations within groups), 15 of these 23 pairs were no longer significant. No excess in number of pairs of loci showing significant association was left when tested under the appropriate null hypothesis as only 8 pairs out of 171 remained in significant LD at the 5% level.
Discussion
The present study clearly shows the presence of a large-scale structure in A. thaliana. When compared to the unique analogous study of large-scale population structure recently published that utilized 876 markers (Nordborg et al. 2005), only 19 markers were sufficient here to uncover genetic stratification, without using prior information on the population of origin of any of the clustered accessions. This was confirmed here by significant genetic isolation by geographical distance at the group level. Traces of the colonization route in Europe were suggested by a decreasing gradient in allelic richness from West to East. More importantly, our study revealed that most significant LD detected in the sample was due to the population structure detected. Below, we discuss possible caveats, and contrast in more detail our results with previous studies describing various aspects of polymorphism in Arabidopsis thaliana at different geographical scales.
SNP vs. microsatellite markers
When using the complete data set of markers, a robust stratification characterized by stable and highly contrasted individual proportions of membership was found. In contrast, neither the microsatellite nor the SNP markers allowed for the detection of such genetic stratification when used alone. This may reflect the reduced power that comes from examining only ∼10 loci of each type. It is important to note, however, that the precise clustering obtained is likely to depend on both the sampling of accessions and the choice of loci. But as shown by Nordborg et al. (2005) who used a different set of markers and accessions but a similar model-based method, the clustering solution found is consistent a posteriori with geography. The structure algorithm indirectly utilizes LD among unlinked loci to infer group composition (but see Pritchard et al. 2000a). Most pairs of unlinked loci involved a microsatellite and an SNP (90 pairs of 171 possible pairs). Accordingly, most pairs exhibiting significant LD were found in this category. This suggests that in our study both subsets of markers were necessary to provide enough loci for the population structure to be inferred. Incidentally, the fact that no significant LD remained when tested under the appropriate hypothesis may also reflect a lack of power in our study. Nevertheless, this brings about the question of whether an extensive number of markers are necessary to detect a large-scale population structure in this species. Most previous studies only characterized either a few genetic groups with some geographical consistency (e.g. Barth et al. 2002) or diversity zones (Hoffman et al. 2003). In the only previous study uncovering the existence of a large-scale population structure in A. thaliana, the authors suggested that this result was probably due to the extremely large number of markers (876) they used (Nordborg et al. 2005). Our results rather suggest that the model-based method we both used can uncover a broad-scale stratification with many fewer markers.
Because of the density of the markers included in their study, Nordborg et al. (2005) used a more parameter-rich model than we did for inferring population structure. Although the model they used allows a more detailed analysis, such as inferring the ancestral population of origin of particular chromosomal regions within individuals, the global picture obtained is similar in both studies. Note that only 17% of accessions were common between the two studies. Some differences were observed and are discussed below.
Pattern of the genetic differentiation between clusters
Considering the large geographical range of this study, groups uncovered by our analysis should not be considered as populations. These groups instead reflect a regional level of genetic differentiation comprising more closely related populations. The existence of a distinct Eurasian group agrees with previous analyses (AFLP data, Sharbel et al. 2000; Nordborg et al. 2005), as well as the existence of a genetic differentiation between Western Europe and Eastern Europe (Nordborg et al. 2005). In addition, the clustering of the accessions from the West Mediterranean region provides support for the hypothesis of the existence of a glacial refuge during glacial cycles in this region (see for instance, Comes & Kadereit 1998). Note that this region was not clearly discriminated from the others in the study of Nordborg et al. (2005). This might be due to the fact that seven of the eight accessions that were assigned to the West Mediterranean group in our study were not included in the sample used by Nordborg et al. (2005).
When including six accessions from North America in our sample, these were sequentially clustered with the Western Europe cluster (at K = 4) and then grouped in a single cluster distinct from the Western Europe cluster (data not shown). This is very similar to what was obtained by Nordborg et al. (2005) and consistent with previous results that suggested a possible long-distance dispersal from Western Europe to North America as a result of human activities (Kawabe & Miyashita 1999; Hoffman et al. 2003). More detailed analysis (not shown) revealed that the six accessions from North America could be divided into two distinct groups of highly similar genotypes, which suggests a strong recent founder effect in this region. Including seven Japanese accessions in the sample did not change the clustering solution presented here. However, it is interesting to note that accessions originating from Japan were assigned to several different clusters. This could be due to recent migration/colonization events.
No genetic isolation by distance was detected at the individual level. Genetic distances between pairs of individual accessions were very large with low variance, even between accessions assigned to the same group and somewhat geographically closer. A similar pattern emerged in the study of Nordborg et al. (2005). Nevertheless, our analysis revealed a significant isolation by distance relationship at the group level. Indeed, the correlations observed between geographical and genetic distances among groups estimated using either the microsatellite markers alone or both sets of markers were positive and significant. The correlation obtained when using the SNP markers alone was also positive but not significant. When pairwise distances were estimated using all the markers, the correlation between geographical and genetic distances increased dramatically (R2 = 0.88). This suggests that the weaker positive correlation based on SNP markers was not due to chance. Differences in mutation processes between microsatellites and SNPs are expected to affect (i) levels of differentiation at equilibrium and (ii) rates of convergence to new equilibrium values after colonization events or recent gene flow. These mutational differences can explain the variation in the strength of the observed correlations between the types of markers.
Footprints of ancient glacial refugia in the data?
Our data may be discussed with regard to the scenario of postglacial colonization of Europe from putative glacial refugia (about 17 000 years) proposed by Sharbel et al. (2000). These authors proposed that Europe may have been recolonized from a glacial refugium in Asia and to a lesser extent from another refugium located in Iberia. However, they found no increase in genetic diversity (measured as HE) in central Europe relative to any of the two putative refugia. This was interpreted as consistent with a scenario whereby the genetic diversity of migrant populations derived from each contributing refugium had been decreased by drift during the recolonization. Here, we found a significant gradient in allelic richness from West to East. This could be interpreted as consistent with a recolonization of Europe from a single glacial refugium in the West Mediterranean region, up to Eurasia. This scenario would also be consistent with the genetic isolation-by-distance relationship we found at the group level. Note that other scenarios may be consistent with these observations. The observed gradient in allelic richness may simply reflect, for instance, differences in geographical distance separating clusters of current ‘hybrid’ populations from different refugia. As stressed by Sharbel et al. (2000) and Hoffman et al. (2003), the Balkans are the least sampled area for A. thaliana and this is problematic since this region was identified as a putative glacial refugia (see Hewitt 1999). Further sampling in that region and other undersampled regions such as the West Mediterranean will certainly help in assessing most probable scenarios.
Impact of genetic stratification on patterns of LD
A large amount of diversity is required in association mapping studies, which, especially in highly selfing species, often leads to the use of accessions of heterogeneous geographical origin. Our study documents the known theoretical risk of detecting spurious associations (LD) when using worldwide samples of accessions of A. thaliana. Here, the regional genetic stratification that was inferred was shown to be the main source of ‘spurious’ LD among essentially unlinked markers. When testing LD using the appropriate null hypothesis — one that takes into account the underlying genetic stratification — no excess in number of significantly associated pairs of loci was found between unlinked markers. This is consistent with the fact that the model-based approach we use to infer population structure assumes no LD within groups between unlinked markers. Although genomic control would necessitate using a larger number of markers than we did (but see Pritchard et al. 2001 for a review), this finding also suggests that methods for performing tests of association that account for genetic stratification (see, for instance, Bacanu et al. 2000; Pritchard et al. 2000b) should be mandatory when performing association mapping studies on a large geographical scale in A. thaliana.
This study provides evidence for a regional structure in A. thaliana and confirms a recent finding based on a large-scale survey of sequence polymorphism (Nordborg et al. 2005). We have shown that (i) genetic stratification can be assessed in A. thaliana species using a moderate number of loci and (ii) that accounting for such genetic structure eliminates most ‘spurious’ LD between unlinked markers. Accounting for a regional stratification in A. thaliana will benefit future association studies and more generally, work aiming to estimate different population parameters in this model species. Indeed, together with assessing the most probable demographic scenarios in A. thaliana (Schmid et al. 2005), taking regional structure into account should improve future modelling of the nucleotidic diversity in the genome of this species. This knowledge will be instrumental for building future tools for (i) association-based mapping and (ii) the reliable detection of genomic regions with patterns of diversity suggestive of selection.
Acknowledgements
This work was supported by the funds of the Institut National de la Recherche Agronomique (INRA, France). Marie-France Ostrowski was supported by a postdoctoral fellowship from the project ARACORE. We thank Joëlle Ronfort, Haya-Anne Tsitrone, Jean-Baptiste Vaquieras, Philippe Jarne, Patrice David and Thomas Lenormand for helpful discussions and comments on the manuscript.
Appendix
| E | EE | WE | WM |
|---|---|---|---|
| Te-0 | In-0 | Pi-0 | Can-0 |
| Kas-1 | Ka-0 | Ta-0 | Cvi-0 |
| Mir-0 | Gr-3 | Br-0 | JEA |
| Ms-0 | Dra-0 | Blh-1 | Ita-0 |
| 9481B | Jl-3 | Bur-0 | Alc-0 |
| N6 | Sap-0 | LDV-5 | Sah-0 |
| N8 | Sav-0 | RAN | St-0 |
| N10 | Fl-1 | Bay-0 | Ge-0 |
| N13 | PYL-1 | No-0 | |
| N14 | Sp-0 | Db-1 | |
| N15 | Bl-1 | Enkheim-T | |
| N17 | Pa-1 | Ct-1 | |
| N11 | Kn-0 | Mt-0 | |
| Kondara | Wil-1 | Nok-1 | |
| Hodja-Obi-Garm | Oy-0 | Col-0 | |
| Shakdara | Lip-0 | Stw-0 | |
| Rubezhnoe-1 | Mh-0 | Bla-1 | |
| Ler-1 | |||
| Est-0 | |||
| Chi-0 | |||
| Rsch-4 | |||
| Petergof | |||
| Rld-2 | |||
| Ws | |||
| N4 | |||
| N7 | |||
| Ost-0 | |||
| Edi-0 | |||
| Abd-0 |
References
This work was done within the framework of ARACORE, a collaborative project involving several INRA labs and the CNG (Centre National de Génotypage). The goal of the project was to investigate patterns of naturally occurring variation in the model species Arabidopsis thaliana, and to establish a set of tools enabling the optimal use of natural variation for important adaptive traits. These tools include (1) a sample of lines comprising the bulk of the diversity present in current stock centers and (2) sets of segregating populations to allow mapping of QTL in a variety of genetic backgrounds. More info is available at http://dbsgap.versailles.inra.fr/vnat/.




