Interspecies allometric scaling. Part I: prediction of clearance in large animals
Abstract
Interspecies scaling is a useful tool for the prediction of pharmacokinetic parameters from animals to humans, and it is often used for estimating a first-time in human dose. The knowledge of pharmacokinetics in veterinary species is important for dosage selection, particularly in the treatment of large zoo animal species, such as elephants, giant cats and camels, for which pharmacokinetic data are scant. Therefore, the accuracy in clearance predictions in large animal species, with and without the use of correction factors (rule of exponents), and the impact of species selection in the prediction of clearance in large animal species was examined. Based upon this analysis, it was determined that there is a much larger risk of inaccuracies in the clearance estimates in large animal species when compared with that observed for humans. Unlike in humans, for large animal species, correction factors could not be applied because there was no trend between the exponents of simple allometry and the appropriate correction factor for improving our predictions. Nevertheless, we did see an indication that the exponents of simple allometry may alert us as to when the predicted clearance in the large animal may be underestimated or overpredicted. For example, if a large animal is included in the scaling, the predicted clearance in a large animal should be considered overestimated if the exponent of simple allometry is >1.3. Despite the potential for extrapolation error, the reality is that allometric scaling is needed across many veterinary practice situations, and therefore will be used. For this reason, it is important to consider mechanisms for reducing the risk of extrapolation errors that can seriously affect target animal safety, therapeutic response, or the accuracy of withdrawal time predictions.
Introduction
Interspecies scaling is a useful tool for the prediction of pharmacokinetic parameters from animals to humans. With the advent of new approaches, it is now possible to predict human pharmacokinetic parameters with greater accuracy than was possible a decade earlier. The first-in-human dose can be selected based on pharmacokinetic data from small laboratory animals (mice, rat, rabbit, guinea pig, monkey, and dog). The principles and methods of extrapolation of pharmacokinetic parameters from laboratory animals to man have been extensively discussed (Boxenbaum & Fertig, 1984; Boxenbaum & Dilea, 1995; Lave et al., 1997; Obach et al., 1997; Mahmood, 2005). Similarly, the knowledge of pharmacokinetics in veterinary species is important for dosage selection, particularly in the treatment of large zoo animal species, such as elephants, giant cats and camels, for which pharmacokinetic data are scant. Without an understanding of the factors that can influence the accuracy of these predictions, such extrapolations can lead to ineffective doses or excessively high doses that can cause serious toxicity.
It is now well-established that clearance can be extrapolated from small laboratory animals to man with a fair degree of accuracy, provided that the rule of exponents (RE) is used (Mahmood, 2005). However, it is not known if the clearance from small animals can be extrapolated to large animals with the same degree of accuracy and whether correction factors shown to improve the accuracy of drug clearance predictions in humans can likewise be used to improve predictions in large veterinary species.
This report addresses this issue and highlights many important factors related to the prediction of clearance from small to large animals. In part II of this report, we explore some of the mathematical attributes of the regression analysis that may contribute to errors in allometric predictions in large animal species.
Methods
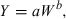 (1)
(1)Method 1: simple allometry
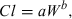 (2)
(2)Method 2: product of maximum life span potential and clearance
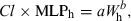 (3)
(3)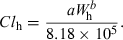 (4)
(4)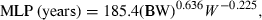 (5)
(5)Method 3: product of brain weight and clearance
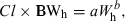 (6)
(6)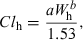 (7)
(7)The aforementioned three methods can only be used under specific conditions. Mahmood and Balian (1996) and Mahmood (2005) formulated a rule so that only one of these methods could be used to predict drug clearance in man from animal data. These authors termed this rule as ‘the rule of exponents’. When scaling from small animal to man, if the exponents of the simple allometry lie between 0.55 and 0.70, simple allometry will predict clearance more accurately than Cl × MLP or Cl × BW. Alternatively, the use of MLP is appropriate for drugs whose exponents lie between 0.71 and 0.99. If the exponent of simple allometry is ≥1.0, then the product of Cl × BW is the most suitable approach for predicting clearance in humans. If the exponents of the simple allometry are >1.3, it is likely that the prediction of clearance from animals to humans will be substantially higher than the observed human clearance, even if using the approach of Cl × BW. If the exponents of simple allometry are below 0.55, the predicted clearance will likely be lower than the observed human clearance.
To predict the clearance from small to large animal species, 12 drugs (Table 1) for which clearance values were available following intravenous administration in both small and large animal species were selected from the literature. For eight drugs, human data were also available. For each set of extrapolations, no less than three species were used to predict clearance in man or in large animals. The following three methods were used to predict the pharmacokinetic parameters in large animals:
| Drugs | Small animals without man | Small animals with man | Species used | Body weight range (kg) | References | ||
|---|---|---|---|---|---|---|---|
| Exponents | R | Exponents | R | ||||
| Caffeine | 0.748 | 0.981 | 0.698 | 0.987 | m, r, rab, mk | 0.03–5.1 | Bonati et al. (1984–85), Bachmann (1989), Peck et al. (1997), Wasfi et al. (2000) |
| Antipyrine | 0.589 | 0.999 | 0.560 | 0.998 | m, r, rab | 0.025–2.75 | Elsheikh et al. (1991), Ben-Zvi et al. (1995), Dyke et al. (1998), Balani et al. (2002) |
| Theophylline | 0.657 | 0.954 | 0.667 | 0.974 | m, r, rab, d | 0.023–10 | Ingvast-Larsson et al. (1985), Gascon et al. (1994), Elsheikh et al. (2001) |
| Fluconazole | 0.728 | 0.999 | 0.616 | 0.953 | m, r, gp, rab, d | 0.02–13.2 | Jezequel (1994), Latimer et al. (2001) |
| Cefoperazone | 0.578 | 0.907 | 0.573 | 0.865 | m, r, rab, mk, d | 0.021–10.7 | Sawada et al. (1984), Soraci et al. (1996) |
| Gentamicin | 0.668 | 0.944 | 0.722 | 0.977 | r, rab, d | 0.23–9.2 | Tanira et al. (1997), Martin-Jimenez and Riviere (2001), McNamara et al. (2001) |
| Propranolol | 0.679 | 0.923 | 0.701 | 0.959 | r, d, mk | 0.25–14.2 | Evans et al. (1973), Aramaki et al. (2000) |
| Furosemide | 1.081 | 0.995 | 0.844 | 0.962 | r, mk, d | 0.2–12 | Doyle et al. (1982), Ali et al. (1998) |
| Thiamphenicol | 0.674 | 0.999 | NA | NA | m, r, rab, d | 0.029–16.6 | Castells et al. (2001) |
| Sulphadimidine | 1.015 | 0.989 | NA | NA | r, d, goat | 0.33–30 | Riffat et al. (1982), Nouws et al. (1987), Witkamp et al. (1992) |
| Flunixin | 0.497 | 0.883 | NA | NA | rab, cat, d | 2.7–10 | Hardie et al. (1985), Lees and Taylor (1991), Landoni et al. (1995), Cheng et al. (1998), Wasfi et al. (1998), Coakley et al. (1999) |
| Enrofloxacin | 0.863 | 0.987 | NA | NA | m, r, rab, d | 0.03–13.4 | Kung et al. (1993), Gavrielli et al. (1995), Bregante et al. (1999); Haines et al. (2000) |
- m, mouse; r, rat; rab, rabbit; gp, guinea pig; mk, monkey; d, dog.
- When man was included in the scaling a body weight of 70 kg was used.
- NA, Human data not available.
- 1
The pharmacokinetic parameters were first predicted from small laboratory animals to humans as well as in large animals. The RE was used to predict clearance in humans but not in large animals (methods 1–3, depending on the exponents of the simple allometry).
- 2
The observed human data were then included with the small laboratory animal data to predict pharmacokinetic parameters in large animal species and to evaluate if the inclusion of human data in the analysis improved the prediction in large animals.
- 3
The clearance was predicted by including at least one large animal species in the scaling. In this method of scaling, the fitted dataset included no animal species whose body weight was less than that of the dog. Wherever possible, human data were included in the scaling. If data from two or three large animal species such as horse, camel, cow or donkey were available, the scaling was repeated sequentially, replacing one large animal by another. Prediction was always made in the species that was not included in the scaling.

Results
Prediction of clearance from laboratory animals to large animal species with and without human data
Table 1 summarizes the allometric exponents and the corresponding correlation coefficients (R) of the regression of log clearance vs. log body weight. A good correlation between body weight and clearance was noted across all drugs with or without the inclusion of human data. The exponent of the simple allometry (without human data) for clearance ranged from 0.497 to 1.081 and from 0.560 to 0.844 with human data. For some drugs, inclusion of human data with the small animal data altered the exponent of the allometry almost by ≥0.1. This difference had a substantial impact on the prediction of clearance in large animal species.
The prediction error associated with the allometric scaling of clearance for these compounds is provided in Table 2. The clearances of all eight drugs in humans (for which human data were available) were predicted with great accuracy when the RE was applied. However, despite the very high correlation coefficient, the predicted clearances in large animals were grossly in error. No particular pattern of error was identified and depending upon the drug, predicted values could be either substantially lower or higher than the observed values. The error in the predicted clearances for some drugs was several-fold. For several compounds, the inclusion of human data with small laboratory animal data improved the prediction of clearance. To evaluate the accuracy in smaller animal species, clearance in cat, goat and sheep was also predicted for some compounds. Unlike that seen with the large animal species, but similar to that seen for humans, the predicted clearance values in cat, goat, and sheep were reasonably accurate when derived from equations based solely on laboratory animals and without the RE.
| Drugs | Body weight (kg) | Observed | Predicted | Predicted with man | Error | Error with man |
|---|---|---|---|---|---|---|
| Caffeine | ||||||
| Man | 70 | 98 | 71 | NA | 0.72 | NA |
| Horse | 400 | 340 | 566 | 393 | 1.66 | 1.16 |
| Donkey | 270 | 221 | 422 | 299 | 1.91 | 1.35 |
| Camel | 365 | 82 | 528 | 369 | 6.44 | 4.50 |
| Antipyrine | ||||||
| Man | 70 | 43 | 55 | NA | 1.28 | NA |
| Horse | 450 | 2790 | 164 | 133 | 0.06 | 0.05 |
| Camel | 375 | 1613 | 148 | 120 | 0.09 | 0.07 |
| Sheep | 25 | 20 | 30 | 26 | 1.50 | 1.30 |
| Goat | 15 | 22 | 23 | 20 | 1.05 | 1.10 |
| Theophylline | ||||||
| Man | 70 | 45 | 42 | NA | 0.93 | NA |
| Horse | 450 | 387 | 138 | 149 | 0.36 | 0.39 |
| Camel | 375 | 2288 | 123 | 132 | 0.05 | 0.06 |
| Goat | 30 | 267 | 23 | 24 | 0.09 | 0.09 |
| Fluconazole | ||||||
| Man | 70 | 22 | 29 | NA | 1.32 | NA |
| Horse | 500 | 167 | 119 | 43 | 0.71 | 0.26 |
| Cat | 2.4 | 1.5 | 2.4 | 1.6 | 1.60 | 1.07 |
| Cefoperazone | ||||||
| Man | 70 | 74 | 79 | NA | 1.07 | NA |
| Horse | 415 | 4981 | 220 | 215 | 0.04 | 0.04 |
| Calf | 80 | 653 | 85 | 83 | 0.13 | 0.13 |
| Sheep | 40 | 107 | 57 | 56 | 0.53 | 0.52 |
| Gentamicin | ||||||
| Man | 70 | 100 | 72 | NA | 0.72 | NA |
| Horse | 318 | 567 | 230 | 318 | 0.41 | 0.56 |
| Sheep | 94 | 87 | 75 | 94 | 0.86 | 1.08 |
| Goat | 28 | 32 | 24 | 28 | 0.75 | 0.88 |
| Cat | 11 | 7 | 11 | 11 | 1.57 | 1.57 |
| Propranolol | ||||||
| Man | 70 | 850 | 728 | NA | 0.86 | NA |
| Horse | 533 | 12 181 | 2891 | 3303 | 0.24 | 0.27 |
| Furosemide | ||||||
| Man | 70 | 154 | 296 | NA | 1.92 | NA |
| Horse | 500 | 6450 | 5878 | 1384 | 0.91 | 0.21 |
| Camel | 247 | 1334 | 2744 | 737 | 2.06 | 0.55 |
| Thiamphenicol | ||||||
| Calf | 75 | 327 | 244 | NA | 0.75 | NA |
| Sheep | 66 | 449 | 224 | NA | 0.50 | NA |
| Pig | 26.6 | 356 | 121 | NA | 0.34 | NA |
| Sulphadimidine | ||||||
| Horse | 275 | 253 | 159 | NA | 0.63 | NA |
| Cattle | 603 | 498 | 352 | NA | 0.71 | NA |
| Camel | 200 | 136 | 115 | NA | 0.85 | NA |
| Sheep | 25 | 19 | 14 | NA | 0.74 | NA |
| Flunixin | ||||||
| Horse | 237 | 492 | 69 | NA | 0.14 | NA |
| Donkey | 447 | 427 | 50 | NA | 0.12 | NA |
| Mule | 467 | 654 | 70 | NA | 0.11 | NA |
| Camel | 475 | 705 | 71 | NA | 0.10 | NA |
| Calf | 119 | 397 | 35 | NA | 0.09 | NA |
| Sheep | 45 | 29 | 22 | NA | 0.76 | NA |
| Enrofloxacin | ||||||
| Mare | 540 | 3331 | 6388 | NA | 1.92 | NA |
| Camel | 453 | 2088 | 5919 | NA | 2.83 | NA |
| Cow | 710 | 5775 | 8723 | NA | 1.51 | NA |
| Sheep | 45 | 209 | 807 | NA | 3.86 | NA |
- NA, not applicable.
Inability of RE to improve allometric predictions in large animal species
In humans, the prediction of clearance was improved by the incorporation of MLP or brain weight. The application of these correction factors depends on the exponents of the simple allometry as described previously. To determine whether or not the RE can be applied to allometric scaling in large animal species, the influence of MLP and brain weight was examined using two drugs whose clearance values have been estimated across a wide variety of animal species: enrofloxacin and furosemide (Table 3).
| Species | Body weight (kg) | Observed Cl | Predicted Cl (SA) | Predicted Cl (MLP) |
|---|---|---|---|---|
| Enrofloxacin | ||||
| Sheep* | 45 | 209 | 863 | 903 |
| Cow* | 700 | 5775 | 9216 | 16 992 |
| Horse* | 550 | 3392 | 7484 | 10 188 |
| Camel* | 453 | 2088 | 6330 | 8142 |
| Horse† | 550 | 3392 | 3635 | 3155 |
| Camel† | 453 | 2088 | 3121 | 2384 |
| Furosemide | Predicted Cl (BRW) | |||
| Horse‡ | 500 | 6450 | 2730 | 24 057 |
| Camel‡ | 247 | 1334 | 1349 | 4576 |
- *Allometric relationships obtained with SA or MLP × Cl using small animals (mouse, rat, rabbit, dog) was as follows: SA: Cl = 32.3W0.863, r = 0.991; MLP × Cl = 21.2W1.169, r = 0.989.
- †Allometric equation is based upon data from dog, sheep and cow (SA: Cl = 25.5W3, r = 0.89; MLP × Cl = 35.3W0.864, r = 0.915).
- ‡Allometric relationships obtained with SA or brain weight × Cl using small animals (rat, rhesus monkey, and dog) was as follows: SA: Cl = 5.46W1.0, r = 0.979; Cl × BRW = 0.051W2.0, r = 0.999.
In large animal species, the RE did not improve prediction of clearance (Table 3). Furthermore, unlike that seen with humans, there was no trend in the exponents of the simple allometry that could guide in the selection of a particular correction factor. Nevertheless, for these same compounds, RE did substantially improve our estimates of clearance in humans. For example, the human clearance of furosemide using simple allometry (based upon rat, rhesus monkey and dog) was 381 mL/min. This is substantially higher than the observed human Cl value of 154 mL/min. However, when brain weight was used as a correction factor (allometric exponent in this case = 1.0), the prediction improved substantially (163 mL/min). On the other hand, the application of brain weight introduced substantial error in the predicted clearance of camel and horse.
In the case of enrofloxacin (for which there is no human data), our clearance prediction (based upon data in mice, rat, rabbit and dog) went from 1263 mL/min when using simple allometry to 370 mL/min when using MLP (allometric coefficient was 0.863). Application of the MLP introduced substantial error in the predicted clearance of cattle, horses, and camels. The analysis from these two drugs (and several others not shown here) indicates that although the RE substantially helps in improving the predicted human clearance, it is not applicable to the large animals. At this time, the reasons for this are not known.
Impact of species selection in the prediction of clearance in large animal species
In this set of evaluations, the smallest animal included in the data set for the prediction of clearance was the dog. Human data were included in the scaling when available. At least one large animal species (horse, camel, donkey, mule, or cattle) was included in the scaling. The results of this analysis are shown in Table 4. The errors associated with the predicted clearance based upon the inclusion of larger animal species (termed ‘current’) were compared with the errors in predictions when the scaling was based upon data solely from the small laboratory animal species (as reported in Table 2). These ‘Table 2’ error values represent those error estimates obtained when human data were excluded from the regression analysis. Treating each scaling event for each animal species as a single ‘observation’, the magnitude of error observed across compounds when using either the species included in Table 2 vs. those in Table 4 (termed ‘current’), was compared to assess if there are differences in the overall accuracy characteristics of these allometric estimates (Fig. 1). Note that when error = 1, the clearance value predicted by scaling equals the observed clearance value.
| Species used | Exponents | R | Species predicted | Observed Cl | Predicted Cl | Error | |
|---|---|---|---|---|---|---|---|
| Current | Table 2 | ||||||
| Caffeine | |||||||
| Dog, man, donkey | 0.727 | 0.998 | Horse | 312 | 340 | 0.92 | 1.66 |
| Camel | 292 | 82 | 3.56 | 6.44 | |||
| Dog, man, horse | 0.762 | 0.999 | Donkey | 221 | 256 | 1.16 | 1.91 |
| Camel | 82 | 323 | 3.94 | 6.44 | |||
| Antipyrine | |||||||
| Dog, man, camel | 0.827 | 0.765 | Horse | 2790 | 860 | 0.31 | 0.06 |
| Dog, man, horse | 0.951 | 0.795 | Camel | 1613 | 1038 | 0.64 | 0.09 |
| Theophylline | |||||||
| Dog, goat, horse | 0.688 | 0.793 | Camel | 2288 | 478 | 0.21 | 0.05 |
| Dog, goat, camel | 1.261 | 0.957 | Horse | 387 | 3657 | 9.45 | 0.36 |
| Enrofloxacin | |||||||
| Dog, sheep, cow | 0.784 | 0.897 | Mare | 3331 | 3552 | 1.07 | 1.92 |
| Camel | 2088 | 3095 | 1.47 | 2.83 | |||
| Dog, sheep, mare | 0.676 | 0.969 | Cow | 5775 | 3063 | 0.53 | 1.51 |
| Camel | 2088 | 2261 | 1.08 | 2.83 | |||
| Dog, mare, camel | 0.554 | 0.987 | Cow | 2088 | 3230 | 1.55 | 1.51 |
| Sheep | 209 | 703 | 3.36 | 3.86 | |||
| Cefoperazone | |||||||
| Dog, man, horse | 1.189 | 0.875 | Calf | 653 | 348 | 0.53 | 0.13 |
| Sheep | 107 | 153 | 1.43 | 0.53 | |||
| Dog, man, calf | 0.703 | 0.504 | Horse | 4981 | 758 | 0.15 | 0.04 |
| Sheep | 107 | 146 | 1.36 | 0.53 | |||
| Furosemide | |||||||
| Dog, man, horse | 1.149 | 0.934 | Camel | 1334 | 1740 | 1.30 | 2.06 |
| Dog, man, camel | 0.864 | 0.923 | Horse | 4981 | 1632 | 0.33 | 0.91 |
| Sulphadimidine | |||||||
| Dog, goat, horse | 1.248 | 0.990 | Cattle | 498 | 737 | 1.48 | 0.71 |
| Camel | 136 | 186 | 1.37 | 0.85 | |||
| Sheep | 19 | 14 | 0.74 | 0.74 | |||
| Dog, goat, cattle | 1.161 | 0.993 | Horse | 253 | 217 | 0.86 | 0.63 |
| Camel | 136 | 150 | 1.10 | 0.71 | |||
| Sheep | 19 | 13 | 0.68 | 0.74 | |||
| Dog, goat, camel | 1.175 | 0.988 | Cattle | 498 | 555 | 1.11 | 0.71 |
| Horse | 253 | 220 | 0.87 | 0.63 | |||
| Sheep | 19 | 13 | 0.68 | 0.74 | |||
| Flunixin | |||||||
| Sheep, calf, donkey | 1.690 | 0.920 | Horse | 492 | 1868 | 3.80 | 0.14 |
| Mule | 654 | 2012 | 3.08 | 0.11 | |||
| Camel | 705 | 2070 | 2.94 | 0.10 | |||
| Sheep, mule, donkey | 1.386 | 0.987 | Horse | 492 | 754 | 1.53 | 0.14 |
| Calf | 397 | 120 | 0.30 | 0.09 | |||
| Camel | 705 | 820 | 1.16 | 0.10 | |||
| Dog, sheep, donkey | 1.173 | 0.973 | Horse | 492 | 707 | 1.44 | 0.14 |
| Calf | 397 | 150 | 0.38 | 0.09 | |||
| Camel | 29 | 759 | 1.08 | 0.10 | |||
| Mule | 654 | 744 | 1.14 | 0.11 | |||
| Dog, sheep, camel | 1.109 | 0.986 | Horse | 492 | 565 | 1.15 | 0.14 |
| Calf | 397 | 130 | 0.33 | 0.10 | |||
| Sheep | 29 | 44 | 1.52 | 0.76 | |||
| Mule | 654 | 593 | 0.91 | 0.11 | |||
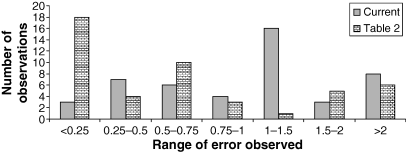
Comparison of error seen from large animal predictions based on small species vs. larger animal species.
From these results, we see that for any of the large animal species, the predicted clearances are highly dependent upon the species included in the regression analysis. For some species and compounds, there were large discrepancies between the predicted clearance values, depending upon the large animal species included in the allometric assessment. With regard to comparing the error from this ‘current’ assessment to the error values reported in Table 2, for most (but not all) compounds, the magnitude of the error was substantially reduced when at least one large animal species was included in data set used for the predictions. As seen in Fig. 1, there was a much greater proportion of error falling within the range of 0.5–1.5 (i.e., more accurate predictions) when large animal species were included in the data set when compared with when only laboratory animals were included in the analysis. This is consistent with the importance of including large animal species in the allometric analysis, even though there was a slightly greater risk of overestimating the true clearance values when large animal species were included in the regression analysis.
In general, when the equation is based solely upon small laboratory species, there is a great propensity for substantially underestimating clearance and, unlike that observed for humans, the drug clearance in large animal species is generally poorly predicted based on data obtained in laboratory animals.
Discussion
Despite the potential for extrapolation error, the reality is that allometric scaling is needed across many veterinary practice situations and therefore will be used. For this reason, it is important to consider mechanisms for reducing the risk of extrapolation errors that can seriously affect target animal safety, therapeutic response, or the accuracy of withdrawal time predictions. Based upon this analysis, it appears that inclusion of at least one large animal in the scaling (with or without human data) can improve predictions. As discussed in part II, there may be several reasons for this finding.
Another important consideration is the exponent of allometry. As mentioned previously, if the exponents of the simple allometry are <0.55 then the predicted clearance in humans is likely to be lower than the observed values. The magnitude of this underestimation cannot be determined by the value of the exponent. If the exponents of the simple allometry are >1.3, the predicted clearance in humans will be overestimated by several orders of magnitude, even when using brain weight as a correction factor. In large animals, correction factors could not be applied because there was no trend seen between the exponents of the simple allometry and the appropriate correction factor for improving our predictions. Nevertheless, we did see an indication that the exponents of simple allometry may alert us to when the predicted clearance in the large animal may be underestimated or overpredicted. An example of this was seen with flunixin. The exponent of allometry based upon small laboratory animals was 0.497. The predicted clearances of flunixin in six large animal species were substantially underestimated (Table 2). When the large animal species were included in the scaling, the exponents of allometry increased (Table 4). Depending upon the species included in the regression analysis, the allometric exponents ranged from 1.11 to 1.69. The predicted clearances of flunixin were near the observed clearances for large animal species when the exponent of the allometry was either 1.173 or 1.109. However, clearance values were grossly overestimated when the allometric exponent was 1.69. Therefore, it is suggested that if a large animal species is included in the scaling, the predicted clearance in the other large animal species should be considered overestimated if the exponent of the simple allometry is >1.3.
The use of allometric scaling to predicted clearance across species always has the risk of ignoring potential differences in clearance mechanisms and metabolic pathways. For example, most species either convert ketoprofen from the R to the S enantiomer (rodents, dogs, rabbits, monkey, horse, cat) or do not convert at all (cattle and llamas). Asian elephants are the only studied species that appears to convert S to R. Elephants also appear to produce a glycine conjugate not reported in other species (Hunter et al., 2003). In addition, the vast majority of large animals for which pharmacokinetic data are available are herbivores. Conversely, the smaller animal species are either omnivores (mouse, rat, monkey and human) or carnivores (dogs and cats). This difference in feeding behavior itself can influence drug metabolism and renal elimination. A detailed discussion of the differences in drug metabolism that may influence extrapolation error when small animals are used for human preclinical drug development has been reviewed elsewhere (Martinez, 2006). While large carnivore data (lion, tiger, polar bear, etc) would be helpful, the obvious dangers hinder this area of research. Some marine mammal species may be worthy of consideration, but due to body fat composition of species such as killer whales (Orcinus orca), the results would be of limited use.
Another point of consideration is the interspecies differences in the contribution of various organ systems and differences in body composition as it pertains to the body weight estimates. For example, when using ruminants in an allometric evaluation, we also need to consider the percentage of the estimated value of weight that is associated with rumen fluids. In an adult cow (e.g., 1300 lb), the rumen can contain more than 80 gallons of grain and fluid (Ensminger et al., 1990). When we consider sheep, 13% of their body weight is attributable to rumen contents and almost 12% of their live weight is associated with fleece and pelt (MacGregor, 1980). On the other hand, the wet weight of digestive contents in 10 African wild elephants in Kruger National Park was estimated to be approximately 10% of the total body weight (A. Craigmill, personal communication; Isaza & Hunter, 2004). When considering this value on a log scale, the latter translates into W = 2.7 for digestive contents and 3.7 for the body weight (where an adult African elephant is estimated to weigh between 4100 and 5000 kg) (Schmidt, 1986). From these values, we can see how these certain species-specific anatomical traits can greatly influence the accuracy of the predicted clearance.
Even if these normal physiological differences could be ignored, there remains the error attributable simply to extrapolation. For large animal species, when generating an equation using data derived from mice, rats and dogs, there is almost a 600-fold range of weights. When using that equation to extrapolate to man, there is a five- to sixfold difference in weight between actual (dog) data vs. extrapolated (human) data. On the other hand, if an allometric equation is established solely on the basis of data obtained in large animal species such as cattle, horses, and donkeys, there is less than a twofold range in weights. Therefore, using only large animal species for generating the allometric equation will compromise our ability to adequately describe the slope and intercept as a function of body weight. These potential sources of extrapolation error are further examined in part II.




