Do dams and levees impact nitrogen cycling? Simulating the effects of flood alterations on floodplain denitrification
Abstract
A fundamental challenge in understanding the global nitrogen cycle is the quantification of denitrification on large heterogeneous landscapes. Because floodplains are important sites for denitrification and nitrogen retention, we developed a generalized floodplain biogeochemical model to determine whether dams and flood-control levees affect floodplain denitrification by altering floodplain inundation. We combined a statistical model of floodplain topography with a model of hydrology and nitrogen biogeochemistry to simulate floods of different magnitude. The model predicted substantial decreases in NO3-N processing on floodplains whose overbank floods have been altered by levees and upstream dams. Our simulations suggest that dams may reduce nitrate processing more than setback levees. Levees increased areal floodplain denitrification rates, but this effect was offset by a reduction in the area inundated. Scenarios that involved a levee also resulted in more variability in N processing among replicate floodplains.
Nitrate loss occurred rapidly and completely in our model floodplains. As a consequence, total flood volume and the initial mass of nitrate reaching a floodplain may provide reasonable estimates of total N processing on floodplains during floods. This finding suggests that quantifying the impact of dams and levees on floodplain denitrification may be possible using recent advances in remote sensing of floodplain topography and flood stage. Furthermore, when considering flooding over the long-term, the cumulative N processed by frequent smaller floods was estimated to be quite large relative to that processed by larger, less frequent floods. Our results suggest that floodplain denitrification may be greatly influenced by the pervasive anthropogenic flood-control measures that currently exist on most majors river floodplains throughout the world, and may have the potential to be impacted by future changes in flood probabilities that will likely occur as a result of climate shifts.
Introduction
One of the largest anthropogenic alterations to global biogeochemical cycling is the disruption of the nitrogen cycle (Vitousek et al., 1997a). Human activities have doubled the rate of nitrogen input to terrestrial systems (Vitousek et al., 1997a). In some cases, this has greatly increased nitrogen loadings to rivers, estuaries and oceans (Vitousek et al., 1997a). For example, average nitrate concentrations in the Mississippi River have increased over 10-fold since the 19th century (Goolsby & Battaglin, 2001), contributing to eutrophication and diminished quality of drinking water (Carpenter et al., 1998; Mosier et al., 2001). Yet in other cases, in-stream nitrogen levels have remained low relative to massive N loading (Boyer et al., 2002). It is unknown whether this unaccounted for N is lost quickly via denitrification (the conversion of NO3-N to atmospheric N2) or stored in long-term pools (van Breemen et al., 2002). Thus, a fundamental challenge to quantifying widespread changes in the nitrogen cycle is understanding the significance of denitrification.
Floodplains may be particularly important sites for denitrification and retention of nitrogen. While the anoxic sediments of lakes, rivers and wetlands are all active sites of denitrification (Jannson et al., 1994; Howarth et al., 1996), fluvial lakes retain more NO3-N than river fragments (Hillbricht-Ilkowska, 1999) and wetlands retain more N than rivers (Saunders & Kalff, 2001). Work in tropical (Kern et al., 1996; Esteves et al., 2001) and temperate systems (Brinson et al., 1983; Tockner et al., 1999) suggest that floodplains can retain N well. For example, diversion of a portion of Mississippi River through the Bonnet Carre Spillway resulted in a 28–42% decrease in nitrate concentrations (Lane et al., 2001). Also, fluctuating water levels resulting from floods create the aerobic and anaerobic conditions particularly effective for enhancing nitrification and denitrification (Reddy & Patrick, 1975; Groffman & Tiedje, 1988) in alluvial soils (Ponnamperuma, 1972; Keeney, 1973). Lastly, more denitrification occurs in forested wetlands when the hydrologic regime is maintained than in restored wetlands where the hydrologic regime has not been reestablished (Hunter & Faulkner, 2001).
Flooding patterns on most major river floodplains in the northern hemisphere have been massively altered for flood control and navigation, however (Dynesius & Nilsson, 1994; Power et al., 1995; Nilsson et al., 1997; Vitousek et al., 1997a). Dams have lowered the height of flood peaks in many rivers, reducing the frequency and amount of overbank inundation. Flood-control levees restrict the lateral flow of water and accompanying nutrients from rivers to their floodplains (Sparks, 1995). While the effect of water level changes on biogeochemistry has been established at local scales (reviewed by Hill, 2000), predicting the impact of changing hydrology on biogeochemical fluxes over broad scales remains an enormous challenge (Pinay et al., 2002). Not too surprisingly, the effect of flood modifications on denitrification in large rivers is poorly described (Vitousek et al., 1997a).
We ask whether dams and levees impact floodplain denitrification by altering patterns of floodplain inundation, and attempt to surmount several obstacles to addressing this question by using a spatial simulation model. Floodplain denitrification rates are highly variable because of the spatial variability of floodplain soils and topography, as well as the hydrologic variability resulting from the rise and fall of floodwaters (Johnston et al., 2001). Such pronounced spatial heterogeneity poses a severe challenge for direct measurements of floodplain-scale denitrification as well as the extrapolation of fine-scale measurements to broader spatio-temporal scales. Also, experimental floods at the scale of entire floodplains are not common, as they are expensive, infeasible or even impossible to perform, much less replicate. Using a simulation model, we can simulate experimental addition or removal of levees and dams and examine differences because of flood magnitude while replicating over multiple floodplains. While not a replacement for field measurements and experiments, heuristic models provide an important first step towards the systematic examination of scenarios impossible or difficult to address in any other way. Here, we present a simulation modelling approach that includes spatial variability in floodplain topography, temporal variability of floods, and a replicated experimental design.
Our goal is to assess the potential effects of dams and levees using a generalized floodplain denitrification model. While not intended to capture the detail of any particular floodplain precisely, the simulations are representative of floodplains typical of the Upper Mid-western USA. Our model includes several of the potential sources of variability in floodplain-scale denitrification: variable pond size, duration, and location relative to flood-control levees, as well as floods of different magnitude. We combine a general statistical model of floodplain topography (Gergel, 2002) with a model of floodplain pond hydrology and biogeochemistry of dissolved organic carbon, oxygen and nitrate. First, we examine the behavior of our model at the scale of an individual pond. We then compare denitrification on entire floodplains subject to different hydrologic modifications (dams and levees) for floods of different magnitude. We then suggest some priorities for further research.
It is extremely important to note that while many, many factors could impact the total nitrate processed in any particular circumstance (e.g. flood timing, temperature, etc.) the goal of our model was not to predict the exact amount of nitrate processed on a particular floodplain. Instead, our goal is to generate hypotheses about the relative differences in N processing on floodplains subject to dams vs. flood-control levees. Our question was implicitly: How do levees and dams influence N processing while holding a variety of other important factors consistent.
Methods
We simulated floodplain landscapes using a previously developed fractal terrain model for floodplains of the Upper Mid-western USA (Gergel, 2002). When flooded, depressions in the simulated terrain received NO3-N, dissolved organic carbon (DOC) and well-oxygenated water. As ponds drained, nitrogen losses because of biotic assimilation and denitrification were determined for both the water column and the underlying sediments. Scenarios compared N processing among four different types of anthropogenic modifications: (1) natural, unmodified river floodplains; (2) leveed floodplains; (3) floodplains with upstream regulated flows (the dam scenario) and (4) both modifications (upstream dam+levee). Each scenario was examined for a range of flood magnitudes. An overview of the major steps of the modeling process is shown in Fig. 1.
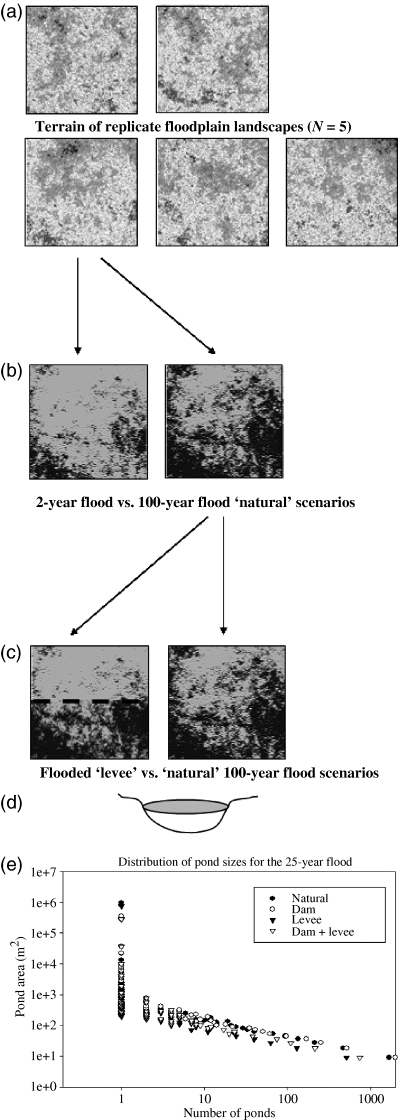
Conceptual overview of modelling process. (a) Floodplain topography for five simulated replicate floodplains (1500 × 1500 m2) used in this model (originally developed by Gergel, 2002). Topographic relief (in 0.5 m intervals) is shown. The main channel is adjacent to the lower boundary of each landscape, and there is a gradient in topographic relief from the main channel towards the uplands. (b) Example floods of different magnitude on the same simulated landscape showing the 2- and 100-year floods. Black areas are inundated. Pond density reflects the topographic gradient across the floodplain from the lowest to higher areas. 2-, 5-, 25-, 50-, 100- and 500-year floods were simulated on each of the five floodplain replicates. (c) Four flood modification scenarios were considered: Natural, Unmodified floodplain; Regulated Flows (Dam); Leveed floodplain; and Dam+Levee. Shown here are the flooded ‘Levee’ vs. ‘Natural’ floodplain scenarios for the 100-year flood. Levee is shown by broken line bisecting the floodplain. (d) Hydrology and biogeochemistry models run in each individual pond: after filling of ponds, the denitrification model was run in each pond using the biogeochemistry model outlined in Fig. 2 and explained further in Appendix 2. (e) Distribution of pond sizes for 25-year flood subject to different modifications (dams, levees, dams and levees, or natural). To compare among the different modification scenarios, the total nitrogen processed (kg NO3-N) by each pond (for a given magnitude flood) was summed for the entire floodplain.
Floodplain terrain
Terrain was simulated to create five replicate floodplains 230 ha in size (Fig. 1a). Simulated terrain was used to control for topographic factors that could influence our results, as well as provide appropriate replication. The area inundated during a flood was governed by the floodplain terrain at given elevations relative to flood stage. Furthermore, the number of ponds on a floodplain was a result of the spatial auto-correlation of the terrain. Highly correlated terrain generally produces fewer, more connected ponds, whereas less auto-correlation in terrain produces many disconnected ponds. Both the auto-correlation of the terrain and the area at different elevations can vary greatly within and among floodplains. However, our simulated terrain controlled for these factors, enabling us to isolate the variability in nitrogen processing solely because of levees and dams (and flood magnitude). The procedure used to create synthetic floodplain landscapes and simulate floods was identical to that described in Gergel (2002) based on the terrain and hydrologic characteristics of Wisconsin River floodplain near Portage, WI (Gergel, 2002; Gergel et al., 2002). Each of the five replicate landscapes were generated using RULE software designed for creating fractal landscapes (Gardner, 2000). RULE allowed the initialization of each landscape with a unique random number while holding constant both the area of land at different elevations and the spatial auto-correlation of the terrain. This approach produced five statistically similar, yet unique, replicate landscapes (Fig. 1a). When flooded, the fractal distribution of pond sizes was a result of the fractal geometry of the terrain (Gergel, 2002) and the degree of spatial auto-correlation of the terrain (Fig. 1e). Stochastic processes such as fractional-Brownian motions provide realistic representations of lake-rich, scale-free terrain (Goodchild, 1988). While not appropriate for all types of terrain (Klinkenberg & Goodchild, 1992), this fractal model is useful for producing a range of pond sizes when inundated (Fig. 1e), including many smaller ponds and few large ponds (Hamilton et al., 1992; Gergel, 2002).
Flooding experiments
Flood simulation experiments used a factorial design: four flood modification scenarios (natural, dam, levee, dam+levee) with five different flood magnitudes (2-, 5-, 25-, 100-, and 500-year floods), with the terrain of five replicate floodplains underlying each (Fig. 1a). The levee scenarios involved a setback levee, centered between the channel and the upland edge of the floodplain (Fig. 1c). The effect of an upstream dam was simulated by incorporating the dampening effect on peak flows, a common response of rivers to regulation (Poff et al., 1997). This was accomplished using a lower discharge for a given flood probability (Gergel, 2002) based on simulated regulated and unregulated discharges for the Wisconsin River (Krug & House, 1980) which were used to develop flood probability curves representing dammed and un-dammed conditions (Gergel, 2002). Thus, the 100-year regulated flows were lower than the 100-year unregulated flows, leading to lower water surface elevations during floods. The ‘dam+levee’ scenario incorporated both the dampening of flood stage and the ‘cut off’ of the floodplain by a levee. The natural scenario represented a floodplain unmodified by either an upstream dam or a levee.
The pattern of inundation is adapted from the results of Hydrologic Engineering Center – River Analysis System, U.S. Army Corps of Engineers 1998 (HEC-RAS) (US Corps) simulations along the Wisconsin River (Gergel et al., 2002, Gergel, 2002). Simulated floods were based on the Wisconsin River flood regime, and approximated the timing, flood probabilities and stage/discharge relationships of the Wisconsin River below the Wisconsin Dells, WI. Each simulated flood represented the passing of the flood peak (for one spring flood), set to occur on April 1. Flood probability curves for the Wisconsin River were obtained using PeakFQ software with simulated regulated and unregulated gauge data from Wisconsin Dells (Krug & House, 1980). Floods of several different recurrence intervals were modeled (2, 5, 25, 100, 500 year). Using HEC-RAS and accompanying cross-sections for the Wisconsin River, a stage/discharge curve was developed (Gergel et al., 2002). These simulations used HEC-RAS to determine flood heights associated with 5-, 10-, and 25-year floods. When rounded to the nearest 0.5 m, the curve shows an approximate 0.5 m successive incremental increase in stage between each magnitude flood (Gergel, 2002). Thus, each successive increase in flood magnitude (2-, 5-, 25-, 100-, and 500-year floods) was represented as a 0.5 m increase in flood stage (Gergel, 2002; Fig. 1b). Peak flood stage relative to the elevation of each replicate landscape was used to determine which areas were inundated by a flood. Any depression at an elevation equal to or lower than the flood stage was considered inundated (Gergel, 2002).
These scenarios were representative of a slow rising flood with significant lateral and subsurface movement of floodwaters across a floodplain with sandy soils of high hydraulic conductivity (Gergel, 2002). Bates et al. (1998) have developed synthetic fractal floodplains based on real terrain to evaluate and parameterize a hydraulic floodplain model. On such terrain he examined four stages: (a) bank-full, (b) initial flooding, (c) peak inundation extent and (d) ponding after the floodwave has passed (Bates et al., 1998). Unlike the Bates et al. (1998) model, the model in this current research presents a phenomenological approach to floodplain inundation, mimicking the pattern of overbank inundation, not unlike the flood patterns left after the passage of the floodwave in Bates et al. (1998). Some topographically isolated ponds are filled during the peak flows which then subside, leaving discontinuous ponded areas. Furthermore, sandy soils with extremely high hydraulic conductivity (such as those along the floodplain of the Wisconsin River) likely allow for significant lateral, shallow subsurface movement of floodwaters. Although not modeled explicitly in this phenomenological approach, the inundation patterns assume a quickly rising hydrograph and a floodwave of short duration. Along the Wisconsin River, the floodwave from overbank inundation moves across the floodplain faster than the floodwave associated with the groundwater table, however. A longer duration flood, dominated by a rising groundwater table, would have the potential to fill areas both inside and outside the levee and allow for greater seepage through the levee. No seepage through the levee was modelled.
The distribution of pond sizes is shown for the 25-year flood under the four different scenarios of hydrologic modification (Fig. 1e). The volume and surface area of each pond was exported from ARC/INFO (ESRI 2000) to Matlab 6.5 (Matlab, 2003). The initial depth of each pond was determined by dividing the initial pond volume by the initial pond area. Pond drainage was loosely based on parameters used by Gergel (2002) and described further in Appendix 1. Mean monthly evaporation and rainfall data (Midwestern Regional Climate Center, 1998) resulted in net losses of 5% of the total pond volume per day. As the basins of individual ponds accumulate particulates such as silt, clay, and detritus, drainage parameters in individual pond basins represented seepage rates expected through soils of low hydraulic conductivity (Freeze & Cherry, 1979), in contrast to the intervening areas of sandy loam floodplain soils.
Pond biogeochemistry
The fate of NO3-N delivered to the floodplain by floods was investigated using a model of the dynamics of oxygen, carbon and nitrogen (Fig. 2, Appendix 1). The mass of NO3-N processed in ponds was a function of biotic assimilation and denitrification, and N removal was summed for each floodplain to determine the total mass processed on each floodplain (Figs 1 (d) and (e)).
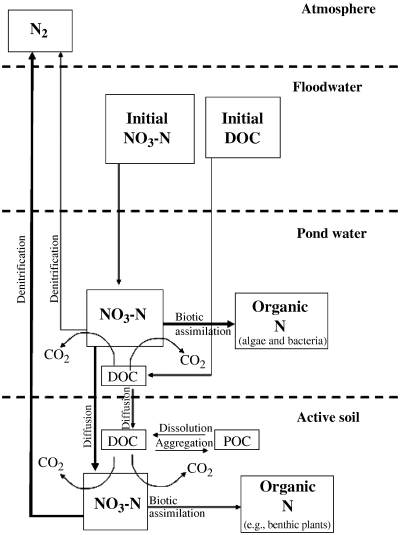
Conceptual diagram of nitrogen biogeochemistry model, showing four major compartments: incoming floodwaters, water column of pond, pore waters of active soil layer, and losses to the atmosphere. The reduction of oxygen levels in ponds (not shown) is a function of respiration. The differential equations used to simulate changes in O2, DOC, and NO3− are described in Appendix 1.
O2 dynamics
Oxygen dynamics in the water column and soil were modeled because conditions of hypoxia are necessary for denitrification to occur. Dissolved oxygen in the water column was modeled as the balance between O2 inputs from the atmosphere, O2 losses to sediment and heterotrophic metabolism. Soil O2 concentrations were the result of inputs from the water column and soil metabolic losses. We assumed no O2 inputs from primary production. We assumed initial saturation of floodwaters and determined the saturating O2 concentration empirically (Rich, 1973). Pond water undersaturated with dissolved oxygen underwent aeration from the atmosphere by turbulent diffusion (Rich, 1973) as described in Appendix 1. Losses from the water column to the sediment were also governed by turbulent diffusion through the water column and the concentration gradient of oxygen between the water and soil. Metabolic losses of O2 in the water (as well as in the soil) were calculated based on the amount of C respired using a molar respiratory quotient of 1 mol CO2 released per mole O2 consumed. Soil O2 concentrations were governed by Fickian diffusion through the active soil layer (Appendix 1).
Dissolved organic carbon (DOC)
We assumed that DOC was the energy source for heterotrophic bacteria because this fraction typically represents 75–95% of the total organic C fraction in aquatic ecosystems (Wetzel, 2001). DOC concentrations were governed by the biotic assimilation of NO3-N, respiration (which determines anoxia), and denitrification. We used a nominal value of 10 mg L DOC in incoming floodwaters, which is typical of instream and floodplain concentrations in the Wisconsin River during spring, including periods of floodplain inundation (USGS, 2000; E. H. Stanley, unpublished data, University of Wisconsin, Madison, WI, USA). The DOC budget included metabolic losses from the water column, losses from turbulent diffusion of DOC from the water to the soil, and metabolic losses in the soil. Metabolic losses were governed by a carbon metabolic coefficient of 0.02 g day−1 (Carpenter & Pace, 1997). In the soil, carbon dynamics were also influenced by dissolution and aggregation of carbon between dissolved and particulate forms which was necessary to stabilize the model's organic carbon dynamics (Appendix 1).
Nitrate (NO3-N)
Initial NO3-N concentrations of floodwaters was 10 mg L to represent conditions characteristics of flood flows in enriched river systems in the Mid-western U.S. (Goolsby et al., 1999). NO3-N losses from pond water included biotic assimilation, diffusion into the soil, and losses to denitrification. Soil NO3-N was governed by inputs via turbulent diffusion from the water column into the soil, losses due to biotic assimilation of NO3-N, and denitrification. Denitrification occurred when the concentration of O2 in the water column or soil was below 1 mg L (Tiedje, 1988). Thus, N losses in the water column and soil were due only to biotic assimilation during oxygenated conditions. N loss through denitrification was calculated using a coefficient of 8.27 g NO3 consumed/C consumed (Seitzinger, 1994). Losses of nitrate to the soil compartment were modeled based on Fickian diffusion (Golterman, 1995; Appendix 1).
The simulations ended when pond depth went below 0.20 m or all nitrate was depleted from the soil and water column. Numerical solutions of the oxygen dynamics became unstable when the pond became too shallow. This effect was eliminated by terminating simulations when pond depth reached 0.20 m. In the simulations, pond duration ranged from 13 to 49 days. The simulated example (pond mean depth=1 m, Fig. 3) lasted 13 days, with soil hypoxia occurring after approximately 2 days (Fig. 3c), and cumulative NO3 processing increasing within a few days post-flood (Fig. 3e).
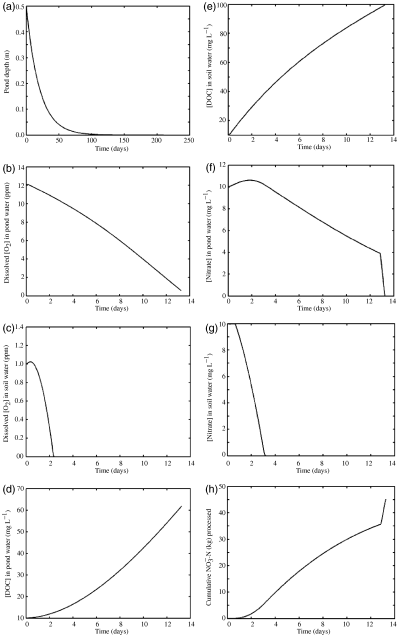
Dynamics for an individual pond (described further in Appendix 2). (a) Pond drainage through time (5% of volume day−1), represented as a change in depth for one hypothetical pond (area=9.0 m−2, depth=0.5 m). (b) and (c) Dissolved oxygen (O2) concentrations in the water column (b) and soil water (c). Oxygen loss is coupled to carbon respiration (Fig. 2). (d) and (e) Simulated dissolved organic carbon concentrations (DOC) for one hypothetical pond in the water column (d) and soil water (e) through time. Initial [DOC] is from floodwaters; DOC losses in the water column and soil are because of respiration. Increases in soil DOC are from breakdown of soil particulate organic carbon (POC) and diffusion from the water column. (f) and (g) Simulated nitrate losses are because of biotic assimilation during oxygenated conditions, and denitrification during conditions of hypoxia (<1 mg l) in the water column (f) and soil (g). (h) Simulated cumulative NO3-N processed over time.
Assumptions
The model included several important simplifying assumptions. It addressed only the fate of NO3-N from floodwaters as this fraction of N dominates in anthropogenically enriched rivers (Goolsby et al., 1999, Arheimer & Wittgren, 2002) and represents >80% of the total N in floodwaters of the Wisconsin River (with NH4-N<10% and low DON) (Forshay & Stanley, 2005). Further, depletion of total N on floodplains is often driven by the loss of the nitrate fraction (Knowlton & Jones, 1997; Tockner et al., 1999). Because we were interested in the fate of river-derived nitrate, N inputs from nitrification were not modeled. Nitrification occurs in oxygenated sediments which are rarely available during flooding (Robertson et al., 1999), and thus this process appears to be responsible for only 10% or less of the nitrate that is denitrified during flooding (Lindau et al., 1994; DeLaune et al., 1996). However, this assumption may exclude some fraction of river-derived N from previous flooding. Specifically, NO3 that is assimilated (i.e. converted to organic N) during flooding may subsequently be converted back to NO3 via mineralization and nitrification during the interflood period and released into the water column when flooding returns. The importance of this delayed cycling of N is unknown for floodplain systems, thus we considered its inclusion to be beyond the scope of this study. Inputs from N-fixation were also not included, but are likely quite minor given the high concentration of N in the floodwaters. As a result, our model's estimates of potential total N loss are probably conservative.
Sensitivity and statistical analyses
Sensitivity analyses were used to determine the influence of select variables and parameters on total NO3-N processed in individual ponds (Appendix 2). Several parameters of interest were varied from a fraction of, to several orders of magnitude greater than, their nominal values. The procedure is described further in Appendix 2.
The mass of incoming NO3-N was calculated as the initial NO3-N concentration in the floodwaters multiplied by the volume of each pond, summed for all ponds on the floodplain. For each replicate floodplain (N=5), we determined the total amount of NO3-N processed for different flood magnitudes under different scenarios. The means across replicate landscapes were compared among the four treatments (natural, dam, levee, dam+levee) using SAS (1989). The coefficient of variation among replicates was determined for the total mass of NO3-N processed. Areal processing rates (NO3-N, kg ha−1) were calculated as the total mass of NO3-N processed divided by the area inundated for the corresponding flood magnitude.
Results
First, we present results for the biogeochemical dynamics of an individual pond. Second, we present our results for simulated floodplains and evaluate the relative impacts of levees and dams. The sensitivity analyses for a set of 100 ponds of equivalent size are presented in Appendix 2.
Biogeochemistry of individual ponds
At the level of an individual pond, available nitrate was lost quickly, in approximately 2 weeks. Dynamics of one hypothetical pond are presented in Fig. 3(a)–(h). Drainage is shown as change in mean depth through time (Fig. 3a), where time 0 is the start of the flood. The gradual depletion of oxygen in water (Fig. 3b) and soil (Fig. 3c) layers over time was followed by the depletion of nitrate in the soil (Fig. 3g) and water (Fig. 3f). Most of the denitrification occurred in the soil compartment of the model. Cumulative NO3-N processed by assimilation and denitrification in both the soil and water column (Fig. 3h) showed that denitrification in the water column was meager because of high oxygen concentrations. Nitrate loss from the water column was primarily the result of biotic assimilation and diffusion into sediments where it was denitrified.
Floodplain dynamics
The first important difference among flood scenarios was the area inundated (Fig. 4a). For the 2-year flood, the total area flooded ranged from 6 ha (dam+levee scenario) to 47 ha (natural scenario). Dams reduced the area flooded (12 ha) more so than the flood-control levees (18 ha). Whether dams or levees had a greater impact on the area flooded, however, depended on flood magnitude. The area inundated in the dam scenario was less than for the levee scenario for 2- and 100-year floods, but greater for the 5- and 25-year events. In all scenarios, the area flooded was equivalent for the 500-year flood as the levees were breached (i.e. over-topped). The combined impacts of a levee and a dam were greatest for the 100-year flood event, as the lowering of the flood peak because of the dam inhibited the levee breach that would otherwise occur (Fig. 4a). Data are summarized by hydroperiod in Gergel (2002).
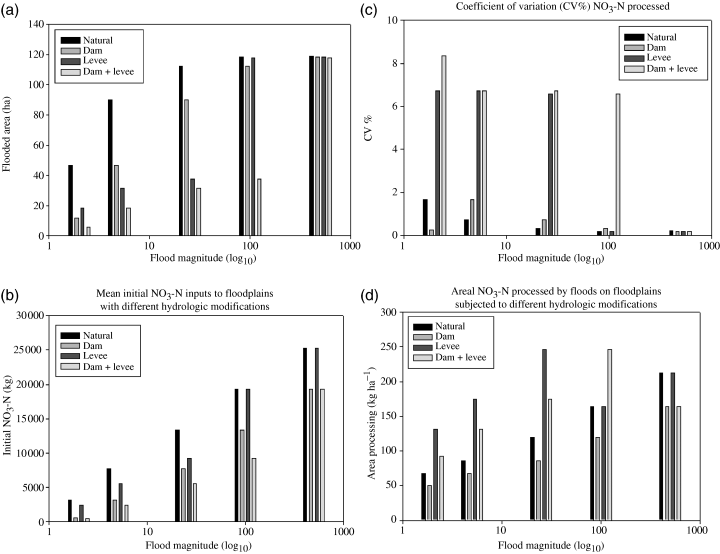
Simulation results. Values are means among replicated simulated floodplains (N=5). (a) Total area flooded (ha) (b) Initial NO3− transported to the floodplain by different inundation scenarios (c) Coefficient of Variation (%) in NO3-N processed under different scenarios (d) Areal NO3-N processing for different magnitude flood events under different scenarios.
Levees and dams also altered the total amount of nitrate processed (Fig. 4b). In every scenario examined here, the entire amount of nitrate reaching the floodplain was processed either through assimilation or denitrification. Dams always reduced nitrogen processing relative to the levee and natural scenarios, regardless of flood magnitude. N processed in the levee scenario was less than in the natural scenarios except for floods large enough to breach the levee. For a given modification, the amount of NO3-N processing increased with flood magnitude (Fig. 4b). For a 2-year flood, the mean total NO3-N processed on unmodified ‘natural’ river floodplains was 3147 kg. Dammed river floodplains processed the lowest amount of total nitrate, averaging 593 kg. The floodplain with a setback levee processed an amount of NO3-N intermediate between the natural and dam scenarios, averaging 2425 kg. The combined effect of an upstream dam and a levee resulted in 514 kg NO3-N processed, the lowest of any scenario. The relative trends for 5- and 25-year floods were similar to those of the 2-year event. For the 5-year flood, the amount of NO3-N processed decreased from natural, to levee, to dam, to the dam+levee scenario, with means of 7743, 3147, 5530, and 2425 kg, respectively, (Fig. 4b). For the 25-year flood, the mean total NO3-N processed was 13368 kg for the natural floodplain, 9228 for the levee scenario, 7743 for the dam scenario, and 5530 for dam+levee. For the 100- and 500-year events, the mean NO3-N processed in the natural scenario (19,299 and 25,242 kg) was similar to that processed in the leveed scenario (19,271 and 25,203 kg) for the respective flood magnitudes. Less NO3-N was processed in the dam scenario for both magnitude events, with means of 13,368 and 19,299 for the 100- and 500-year events, similar to the dam+levee scenario.
The variability in total nitrate processed among replicate floodplains differed substantially among the various treatment scenarios, and among different flood magnitudes. The variability (CV%) for scenarios involving levees (either in the levee only or dam+levee scenarios) was the greatest, ranging from 6.6% to 8.4% (Fig. 4c). This held except in the scenarios where the levee was breached (e.g. 100-year dam+levee and 100- and 500-year levee scenarios). For other scenarios, the CV% was less than 1.7%, and often less than 0.3%. Areal processing rates varied widely by treatment and flood magnitude, from as low as 50 kg ha−1 in the dam 2-year flood to just over 246 kg ha−1 in the levee 25 and dam+levee 100-yr (Fig. 4d). Within a given flood magnitude for the 2-, 5-, and 25-year floods, the areal rates were always greatest for the levee scenarios (Fig. 4d).
Discussion
Floodplain model evaluation
Our floodplain-scale simulations yield several important patterns. Results are comparable with the per cent processed, total nitrate processed, and areal processing rates reported for other floodplains and wetlands. In our simulations, dams reduced the total nitrate processed by floodplains from <25% to ∼60% of the amount processed in the natural (unmodified) scenarios. The effect of a levee was less severe, as the leveed floodplains always processed well over half as much nitrate as the natural scenario. While levees increased areal denitrification, total N processing was largely offset by the reduction in area over which denitrification occurred. Floods of larger magnitude resulted in more nitrate processing than smaller magnitude events (for a given modification scenario) because larger floods transported a greater initial volume of nitrate-rich floodwaters to the floodplain. Scenarios that involved a levee (either the ‘levee only’ or ‘dam+levee’ scenarios) resulted in the most variability in N processing among replicate floodplains. In the following sections, we discuss each of these points in more detail.
The general pattern of complete and rapid loss of nitrate in ponds, and thus, in the entire floodplain, is not unrealistic. A hydraulic residence of time of at least five days has been suggested to promote efficient nitrogen retention (Kadlec & Knight, 1996), as this period of time is assumed to be long enough to promote denitrification of inflowing nitrate and sedimentation of solids. Experimental additions of NO3− to wetlands can result in its attenuation in a matter of hours (Casey & Klaine, 2001) or days. Experimental additions resulting in >10 mg L NO3-N in flooded sloughs of the Wisconsin River were depleted in under 6 days (Forshay and Stanley, 2005). Thus, the rapid N removal in our model is reasonable at the scale of individual ponds and wetlands. At the scale of the entire floodplain, this rapid removal resulted in 100% of NO3-N being processed.
When compared with sewage treatment wetlands, the total nitrate processed by a 230 ha area of floodplain (the size of our simulated landscapes) is not an inconsequential component of a local nitrogen budget. Jackson Creek wetland (a 39 ha wetland near Lake Delavan, WI) contains several sewage treatment ponds. The average daily load of dissolved NO2+NO3-N from May to June was approximately 340 kg during a high precipitation year, and <45 kg for a dry year (Elder & Goddard, 1996). The yearly load of NO2+NO3-N in the dry year was just over 19 000 kg. The natural floodplain scenario in our model processed a similar 20 000 kg during the 100-year flood.
In rivers with large-floodplains, quite substantial areas may be flooded, leading to great potential for denitrification. For example, Gergel et al. (2002) estimate for the Wisconsin River (the river which loosely provided some of the basis for our hypothetical scenarios), a difference in area inundated along a 4 km reach varied from 400 ha (for a 2-year flood) to 1200 ha (for a 500-year flood), assuming the reach was not leveed. Data from sampling during floods, as well as nitrate addition experiments, on that same 4 km reach of the Wisconsin River suggest rough estimates that a 2-year flood might process 37% of the entire load of floodwater N entering the reach (Forshay & Stanley, 2005).
Our areal estimates of NO3-N processing are well within the range of other reported measurements for wetlands and inundated areas. Our highest estimated areal NO3-N removal rates were for floods in the levee treatment, and specifically for the 25-year levee and 100-year dam+levee scenarios (∼246 kg ha−1) (Fig. 4d). Because the floodplain areas between the levee and the main channel were lower in elevation than areas further from the channel, these areas allowed for greater depth of inundation. Thus, areas inside the levees contained a greater volume of floodwater (per unit floodplain area), and a correspondingly greater mass of initial NO3-N per unit floodplain, resulting in greater areal processing than in areas closer to uplands. Our lowest areal estimate (∼50 kg ha−1) was for the 2-year flood dam scenario.
For comparison, areal NO3-N removal capacity of the Ill floodplain was 559 t N yr−1 or 1398 kg N ha−1 yr−1 for the modeled surface area of 40 km2 (Perez et al., 1999). Average N removal in wetlands has been estimated as ranging from 200–500 kg ha−1 yr−1 (Paludan & Fuglsang, 2000; Arheimer & Wittgren, 2002) and less than 100 kg ha−1 yr−1 (Arheimer & Wittgren, 1994). Comparisons of nonflooded (or well-drained) vs. flooded (or poorly drained) conditions have yielded the following ranges: 7 vs. 39 kg N ha−1 yr−1 (Hanson et al., 1994); 4 vs. 10 kg N ha−1 month−1 (Davidsson & Leonardson, 1997); 22 vs. 38 kg N ha−1 month−1 (Davidsson & Leonardson, 1997). However, recall that each flood is of a different length of time depending on flood magnitude (and thus the size of the biggest pond on the landscape). We compare our results with yearly estimates as it is not unreasonable to have just one flood in a year. Multiple floods in a given year would make our results conservative estimates of the nitrate processing capacity of a floodplain. However, when comparing our simulations to data calculated on a “per flood” basis, our areal estimates are not unreasonable. For example, experimental nitrate additions by Forshay and Stanley (2005) led to estimated areal processing rates of 10 mg N m−2 h−1 along the same reach of the Wisconsin River upon which our modeling scenarios are very loosely based. While these estimates are based on measurements made during several days of one flood, when scaled up, such estimates would lead to estimates of 10 kg N ha day−1.
While few such models exist, our model is similar in some ways to Arheimer & Wittgren's (2002) landscape-level denitrification model; however, quite different in some important aspects. Arheimer & Wittgren (2002) compare annual inflows and outflows of total N for eight surface-flow wetlands ranging from 0.1 to 3.0 ha in Southern Sweden and calibrated several models of N loss. The final concentration of N in the outflow was based on: N concentration in the inflow, the area and volume of the wetlands, net N removal rate (g m−2 day−1) and an area/temperature-dependent removal rate coefficient, integrated over time. They also compared several variations of their general model that accounted for temperature differences, as well as, resuspension of nitrogen. Their best model (from N=8 wetlands) was then extrapolated to 40 wetlands (0.5–7.0 ha in size), covering an area of 0.92 km2 (92 ha) within a larger catchment (224 km2). Their estimated removal rates ranged from 57 to 466 kg ha−1 yr−1 depending on different features of the wetlands (Arheimer & Wittgren, 2002), which fall within the range of our areal estimates. Unlike our model, average removal was 10% of inputs (in contrast to our 100% removal). Their simulated wetlands removed on average 358 kg N yr−1, with an average residence time of 41 days. One of the reasons lower nitrate removal rates and percentages may have been observed in other studies may be because of the flow through of wastewater, however.
As with many biogeochemical fluxes, areal field measurements of denitrification made at the plot-level cannot necessarily be scaled up across large heterogeneous watersheds; rendering, simple extrapolation of aerial estimates misleading (McClain et al., 2003). Thus, at the scale of whole watersheds, denitrification is often estimated as the difference between watershed inputs and stream outputs (van Breemen et al., 2002) and can account for almost 40% of storage and losses (van Breemen et al., 2002). Our results expose some of the challenges and assumptions of estimating landscape-scale denitrification for floodplains. Our areal estimates of NO3-N processing ranged from 50 to 246 kg ha−1. The variability in topographic relief resulted in higher areal rates near the main channel, making the scaling up of areal processing rates problematic. The variability in total N processed was always higher for scenarios involving a levee due the importance of the specific location of the lowest lying areas and largest ponds relative to the levee. Such variability was apparent even after using simulated, statistically similar landscapes, which were arguably much more similar than any other paired floodplain landscapes one might compare.
Our estimates of floodplain-scale denitrification are likely conservative because of aspects of nitrogen biogeochemistry not included in the model which were discussed in the methods. Further, several impacts of dams and levees not simulated in our model could influence our results. For example, the levee scenario included only one levee location – a setback levee scenario – where half of the floodplain was available for inundation. Thus, the impact of levees was under-estimated, as levees located closer to the main channel (e.g. mainline levees) would restrict all overbank flooding, thereby reducing the NO3-N processing ability of the floodplain to nil for small floods that do not breach or break the levee. Our model did not include increases in flood stage that often accompany levees (Belt, 1975), but this effect can be minor in setback levee situations (Gergel et al., 2002). Also, impoundments along rivers can increase denitrification because of the increased retention time and contact between nitrate-rich river flows and anoxic reservoir water and/or sediments (Howarth et al., 1996; Garnier et al., 2000). Our simulations did not address this aspect of dams; however, others have suggested this impact may not be significant at the scale of river networks (Seitzinger et al., 2002). Furthermore, the rise in stage associated with increasing flood magnitude varies substantially among floodplains depending on floodplain and channel morphology, so our reported differences in total processing for different magnitude floods are not directly translatable to other floodplains.
Implications
It has been suggested that ‘Further research is needed to better understand the processes controlling N transport and transformations and on how to represent those processes in models that allow assessment at the scale of large regions’ (van Breemen et al., 2002). We agree and would like to suggest several specific points of focus related to this challenge for large river floodplains.
Because 100% of NO3-N was processed in all scenarios, the primary impact of dams and levees on nitrate processing was to reduce the amount of NO3-N initially reaching the floodplain. An upstream dam always caused a greater reduction in the total NO3-N processed than a setback levee for the same magnitude flood (Fig. 4b), but this was not simply because of a reduction in area flooded (Fig. 4a). For example, in the 5-year flood, the area inundated in the dam scenario was greater than in the levee scenario (Fig. 4a), but the total nitrate processed was roughly half as much as the levee scenario (Fig. 4b). In other words, the reduction of flood peaks because of dams always lowered the total volume of floodwaters and initial mass of NO3-N reaching the floodplain (as compared with the levee scenarios), but did not necessarily decrease the area inundated. Setback levees decreased the total NO3-N processed as compared with the natural scenarios, but only for the smaller magnitude events that did not breach the levee (Fig. 4a). By reducing the area inundated relative to the natural scenario (Fig. 4a), a levee reduced the total input of NO3-N to the floodplain.
These findings suggest hypotheses for further evaluation using field measurements. Because the primary impact of dams and levees was reducing the total mass of NO3-N initially reaching the floodplain (Fig. 4b) and nitrate loss occurred rapidly and completely, the volume of floodwaters and mass of nitrate initially reaching the floodplain was of greater concern than characterizing the postflood hydrology of individual ponds. A fortuitous simplification may arise if floodplain denitrification can be assessed by estimating flooded area, pond volume and flood stage, without tracking postflood hydrology and biogeochemistry. Flood stage corresponding to different magnitude events can be estimated using well-developed hydraulic simulation models (e.g. HEC-RAS, USACE 1998). Highly accurate measurements of the height of floodplain inundation can be obtained using both laser and radar altimetry (Mertes, 2002). Interferometric synthetic aperture radar data from the Amazon has been used to track changes in flood stage to centimeters (Alsdorf et al., 2000). These rapidly improving techniques for remote sensing of floods could be used in conjunction with actual flood manipulation experiments that quantify floodplain-scale nitrogen budgets. If our hypothesis is confirmed through field work and broad-scale experiments, this would suggest that monitoring the broad-scale impact of dams and levees on floodplain denitrification may be possible, if tracking of individual pond dynamics is not of primary concern, and remote sensing of flood volume and corresponding incoming nitrate loads can reasonably be accomplished.
Our simulation approach enables an examination of the impacts of anthropogenic modifications in relation to the probabilities associated with different magnitude floods. Because the effects of dams and levees vary so much with flood magnitude, the full significance of these different modifications can really only be appreciated when viewed in light of their likelihood of occurring in the long-term. When examining individual floods, larger magnitude floods appeared quite important for floodplain nitrogen budgets, as significantly more nitrogen was processed during these events (Fig. 4d). However, when accounting for flood probabilities over the long-term, a different picture emerges. Over time, cumulative N processed by recurring smaller floods would be quite large relative to that processed by larger, less frequent floods (Fig. 5). The reduction in N processing because of regulation (dams) is amplified by this long-term perspective (Fig. 5), as the proportional reduction by dams (as compared with the natural scenario) is greatest for these smaller magnitude floods. In contrast, areal processing rates on leveed floodplains were higher than the natural floodplain for these smaller-sized floods. Thus, when viewed from the longer-term perspective, the impact of dams may be of more concern than the impact of setback levees.
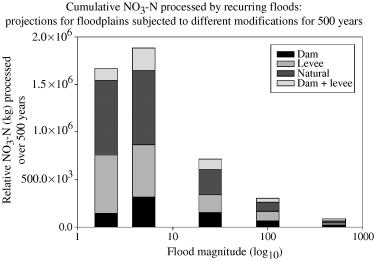
Projected NO3-N processed from recurring floods of different magnitude over 500 years. This suggests the cumulative amount of nitrate likely to be processed by frequent 2-year floods on a given floodplain (over the course of 500 years) could vary substantially if that floodplain were subjected to modifications of different types. These data are intended to account for the fact that different magnitude floods have a different probability of occurring. Thus, the differential impact of human modifications on floods of different magnitude may be amplified in the long-term by accounting for the associated flood probabilities. Shown are averages among five replicate floodplains.
Furthermore, the long-term consequences of the interactions between levees, dams and flood frequencies become even more important when viewed in light of climate change. Changes in the timing, frequency and severity of floods are expected throughout North America as a result of climate shifts (IPCC 2001). The Mid-west USA and Canadian prairies are expected to see both increases and decreases in streamflow along with an increasing likelihood of severe drought (IPCC 2001). Paleo-flood records also reveal that periods of rapid climate change are associated with higher frequencies of large and extreme floods (Knox, 2000). Changes in land use can also alter flood patterns and flood frequencies (Fitzpatrick et al., 1999). Agricultural conversion has accelerated runoff and increased the flood magnitudes across a wide range of recurrence frequencies (Knox, 2001). Peak discharges of high-frequency floods have increased 200–400% since preagricultural periods in the Upper Mississippi Valley (Knox, 2001). Land use change may have the greatest impact on the flood peaks of smaller floods (Knox, 2001), because extreme floods may not be as affected (proportionally) by in part reductions in wetland storage capacity wetland loss and concomitat (Pitlick, 1997). Thus, conversion of wetlands to agriculture may not only contribute to increased nitrogen loading to surface waters, but also affect the small magnitude floods which our simulations suggest may be responsible for the most denitrification in the long-term. Thus, a long-term perspective on changing flood probabilities provides important context for understanding the potential impact of levees and dams on river floodplains.
The development of restoration techniques for aquatic systems is a research priority (National Research Council, 1992); however, predicting the success of large river restorations remains problematic (Gore & Milner, 1990). Because of prohibitive costs very few large river restorations have occurred (Regier et al., 1989; Kern, 1992). Although millions of dollars have been spent on, flow management and manipulation of large riverine systems in the Grand Canyon, Patten & Stevens, 2001; the Snowy River in Australia, Pigram, 2000) as well as others (Poff et al., 2004). Dam removal is also becoming increasingly common, and a recently compiled database includes information on over 400 dams dismantled in the US (Pohl, 2002). However, most dam removal has been confined to smaller river systems (Stanley & Doyle, 2003). Unplanned levee breaks have occurred (Magilligan et al., 1998), but intentional levee removal is not common. Further, because unmodified large riverine systems are not abundant, controlled, replicated experimental systems are challenging to find. As a result, understanding the full extent of anthropogenic alterations on large rivers has been problematic at best. While heuristic models (such as that presented here) will likely continue to make important contributions to our understanding of landscape-scale denitrification and flooding, they are unlikely to reduce uncertainties to the level demanded by decision-makers in this contentious area. Whole floodplain experiments are needed in which N budgets are determined before and after dams and levees are added or removed. Experimental floods are needed to validate our results and hypotheses, and test the robustness of our different assumptions. Until such experiments are performed, management of landscape-level floodplain denitrification will be complicated by uncertainty on several fronts.
As human domination of the earth increases (Vitousek et al., 1997b), significant alterations to ecosystem services can be expected. This may have important economic consequences, as nutrient cycling constitutes over half the economic value of the world's ecosystem services (Costanza et al., 1997). Denitrification is a critical component of global and regional N cycling as a mechanism for return of excess N to the atmosphere, and at the scale of large river basins, the majority of N inputs are likely lost via this process (Howarth et al., 1996). Up to 90% of floodplains have been cultivated and modified in Europe and North America, substantially diminishing their role in N processing (Tockner & Stanford, 2002). There may be tens of thousands of kilometers of flood-control levees, floodwalls, embankments and dikes in the US (Johnston Associates, 1989; Tobin, 1995) and 98% of rivers are regulated in the US (Vitousek et al., 1997b). The effects of anthropogenic modifications on nitrogen cycling in large rivers remain poorly described (Vitousek et al., 1997a), although the economic value of floodplains as nutrient sinks is likely substantial. For example, along the Danube, the value of nutrient processing services accounted for roughly half the total economic value of ecosystem services (Gren et al., 1995); and wetland restoration has been suggested as the most cost-effective way to decrease nonpoint source pollution (Rosenberg et al., 1991; Gren, 1995). Here, we showed substantial decreases in the amount of NO3-N processed by river floodplains altered by levees and upstream dams through reductions in the nutrient processing services provided by floodplain wetlands. Because floodplains occupy an area over 2 × 106 km2 (Tockner & Stanford, 2002), levees and dams may significantly diminish the processes responsible for nitrogen return to the atmosphere and thus, maintenance of water quality.




