A cladistic reconstruction of the ancestral mite harvestman (Arachnida, Opiliones, Cyphophthalmi): portrait of a Paleozoic detritivore
Abstract
Two character sets composed of continuous measurements and shape descriptors for mite harvestmen (Arachnida, Opiliones, Cyphophthalmi) were used to reconstruct the morphology of the cyphophthalmid ancestor and explore different methods for ancestral reconstruction as well as the influence of terminal sets and phylogenetic topologies. Characters common to both data sets were used to evaluate linear parsimony, averaging, maximum likelihood and Bayesian methods on seven different phylogenies found in earlier studies. Two methods—linear parsimony implemented in TNT and nested averaging—generated reconstructions that were (i) not predisposed to comprising simple averages of characters and (ii) in broad agreement with alternative methods commonly used. Of these two methods, linear parsimony yielded significantly similar reconstructions from two independent Cyphophthalmi data sets, and exhibited comparatively low ambiguity in the values of ancestral characters. Therefore complete sets of continuous characters were optimized using linear parsimony on trees found from “total evidence” data sets. The resulting images of the ancestral Cyphophthalmi suggest it was a small animal with robust appendages and a lens-less eye, much like many of today’s species, but not what might be expected from hypothetical reconstructions of Paleozoic vegetation debris, where Cyphophthalmi likely originated.
© The Willi Hennig Society 2012
The aggregate optimization of several morphological characters can be used to generate a rough visual image of an ancestor—a convenient summary of a taxon’s plesiomorphic morphological character states and a prediction of paleontological discoveries (Pagel, 1999). The morphology of hypothetical progenitors can also suggest a lineage’s original physiology, behavior, and ecology. These scenarios can be compared with ancestral reconstructions of non-morphological characters and other associated data (such as web architecture in spiders, Blackledge et al., 2009; Dimitrov et al., 2012), something that has become more feasible with the handling of continuous data by phylogenetic programs. Obviously, ancestral reconstructions are highly influenced by the underlying phylogenies and the implicit hypotheses about character state polarities derived from the arrangement of clades. But do they also depend on the number of terminals included and the degree of redundancy with which one clade is represented, and are they fundamentally just averages across the character matrix? Such influences would make ancestral reconstructions largely dependent on the particulars of the terminal set and thus not highly informative.
We decided to explore the ancestral reconstruction of our arachnid of interest, the mite harvestmen (Opiliones, Cyphophthalmi), to gain insight into this ancient terrestrial animal and the algorithms for reconstructing morphology. Cyphophthalmi are a suborder of the daddy-long-legs (Opiliones, also known as harvestmen), but they look and behave quite differently from Opiliones commonly encountered: they have rounded bodies about 1–6 mm long, with thick, short legs, and they live almost exclusively below the upper layer of leaf litter (Giribet, 2000). It would be interesting to see the morphology of transitional forms between Cyphophthalmi and its spindly-legged sister groups in Opiliones and understand how such divergent morphologies arose in one group, but no such lineages exist today, and no transitional fossils have been found. Indeed, the oldest Opiliones fossil known, a 410 Ma specimen from the Early Devonian Rhynie cherts (Dunlop et al., 2004), already displays the morphology of modern daddy-long-legs in the suborder Eupnoi, with extremely long, thin legs.
Cyphophthalmi are distributed globally (Giribet, 2000) and have been the subject of numerous phylogenetic analyses (Giribet and Boyer, 2002; Boyer and Giribet, 2004; Boyer et al., 2007; Clouse et al., 2009; Murienne and Giribet, 2009; Sharma and Giribet, 2009; de Bivort and Giribet, 2010; de Bivort et al., 2010; Clouse and Giribet, 2010; Giribet et al., 2012). We have at our disposal phylogenetic hypotheses derived from molecular and morphological data, the latter being both discrete and continuous. Just by looking at traits consistent across the whole suborder, we are already able to make some assertions about the ancestor of all extant Cyphophthalmi—what we have called the “phylogenetically inferred progenitor of the Cyphophthalmi” (PIPC). We surmise that Cyphophthalmi originated between 425 and 410 Ma, not only because their sister group within the Opiliones was already present by this time, but also because the likely sister group to all Opiliones, Scorpiones, appeared in the Late Silurian (Dunlop, 2007). The Silurian also saw the first appearance of large plants in communities along waterways, and it seems likely that Cyphophthalmi—which today inhabits almost exclusively humid forest litter—originated in detritus along Silurian streams (Labandeira, 2005). Cyphophthalmi can be kept alive on a diet of dead Drosophila (P. Sharma, pers. commun.) and have been observed ingesting amorphous masses of dead soft-bodied invertebrates (P. Sharma, pers. commun.), and a scavenging diet is consistent with their habitat, morphology, and behaviour; it would also have been an available diet in the Silurian, with a variety of terrestrial arthropods providing a steady flow of carcasses on which to feed. Thus Cyphophthalmi likely were, like many early terrestrial arthropods, detritivores, but not on plant material (Shear and Kukalová-Peck, 1990).
Cyphophthalmi are not as morphologically conserved as may first appear, and their ancestral condition gives us a small window into Paleozoic life for terrestrial detritivores, which was not entirely the same as it is today. It has been asserted that until the Devonian, forest litter was composed of woody parts and stems, not leaves, and was found mostly on floodplains and embankments (Shear and Kukalová-Peck, 1990). This is evocative of the habitat of the Southeast Asian cyphophthalmid family Stylocellidae, which not only lives mostly in rainforests but also appears to be unique in the suborder in being capable of crossing large bodies of water (Clouse and Giribet, 2007). Stylocellidae also includes the largest species in the suborder, and most species in the family have prominent eye lenses. We have suggested elsewhere (Clouse et al., 2011) that these stylocellid characters may give the family an intrinsic advantage to dispersing over water, and perhaps the ancestral cyphophthalmid in the Paleozoic would have also been best suited as a nimble form, capable of climbing through debris being regularly disturbed by floods. Still, Stylocellidae includes small, eyeless forms, like most other species in the suborder, and only a phylogenetic reconstruction can help us draw any possible parallels between modern and ancient morphologies and habitats.
The data we optimized to reconstruct PIPC are continuous data, and when we previously used these data for phylogenetic reconstruction (Clouse et al., 2009; de Bivort et al., 2010), they were treated as Farris characters under linear parsimony. Also known as “ordered” or “additive” characters, their cost for any state change is simply the size of the interval between states (Farris, 1970; Goloboff et al., 2006, 2008). Linear parsimony has been contrasted with squared-change parsimony (Rogers, 1984; Maddison, 1991), in which costs are the squares of the intervals between states. Squared-change parsimony tends to distribute state changes evenly across trees (Maddison, 1991; Butler and Losos, 1997; Goloboff et al., 2006) and can produce ancestral values that are just averages of the descendants (Huey and Bennett, 1987; Maddison, 1991; Rohlf, 2002). Most recently, landmarks can be input for phylogenetic analysis (Catalano et al., 2010; Goloboff and Catalano, 2010) and the linear distances between their changes used to score trees and thus find the optimal phylogeny.
Our goals here were to explore the ancestral condition of the Cyphophthalmi and the behaviour of new algorithms for optimizing continuous data, especially linear parsimony in the program TNT (Goloboff et al., 2008). We also compare these reconstructions with those found with averaging methods, squared-change parsimony, maximum likelihood, and Bayesian methods, and we investigate the influence of branch lengths and outgroups. In most algorithms, the basal node is treated differently from internal nodes, so the inclusion of outgroups can be key. For example, in TNT, nodes are reconstructed during “down-pass optimization” using character information from the descendants, but additionally a subsequent “up-pass optimization” uses information from ancestral and sister nodes (which are not available for the basal node) (Goloboff et al., 2006).
Cyphophthalmi were likely some of the earliest scavengers in terrestrial plant debris, and their trends in morphological evolution could parallel long-term changes in forest-floor habitats. TNT’s (Goloboff et al., 2006, 2008) implementation of algorithms for continuous data have allowed the testing of quantitative hypotheses such as ancestral wasp relatedness (Pickett et al., 2006), preferred plant habitats (Catalano et al., 2008), and genome thermodynamic stability (Catalano et al., 2009). Thus we find it useful to continue testing those algorithms against alternative reconstruction methods to understand how they are handling character data, while at the same time starting to investigate deep trends in character evolution in mite harvestmen.
Methods
Our approach to characterizing PIPC was rooted in a comparison of several plausible reconstruction methods, evaluated on trees with: (i) differing terminals and (ii) differing topology. In particular, using our cyphophthalmid data sets, we sought to evaluate which reconstruction methods are robust to the variation in terminals and alternative topologies, and which reconstructed characters represent the best consensus across methods. Practically, we divided the task into two parts. In the first we asked how linear parsimony reconstructions compare with averaging methods across terminal sets and topologies. In the second part, we focused on a single tree to compare linear parsimony with diverse alternative approaches such as maximum likelihood, Bayesian, and landmark optimization.
Part 1: Linear parsimony and averaging
We first selected two distinct terminal sets that each: (i) contained representative animals from all the major lineages of the Cyphophthalmi (the families Stylocellidae, Pettalidae, Sironidae, Neogoveidae and Troglosironidae), and (ii) had been used previously to generate phylogenetic hypotheses for Cyphophthalmi. The first of these terminal sets (PET) includes 50 cyphopthalmid terminals predominantly representing the family Pettalidae (de Bivort and Giribet, 2010). The second terminal set (STY) contains 136 cyphophthalmid terminals, mostly from the family Stylocellidae, and 21 opilionid outgroup taxa (Clouse et al., 2009; Clouse and Giribet, 2010). These particular terminal sets were chosen because each had been used to generate distinct (but plausible) phylogenetic hypotheses from three different character sets each (Fig. 1a). Specifically, the PET terminals were previously analysed using: (i) 62 discrete morphological characters; (ii) 78 continuous morphological characters; and (iii) these two data sets in combination (de Bivort and Giribet, 2010; figs 10A,B and 12A (1 : 1, EW), respectively). The STY terminals were previously analysed using: (i) 6571 molecular characters (Clouse and Giribet, 2010; fig. 3); (ii) 51 continuous morphological characters (Clouse et al., 2009; figs 5 and 6); and (iii) these two data sets in combination (Clouse et al., 2009; figs 5 and 6). We refer to the topologies generated by these analyses as PET-D, PET-C, PET-DC, STY-M, STY-C and STY-MC, respectively. The continuous data in both PET and STY consist of raw measurements and shape descriptors (typically ratios of raw measurements), derived from male specimens, analysed for independence, and subjected to collapse of dependent characters (de Bivort et al., 2010).
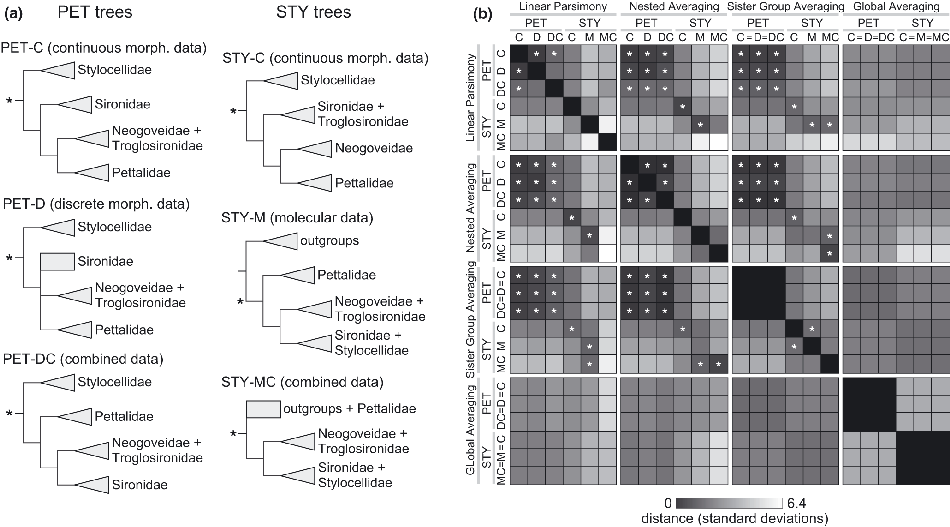
Phylogenetic topologies and data sets analysed, and the respective pairwise distances between their reconstructions of ancestral morphology. (a) Schematics of the six phylogenetic trees analysed. Three PET topologies were analysed (de Bivort and Giribet, 2010) containing 50 cyphophthalmid terminals, and found using either discrete morphological characters (D), continuous morphological characters (C), or both types data (DC). Three STY topologies were analysed (Clouse et al., 2009) containing 136 cyphophthalmid terminals and 21 outgroup terminals, and found using either molecular data (M), continuous morphological characters (C), or both types of data (MC). All trees were rooted either by non-cyphophthalmids (outgroups) or by the family Stylocellidae (Giribet and Boyer, 2002). Shaded triangles indicate clades, rectangles unresolved groups. Asterisks indicate the tree node interrogated for each ancestral reconstruction. (b) Table indicating the pairwise Euclidean distance between the ancestral reconstructions generated from each of the phylogenies presented in (a), for each of four reconstruction methods (see text for descriptions). Reconstructions were calculated post tree-searching for 18 z-score normalized characters available in both the PET-C and STY-C data sets. Because global averaging is topology-independent and sister group averaging varies only if sister group species membership varies, the reconstructions they generate do not vary between some topological variants of the same terminal set (indicated by “=” in labels). Black indicates identical reconstructions; white, reconstructions with little agreement. Asterisks indicate pairs of reconstructions that are non-trivially closer than expected by chance (P < 0.05, Methods).
We evaluated four reconstruction methodologies against each of the six terminal/topology combinations, as follows.
- 1
Linear parsimony, as implemented for continuous characters in TNT.
- 2
Nested averaging: for each reconstructed character, the average of that character was calculated for each pair of sister terminals, the pairs of sister terminals were respectively replaced with their average, and this process was repeated until the root was calculated. For example, for the tree (outgroups, (A, ((B, C), (D, E)))), one would reconstruct the ancestral character value of the ingroups as [average(A, average(average(B, C), average(D, E)))].
- 3
Sister group averaging: the ancestral character value was calculated as the average of the un-nested averages of the two clades (or more, in the case of unresolved ancestral nodes) descending directly from the ancestral node. For the tree described above, the ancestral value would be [average(A, average(B, C, D, E))].
- 4
Global averaging: the reconstructed value was simply the average value across all terminals: [average(A, B, C, D, E)].
In order to evaluate the “robustness” of methodologies (to variation in terminal set and topology) and “consistency” of particular reconstructions (across methods), we used 18 continuous morphological characters available in both the PET and STY data sets (Table 1). These were identified by first finding any characters in both the STY-C and PET-C continuous data sets that were defined in precisely the same way. Then additional characters were defined using simple mathematical operations on pre-existing STY-C characters so that they would be directly comparable with PET-C characters. The raw 18 characters from both data sets were combined and z-score normalized so that they would be comparable between the STY and PET data sets, and each contributes equally to comparison metrics such as the correlation or Euclidean distance between character reconstructions. In this form, the 18 characters were used to reconstruct their ancestral states on each of the six terminal/topology combinations, using each of the four reconstruction methods. These comparisons evaluate the robustness and consistency of the reconstruction. Previously, the 18 characters were all found to be phylogenetically informative (Clouse et al., 2009; de Bivort et al., 2010); however, basically all continuous characters show some degree of homoplasy because of the flexibility in the states they can assume and their precision.
| Character description | Measurement formula in PET-C (de Bivort et al., 2010) | Measurement formula in STY-C (Clouse et al., 2009) | |
|---|---|---|---|
| 1 | Length of dorsal soma | 1 | D1 |
| 2 | Soma length-to-width ratio | 1/3 | D1/D5 |
| 3 | Relative width between ozophores | 8/2 | D7/D6 |
| 4 | Anal plate relative length | 21/1 | A2/D1 |
| 5 | Anal plate length-to-width ratio | 21/20 | A2/A1 |
| 6 | Gonostome relative length | 35/1 | G2/D1 |
| 7 | Gonostome length-to-width ratio | 35/34 | G2/G1 |
| 8 | Sternite 8 relative maximum length | 25/1 | (V14–V13)/D1 |
| 9 | Sternite 7 relative maximum length | 26/1 | (V15–V14)/D1 |
| 10 | Sternite 6 relative maximum length | 27/1 | (V16–V15)/D1 |
| 11 | Coxae IV suture relative length | 38/1 | V29/D1 |
| 12 | Sternal region relative length | 37/1 | V2/D1 |
| 13 | Relative width between spiracles | 33/3 | V1/D5 |
| 14 | Second cheliceral article relative length | 51/1 | C1/D1 |
| 15 | Moveable digit local relative length | 52/51 | C2/C1 |
| 16 | Second cheliceral article relative width | 54/2 | C5/D6 |
| 17 | Widest part of second cheliceral article position | 58/51 | C6/C1 |
| 18 | Percentage of second cheliceral article ornamented | 143N/51 | C4/C1 |
Trees in the PET terminal set did not contain non-cyphophthalmid outgroups, and were re-rooted manually so that Stylocellidae was sister to the remaining Cyphophthalmi as per Boyer et al. (2007). Reconstructed ancestral characters were extracted from TNT using a custom script. The calculation of nested averaging reconstructions was performed in MATLAB using custom scripts that read parenthetical tree files. Sister group averaging and global averaging methods were performed in Microsoft Excel.
For analyses that could not accommodate a range in reconstructed ancestral character values (such as Euclidean distances and correlation coefficients), we replaced the reconstructed range with its average. P values were assigned to Euclidean distances between alternative reconstructions (Fig. 1b) by a bootstrapping method because we could not identify a statistical distribution known to generically characterize Euclidean distances. Specifically, we assumed that the (16) different reconstructions of character (from the different methods) reflect a distribution of its reconstructed value. By sampling those values independently for each of the 18 characters, we generated randomized “reconstructions” that removed any mutual information between reconstructed characters introduced by each method. Pairs of random reconstructions were generated 105 times, and the Euclidean distance between each pair recorded. The 95th percentile of these values was used as the P = 0.05 cutoff. This approximates the alpha value because bootstrap resampling provides an unbiased estimate of parameters of an unknown distribution, in this case, its 95th percentile.
In order to visualize the respective distances between all pairs of reconstructions simultaneously, we used the data visualization technique multidimensional scaling (Cox and Cox, 2001) to place the reconstructions in a two-dimensional (rather than 18-dimensional) space. This was performed in MATLAB using built-in functions and default non-metric scaling. This option preserves the ordering of the pairwise distances between reconstructions—that is, if one pair of reconstructions is farther apart than another pair, that relationship will also hold in the 2D visualization. The error introduced by this monotonicity requirement was small.
Part 2: Broader reconstruction comparisons
We measured the 18 characters common to PET-C and STY-C for five species in all three non-cyphophthalmid suborders of Opiliones: Eupnoi, Dyspnoi, and Laniatores. These groups lack ozophores and sometimes coxae IV meeting at the midline, so these new character sets were missing some values. This expanded Opiliones continuous data set (OPI-C) was optimized on a tree reflecting the most recent molecular phylogenetic evidence (Giribet et al., 2012), using a wide variety of methodologies, including linear parsimony, squared-change parsimony, averaging, maximum likelihood, and Bayesian. This tree was generated in the program BEAST ver. 1.6.1 (Drummond et al., 2006; Drummond and Rambaut, 2007), and, having been dated, was ultrametric and had branch lengths; this was different from topologies used in Part 1, which lacked branch lengths. The influence of branch lengths for the tree in Part 2 was evaluated by comparing reconstructions using the original tree with those when the branch lengths were all changed to 1. In a landmark version of OPI-C, we retained the original x- and y-coordinates used to calculate the 18 character values and optimized them directly (Catalano et al., 2010) in TNT (Goloboff and Catalano, 2010), using a method that treats the distance between inferred ancestral landmarks like additive characters under a parsimony criterion. The reconstructed landmarks were then used to re-derive the 18 continuous characters for comparison.
We generated ancestral reconstructions with and without branch lengths and outgroups in the programs Mesquite ver. 2.74 (Maddison and Maddison, 2011), BayesTraits (beta version, available from the developers upon request), and the APE phylogenetic analysis package (Paradis et al., 2004) in the R software environment (R Development Core Team 2011). We also performed internal checks to see if different optimizations that are equivalent in theory did give the same ancestral reconstructions, such as comparing squared-change parsimony reconstructions unweighted by branch lengths with squared-change reconstructions weighted by branch lengths but on a tree with all branch lengths set to zero; such tests did result in identical reconstructions.
The Bayesian reconstruction in BayesTraits beta requires an initial Markov Chain Monte Carlo (MCMC) run to generate model parameters, then a final MCMC run for the reconstructions. A two-character test data set did settle on reasonable character reconstructions, but our full data set showed no evidence of settling, even after 55 million generations on one run and 40 million in another. Thus our reconstruction values are the average of 800 000 generations, sampled every 100, after a 250 000-generation burn-in. When testing reconstructions on trees with no outgroups (which required an MRCA at the base of the tree) or using the directional model, reconstructions settled on zeros (i.e. simple global averages given our normalized characters), so these functions appear not to be fully implemented. Because we used normalized data, the constant parameter “datadev” (the Monte Carlo step size, which we kept at the program’s default setting) had the same effect on all characters, regardless of their original magnitude. For all other methodologies, default parameters and settings were used.
Once we identified the methodology that yielded the most robust and consistent reconstructions, we reconstructed all the continuous characters in the original continuous data sets on their corresponding total evidence trees to generate the final set of reconstructed characters. PIPC illustrations were constructed by hand in Adobe Illustrator, beginning with a generic outline of a cyphophthalmid and sequentially imposing the constraints of each reconstructed character, at each step smoothly warping the outline to accommodate the new constraint. Slight contradictions in the position of spatially constrained morphological features (for example, arising from it being possible to determine a constrained position using a sequence of reconstructed characters anterior to posterior as well as posterior to anterior) were resolved if possible by preferring the position constrained most directly (i.e. involving the fewest characters), and then by averaging the alternative positions. Ranges in reconstructed values were replaced with their average for purposes of the illustration.
Results
Part 1: Linear parsimony and averaging
The pairwise Euclidean distances between the reconstructions of each of the 24 terminal/topology/methodology combinations are shown in Fig. 1b. The Euclidean distance between two reconstructions equaled 0 if the reconstructions were identical, and has units of standard deviations, since the characters were z-score normalized. We found little agreement between global averaging and the other three reconstruction methods in Part 1. Reconstructions based on the PET terminal set were in broad agreement, whether the reconstruction method was linear parsimony, nested averaging, or sister group averaging. Only one pair of PET reconstructions (PET-DC and PET-D under linear parsimony) was not more similar than expected by chance alone (P < 0.05, uncorrected for multiple comparisons; see Methods).
This pattern of broad agreement was not observed with the STY trees—suggesting that the robustness of reconstructions to topological variation depends on the terminal set being analysed. However, agreement among STY reconstructions was found in a number of specific instances. For example, STY-M under linear parsimony agreed significantly with STY-M under nested averaging and sister group averaging, as well as STY-MC under sister group averaging. Of 45 non-trivial comparisons made between STY reconstructions, nine were found to be significantly similar. It should be noted that global averaging is independent of topology, and sister group averaging is topology-independent among trees that preserve sister group composition. Thus both of these methods yielded identical reconstructions for each of the three topologies associated with the PET terminal set, and global averaging yielded identical reconstructions for all STY trees. In some cases, some STY reconstructions were surprisingly far from one another (e.g. STY-C and STY-M under linear parsimony). No pairs of STY and PET reconstructions were found to be closer than expected by chance. However (particularly because of the frequent agreement between PET reconstructions) far more agreement between reconstructions was generally found than would be expected by chance (41 of 153 non-trivial comparisons were significant with P < 0.05).
Visualizing the differences between all reconstructions in two dimensions (Fig. 2a) reveals that, while there was little significant pairwise agreement between the STY reconstructions, they do “cluster” together more with each other than with the PET reconstructions, with the exception of the linear parsimony reconstruction of STY-MC. Reconstructions based on STY-C tree under any method other than global averaging exhibit moderate similarity to reconstructions based on any of the PET trees under any method other than global averaging. Considering the topology of the various trees, we observe that all the trees which were rooted with Stylocellidae as sister to the remaining Cyphophthalmi (STY-C and all PET trees) have fairly close reconstructions. STY-MC and STY-M have identical topologies at the family level, except for their resolution at the root, but the STY-M reconstructions are closer to the STY-C reconstructions than they are to those of STY-MC. Moreover, the STY-MC and STY-M reconstructions are farther apart than any other pair of reconstructions, suggesting that reconstructions are more sensitive to the degree of resolution at the optimized node than topology of groups descending from it.
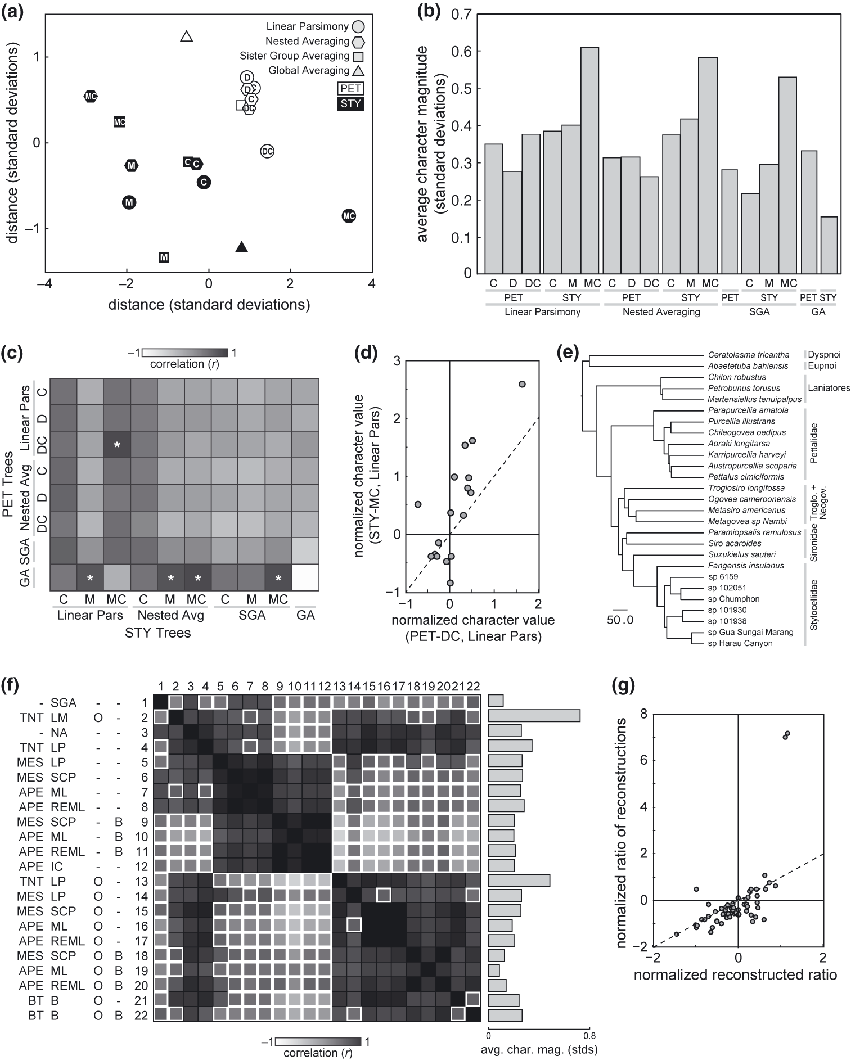
Evaluation of reconstructions across data sets, topologies and methods. (a) Spatial visualization of the approximate Euclidean distances between reconstructions, generated by multidimensional scaling (see Methods). Closer icons indicate more similar reconstructions and vice versa. Black indicates STY reconstructions; white, PET reconstructions. Letters indicate the topologies presented in Fig. 1a, and shapes the reconstruction method. Global averaging methods are topology-independent (with respect to PIPC), thus their icons are unlettered. Sister group averaging is topology-independent for the PET trees. (b) Average magnitude of the values of the 18 reconstructed (normalized) characters at the ancestral node for all topologies and reconstruction methods. Taller bars indicate reconstructions in which reconstructed character values are farther from their respective means across terminals. SGA, sister group averaging; GA, global averaging. (c) Pairwise correlation coefficients between reconstruction values generated using the PET and STY topologies, for all reconstruction methods. Asterisks indicate pairs of reconstructions that are more correlated than expected by chance (P < 0.05). (d) Scatter plot of reconstructed character values generated using linear parsimony of the STY-MC topology versus the PET-DC topology (r = 0.62, P = 0.0043). (e) Tree, based on recent molecular analysis of Cyphophthalmi (Giribet et al., 2012), with branch lengths used for reconstructing the OPI-C data set. (f) Pairwise correlation coefficients between reconstructions generated using the OPI-C data set, as implemented in TNT, Mesquite (MES), APE in R, or BayesTraits (BT). Methods include sister group averaging (SGA), landmark optimization (LM), nested averaging (NA), linear parsimony (LP), squared-change parsimony (SCP), maximum likelihood under a Brownian motion model (ML), restricted ML model (REML), independent contrasts (IC), and Bayesian reconstruction (B). –/O indicates the inclusion of outgroup data, –/B, branch lengths. Entries with white borders are not statistically significant (P > 0.05, r < 0.47). Bar graph at right shows the average character magnitude for each reconstruction, as in (B). (g) Scatter plot of the ratio of pairs of reconstructed character values versus the reconstructed value of the character consisting of the ratio of those characters (r = 0.61, P < 10−6), plotted for all ratio characters in the PET-C data set, reconstructed by linear parsimony.
To the extent that the averaging methods (nested, sister group, and global averaging) are insensitive to tree topology, their estimates of ancestral characters will trend toward the mean value of each character across the represented terminals (that is, regress toward the mean). In the case of z-score normalized characters, this mean value is encoded as 0. Thus observing many or all reconstructed ancestral characters to have magnitudes near zero is evidence of this pitfall of averaging methods. We tested this by calculating the average magnitude of the 18 reconstructed character values, for each terminal/topology and reconstruction method (Fig. 2b). Characters reconstructed using global averaging had a comparatively low magnitude, and both linear parsimony and nested averaging tended to produce greater magnitudes, particularly in the STY reconstructions. Reconstructions performed under sister group averaging yielded low-magnitude reconstructions except in STY-MC, which yielded higher magnitude reconstructions because of the presence of several single-species branches emanating from its unresolved root. Note that the reconstructed character values using global averaging (and the standard deviation across them) are not strictly 0, despite the characters being normalized and the method being a simple average. This is because, although global averaging was done separately on PET-C and STY-C, the two data sets were normalized beforehand together.
While the Euclidean distance between two reconstructions (1, 2) reveals their overall similarity, it can potentially obscure agreement in the trends of reconstructed characters, if not their magnitudes. Therefore we looked at the pairwise correlation coefficients between the PET and STY reconstructions to see if agreement could be found in the trends of the reconstructions (Fig. 2c). Indeed, the reconstruction generated using linear parsimony on the PET-DC and STY-MC (Fig. 2d) was highly significant (r = 0.62, P = 0.0043). Since we had originally observed less agreement among STY reconstructions than among PET reconstructions (Fig. 1b), it was not surprising to observe that the correlation between particular STY and PET reconstructions was dependent primarily on which STY reconstruction was being considered. The exception to this was the PET global averaging reconstruction, which was positively correlated with a number of STY reconstructions, despite it being considerably far from them as measured by Euclidean distance (Fig. 2a). The most negative correlation was found between STY and PET under global averaging, but this is an artifact of both character sets being normalized together, while undergoing global averaging separately.
Since the Euclidean distance between the linear parsimony reconstructions of the STY-MC and PET-DC is not especially great (Fig. 2a), and they strongly agree about the trends in ancestral characters (Fig. 2c,d) we concluded that these topologies and this methodology could ultimately form the basis of our visualizations of PIPC. However, before presenting these reconstructions as definitive, we needed to confirm several points. First, the original PET-C and STY-C data sets did not include character values for any outgroup species, thus this information was unavailable during reconstruction, even if the tree being used for reconstruction itself contained outgroups. To what extent does this distort the reconstruction? Second, we have focused on linear parsimony in contrast to averaging as a reconstruction method. Perhaps philosophical alternatives, such as maximum likelihood and Bayesian reconstruction, are definitively preferable. Lastly, such methods allow us to incorporate branch length information. Does that greatly affect reconstructed character values?
Part 2: Broader reconstruction comparisons
To address these questions, we generated a new data set (OPI-C), with measurements of the 18 characters common to PET-C and STY-C for five outgroup species in suborders of Opiliones other than Cyphophthalmi (Gruber, 1978; Tourinho, 2004; Schwendinger, 2006; Bauer and Prieto, 2009; Sharma and Giribet, 2011). We optimized OPI-C on a tree derived from the most recent comprehensive molecular phylogeny of the Cyphophthalmi (Giribet et al., 2012), which included all suborders of Opiliones, all families of Cyphophthalmi, representatives of Pettalidae and Stylocellidae in similar proportions, and branch lengths (Fig. 2e). We also produced a landmark version of OPI-C in which the x- and y-coordinates of all features on the animals (required to calculate the 18 character values) were retained as such for landmark analysis in TNT.
OPI-C was reconstructed on this tree using many different methods: averaging, linear parsimony, landmark optimization, squared-change parsimony, maximum likelihood (under Brownian motion, supported by an analysis of evolutionary model selection described below, and restricted likelihood models), independent contrasts, and Bayesian. The pairwise correlation coefficients between these methods are presented in Fig. 2f. We found that the primary determinant of whether two reconstructions were in agreement was whether they utilized outgroup information. Important exceptions to this pattern were nested averaging (which performs only down-pass calculations, thereby ignoring outgroup information) and linear parsimony implemented in TNT.
Reconstructions generated using linear parsimony in TNT and nested averaging were in the broadest agreement with other reconstructions. They correlated significantly with the reconstructions of essentially all other methods, with the exception of the maximum likelihood methods that ignored outgroups but utilized branch lengths. The only other method that displayed similarly broad agreement was landmark optimization in TNT, although this approach (which uses outgroup information) was not significantly correlated with three of the maximum likelihood and Bayesian methods that also used outgroup information. Sister group averaging exhibited the least agreement. The inclusion or exclusion of branch length information increased the correlation between differing methods only slightly. We expected (Felsenstein, 1985), and observed, that independent contrasts and squared-change parsimony weighted by branch lengths and lacking outgroup data gave identical results.
We tested our 18 overlapping morphometric characters for the best-fit model of evolution on a tree with outgroups and branch lengths using the GEIGER package (Harmon et al., 2008) in R (R Development Core Team, 2011). Each character was fitted to the evolutionary model independently of the other characters. Using the “fitContinuous” command, we generated two comparisons for each character: differences in the log-likelihood between the fit of each model and Brownian motion, and the Akaike information criterion (AIC) measure of information content. The evolutionary models tested included Pagel’s (1999) lambda, kappa, and delta models, Brownian motion, Ornstein–Uhlenbeck (which is Brownian motion with stabilizing selection), and “white noise”, which models a lack of phylogenetic signal. Missing data were replaced by the average of other values for the character when needed.
The log-likelihoods of the fits of evolutionary models for the majority of our 18 characters were not significantly different from the Brownian motion model. Only seven characters had a significantly different likelihood of fit by a model other than Brownian motion, and for all of these the fit of the alternate model was more likely. Using AIC, the same seven characters plus an additional one were better explained by models other than Brownian motion. Three characters were best fit by the white noise model, but for all other characters the white noise model was significantly worse in both the lnL and AIC comparisons.
Maximum likelihood methods generate 95% confidence intervals on reconstructed characters, and linear parsimony in TNT generates ranges for reconstructed characters. Both of these indicate the degree of uncertainty in the reconstruction, and we found them to be of the same order of magnitude—respectively 36% and 12% on average across characters. There was no consistent relationship across methods between the inclusion or exclusion of outgroups and the size of the confidence intervals. For example, the addition of outgroup data to a linear parsimony analysis broadened the range of the reconstruction of body size (character 1) from 2.7% to 25%, but reduced the 95% confidence interval of that character under a Brownian motion model from 50% to 42%.
As an indication of the predisposition of a reconstruction method simply to average character values across taxa, we again calculated the average magnitude of our normalized characters in each reconstruction (Fig. 2f, right) of OPI-C. Sister group averaging and maximum likelihood under Brownian motion (using outgroup data and branch lengths) produced the smallest-magnitude reconstructed characters, i.e. those closest to an average. Landmark optimization produced reconstructed characters with the greatest magnitude, followed by linear parsimony using outgroup data and linear parsimony not using outgroup data. All other methods produced reconstructions with intermediate magnitude characters.
Only one method differed from the others by analysing characters under spatial constraints: landmark optimization, which acts directly on the x- and y-coordinates of the animal features used to measure the continuous characters. This method has the potential advantage of bypassing distortions in the independent optimization of characters that are respectively constrained. For example, optimization could be performed independently on three non-independent characters encoding a numerator, a denominator, and their ratio. We tested whether this distortion was occurring in the linear parsimony reconstructions as follows. The original PET-C and STY-C character sets contain many characters that are the ratio of two raw measurements of the animals. If their reconstructions are to be believed, then the ratio of two reconstructed raw characters should correlate with the reconstructed value of the corresponding ratio character. We evaluated this using the 59 ratio characters present in the PET-C character set (Fig. 2g) and found strong agreement (r = 0.61, P < 10−6). The two characters falling farthest from the trend line encode two measurements of the width of the ozophores (cone-like scent organs) relative to the body width.
From the comparison of these methods, we conclude the following about the reconstructions generated using linear parsimony in TNT:
- 1
They are similar to each other (with statistical significance), irrespective of the inclusion of outgroup data.
- 2
They are significantly correlated with those of numerous other methods, including maximum likelihood and Bayesian analysis, performing in this respect nearly as well as nested averaging. Moreover, they are correlated in the specific cases of two previously published “total evidence” phylogenies for the Cyphophthalmi (Fig. 2c,d).
- 3
The ranges in reconstructed characters provide a measure of the precision with which characters are resolved, given the data, tree topology, and algorithm. In some sense, these ranges are analogous to confidence intervals output by maximum likelihood algorithms, inasmuch as the latter derive from the same sources of uncertainty. In the case of STY-C and PET-C, these ranges were fairly small, averaging 9% and 12% of character magnitude, respectively.
- 4
They appear to resist simply reporting an average of character values (Fig. 2b,f), second in this respect only to landmark optimization.
- 5
Their ratio characters appeared to not be greatly distorted by the independent reconstruction of their numerators and denominators (Fig. 2g).
Using linear parsimony in TNT, we reconstructed the ancestral values of the original 78 PET-C and 51 STY-C continuous morphological characters on the PET-DC and STY-MC trees, respectively. These values were then un-normalized to yield raw character values that provided constraints for two illustrations of PIPC (Fig. 3), one for each character set. Not surprisingly, given that we chose the reconstruction method that was the most consistent, there is broad agreement in the morphology of PIPC illustrations generated using the PET-C and STY-C characters. Both visualizations reveal small Cyphophthalmi (total body length excluding chelicers 2.5 and 2.9 mm, respectively) with a wide prosoma, entire posterior tergites (i.e. lacking the bilobed posterior found as a sexual dimorphism in the males of many species), lateral ozophores raised from the edge of the carapace (type 2 of Juberthie, 1970), coxae of legs III meeting at the midline, robust second cheliceral articles widest close to their proximal end, and an anal plate in a posterior position. The reconstructions differ qualitatively in a few ways: the ornamentation on the second cheliceral article, the midline modification of the anal plate, and the distance between the lateral margins of the opisthosomal sternites and the lateral margins of the body.
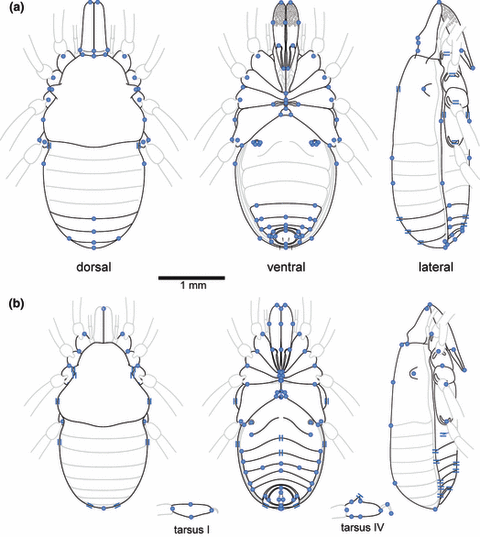
Visualizations of PIPC. (a) Reconstruction generated using PET-C data optimized by linear parsimony on the PET-DC topology. (b) Reconstruction generated using STY-C data optimized by linear parsimony on the STY-MC topology. Circles indicate the reconstructed position of features that are constrained in two dimensions. Parallel lines indicate the reconstructed position of features that are constrained perpendicularly to those lines, but not to displacement of that feature in directions parallel to the lines. Grey lines are features of the animals shown for completeness, but not directly evaluated in the reconstruction. All diagrams are shown to scale.
Characters present in PET-C but not in STY-C imply that PIPC had first cheliceral articles tightly articulated with the dorsal scutum and bearing a small dorsal crest, a broad sternal plate, caudal setae (scopulae) of typical length, and thickness typical of most species. Characters present in STY-C but not in PET-C imply that PIPC had either lens-less eyes or no eyes, a larger than average anal gland opening, a bilobed tergite IX, an oval gonostome, short tarsi on the first and fourth legs, with the latter bearing a small adenostyle (a secretory gland of unknown function found on the tarsus of walking leg IV in males of all species,). Notably, the smaller of the two PIPC representations (based on the STY-C data set, Fig. 3b) is based on a data set containing the larger animals (stylocellids, which are on average larger than pettalids). This provides further evidence that, unlike the topology-independent averaging methods, linear parsimony does not simply report the mean character values across terminals. Moreover, the overall appearance of the PIPC image based on the PET-C data set is more like a primitive stylocellid (Giribet, 2002,Clouse et al., 2009) than the image based on the STY-C data set.
Discussion
We recovered two images for the ancestor of all extant Cyphophthalmi (PIPC). These images were in strong qualitative agreement, revealing small animals with robust chelicerae and lacking the posterior modifications characteristic of sexual dimorphism in many extant species. The reconstructions differed in a small number of qualitative ways, and in these instances of disagreement, the preferred character states may be those implied by the PET data set (Fig. 3a), since these data yielded reconstructions considerably more robust to topological and methodological variation.
Given Stylocellidae’s morphology (often large, long-legged, with eyes bearing lenses), habitat (rain-drenched mountainsides), and dispersal events (the only known crossing of an oceanic barrier) (Clouse, 2010), a large PIPC would seem to fit the ecological challenges of coarse riverbank debris available to Paleozoic detritivores. Indeed, a small, short-legged PIPC with diminished eyes is not consistent with the idea of a large, gangly ancestor climbing over sopping pieces of plant debris along Paleozoic streams. Therefore our small reconstructed animal prompted us to consider more closely size variation within Cyphophthalmi, and to ask whether this reconstruction can still be consistent with life on a Paleozoic floodplain. Within Stylocellidae, species sizes can vary in the same habitat; conspecific species often differ markedly by size, so without knowing much about their ecology, we can at least say that general environmental effects do not exert strong selective pressure on body size. Perhaps species of differing sizes segregate within a leaf litter habitat on a smaller scale, or have different strategies during disturbance.
But in general, larger species may have less chance to dig deep in the soil during adverse environmental conditions; large sizes may be favourable in more humidity-stable environments. This is consistent with the observation that cave-dwelling species of Cyphophthalmi are amongst the largest, and live in some of the most stable humidity conditions. In addition, this matches the observation that smaller Mediterranean cyphophthalmids are seldom collected from leaf litter during the dry season (G. Giribet., pers. obs.). They presumably burrow deeply into the soil to avoid dehydration, rather than undergoing a generational die-off, as they have been observed to live up to 9 years (Juberthie, 1960). But for those tropical forest species for which phenology is known, they are eurychrones (present throughout the year) (Legg and Pabs-Garnon, 1989).
Despite the lack of leaves on early macrophytes, sufficiently decomposed plant debris in the Paleozoic likely still generated the deep, soft duff so commonly favoured by Cyphophthalmi today, and PIPC reminds us of one species that flourishes in deep duff on a floodplain today: Metasiro americanus Davis 1933. It ranges from upland areas of the Florida panhandle to the southern Appalachians, but it also has populations in the Savannah River Floodplain along the coast of South Carolina. These latter populations likely experience complete inundations, yet they can be found in great numbers in the deep, humid, fine debris of certain hardwood hammocks in the area. Like PIPC, this species is comparatively small, short-limbed, lens-less (and eyeless), and exhibits minimal sexual dimorphism. We wonder if small size allows species to live deep in the duff, where eyes are less useful, and whether this habitat affords protection from periodic floods as well as dehydration during dry seasons. Additionally, a small body with short, robust limbs would be less susceptible to shearing forces during a flood. Present cyphophthalmid ecology is poorly known, and attempting to project it back over 410 million years is highly speculative, but we offer these thoughts as a first step toward testable hypotheses for the evolutionary trends we see in the suborder.
The behaviour of character reconstruction methods
In Part 1, we first tested four different reconstruction methods against six different phylogenetic hypotheses, three of which contained mostly pettalid terminals (PET), and three of which were predominantly stylocellid terminals (STY). With the exception of the simplest reconstruction method, global averaging, there was good agreement in the reconstructions generated using the PET terminal set, but only sporadic agreement between pairs of reconstructions generated using the STY terminal set. Nevertheless, reconstructions agreed more within a terminal set than between the two, suggesting that reconstructions are generally sensitive to terminal selection. Moreover, sensitivity to reconstruction methodology also varied with terminal set—PET reconstructions were robust to methodology as well as topology, but STY reconstructions were more sensitive to both topological and methodological changes. The latter data set also revealed that a lack of resolution at the reconstructed node introduces considerable sensitivity to reconstruction method. The robustness to variation in topology and methodology of a particular terminal set should therefore be evaluated while determining what confidence can be placed on an ancestral reconstruction.
By considering the correlation between reconstructions, rather than simply the Euclidean distance between them, we were able to identify reconstructions using either terminal set that agreed about the trends of ancestral characters, if not the magnitude of those characters. Using this comparison, we also considered a wide variety of methods to optimize the OPI-C data set (containing outgroup data for five non-cyphopthalmid species) on an updated molecular tree with branch lengths. Squared-change parsimony and maximum likelihood methods yielded congruent reconstructions, irrespective of the inclusion of branch length data, but dependent on the inclusion or exclusion of outgroup data. Bayesian reconstructions were consistent, irrespective of the inclusion of outgroup data, with the other reconstructions that used outgroup data. Reconstructions by landmark optimization, nested averaging, and linear parsimony in TNT were correlated to all other categories of reconstruction, except squared-change parsimony and maximum likelihood without outgroup data but with branch lengths.
Linear parsimony as implemented in TNT showed broad agreement with the reconstruction method used, as well as insensitivity to the inclusion or exclusion of outgroup data. Moreover, this method also generated the greatest agreement between reconstructions based the distinct STY and PET trees, specifically the PET-DC and STY-MC trees. It is encouraging that the greatest agreement between reconstructions generated with different terminal sets was found using trees based on “total evidence” analyses (combining different data sets), suggesting that the inclusion of as many characters as possible reveals consistent phylogenetic relationships even when the terminal set varies significantly. Consistently, we observed that the reconstruction methods most likely to yield sets of reconstructed characters with values far from the overall mean across terminals were landmark optimization, linear parsimony, and nested averaging. Conversely, global and sister group averaging generally yielded reconstructions less distinct from the mean across terminals.
For the topology tested in Part 2, the inclusion or exclusion of branch length information was not found greatly to affect the ancestral reconstruction. This was a surprising result, as we expected our reconstructions using branch lengths to cluster together. Instead, it seems that the reconstruction of PIP-C is more sensitive to tree topology and the position of the reconstructed node within the tree.
When an ancestral reconstruction is optimized at the root of a tree, the selection of the outgroup would seem to be of critical importance, since its ancestral character states are only one edge away from the root. We chose to root our Cyphophthalmi-only trees using Stylocellidae, based on the best previously available evidence (Boyer et al., 2007). However, recent results (Giribet et al., 2010, 2012) suggest that Pettalidae may be sister to the remaining Cyphophthalmi, as they were found in the STY-M and STY-MC trees. Re-analysis of PET and STY-C trees under this alternative topology did not change the most prominent characteristics of PIPC, which were found to be more pettalid-like already. Specifically, pettalids have the following in common with PIPC: they are, on average, smaller than stylocellids, possess robust chelicerae with only partial ornamentation, and are eyeless or lens-less. PIPC’s most distinctively stylocellid characteristic is its dorsal outline, rather than any specific set of reconstructed characters. This suggests the reconstruction is surprisingly robust to the choice of sister group within Cyphophthalmi, at least with respect to the choice of Stylocellidae or Pettalidae. It is not evident what is causing the dilution of stylocellid characters, even when they are placed as sister to the remaining Cyphophthalmi. The earliest lineages in Stylocellidae are the cave-dwelling members of Fangensis, which have reduced (with a lens) or missing eyes, but those species are also large and long-legged, so their placement at the base of Stylocellidae seems unlikely to drive the reduction of eyes in PIPC while having no effect on overall body and limb size.
PIPC is remarkably at odds with non-cyphophthalmid Opiliones, which are usually larger, extremely long-legged, and distinctly eyed (with eyes that appear to be homologous to those in Cyphophthalmi; Alberti et al., 2008). It would have been a convenient reconstruction if PIPC had appeared stylocellid-like, for this would have suggested a gradual evolution of the usual small cyphophthalmid form from an ancestor that is superficially closer to their sister Opiliones. However, given the appearance of PIPC here, the morphology of the ancestor of all Opiliones is not at all obvious, and remains fruitful ground for further inquiry. From that ancestor, two radically different forms of Opiliones emerged in the Paleozoic, raising interesting questions about the evolution of Opiliones: which characters are more derived, and what ecological factors drove their divergence?
A broader consideration of reconstruction methods
De Queiroz (2000) has argued that differences between the data being optimized for the reconstruction and those used to find the tree are desirable, since optimality criteria minimize the number of ancestral origins for characters of interest and can bias reconstructions. We did this in many cases, optimizing, for example, continuous characters in trees found using molecular data; still, without a detailed examination of this issue, we offer no explicit insight here. But this and other studies—discrete characters on a molecular phylogeny (Hibbitts and Fitzgerald, 2005), continuous morphological data on a discrete morphological phylogeny (Gasparini et al., 2006), and generic averages on a supertree constructed from trees searched off discrete morphological and behavioral data (Hormiga et al., 2000)—emphasize a lack of restrictions in this regard.
Maddison (1991) showed that character reconstructions under parsimony are related to those under maximum likelihood in that squared-change parsimony derives from probabilistic models of tree estimation (Edwards and Cavalli-Sforza, 1964; Cavalli-Sforza and Edwards, 1967). Additionally, Webster and Purvis (2002a) have provided a map of rate and reconstruction equivalencies among different parsimony and likelihood methods. From their map, we were able to confirm the equivalence between unweighted squared-change parsimony and weighted squared-change parsimony when branch lengths are equal; that linear parsimony produces different reconstructions from squared-change parsimony; and that both parsimony methods differ from maximum likelihood with a Brownian motion model of evolution. Webster and Purvis (2002a) do not indicate that independent contrasts gives equivalent reconstructions to other methods, although at the root of the tree it should be the same as squared-change parsimony and likelihood with a Brownian motion model (Felsenstein, 1985; Grafen, 1989); indeed, in our reconstructions, independent contrasts in APE at the base of Cyphophthalmi when there were no outgroups (i.e. at the base of the entire tree) gave equivalent reconstructions to unweighted squared-change parsimony with no outgroups and restricted ML under a Brownian motion model with no outgroups and no branch lengths. Independent contrasts reconstructions were not affected by branch lengths, but rather by optimizing at the base of the tree or an internal node (as when outgroup data were included); independent contrasts reconstructions at internal nodes were equivalent to weighted squared-change parsimony with no outgroups and very close to those from restricted maximum likelihood with no outgroups but branch lengths.
Normally, the model behind the evolution of continuous characters under maximum likelihood is Brownian motion, a random divergence of character state means. The Ornstein–Uhlenbeck modification of this process (Lande, 1976) can be used to constrain divergences, essentially introducing stabilizing selection, and a further modification is to remove the up-pass optimization. Using a stabilizing model and only a down-pass with squared-change calculations leads to Felsenstein’s (1985) independent contrasts, which for any one node is the weighted average of descendant character states (weighted by the branch lengths). The package APE considers Ornstein–Uhlenbeck Brownian motion a generalized Brownian motion model, and indeed, the reconstructions it calculated from our data under maximum likelihood with a Brownian motion model were almost identical to the global average for each character across all terminals. For some characters, including body size, they were strictly identical to the global average (although with confidence intervals).
Other likelihood method variants were difficult to test due to our uncertainty over use of the program. In APE, generalized least squares methods can be used with a variety of correlation models, but produced error messages in our hands. These warnings seemed spurious, but could have indicated problems that led to nonsensical reconstructions (such as an ancestral Cyphophthalmi five times larger than any that exist today or are in the fossil record, under the correlation structure of Martins and Hansen, 1997). As for Bayesian reconstructions, Maddison (1991) has argued that a weighted squared-change parsimony reconstruction also maximizes the posterior probability of the reconstruction, making it equivalent to a Bayesian method. We did not find this to be the case, but we also had large variances from different runs of BayesTraits, uncertainty in the proper settings of the various parameters, and evidence that some functions are still under development.
The fact that various reconstruction methods are related and some of these are equivalent to averages raises the question of whether we gain anything from character optimizations that is not available from just calculating nested averages down the tree, or, worse, a simple global average across terminals. We found here that reconstructions using global averaging were distant from other reconstructions (except maximum likelihood in APE). However, results from nested averaging performed essentially as consistently as linear parsimony in most analyses, with the important exception of not finding congruity between reconstructions based on the STY and PET data sets (Fig. 2c).
A test of optimization methods by Webster and Purvis (2002b) resulted in ancestral reconstructions of Foraminifera that were also different from the average of all the terminals, but just such an average turned out to be a better match for known fossil ancestors than any of the reconstructions. The lesson of their study, however, may be that reconstructions are ultimately dependent on the phylogeny upon which characters are optimized, and its reliability is key. Webster and Purvis (2002b) used a phylogeny constructed using a “stratophenetic” approach, where the author (Fordham, 1986) created species groups with “intuitively defined boundaries” and traced their evolution through geological strata. Thus it is perhaps not surprising that its ancestral nodes were occupied by forms most closely resembling descendant averages, since the author may have been merely averaging shapes when exercising his intuition during tree inference. A second test of reconstruction methods conducted by Webster and Purvis (2002a) on a primate data set also relied on phylogenic estimations, dates, and ancestor hypotheses (including a composite phylogeny with fairly subjective branch lengths; Purvis, 1995) perhaps too rough to indicate which of these methods found the “correct” ancestral morphology. It is important that these methods do not produce just global averages, but ultimately it is difficult to judge their accuracy using such problematic historical hypotheses.
Given the differing philosophies on phylogenetic reconstruction, historical speculation, and assertions about ancient life, acceptance of ancestral reconstruction as a general exercise is varied. However, we feel our work here formalizes a process done casually by ourselves and other opilionid biologists as part of developing new phylogenetic hypotheses and describing newly discovered fossils, which is to wonder what the origins of Opiliones were like (e.g. Garwood et al., 2011). We have shown here that linear parsimony generates reconstructions robust to changes in terminals and topologies, which are quite distinct from simple averages but consistent with reasonable alternative methods, and we have used it to generate an ancestral reconstruction that currently stands as our best estimate of the progenitor for this very old, worldwide group of arthropods.
Acknowledgements
We are indebted to Dennis Stevenson, Cladistics Editor-in-Chief, and two anonymous referees who encouraged us to improve and expand the manuscript. B. de Bivort was supported by the Rowland Junior Fellows Program. This research was funded in part by the National Science Foundation (grant DEV-0236871 to G. Giribet).




