A consensus- and harmony-based feedback mechanism for multiple attribute group decision making with correlated intuitionistic fuzzy sets
Abstract
In this study, an interactive consensus model is proposed for correlated multiple attribute group decision making (MAGDM) problems with intuitionistic triangular fuzzy numbers (ITFNs). The harmony degree (HD) is investigated to determine the degree of maintaining experts' original information while the consensus level is defined as the proximity degree (PD) between an expert and other experts on three levels: evaluation elements of alternatives, alternatives, and decision matrices. Combining HD and PD, a three-dimensional feedback mechanism is proposed to identify discordant experts, alternatives, and corresponding preference values that contribute less to consensus, and provides advice to reach a higher consensus level. Additionally, visual representation of experts' consensus position within the group is provided. Furthermore, a graphical simulation of future consensus and harmony status, if the recommended values were to be implemented, is also provided. Therefore, our proposed feedback mechanism guarantees that it increases the consensus level of the set of experts while maintaining, as much as possible, experts' original information. Then, the PD-induced intuitionistic triangular fuzzy correlated averaging (PD-IITFCA) operator is investigated to aggregate the interactive individual opinions between experts. Finally, the intuitionistic triangular fuzzy correlated averaging (ITFCA) operator is developed to aggregate the evaluation elements of alternatives under correlative attributes. Based on the score and accurate functions of ITFNs, an order relation is proposed to obtain the final solution of alternatives.
1. Introduction
Multiple attribute group decision making (MAGDM) problems address decision situations in which a group of experts express preferences on multiple attributes and interact to derive a common solution (Ölçer and Odabaşi, 2005). During the past decades, significant work has been done to develop decision-making models for this issue. For example, recent proposals to deal with MAGDM can be found in the literature (Park and Kim, 1997; Wei et al., 2000; Cao and Wu, 2011). However, the MAGDM problems generally involve many conflicting aspects prevalent among its experts because different actors have diverse and conflicting value systems. It is preferable that the set of experts reach consensus before applying a selection process to derive the decision solution (Altuzarra et al., 2010; Wu and Cao, 2010; Wu et al., 2011).
Consequently, one key issue that needs to be addressed in an MAGDM problem is the evaluation of the consensus level of group experts. A comprehensive review of the literature (Herrera-Viedma et al., 2014) indicates the existence of different approaches to model consensus under group decision making (GDM). The GDM models usually have the following preference relations: the crisp numbers (Chiclana et al., 1998, 2007, 2009, 2013; Wu and Xu, 2012), interval numbers (Xu, 2004; Wu et al., 2009; Wu and Cao, 2010; Wu and Chiclana, 2014a), linguistic information (Herrera et al., 1996a, 2009; Zhou and Chen, 2013), fuzzy numbers (Bryson, 1997; Dong et al., 2008, 2010; Su et al., 2013), intuitionistic fuzzy numbers (Szmidt and Kacprzyk, 2003; Xu, 2007; Xu and Yager, 2009; Yu, 2014), and extended intuitionistic fuzzy numbers (Wu and Chiclana, 2012; Wu and Liu, 2012; Wu and Cao, 2013). However, these approaches are static in nature, that is, they do not include any type of feedback mechanism to produce rules or recommendations on how to increase consensus when it is unacceptably low. Cabrerizo et al. (2010) made a comprehensive comparison of different consensus measures, and then some interactive consensus models (Alonso et al., 2010; Dong et al., 2014; Herrera-Viedma et al., 2007; Wu and Chiclana, 2014b; Xu and Wu, 2013; Xu et al., 2013;) were developed for experts to change their opinion to a higher consensus level by a feedback mechanism. Furthermore, these interactive consensus models are extended into the following decision-making contexts: network (Pérez et al., 2010; Alonso et al., 2013), unbalanced fuzzy linguistic information (Cabrerizo et al., 2009, 2010), and discrete fuzzy linguistic information (Massanet et al., 2014). However, these interactive consensus models use the two comparison preference relations, therefore they are only suitable to deal with single-attribute GDM problems. Recently, Xu (2009) extended these models to the case of MAGDM problems. But, Xu's interactive consensus model contains a feedback mechanism that experts must change all of their opinions, if one expert has not reached the threshold value of consensus level. Later, Xu and Wu (2011) proposed an improved feedback mechanism in which every expert has to update only part of his/her opinion (some elements in the decision matrices).
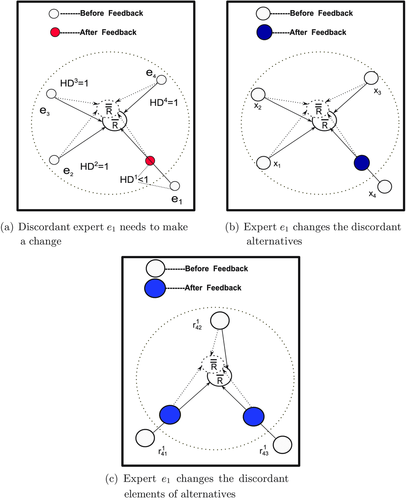
Although these interactive consensus models are successful in investigating different kinds of consensus levels and proposing feedback mechanisms to provide advice to reach higher consensus degree, these models neglected a reality that if the recommended advice makes experts deviate from their original opinions, they may not accept these advice. Therefore, in nature, these approaches are forcing the discordant experts to change their opinions without considering whether they agree or not. However, in practice, it is up to the decision maker (DM) whether to implement the recommendations given to him/her (Eklund et al., 2008). A more reasonable policy should rest on this premise and, consequently, it would allow the DM to revisit his/her evaluations using appropriate and meaningful consensus information representation (Wu and Chiclana, 2014b). Also, Herrera-Viedma et al. (2014) recently pointed that some new decision rules should be taken into the consensus process of GDM. Inspired by these ideas, this article defines the concept of the harmony degree (HD) to determine the degree of maintaining the original information of expert. Then, the consensus level is defined as the proximity degree (PD) between an expert and other experts in the group. Particularly, the PD is computed on three levels: evaluation elements of alternatives, alternatives, and decision matrix. Combining the PD and HD, a three-dimensional (3D) feedback mechanism is proposed to show the consensus and harmony status of every expert with figures. Furthermore, a graphical simulation of future consensus and harmony status, if the recommended values were to be implemented, has been depicted (see Fig. 2(a)–(c) in the final numerical example). In the light of this extra visual information, a discordant expert can revisit his evaluations and make changes if considered appropriate to achieve a higher consensus level. Consequently, the novelty of our feedback mechanism is that it increases the consensus level of the set of experts and maintains, as much as possible, experts' original information simultaneously.
Considering that there may exist some degree of interactive characteristics in experts or interdependence in criteria (Grabisch, 1995; Grabisch et al., 2000; Torra, 2003; Tan, 2011), it could be interesting to investigate an interactive approach for MAGMD in which the preferences of experts are interactive and the attributes are interindependent. Because of the fuzziness in MAGDM, this article applies the intuitionistic triangular fuzzy numbers (ITFNs) to describe the evaluation elements (Zhang and Liu, 2010) that are an extension of triangular fuzzy sets (Zadeh, 1965) and intuitionistic fuzzy sets (Atanassov, 1986). After the group consensus level reaches a satisfied value, the individual decision matrices need to be aggregated into a collective matrix. Therefore, the aggregate operator is a key issue in GDM (Merigó and Casanovas, 2011; Merigó and Gil-Lafuente, 2011, 2013; Zhou et al., 2012a, 2012b). To deal with interactive characteristics between experts, a new PD-induced intuitionistic triangular fuzzy correlated averaging (PD-IITFCA) operator is investigated to compute the collective decision matrix. The PD-IITFCA operator associated weighting vector is derived using the PD of individual expert, providing a monotonic increasing mapping between the experts' consensus levels and their contribution weight in the collective decision matrix. Furthermore, this PD-IITFCA operator has the advantage that it does not require to assign the weight of each expert beforehand, while Pérez et al. (2013) assumed that the weights of experts are to be obtained directly. To rank the best alternative, an intuitionistic triangular fuzzy correlated averaging (ITFCA) operator is investigated to aggregate the evaluation elements of alternatives under correlative attributes, which can also be regarded as the generalization of these correlated aggregating operators in the literature (Wei and Zhao, 2012; Yang and Chen, 2012; Meng et al., 2013; Wu et al., 2013).
The rest of the article is organized as follows. Section 2. develops the score and accurate functions of ITFNs, then an order relation for ranking ITFNs is proposed. In Section 3., the definition of PD is proposed on three levels. Then, an interactive consensus model for MAGDM with ITFNs is covered with special attention paid to the design of the PD-based feedback mechanism. Section 4. proposes an approach for the selection process of MAGDM problems based on the PD-IITFCA and ITFCA operators. Section 5. gives an illustrative example to show the validity of our proposed method. Finally, Section 6. gives an analysis of the proposed consensus model highlighting the main differences with respect to existing consensus models in the literature, and then draws the conclusions.
2. Score and accurate functions for ranking ITFNs
Intuitionistic fuzzy sets (IFSs) were introduced by Atanassov (1986).
Definition 1. (IFS)An IFS A over a universe of discourse X is represented as
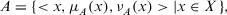 (1)
(1)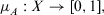
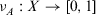 , and
, and 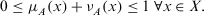 For each
For each 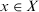 , the numbers
, the numbers  and
and 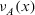 are known as the degree of membership and degree of nonmembership of x to A, respectively.
are known as the degree of membership and degree of nonmembership of x to A, respectively.
To express more fuzzy information, Atanassov and Gargov (1989) introduced the definition of interval-valued IFSs (IVFSs), which was later generalized by Zhang and Liu (2010) with ITFNs. A prominent characteristic of ITFNs is that its membership values and nonmembership values are triangular fuzzy numbers (TFNs).
Definition 2. (ITFNs)An ITFN is denoted as 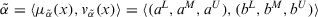 . Its membership function can be given as
. Its membership function can be given as
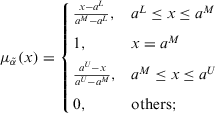 (2)
(2)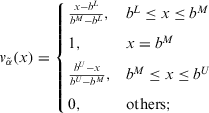 (3)
(3)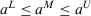 ,
, 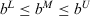 , and
, and 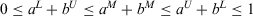 .
.
Note 1.When the nonmembership function 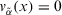 , then an ITFN is reduced to a TFN. If
, then an ITFN is reduced to a TFN. If 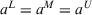 and
and 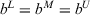 , then an ITFN is reduced to an intuitionistic fuzzy number.
, then an ITFN is reduced to an intuitionistic fuzzy number.
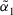 and
and 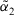 be two ITFNs, and
be two ITFNs, and 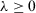 , then ITFNs have the following operational laws:
, then ITFNs have the following operational laws:
- 1.
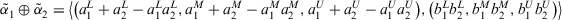 .
. - 2.
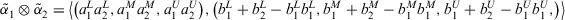 .
. - 3.
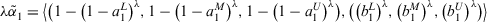 .
. - 4.
 .
.
To rank TFNs, Liou and Wang (1992) proposed the following index.
Definition 3.Let 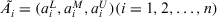 is a collection of TFN with left membership function
is a collection of TFN with left membership function  and right membership function
and right membership function 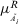 . Suppose that
. Suppose that 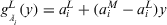 is the inverse function of
is the inverse function of 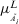 , and
, and 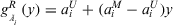 is the inverse function of
is the inverse function of 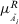 , then ordering index is defined by
, then ordering index is defined by
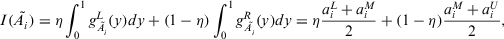 (4)
(4)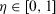 is the optimism index reflecting the optimism degree of a decision maker. The larger η is, the more optimistic the decision maker is.
is the optimism index reflecting the optimism degree of a decision maker. The larger η is, the more optimistic the decision maker is.
Recall that TFNs are particular cases of ITFNs, we can apply this index to propose the score and accurate functions of ITFNs.
Definition 4. (Score function of ITFNs)Let 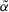 be an ITFN. Then, a score function of ITFNs can be represented as follows:
be an ITFN. Then, a score function of ITFNs can be represented as follows:
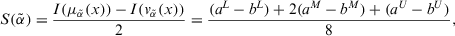 (6)
(6)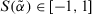 , the larger the value of
, the larger the value of 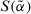 , the more the degree of score of the ITFN
, the more the degree of score of the ITFN 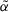 .
. 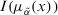 and
and 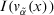 are computed by expression 5, respectively.
are computed by expression 5, respectively.
Definition 5. (Accuracy function of ITFNs)An accuracy function of ITFNs can be represented as follows:
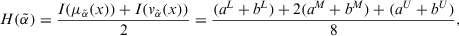 (7)
(7)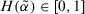 , the larger the value of
, the larger the value of 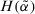 , the more the degree of accuracy of the ITFN
, the more the degree of accuracy of the ITFN 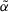 .
. 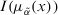 and
and 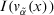 are computed by expression 5, respectively.
are computed by expression 5, respectively.
Definition 6. (Order relations of ITFNs)Let 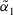 and
and 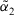 be two ITFNs, then
be two ITFNs, then
- 1. If
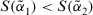 , then
, then 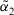 is greater than
is greater than  , denoted by
, denoted by 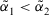 .
. - 2. If
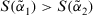 , then
, then 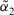 is smaller than
is smaller than 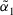 , denoted by
, denoted by 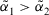 .
. - 3. If
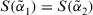 , then
, then
- (a) if
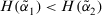 , then
, then 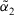 is greater than
is greater than 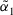 , denoted by
, denoted by 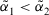 ;
; - (b) if
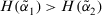 , then
, then 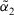 is smaller than
is smaller than  , denoted by
, denoted by 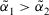 ;
; - (c) if
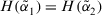 , then
, then 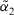 is equal to
is equal to 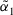 , denoted by
, denoted by 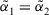 .
.
- (a) if
3. Interactive consensus model for correlated MAGDM
- 1. “the consensus process” and
- 2. “the selection process.”
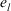 does not reach the threshold value of consensus level, then the interactive algorithm (Xu, 2009) changes every original decision matrix
does not reach the threshold value of consensus level, then the interactive algorithm (Xu, 2009) changes every original decision matrix
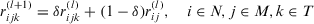 (8)
(8)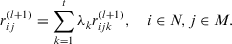 (9)
(9)But this interactive consensus model has some drawbacks that force experts to change all of their opinions (Xu and Wu, 2011). This policy may not be acceptable to those experts with acceptable consensus level as it will make them deviate from their original opinions. A more reasonable policy of interactive consensus process is to increase the level of agreement and, at the same time, maintain the original information as much as possible. To achieve these “rational” criteria, this article introduces the definition of proximity degree (PD) to measure the actual consensus on three levels: evaluation elements of alternatives, alternatives, and decision matrix. If 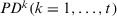 satisfies a minimum satisfaction threshold value
satisfies a minimum satisfaction threshold value 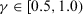 , agreed by the group experts, then the selection process of GDM is carried out; otherwise a 3D feedback mechanism is proposed to identify the discordant experts, the discordant alternatives and the discordant evaluation elements at a fast speed. Also, this article will determine the degree of maintaining the original information of expert, named harmony degree (or HD). Combining the PD and HD, this feedback mechanism provides figures to show the consensus status of every expert. Furthermore, a graphical simulation of future consensus and harmony status, if the recommended values were to be implemented, is also presented.
, agreed by the group experts, then the selection process of GDM is carried out; otherwise a 3D feedback mechanism is proposed to identify the discordant experts, the discordant alternatives and the discordant evaluation elements at a fast speed. Also, this article will determine the degree of maintaining the original information of expert, named harmony degree (or HD). Combining the PD and HD, this feedback mechanism provides figures to show the consensus status of every expert. Furthermore, a graphical simulation of future consensus and harmony status, if the recommended values were to be implemented, is also presented.
- 1. “the aggregation process” and
- 2. “the exploitation of the alternatives” (Herrera-Viedma et al., 2004).
In order to aggregate the individual decision matrix into a collective one, it is necessary to determine the weights associated to each expert. Because consensual information is considered more relevant or important than discordant information, we develop the PD-IITFCA operator that associates higher weights with more consensual information. This operator has the advantage that it does not need any weight information beforehand and assigns the experts' weights by their associated PDs. Furthermore, the PD-IITFCA operator aggregates individual opinions in such a way that more emphasis is given on higher consensus level. Finally, we develop the ITFCA operator to aggregate the correlative attribute values and derive the final priority of the alternatives.
- Computing proximity indexes.
- Feedback mechanism.
- The PD-IITFCA operator based aggregation.
- The ITFCA operator based exploitation.
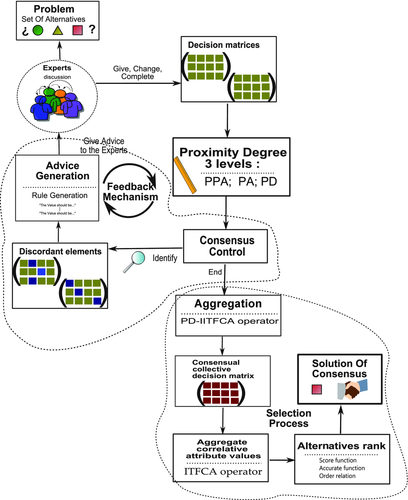
These steps will be presented in more detail in the following subsections. A step-by-step example to illustrate the computation processes involved in each step is also provided.
3.1. The definition of PD with ITFNs
Based on the Hamming distance (Yang and Chiclana, 2012), we can define a distance function between ITFNs as follows:
Definition 7.Let 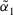 and
and 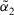 be two ITFNs, then we define the distance between
be two ITFNs, then we define the distance between 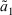 and
and 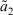 as follows:
as follows:
 (10)
(10)Xu and Yager (2009) defined the similarity degree between two intuitionistic fuzzy numbers for consensus analysis in GDM. We extend it to the case of ITFNs.
Definition 8. (Similarity degree)Let 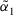 and
and  be two ITFNs, and
be two ITFNs, and 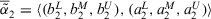 be the complement of
be the complement of 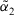 , then
, then
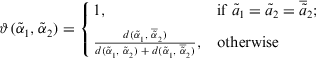 (11)
(11)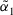 and
and 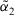 , where
, where 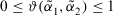 .
.
- 1.
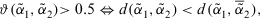 which means
which means 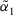 is more similar to
is more similar to 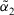 than
than 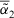 . Especially,
. Especially, 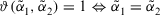 , which means the identity of
, which means the identity of 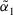 and
and 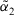 .
. - 2.
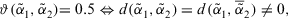 which means
which means 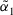 is similar to
is similar to 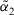 than
than 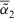 .
. - 3.
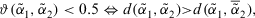 which means
which means 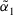 is more similar to
is more similar to 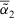 than
than 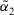 . Especially,
. Especially, 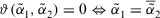 , which means the complete dissimilarity of
, which means the complete dissimilarity of 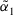 and
and 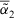 .
.
In the following definition, we will apply the developed similarity to measure the PD for each expert.
Definition 9.Let 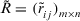 be a
be a  decision matrix. If all
decision matrix. If all 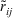 are ITFNs, and
are ITFNs, and
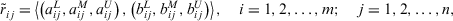
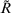 an intuitionistic triangular fuzzy decision matrix.
an intuitionistic triangular fuzzy decision matrix.
To compute the PD between an expert and other experts in the group, we need to aggregate decision matrices into a collective matrix. However, in most cases, the weight information of experts is usually not known beforehand. Therefore, the arithmetic or geometric average operators are usually used for aggregating individual opinions (Bryson, 1997; Xu and Yager, 2009; Yu and Lai, 2011; Wu and Xu, 2012).
Definition 10.Let  be a collection of intuitionistic triangular fuzzy decision matrices given by experts, respectively, then the average aggregated intuitionistic triangular fuzzy decision matrix
be a collection of intuitionistic triangular fuzzy decision matrices given by experts, respectively, then the average aggregated intuitionistic triangular fuzzy decision matrix 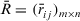 is defined as:
is defined as:
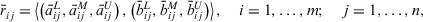
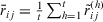 .
.
- Level 1. PD on elements of alternatives. The PD of an expert
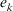 to the group on the alternatives
to the group on the alternatives 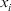 under attribute
under attribute 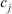 is
is
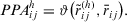 (12)
(12) - Level 2. PD on alternatives. The PD of an expert
 to the group on the alternative
to the group on the alternative 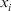 is
is
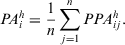 (13)
(13) - Level 3. PD on decision matrix. The PD of an expert
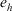 to the group on decision matrix is
to the group on decision matrix is
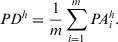 (14)
(14)
The greater the value of 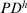 , the greater the PD between intuitionistic triangular fuzzy decision matrices
, the greater the PD between intuitionistic triangular fuzzy decision matrices  and
and 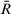 . The PD has the following desirable properties.
. The PD has the following desirable properties.
Proposition 1.Let 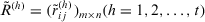 be t intuitionistic triangular fuzzy decision matrices, and
be t intuitionistic triangular fuzzy decision matrices, and 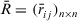 be their averaged aggregated decision matrix, then
be their averaged aggregated decision matrix, then
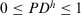 .
.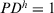 if and only if
if and only if  and
and  are identical.
are identical.
Proof 1.By expression 12, we have
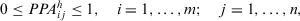
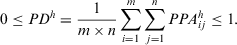
2. Necessity. If 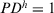 , then
, then 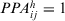 , for all
, for all 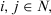 that is,
that is,  , for all
, for all 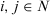 . Therefore,
. Therefore, 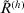 and
and 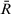 are identical.
are identical.
3. Sufficiency. If  and
and 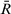 are identical, then
are identical, then 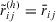 , for all
, for all 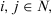 that is,
that is, 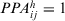 , for all
, for all 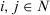 . Therefore,
. Therefore,  .
. 
The PD can be used to decide when the feedback mechanism should be applied to give advise to the experts, or when the consensus reaching process has to come to an end. When 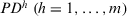 satisfies a minimum satisfaction threshold value
satisfies a minimum satisfaction threshold value 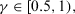 the consensus reaching process ends, and the selection process is applied to achieve the solution of consensus.
the consensus reaching process ends, and the selection process is applied to achieve the solution of consensus.
Note 2.In GDM problems, it is rare to achieve complete consensus. Therefore, the threshold value 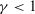 . And in most cases, if more than half of experts can achieve consensus, the decision-making result may be acceptable. Thus,
. And in most cases, if more than half of experts can achieve consensus, the decision-making result may be acceptable. Thus,  . Consequently, we have the threshold value
. Consequently, we have the threshold value 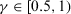 . The bigger the threshold value, the more experts should change their preference relation.
. The bigger the threshold value, the more experts should change their preference relation.
3.2. Three-dimensional feedback mechanism
When at least one of the experts' consensus levels is below the fixed threshold value, a feedback mechanism is activated to generate personalized advice to those experts, which includes two steps: “identification of the evaluation values” that should be changed and “generation of advice.”
3.2.1 Identification of the evaluation values
- Step 1. The experts with a PD lower than the threshold value γ are identified:
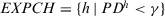 .
. - Step 2. For the identified experts, their alternatives with a
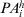 lower than the satisfaction threshold γ are identified:
lower than the satisfaction threshold γ are identified: 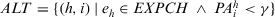 .
. - Step 3. Finally, the values to be changed are
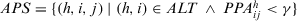 .
.
3.2.2 Generation of advice
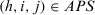 , the personalized recommendation rules are identified as follows:
, the personalized recommendation rules are identified as follows:
- 1.
If
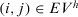 , the recommendation generated for expert
, the recommendation generated for expert 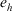 is: “You should change your evaluation value for the alternatives
is: “You should change your evaluation value for the alternatives 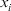 under attribute
under attribute 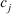 ,
, 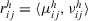 , to a value closer to
, to a value closer to 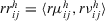 .''
.''
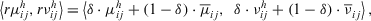
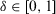 is a parameter to control the degree of recommendation.
is a parameter to control the degree of recommendation.To determine the degree of maintaining the original information of expert before and after adopting the recommended advice, this article provides the definition of the HD as follows.
Definition 11.After accepting the recommended advice by feedback mechanism, the HD of expert 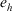 can be as defined as
can be as defined as
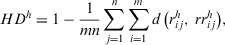 (15)
(15)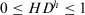 . The bigger the
. The bigger the 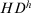 , the less original opinion the expert
, the less original opinion the expert 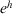 changes.
changes.
Definition 12.The general HD (GHD) of experts can be as defined as
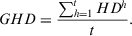 (16)
(16)Note 3.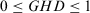 . The bigger the GHD, the more original opinion is preserved in every feedback round. Therefore, a more reasonable policy of feedback mechanism is to arrive at the threshold value of consensus level and the maximum value of GHD simultaneously.
. The bigger the GHD, the more original opinion is preserved in every feedback round. Therefore, a more reasonable policy of feedback mechanism is to arrive at the threshold value of consensus level and the maximum value of GHD simultaneously.
4. Selection process based on the PD-IITFCA and ITFCA operators
4.1. The PD-IITFCA operator for aggregating individual decision matrices
Let 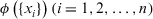 be the weights of the elements, where ϕ is a fuzzy measure. Wang and Klir (1992) gave the definition of ϕ as follows.
be the weights of the elements, where ϕ is a fuzzy measure. Wang and Klir (1992) gave the definition of ϕ as follows.
Definition 13.A fuzzy measure ϕ on set Y is a set function ϕ : 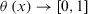
- 1.
 .
. - 2.
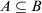 ; implies
; implies 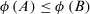 , for all
, for all 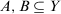 .
. - 3.
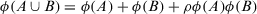 , for all
, for all 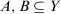 and
and 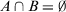 , where
, where 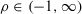 .
.
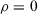 , then the condition (3) reduces to the axiom of additive measure:
, then the condition (3) reduces to the axiom of additive measure:
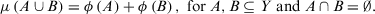
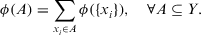 (17)
(17)Combining the above definition and the well-known Choquet integral (Choquet, 1953), Xu (2009) developed some intuitionistic fuzzy aggregation operators that consider the importance of the elements or their ordered positions and reflect the correlations among the elements or their ordered positions simultaneously. In the following, we develop the PD-ITIFCA operator for aggregating decision-making matrices with ITFNS in which the weights of experts are correlative.
Definition 14.Let 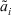 be a collection of ITFNs on X, a PD-IITFCA operator of dimension is a mapping PD-IITFCA:
be a collection of ITFNs on X, a PD-IITFCA operator of dimension is a mapping PD-IITFCA: 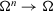 such that
such that
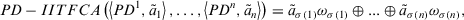 (18)
(18)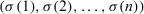 is a permutation of
is a permutation of 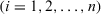 such that
such that 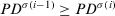 for all
for all 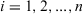 , that is,
, that is, 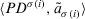 is the 2-tuple with
is the 2-tuple with 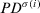 the tth largest values in the set
the tth largest values in the set  , and
, and 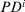 in
in 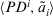 is referred as the order inducing variable and
is referred as the order inducing variable and 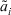 as the ITFNs.
as the ITFNs. 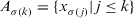 for
for  and
and 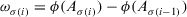 .
.
By Definition 14, we get the following result using mathematical induction on n.
Theorem 1.Let 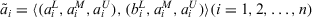 be a collection of intuitionistic triangular fuzzy values on X and ϕ be a fuzzy measure on Y, then their aggregated value using the PD-TIFCA operator is also an ITFN, and
be a collection of intuitionistic triangular fuzzy values on X and ϕ be a fuzzy measure on Y, then their aggregated value using the PD-TIFCA operator is also an ITFN, and
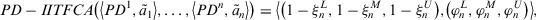 (19)
(19)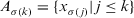 for
for 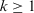 , and
, and 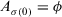 , and
, and 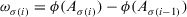 .
. 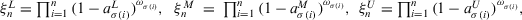
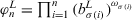 ,
,  , and
, and 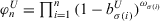 , respectively.
, respectively.
Proof.Clearly, the first result follows from Equation 18. In the following equation, we prove Equation 19 using mathematical induction on n. For  , we have
, we have

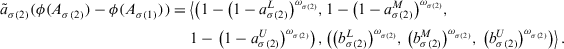
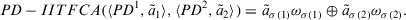
That is, for n = 2, Equation 19 holds. Suppose if for 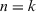 , Equation 19 holds, that is,
, Equation 19 holds, that is,
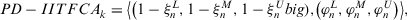
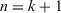 , according to Definition 14, we have
, according to Definition 14, we have
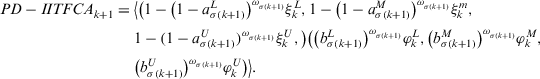
That is, for 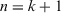 , expression 19 always holds. Therefore, for all n, expression 19 always holds, which completes the proof of Theorem 1.
, expression 19 always holds. Therefore, for all n, expression 19 always holds, which completes the proof of Theorem 1. 
 :
: 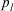 is the argument value to aggregate,
is the argument value to aggregate, 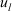 is the importance weight value associated with
is the importance weight value associated with 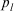 , and
, and 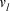 is the order inducing value, the aggregation is
is the order inducing value, the aggregation is
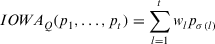 (20)
(20)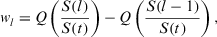 (21)
(21)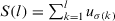 , and σ is the permutation such that
, and σ is the permutation such that 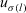 in
in 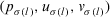 is the lth largest value in the set
is the lth largest value in the set  . Q is a function: [0, 1] → [0, 1] such that
. Q is a function: [0, 1] → [0, 1] such that 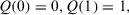 and if
and if 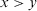 then
then 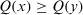 .
.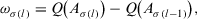 (22)
(22)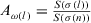 ,
, 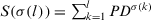 , and σ is the permutation such that
, and σ is the permutation such that 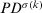 is the lth largest value in the set
is the lth largest value in the set  .
.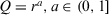 (Chiclana et al., 2007), we can verify that the higher the consensus of an expert the higher the weighting value of that expert in the aggregation, that is,
(Chiclana et al., 2007), we can verify that the higher the consensus of an expert the higher the weighting value of that expert in the aggregation, that is,
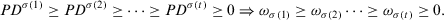
4.2. The exploitation of the alternatives
Definition 15.Let 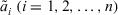 be a collection of intuitionistic triangular fuzzy values on X. Based on fuzzy measure, an ITFCA operator of dimension n is a mapping TIFCA:
be a collection of intuitionistic triangular fuzzy values on X. Based on fuzzy measure, an ITFCA operator of dimension n is a mapping TIFCA: 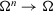 such that
such that
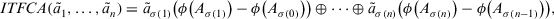 (23)
(23)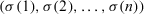 is a permutation of
is a permutation of 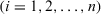 such that
such that 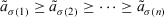 ,
, 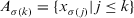 , for
, for 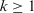 and
and 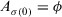 .
.
We can also obtain the following result for aggregating ITFNs using mathematical induction on n.
Theorem 2.Let 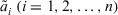 be a collection of intuitionistic triangular fuzzy values on X, then their aggregated value using the ITFCA operator is also an intuitionistic triangular fuzzy value, and
be a collection of intuitionistic triangular fuzzy values on X, then their aggregated value using the ITFCA operator is also an intuitionistic triangular fuzzy value, and
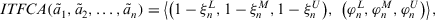 (24)
(24)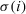 indicates a permutation on X such that
indicates a permutation on X such that 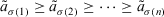 ,
, 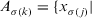
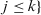 for
for 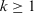 , and
, and 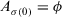 , and
, and 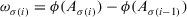 .
. 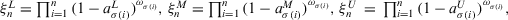
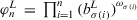 ,
, 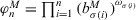 , and
, and 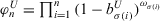 ,respectively.
,respectively.
5. Numerical example
Example 1.A computer producing company wants to select the most appropriate green supplier for one of the key elements in its manufacturing process. After preevaluation, four suppliers have remained as alternatives for further evaluation. Three criteria are considered as follows: C1, environmental costs; C2, remanufacturing/reuse activity; C3, hazardous waste management. Four experts from different departments organized this evaluation whose important degrees are not known beforehand. Procedure for the selection of most appropriate green supplier contains the following steps:




Step 1. According to Definition 10, all the decision matrices 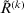 are synthesized into an aggregated decision matrix
are synthesized into an aggregated decision matrix 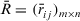 :
:

Step 2. Taking a minimum threshold value of 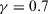 , we calculate the PDs on the relation for each expert as follows:
, we calculate the PDs on the relation for each expert as follows: 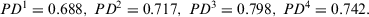
Therefore, the feedback mechanism is activated to assist expert e1.
Step 3. The following 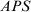 set is obtained:
set is obtained:
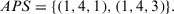
Step 4. Taking a value of 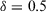 , the recommendations for expert e1 are as follows:
, the recommendations for expert e1 are as follows:
- You should change your evaluation value of alternative x4 under attribute c1 to a value closer to
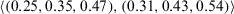 .
. - You should change your evaluation value of alternative x4 under attribute c3 to a value closer to
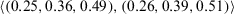 .
.
We can obtain the  . Obviously, it is very close to 1, which means experts just need to make a little change of their original opinions. Therefore, expert e1 may be glad to implement the changes in his evaluation values to a higher consensus levels. Furthermore, a visual graphical simulation of future consensus status after the recommended values were to be implemented is shown in Fig. 2(a)–(c).
. Obviously, it is very close to 1, which means experts just need to make a little change of their original opinions. Therefore, expert e1 may be glad to implement the changes in his evaluation values to a higher consensus levels. Furthermore, a visual graphical simulation of future consensus status after the recommended values were to be implemented is shown in Fig. 2(a)–(c).
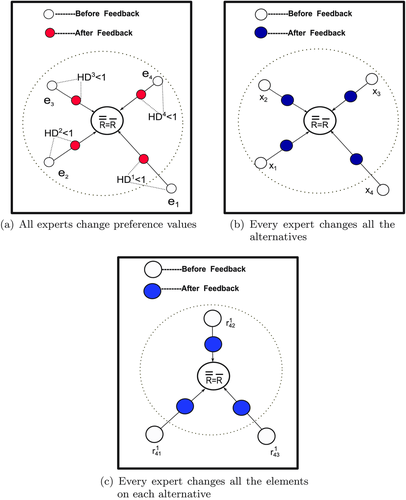
Adopting Xu's feedback mechanism (Xu, 2009), we can calculate the 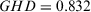 , which is obviously lower than our
, which is obviously lower than our 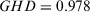 . The reason for this is that Xu's feedback mechanism forces every expert to change the preference values regardless of whether they achieve the threshold value of consensus level shown in Fig. 3. In addition, Fig. 3(b) and (c) shows that all the alternatives and elements are changed. Obviously, our proposed feedback mechanism advises the discordant expert to change only his part evaluation values, and therefore it reduces the computation burden and can be easily accepted.
. The reason for this is that Xu's feedback mechanism forces every expert to change the preference values regardless of whether they achieve the threshold value of consensus level shown in Fig. 3. In addition, Fig. 3(b) and (c) shows that all the alternatives and elements are changed. Obviously, our proposed feedback mechanism advises the discordant expert to change only his part evaluation values, and therefore it reduces the computation burden and can be easily accepted.
Step 5. Second consensus round: Assuming e1 implements the values recommended above, he/she gives the new decision matrix 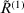 as
as

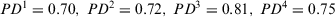 , which are over the threshold value
, which are over the threshold value 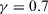 .
.Step 6. Apply the new consensus levels : 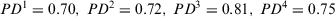 and assume the basic unit-interval monotonic (BUM) function
and assume the basic unit-interval monotonic (BUM) function 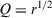 , we calculate the correlated weights of experts by expression 22.
, we calculate the correlated weights of experts by expression 22.

Then, by the PD-IITFCA operator 18, the collective decision matrix is computed as

Step 7. Thus, the exploitation of the alternatives would be activated.
Suppose that the fuzzy measure of attribute of 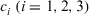 as follows:
as follows:
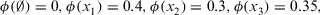
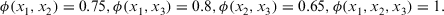
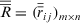 and the ITFCA operator, we derive the collective overall preference values
and the ITFCA operator, we derive the collective overall preference values 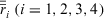 of the alternative:
of the alternative:
 (25)
(25)According to expression 6, we calculate the score functions as

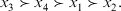
6. Conclusions
- 1. It investigates the HD to determine the degree of maintaining the original information of expert before and after adopting the recommended advice. Therefore, the discordant expert can decide whether to adopt the recommended advice produced by feedback mechanism. It is worth noting that this issue has not been successfully addressed by any previous GDM model.
- 2. It defines the consensus level as the PD between an expert and other experts in the group on three levels: evaluation elements, alternatives, and decision matrices. Once the discordant experts are identified, the consensus model proceeds to identify their alternatives and the corresponding evaluation elements at the level of pair of alternatives.
- 3. Combining the HD and PD, this article proposes a 3D feedback mechanism, which produces a visual graphical simulation of future consensus status after the recommended values were to be implemented. The novelty of our feedback mechanism is that the acceptable consensus level of the set of experts is achieved, simultaneously maintaining experts' original information to maximum degree.
- 4. It investigates the PD-IITFCA operator to aggregate the interactive opinion of experts, which does not require assigning a weight to each expert beforehand and its associated weighting vector is derived using the PD of individual expert. Then, the ITFCA operator is proposed to aggregate the evaluation elements of alternatives under correlative attributes.
- 1. The definitions of PD do not take into account the weights of attributes. Therefore, the correlative relation in the attributes does not reflect in the feedback mechanism.
Finally, the feedback mechanism of the proposed consensus model is designed following a top-to-bottom methodology, and therefore it identifies the discordant experts in the following order: (a) their decision matrices, (b) their alternatives, and (c) their evaluation elements. Then, the experts only need to update their discordant evaluation elements to consensus, that is, it preserves the original decision opinions and independence in maximum degree, and also reduces the computation burden with respect to other consensus method in the literature.
Acknowledgments
The authors are very grateful to General Editor Prof. Celso Ribeiro and the anonymous referees for their valuable comments and suggestions that have helped us to improve considerably the quality of this article. This work was supported by the National Natural Science Foundation of China (NSFC) under the grant nos. 71101131 and 71331002, Zhejiang Provincial National Science Foundation for Distinguished Young Scholars of China (no. LR13G010001), Zhejiang Provincial Planted Talent Foundation of China (no. 2014R404046), and Zhejiang Provincial Qianjiang Talent Foundation of China.



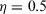 , then expression
, then expression