Internet Search Intensity and Its Relation with Trading Activity and Stock Returns*
Abstract
Using Google search volume as a proxy for investor attention, this paper provides evidence on the role attention plays in financial markets. We first show that abnormal Google search volume (ASVI) helps explain cross-sectional variations in trading activity, even after controlling for its important determinants. Specifically, ASVI is positively related to trading volume, order imbalance and liquidity. When the relation between stock returns and ASVI is examined, we find a strong positive relation in the month after attention shocks and a reversal over a longer holding period. We further conjecture that the attention effect is more pronounced in stocks with higher limits to arbitrage. For this purpose, we construct a limits-to-arbitrage index and show that limits to arbitrage play an important role in explaining the attention effect.
I INTRODUCTION
The efficient market hypothesis assumes that stock prices should instantaneously reflect new information as it arrives (Fama 1970). This assumption requires investors to be aware of the full set of information available in the market. However, psychological evidence suggests that investors can only handle a certain amount of information at any point in time and thus, as Kahneman (1973) has argued, attention is a scarce cognitive resource. The study by Barber and Odean (2008) establishes the theory in investor attention. They argue that investors face a search problem when selecting which stocks to buy. However, the search problem is not as formidable when investors sell stocks, since they can only sell the stocks that they already own.1 Thus, when facing a search problem, investors are more likely to buy rather than sell stocks that attract their attention. This prediction leads to short-term positive price pressure at an attention-grabbing event and this price pressure dissipates as attention wears off over time.
The purpose of this paper is to examine the role attention plays in financial markets. We first hypothesize that attention helps explain the cross-sectional variation in trading activity. Chordia et al. (2007) argue that trading activity is a function of liquidity trading, the number of informed agents, the degree of learning by investors on how asset returns are generated, and the dispersion of agents’ information signals. The authors further point out that investors’ liquidity needs are realized only in stocks that are more visible to investors. Chordia et al. (2007) find that proxies for visibility such as size, firm age, the book-to-market ratio, and price levels are important determinants of cross-sectional variation in trading activity. Since attention is a necessary condition for a firm to be publicly recognized, this should lead to a positive relation between attention and trading activity in the cross section when combined with the view that the buying behavior of investors is influenced by attention-grabbing events.
In classical finance theories with a no-arbitrage argument, profitable opportunities from trading securities are exploited by arbitragers and their arbitrage activities should correct mispriced securities. This argument is built on the assumption that information is readily available to investors. However, arbitrage opportunities could become less obvious when information is sparse or even ignored (e.g., Zhang 2006). Trade barriers such as transaction costs and short-sale constraints could further hinder arbitrage activities. If the attention effect is due to ignorance of price relevant information or to constraints in allocating attention, the effect should be more pronounced in the presence of severe limits to arbitrage. This is because investors who have a greater capacity to obtain information and exploit mispricing will be more likely to avoid stocks where arbitrage is difficult.
This paper employs monthly share price data drawn from the Australian market from 2004 to 2015. Our proxy for investor attention is the Google search volume index (SVI) following Da et al. (2011). The use of the Australian market is motivated by two facts. First, how attention can be directly captured remains an open question and many alternative proxies have been employed in empirical analysis. With the development and convenience of the Internet, online resources are rapidly becoming one of the most important information sources for investors. However, compared to other alternative proxies, the use of Internet search as a proxy for attention is fairly limited in markets outside the United States.2 In Australia, Google is the dominant search engine, with over 90% of all searches run, greater than the 72% reported in the US market.3 The second most popular search engine in Australia is Bing, but it comprises only about 4% of the market. Thus, Google search engine is arguably an important information source for Australian investors. Second, the Australian market is of interest in its own right. As noted in Chiah et al. (2016), about 70% of the listed stocks on the Australian Securities Exchange (ASX) are priced below AU$1. Thus, the distribution of share prices is highly skewed and companies with low share prices are common in this market. Dyl and Elliott (2006) point out that small and less well-known firms tend to have low share prices in order to broaden their investor base. Accordingly, attention is expected to play a nontrivial role in this market.
We find that abnormal Google search volume (ASVI), which is defined as the difference between the current SVI and the mean SVI over the past 12 months, scaled by the standard deviation of the SVI over the past 12 months, is positively related to turnover, order imbalance (OIB) and liquidity in the cross section. These relationships remain robust when other important determinants of trading activity are included in the analysis. The positive relation between ASVI and the OIB between buy and sell orders is consistent with the view that attention attracts more buying than selling. We also find that high investor attention shocks lead to an increase in trading volume, OIB and stock liquidity in the subsequent month.
Consistent with the literature, the existence of the attention effect is unambiguous. At the portfolio level, the return difference between stocks experiencing a high ASVI and stocks experiencing a low ASVI is positive in the short run and this return difference falls considerably as the holding period is extended. This return pattern is also confirmed at the individual stock level after controlling for other firm characteristics, which are known to affect stock returns. Our results are robust to a number of sensitivity checks, including (i) employing different search terms, (ii) examining whether the relation between ASVI and stock returns is caused by price-sensitive announcements, (iii) considering seasonality in returns, (iv) testing the existence of the attention effect after controlling for turnover and liquidity shocks, and (v) using weekly rather than monthly stock return data. Our results provide strong out-of-sample evidence on the relation between search intensity and stock returns. The explanatory power of ASVI on trading activity and stock returns is consistent with the theoretical prediction of Barber and Odean (2008) that the proportion of stocks being purchased relative to stocks being sold will be greatest following periods of high attention.
Having confirmed the existence of the attention effect, we formally test how limits to arbitrage contribute to the effect. An important methodological consideration is how limits to arbitrage are measured. The most common measure of arbitrage risk is idiosyncratic stock volatility (e.g., Pontiff 1996; Wurgler and Zhuravskaya 2002). The other common measure is information uncertainty, which is often proxied by analyst coverage (Hong et al. 2000) and dispersion in earnings forecasts (e.g., Diether et al. 2002; Zhang 2006). Trading costs are also linked to limits to arbitrage and proxies include stock prices, firm size, and trading volume (e.g., Bhushan 1994; Stoll 2000; Nagel 2005). In this paper, we construct a limits-to-arbitrage index based on five popular limits-to-arbitrage measures following a recent methodological innovation by Stambaugh et al. (2015). The measures include idiosyncratic volatility, analyst coverage, share price, firm size, and share turnover. Our tests involve an examination of portfolios double-sorted on ASVI and the limits-to-arbitrage index and cross-sectional regressions performed for stocks with different levels of arbitrage risk. Consistent with our conjecture, we find that the attention effect is most pronounced in stocks with high arbitrage costs. Specifically, these stocks exhibit stronger short-run price pressure and subsequent reversal.
Our paper contributes to the literature in two major ways. First, an investigation of the attention effect in Australian equity returns not only provides a comparison with other markets, but also establishes evidence of common components of attention in stock returns through similar findings. Our results suggest that Google search volumes contain useful information in generating asset returns. Second, the paper contributes to the literature on investor attention in asset pricing dynamics by introducing the role limits to arbitrage play. In particular, we show that attention shocks lead to strong stock price reactions, especially in those stocks that are informationally constrained.
The remainder of this study is organized as follows. Section II describes the data and the research design. Section III reports the findings on the relation between attention and trading activity. Section IV examines the relation between attention and stock returns. Section V explores the role limits to arbitrage play in explaining the attention effect. Finally, Section VI concludes the paper.
II DATA AND METHODS
A Data
The analysis is conducted at the monthly level from 2004 to 2015.4 The start date is restricted by the availability of Google search volume data. The data come from several different sources. The return data are obtained from several databases through the Securities Industry Research Centre of Asia-Pacific (SIRCA). This includes monthly stock information from the Share Price and Price Relatives database, daily stock information from the Core Research Data database, and order flow data from the AusEquities database. Accounting information is collected from the Morningstar Aspect Huntley database.
Monthly SVI data are downloaded from Google trends for all available stocks in the sample. If a stock has no SVI data, it is dropped from the sample. Investors may search for a stock in Google using either its ticker symbol or company name. However, the ASX tickers for listed stocks may not be a meaningful search term. For instance, the ASX ticker for David Jones Limited is DJS. Searching DJS returns information not relevant to David Jones. Table A1 in Appendix A shows the sample coverage when SVI is searched by tickers. The coverage (by number of observations) is only 46%, on average, from 2004 to 2015. A comparison based on market capitalization suggests that many smaller firms are excluded from the search. Therefore, the company name is used in this study as the search keyword in Google Trends.5 This procedure is in line with studies such as those of Bank et al. (2011), Takeda and Wakao (2013), and Vlastakis and Markellos (2012). We first use the full company name as the search keyword. The incorporated suffix, such as Co., Ltd., Inc., and Holdings, is excluded from the search. The search is performed based on all categories in Australia.6
Table 1 presents summary statistics of the sample stocks against the population of all available ordinary stocks in the Australian market. Generally, the number of firms and total market capitalization for both the sample and population show an overall upward trend throughout the sample period. The percentage of stocks covered (market capitalization covered) increases from 62.26% (91.62%) in 2004 to 75.29% (98.00%) in 2013, followed by a moderate decrease to 72.72% (95.95%) in 2015. The fact that the percentage covered for market capitalization is over 90% implies that stocks excluded from the sample (i.e., those that do not have SVI data) are mostly very small in size. In addition, Table 1 shows that, for both the sample and the population, the median market capitalization is substantially smaller than the mean market capitalization across all sample years. This finding shows that the Australian equity market is comprised of a few mega-cap stocks and a relatively large number of small-cap stocks, a well-known market characteristic (e.g., Gray and Tutticci 2007). Da et al. (2011) and Ben-Rephael et al. (2017) show that SVI mostly captures retail investor attention. Australia is thus a particularly interesting market in which to employ this proxy, as most listed stocks are small and outside the investable universe of institutional investors. Retail investor attention should matter more in these stocks.
| Year | Sample | Population | Coverage percentage | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Min ($M) | Median ($M) | Max ($B) | Mean ($M) | Total ($B) | N | Min ($M) | Median ($M) | Max ($B) | Mean ($M) | Total ($B) | By N (%) | By market cap (%) | |
| 2004 | 861 | 0.1024 | 42.23 | 49.52 | 741.82 | 638.45 | 1383 | 0.0202 | 23.38 | 49.52 | 503.60 | 696.84 | 62.26 | 91.62 |
| 2005 | 953 | 0.2020 | 40.42 | 69.21 | 804.91 | 767.89 | 1480 | 0.0187 | 24.25 | 69.21 | 567.40 | 840.23 | 64.42 | 91.39 |
| 2006 | 1054 | 0.2690 | 47.63 | 95.13 | 914.59 | 964.39 | 1571 | 0.0270 | 29.95 | 95.13 | 653.42 | 1026.63 | 67.12 | 93.94 |
| 2007 | 1182 | 0.7747 | 58.97 | 120.76 | 1039.84 | 1230.70 | 1697 | 0.1714 | 37.49 | 120.76 | 754.17 | 1280.64 | 69.69 | 96.10 |
| 2008 | 1287 | 0.4303 | 32.00 | 124.02 | 802.35 | 1031.95 | 1804 | 0.0845 | 21.02 | 124.02 | 589.33 | 1062.96 | 71.34 | 97.08 |
| 2009 | 1295 | 0.0834 | 25.37 | 119.74 | 754.05 | 976.07 | 1791 | 0.0586 | 17.04 | 119.74 | 558.42 | 999.08 | 72.31 | 97.70 |
| 2010 | 1308 | 0.0407 | 35.37 | 136.12 | 864.67 | 1131.21 | 1789 | 0.0385 | 23.22 | 136.12 | 648.07 | 1159.20 | 73.11 | 97.59 |
| 2011 | 1357 | 0.0142 | 37.89 | 132.76 | 821.01 | 1113.70 | 1837 | 0.0102 | 24.60 | 132.76 | 621.24 | 1141.21 | 73.87 | 97.59 |
| 2012 | 1366 | 0.0016 | 29.28 | 108.27 | 753.65 | 1029.56 | 1831 | 0.0016 | 18.98 | 108.27 | 574.75 | 1052.24 | 74.60 | 97.84 |
| 2013 | 1364 | 0.0016 | 24.06 | 117.99 | 889.61 | 1213.11 | 1812 | 0.0016 | 15.83 | 117.99 | 683.46 | 1237.87 | 75.29 | 98.00 |
| 2014 | 1361 | 0.0016 | 25.12 | 129.08 | 963.42 | 1310.35 | 1818 | 0.0016 | 16.86 | 129.08 | 738.80 | 1342.78 | 74.86 | 97.58 |
| 2015 | 1340 | 0.0027 | 23.16 | 139.44 | 975.00 | 1305.90 | 1843 | 0.0027 | 17.17 | 139.44 | 738.13 | 1361.06 | 72.72 | 95.95 |
- This table shows summary statistics on stocks’ market capitalization in the sample (stocks with valid SVI) and in the Share Price and Price Relatives database (population). The table reports the monthly average minimum (min), median, maximum (max), mean, and total capitalization of both the sample and the population (all ordinary stocks) from 2004 to 2015. The number of stocks (N) is the average number of stocks per year. The values for the minimum, median, and mean are in millions of dollars ($M) and the maximum and total market capitalization values are in billions of dollars ($B). The coverage percentage of N is the ratio of the number of sample stocks to the number of stocks in the population. The coverage percentage by market cap is the ratio of the total market capitalization of the sample to the total market capitalization of the population.
B Attention shocks and trading activity
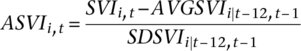 (1)
(1)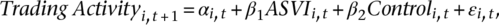 (2)
(2)Chordia et al. (2007) show that trading activity measures such as turnover and OIB depend on the degree of liquidity trading, informed trading, and the level of uncertainty and disagreement about fundamental values. Accordingly, we examine the extent to which ASVI explains cross-sectional variation in turnover and OIB. Moreover, when individual investors acquire useful information relevant to a stock via Google searches, the information asymmetry problem for the stock is mitigated. Noise trading may also increase following retail investor attention. As a result, liquidity should improve for stocks with better attention. In fact, Ding and Hou (2015) find a positive relation between investor attention and stock liquidity for similar reasons. We therefore include liquidity as a trading activity measure.
Turnover is monthly trading volume scaled by the number of shares outstanding. OIB in a month is the average of daily OIB defined as the difference between total buy orders and total sell orders divided by total daily orders. Following Barber and Odean (2008), OIB is calculated using value rather than number of trades. The order flow data is not available for all stocks in our sample (about half of our sample) and the data starts in 2006. Analyses related to OIB are thus limited to a subset of stocks with available data. The Amihud (2002) illiquidity ratio is used as a proxy for liquidity, and it is defined as the average ratio of daily absolute stock returns to daily trading volume in a month. Since the Amihud ratio is highly right skewed and a higher value corresponds to a lower level of liquidity, following Edmans et al. (2013), we log-transform the measure first and then, for ease of interpretation, multiply the measure by −1. Since trading activity variables exhibit high autocorrelations, we adjust the variables following the method outlined in Chordia et al. (2007) to eliminate nonstationarity.
According to Chordia et al. (2007), trading activity can be explained by stock visibility, portfolio rebalancing needs, differences of opinion, and uncertainty about firm fundamental values. The control variables in equation () therefore follow those used by Chordia et al. (2007). We use firm size, age, the book-to-market ratio, and stock price to measure stock visibility. Age is the number of listing months since the initial public offering. For rebalancing needs, we separate the returns of the past month into POS and NEG, where POS (NEG) is defined as the monthly return of an individual stock if it is positive (negative) and zero otherwise. Finally, we use leverage to measure differences of opinion and beta to measure uncertainty about firm fundamental values. Leverage is computed by using the book value of debt divided by total assets. Beta is estimated using the market model over the past 252 trading days. Following Chordia et al. (2007), both size and price are logged and adjusted for nonstationarity.
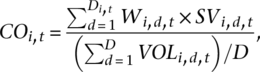 (3)
(3)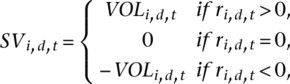 (4)
(4)To strengthen the regression analysis, we use portfolio sorts to further test the relation between ASVI and trading activity. In each month over the sample period, stocks are first sorted by their ASVI into 10 portfolios. Decile 1 contains stocks with the lowest ASVI values and decile 10 contains stocks with the highest. The average trading activity is then calculated for each decile over the subsequent months. This approach reveals a simple picture of how trading activity varies across the spectrum of attention shocks.
C Asset pricing tests
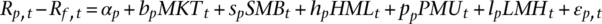 (5)
(5)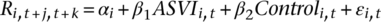 (6)
(6) (7)
(7)III ATTENTION AND CROSS-SECTIONAL VARIATIONS IN TRADING ACTIVITY
Table 2 presents the regression results. Panels A and B report the time-series average of the monthly cross-sectional regression estimates using turnover, OIB and liquidity as the measure of trading activity, respectively. For the baseline model without the control variables (regression (1)), the coefficients of ASVI are all positive and significant at the 1% level. This finding suggests a significant positive relation between trading activity and ASVI. Regressions (2) and (3) include the control variables. Given the high correlation between size and share price, we separately include size (regression (2)) and share price (regression (3)) in the analysis. Across the trading activity measures, the impact of the control variables seems rather mixed. For example, when liquidity is used as the dependent variable, the coefficients of the book-to-market ratio and leverage are negative. Past negative returns also exhibit somewhat different patterns in predicting trading activity variables. This may be because these variables capture different aspects of trading activity. Nevertheless, the main takeaway in Table 2 is that the relation between ASVI and trading activity is robust after we control for important determinants of trading activity.
| Regression | Constant | ASVI | AGE | SIZE | BM | BETA | PRICE | LEV | POS | NEG | CO | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: TURNOVER | ||||||||||||
| 1 | 0.0579 | 0.0063 | ||||||||||
| (31.31)*** | (9.70)*** | |||||||||||
| 2 | 0.1331 | 0.0067 | −0.0022 | −0.0023 | 1.4423 | 0.0009 | 0.0345 | 0.0581 | −0.0553 | 0.0089 | ||
| (9.93)*** | (7.65)*** | (−1.77)* | (−4.21)*** | (4.39)*** | (1.63) | (8.53)*** | (5.62)*** | (−3.27)*** | (13.87)*** | |||
| 3 | 0.0838 | 0.0066 | −0.0042 | 1.7581 | 0.0007 | 0.0053 | 0.0288 | 0.0691 | −0.0831 | 0.0082 | ||
| (12.62)*** | (7.59)*** | (−3.37)*** | (5.10)*** | (1.31) | (4.86)*** | (7.31)*** | (6.96)*** | (−5.15)*** | (13.09)*** | |||
| Panel B: LIQUIDITY | ||||||||||||
| 1 | 0.0368 | 0.0291 | ||||||||||
| (1.13) | (9.76)*** | |||||||||||
| 2 | 0.8119 | 0.0200 | 0.0083 | −0.0269 | −11.9230 | 0.0066 | −0.0474 | 0.3119 | 0.4155 | 0.0277 | ||
| (3.14)*** | (4.40)*** | (1.03) | (−2.72)*** | (−12.01)*** | (1.91)* | (−1.55) | (4.99)*** | (4.29)*** | (6.51)*** | |||
| 3 | 0.2554 | 0.0165 | −0.0249 | −7.8838 | 0.0048 | 0.0989 | −0.1102 | 0.4185 | −0.0230 | 0.0188 | ||
| (4.03)*** | (3.92)*** | (−2.81)*** | (−8.03)*** | (1.29) | (11.68)*** | (−3.24)*** | (6.28)*** | (−0.23) | (4.06)*** | |||
| Panel C: OIB | ||||||||||||
| 1 | −0.0035 | 0.0046 | ||||||||||
| (−1.56) | (10.04)*** | |||||||||||
| 2 | −0.0402 | 0.0043 | 0.0004 | 0.0021 | −0.2217 | −0.0004 | 0.0005 | −0.0044 | 0.0577 | 0.0188 | ||
| (−2.45)** | (9.80)*** | (0.49) | (2.78)*** | (−1.63) | (−0.85) | (0.14) | (−0.76) | (4.69)*** | (2.07)** | |||
| 3 | −0.0037 | 0.0043 | 0.0011 | −0.2203 | −0.0003 | 0.0019 | 0.0003 | −0.0052 | 0.0582 | 0.0188 | ||
| (−0.74) | (9.82)*** | (1.32) | (−1.67)* | (−0.74) | (2.99)*** | (0.09) | (−0.92) | (4.84)*** | (2.07)** | |||
- This table reports estimates from Fama and MacBeth (1973) cross-sectional regressions for the sample using equation (). In each month t, trading activity in month t + 1 are regressed on ASVI and a set of control variables in month t. Different regression specifications are performed. This procedure is repeated every month over the sample period. Panels A and B report the time-series averages of the monthly cross-sectional regression estimates within the entire sample using turnover and liquidity as the measure of trading activity, respectively. Newey and West (1987) standard errors are used to calculate t statistics; TURNOVER is share turnover; LIQUIDITY is the log-transformed Amihud illiquidity ratio, with a reversed sign to represent liquidity; OIB is order imbalance defined as the difference between total buy orders and total sell orders divided by total daily orders. AGE is the number of listing months on the ASX; SIZE is market capitalization; BM is the book-to-market ratio; BETA is the beta of a stock estimated using the market model over the past 252 trading days; PRICE is the stock price at the end of the month; LEV is leverage calculated by dividing book debt by total assets; POS (NEG) is defined as the monthly return of an individual stock if it is positive (negative) and zero otherwise; CO is the measure of continuing overreaction, defined in equation (); and AGE, SIZE, BM, PRICE, and CO are the natural logarithms of firm age, market capitalization, the book-to-market ratio, stock price, and continuing overreaction, respectively. TURNOVER, LIQUIDITY, OIB, SIZE and PRICE are adjusted following the method outlined in Chordia et al. (2007) to eliminate nonstationarity. All the variables are winsorized at the first and 99th percentiles.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
To further explore the relation between ASVI and trading activity, we form decile portfolios on ASVI at time t and calculate the trading activity for each portfolio at times t, t + 1, and t + 2, respectively. Showing trading activities at different time periods allows us to investigate how they change over time. Table 3 presents the results. At time t, from the low-ASVI group to the high-ASVI group, trading activity exhibits an overall increasing trend. A positive relation between ASVI and OIB is also consistent with the view that attention attracts more buying than selling. The differences between the high- and low-ASVI groups are positive and significant at the 1% level for all the trading activity variables. At time t + 1, the increasing pattern in trading activity becomes more obvious. For example, turnover (liquidity) increases from 0.0417 (−1.4933) in the low-ASVI group to 0.0608 (−1.1537) in the high-ASVI group. This finding implies that stocks with a higher ASVI are traded more than stocks with a lower ASVI. The result from OIB is less apparent but the difference remains statistically significant. The difference in trading activity between the low- and high-ASVI groups continues to be significant at t + 2 except for OIB. However, compared to times t and t + 1, the trend is less obvious. As the OIB related results are based on the sample of stocks with available order flow data, the finding may be influenced by firm size.
| Trading activity (t) | Trading activity (t + 1) | Trading activity (t + 2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| TURNOVER | LIQUIDITY | OIB | TURNOVER | LIQUIDITY | OIB | TURNOVER | LIQUIDITY | OIB | |||
| Low | 0.0432 | −1.4775 | −0.0117 | 0.0417 | −1.4933 | −0.0099 | 0.0431 | −1.4992 | −0.0042 | ||
| 2 | 0.0438 | −1.3333 | −0.0047 | 0.0428 | −1.3575 | −0.0114 | 0.0447 | −1.3626 | −0.0077 | ||
| 3 | 0.0468 | −1.2725 | −0.0058 | 0.0446 | −1.2946 | −0.0090 | 0.0469 | −1.3025 | −0.0079 | ||
| 4 | 0.0487 | −1.3261 | −0.0071 | 0.0463 | −1.3522 | −0.0069 | 0.0481 | −1.3658 | −0.0072 | ||
| 5 | 0.0453 | −1.399 | −0.0059 | 0.0443 | −1.4053 | −0.0079 | 0.0446 | −1.4202 | −0.0035 | ||
| 6 | 0.0454 | −1.4229 | −0.0062 | 0.0448 | −1.4099 | 0.0024 | 0.0456 | −1.4056 | −0.0007 | ||
| 7 | 0.0480 | −1.3253 | −0.0047 | 0.0478 | −1.3502 | −0.0048 | 0.0473 | −1.3407 | −0.0021 | ||
| 8 | 0.0514 | −1.3063 | 0.0008 | 0.0506 | −1.2914 | −0.0026 | 0.0492 | −1.2924 | −0.0045 | ||
| 9 | 0.0489 | −1.2563 | 0.0034 | 0.0504 | −1.2296 | 0.0007 | 0.0483 | −1.2278 | −0.0025 | ||
| High | 0.0526 | −1.2185 | 0.0105 | 0.0608 | −1.1537 | 0.0080 | 0.0540 | −1.1279 | −0.0030 | ||
| H – L | 0.0094 | 0.2590 | 0.0221 | 0.0191 | 0.3396 | 0.0178 | 0.0110 | 0.3712 | 0.0012 | ||
| (5.73)*** | (9.31)*** | (8.47)*** | (11.48)*** | (11.56)*** | (7.55)*** | (7.02)*** | (12.74)*** | (0.52) | |||
- For each month t, from 2004 to 2015, stocks are sorted into deciles based on ASVI in that month. The low (high) portfolio is the decile that contains stocks with the lowest (highest) level of ASVI. The table reports trading activity in months t, t + 1, and t + 2 for each ASVI decile portfolio. The term TURNOVER is defined as trading volume divided by the number of shares outstanding. LIQUIDITY is the log-transformed Amihud illiquidity ratio with a reversed sign to represent liquidity. OIB is order imbalance defined as the difference between total buy orders and total sell orders divided by total daily orders. These variables are adjusted following the method outlined in Chordia et al. (2007) to eliminate nonstationarity.
- *** Statistical significance at the 1% level.
IV ATTENTION AND STOCK RETURNS
A Main results
Table 4 show returns to portfolios sorted on ASVI over different holding periods. Panel A displays the raw returns and Panel B shows the risk-adjusted returns (the regression intercepts from equation ()). There is an almost monotonic increase in returns from low- to high-ASVI portfolios, particularly over short-term holding periods. The return differences between the highest- and lowest-ASVI deciles are all significant over the holding period analyzed. However, the difference in returns declines as the holding period increases. For example, the average monthly return generated by the high-minus-low strategy decreases from 4.38% (t = 11.92) when K = 1 to 0.38% (t = 3.84) when K = 12. This result implies a reversal in the return premium when the holding period is extended. This return pattern is consistent with those documented by Barber and Odean (2008) and Da et al. (2011) for the US market and by Bank et al. (2011) for the German market. For example, Da et al. (2011) find that an increase in Google search volume predicts higher stock prices in the next 2 weeks and a price reversal after the third week.
| Low | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | High | High – Low | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Raw return | |||||||||||
| K = 1 | −0.0084 | −0.0093 | −0.0055 | −0.0030 | −0.0029 | 0.0031 | 0.0100 | 0.0080 | 0.0129 | 0.0354 | 0.0438 |
| (−1.64) | (−1.87)* | (−1.12) | (−0.58) | (−0.55) | (0.59) | (1.71)* | (1.43) | (2.32)** | (5.31)*** | (11.92)*** | |
| K = 3 | −0.0008 | −0.0014 | −0.0007 | 0.0012 | 0.0000 | 0.0024 | 0.0052 | 0.0053 | 0.0064 | 0.0125 | 0.0132 |
| (−0.15) | (−0.29) | (−0.15) | (0.22) | (0.01) | (0.46) | (0.96) | (1.00) | (1.24) | (2.24)** | (7.69)*** | |
| K = 6 | 0.0005 | 0.0017 | 0.0005 | 0.0022 | 0.0013 | 0.0032 | 0.0052 | 0.0049 | 0.0045 | 0.0078 | 0.0073 |
| (0.10) | (0.35) | (0.10) | (0.42) | (0.26) | (0.62) | (0.99) | (0.97) | (0.89) | (1.47) | (5.62)*** | |
| K = 12 | 0.0023 | 0.0031 | 0.0024 | 0.0023 | 0.0027 | 0.0032 | 0.0053 | 0.0044 | 0.0046 | 0.0062 | 0.0038 |
| (0.48) | (0.64) | (0.50) | (0.46) | (0.53) | (0.63) | (1.06) | (0.89) | (0.94) | (1.21) | (3.84)*** | |
| Panel B: Risk-adjusted return | |||||||||||
| K = 1 | −0.0118 |
−0.0122 | −0.0084 | −0.0064 | −0.0051 | 0.0024 | 0.0098 | 0.0070 | 0.0125 | 0.0460 | 0.0578 |
| (−5.46)*** | (−5.21)*** | (−3.70)*** | (−2.92)*** | (−2.21)** | (1.44) | (3.51)*** | (2.71)*** | (5.52)*** | (7.71)*** | (9.05)*** | |
| K = 3 | −0.0046 | −0.0053 | −0.0047 | −0.0022 | −0.0034 | −0.0013 | 0.0016 | 0.0016 | 0.0025 | 0.0092 | 0.0138 |
| (−2.56)*** | (−3.29)*** | (−2.90)*** | (−1.38) | (−1.92)* | (−0.85) | (0.88) | (0.78) | (1.81)* | (4.73)*** | (6.95)*** | |
| K = 6 | −0.0035 | −0.0019 | −0.0034 | −0.0013 | −0.0019 | −0.0006 | 0.0016 | 0.0013 | 0.0007 | 0.0046 | 0.0081 |
| (−2.47)** | (−1.21) | (−2.17)** | (−0.92) | (−1.19) | (−0.40) | (0.98) | (0.70) | (0.48) | (3.00)*** | (6.21)*** | |
| K = 12 | −0.0016 | −0.0006 | −0.0015 | −0.0012 | −0.0008 | −0.0007 | 0.0017 | 0.0009 | 0.0008 | 0.0026 | 0.0042 |
| (−1.18) | (−0.40) | (−0.95) | (−0.87) | (−0.49) | (−0.46) | (1.19) | (0.57) | (0.60) | (1.86)* | (4.90)*** | |
- At the end of each month over the sample period, stocks are sorted into deciles by ASVI. The low (high) portfolio is the decile that contains stocks with the lowest (highest) level of ASVI. Monthly portfolio returns over the next K months (K = 1, 3, 6, 12) are calculated for each decile portfolio. Portfolios are updated monthly. Panels A and B report the raw and risk-adjusted portfolio returns (regression intercept) from the Fama and French (2015) five-factor model, respectively. The column denoted High – Low is the return difference between the high- and low-ASVI portfolios. The t statistics listed in parentheses are estimated based on Newey and West (1987) standard errors.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
To further examine the role firm size plays, we divide stocks into three groups based on their market capitalization, following Gray and Johnson's (2011) definition. In particular, at the end of each month during the sample period, large stocks are those that comprise the top 90% of the total market capitalization of the sample. Medium stocks are those that comprise the next 7% of total market capitalization and small stocks represent the remaining 3%. Since there are fewer stocks within each size group, we form quintile ASVI portfolios to ensure sufficient observations in each of the portfolios. Our unreported results confirm that the attention effect is strongest in small stocks. Although the reversal is considerable in this group, the hedge return remains significant after 12 months. In contrast, the return premium is only significant in the first holding month for both medium-sized and large firms. This finding is consistent with the view that attention is a scarce resource among smaller stocks.
We run equation () to investigate further the relation between ASVI and stock returns at the individual stock level. To better understand the relation between ASVI and future returns, unlike the holding periods used in the portfolio sorts, we consider returns over the next one, two to six, and seven to 12 months. Table 5 reports the results and Panels A to C show the outcomes when the dependent variables are returns over the next one, two to six, and seven to 12 months, respectively.
| Regression | Constant | ASVI | SIZE | BM | MOM | IVOL | MAX | BETA | CO | REV |
|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Return [t + 1] | ||||||||||
| 1 | 0.0042 | 0.0111 | ||||||||
| (0.72) | (12.75)*** | |||||||||
| 2 | 0.0116 | 0.0112 | −0.0007 | 0.3452 | 0.0090 | |||||
| (0.72) | (12.36)*** | (−1.04) | (2.80)*** | (2.52)*** | ||||||
| 3 | 0.0513 | 0.0112 | −0.0024 | 0.3673 | 0.0106 | −0.2139 | ||||
| (4.22)*** | (12.16)*** | (−4.21)*** | (2.86)*** | (3.00)*** | (−2.89)*** | |||||
| 4 | 0.0483 | 0.0114 | −0.0022 | 0.3916 | 0.0106 | −0.1015 | −0.0558 | −0.0003 | −0.0013 | 0.0149 |
| (2.95)*** | (11.91)*** | (−3.03)*** | (2.96)*** | (3.44)*** | (−1.72)* | (−5.16)*** | (−0.11) | (−0.97) | (2.78)*** | |
| Panel B: Return [t + 2, t + 6] | ||||||||||
| 1 | 0.0225 | −0.0004 | ||||||||
| (1.06) | (−0.27) | |||||||||
| 2 | 0.0136 | −0.0013 | −0.0002 | 0.5854 | 0.0423 | |||||
| (0.26) | (−1.00) | (−0.10) | (1.87)* | (2.72)*** | ||||||
| 3 | 0.1718 | −0.0011 | −0.0070 | 0.5660 | 0.0472 | −0.8222 | ||||
| (3.93)*** | (−0.85) | (−3.73)*** | (1.77)* | (3.17)*** | (−3.61)*** | |||||
| 4 | 0.1775 | −0.0012 | −0.0067 | 0.7503 | 0.0463 | −0.7908 | −0.0616 | −0.0076 | 0.0100 | 0.0661 |
| (3.06)*** | (−0.87) | (−2.78)*** | (2.09)** | (3.72)*** | (−4.09)*** | (−2.57)** | (−0.98) | (3.82)*** | (4.44)*** | |
| Panel C: Return [t + 7, t + 12] | ||||||||||
| 1 | 0.0236 | 0.0009 | ||||||||
| (0.95) | (0.58) | |||||||||
| 2 | 0.0310 | 0.0007 | −0.0007 | 0.5503 | 0.0232 | |||||
| (0.50) | (0.41) | (−0.32) | (1.35) | (2.74)*** | ||||||
| 3 | 0.1342 | 0.0005 | −0.0053 | 0.5238 | 0.0247 | −0.4359 | ||||
| (2.60)*** | (0.33) | (−2.30)** | (1.32) | (3.11)*** | (−1.36) | |||||
| 4 | 0.1548 | 0.0002 | −0.0055 | 0.9195 | 0.0238 | −0.5711 | −0.0329 | −0.0078 | 0.0093 | 0.0606 |
| (2.49)** | (0.16) | (−2.13)** | (2.46)** | (3.77)*** | (−2.68)*** | (−0.96) | (−0.82) | (2.93)*** | (3.99)*** | |
- At the end of each month over the sample period, we run Fama and MacBeth (1973) regressions using equation (). The dependent variables are the individual stock buy-and-hold returns over the next 1 month (Panel A), 2–6 months (Panel B), and 7–12 months (Panel C), respectively. Different regression specifications are performed. The term SIZE is market capitalization; BM is the book-to-market ratio; MOM is the cumulative return of the past six months with a 1-month lag; IVOL is idiosyncratic volatility estimated over the past 252 trading days; MAX is the maximum daily return within month t; BETA is the beta of a stock estimated using the market model over the past 252 trading days; CO is the measure of continuing overreaction defined in equation (); REV is the stock return in month t; and SIZE, BM, and CO are natural log transformed. All variables are winsorized at the first and the 99th percentiles. The table reports the time series average of the monthly cross-sectional regression estimates. The t statistics are adjusted for Newey and West (1987) standard errors.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
The results of the baseline model (i.e., regression (1)) across the three panels show that the positive relation between ASVI and stock returns exists only in the first month.8 This is consistent with Barber and Odean's (2008) attention theory, where attention has a short-term price impact. This is also in line with the empirical findings of Da et al. (2011). When other firm characteristic variables are included in the baseline model (i.e., regressions (2) to (4)), the magnitude of the coefficients of ASVI remains consistent. This finding shows a robust relation between ASVI and returns. In a nutshell, the regression analysis at the individual stock level supports the findings at the portfolio level and ASVI remains important in the presence of variables that are known to affect stock returns. It is worth noting that the effect is short-lived; the significant buy-and-hold portfolio returns over a longer holding period documented in Table 4 is mainly driven by the first month.
B Robustness checks
Trading activity can increase due to informed trading at the time of an earnings announcement (Kim and Verrecchia 1994; Kim et al. 1997). Therefore, during the earnings announcement period, higher returns could have little to do with increases in attention. Motivated by this rationale, it is possible that a high value of ASVI is associated with price-sensitive announcements. Accordingly, we test whether the relation between ASVI and stock returns remains robust after removing stocks experiencing price-sensitive announcements.9 The announcement data are downloaded from the Australian Company Announcements database maintained by SIRCA. In addition to scheduled earnings announcements, whenever there are circumstances that are likely to affect earnings, firms are required to update the market. Chai and Do (2016) point out that these updates are typically followed by strong market reactions. Thus, our announcements data consist of both scheduled earning announcements and any market updates that are tagged as price sensitive by the ASX. We follow the same method applied in prior Australian studies (e.g., Zhong and Gray 2016) to remove stocks with price-sensitive announcements and repeat the portfolio analysis undertaken in Table 4. Panel A of Table 6 shows that the high-minus-low return remains significantly positive and is similar to those in Table 4.
| Low | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | High | High – Low | Alpha |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Excluding price-sensitive announcements | |||||||||||
| −0.0114 | −0.0148 | −0.0099 | −0.0051 | −0.0059 | 0.0003 | 0.0079 | 0.0107 | 0.0147 | 0.0434 | 0.0548 | 0.0565 |
| (−2.02)** | (−2.69)*** | (−1.80)* | (−0.84) | (−1.03) | (0.05) | (1.22) | (1.64) | (2.35)** | (5.58)*** | (11.23)*** | (11.08)*** |
| Panel B: Excluding January and July | |||||||||||
| −0.0144 | −0.0148 | −0.0123 | −0.0086 | −0.0084 | −0.0021 | 0.0041 | 0.0039 | 0.0083 | 0.0303 | 0.0448 | 0.0488 |
| (−2.67)*** | (−2.76)*** | (−2.41)** | (−1.52) | (−1.52) | (−0.37) | (0.65) | (0.64) | (1.40) | (4.20)*** | (10.75)*** | (9.99)*** |
| Panel C: Alternative search keywords | |||||||||||
| −0.0092 | −0.0060 | −0.0066 | −0.0011 | −0.0025 | 0.0026 | 0.0091 | 0.0102 | 0.0138 | 0.0341 | 0.0433 | 0.0442 |
| (−1.86)* | (−1.20) | (−1.36) | (−0.22) | (−0.48) | (0.51) | (1.61) | (1.81)* | (2.57)*** | (5.24)*** | (11.67)*** | (9.72)*** |
| Panel D: SVI searched by tickers | |||||||||||
| 0.0024 | 0.0007 | 0.0048 | 0.0054 | 0.0052 | 0.0060 | 0.0085 | 0.0069 | 0.0065 | 0.0129 | 0.0106 | 0.0102 |
| (0.48) | (0.13) | (0.91) | (1.06) | (1.02) | (1.13) | (1.65) | (1.31) | (1.24) | (2.41)** | (4.48)*** | (3.78)*** |
| Panel E: Up market | |||||||||||
| −0.0122 | −0.0151 | −0.0097 | −0.0096 | −0.0093 | −0.0015 | 0.0022 | 0.0037 | 0.0070 | 0.0284 | 0.0407 | 0.0437 |
| (−2.24)** | (−2.97)*** | (−1.76)* | (−1.73)* | (−1.64) | (−0.26) | (0.37) | (0.61) | (1.20) | (3.96)*** | (9.96)*** | (8.08)*** |
| Panel F: Down market | |||||||||||
| 0.0141 | 0.0209 | 0.0175 | 0.0333 | 0.0303 | 0.0326 | 0.0504 | 0.0359 | 0.0448 | 0.0767 | 0.0626 | 0.0570 |
| (0.92) | (1.34) | (1.52) | (2.20)** | (2.27)** | (2.45)** | (2.84)*** | (2.30)** | (2.77)*** | (4.22)*** | (6.19)*** | (4.58)*** |
- At the end of each month over the sample period, stocks are sorted into deciles by ASVI. The low (high) portfolio is the decile that contains stocks with the lowest (highest) level of ASVI. Monthly portfolio returns over the next month are calculated for each decile portfolio. Portfolios are updated monthly. This table shows the raw and risk-adjusted (alpha from the Fama–French five-factor model) returns when price-sensitive announcements are excluded (Panel A), when the months of January and July are excluded (Panel B), when ASVI is computed using the SVI downloaded by searching the abbreviated company names from Share Price and Price Relatives (Panel C) and by searching ASX tickers (Panel D), and in UP (Panel E) and DOWN (Panel F) markets based on the value-weighted market index over months t – 36 to t – 1. The column denoted High – Low shows the return differences between the high- and low-ASVI portfolios. The t statistics are adjusted for Newey and West (1987) standard errors.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
Prior studies, such as those of Brown et al. (1983), Gaunt et al. (2000), and Gray and Tutticci (2007), show that higher returns are exhibited in January and July in Australia. Therefore, to check that our results are not driven by seasonality, we rerun the portfolio analysis excluding January and July. Panel B of Table 6 shows that the attention effect is robust to such an omission. This finding demonstrates that the existence of the attention effect is not due to seasonality.
In the main analysis, we use a company's full name to download its Google search volume. Considering that different investors could search for the same firm using several variations of its name, we test the robustness of our results using the abbreviated name (from the database) as the search keyword. As in the main analysis, the incorporation suffix, such as Co., Ltd., Inc., and Holdings, are excluded from the search. We then replicate the portfolio-level analysis and the results, reported in Panel C of Table 6, are insensitive to alternative search keywords. To complement this finding, we also repeat the portfolio analysis using SVI searched by tickers. The results, displayed in Panel D of Table 6, confirm the existence of the ASVI effect. However, the magnitude of the hedge return is lower compared to those found in Table 4. This is justifiable, as the sample size is much smaller and is biased towards large firms (see Table A1 in Appendix A).
The sample in this study includes periods of extreme market shocks with significant losses (i.e., the 2007–2009 financial crisis). This downward market movement affects investors’ risk aversion and how they react to new information. Therefore, it is worth checking the relation between ASVI and stock returns conditioned on different market states. Following Cooper et al. (2004), at the end of each month during the sample period, the market is defined as UP (DOWN) if the value-weighted market index over the past 36 months is nonnegative (negative). The results of decile portfolio sorts are then separated into UP and DOWN markets. Panels E and F of Table 6 present the results. The high-minus-low return is significant in both states of the market and seems to be stronger in DOWN markets. However, caution is needed when interpreting these results, since our sample period is dominated by UP markets.
Our final robustness test is to examine whether our finding remains robust when the analysis is conducted using weekly data. To address this, we repeat the portfolio level analysis using weekly SVI with holding periods of 1, 2, 4, 26, and 52 weeks. ASVI at the weekly level is calculated based on equation () but with an estimation period of 8 weeks. As in the main analysis, we use the weekly Fama–French five-factor model to adjust for risk. Table A2 in Appendix A show the results. There is strong evidence of the ASVI effect in weekly data, and the return pattern is similar to that reported in Table 4.
C ASVI and abnormal trading activity
The relation between trading activity and stock returns has been well documented in the literature. A number of studies show that stocks with an unusually high trading volume have higher subsequent returns than stocks with an unusually low trading volume (Karpoff 1986; Gallant et al. 1992; Blume et al. 1994; Gervais et al. 2011). Bali et al. (2014) show that liquidity shocks predict future returns up to 6 months ahead. Unusual trading volume has been indirectly used as a proxy for attention by a number of studies (e.g., Barber and Odean 2008). Bali et al. (2014) suggest that the liquidity shock effect is caused by stock market underreaction driven by investor inattention as well as illiquidity.
Given the findings in Section III, it is possible that the observed relation between ASVI and returns is caused by volume or liquidity shocks. In this section, we investigate the extent to which ASVI and trading activity shocks have a standalone influence on cross-sectional returns. For this purpose, we rerun equation () and include liquidity and volume shocks as control variables. Volume and liquidity shocks are defined the same way as ASVI is defined (equation ()), measured by share turnover and the Amihud illiquidity ratio. The calculation is in line with prior studies, such as those of Bali et al. (2014) and Chen et al. (2001).
The regression results are displayed in Table 7. The positive and statistically significant coefficients of both volume and liquidity shocks confirm the findings of past studies. However, the relation between ASVI and returns remains strong in the presence of both volume and liquidity shocks and when all the control variables are considered. The magnitudes of the coefficients (albeit significant) of both volume and liquidity shocks decline when ASVI are included in the regressions. This finding establishes the robustness of our results and indicates that ASVI contains important information beyond that captured by trading activity shock measures.
| Regression | Constant | ASVI | VOSH | LISH | SIZE | BM | MOM | IVOL | MAX | BETA | CO | REV |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0042 | 0.0111 | ||||||||||
| (0.72) | (12.75)*** | |||||||||||
| 2 | 0.0045 | 0.0030 | ||||||||||
| (0.74) | (5.66)*** | |||||||||||
| 3 | 0.0042 | 0.0027 | ||||||||||
| (0.66) | (2.54)** | |||||||||||
| 4 | 0.0046 | 0.0113 | 0.0018 | 0.0020 | ||||||||
| (0.73) | (11.89)*** | (3.12)*** | (1.90)* | |||||||||
| 5 | 0.0096 | 0.0114 | 0.0014 | 0.0020 | −0.0006 | 0.3763 | 0.0093 | |||||
| (0.47) | (11.50)*** | (2.59)*** | (1.76)* | (−0.65) | (2.50)** | (2.47)** | ||||||
| 6 | 0.0542 | 0.0113 | 0.0014 | 0.0020 | −0.0025 | 0.3435 | 0.0107 | −0.2145 | ||||
| (3.37)*** | (11.33)*** | (2.71)*** | (1.73)* | (−3.51)*** | (2.31)** | (2.88)*** | (−2.76)*** | |||||
| 7 | 0.0501 | 0.0112 | 0.0022 | 0.0012 | −0.0023 | 0.3875 | 0.0102 | −0.0846 | −0.0605 | −0.0001 | −0.0015 | 0.0149 |
| (2.84)*** | (11.32)*** | (4.14)*** | (1.04) | (−2.88)*** | (2.72)*** | (3.18)*** | (−1.29) | (−4.95)*** | (−0.02) | (−1.05) | (2.70)*** |
- At the end of each month from 2004 to 2015, we run Fama and MacBeth (1973) regressions using equation (). The dependent variables are the individual stock buy-and-hold returns over the next month. The term SIZE is market capitalization; BM is the book-to-market ratio; MOM is the cumulative return of the past 6 months with a 1-month lag; IVOL is idiosyncratic volatility estimated over the past 252 trading days; MAX is the maximum daily return within month t; BETA is the beta of a stock estimated using the market model over the past 252 trading days; CO is the measure of the continuing overreaction defined in equation (); REV is the stock return in month t, where SIZE, BM, and CO are natural log transformed; and VOSH and LISH are volume and liquidity shocks, respectively. All variables are winsorized at the first and the 99th percentiles. The regression is estimated each month and the table reports the average of the regression estimates. The t statistics are adjusted for Newey and West (1987) standard errors.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
V ATTENTION AND LIMITS TO ARBITRAGE
Our results thus far demonstrate a robust relation between ASVI and stock returns. In this section, we test the role limits to arbitrage play in the ASVI–return relation. Recently, Stambaugh et al. (2015) built a simple proxy for mispricing based on a composite rank of numerous firm characteristics known to be associated with anomalous returns. Motivated by their work and the fact that there are a few proxies for limits to arbitrage, we construct a limits-to-arbitrage index for each firm in our sample.
Our limits-to-arbitrage index is constructed based on five proxies for arbitrage costs, including idiosyncratic volatility, analyst coverage, share price, firm size, and share turnover. Among existing proxies for limits to arbitrage, idiosyncratic volatility is the most popular measure. For example, Pontiff (2006) shows that arbitrageurs prefer to hold fewer stocks with higher idiosyncratic volatility. McLean (2010), using idiosyncratic volatility as a proxy for arbitrage costs, shows that lower arbitrage costs are associated with a weaker (negative) relation between short interest and subsequent stock returns. Analyst coverage is used as a proxy for information uncertainty. More analyst coverage indicates a stronger information environment (Hong et al. 2000) and will mitigate mispricing (e.g., Zhang 2006). Share price, firm size, and share turnover are related to potential transaction costs. Share price has been found to be inversely related to the bid–ask spread and brokerage costs (Bhardwaj and Brooks 1992; Stoll 2000). Small firms are generally less liquid and have high short-sale constraints. Share turnover is a common measure for stock liquidity, capturing the time required to execute an order or to trade a large block of shares.
The limits-to-arbitrage index is constructed as follows. Each month, stocks are assigned a percentile rank based on one of the limits-to-arbitrage measures. For example, stocks with the highest (lowest) idiosyncratic volatility receive the highest (lowest) rank. In other words, stocks with the highest arbitrage costs receive the highest rank, while stocks with the lowest arbitrage costs receive the lowest rank. An exception is made with analyst coverage, since the variation across firms is low. We thus assign the highest rank (i.e., 100) to stocks without analyst coverage and the lowest rank (i.e., zero) to stocks with the highest number of analysts. The interval in ranking depends on the highest number for analyst coverage. The limits-to-arbitrage index for each stock is the simple average of the ranks across the five measures. By construction, a high index value indicates a high level of arbitrage cost.
To explore the interaction between limits to arbitrage and attention, stocks are independently double sorted into quintiles based on the constructed limits-to-arbitrage index and ASVI, resulting in 25 portfolios. The equal-weighted returns to each portfolio are calculated for the following month, after which the double sorting is repeated. The results are reported in Table 8. There are several notable findings. First, reading the results across the ASVI quintiles, there is no attention effect in stocks with the lowest arbitrage costs. However, in the rest of the limits-to-arbitrage groups, returns increase monotonically across the ASVI quintiles and the high-minus-low returns are statistically significant. The high-minus-low return also increases monotonically from the lowest to the highest limits-to-arbitrage index quintiles. This result is consistent with our conjecture that the attention effect is more pronounced in stocks with high arbitrage costs. Second, reading each column, the return difference between high- and low-arbitrage quintiles is only significant in extreme ASVI groups. Interestingly, the return is negative (albeit only marginally significant) in the lowest-ASVI quintile and is positive in the two high-ASVI quintiles. The magnitude of the return difference also increases with ASVI.
| Low ASVI | 2 | 3 | 4 | High ASVI | High – Low | Alpha | |
|---|---|---|---|---|---|---|---|
| Low LTA | 0.0027 | 0.0075 | 0.0056 | 0.0060 | 0.0054 | 0.0026 (0.97) | 0.0033 (1.19) |
| 2 | 0.0006 | −0.0019 | 0.0001 | 0.0105 | 0.0218 | 0.0211 (5.60)*** | 0.0203 (5.56)*** |
| 3 | −0.0174 | −0.0103 | −0.0037 | 0.0047 | 0.0420 | 0.0594 (10.72)*** | 0.0591 (7.50)*** |
| 4 | −0.0208 | −0.0151 | −0.0047 | 0.0118 | 0.0417 | 0.0625 (9.13)*** | 0.0631 (8.54)*** |
| High LTA | −0.0064 | 0.0024 | 0.0149 | 0.0245 | 0.0661 | 0.0726 (7.15)*** | 0.0708 (6.77)*** |
| High – Low | −0.0092 | −0.0051 | 0.0093 | 0.0186 | 0.0608 | ||
| (−1.66)* | (−0.93) | (1.55) | (2.44)** | (5.77)*** | |||
| Alpha | −0.0095 | −0.0055 | 0.0089 | 0.0150 | 0.0579 | ||
| (−1.84)** | (−0.83) | (1.33) | (2.19)** | (5.06)*** |
- At the end of each month, all sample stocks are independently sorted into quintile portfolios on the constructed limits-to-arbitrage (LTA) index and ASVI. The independent double sort creates 25 intersection portfolios for which equal-weighted portfolio returns are calculated in month t + 1. The table reports the average return for each portfolio. High – Low shows the differences in returns between high- and low-ASVI portfolios and between high- and low-LTA portfolios. Alpha is the intercept from the Fama–French five-factor model. The t statistics using Newey and West (1987) standard errors are shown in parentheses.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
A stronger attention effect in stocks with high limits to arbitrage should result in higher short-run price pressure and subsequent reversal. To confirm this, we examined the portfolio returns in the limits-to-arbitrage groups over longer holding periods of 3, 6, and 12 months. Table 9 displays the results. To conserve space, we only show ASVI quintiles in both high and low limits-to-arbitrage groups. Reversal is observed in the high limits-to-arbitrage group. For the low limits-to-arbitrage group where the 1-month ahead hedge return is not significant there is also no reversal. This confirms that the short-run price pressure and subsequent reversal is concentrated in stocks where arbitrage is more difficult. Overall, the results confirm that attention is a scarce cognitive resource for stocks with high limits to arbitrage.
| Low ASVI | 2 | 3 | 4 | High ASVI | High – Low | Alpha | |
|---|---|---|---|---|---|---|---|
| Panel A: K = 3 | |||||||
| Low LTA | 0.0058 | 0.0063 | 0.0056 | 0.0067 | 0.0059 | 0.0001 (0.06) | 0.0011 (0.57) |
| High LTA | −0.0031 | 0.0002 | 0.0029 | 0.0059 | 0.0098 | 0.0129 (3.62)*** | 0.0138 (5.04)*** |
| High – Low | −0.0089 | −0.0060 | −0.0027 | −0.0007 | 0.0039 | ||
| (−1.94)* | (−1.36) | (−0.58) | (−0.15) | (0.78) | |||
| Alpha | −0.0070 | −0.0036 | −0.0004 | 0.0002 | 0.0058 | ||
| (−1.76)* | (−0.97) | (−0.12) | (0.05) | (1.53) | |||
| Panel B: K = 6 | |||||||
| Low LTA | 0.0072 | 0.0066 | 0.0056 | 0.0063 | 0.0052 | −0.0020 (−1.40) | −0.0012 (−0.95) |
| High LTA | −0.0011 | 0.0008 | 0.0040 | 0.0056 | 0.0053 | 0.0065 (2.47)** | 0.0073 (2.74)*** |
| High – Low | −0.0084 | −0.0058 | −0.0016 | −0.0008 | 0.0001 | ||
| (−1.97)* | (−1.54) | (−0.36) | (−0.17) | (0.03) | |||
| Alpha | −0.0065 | −0.0033 | 0.0008 | 0.0009 | 0.0020 | ||
| (−2.11)** | (−1.04) | (0.23) | (0.27) | (0.60) | |||
| Panel C: K = 12 | |||||||
| Low LTA | 0.0072 | 0.0067 | 0.0057 | 0.0066 | 0.0055 | −0.0016 (−1.75)* | −0.0011 (−1.33) |
| High LTA | 0.0007 | 0.0002 | 0.0046 | 0.0042 | 0.0047 | 0.0040 (2.14)** | 0.0036 (1.72)* |
| High – Low | −0.0064 | −0.0065 | −0.0010 | −0.0025 | −0.0008 | ||
| (−1.57) | (−1.65) | (−0.25) | (−0.59) | (−0.20) | |||
| Alpha | 0.0005 | 0.0000 | 0.0050 | 0.0039 | 0.0052 | ||
| (0.15) | (0.01) | (1.53) | (1.18) | (1.76)* | |||
- At the end of each month, all sample stocks are independently sorted into quintile portfolios on the constructed limits-to-arbitrage (LTA) index and ASVI. The independent double sort creates 25 intersection portfolios for which equal-weighted portfolio returns are calculated for K = 3, 6, and 12 months. The table reports the average returns for ASVI quintiles in high and low LTA groups. High – Low shows the differences in returns between high- and low-ASVI portfolios and between high- and low-LTA portfolios. Alpha is the intercept from the Fama–French five-factor model. The t statistics using Newey and West (1987) standard errors are shown in parentheses.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
To further strengthen our findings, we run equation () in different limits-to-arbitrage groups. Specifically, each month, stocks are first sorted into three portfolios using a 30:40:30 split based on the limits-to-arbitrage index. Within each group, different specifications of equation () are estimated. Table 10 presents the results. The baseline model (regression (1)) shows that ASVI is statistically significant in all three limits-to-arbitrage groups. However, the magnitude of the ASVI coefficient is much larger in the high limits-to-arbitrage group. The results remain consistent in the presence of control variables. It is worth mentioning that we include both idiosyncratic volatility and size, which are also used to construct our limits-to-arbitrage index, in the regressions. The purpose is to investigate whether the ASVI–return relation is altered by these variables in different limits-to-arbitrage groups. Our untabulated results show that the difference in the ASVI coefficients between the high and low limits-to-arbitrage groups is 0.0074 (t = 6.92), 0.0075 (t = 7.00), 0.0073 (t = 6.92), and 0.0073 (t = 6.86) for regressions (1) to (4), respectively. These results show strong support for our conjecture that the attention effect is most pronounced in stocks with high limits to arbitrage.
| Regression | Constant | ASVI | SIZE | BM | MOM | IVOL | MAX | BETA | CO | REV |
|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Low | ||||||||||
| 1 | 0.0069 | 0.0027 | ||||||||
| (1.30) | (3.52)*** | |||||||||
| 2 | 0.0044 | 0.0022 | 0.0000 | −0.4348 | 0.0195 | |||||
| (0.20) | (3.06)*** | (0.01) | (−1.63) | (3.31)*** | ||||||
| 3 | 0.0267 | 0.0021 | −0.0009 | −0.3122 | 0.0219 | −0.2262 | ||||
| (1.33) | (2.81)*** | (−1.06) | (−1.22) | (4.17)*** | (−0.98) | |||||
| 4 | 0.0170 | 0.0021 | −0.0004 | −0.2562 | 0.0190 | −0.0998 | −0.0046 | 0.0219 | −0.0001 | 0.0391 |
| (0.82) | (2.89)*** | (−0.42) | (−1.18) | (3.92)*** | (−0.59) | (−1.31) | (0.73) | (−0.09) | (3.88)*** | |
| Panel B: Medium | ||||||||||
| 1 | 0.0062 | 0.0084 | ||||||||
| (1.07) | (9.63)*** | |||||||||
| 2 | 0.0094 | 0.0086 | −0.0005 | 0.4811 | 0.0081 | |||||
| (0.57) | (9.41)*** | (−0.77) | (3.94)*** | (1.83)* | ||||||
| 3 | 0.0491 | 0.0084 | −0.0022 | 0.4708 | 0.0088 | −0.1967 | ||||
| (3.64)*** | (9.09)*** | (−3.85)*** | (3.78)*** | (2.01)** | (−2.76)*** | |||||
| 4 | 0.0415 | 0.0086 | −0.0018 | 0.4936 | 0.0104 | −0.1056 | −0.0376 | −0.0007 | −0.0023 | 0.0138 |
| (2.20)** | (8.90)*** | (−2.20)** | (3.51)*** | (2.56)** | (−1.48) | (−2.55)** | (−0.28) | (−1.60) | (1.84)* | |
| Panel C: High | ||||||||||
| 1 | 0.0034 | 0.0101 | ||||||||
| (0.59) | (11.30)*** | |||||||||
| 2 | −0.0175 | 0.0097 | 0.0010 | −0.1084 | 0.0115 | |||||
| (−0.90) | (10.64)*** | (1.22) | (−0.52) | (3.03)*** | ||||||
| 3 | 0.0413 | 0.0094 | −0.0014 | −0.1709 | 0.0154 | −0.3909 | ||||
| (3.04)*** | (10.29)*** | (−2.38)** | (−0.87) | (4.33)*** | (−3.05)*** | |||||
| 4 | 0.0482 | 0.0094 | −0.0017 | −0.0643 | 0.0141 | −0.2977 | −0.0596 | 0.0001 | 0.0004 | 0.0242 |
| (3.03)*** | (10.17)*** | (−2.51)** | (−0.37) | (4.64)*** | (−2.86)*** | (−3.85)*** | (0.03) | (0.31) | (4.32)*** | |
- At the end of each month over the sample period, stocks are classified into three groups using a 30:40:30 split based on the limits-to-arbitrage index. We then run equation () within each group of stocks. The dependent variables are the individual stock return in month t + 1. Different regression specifications are performed. The term SIZE is market capitalization; BM is the book-to-market ratio; MOM is the cumulative return of the past 6 months with a 1-month lag; IVOL is idiosyncratic volatility estimated over the past 252 trading days; MAX is the maximum daily return within month t; BETA is the beta of a stock estimated using the market model over the past 252 trading days; CO is the measure of continuing overreaction defined in equation (); REV is the stock return in month t; and SIZE, BM, and CO are natural log transformed. All variables are winsorized at the first and the 99th percentiles. The table reports the time-series average of the monthly cross-sectional regression estimates, in low (Panel A), medium (Panel B), and high (Panel C) limits to arbitrage groups. The t statistics are adjusted for Newey and West (1987) standard errors.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.
VI CONCLUSION
Limited attention is a consequence of limited information processing power on the vast amount of information available in financial markets. This paper contributes to the growing literature on theories and evidence of limited attention and information processing and their implications in asset pricing. In the age of information technology, obtaining information from the Internet is easy and cheap for investors. Motivated by this reasoning, we use hand-collected Google search volume as a proxy for attention. The findings of this paper provide strong out-of-sample evidence to the attention literature.
We find that ASVI helps explain the cross-sectional variation in trading activity. An increase in ASVI leads to higher turnover, a greater OIB between buy and sell orders, and increased liquidity. Consistent with attention theory, there is a positive relation between ASVI and stock returns over a short investment horizon and then reversal over a longer period. Our results are robust to a number of sensitivity checks. Furthermore, we document that the attention effect is more pronounced in stocks with high arbitrage costs. Our empirical findings provide new insights on the cause of the attention effect.
Overall, the findings of this paper are consistent with the view that information technology has shaped the operations of financial markets. The open and public nature of the Internet facilitates information sharing and has become an important source in obtaining information. For practitioners, Google keyword search volume can be used to predict macroeconomic and company trends, which could be applied to developing advanced investment strategies.
APPENDIX A
| Year | Sample | Population | Coverage percentage | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Min ($M) | Median ($M) | Max ($B) | Mean ($M) | Total ($B) | N | Min ($M) | Median ($M) | Max ($B) | Mean ($M) | Total | By N (%) | By Market Cap (%) | |
| ($B) | ||||||||||||||
| 2004 | 500 | 0.1039 | 51.91 | 49.52 | 936.64 | 468.47 | 1383 | 0.0202 | 23.38 | 49.52 | 503.60 | 696.84 | 36.15 | 73.38 |
| 2005 | 552 | 0.1620 | 47.31 | 69.21 | 1061.33 | 586.77 | 1480 | 0.0187 | 24.25 | 69.21 | 567.40 | 840.23 | 37.33 | 76.41 |
| 2006 | 617 | 0.1021 | 55.49 | 95.13 | 1190.17 | 734.29 | 1571 | 0.0270 | 29.95 | 95.13 | 653.42 | 1026.63 | 39.28 | 76.14 |
| 2007 | 693 | 0.2075 | 64.44 | 120.76 | 1339.21 | 928.59 | 1697 | 0.1714 | 37.49 | 120.76 | 754.17 | 1280.64 | 40.84 | 75.45 |
| 2008 | 760 | 0.2506 | 34.83 | 124.02 | 1016.74 | 771.94 | 1804 | 0.0845 | 21.02 | 124.02 | 589.33 | 1062.96 | 42.14 | 74.80 |
| 2009 | 785 | 0.1944 | 26.89 | 119.74 | 945.50 | 742.71 | 1791 | 0.0586 | 17.04 | 119.74 | 558.42 | 999.08 | 43.84 | 76.09 |
| 2010 | 819 | 0.1725 | 37.06 | 136.12 | 1062.67 | 870.00 | 1789 | 0.0385 | 23.22 | 136.12 | 648.07 | 1159.20 | 45.78 | 76.91 |
| 2011 | 902 | 0.0150 | 34.53 | 132.76 | 974.91 | 878.63 | 1837 | 0.0102 | 24.60 | 132.76 | 621.24 | 1141.21 | 49.11 | 78.89 |
| 2012 | 940 | 0.0150 | 25.11 | 108.27 | 873.52 | 821.48 | 1831 | 0.0016 | 18.98 | 108.27 | 574.75 | 1052.24 | 51.35 | 79.79 |
| 2013 | 991 | 0.0016 | 20.39 | 117.99 | 985.66 | 976.69 | 1812 | 0.0016 | 15.83 | 117.99 | 683.46 | 1237.87 | 54.70 | 80.51 |
| 2014 | 1050 | 0.0016 | 20.60 | 129.08 | 1008.20 | 1057.43 | 1819 | 0.0016 | 16.86 | 129.08 | 738.80 | 1342.78 | 57.75 | 80.70 |
| 2015 | 1119 | 0.0031 | 18.72 | 139.44 | 951.32 | 1064.08 | 1843 | 0.0027 | 17.17 | 139.44 | 738.13 | 1361.06 | 60.73 | 81.48 |
- This table shows summary statistics on stocks’ market capitalization in the sample (stocks with valid SVI) and in the Share Price and Price Relatives database (population). The table reports the monthly average minimum (min), median, maximum (max), mean, and total capitalization of both the sample and the population (all ordinary stocks) from 2004 to 2015. The number of stocks (N) is the average number of stocks per year. The values for the minimum, median, and mean are in millions of dollars ($M) and the maximum and total market capitalization values are in billions of dollars ($B). The coverage percentage of N is the ratio of the number of sample stocks to the number of stocks in the population. The coverage percentage by market cap is the ratio of the total market capitalization of the sample to the total market capitalization of the population.
| Low | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | High | High – Low | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Raw return | |||||||||||
| K = 1 | 0.0009 | 0.0007 | 0.0007 | 0.0013 | 0.0013 | 0.0023 | 0.0026 | 0.0025 | 0.0022 | 0.0029 | 0.0020 |
| (0.97) | (0.83) | (0.79) | (1.36) | (1.39) | (2.59)*** | (3.00)*** | (2.70)*** | (2.55)** | (3.08)*** | (2.65)*** | |
| K = 2 | 0.0008 | 0.0010 | 0.0005 | 0.0013 | 0.0019 | 0.0016 | 0.0023 | 0.0020 | 0.0017 | 0.0025 | 0.0017 |
| (0.93) | (1.30) | (0.59) | (1.53) | (2.30)** | (1.95)* | (2.82)*** | (2.41)** | (2.13)** | (2.93)*** | (3.21)*** | |
| K = 4 | 0.0009 | 0.0010 | 0.0009 | 0.0012 | 0.0017 | 0.0013 | 0.0021 | 0.0018 | 0.0012 | 0.0018 | 0.0010 |
| (1.14) | (1.33) | (1.14) | (1.47) | (2.20)** | (1.63) | (2.65)*** | (2.25)** | (1.61) | (2.34)** | (2.46)** | |
| K = 26 | 0.0014 | 0.0012 | 0.0015 | 0.0013 | 0.0014 | 0.0015 | 0.0016 | 0.0016 | 0.0017 | 0.0017 | 0.0003 |
| (1.91)* | (1.65) | (2.07)** | (1.66)* | (1.92)* | (2.04)** | (2.14)** | (2.16)** | (2.31)** | (2.28)** | (1.64) | |
| K = 52 | 0.0017 | 0.0014 | 0.0016 | 0.0016 | 0.0016 | 0.0016 | 0.0018 | 0.0018 | 0.0019 | 0.0020 | 0.0003 |
| (2.28)** | (1.89)* | (2.23)** | (2.10)** | (2.18)** | (2.17)** | (2.47)** | (2.49)** | (2.59)*** | (2.72)*** | (2.64)*** | |
| Panel B: Risk-adjusted return | |||||||||||
| K = 1 | −0.0004 | −0.0006 | −0.0007 | −0.0002 | 0.0000 | 0.0008 | 0.0013 | 0.0013 | 0.0010 | 0.0017 | 0.0021 |
| (−0.81) | (−1.22) | (−1.29) | (−0.25) | (0.05) | (1.44) | (2.46)** | (2.26)** | (1.85)* | (2.59)*** | (2.79)*** | |
| K = 2 | −0.0006 | −0.0003 | −0.0009 | −0.0001 | 0.0006 | 0.0002 | 0.0010 | 0.0008 | 0.0004 | 0.0012 | 0.0017 |
| (−1.34) | (−0.85) | (−2.03)** | (−0.20) | (1.45) | (0.52) | (2.28)** | (1.72)* | (0.98) | (2.48)** | (3.36)*** | |
| K = 4 | −0.0005 | −0.0003 | −0.0004 | −0.0002 | 0.0004 | 0.0000 | 0.0007 | 0.0005 | −0.0001 | 0.0005 | 0.0009 |
| (−1.46) | (−0.95) | (−1.21) | (−0.42) | (1.22) | (−0.10) | (2.01)** | (1.28) | (−0.23) | (1.31) | (2.65)*** | |
| K = 26 | 0.0000 | −0.0001 | 0.0002 | −0.0001 | 0.0001 | 0.0001 | 0.0002 | 0.0002 | 0.0004 | 0.0003 | 0.0003 |
| (0.15) | (−0.45) | (0.61) | (−0.27) | (0.28) | (0.48) | (0.72) | (0.77) | (1.06) | (1.11) | (1.63) | |
| K = 52 | 0.0003 | −0.0000 | 0.0003 | 0.0002 | 0.0002 | 0.0002 | 0.0004 | 0.0005 | 0.0005 | 0.0006 | 0.0003 |
| (0.87) | (−0.01) | (0.83) | (0.73) | (0.76) | (0.72) | (1.32) | (1.39) | (1.41) | (1.88)* | (2.75)*** | |
- At the end of each week over the sample period, stocks are sorted into deciles by ASVI. The low (high) portfolio is the decile that contains stocks with the lowest (highest) level of ASVI. Weekly portfolio returns over the next K weeks (K = 1, 2, 4, 26, 52) are calculated for each decile portfolio. Portfolios are updated weekly. Panels A and B report the raw and risk-adjusted portfolio returns (regression intercept) from the Fama and French (2015) five-factor model, respectively. The column denoted High – Low is the return difference between the high- and low-ASVI portfolios. The t statistics listed in parentheses are estimated based on Newey and West (1987) standard errors.
- * Statistical significance at the 10% level.
- ** Statistical significance at the 5% level.
- *** Statistical significance at the 1% level.




