MEASURING ECONOMIC INSECURITY
Abstract
We provide an axiomatic treatment of the measurement of economic insecurity, assuming that individual insecurity depends on the current wealth level and its variations experienced in the past. The first component plays the role of a buffer stock to rely on in case of an adverse future event. The second component determines the confidence an individual has on her ability to overcome a loss in the future. Two classes of linear measures are characterized with sets of plausible and intuitive axioms and, for each of these classes, an important subclass is identified.
1. INTRODUCTION
The notion of economic insecurity has received an increasing amount of public attention in the recent past and is appearing frequently in policy debates. In spite of its widespread use, a precise definition of the term “economic insecurity” has remained elusive, and the phenomenon has not yet been analyzed from a thorough theoretical perspective.
There have been several attempts to design measures of economic insecurity. They include (i) an initiative of the French–German Ministerial Council in response to the report of the Commission on the Measurement of Economic Performance and Social Progress (Stiglitz et al., 2009); (ii) the Rockefeller Foundation's Economic Security Index (Hacker et al., 2010); and (iii) a proposal by the International Labour Organization (2004) and by Osberg and Sharpe (2009). The respective recommended measures can roughly be described as (i) the share of the population facing the risk of poverty; (ii) the fraction of the population who experience a drop in disposable family income of at least 25% from the previous year and lack an adequate financial safety net; and (iii) a weighted average of the “scores” achieved in different attributes.
The objective of our contribution is to formulate an axiomatic framework that we consider suited to the task of measuring the economic insecurity faced by an individual and characterize classes of insecurity measures on the basis of our axioms. The axiomatic method is a fundamental tool in economics and other social sciences. It has been applied in numerous path-breaking contributions, such as those of Nash (1950), Arrow (1951), Shapley (1953), and Sen (1970), to name but a few. Briefly, the main purpose of an axiomatic study is to identify properties that are considered plausible for the objects under consideration (here, measures of economic insecurity) and to derive the class of measures that are the only ones with these properties, thus obtaining a characterization. This is an essential task in discussing the design of economic index numbers because it provides us with a precise answer to the question of what measures are suitable for the problem at hand. A more detailed account of the axiomatic method can be found in Thomson (2001).
Clearly, economic insecurity is a multifaceted issue, and a comprehensive formal definition that subsumes all possible aspects of it is likely to remain difficult to be agreed upon for some time to come. According to Osberg (2010, p. 23), “[A] definition of ‘economic insecurity' which reflects the common usage meaning of the term ‘insecure' might be: ‘the anxiety produced by the lack of economic safety.’” The United Nations Department of Economic and Social Affairs (2008, p. vi) writes that, “It is not easy to give a precise meaning to the term economic insecurity. Partly because it often draws on comparisons with past experiences and practices, which have a tendency to be viewed through rose-tinted lenses, and also because security has a large subjective or psychological component linked to feelings of anxiety and safety, which draw heavily on personal circumstances. Still in general terms economic insecurity arises from the exposure of individuals, communities and countries to adverse events, and from their inability to cope with and recover from the costly consequences of those events.” Jacobs (2007, p. 1) suggests that, “Economic insecurity is perhaps best understood as the intersection between ‘perceived' and ‘actual' downside risk.” According to Stiglitz et al. (2009, p. 198), “Economic insecurity may be defined as uncertainty about the material conditions that may prevail in the future. This insecurity may generate stress and anxiety in the people concerned, and make it harder for families to invest in education and housing.”
A plausible summary and synthesis of the above considerations can be captured in the following phrase: Economic insecurity is the anxiety produced by the possible exposure to adverse economic events and by the anticipation of the difficulty to recover from them.
Past, present, and future are all involved. We are insecure about a future event, and the anticipation of some difficulty in recovering generates anxiety in an individual. The resources we have today are important: The wealthier we are, the bigger the buffer stock we can rely on in case of an adverse future event. Our past experiences play a role in shaping our self-confidence on how well we can do in case of an adverse event. We remember gains and losses in our resources over time. Evidence from psychology and economics supports this view. For instance, Knight (1921, p. 199) states that, “all reasoning rests on the principle of analogy. We know the absent from the present, the future from the now, by assuming that connections or associations among phenomena which have been valid will be so; we judge the future by the past.” The idea that the memories of the past influence an individual's behavior is also central to the work of numerous other authors. To pick a prominent example, some of the fundamental contributions due to Allais (1966, 1972, 1974) make this point. See also Munier (1991) for a thorough discussion.
What we are interested in is the subjective forecast of how well someone can handle a loss in the future. Past gains and losses determine the confidence an individual has today. We focus on wealth variations in the past and the current wealth level as the basic determinants of insecurity. Thus, the measures of individual insecurity we propose have as their domain wealth streams of varying lengths. The length of these streams is not assumed to be fixed because individuals are of different ages in a given time period and, moreover, the availability of data may impose restrictions on how far back in the past we can go when assessing economic insecurity.
Although there are, of course, many aspects of life that may play an important role in assessing the economic insecurity faced by an agent, it seems to us that an adequate (and, from an applied perspective, realistic) option is to use a comprehensive notion of wealth as the relevant variable. By doing so, we abstract from determinants of insecurity that cannot be captured by a monetary variable (see Stiglitz et al., 2009, pp. 53–54, for a discussion and examples). However, this simplification does not seem to pose much of a problem if the notion of wealth employed is indeed defined in a comprehensive manner—wealth is assumed to encompass everything that may help an individual in coping with adverse events. The wealth of an individual includes, for instance, claims on governments, family, friends, etc. Sen (1976) refers to these claims as entitlements—consumption bundles available to an agent given her rights and opportunities; see also Sen (1984, p. 497).
We fully acknowledge that the use of wealth as the crucial variable—be it in terms of financial wealth or in the form of a more comprehensive notion—represents a simplifying assumption and, as such, is not without its difficulties. This is a feature shared by many approaches to phenomena such as poverty, inequality, and deprivation, all of which were originally analyzed in terms of relatively straightforward models based on wealth or income only in order to capture the essentials of the issue at hand. In fact, all of economic modeling is, by its very nature, based on the notion of constructing a simplified and tractable representation of real-world economic interactions and observations. In the economic-insecurity model under consideration here, it deserves to be mentioned that claims and entitlements are often of a conditional nature and, thus, expectations of wealth levels may be more suitable in some circumstances. Moreover, it may be argued that insecurity resulting from variations in wealth levels that are due to choices of the agent should be distinguished from those that result from externally imposed shocks. As a possible response to the latter qualification, we note that we focus on the sentiment of insecurity experienced by an individual rather than on notions of responsibility that are addressed in a different branch of the literature. In any case, we believe that it is of importance to develop a coherent and formally precise model of measuring economic insecurity even though this inevitably comes at the cost of some simplifications.
We suggest two classes of linear measures of insecurity and characterize them by means of plausible sets of axioms. These measures bear a strong formal resemblance to the generalized Gini indices familiar from the literature on the measurement of inequality. In particular, single-series Ginis and single-parameter Ginis (Weymark, 1981) have become standard tools in this area. In recognition of earlier achievements and in order to place our contribution in context, we refer to our measures as two-sequences Ginis and two-parameters Ginis. These labels parallel those employed in the existing literature for measures that share this linear structure, and, moreover, they provide intuitive descriptions of their distinguishing features.
First, we identify economic insecurity in terms of the current wealth level multiplied by minus one plus weighted sums of the wealth gains (losses) experienced in the past. Two sequences of coefficients are employed—one applies to gains, the other to losses. The coefficients are such that recent experiences are given higher weight than experiences that have occurred in the more distant past. A subclass of these measures is obtained by giving higher weights to the absolute values of past losses than to those of past gains, thereby reflecting an attitude that we may label loss aversion in analogy to loss aversion in prospect theory; see Kahneman and Tversky (1979) and Tversky and Kahneman (1992).
Second, we consider linear measures such that all coefficients applied to gains are equal and all coefficients applied to losses are equal. This reduces the two sequences to two parameters. Again, a subclass that corresponds to loss-averse measures is identified.
Although we use individual wealth streams as the primitives of our analysis, we arrive at measures that depend on wealth changes in the past in addition to current wealth. To further motivate such measures based on gains and losses, note that Tversky and Kahneman (1992) make such an assumption in the context of choice under uncertainty.
2. WEALTH STREAMS AND INDIVIDUAL INSECURITY
For any 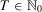 , let
, let 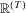 be the
be the 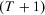 -dimensional Euclidean space with components labeled
-dimensional Euclidean space with components labeled 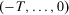 . Zero is interpreted as the current period and T is the number of past periods taken into consideration. We allow T to vary because people alive in the current period may have been born (or have become economic agents) in different periods. A measure of individual insecurity is a sequence of functions
. Zero is interpreted as the current period and T is the number of past periods taken into consideration. We allow T to vary because people alive in the current period may have been born (or have become economic agents) in different periods. A measure of individual insecurity is a sequence of functions 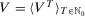 where, for each
where, for each 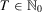 ,
, 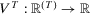 . This index assigns a degree of insecurity to each individual (net) wealth stream
. This index assigns a degree of insecurity to each individual (net) wealth stream 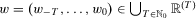 . We employ a comprehensive notion of wealth, and we allow net wealth to be negative. The wealth stream
. We employ a comprehensive notion of wealth, and we allow net wealth to be negative. The wealth stream 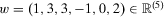 is illustrated in Figure 1.
is illustrated in Figure 1.

We want to design a class of measures the members of which capture the dependence of a sentiment of insecurity on past wealth movements in addition to today's wealth level. Our first property is a difference monotonicity axiom. To motivate it, consider, for example, a temporary shock that precedes a given wealth stream. If the shock results in a gain in wealth, this is likely to reduce insecurity concerns because the individual now has further opportunities to mitigate possible negative future shocks in wealth. Analogously, if the shock involves a loss, the opposite reaction in terms of insecurity is to be expected. Thus, we arrive at the following property:
Difference Monotonicity
For all  , for all
, for all  and for all
and for all 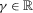 ,
, 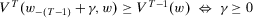 .
.
Difference monotonicity requires a decrease in insecurity as a consequence of the ceteris paribus addition of another period  that introduces a gain between periods
that introduces a gain between periods 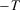 and
and 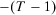 , thus allowing past gains to work against insecurity. Analogously, the measure of insecurity is assumed to increase if a period
, thus allowing past gains to work against insecurity. Analogously, the measure of insecurity is assumed to increase if a period 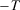 is added in a way such that wealth decreases, ceteris paribus, when moving from
is added in a way such that wealth decreases, ceteris paribus, when moving from 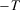 to
to 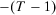 . Finally, if the addition of period
. Finally, if the addition of period 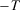 involves a wealth level identical to that of period
involves a wealth level identical to that of period 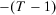 , insecurity is unchanged. This is a monotonicity requirement that appears to be essential in capturing the notion of increased (decreased, unchanged, respectively) insecurity as a response to additional losses (additional gains, no changes, respectively) in past wealth levels. Note that the axiom does not imply that gains and losses have to be treated symmetrically; it is possible, for instance, that adding a gain of a certain magnitude, ceteris paribus, decreases insecurity by less than a loss of the same magnitude increases insecurity. We will return to this issue in more detail at the end of the following section. The axiom is illustrated in Figure 2. Starting from
, insecurity is unchanged. This is a monotonicity requirement that appears to be essential in capturing the notion of increased (decreased, unchanged, respectively) insecurity as a response to additional losses (additional gains, no changes, respectively) in past wealth levels. Note that the axiom does not imply that gains and losses have to be treated symmetrically; it is possible, for instance, that adding a gain of a certain magnitude, ceteris paribus, decreases insecurity by less than a loss of the same magnitude increases insecurity. We will return to this issue in more detail at the end of the following section. The axiom is illustrated in Figure 2. Starting from 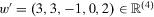 , an additional period −5 is added to arrive at the stream
, an additional period −5 is added to arrive at the stream 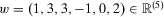 . The move from period −5 to period −4 involves a gain in net wealth and, thus, difference monotonicity demands that
. The move from period −5 to period −4 involves a gain in net wealth and, thus, difference monotonicity demands that 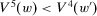 .
.

Next, we state a property that captures the observation that recent experiences carry a higher weight than experiences that occurred in the more distant past.
Proximity Monotonicity
For all 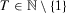 , for all
, for all  and for all
and for all  ,
,
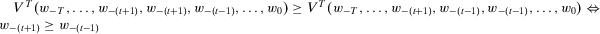 .
.
Proximity monotonicity ensures that a gain (loss) of a given magnitude reduces (increases) insecurity, ceteris paribus, to a higher extent the closer to the present this gain (loss) occurs. That is, changes in wealth from one period to the next have a more severe impact the closer they are to the present period. Figure 3 illustrates the axiom. Comparing the streams 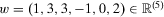 and
and 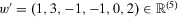 , we see that
, we see that 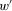 can be obtained from w by shifting the drop from 3 to −1 one period further into the past. According to proximity monotonicity, the earlier loss affects the current sentiment of insecurity to a lesser extent than the original one and, thus, insecurity in
can be obtained from w by shifting the drop from 3 to −1 one period further into the past. According to proximity monotonicity, the earlier loss affects the current sentiment of insecurity to a lesser extent than the original one and, thus, insecurity in 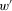 is less than insecurity in w.
is less than insecurity in w.

A common property in the design of economic index numbers is homogeneity, an axiom that ensures that proportional changes in wealth are mirrored in the corresponding insecurity values. Thus, homogeneity requires insecurity to be measured by means of a ratio scale.
Homogeneity
For all 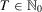 , for all
, for all  and for all
and for all 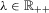 ,
, 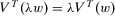 .
.
An analogous property applies to absolute instead of proportional changes. Formulated for insecurity measures, it is defined as follows. We use 1r to denote the vector consisting of 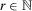 ones.
ones.
Translatability
For all 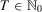 , for all
, for all  , and for all
, and for all 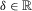 ,
, 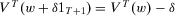 .
.
Translatability differs from the usual translation-scale property in that the value of δ is subtracted from the level of insecurity when δ is added to the wealth level in each period. This is a consequence of the inverse relationship between wealth and insecurity.
Homogeneity and translatability are familiar from the measurement of welfare and inequality; see, for instance, Kolm (1976a, 1976b) for detailed discussions and interpretations. Each of the two properties by itself is too weak to impose a linear structure on a measure of economic insecurity. Taken together, however, they play an important role in arriving at the classes of measures that we focus on here. A first indication of this is given in the following lemma: The conjunction of homogeneity and translatability implies that 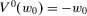 for all
for all 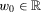 . Thus, V0 is a decreasing linear function of w0. This observation is of importance in proving our subsequent results.
. Thus, V0 is a decreasing linear function of w0. This observation is of importance in proving our subsequent results.
Lemma 1.If a measure of individual insecurity V satisfies homogeneity and translatability, then
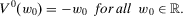 (1)
(1)Proof.Setting 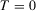 and
and 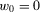 , homogeneity implies
, homogeneity implies
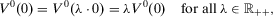
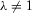 , it follows that
, it follows that
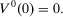 (2)
(2)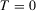 and
and 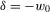 in the definition of translatability and using 2, we obtain
in the definition of translatability and using 2, we obtain
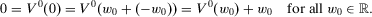 (3)
(3)
Note that the full force of homogeneity and translatability is not needed for the above lemma; as is evident from the proof, it is sufficient to use the respective properties that are obtained by restricting the scopes of the axioms to the cases in which 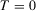 .
.
The next axiom combines a recursivity condition with the assumption that the role of past wealth enters through wealth differences only. Thus, in addition to the separability property encompassed by the axiom, this aggregation property expresses the assumption that past gains and losses are what matters to an agent; see also the discussion in the introduction and note, again, the motivation of such an approach provided by Tversky and Kahneman (1992).
Temporal Aggregation Property
For all 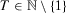 , there exists a function
, there exists a function 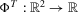 such that, for all
such that, for all  ,
, 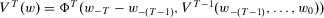 .
.
The temporal aggregation property is a separability condition that allows a measure of insecurity to be calculated by recursively moving back from the current period to the earliest relevant period where, in the step involving period 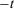 , the part of insecurity that takes into consideration all periods from
, the part of insecurity that takes into consideration all periods from 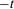 to the current period is obtained as an aggregate of the insecurity resulting from considering periods
to the current period is obtained as an aggregate of the insecurity resulting from considering periods 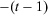 to period zero only and the change experienced in the wealth level between periods
to period zero only and the change experienced in the wealth level between periods 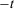 and
and 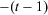 ; see Blackorby et al. (1978) for a detailed discussion of various recursivity properties.
; see Blackorby et al. (1978) for a detailed discussion of various recursivity properties.
3. TWO-SEQUENCES GINI MEASURES
In order to formalize our first approach to economic insecurity, we characterize a specific class of measures that are inspired by the single-series Gini measures of inequality. The Gini index is one of the most established and well-known measures of income or wealth inequality. The generalized Gini measures retain the linear structure of the Gini on sets of distributions that are rank-ordered but allow for alternative degrees of inequality aversion by generalizing the coefficients to any rank-ordered sequence of parameters. To illustrate the notion of a rank-ordered set, consider the two-person case. The distributions on or below the 45-degree line form a rank-ordered set, namely, the set of distributions such that the first component is greater than or equal to the second. Analogously, the distributions on or above the 45-degree line also form a rank-ordered set—the set of distributions such that the second component is greater than or equal to the first.
A subclass of the generalized Ginis is given by the single-series Ginis, characterized in Bossert (1990). They are generalized Ginis such that the sequence of coefficients is the same for all population sizes. See, for instance, Donaldson and Weymark (1980), Weymark (1981), and Bossert (1990) for a discussion of the generalized and the single-series Ginis. Zank (2007) includes the generalized Ginis in his analysis of welfare functions with a reference income. The use of terms such as single-series Ginis is standard in all of the literature on economic measures that are linear on rank-ordered sets of distributions. We follow this convention because these terms are well established and because we consider it essential to acknowledge these earlier contributions to the relevant literature.
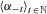 and
and 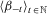 be two sequences of parameters such that
be two sequences of parameters such that
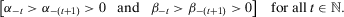 (4)
(4)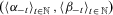 satisfying 4 such that, for all
satisfying 4 such that, for all 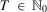 and for all
and for all  ,
,
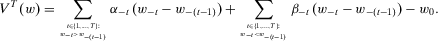
Theorem 1.A measure of individual insecurity V satisfies difference monotonicity, proximity monotonicity, homogeneity, translatability, and the temporal aggregation property if and only if V is a two-sequences Gini measure of insecurity.
Proof.“If.” That the two-sequences Gini measures of insecurity satisfy homogeneity and translatability is immediate. Difference monotonicity follows from the positivity of the coefficients  and
and 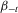 ; see 4. Proximity monotonicity is satisfied because of the inequalities that apply to the sequences of parameters; see, again, 4. To see that the temporal aggregation property is satisfied, define, for all
; see 4. Proximity monotonicity is satisfied because of the inequalities that apply to the sequences of parameters; see, again, 4. To see that the temporal aggregation property is satisfied, define, for all 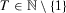 , the function
, the function 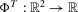 by letting, for all
by letting, for all 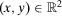 ,
,

“Only if.” Suppose V satisfies the required axioms. We prove the requisite implication by inductively constructing a pair of sequences 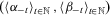 such that 4 is satisfied and
such that 4 is satisfied and
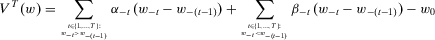 (5)
(5) and for all
and for all  .
.If  , 5 is satisfied for all
, 5 is satisfied for all 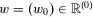 (trivially, for any pair of sequences of coefficients and, in particular, for the pair of sequences to be constructed below) because of 1.
(trivially, for any pair of sequences of coefficients and, in particular, for the pair of sequences to be constructed below) because of 1.
Now let  .
.
If  is such that
is such that 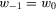 , difference monotonicity and 1 together imply
, difference monotonicity and 1 together imply
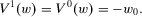 (6)
(6)If w is such that 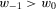 , translatability with
, translatability with 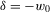 implies
implies
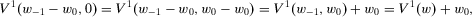
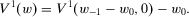 (7)
(7) , it follows that
, it follows that
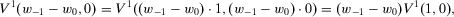
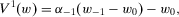 (8)
(8)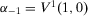 . By difference monotonicity,
. By difference monotonicity,  .
.If w is such that 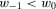 , a parallel argument yields
, a parallel argument yields
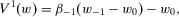 (9)
(9)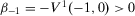 .
.Combining 6, 8, and 9, we obtain
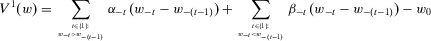
 .
.Now suppose that  and
and
 (10)
(10)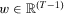 where
where 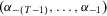 and
and 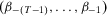 are such that
are such that 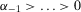 and
and 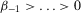 . We have to show that there exist
. We have to show that there exist 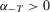 and
and 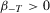 such that
such that
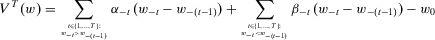 (11)
(11) and that the pair of sequences
and that the pair of sequences 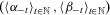 thus constructed satisfies 4.
thus constructed satisfies 4.Together with 10, the temporal aggregation property implies the existence of a function 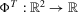 such that
such that
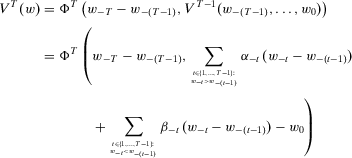 (12)
(12) .
.First, consider  such that
such that 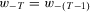 . Difference monotonicity and 10 together imply
. Difference monotonicity and 10 together imply
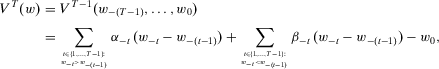
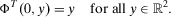 (13)
(13)Now consider the case in which w is such that 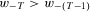 . Homogeneity implies that
. Homogeneity implies that 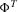 satisfies
satisfies
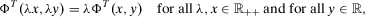 (14)
(14)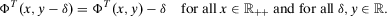 (15)
(15)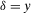 , 15 implies
, 15 implies 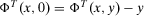 and, thus,
and, thus,
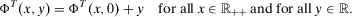 (16)
(16)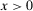 , 14 implies
, 14 implies
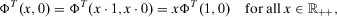
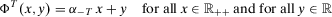 (17)
(17)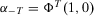 . By difference monotonicity,
. By difference monotonicity, 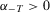 .
.If w is such that 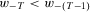 , an argument parallel to that used above to derive 17 can be employed to obtain
, an argument parallel to that used above to derive 17 can be employed to obtain
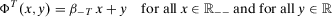 (18)
(18)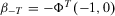 . By difference monotonicity,
. By difference monotonicity, 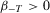 .
.Combining 13, 17, and 18, it follows that
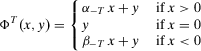 (19)
(19)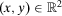 . Substituting back into 12, we obtain 11, that is,
. Substituting back into 12, we obtain 11, that is,
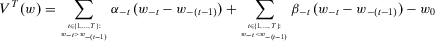
 .
.It remains to be shown that 4 is satisfied. Because the positivity of the coefficients has already been established, all that is left to prove is
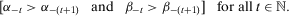
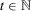 . Let
. Let 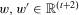 be such that
be such that
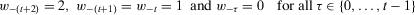
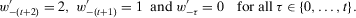
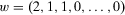 and
and 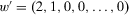 . Using 12 and 19, it follows that
. Using 12 and 19, it follows that
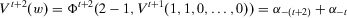
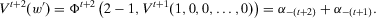
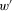 can be obtained from w by shifting the drop from 1 to 0 one period further into the past. According to proximity monotonicity, the earlier loss in
can be obtained from w by shifting the drop from 1 to 0 one period further into the past. According to proximity monotonicity, the earlier loss in 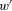 affects insecurity to a lesser extent than the later loss in w and, thus, insecurity in
affects insecurity to a lesser extent than the later loss in w and, thus, insecurity in 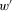 must be less that insecurity in w. Thus, proximity monotonicity requires
must be less that insecurity in w. Thus, proximity monotonicity requires
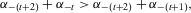 (20)
(20)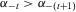 , as was to be established.
, as was to be established. 
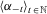 and
and 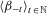 . A plausible assumption appears to be the requirement that ceteris paribus losses of a certain magnitude in a given period have a stronger impact on insecurity than ceteris paribus gains of the same magnitude in the same period. This assumption is captured in the loss-priority axiom. If this property is added to those of Theorem 1, the parameter values must be such that losses carry a higher weight than gains in each period, which leads to a subclass of the measures identified in the previous characterization. This subclass is defined in terms of those pairs of sequences
. A plausible assumption appears to be the requirement that ceteris paribus losses of a certain magnitude in a given period have a stronger impact on insecurity than ceteris paribus gains of the same magnitude in the same period. This assumption is captured in the loss-priority axiom. If this property is added to those of Theorem 1, the parameter values must be such that losses carry a higher weight than gains in each period, which leads to a subclass of the measures identified in the previous characterization. This subclass is defined in terms of those pairs of sequences 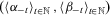 that satisfy
that satisfy
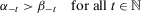 (21)
(21)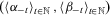 satisfying 4 and 21 such that, for all
satisfying 4 and 21 such that, for all 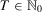 and for all
and for all  ,
,
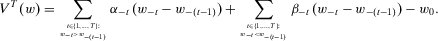
The property of loss priority alluded to above is defined formally as follows:
Loss Priority
For all 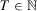 , for all
, for all 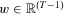 and for all
and for all 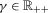 ,
, 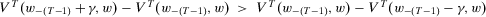 .
.
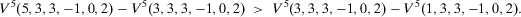

Adding loss priority to the axioms of Theorem 1 leads to a characterization of the loss-averse measures defined above. This is stated in the following theorem, the proof of which is straightforward and left to the reader.
Theorem 2.A measure of individual insecurity V satisfies difference monotonicity, proximity monotonicity, homogeneity, translatability, the temporal aggregation property, and loss priority if and only if V is a two-sequences loss-averse Gini measure of insecurity.
 and
and 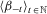 so that
so that
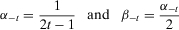
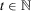 . The coefficients according to the sequence
. The coefficients according to the sequence 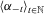 are the inverses of the coefficients corresponding to the Gini social evaluation function; see, for instance, Donaldson and Weymark (1980) and Weymark (1981).
are the inverses of the coefficients corresponding to the Gini social evaluation function; see, for instance, Donaldson and Weymark (1980) and Weymark (1981).4. TWO-PARAMETERS GINI MEASURES
The recollection of past experiences is a key determinant of an individual's current behavior. Allais (1966, p. 1128) argues that, in some circumstances, “forgetfulness per unit of time is constant.” To capture this alternative notion, past experiences should not be discounted. The purpose of this section is to suggest and characterize classes of insecurity measures that conform to this alternative idea formulated by Allais (1966).
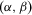 such that, for all
such that, for all 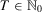 and for all
and for all  ,
,
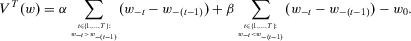
Proximity Indifference
For all 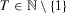 , for all
, for all  , and for all
, and for all  ,
, 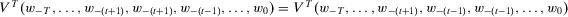 .
.
As opposed to proximity monotonicity, proximity indifference requires that a ceteris paribus shift in time of a gain or loss of a given magnitude leaves insecurity unchanged. Again, Figure 3 can be referred to as an illustration of the axiom; this time, however, insecurity in w and in 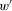 must be identical.
must be identical.
We now obtain the following characterization of the two-parameters Gini measures of insecurity.
Theorem 3.A measure of individual insecurity V satisfies difference monotonicity, proximity indifference, homogeneity, translatability, and the temporal aggregation property if and only if V is a two-parameters Gini measure of insecurity.

 such that
such that  and, for all
and, for all 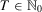 and for all
and for all  ,
,
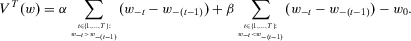
We state the final theorem of the article without a proof.
Theorem 4.A measure of individual insecurity V satisfies difference monotonicity, proximity indifference, homogeneity, translatability, the temporal aggregation property, and loss priority if and only if V is a two-parameters loss-averse Gini measure of insecurity.
5. CONCLUDING REMARKS
In this article, we propose classes of measures of economic insecurity analyzed from a thorough theoretical perspective. The measures of individual insecurity characterized in this article share a linear structure with the generalized Gini social evaluation functions used in ethical approaches to inequality measurement. Furthermore, they resemble rank-ordered decision criteria employed in theories of choice under uncertainty.
We provide a detailed treatment of individual insecurity based on wealth considerations. This leaves open the problem of aggregating individual insecurity values into a social index. Although the design of social rather than individual measures of economic insecurity also is an issue of considerable interest, we focus on the individual problem in this article. We justify this choice by appealing to the observation that economic insecurity is very much a sentiment experienced by each individual. To draw a parallel to other questions involving economic index numbers, consider the measurement of deprivation as a prominent example. As illustrated in Yitzhaki (1979) and much of the subsequent literature, it is natural to first obtain an individual value of deprivation for any income distribution and then, in a second stage, aggregate these individual deprivation values into a social deprivation index. This second stage is frequently performed by calculating the arithmetic mean of the individual deprivation values, and the more substantive problem is that of designing the individual index. The measurement of economic insecurity is similar in this respect: once an individual index of insecurity is established, a social index can easily be obtained by applying a (possibly but not necessarily arithmetic) mean to the individual insecurity values. Note that this contrasts with economic measures of inequality: There is no “individual” inequality because the phenomenon in itself is defined in terms of the disparity present in a distribution. Thus, an explicit study of economic insecurity for society as a whole is another task to be undertaken in future work. In addition, one may want to explore the possibility of including (nonmonetary) variables other than wealth in order to arrive at a more comprehensive notion of insecurity.
We conclude with two recommendations. The first is addressed to policy makers and the second pertains to possible further related research programs.
A central role in our index of economic insecurity is played by the memory of an individual of her economic past. Because insecurity appears to have become a key variable in measures of well-being intended to go beyond GDP, a recommendation for policy makers is to be more inclusive in determining the data to be considered. Allais (1974, p. 323) expresses a similar view by saying that, “a policy for bringing about a collective optimum should take into account not the future developments, but the past evolution.”
A recommendation for future research is to continue with the effort to incorporate an individual's past as a determinant of present well-being. This line of research appears to be, together with multidimensionality, very promising in understanding the complexity of well-being.




