Decoupled erosion of amphibians’ phylogenetic and functional diversity due to extinction

1 INTRODUCTION

Rapid loss of biological diversity from human actions has triggered a mass extinction during the Anthropocene (Barnosky et al., 2011; Ceballos et al., 2017). This might include the loss of species that play important ecological roles within communities (Boyer & Jetz, 2014; Fonseca & Ganade, 2001), owing to their unique traits (Faith, 2018) and evolutionary history (Veron, Davies, Cadotte, Clergeau & Pavoine, 2017). A common assumption is that closely related species share more similar ecologies than distant related ones (Wiens & Graham, 2005), thus protecting phylogenetic diversity (PD) may help to preserve functional diversity (FD) (Faith, 1992, 2008; Vane-Wright, Humphries & Williams, 1991; Veron et al., 2017; Winter, Devictor & Schweiger, 2013). The correlation between PD and FD is a topic of intense debate (Gerhold, Cahill, Winter, Bartish & Prinzing, 2015; Pavoine, Vela, Gachet, Bélair & Bonsall, 2011; Tucker, Davies, Cadotte & Pearse, 2018), with evidence both for it (Collen, Turvey, et al., 2011; Huang, Stephens & Gittleman, 2012; Redding, Dewolff & Mooers, 2010) and against it (Kelly, Grenyer & Scotland, 2014; Mazel et al., 2018; Oliveira et al., 2016). However, whether the loss of PD yields concomitant loss of FD remains poorly understood, therefore undermining our capacity to predict the impact of extinctions on evolutionary and ecological dimensions of biodiversity.

The magnitude of PD loss and FD loss from any species’ extinction ultimately depends on its shared evolutionary history and ecological similarity with extant species, respectively. Due to phylogenetic constraints on trait and niche evolution (Felsenstein, 1985; Wiens & Graham, 2005), the simplest scenario predicts that the loss of PD and FD should be coupled. For instance, the extinction of a species in an older monotypic clade with few relatives could have a greater impact on the loss of both PD and FD than the loss of a species in a recently diverged clade with many close relatives (Nee & May, 1997; Redding et al., 2010). This is because the former species might carry more distinct evolutionary history and ecological traits not found elsewhere than the latter species. However, different pathways exist that can lead to decoupled losses between PD and FD. For instance, a large portion of PD would be lost with the extinction of phylogenetically isolated species, but FD loss could be low if remaining species share similar ecological roles (i.e., functional redundancy, Rosenfeld, 2002). This can occur via convergent evolution (Winemiller, Fitzgerald, Bower & Pianka, 2015), or strong environmental selection (Li et al., 2018; Webb, Ackerly, McPeek & Donoghue, 2002), that expresses similar suites of traits among phylogenetically distant lineages. Conversely, high FD can be lost if some traits correlate strongly with extinction risk. Species with small geographical range size, low population density, long life span, slow reproductive rates and large body size are disproportionately more threatened (Collen, McRae, et al., 2011; Davidson, Hamilton, Boyer, Brown & Ceballos, 2009; Fritz, Bininda-Emonds & Purvis, 2009; Jenkins, Pimm & Joppa, 2013), and so the loss of these traits by extinction may disproportionately reduce FD relative to PD (Fritz & Purvis, 2010).

Studies concerning the loss of biodiversity by extinction often focus on single dimensions of biodiversity at a time (e.g., Batista, Gouveia, Silvano & Rangel, 2013; Boyer & Jetz, 2014; Jernvall & Wright, 1998; Jono & Pavoine, 2012), but there is clearly a need for more integrated approaches that account for multiple dimensions jointly (Brum et al., 2017; Cadotte, Davies & Peres-Neto, 2017; Cadotte & Tucker, 2018; Pollock, Thuiller & Jetz, 2017). Global analyses with mammals showed that the loss of PD, inferred by the extinction of threatened species in accordance to the International Union for Conservation of Nature (IUCN) Red List, did not match losses of FD estimated by variance in body mass (Davis, Faurby & Svenning, 2018; Fritz & Purvis, 2010). Such decoupling undermines the use of PD loss as a surrogate for FD loss. Although body mass is arguably an indicator of many facets of species’ ecology and life history, combinations of traits corresponding to multiple ecological dimensions should yield more holistic representation of FD (Kraft, Godoy & Levine, 2015; Petchey & Gaston, 2006). For instance, Tucker et al. (2018) found that the strength of the PD–FD relationship increases with increasing number of traits used in the FD measure.

PD theoretically reflects the aggregated expectation of multiple, including hard-to-measure, traits. Consequently, PD has been widely used as a proxy of FD. Furthermore, Faith (1992, 2018) argued that PD may also help to protect unknown FD of unanticipated future benefits for humanity, an outcome referred to as its “option-value”. In this study, we focus on the “proxy-value” of PD, not its “option-value”, both being important reasons for conserving PD (Faith, 2015; Forest, Crandall, Chase & Faith, 2015; Owen, Gumbs, Gray & Faith, 2019).

Here, we integrate phylogeny (Jetz & Pyron, 2018), traits (Oliveira, São-Pedro, Santos-Barrera, Penone & Costa, 2017), distribution and threat status (IUCN, 2018) for amphibians globally (6,097 species) to predict how extinctions will impact their PD and FD. We do this by first calculating current amphibian PD and FD, and then estimating the loss of PD and FD given probabilities that currently threatened species will go extinct in the near future (Mooers, Faith & Maddison, 2008). We assess the impact of extinctions on total amphibian diversity, as well as patterns of diversity loss across space according to species assemblage within grid cells. Understanding the consequences of extinctions on amphibian diversity is crucial for prioritizing conservation because they face high extinction pressure from human impacts, with 41% of species threatened with extinction (IUCN, 2018). Our study reveals that although patterns of current amphibian PD are FD associated, extinctions would result in strongly decoupled losses of amphibian PD and FD.

2 METHODS

3 RESULTS

3.1 Global scale diversity loss

Our models indicate that over 32% (SD = ±0.33) of all amphibians (median = 1,979; SD = ±20) would be lost within the next 100 years. The extinction of these species eroded 26,046 Myr (SD = ±420) of unique evolutionary history, which corresponds to 20.4% (SD = ±0.33) of all amphibian PD and 5.3% (SD = ±0.55) of their FD (4PD:1FD ratio) (Figure 1). The imminent disappearance of at risk amphibians would remove far more of each dimension of diversity than expected by random extinctions (Figure 1), leaving a large PD and FD debt as unique lineages and trait diversity are at risk of becoming completely lost in the near future.

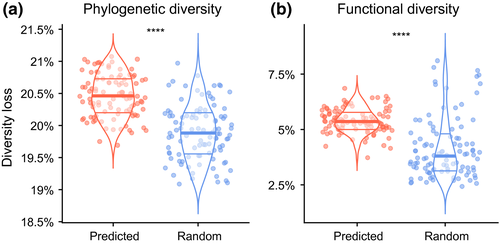
3.2 Regional scale diversity loss

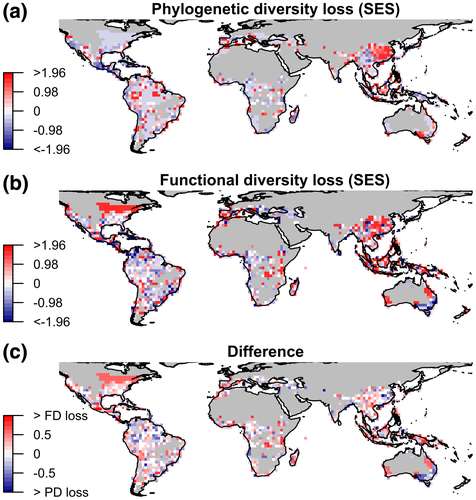
The loss of amphibian dimensions of diversity varied widely in space (Figure 2), regardless of the richness of extant species in assemblages (Supporting Information Figure S4 and Table S1). The loss of species richness was closely associated with PD loss within assemblages [standardized coefficient (std. coeff.) = .91, R² = .85, p-value < .001], but not with FD loss (std. coeff. = .22, R² = .4, p-value < .001) (Figure 2). Moreover, hotspots of species richness loss were mostly congruent with those of PD loss, but not with those of FD loss (Supporting Information Figure S5). Assemblages would lose on average more of their FD (7.8%) than PD (3.6%) (2.2FD:1PD), a pattern opposite to what was observed in the global scale assessment. Regions at risk of losing high proportions of both PD and FD were concentrated in Central America, the Caribbean islands, the Andes and northern Amazon of South America, eastern China, Southeast Asia and eastern Australia (Figure 2).

Our results revealed large geographical variation concerning the departure of PD loss and FD loss from random extinctions (Figure 3). The loss of PD and FD did not differ from random in most assemblages (denoted by a distribution of SES values centred on zero; Supporting Information Figure S6), but when they did they were more positive than negative, indicating higher loss of PD and FD than random (Figure 3; Supporting Information Figure S7). While all major regions of the world contained a mix of higher and lower loss for PD and FD, in most assemblages FD losses exceeded PD losses (Figure 3c), indicating elevated trait uniqueness in imperilled species. Exceptions were located mostly in the Neotropics and eastern Australia, where assemblages lost more PD than FD (Figure 3c).

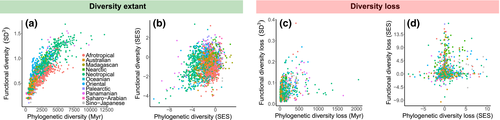
The PD and FD of currently extant amphibians were positively associated and followed an asymptotic relationship [Figure 4a; second-order polynomial function: R² = .9, Akaike information criterion (AIC) = 524, p < .001; linear function: R² = .87, AIC = 735, p < .001]. This positive association remained even after controlling for richness (Figure 4b). However, projected extinctions broadly decoupled the loss of PD and FD (Figure 4c,d), indicating that the loss of evolutionary history responded independently from the loss of ecological functions. Spatial models confirmed that the predictive power of PD on FD was greater than the predictive power of PD loss on FD loss (Table 1). These results again held after controlling for richness (Table 1, Figure 4d).

Table 1. Summary of spatial models testing phylogenetic diversity (PD) as a surrogate of functional diversity (FD)

Model	Std. coeff.	Pseudo-R2
		Predictor + space	Predictor only
Extant diversity
FD ~ PD	.7	.79	.65
FD SES ~ PD SES	.35	.23	.1
Diversity loss
FD loss ~ PD loss	.34	.23	.12
FD loss SES ~ PD loss SES	.11	.27	.02

Note

• Std. coeff. = standardized coefficient. The predictive power of models for extant diversity are much higher than the ones for diversity loss. Spatial models were calculated using raw PD and FD values, as well as using standardized effect sizes (SES) of these same metrics. Spatial models were fitted with simultaneous autoregressive models with the error term. Pseudo-R² was partitioned into the variance explained by predictor variable and the combination of predictor variable + space. All std. coeffs. are significant (p-values < .05).

4 DISCUSSION

Understanding how extinctions may erode evolutionary and ecological dimensions of diversity is fundamental for conservation planning, especially when one dimension is used as a surrogate for another (Cadotte & Tucker, 2018; Devictor et al., 2010; Hidasi-Neto, Loyola & Cianciaruso, 2015; Mazel, Mooers, Riva & Pennell, 2017; Sobral et al., 2014). If shared evolutionary history among species infers ecological similarity (Felsenstein, 1985), then losing PD might result in the loss of FD (Faith, 2008; Forest et al., 2015; Nee & May, 1997; Veron et al., 2017). Our results indicate a weak association between the loss of PD and FD (Figure 4), therefore challenging the notion that PD loss is an appropriate surrogate of FD loss. Interestingly, this decoupling occurred even though a strong correlation exists between extant amphibian PD and FD across assemblages globally (Figure 4).

Although highly threatened (Brum et al., 2013; Pounds, 2001; Sodhi et al., 2008), analyses of projected impacts by extinctions on amphibian diversity are scarce. Batista et al. (2013) simulated the extinction of threatened New World anurans and found a spatial pattern in PD loss that closely resembles our results. However, as a consequence of knowledge gaps regarding traits, studies on amphibian FD have had narrow taxonomic and geographical scope (Ernst, Linsenmair & Rödel, 2006; Ochoa-Ochoa et al., 2019; Tsianou & Kallimanis, 2016). We provide the first global estimate of current patterns, and predicted future loss, of amphibian PD and FD. We found that current amphibian PD and FD are related to each other globally (Figure 4a,b), consistent with the hypothesis that closely related species are ecologically similar (Faith, 1992; Wiens & Graham, 2005). This association remains after controlling for richness using SES. Further support for this association comes from strong phylogenetic signal in the traits used for calculating FD (Supporting Information Table S2). However, there is little evidence that losses in PD and FD by extinctions will retain this similarity (Figure 4c,d). The lack of congruence between the loss of amphibian PD and FD indicates that species vulnerable to extinction vary in the magnitude of shared ancestry and functional redundancy with survivors. Importantly, this mismatch is geographically uneven, with some regions losing more FD than PD, whereas the opposite is expected for other regions.

We found that, for most worldwide amphibian assemblages, extinctions are likely to impact more of their current FD than PD (Figure 3c). This suggests threatened species carry more unique traits, or hang in shorter phylogenetic branches, relative to coexisting species. Previous studies of amphibians have shown that some traits correlate strongly with high threat risk [e.g., large body size, aquatic and arboreal habitat, viviparous reproduction, and small range size (Foden et al., 2013; Sodhi et al., 2008)]. A higher than expected global FD loss (Figure 1) indicates that threatened amphibians occupy a unique trait space. The loss of these species would greatly reduce variance among traits, leaving a high FD loss. Because amphibians show generally low dispersal ability and small range sizes, more diverse assemblages may have many closely related species, inducing phylogenetic redundancy and potentially contributing to a lower loss of PD than FD. Indeed, our data indicate assemblages with high richness of small-range species (range size < 200 km²) lost more species (Supporting Information Figure S8; Pearson’s r = .45, p-value < .001), but less PD than expected by chance (Supporting Information Figure S9; Pearson’s r = −.21, p-value < .001).

However, the Neotropical and eastern Australia regions were an exception for this pattern. Assemblages in these regions would lose more of their PD than FD, suggesting functional redundancy among species (Figure 3c). The Neotropics harbour the highest amphibian diversity and endemism globally, and both the Neotropical and eastern Australia regions concentrate a high number of threatened species (Jenkins et al., 2013). Recent phylogenetic analyses revealed that species-rich amphibian assemblages are composed of many old families that diversified quickly (Jetz & Pyron, 2018; Pyron & Wiens, 2013). The Neotropics hold highly evolutionary distinct species (Supporting Information Figure S10), thus their extinction would contribute to a high PD loss. Yet, rapidly diversifying amphibian clades share a greater number of threatened species compared to slowly diversifying clades (Greenberg & Mooers, 2017). If rates of trait evolution lag behind rates of lineage diversification, as in non-adaptive radiations (Kozak, Weisrock & Larson, 2006), it is possible that extinctions will overwhelmingly erode PD while maintaining FD due to high functional redundancy. This hypothesis is consistent with the observed asymptotic relationship between amphibian PD and FD, which is mainly driven by Neotropical assemblages (Figure 4a).

The relative impact of extinctions upon amphibian PD and FD varied with the scale of our analyses. At the global scale (across all 6,189 species considered in this study) amphibians lost more PD than FD (4PD:1FD ratio), whereas at the assemblage scale [2 ×2 grid cells, considered an appropriate resolution for the data (Hurlbert & Jetz, 2007)] they lost on average more FD than PD (2.2FD:1PD ratio). It is important to note, however, that any loss of PD or FD to extinction is relative to the survivors in the species pool. At the global pool, species from different assemblages overlap in trait space, resulting in higher functional redundancy relative to that at the assemblage scale. This high redundancy ultimately increases the chance that an extinct species will be replaced by a functionally equivalent one, with the loss therefore being less impactful to FD. On the other hand, in the assemblage pool, because amphibians in general have low vagility, diversifying lineages could remain within the same assemblage over time. This would result in high phylogenetic redundancy and potentially translate into less PD loss relative to FD loss. These seemingly contrasting results complement, rather than contradict, each other, allowing a more complete inference of the processes that predominate across different scales.

The poor support for the “proxy-value” of PD loss should not undermine the conservation importance of PD. Conserving PD may help to protect the diversity of evolutionary histories, but also multiple hard-to-measure traits that may be beneficial to society – referred to as the “option-value” (Amado, Bidau & Olalla-Tárraga, 2019; Faith, 2008, 2018; Forest et al., 2015; Owen et al., 2019). Any estimate of FD reflects the choice of traits, which is often arbitrary and determined primarily by data availability. We used traits that might link to ecosystem functions and services amphibians perform in ecosystems, and have been used in other studies with amphibians (Ochoa-Ochoa et al., 2019; Oliveira & Scheffers, 2019; Rapacciuolo et al., 2019). For instance, burrowing behaviour alters soil properties, body size is associated with feeding habits, and reproduction strategy may reflect energy and matter flux (Wells, 2007). Additional levels of detail in amphibian traits may change our representation of FD (Tucker et al., 2018) but high-resolution data remain currently unavailable.

In facing the current biodiversity crisis, conservation biologists have growing concerns over the degree to which future extinctions would erode evolutionary and ecological dimensions of diversity (Cadotte & Tucker, 2018; Davies, 2015; Mazel et al., 2016; Vane-Wright et al., 1991; Veron et al., 2017). Because our simulated extinction scenarios eroded PD and FD independently, we conclude that conserving one dimension of biodiversity as surrogate for another should be avoided. The loss of PD prunes the Tree of Life, and hinders the potential for lineages to evolve and adapt (Forest et al., 2015; Vane-Wright et al., 1991), whereas the loss of FD drives functional homogenization, which potentially reduces the goods and services from ecosystems that benefit humans (Fonseca & Ganade, 2001; Oliver et al., 2015; Petchey & Gaston, 2002). Prioritizing PD is generally a reasonably good method for conserving FD (Mazel et al., 2018), but the loss of one dimension may not yield concomitant loss of the other (Davis et al., 2018; Fritz & Purvis, 2010). Conservation attention should be directed towards regions with high likelihood of losing large portions of their PD and FD. However, a decoupling in the loss of PD and FD will require case-specific conservation strategies in different regions to secure the protection of the biodiversity dimension of interest (Cadotte & Tucker, 2018).

DATA ACCESSIBILITY

Distribution data are available through IUCN (https://www.iucnredlist.org/). Phylogenetic data are available through the Vert Life project (https://vertlife.org/). Trait data are available through the AmphiBIO database (https://figshare.com/articles/Oliveira_et_al_AmphiBIO_v1/4644424). Predicted threat status for Data Deficient species is available at the Supporting Information Appendix S3.

AUTHOR CONTRIBUTION

BFO and GCC planned the research. BFO performed the analyses. BFO wrote the first draft. All authors contributed substantially to the writing.

BIOSKETCHES

Brunno F. Oliveira is interested in macroecology and community ecology. His research integrates phylogenies, maps and traits to understand the mechanisms that generate biodiversity gradients, and how humans disrupt these gradients.

Brett R. Scheffers is interested in biological organization and processes in space and time. Brett’s interests include multidimensional species distributions, community assembly/disassembly, ecophysiology, ecological scaling rules, and thermal complexity of landscapes. He uses these concepts to assess species and habitat vulnerability and resilience under novel climates and human disturbances.

Gabriel C. Costa is an Assistant Professor at Auburn University at Montgomery. His research focuses on understanding what determines the spatial distribution of biodiversity. He is interested in disentangling the roles of ecological and evolutionary drivers of biodiversity in different taxonomic groups and from local to global scales. He is also motivated by using his findings to create instrumental knowledge that can then support conservation decisions.