In order to mitigate the ecological, economical and social consequences of future climate change, we must understand and quantify the response of vegetation to short-term climate anomalies. There is currently no model that quantifies vegetation resistance and resilience at a global scale while simultaneously taking climate variability into account. The goals of this study were therefore to develop a standardized indicator of short-term vegetation resilience and resistance to drought and temperature anomalies, and to improve our understanding of vegetation resistance and resilience in drought-sensitive areas by linking metrics of vegetation stability to the percentage of tree cover, non-tree vegetation and bare soil.

Location

Global.

Methods

The deviation of vegetation behaviour from expectations was quantified using anomalies in the normalized difference vegetation index (NDVI) and modelled as a function of (1) past NDVI anomalies, (2) an instantaneous drought indicator and (3) temperature anomalies. Metrics of resistance and resilience were then extracted from the model and related to the percentages of bare soil, non-tree vegetation and tree cover.

Results

Comparisons of the globally derived resilience and resistance metrics showed low resilience and low resistance to drought in semi-arid areas, low resistance to negative temperature anomalies in high-latitude areas, and low resistance to positive temperature anomalies in the Sahel and Australia. In drought-sensitive areas, resilience was highest for vegetation types with 3–20% bare soil and 5–15% tree cover.

Main conclusions

Our ARx model is the first to simultaneously derive vegetation resistance and resilience metrics at a global scale, explicitly taking into account the spatial variability of short-term climate anomalies and data reliability. Its results highlight the impact of tree cover, non-tree vegetation and bare soil on vegetation resilience.

Introduction

Changing average climate conditions, combined with greater and more frequent climate extremes, are expected to affect the primary productivity of terrestrial vegetation and plant distribution patterns. This may have major economic and ecological implications (Field et al., 2012). For example, climate extremes such as heat waves reduce primary productivity by diminishing water availability and decreasing the net CO₂ exchange of ecosystems. The resulting drought stress, combined with the higher expected incidence of pests and pathogens, might further decrease plant viability and increase mortality (McDowell et al., 2008). The effects of droughts and temperature anomalies on plant mortality have already been observed globally (Allen et al., 2010). To anticipate the consequences of the affected ecosystem functions and the associated ecosystem services, a comprehensive global quantification of the susceptibility of vegetation to droughts and temperature anomalies, and a better understanding of the vegetation characteristics that mediate vegetation response, are essential.

The stability of vegetation in the face of external disturbances has generally been described using measures of resistance and resilience in biomass productivity (Tilman, 1996). ‘Resistance’ expresses the ability of vegetation to withstand environmental disturbances. It has been quantified using the magnitude of vegetation response at the moment of the climate anomaly. ‘Resilience’ measures the speed of recovery after the disturbance (engineering resilience), or the magnitude of disturbance that can be absorbed before the ecosystem's structure changes (ecological resilience; Walker et al., 1981; Holling, 1996). Engineering resilience can be quantified by measuring the time required to return to the biomass state that existed before the stress (Tilman, 1996; Lhermitte et al., 2010, 2011a), or by autocorrelation or the persistence of trends within a time-series of vegetation characteristics (Simoniello et al., 2008; Dakos et al., 2012). Large-scale ecological resilience of tropical savannas and forests, conversely, has been quantified through the probability that forest, savanna or treeless cover will switch states (Hirota et al., 2011).

A variety of studies, ranging from small-scale ecological experiments to global vegetation surveys, have focused on the stability of vegetation after short-term climate anomalies. Such local studies mostly focus on vegetation biomass before, during and after a drought event (e.g. Tilman, 1996). They have the advantage of being based on accurate field measurements (e.g. biomass) but, because they are labour-intensive and often destructive, the same approach cannot be used for large-scale studies. Satellite observations have therefore been used to assess the response of vegetation at larger scales. The cyclic availability of remote-sensing products directly associated with the state of the vegetation, makes them highly valuable for ecosystem monitoring (Zeng et al., 2013). They include the leaf area index (LAI;, e.g. Myneni et al., 2002), the fraction of photosynthetically active radiation (fPAR;, e.g. Myneni et al., 2002), net and gross primary productivity (NPP and GPP;, e.g. Justice et al., 2002) and indicators of biomass and greenness of vegetation, such as the normalized difference vegetation index (NDVI;, e.g. Tucker et al., 2005) and the enhanced vegetation index (EVI;, e.g. Justice et al., 2002). They also exhibit valuable properties, both temporal and spatial, for ecological applications. For example, remote sensing provides information over broad spatial extents, and such data are difficult or impossible to obtain from field studies. Moreover, the continuous data acquisition of satellites over periods of several years enables the establishment of long-term time-series.

Despite the advantages of satellite data in quantifying vegetation responses to climate extremes at continental scales, such time-series also suffer important drawbacks. First, because vegetation stability depends strongly on the characteristics of the climate anomaly, a comparison of the vegetation stability between different parts of the world is impossible without accounting for the varying magnitude of the climatic disturbance. For example, a drought may be extreme at location A but mild at location B; if the vegetation at both locations were to show a similar response, the vegetation of A and B would seem to have similar sensitivities to drought, but when the magnitude of the climate anomaly is accounted for, the vegetation of A is less sensitive than that of B. In order to obtain a reliable assessment of vegetation response to short-term climate anomalies at large spatial scales, vegetation stability metrics must therefore be standardized based on climate data. Second, vegetation has ‘memory’, in that its state depends both on current disturbances and the residual effects of past climate conditions. This ‘memory effect’ should be considered when assessing the immediate response to short-term climate anomalies. Although many studies have quantified ecosystem stability in response to environmental disturbances (e.g. Lloret et al., 2007; Simoniello et al., 2008; Telesca et al., 2008), none has simultaneously taken into account metrics standardizing for short-term climate effects and system memory.

The difficulties in assessing vegetation stability across large spatial scales have contributed to the current lack of a global assessment of the vegetation characteristics that determine short-term vegetation stability. In drought-limited environments, vegetation response is expected to be mediated by the access of plant roots to soil moisture. In savannas, functional diversity in water uptake through interspecific variation in root systems stabilizes the vegetation at large scales (Walter & Mueller-Dombois, 1971; Scanlon et al., 2005). Mixtures of trees and grasses may therefore show greater vegetation stability than vegetation types with only trees or grasses. Scanlon et al. (2005) confirmed this hypothesis using a hydrological model based on tree cover and near-surface moisture using a transect from 12° S to 26° S in southern Africa. This hypothesis has been challenged, however, due to its oversimplified presentation of root-zone profiles, and its failure to take herbivory, fire and competition between grasses and tree seedlings into account (Bond, 2008).

Given the lack of a suitable model that quantifies vegetation resistance and resilience at a global scale, and in order to assess the vegetation characteristics that determine short-term vegetation stability, the overall objectives of this study were (1) to present a model that globally quantifies short-term vegetation stability by explicitly taking the magnitude of short-term climate anomalies into account; and (2) to improve our understanding of the drivers of drought resistance and engineering resilience in drought-sensitive areas. More specifically, we aimed to present standardized indicators of short-term vegetation resilience and resistance to drought and temperature anomalies, and to assess whether mixtures of grassland and trees are more stable than relatively pure grasslands and pure tree vegetation by establishing a relationship between metrics of vegetation stability and the percentage of tree cover, non-tree vegetation and bare soil in drought-sensitive areas. The model presented here is based on a fit between global remote-sensing time-series related to vegetation health (NDVI), and time-series of global drought and temperature anomalies.

Methods

Remote-sensing data

Global Inventory Modeling and Mapping Studies (GIMMS) NDVI bimonthly time-series, acquired between July 1981 and December 2006 with a spatial resolution of 0.072° were used to quantify the temporal vegetation status. NDVI quantifies the amount and greenness of vegetation, and so correlates with vegetation biomass, vegetation dynamics and the fraction of absorbed photosynthetically active radiation (fAPAR), and provides a widely used estimator of vegetation health (Zeng et al., 2013). NDVI time-series generally consist of: (1) a seasonal component, such as phenology; (2) anomalies, such as the response to environmental factors; and (3) noise, including sensor noise and atmospheric influences (Lhermitte et al., 2011b). To study vegetation anomalies, the seasonal component must be removed and noise must be reduced. To that extent, low-quality data was removed from the bimonthly time-series using the associated quality flags (Tucker et al., 2005). The bimonthly NDVI time-series were then resampled to monthly series using maximum-value compositing (Holben, 1986) in order to be compatible with the monthly climate time-series. Finally, the seasonal component was removed by subtracting the monthly mean NDVI value.

The fractions of bare soil, tree cover and non-tree vegetation (i.e. shrubs, crops and other herbaceous vegetation) were extracted from the MODIS Vegetation Continuous Fields (MOD44B.003; Hansen et al., 2003) to study the relationship of the vegetation stability metrics with vegetation cover. This dataset was subsequently resampled to the GIMMS grid by assigning to each GIMMS pixel the average fraction of all MODIS pixels situated within it.

Climate data

Monthly temperature anomaly time-series from July 1981 to December 2006 were obtained from the 0.5° Goddard Institute for Space Studies (GISS) data set (1200 km smoothing radius; New et al., 2000). Droughts were quantified using monthly time-series of the standardized precipitation–evapotranspiration index, SPEI, from 1981 to 2006 (Vicente-Serrano et al., 2010). SPEI is a site-specific drought indicator based on deviations from the average water balance. The latter is calculated as precipitation minus potential evapotranspiration over a specified time-scale. Both the temperature and SPEI time-series were spatially resampled to the GIMMS grid using nearest-neighbour resampling. A three-month time-scale – i.e. SPEI calculated for the cumulative water balance over the previous three months – was used, because this approach has been shown to produce the highest correlation with NDVI while reducing the influence of noise (Vicente-Serrano et al., 2013; Zeng et al., 2013). As such, positive temperature anomalies and SPEI values indicate warmer and wetter conditions than average, respectively, whereas negative values represent cooler conditions or a negative water balance. (See Table 1 for an overview of the datasets.)

Table 1. Overview of the data properties

Dataset	URL	Base period	Resolution	Reference
GIMMS NDVI	http://gcmd.nasa.gov/records/GCMD_GLCF_GIMMS.html	07/1981–12/2006	0.072°	Tucker et al. (2005)
GISS Temperature anomaly (1200 km smoothing)	http://www.giss.nasa.gov/	1961–1990	0.5°	Hansen et al. (1999); New et al. (2000)
SPEI	http://sac.csic.es/spei/database.html	01/1901–12/2011	0.5°	Vicente-Serrano et al. (2010)
Land Cover Fractions	https://lpdaac.usgs.gov/data_access/	–	500 m	Hansen et al. (2003)

Because our objective was to characterize the short-term response of vegetation to short-term climate anomalies, long-term NDVI trends were of no interest. Such trends are considered to represent changes in the equilibrium state of the vegetation (e.g. due to overgrazing or long-term successional cycles) instead of being anomalies resulting from short-term climate anomalies. Time-series of NDVI anomalies, SPEI and temperature anomalies were therefore detrended whenever a significant temporal linear trend was detected (Appendix S1).

Vegetation stability

The vegetation response to short-term climate anomalies was modelled by considering the NDVI anomaly as a linear combination of the temperature anomaly, drought index (SPEI) and NDVI anomaly history:

$urn:x-wiley:1466822X:media:geb12279:geb12279-math-5001$

where Y_t is the standardized NDVI anomaly at time t, SPEI_t is the standardized SPEI index at time t, T_t is the standardized temperature anomaly, and ϵ_t is the residual term at time t; α, β and ϕ are the model's coefficients. Standardization of the time-series was performed in order to assure comparability between the model coefficients. This model is known by the acronym ARx.

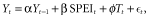
Each of the model coefficients of the ARx model can be related to metrics of ecosystem stability (Table 2). The coefficient of the standardized temperature anomaly time-series, ϕ, is an indicator of the vegetation anomaly related to instantaneous temperature changes, and thus represents a temperature-resistance metric. Similarly, the coefficient of the standardized SPEI time-series, β, represents the drought-resistance metric. Finally, α gives an indication of the dependence of the anomalies on the previous response values. Where α is large, anomalies are strongly determined by the anomaly at time t−1 and the ecosystem recovers slowly from any disturbance; where α is small, ecosystems tend to recover quickly. As such, α is related to ecosystem resilience and can be considered a resilience metric that quantifies memory effects.

Table 2. Interpretation of the ARx coefficients

Coefficient

Interpretation magnitude

Interpretation sign

α (coefficient of Y_t₋₁)

Absolute values between zero and one represent systems returning to equilibrium, with large absolute values indicating a low resilience, i.e. a slow return to equilibrium

Positive Anomalies are similar to the previous anomaly. In case α is smaller than one, the anomaly gradually diminishes over time.

Negative Anomalies are similar to the previous anomaly, but with the opposite sign. In case α is larger than −1, the system returns to equilibrium in an oscillating way

β (coefficient of SPEI_t) and ϕ (coefficient of T_t)

Large absolute values indicate a low resistance to droughts/temperature anomalies, i.e. a large vegetation response to short term droughts/temperature anomalies.

Positive Wetter conditions/higher temperatures than average induce a positive NDVI response, i.e. an increase in biomass or vegetation greenness. Dryer conditions/lower temperatures than average induce a negative NDVI response, i.e. lower biomass or vegetation greenness.

Negative Wetter/higher temperatures conditions than average induce a negative NDVI response, i.e. a decrease in biomass or vegetation greenness. Dryer conditions/lower temperatures than average induce a positive NDVI response, i.e. higher biomass or vegetation greenness

In order to obtain a parsimonious fitted model with significant coefficients, the ARx model was fitted for all combinations of model terms, and the model with the lowest Schwarz information criterion (Schwarz, 1978) was selected as optimal. This optimal model was screened based on the root mean squared error (RMSE) of the residuals and only pixels with RMSE < 0.9 were considered to show a good fit and were retained.

Finally, to achieve a better understanding of the vegetation characteristics that mediate vegetation resistance and resilience in drought-sensitive areas, each of the ARx coefficients was related to the fractions of bare soil, non-tree vegetation and tree cover.

Results

Global resilience and resistance

The ARx model could be fitted in 77.5% of terrestrial pixels; it did not converge for the remaining 22.5%. Half of the fitted pixels showed a fit with RMSE lower than 0.9, and 62.8% of the pixels with poor fit were located in arid, semi-arid or temperate regions with trees and bare soil each covering less than 50% of the pixels. Regions of poor fit were largely located in the upper northern latitudes and in coastal, desert or tropical regions (Fig. 1a). Consequently, our model did not provide information regarding the stability of these regions, mostly consisting of either dense forests or sites with extremely sparse vegetation.

**Figure 1**
Open in figure viewer PowerPoint

Global overview of vegetation cover fractions and vegetation stability, i.e. the percentage of tree, non-tree vegetation and bare cover (a), vegetation resilience (b), vegetation resistance against drought (c) and vegetation resistance against temperature anomalies (d) and the RMSE of the model (e). For panels (b)–(e), only pixels with a RMSE < 0.9 are represented.

The vegetation resilience metric (Fig. 1b), was positive for 99.9% of the pixels fitted by the model and explained the largest part of the variation. Low resilience (large values of α) was found in semi-arid areas, and more specifically in west-central USA, Argentina, southern Europe, the Sahel, southern Africa, Australia and semi-arid Asia. These regions had a relatively good fit (RMSE ≈ 0.65) (Fig. 1e). The vegetation drought-resistance metric (Fig. 1c) was mostly positive (91.9% of the pixels), whereas the vegetation temperature-resistance metric (Fig. 1d), was positive in some regions and negative in others. The resistance metrics had contrasting spatial patterns: the temperature-resistance metric (Fig. 1d) had positive values in northern USA, western and eastern Europe, and negative values were present in southern Africa, the Sahel, northern Australia and eastern Brazil. In contrast, most semi-arid regions showed large positive values for the drought-resistance metric, especially Australia (Fig. 1c). The vegetation drought-resistance pattern was similar to the resilience pattern, but with subtle differences. For example, high values of the drought-resistance metric were found in northern Argentina although the metric was not significant in southern Argentina. The vegetation resilience metric showed the reverse pattern, with large positive values in southern Argentina and small positive values in north Argentina. Similarly, central and western Australia showed the highest values for the vegetation resilience metric, and eastern Australia had the highest values for the drought-resistance metric.

Relationship between resistance, resilience and land cover

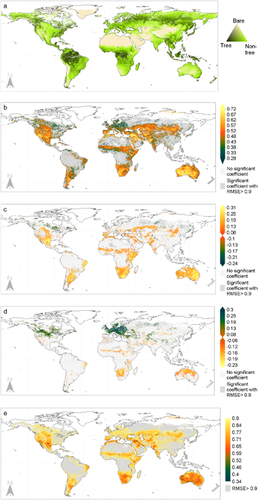
Analysis of the vegetation temperature-resistance, drought-resistance and resilience metrics as a function of vegetation cover fractions (Fig. 2) demonstrated the importance of tree cover, non-tree vegetation and bare soil cover on vegetation stability. In order to allow comparisons with earlier studies on savanna systems, only pixels with vegetation sensitive to drought (positive drought-resistance metric) were selected. In addition, for the analysis of resistance versus temperature anomalies, only negative values of ϕ were selected. Drought-sensitive vegetation with a low non-tree vegetation cover or a high fraction of bare soil showed the least resilience (values higher than 0.5) and the strongest vegetation memory effects. The area of low vegetation resilience is indicated by point P₁ in Fig. 2(a), having a resilience value greater than 0.6 and tree cover, non-tree vegetation and bare soil fraction of 15%, 57% and 28%, respectively. In contrast, vegetation types with high levels of tree cover (40–50%) and low bare-soil fractions (0–5%) showed the highest resilience (low values of α). For example, point P₂ in Fig. 2(a) (tree cover 42%, non-tree vegetation 56%, bare soil 2%) shows a resilience value below 0.5.

**Figure 2**
Open in figure viewer PowerPoint

The mean vegetation resilience (a), mean vegetation resistance against drought (b), mean vegetation resistance against temperature anomalies for pixels with a negative metric (c) as a function of the fractions of tree cover, non-tree vegetation and bare cover for pixels with a significant positive SPEI metric and an RMSE < 0.9. Points P₁ to P₅ indicate vegetation with a tree cover of 15%, 42%, 14%, 10% and 1%; a non-tree vegetation cover of 57%, 56%, 83%, 80% and 86%; and a bare soil cover of 28%, 2%, 3%, 10% and 13% respectively. Lines T₁ and T₂ in (a) illustrate the transect for a bare cover of 1% and 5% respectively.

Two cross-sections (T₁ and T₂ in Fig. 2a) reveal the change in resilience as a function of tree cover and non-tree vegetation cover. For very low bare-soil fractions (< 5%) (cross-section T₁: 1% bare cover), resilience decreases as the fraction of non-tree vegetation increases. For higher bare-soil fractions (e.g. cross-section T₂, at 5% bare cover), this decrease was no longer present; instead, resilience shows an optimum around a non-tree vegetation fraction of 85% (point P₃ in Fig. 2a). Finally, for bare-soil fractions above 20%, the resilience optimum was no longer present and the resilience showed a positive linear relationship with the non-tree vegetation cover fraction. This implies that for very low bare-soil fractions, the highest resilience and the lowest vegetation memory effects are observed when there are more trees, whereas for high bare-soil fractions the opposite is true: the highest resilience is observed where trees are less abundant.

The vegetation temperature-resistance (Fig. 2c) and drought-resistance (Fig. 2b) metrics showed contrasting patterns when analysed as a function of cover fractions. For example, the lowest drought-resistance (high values of β) was found for ecosystems with a tree cover of approximately 10% (e.g. point P₄ in Fig. 2b). In contrast, ecosystems with no tree cover and 80–90% non-tree cover showed the highest sensitivity to temperature anomalies (e.g. point P₅ in Fig. 2c).

Although the two resistance metrics showed clear patterns in terms of the cover fractions, the mean value of the resistance metric (signal) is relatively low compared to its standard deviation (noise; Appendix S2). The signal-to-noise ratio (SNR) of the resilience metrics varied mostly between 6 and 8, whereas for the relationships between resistance and anomalies in drought and temperature, the SNR varied mostly between 2 and 4 and between 4 and 6, respectively. The low SNR or relatively high variability of the resistance metrics limits comparisons between vegetation cover fractions. Factors other than tree cover, bare soil and non-tree vegetation may play an important role in the distribution of these stability metrics.

Discussion

Model

We have presented a simple ARx model for extracting global metrics for vegetation resilience and resistance against drought and temperature anomalies based on NDVI and climate time-series. This model assesses vegetation response to short-term climate anomalies, and not the effect of vegetation state on short-term climate anomalies. The proposed ARx model therefore describes only one part of the whole feedback system.

The ARx model differs from previous approaches in five important ways.

Vegetation stability is estimated based on the vegetation response to short-term climate anomalies. The explicit inclusion of climate data allows us to standardize the response for the timing and magnitude of the impact, thus enhancing the comparability of the metrics over large spatial scales.
Short-term climate anomalies – any deviation from average climate conditions – are taken into account. This implies that the response characteristics are based on the complete range of vegetation response, and not only on climate extremes. The ARx method therefore gives an indication of the immediate response if the climate turns drier, wetter, colder or hotter, unlike methods that focus on climate extremes (e.g. Liu et al., 2013a).
The ARx model estimates the short-term response of vegetation, which contrasts with the more common trend-analysis studies, such as trends in GPP from 1982 to 1999 (Nemani et al., 2003) or trends in vegetation optical depth from 1988 to 2008 (Liu et al., 2013b). In these long-term studies, changes in vegetation cycle and/or responses to climate change or management were assessed. Furthermore, our method allows for the quantification of short-term vegetation resilience (engineering resilience) on a global scale.
Anomalies in vegetation response might either result from previous short-term climate anomalies (memory effect) or from the instantaneous effect of a climate anomaly. The simultaneous estimation of vegetation resistance and resilience allows us to take into account the memory effect of vegetation when estimating vegetation resistance. This approach differs from simple cross-correlations between vegetation and climate time-series (e.g. Zeng et al., 2013), which can be interpreted as simplified versions of the ARx model estimating the (lagged) response of vegetation but without including the memory effect.
One of the primary advantages of the ARx model approach is that it provides an opportunity to assess the quality of the model's fit and the significance of the model's coefficients simultaneously. If desired, insignificant coefficients or pixels with poor fit can be excluded. The exclusion of low-quality data is crucial in remote-sensing studies on vegetation stability, because such data may contribute to spurious and contradictory results (Samanta et al., 2010; De Keersmaecker et al., 2014a). This is especially important when using anomaly data, which have a lower signal-to-noise ratio (SNR) and higher uncertainty than the original data. Most of the pixels excluded in this study were found at northern latitudes in densely forested or bare areas. This might be explained by (i) a high probability of noise in these areas (e.g. presence of clouds, snow or high levels of aerosols) or (ii) small anomalies, causing a low SNR (Hird & McDermid, 2009; De Keersmaecker et al., 2014a,b). The latter might occur in high-biomass systems (e.g. forests), as the relationship between NDVI and vegetation properties such as LAI tends to saturate (Delalieux et al., 2008). It should therefore be stressed that the influence of noise can be severe and is spatially dependent (De Keersmaecker et al., 2014a).

Global vegetation resilience

The ARx model estimates the short-term or engineering resilience of ecosystems on a global scale using the relationship of NDVI anomalies with past anomalies. This approach contrasts with earlier studies that derived resilience from the persistence of trends, based on the method of Simoniello et al. (2008). For example, Harris et al. (2014) note that the resilience derived from persistence depends on the sequence of wet and dry years. Consequently, it is unknown whether the observed spatial variation of the persistence metric is due to the sequence of climate variation or due to ecosystem properties. This stresses the importance of explicitly taking climate variability into account.

The ARx approach to deriving engineering resilience also differs from earlier studies that focused on ecological resilience (e.g. Hirota et al., 2011). Engineering resilience gives an estimate of the recovery time if equilibrium is assumed, whereas ecological resilience quantifies the probability of an ecosystem switching to another state. These two resilience metrics inherently differ by definition, but our results also show that they are closely related. For example, the areas with low engineering resilience and strong memory effects are generally situated in semi-arid areas. In Australia, Africa and South America, these regions coincide with locations with a high probability of converting from a ‘savanna state’ to a treeless state or of remaining in a treeless state (Hirota et al., 2011). This suggests that low engineering resilience leads to low ecological resilience where the ARx provided reliable fits: ecosystems that struggle to recover from disturbances in the short-term also have a higher chance of switching to another state.

Finally, the results of the ARx model suggest that engineering resilience is related to the fractions of tree cover, non-tree vegetation and bare soil. To take one example, for a bare soil cover of 5%, the optimal resilience occurs at 80–90% non-tree vegetation and 5–15% trees. Lower or higher tree-cover fractions lead to a more unstable state. This agrees with the results of Scanlon et al. (2005) and Walter & Mueller-Dombois (1971), who studied the water efficiency in water-limited savanna ecosystems across a transect in Botswana. They found that dynamic grass cover stabilizes the precipitation that reaches the tree roots in the wet season: more precipitation than average will result in a higher grass cover, which in turn diminishes the water percolation to the tree roots. This might be reflected in the ARx resilience with an optimum for a tree-cover fraction between 10% and 20%. This relationship, however, does not hold for very low or high fractions of bare soil. Where there is a lot of bare soil, the range of fractions of tree cover and non-tree vegetation cover with significant coefficients becomes very small, although the total vegetative fraction might be too low to benefit from any hydrological optimization. Where there is very little bare soil, the drought stress might not be severe enough for the vegetation to benefit from the optimization. Furthermore, other disturbances such as wildfires or herbivory may also affect the vegetation composition, thus confounding this relationship (Spessa et al., 2005; Bond, 2008).

Global vegetation resistance

To a certain extent, the extracted vegetation resistance metrics correspond to published ecosystem sensitivity metrics. For example, comparing the output of the ARx model with the drought- or heat-induced tree mortalities of Allen et al. (2010) shows that the reported tree mortality in southern Africa, the eastern Sahel, northern Morocco, eastern Australia, Mediterranean Europe and east-central USA coincides with regions of low drought- or temperature-resistance extracted from the ARx model. The ARx model does not, however, detect tree mortality in eastern and north-western USA, the Amazon forest, Scandinavia, Indonesia or the Philippines, because it provides insufficient fit for forests or dense tree vegetation. Furthermore, the resistance patterns closely resemble the spatial patterns of correlation between NDVI anomalies and SPEI drought index (Vicente-Serrano et al., 2013), the vegetation growth simulations using the dynamic global vegetation model (Notaro, 2008) and the predicted suitability for crop production using a Global Crop Model for four different global climate change models (Ramankutty et al., 2002). Ramankutty et al. (2002) also found positive effects of a temperature increase on crop production in northern latitudes and negative effects of precipitation decrease or temperature increase in semi-arid regions. Moreover, several regional and continental studies support the high sensitivity of areas in North America (Zhang et al., 2010), Europe (Reichstein et al., 2007), Africa (Propastin et al., 2010), Asia (Mohammat et al., 2013; Poulter et al., 2013) and Australia (McAlpine et al., 2009). As such, local as well as other global studies confirm the sensitivity of the low-resistance areas.

Comparing the outputs of the ARx model with the vegetation and climate extremes of Liu et al. (2013a) illustrates that areas with low resistance to drought and temperature anomalies correspond to areas with frequent vegetation–climate extremes (e.g. central USA, southern Europe, the Sahel, northern Patagonia and eastern Australia). The spatial patterns of the vegetation–climate extremes and ARx resistance metrics also show some discrepancies, however: Liu et al. (2013a) found few vegetation extremes in southern South Africa, large parts of Australia, the Horn of Africa and eastern Brazil, whereas these areas show low resistance in the ARx model. Moreover, Liu et al. (2013a) demonstrated frequent vegetation extremes in the Amazon forest and eastern USA, both of which have significant resistance or low-quality fit in the ARx model. The discrepancy between these studies might originate from (1) a low frequency of climate extremes, (2) low-quality time-series or (3) other causes of extreme vegetation responses, such as management or pests. Although vegetation may be sensitive to short-term climate anomalies, it may not show an extreme NDVI anomaly in cases where no climate extremes occur. Regions with low resistance may thus show few NDVI extremes.

Furthermore, low-quality time-series may show NDVI extremes (negative spikes) that are related not to climate extremes, but to cloud cover, aerosol concentration or snow. These types of noise result in a high RMSE values of the ARx model and the stability metrics of these pixels are not represented. As such, some regions may show no ARx metrics, although many NDVI extremes occur. NDVI extremes may also occur due to management or pests (e.g. an early harvest might cause an NDVI anomaly) and are thus not related to short-term climate anomalies. They will not, therefore, directly affect the resistance metrics, resulting in the common occurrence of a high frequency of NDVI extremes and a high resistance to short-term climate anomalies.

These three explanations for the low-quality ARx fit to the results of Liu et al. (2013a) highlight the importance of properly identifying the factors that drive ecosystem anomalies and of understanding the data quality when using the ARx model, because only then can a correct interpretation of ecosystem stability be reached.

Vegetation stability and management

Large-scale stability metrics can support management in two ways. First, they allow a holistic comparison of management regimes over similar vegetation types. Second, the mapping of vegetation stability allows highly vulnerable regions to be identified. These may become a focus for further research or their management may be revised. For example, engineering resilience has been related to ecological resilience and the fractions of bare soil, tree cover and non-tree vegetation, offering a real-time management opportunity. It must be noted, however, that additional factors, such as the occurrence of wildfires, may have to be taken into account to provide more accurate management guidelines. Furthermore, as noise may have an impact on the availability of stability metrics, resulting in a lack of data over forests, for example, the addition of field assessments is recommended, if not a necessity. Such small-scale studies further provide a relatively tight control on environmental conditions and the composition of the vegetation, giving a detailed insight into the factors that regulate stability (such as fertilization, grazing and diversity; Tilman, 1996). This insight can lead to more detailed guidelines on how to adapt the system given the management goals (Mitchell et al., 2000).

To conclude, we have presented a model that quantifies vegetation resistance and resilience metrics while explicitly taking short-term climate anomalies into account. We demonstrate that this method contributes to vegetation management through the identification of vulnerable regions with respect to short-term climate anomalies and that it provides better insight of the factors that drive vegetation response.

Acknowledgements

This research was made possible through the support of KU Leuven, VLIR-UOS (‘Flemish Interuniversity Council – University Development Cooperation’; www.vliruos.be), DGD (the Directorate General for Development Cooperation; www.dgos.be) through the KLIMOS consortium; www.kuleuven.be/klimos and the FWO-project G.0320.12. S. Lhermitte was supported as postdoctoral researcher for Fonds Wetenschappelijk Onderzoek – Vlaanderen.

Supporting Information

References

Allen, C.D., Macalady, A.K., Chenchouni, H., Bachelet, D., McDowell, N., Vennetier, M., Kitzberger, T., Rigling, A., Breshears, D.D., Hogg, E.H., Gonzalez, P., Fensham, R., Zhang, Z., Castro, J., Demidova, N., Lim, J.-H., Allard, G., Running, S.W., Semerci, A. & Cobb, N. (2010) A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. Forest Ecology and Management, 259, 660–684.
10.1016/j.foreco.2009.09.001
Web of Science® Google Scholar
Bond, W.J. (2008) What limits trees in C₄ grasslands and savannas? Annual Review of Ecology, Evolution, and Systematics, 39, 641–659.
10.1146/annurev.ecolsys.39.110707.173411
Web of Science® Google Scholar
Dakos, V., Carpenter, S.R., Brock, W.A., Ellison, A.M., Guttal, V., Ives, A.R., Kéfi, S., Livina, V., Seekell, D.A., van Nes, E.H. & Scheffer, M. (2012) Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE, 7, e41010.
10.1371/journal.pone.0041010
CAS PubMed Web of Science® Google Scholar
De Keersmaecker, W., Lhermitte, S., Honnay, O., Farifteh, J., Somers, B. & Coppin, P. (2014a) How to measure ecosystem stability? An evaluation of the reliability of stability metrics based on remote sensing time series across the major global ecosystems. Global Change Biology, 20, 2149–2161.
10.1111/gcb.12495
PubMed Web of Science® Google Scholar
De Keersmaecker, W., Lhermitte, S., Tits, L., Honnay, O., Somers, B. & Coppin, P. (2014b) Resilience and the reliability of spectral entropy to assess ecosystem stability. Global Change Biology, doi:10.1111/gcb.12799.
10.1111/gcb.12799
Google Scholar
Delalieux, S., Somers, B., Hereijgers, S., Verstraeten, W.W., Keulemans, W. & Coppin, P. (2008) A near-infrared narrow-waveband ratio to determine Leaf Area Index in orchards. Remote Sensing of Environment, 112, 3762–3772.
10.1016/j.rse.2008.05.003
Web of Science® Google Scholar
C.B. Field, V. Barros, T.F. Stocker, Q. Dahe, D.J. Dokken, K.L. Ebi, M.D. Mastrandrea, K.J. Mach, G.-K. Plattner, S.K. Allen, M. Tignor & P.M. Midgley (eds) (2012) Managing the risks of extreme events and disasters to advance climate change adaptation. Special report of Working Groups I and II of the Intergovernmental Panel on Climate Change. Cambridge University Press, New York.
Google Scholar
Hansen, J., Ruedy, R., Glascoe, J. & Sato, M. (1999) GISS analysis of surface temperature change. Journal of Geophysical Research: Atmospheres, 104, 30997–31022.
10.1029/1999JD900835
Web of Science® Google Scholar
Hansen, M.C., DeFries, R.S., Townshend, J.R.G., Carroll, M., Dimiceli, C. & Sohlberg, R.A. (2003) Global percent tree cover at a spatial resolution of 500 meters: first results of the MODIS vegetation continuous fields algorithm. Earth Interactions, 7, 1–15.
10.1175/1087-3562(2003)007<0001:GPTCAA>2.0.CO;2
Web of Science® Google Scholar
Harris, A., Carr, A.S. & Dash, J. (2014) Remote sensing of vegetation cover dynamics and resilience across southern Africa. International Journal of Applied Earth Observation and Geoinformation, 28, 131–139.
10.1016/j.jag.2013.11.014
Web of Science® Google Scholar
Hird, J.N. & McDermid, G.J. (2009) Noise reduction of NDVI time series: an empirical comparison of selected techniques. Remote Sensing of Environment, 113, 248–258.
10.1016/j.rse.2008.09.003
Web of Science® Google Scholar
Hirota, M., Holmgren, M., van Nes, E.H. & Scheffer, M. (2011) Global resilience of tropical forest and savanna to critical transition. Science, 334, 232–235.
10.1126/science.1210657
CAS PubMed Web of Science® Google Scholar
Holben, B.N. (1986) Characteristics of maximum-value composite images from temporal AVHRR data. International Journal of Remote Sensing, 7, 1417–1434.
10.1080/01431168608948945
Web of Science® Google Scholar
Holling, C.S. (1996) Engineering resilience versus ecological resilience. Foundations of ecological resilience (ed. by L.H. Gunderson, C.R. Allen and C.S. Holling), pp. 51–66. Island Press, Washington, DC.
Google Scholar
Justice, C.O., Townshend, J.R.G., Vermote, E.F., Masuoka, E., Wolfe, R.E., Saleous, N., Roy, D.P. & Morisette, J.T. (2002) An overview of MODIS Land data processing and product status. Remote Sensing of Environment, 83, 3–15.
10.1016/S0034-4257(02)00084-6
Web of Science® Google Scholar
Lhermitte, S., Verbesselt, J., Verstraeten, W.W. & Coppin, P. (2010) A pixel based regeneration index using time series similarity and spatial context. Photogrammetric Engineering and Remote Sensing, 76, 673–682.
10.14358/PERS.76.6.673
Web of Science® Google Scholar
Lhermitte, S., Verbesselt, J., Verstraeten, W.W., Veraverbeke, S. & Coppin, P. (2011a) Assessing intra-annual vegetation regrowth after fire using the pixel based regeneration index. ISPRS Journal of Photogrammetry and Remote Sensing, 66, 17–27.
10.1016/j.isprsjprs.2010.08.004
Web of Science® Google Scholar
Lhermitte, S., Verbesselt, J., Verstraeten, W.W. & Coppin, P. (2011b) A comparison of time series similarity measures for classification and change detection of ecosystem dynamics. Remote Sensing of Environment, 115, 3129–3152.
10.1016/j.rse.2011.06.020
Web of Science® Google Scholar
Liu, G., Liu, H.-Y. & Yin, Y. (2013a) Global patterns of NDVI-indicated vegetation extremes and their sensitivity to climate extremes. Environmental Research Letters, 8, 025009.
10.1088/1748-9326/8/2/025009
Web of Science® Google Scholar
Liu, Y.-Y., van Dijk, A.I.J.M., McCabe, M.F., Evans, J.P. & de Jeu, R.A.M. (2013b) Global vegetation biomass change (1988–2008) and attribution to environmental and human drivers. Global Ecology and Biogeography, 22, 692–705.
10.1111/geb.12024
Web of Science® Google Scholar
Lloret, F., Lobo, A., Estevan, H., Maisongrande, P., Vayreda, J. & Terradas, J. (2007) Woody plant richness and NDVI response to drought events in Catalonian (northeastern Spain) forests. Ecology, 88, 2270–2279.
10.1890/06-1195.1
CAS PubMed Web of Science® Google Scholar
McAlpine, C.A., Syktus, J., Ryan, J.G., Deo, R.C., McKeon, G.M., McGowan, H.A. & Phinn, S.R. (2009) A continent under stress: interactions, feedbacks and risks associated with impact of modified land cover on Australia's climate. Global Change Biology, 15, 2206–2223.
10.1111/j.1365-2486.2009.01939.x
Web of Science® Google Scholar
McDowell, N., Pockman, W.T., Allen, C.D., Breshears, D.D., Cobb, N., Kolb, T., Plaut, J., Sperry, J., West, A., Williams, D.G. & Yepez, E.A. (2008) Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytologist, 178, 719–739.
10.1111/j.1469-8137.2008.02436.x
CAS PubMed Web of Science® Google Scholar
Mitchell, R.J., Auld, M.H.D., Le Duc, M.G. & Robert, M.H. (2000) Ecosystem stability and resilience: a review of their relevance for the conservation management of lowland heaths. Perspectives in Plant Ecology, Evolution and Systematics, 3, 142–160.
10.1078/1433-8319-00009
Google Scholar
Mohammat, A., Wang, X.-H., Xu, X.-T., Peng, L.-Q., Yang, Y., Zhang, X.-P., Myneni, R.B. & Piao, S.-L. (2013) Drought and spring cooling induced recent decrease in vegetation growth in Inner Asia. Agricultural and Forest Meteorology, 178–179, 21–30.
10.1016/j.agrformet.2012.09.014
Web of Science® Google Scholar
Myneni, R.B., Hoffman, S., Knyazikhin, Y., Privette, J.L., Glassy, J., Tian, Y., Wang, Y., Song, X., Zhang, Y., Smith, G., Lotsch, A., Friedl, M., Morisette, J.T., Votava, P., Nemani, R.R. & Running, S.W. (2002) Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sensing of Environment, 83, 214–231.
10.1016/S0034-4257(02)00074-3
CAS Web of Science® Google Scholar
Nemani, R.R., Keeling, C.D., Hashimoto, H., Jolly, W.M., Piper, S.C., Tucker, C.J., Myneni, R.B. & Running, S.W. (2003) Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science, 300, 1560–1563.
10.1126/science.1082750
CAS PubMed Web of Science® Google Scholar
New, M., Hulme, M. & Jones, P. (2000) Representing twentieth-century space–time climate variability. Part II: development of 1901–96 monthly grids of terrestrial surface climate. Journal of Climate, 13, 2217–2238.
10.1175/1520-0442(2000)013<2217:RTCSTC>2.0.CO;2
Web of Science® Google Scholar
Notaro, M. (2008) Response of the mean global vegetation distribution to interannual climate variability. Climate Dynamics, 30, 845–854.
10.1007/s00382-007-0329-7
Web of Science® Google Scholar
Poulter, B., Pederson, N., Liu, H.-Y., Zhu, Z.-C., D'Arrigo, R., Ciais, P., Davi, N., Frank, D., Leland, C., Myneni, R., Piao, S.-L. & Wang, T. (2013) Recent trends in Inner Asian forest dynamics to temperature and precipitation indicate high sensitivity to climate change. Agricultural and Forest Meteorology, 178, 31–45.
10.1016/j.agrformet.2012.12.006
Web of Science® Google Scholar
Propastin, P., Fotso, L. & Kappas, M. (2010) Assessment of vegetation vulnerability to ENSO warm events over Africa. International Journal of Applied Earth Observation and Geoinformation, 12, S83–S89.
10.1016/j.jag.2009.10.007
Web of Science® Google Scholar
Ramankutty, N., Foley, J.A., Norman, J. & McSweeney, K. (2002) The global distribution of cultivable lands: current patterns and sensitivity to possible climate change. Global Ecology and Biogeography, 11, 377–392.
10.1046/j.1466-822x.2002.00294.x
Web of Science® Google Scholar
Reichstein, M., Ciais, P., Papale, D. et al. (2007) Reduction of ecosystem productivity and respiration during the European summer 2003 climate anomaly: a joint flux tower, remote sensing and modelling analysis. Global Change Biology, 13, 634–651.
10.1111/j.1365-2486.2006.01224.x
Web of Science® Google Scholar
Samanta, A., Ganguly, S., Hashimoto, H., Devadiga, S., Vermote, E., Knyazikhin, Y., Nemani, R.R. & Myneni, R.B. (2010) Amazon forests did not green-up during the 2005 drought. Geophysical Research Letters, 37, L05401.
10.1029/2009GL042154
Web of Science® Google Scholar
Scanlon, T.M., Caylor, K.K., Manfreda, S., Levin, S.A. & Rodriguez-Iturbe, I. (2005) Dynamic response of grass cover to rainfall variability: implications for the function and persistence of savanna ecosystems. Advances in Water Resources, 28, 291–302.
10.1016/j.advwatres.2004.10.014
Web of Science® Google Scholar
Schwarz, G. (1978) Estimating the dimension of a model. Annals of Statistics, 6, 461–464.
10.1214/aos/1176344136
PubMed Web of Science® Google Scholar
Simoniello, T., Lanfredi, M., Liberti, M., Coppola, R. & Macchiato, M. (2008) Estimation of vegetation cover resilience from satellite time series. Hydrology and Earth System Sciences, 12, 1053–1064.
10.5194/hess-12-1053-2008
Web of Science® Google Scholar
Spessa, A., McBeth, B. & Prentice, C. (2005) Relationships among fire frequency, rainfall and vegetation patterns in the wet–dry tropics of northern Australia: an analysis based on NOAA-AVHRR data. Global Ecology and Biogeography, 14, 439–454.
10.1111/j.1466-822x.2005.00174.x
Web of Science® Google Scholar
Telesca, L., Lasaponara, R. & Lanorte, A. (2008) Intra-annual dynamical persistent mechanisms in mediterranean ecosystems revealed SPOT-VEGETATION time series. Ecological Complexity, 5, 151–156.
10.1016/j.ecocom.2007.10.001
Web of Science® Google Scholar
Tilman, D. (1996) Biodiversity: population versus ecosystem stability. Ecology, 77, 350–363.
10.2307/2265614
Web of Science® Google Scholar
Tucker, C.J., Pinzon, J.E., Brown, M.E., Slayback, D.A., Pak, E.W., Mahoney, R., Vermote, E.F. & El Saleous, N. (2005) An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. International Journal of Remote Sensing, 26, 4485–4498.
10.1080/01431160500168686
Web of Science® Google Scholar
Vicente-Serrano, S.M., Beguería, S. & López-Moreno, J.I. (2010) A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. Journal of Climate, 23, 1696–1718.
10.1175/2009JCLI2909.1
Web of Science® Google Scholar
Vicente-Serrano, S.M., Gouveia, C., Camarero, J.J., Beguería, S., Trigo, R., López-Moreno, J.I., Azorín-Molina, C., Pasho, E., Lorenzo-Lacruz, J., Revuelto, J., Morán-Tejeda, E. & Sanchez-Lorenzo, A. (2013) Response of vegetation to drought time-scales across global land biomes. Proceedings of the National Academy of Sciences USA, 110, 52–57.
10.1073/pnas.1207068110
CAS PubMed Web of Science® Google Scholar
Walker, B.H., Ludwig, D., Holling, C.S. & Peterman, R.M. (1981) Stability of semi-arid savanna grazing systems. Journal of Ecology, 69, 473–498.
10.2307/2259679
Web of Science® Google Scholar
Walter, H. & Mueller-Dombois, D. (1971) Ecology of tropical and subtropical vegetation. Oliver & Boyd, Edinburgh, UK.
Google Scholar
Zeng, F.-W., Collatz, G.J., Pinzon, J.E. & Ivanoff, A. (2013) Evaluating and quantifying the climate-driven interannual variability in Global Inventory Modeling and Mapping Studies (GIMMS) normalized difference vegetation index (NDVI3g) at global scales. Remote Sensing, 5, 3918–3950.
10.3390/rs5083918
Web of Science® Google Scholar
Zhang, X.-Y., Goldberg, M., Tarpley, D., Friedl, M.A., Morisette, J., Kogan, F. & Yu, Y.-Y. (2010) Drought-induced vegetation stress in southwestern North America. Environmental Research Letters, 5, 024008.
10.1088/1748-9326/5/2/024008
Web of Science® Google Scholar

Involved authors are researchers within an informal KU Leuven consortium that aims to develop new methods to extract information from ecosystems that may contribute to a better understanding and a sustainable management of ecosystems.

Citing Literature

Volume24, Issue5

May 2015

Pages 539-548

Filename	Description
geb12279-sup-0001-si.pdf297.5 KB	Appendix S1. Trends.
geb12279-sup-0002-si.pdf211.2 KB	Appendix S2. Signal to Noise Ratio (SNR).

A model quantifying global vegetation resistance and resilience to short-term climate anomalies and their relationship with vegetation cover

Abstract