
Distance, dams and drift: what structures populations of an endangered, benthic stream fish?
Summary
- Spatial population structure plays an important role in species persistence, evolution and conservation. Benthic stream fishes are diverse and frequently imperilled, yet the determinants and spatial scaling of their population structure are understudied.
- We investigated the range-wide population genetic structure of Roanoke logperch (Percina rex), an endangered, benthic stream fish of the eastern United States. Fish were sampled from 35 sites and analysed at 11 microsatellite DNA loci. Clustering models were used to sort individuals into genetically cohesive groups and thereby estimate the spatial scaling of population structure. We then used Bayesian generalized linear mixed models (BGLMMs) to test alternative hypotheses about the environmental factors most responsible for generating structure, as measured by the differentiation statistic FST.
- Clustering models delineated seven discrete populations, whose boundaries coincided with agents of fragmentation, including hydroelectric dams and tailwaters. In the absence of hydrological barriers, gene flow was extensive throughout catchments, whereas there was no evidence for contemporary dispersal between catchments across barriers.
- In the best-supported BGLMM, FST was positively related to the spatial distance and degree of hydrological alteration between sites and negatively related to genetic diversity within sites. Whereas the effect of tailwaters was equivocal, dams strongly influenced differentiation: the effect of a dam on FST was comparable to that of a between-site distance of over 1200 km of unimpounded river. Overall, the effect of distance-mediated dispersal was negligible compared to the combined effects of fragmentation and genetic drift.
- The contemporary population structure of P. rex comprises a few geographically extensive ‘islands’ that are fragmented by hydroelectric projects. This information clarifies the importance of a catchment-scale perspective on conserving the species and suggests that its recovery may require genetic and/or demographic reconnection of presently isolated populations.
Introduction
Accurate knowledge of spatial population structure is fundamental to understanding the demography and evolution of species (Waples & Gaggiotti, 2006). There is a particular need to understand the spatial scales over which populations are connected through dispersal and gene flow, the landscape features that regulate connectivity, and the resulting juxtaposition of population boundaries. Such knowledge informs management tasks such as the delineation of conservation units, assessment of population and metapopulation viability, and strategic enhancement of landscape connectivity (Palsbøll, Bérube & Allendorf, 2007).
This information is sorely needed for many stream-dwelling fish species. Stream fishes are disproportionately imperilled worldwide, due largely to loss and fragmentation of habitats, which reduces population viability (Ricciardi & Rasmussen, 1999; Kottelat & Freyhof, 2007). Relative to other taxa, understanding the spatial population structure and connectivity of stream fishes is complicated, for at least three reasons. First, rates and spatial extents of fish dispersal are notoriously difficult to estimate empirically (Fausch et al., 2002). Second, because catchments are extensive landscapes that may comprise hundreds of kilometres of continuous habitat, the locations of population boundaries may not be obvious to the human eye. Third, the vast majority of previous stream-fish studies have focused on salmon and trout (Salmonidae), many of which are large-bodied, pelagic and migratory (i.e. anadromous or potamodromous; Northcote, 1978), and therefore may prove poor models for understanding other life-history types. Additional research on the population structure of non-salmonid taxa, in particular small-bodied, benthic, non-migratory species, is needed to advance our understanding of stream fish ecology, conservation and evolution overall.
Various characteristics of stream fishes and stream habitat are likely to inhibit individual movement, thereby limiting the spatial extent of dispersal and gene flow among populations. Stream fishes have a finite capacity for movement and must move within confined pathways that vary in permeability (Fausch et al., 2002; Campbell Grant, Lowe & Fagan, 2007). As a result, stream fishes tend to move short distances more frequently than long distances (Rodriguez, 2002). Such distance-attenuated movement might give rise to population structure consistent with a one-dimensional isolation-by-distance (IBD) evolutionary model (Wright, 1943; Rousset, 1997), in which genetic differentiation (a common measure of structure) is a linear function of the spatial distance along stream channels separating individuals (e.g. Primmer et al., 2006; Lamphere & Blum, 2012). Under these conditions, population boundaries may be indistinct, with differentiation accruing continuously through space at a rate inversely related to a taxon's mobility (e.g. Slatkin & Maddison, 1990; Peterson & Denno, 1998).
In contrast, connectivity may change abruptly in streams, producing nonlinear IBD and discrete population boundaries. Dispersal pathways in streams are easily and frequently severed by natural and anthropogenic barriers to fish movement (Morita & Yamamoto, 2002). Natural barriers include temporary features such as beaver dams (Schlosser, 1995) and intermittent stream connections (Labbe & Fausch, 2000; Boizard, Magnan & Angers, 2009), as well as permanent features such as large waterfalls (Meeuwig et al., 2010; Whiteley et al., 2010). Anthropogenic barriers include ephemeral and/or semipermeable features such as poor ‘matrix’ habitat conditions (Gilliam & Fraser, 2001; Roberts & Angermeier, 2007) and seasonally passable road crossings (Warren & Pardew, 1998), as well as more permanent features like dams and weirs (Hänfling & Weetman, 2006; Raeymaekers et al., 2008; Beneteau, Mandrak & Heath, 2009; Horreo et al., 2011). Major hydroelectric dams are among the most obvious agents of river fragmentation, but actually introduce features that potentially vary in permeability to movement; whereas a dam may present a complete barrier to fishes, the associated lentic reservoir upstream and hydrologically variable tailwater downstream may contain unsuitable but partially permeable habitat for a lotic species (Mitchell, Johnson & Harp, 2002; Skalski et al., 2008).
Patterns of genetic structure are determined not only by rates of dispersal between populations, but also by rates of genetic drift within populations. Drift is accelerated in populations with a small effective size (Ne), as is characteristic of populations exhibiting low overall abundance, highly variable spawning success, extinction-colonization dynamics and/or isolation from other populations (Waples, 1990). The dynamic nature of stream environments is likely to reduce the size, stability, connectivity and Ne of fish populations (Campbell Grant et al., 2007), and such effects often are exacerbated by human modifications of hydrology and catchment characteristics (Allan, 2004). Although Ne is difficult to estimate in practice, relative variation in population size is indexed reasonably well by within-population genetic diversity (HE; Frankham, 1996), suggesting that such an index could be used to account for the influence of drift on population differentiation. Accounting for drift is necessary to accurately estimate the spatial extent of gene flow and assess its influence on genetic structure (Hutchison & Templeton, 1999; Guillot et al., 2009).
Most stream fishes probably experience a combination of spatially restricted dispersal (i.e. IBD), fragmentation and interpopulation variation in drift. Although the individual effects of these factors have been relatively well investigated, their combined effects have not. Most previous analyses of genetic differentiation have relied on simple linear regression (e.g. Koizumi, Yamamoto & Maekawa, 2006) or Mantel tests (e.g. Primmer et al., 2006), investigating at most two explanatory variables at a time. Unfortunately, Mantel tests provide no measures of effect size, while simple linear models provide misleading estimates of effect size because they do not account for the non-independence of multiple pairwise comparisons involving the same site. A promising alternative is the use of generalized linear mixed models, which do not restrict the number of explanatory variables, can account for non-independence of errors, allow the modelling of interaction terms, and facilitate model selection in an information-theoretical framework (Browne, Goldstein & Rabash, 2001). Using such models, Meeuwig et al. (2010) explored the relative effects of spatial distance and one-way and two-way barriers (i.e. natural waterfalls) on differentiation within a bull trout (Salvelinus confluentus) metapopulation. These authors found that two-way barriers had a greater effect than one-way barriers, and that barriers increased differentiation by the same amount as 70–200 km of stream distance, indicating the fundamental role of fragmentation in structuring this metapopulation. This approach may yield new insight into mechanisms of population structure in other stream fishes as well.
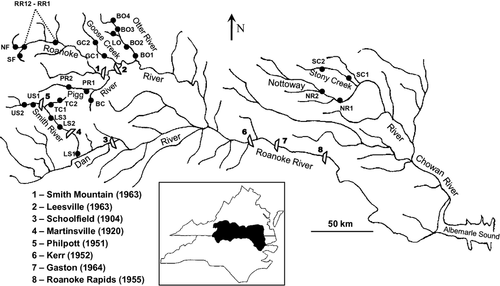
In this study, we investigated the spatial scaling and environmental determinants of population structure in Roanoke logperch Percina rex (Percidae:Etheostomatinae), an endangered, warmwater stream fish of eastern North America. P. rex is benthic, small-bodied (≤165 mm total length), and specializes on lotic habitats with little fine sediment (Rosenberger & Angermeier, 2003). Its dispersal and spatial population structure are poorly understood (Rosenberger, 2007; Roberts et al., 2008). These traits exemplify many members of the speciose darter subfamily, a disproportionately imperilled group of fishes (Jenkins & Burkhead, 1994). P. rex is endemic to the Roanoke, Dan and Nottoway river basins of Virginia and North Carolina, where it persists in several catchments (Rosenberger, 2007; Fig. 1). Occupied catchments are separated by long, unoccupied and potentially uninhabitable stream reaches, major hydroelectric projects, or both. These hydroelectric projects, completed between 1904 and 1964, have introduced various potential agents of fragmentation, including dams, reservoirs and tailwaters. Owing to the species' specialized habitat requirements, limited extant range and presumed decline, P. rex is listed as ‘Endangered’ under the United States Endangered Species Act (U.S. Federal Register 54:34468–34472) and ‘Vulnerable’ on the IUCN Red List (www.iucnredlist.org). Recovery goals focus on monitoring and increasing population sizes, ensuring evolutionary viability and restoring population connectivity (Rosenberger, 2007).
Our objectives were to: (i) estimate the spatial scales over which P. rex populations are structured, (ii) test alternative hypotheses about the environmental factors most responsible for generating structure, including IBD, fragmentation by hydroelectric projects and genetic drift, and (iii) discuss implications for the ecology and conservation of stream fishes.
Methods
Sample collection
Together with biologists from the Virginia Department of Game and Inland Fisheries and the North Carolina Wildlife Resources Commission, we made field collections of P. rex between 2003 and 2008 throughout the species' range. A small section of tissue was excised from the caudal fin of captured individuals, and fish were returned alive to the stream. DNA samples were collected from 578 fish across 35 sites (Table 1; Fig. 1). Each site was 100–300 m long; geographic coordinates were obtained at each. Some sites were sampled in multiple years to estimate temporal genetic variation. Sample sizes varied among sites and years due to variance in our ability to capture P. rex (Table 1).
| Location | Code | Latitude | Longitude | n | A | H E | H O |
|---|---|---|---|---|---|---|---|
| °N | °W | ||||||
| Roanoke basin | |||||||
| Roanoke | |||||||
| Roanoke River | RR1 | 37.26 | −79.91 | 13 | 8.2 | 0.840 | 0.817 |
| RR2 | 37.26 | −79.94 | 18 | 9.3 | 0.845 | 0.837 | |
| RR3 | 37.26 | −79.96 | 24 | 9.7 | 0.832 | 0.782 | |
| RR4 | 37.27 | −79.96 | 16 | 8.5 | 0.822 | 0.811 | |
| RR5 | 37.27 | −79.98 | 12 | 7.6 | 0.808 | 0.784 | |
| RR6 | 37.27 | −80.01 | 12 | 8.0 | 0.843 | 0.818 | |
| RR7 | 37.27 | −80.02 | 10 | 7.4 | 0.836 | 0.764 | |
| RR8 | 37.28 | −80.05 | 27 | 9.4 | 0.837 | 0.818 | |
| RR9 | 37.28 | −80.06 | 15 | 8.5 | 0.834 | 0.824 | |
| RR10 | 37.28 | −80.09 | 16 | 8.9 | 0.846 | 0.789 | |
| RR11 | 37.28 | −80.11 | 11 | 7.2 | 0.803 | 0.835 | |
| RR12 | 37.24 | −80.20 | 8 | 7.0 | 0.838 | 0.727 | |
| North Fork Roanoke River | NF | 37.21 | −80.29 | 9 | 9.0 | 0.851 | 0.818 |
| South Fork Roanoke River | SF | 37.16 | −80.25 | 19 | 7.3 | 0.834 | 0.831 |
| Pigg | |||||||
| Pigg River | PR1 | 36.94 | −79.77 | 70 | 6.0 | 0.653 | 0.642 |
| PR2 | 37.00 | −79.86 | 13 | 4.4 | 0.610 | 0.564 | |
| Big Chestnut Creek | BC | 36.91 | −79.80 | 9 | 4.0 | 0.655 | 0.616 |
| Goose | |||||||
| Goose Creek | GC1 | 37.17 | −79.52 | 6 | 3.1 | 0.532 | 0.448 |
| GC2 | 37.27 | −79.59 | 28 | 3.5 | 0.528 | 0.528 | |
| Otter | |||||||
| Big Otter River | BO1 | 37.21 | −79.30 | 14 | 3.0 | 0.533 | 0.513 |
| BO2 | 37.25 | −79.35 | 36 | 3.7 | 0.568 | 0.598 | |
| BO3 | 37.31 | −79.39 | 13 | 2.8 | 0.536 | 0.573 | |
| BO4 | 37.37 | −79.42 | 26 | 3.5 | 0.569 | 0.549 | |
| Little Otter River | LO | 37.28 | −79.43 | 7 | 2.7 | 0.563 | 0.610 |
| Dan basin | |||||||
| Lower Smith | |||||||
| Lower Smith River | LS1 | 36.50 | −79.76 | 10 | 4.8 | 0.667 | 0.600 |
| Middle Smith River | LS2 | 36.71 | −79.94 | 7 | 4.0 | 0.693 | 0.725 |
| LS3 | 36.72 | −79.94 | 10 | 4.5 | 0.702 | 0.700 | |
| Town Creek | TC1 | 36.80 | −80.00 | 11 | 4.7 | 0.637 | 0.620 |
| TC2 | 36.82 | −80.00 | 9 | 4.5 | 0.683 | 0.636 | |
| Upper Smith | |||||||
| Upper Smith River | US1 | 36.84 | −80.15 | 37 | 8.5 | 0.793 | 0.776 |
| US2 | 36.81 | −80.20 | 5 | 5.1 | 0.811 | 0.782 | |
| Nottway basin | |||||||
| Nottoway | |||||||
| Nottoway River | NR1 | 36.85 | −77.57 | 19 | 5.0 | 0.685 | 0.665 |
| NR2 | 36.90 | −77.67 | 16 | 6.1 | 0.685 | 0.744 | |
| Stony Creek | SC1 | 36.97 | −77.45 | 10 | 4.9 | 0.718 | 0.655 |
| SC2 | 37.06 | −77.57 | 12 | 4.6 | 0.692 | 0.682 | |
Laboratory methods
We extracted template DNA from whole tissue samples using a PureGene DNA Extraction Core Kit A (Gentra Systems, Minneapolis, MN, U.S.A.). We genotyped samples at eleven microsatellite DNA loci (Prex33, Prex36, Prex37, Prex38, Prex41, Prex42, Prex43, Prex44, Prex45, Prex46 and Prex47) developed for P. rex by Dutton et al. (2008), using methods reported therein. Forward primers for these loci were labelled using NED, VIC, PET or FAM fluorescent dye (Applied Biosystems, Inc., Foster City, CA, U.S.A.), and PCR was conducted in a MyCycler Thermal Cycler (BioRad, Hercules, CA, U.S.A.). Amplification products were separated in an ABI 3130 automated sequencer and sized in genemapper 3.5 using a LIZ500HD size standard (Applied Biosystems, Inc.).
Data analysis
To determine whether it was appropriate to combine data across sampling years for subsequent analyses, we used an analysis of molecular variance (amova) in arlequin 3.11 (Excoffier, Laval & Schneider, 2005) to decompose total genetic variance into pure-spatial (i.e. among sites), pure-temporal (i.e. among years within sites) and residual (i.e. among individuals within years within sites) components. For this analysis, we used data only from the 16 sites at which multiple individuals were sampled in multiple years. The magnitude of variance at each hierarchical level was tested for equality with zero based on 104 random permutations of objects among groups at the level being tested. We then tested for Hardy–Weinberg and linkage equilibrium individually for all 35 sites in arlequin. Hardy-Weinberg tests employed 105 recorded Markov Chain Monte Carlo (MCMC) iterations, following a burn-in of 103 iterations, whereas linkage tests employed 105 randomizations. Test results were evaluated using a sequential Bonferroni adjustment for a global α = 0.05. Average allele richness per locus (A), unbiased gene diversity (HE) and observed heterozygosity (HO) were estimated for each site.
We used spatially implicit clustering models to sort individuals into genetically homogeneous groups, and thereby estimate the spatial scale of population structure. Both individual-based and group-based modelling approaches were employed. Based on individual multilocus genotypes (n = 578), the number of discrete genetic clusters (K) in the dataset was estimated using structure 2.1 (Pritchard, Stephens & Donnelly, 2000). To determine whether population structure was hierarchical, we first estimated the number of populations (KP) within the entire dataset, and then estimated the number of subpopulations (KS) within each of the KP inferred populations (e.g. Austin et al., 2011). For KP, we evaluated K values from 1 to 15, whereas for each KS, we evaluated K values from 1 to x, where x = one plus the number of sites sampled in the population in question. All STRUCTURE models allowed for admixture and correlation of allele frequencies among clusters and searched parameter space using 106 recorded MCMC iterations, following a burn-in of 105 iterations. Ten replicates were run for each K value, and the replicate with the lowest Bayesian deviance (= −2 log likelihood) was retained as the best estimate of the likelihood of that K value (Faubet, Waples & Gaggiotti, 2007). The model (i.e. K value) with the lowest deviance was considered the best representation of population structure.
Because not all individuals analysed in STRUCTURE exhibited unambiguous ancestry from a single population (see 3), we used STRUCTURE to estimate the probability that each individual was a first-generation immigrant from a population other than the one from which it was captured. Based on the results of the analysis of population structure, K was fixed at seven for this analysis and capture location was used as a Bayesian prior. The model assumed a background migration rate of 0.5, effectively giving each individual an equal prior probability of being a resident or immigrant. The model also assumed correlation of allele frequencies among populations and searched parameter space using 106 recorded MCMC iterations, following a burn-in of 105 iterations. We concluded that an individual was an immigrant if its posterior probability of origination from another population was greater than 0.5.
For comparison, we also delineated population structure using an unrooted neighbour-joining tree constructed from a matrix of Nei, Tajima & Tateno's (1983) genetic distances (DA) between pairs of sites. Distances and the tree topology were estimated in populations 1.2.3 (O. Langella; http://bioinformatics.org/~tryphon/populations), and the tree was visualized in FigTree 1.3.1 (A. Rambaut; http://tree.bio.ed.ac.uk/). Following the delineation of population structure, we checked whether populations were internally panmictic using an amova to test whether molecular variation among sites within inferred populations differed significantly from zero.
We used Bayesian generalized linear mixed models (BGLMMs) to test alternative hypotheses about the factors most responsible for generating spatial patterns of genetic differentiation among sites. Extension of BGLMMs to pairwise comparison data is possible through the use of random effects that account for non-independence of multiple comparisons involving the same site. A Bayesian approach naturally accommodates this ‘multiple-membership model’ error structure and allows the proper estimation of the posterior mean and credible limits of effect sizes (Browne et al., 2001; Hadfield, 2010).
The response variable in BGLMMs was FST, estimated between all pairs of sites (n = 595 comparisons) in ARLEQUIN. We included predictor variables hypothesized to influence either gene flow or genetic drift, to separate the influences of these two forces on differentiation. Candidate predictors of FST based on gene flow included the spatial distance between sites (measured along stream channels), as well as three alternative characterizations of the degree of fragmentation via hydrological alteration between sites. Potential agents of fragmentation included hydroelectric tailwaters, reservoirs and dams, in order of hypothesized negative influence on connectivity relative to a completely riverine connection. Unfortunately, all sites separated by a reservoir also were separated by a dam, so these influences were confounded. However, some sites separated by a tailwater were not separated by a dam (e.g. GC1 versus BO1; see Fig. 1), so we could independently assess these two features. We recorded the presence or absence of tailwaters and dams between all pairs of sites. The hypothesized effect (or lack of effect) of a feature entered the model as a dummy variable, and alternative characterizations of fragmentation represented all possible combinations of effects. Scenario ‘Alteration1’ posited the effect on FST as riverine < tailwater = dam, ‘Alteration2’ posited the effect as riverine = tailwater < dam and ‘Alteration3’ posited the effect as riverine < tailwater < dam. These scenarios were coded using one, one and two dummy variables, respectively. The candidate predictor of FST based on drift was within-site genetic diversity, calculated as the arithmetic mean heterozygosity (HE) of the two sites being compared, centred to have a mean of zero. We reasoned that, all else being equal, site-pairs with lower HE values had experienced greater rates of drift. We hypothesized that spatial distance and degree of hydrological alteration would be positively related to FST, but that diversity (HE) would be negatively related.
BGLMMs were fit using the MCMCglmm package (Hadfield, 2010) in R 2.13.2 (R Development Core Team, 2011). Models assumed that FST was Gaussian-distributed and included two linked random effects that accounted for the two sites being compared within a given observation. We used diffuse priors for all parameters (mean = 0, variance = 1010) and estimated posteriors based on 1000 MCMC iterations sampled from a total of 20 000 iterations (burn-in = 10 000; thinning interval = 10). Examination of MCMC trace plots indicated that this intensity was sufficient to achieve stationarity, and replicate model runs produced nearly identical posterior estimates (not shown). A total of 31 alternative models were evaluated, consisting of all possible combinations of the fixed effects (spatial distance, genetic diversity and three hydrological-alteration scenarios) and their interactions (distance x diversity, distance x alteration), plus an intercept-only null model. Relative support for competing models was assessed using the deviance information criterion (DIC; Spiegelhalter et al., 2002), with smaller DIC values indicating greater support, and models with DIC values within 2 units of each other considered equally plausible. Model goodness-of-fit was assessed using a pseudo-R2, estimated as the squared correlation between the observed and model-predicted values of FST (Efron, 1978). To evaluate the relative importance of each variable, we estimated the decrease in model predictive ability (i.e. decrease in pseudo- R2) when that variable was removed, averaged across all sets of models (Lindeman, Merenda & Gold, 1980).
Results
Based on the 16 sites in which multiple individuals were captured in multiple years, temporal genetic variation was weak. An amova indicated that only 0.7% of molecular variance was due to differences among years within sites (P = 0.18), whereas 10.2% of variance was due to differences among sites (P < 0.00001) and 89.1% was residual variation among individuals within years within sites (P < 0.00001). We therefore pooled data across years for subsequent analyses. Hardy–Weinberg equilibrium was rejected in only 1 of 385 tests (locus Prex44 in site RR10), indicating a lack of appreciable influence from null alleles or site-scale Wahlund effects. Linkage equilibrium was rejected in only 8 of 1925 tests, and six of these cases occurred at one site (BO2). We therefore retained data from all 11 loci for further analyses.
Both clustering approaches indicated that the range-wide genetic structure of P. rex comprised seven discrete, well-mixed, catchment-scale populations. The individual-based STRUCTURE model with the greatest statistical support exhibited KP = 7, and models with alternative KP values had considerably higher Bayesian deviance scores (see Appendix S1 in Supporting Information). Inferred population memberships (Fig. 2) corresponded closely with geographic sampling locations (Fig. 1). All inferred population boundaries corresponded with one or more agents of hydrological alteration (i.e. dams and/or tailwaters; Fig. 2). Within inferred populations, sites were separated by 1.1–79.2 km (mean 21.2 km), and usually had no intervening barrier. Only two hypothesized barriers, both located within the putative lower Smith River population, failed to produce detectable genetic structure. Individuals from downstream (site LS1) and upstream (sites LS2, LS3, TC1 and TC2) of Martinsville dam clustered together, as did individuals from downstream (sites LS1, LS2 and LS3) and upstream (sites TC1 and TC2) of the Philpott tailwater. Overall, most individuals shared the majority of their ancestry with other individuals captured in the same population, although some admixture was evident between populations occupying Pigg River and Goose Creek and between populations occupying the Roanoke and upper Smith rivers. Although primary population structure was well defined, STRUCTURE showed no evidence for subpopulation structure within any of the seven inferred populations. The optimal KS value was 1 within each population and models with alternative KS values had considerably higher Bayesian deviance scores (Table S1). No individuals were inferred to be first-generation migrants between any of the seven populations delineated by STRUCTURE. The maximum immigrant probability observed was 0.37, well below our threshold of 0.5.
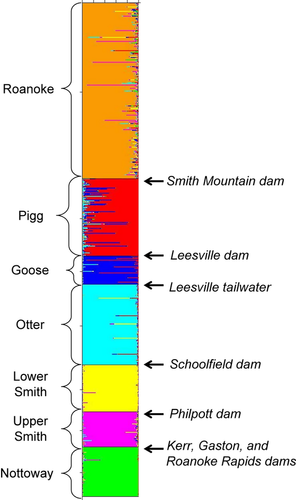
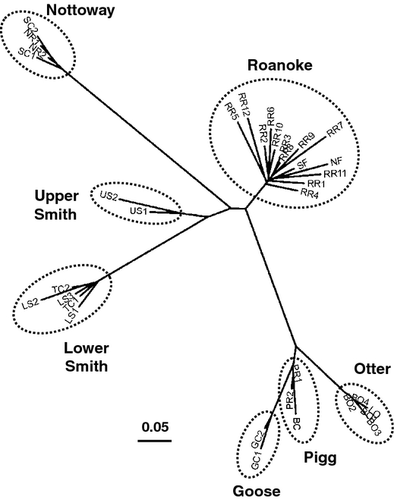
Site-based cluster analysis of population structure provided results concordant with those of the individual-based analysis. A neighbour-joining tree based on Nei et al.'s (1983) DA grouped the 35 sampling sites into seven terminal clusters that matched the seven populations delineated by STRUCTURE (Fig. 3). The topological arrangement of populations in the tree was partly consistent with expectations given the geographic juxtaposition of sites (Figs 1 & 3). As expected, upper and lower Smith populations clustered near each other, as did the three populations occupying the Piedmont physiographic province of the Roanoke basin (Pigg, Goose and Otter), and the Nottoway population was most divergent from other populations. However, the Roanoke population showed an unexpectedly close genetic relationship to the upper Smith population, given the large hydrological distance between these areas. Unlike the arrangement of populations, there was no apparent geographic pattern to the topological arrangement of sites within each population (Fig. 3). Furthermore, the amova indicated that populations were internally panmictic. Whereas 16.9% of total molecular variation was attributable to differences among populations (P < 0.00001), only 0.4% was attributable to differences among sites within populations (P = 0.12), with the remaining 82.3% (P < 0.00001) attributable to residual variation among individuals within sites.
Genetic differentiation, diversity and apparent connectivity varied widely among pairwise comparisons of sites. Estimates of FST, mean HE and riverine distance ranged from −0.01 to 0.36 (mean 0.14), 0.53 to 0.85 (mean 0.72) and 1 to 915 km (mean 344 km), respectively, among site pairs. Of hydrological-alteration classes, 114 site pairs exhibited riverine connections (i.e. no barrier), 14 pairs were separated by a tailwater (but no dam), and 467 pairs were separated by a dam (Fig. 1). Observed FST values were consistently low among riverine comparisons, but variable among dam comparisons (Fig. 4). Two distinct patterns characterized tailwater comparisons: site pairs separated by the Philpott tailwater exhibited low FST values (range −0.012–0.028), whereas site pairs separated by the Leesville tailwater exhibited relatively high FST values (range 0.185–0.254) (Fig. 4).
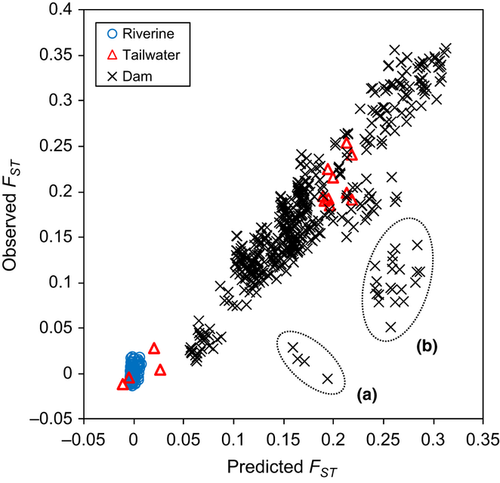
Among the 31 BGLMMs evaluated to predict patterns of genetic differentiation among sites, one model was substantially better-supported than all others based on DIC (Appendix S2 in Supporting Information). No models exhibited a DIC value within two units of this best model, so we focus further discussion on it. In the best-supported BGLMM, and in support of our hypotheses, FST was positively related to the riverine distance and degree of hydrological alteration between sites and negatively related to genetic diversity within sites (Table 2). The model included an alteration x diversity interaction term, which indicated that the negative relationship between diversity and FST was stronger for site pairs separated by tailwaters or dams than for site pairs with riverine connections. Based on variable importance scores (in parentheses), genetic diversity (0.170) and hydrological alteration (0.163) were more influential to models than riverine distance (0.085). In the absence of these effects, the posterior estimate of FST (i.e. model intercept) was approximately zero (mean −0.001, with a 95% credible interval of −0.013 to 0.009). The index of hydrological alteration contained in the best model (‘Alteration3’ in Table S2) consisted of two dummy variables and accounted for three different connectivity situations between sites: riverine connection versus tailwater versus dam. Based on posterior means of effects (in parentheses), dams (0.120) increased the predicted estimate of FST relative to tailwaters (0.012) or riverine connections (−0.001). Tailwaters had an inconsistent influence on FST, given that 95% credible intervals overlapped with zero. The relationship between FST and riverine distance (i.e. IBD slope) was positive and invariant among hydrological-alteration classes (i.e. no interaction), but the effect size was relatively weak; the model predicted that FST would increase by only 0.01 for every 100 km of spatial separation. Thus, the effect of a dam on FST was comparable to that of a between-site distance of over 1200 km of unimpounded river. The effect of genetic diversity on FST depended on between-site connectivity: in site pairs separated by a tailwater or dam, a decrease in mean HE of 0.1 increased FST by 0.14 or 0.10, respectively, whereas in riverine site pairs, the same decrease in mean HE increased FST by only 0.002.
| Model fixed effects | Bayesian posterior estimates | |||
|---|---|---|---|---|
| Mean | 95% credible interval | Importance | ||
| Lower | Upper | score | ||
| Intercept | −0.001 | −0.013 | 0.009 | |
| Riverine distance | 0.010 | 0.008 | 0.012 | 0.085 |
| Hydrological alteration | 0.163 | |||
| Tailwater | 0.012 | −0.043 | 0.063 | |
| Dam | 0.120 | 0.107 | 0.133 | |
| Genetic diversity × Alteration | 0.170 | |||
| Diversity × Riverine | −0.023 | −0.120 | 0.076 | |
| Diversity × Tailwater | −1.374 | −1.708 | −0.980 | |
| Diversity × Dam | −1.014 | −1.089 | −0.931 | |
The best-supported BGLMM exhibited good fit to the observed data, with a pseudo-R2 of 0.81 (Fig. 4). Predicted and observed FST values were in close agreement for comparisons across riverine and tailwater connections and most comparisons across dams. However, FST was noticeably over-predicted within two groups of comparisons across dams. The first group comprised comparisons of site LS1, downstream of Martinsville Dam, to three other sites within the lower Smith River population that were upstream of the dam. The second group comprised comparisons of sites in the Pigg River to those in the Otter River or Goose Creek, on the other (downstream) side of Leesville Dam.
Discussion
Spatial scale of population structure
Our range-wide survey of genetic variation in P. rex unambiguously indicated the presence of seven discrete, well-mixed, catchment-scale populations. The number and geographic extent of these populations were corroborated by both individual- and group-based cluster analyses. Furthermore, neither method showed discernible substructure within any population. We expected that P. rex's discontinuous distribution among suitable reaches and streams (Rosenberger & Angermeier, 2003; Rosenberger, 2007) would lead to detectable differentiation within catchments. Rather, our finding of panmixia within catchments suggests that P. rex readily disperses across reach-scale and stream-scale patch boundaries. Evidence for influences of such boundaries on movements of other fish species is equivocal (Freeman, 1995; Lonzarich, Lonzarich & Warren, 2000; Gilliam & Fraser, 2001; Roberts & Angermeier, 2007; Lamphere & Blum, 2012).
Notably, we observed panmixia over spatial extents of up to 80 river km, considerably greater than the spatial extents over which darters reportedly disperse (Winn, 1958; Roberts & Angermeier, 2007; Schwalb, Poos & Ackerman, 2010). Most direct estimates of darter movement have originated from mark–recapture field studies, which, due to study-design limitations (Albanese, Angermeier & Dorai-Raj, 2004), usually are incapable of detecting movements exceeding 1 km (Schwalb et al., 2010). A noteworthy exception involved P. rex: Roberts et al. (2008) conducted a mark–recapture study for the species throughout an unusually extensive study area (23 km), which enabled detection of two long-distance movements (2.5 and 3.2 km). Yet even this study suffered low detection probabilities that downwardly biased movement estimates (Roberts et al., 2008). In contrast to mark–recapture data, ‘indirect’ estimates of dispersal, for example from spatially extensive studies of gene flow, invasion and recolonization rates and community autocorrelation, provide mounting evidence for catchment-scale mobility of warm-water stream fishes (Hitt & Angermeier, 2008; Waits et al., 2008; Huey et al., 2011), including darters (Ensign et al., 1997; Neely & George, 2006; Austin et al., 2011). These discrepancies between direct and indirect estimates of mobility may partially result from differences in the spatiotemporal extents of studies (Lamphere & Blum, 2012). Regardless, connectivity across whole catchments contradicts conventional wisdom that fish populations are regulated primarily by reach-scale factors and supports the adoption of a riverscape perspective on population regulation (Fausch et al., 2002). Specifically, our results suggest that monitoring and recovery efforts for P. rex should target entire catchments to adequately represent population dynamics.
Although within-catchment connectivity was high, we found no evidence for contemporary exchange between populations occupying different catchments. STRUCTURE analyses indicated that most individuals had ancestry from a single population, and no recent migrants were detected. This information, combined with the distribution of probable anthropogenic barriers to movement (see below), suggests that populations of P. rex are completely isolated and currently on independent demographic and evolutionary trajectories. This situation is best characterized by an ‘isolation’ evolutionary model (Nei & Chakravarti, 1977) or ‘non-equilibrium metapopulation’ demographic model (Schlosser & Angermeier, 1995). Because stream systems are linear networks with few dispersal routes, stream habitats are readily fragmented by natural and anthropogenic barriers to movement (Campbell Grant et al., 2007). Isolated population structures like that of P. rex therefore may be common across stream fish taxa. Such structures are prone to small Ne, increased potential for genetic divergence and increased vulnerability to demographic and environmental stochasticity (Allendorf & Leary, 1986; Morita & Yamamoto, 2002; Neville, Dunham & Peacock, 2006). Optimal management strategies for such taxa will partly depend on the factors that produced isolation, and whether they arose from natural or anthropogenic sources (Frankham et al., 2011).
Determinants of population structure
We used Bayesian generalized linear mixed models (BGLMMs) to tease apart the relative roles of spatially restricted gene flow (i.e. IBD), anthropogenic barriers and genetic drift in producing the contemporary population structure of P. rex. The response variable in these models was the genetic differentiation statistic FST, estimated between pairs of sites. It is important to note that sample sizes were small at many sites (i.e. <15 individuals), which can decrease the precision with which statistics like HE and FST are estimated (Kalinowski, 2005). However, exploratory analyses involving data rarefaction (not shown) indicated little effect of sample size on estimates of HE and FST for P. rex. Furthermore, small-sample-size sites were evenly distributed among geographic areas, which reduced the potential for sample size to inject a systematic bias into BGLMM results. We therefore concluded that site-based samples adequately represented the populations to which they belonged, and proceeded with BGLMM analyses using data from all 35 sites.
The best-supported BGLMM included spatial distance, hydrological alteration and genetic diversity as predictors of pairwise differentiation (FST) between pairs of sites, but the magnitudes of these effects varied widely. One important determinant of genetic differentiation was the presence or absence of a hydroelectric project between sites. The best-supported BGLMM indicated that hydroelectric dams strongly inflated FST values relative to a completely riverine connection, whereas tailwaters had a more nuanced effect, mediating the relationship between genetic diversity and FST. Indeed, all of the population boundaries that we detected coincided with a dam, tailwater or both. Thus, although the catchment was the habitat patch-size that best matched the grain of P. rex's population structure, population boundaries appeared to be more defined by anthropogenic barriers than by natural habitat boundaries per se.
Nearly all populations were isolated from others by a hydroelectric dam, none of which are equipped to allow fish passage. Such isolation is expected to accelerate genetic differentiation relative to a riverine connection (Bessert & Ortí, 2008; Raeymaekers et al., 2008; Junker et al., 2012; Sterling et al., 2012). Dams are pervasive features of riverine landscapes, and with human population growth, economic development, climate change and water shortages predicted for the future, their prevalence is expected to increase (Postel, 2000). The adaptive consequences of resulting anthropogenically induced divergence are only beginning to be investigated (Waples et al., 2007) and warrant additional research, particularly for non-migratory aquatic species.
Although dams usually produced P. rex population boundaries, we noted one exception. P. rex in the most downstream site in the lower Smith River population (Site LS1) were genetically indistinguishable from those in sites further upstream (LS2, LS3, TC1, TC2), despite the bisection of these sections by Martinsville dam and reservoir. Although this is one of the oldest hydroelectric dams in the study area (c. 1920), it also is one of the shortest (~10 m high) and impounds a relatively short reach of river (< 3 km). It therefore may permit enough gene flow to homogenize the gene pools on either side of the dam, even if such gene flow is one-way, from upstream to downstream (e.g. Hänfling & Weetman, 2006; Dehais et al., 2010; Whiteley et al., 2010; Junker et al., 2012). In contrast, the shortest hydroelectric dam in the study area, Schoolfield dam in Danville, Virginia (~9 m high), did coincide with a genetic boundary between the lower Smith and Otter populations. Although modest in height, this dam is flanked by several nearby low-head dams and bisects a 280-km-long, unoccupied segment of river that stretches between Otter River and Smith River. The combined influences of all these features presumably have overwhelmed P. rex's capacity for dispersal and promoted differentiation of the Roanoke and Dan basins.
In another special case, Leesville dam, which separates Pigg River from Goose Creek and Otter River, did coincide with a population boundary and significant genetic differentiation, but model-predicted FST values across this barrier were 12–20% higher than observed values. We can offer no confident interpretation of this finding. Leesville dam is large (~27 m high) and impounds a large reservoir (~1829 ha), so we do not interpret the lower-than-expected FST values as indicative of ongoing gene flow across the barrier. Rather, we hypothesize that the lower differentiation is a legacy of high pre-dam connectivity, coupled with the relatively recent completion of the dam (c. 1963).
Unlike dams, to our knowledge the influence of tailwaters on population structure of stream fishes has not been investigated. We found that tailwaters had inconsistent effects on genetic differentiation of P. rex, seemingly promoting genetic differentiation between Goose Creek and Otter River, but not between Town Creek and lower Smith River. Although Goose Creek and Otter River enter the Roanoke River only 17 river km from each other, pairwise differentiation of sites in these populations was high (FST range 0.20–0.26). Perhaps, hydrologically unstable conditions in the Leesville tailwater make the Roanoke River unsuitable for use as a transit corridor or permanent habitat. In contrast, the Philpott tailwater had little apparent influence on gene flow of P. rex between Town Creek and lower Smith River (FST range −0.01–0.02). The hypolimnetic pulsed release from Philpott dam produces year-round cold water temperatures (~8 °C) that apparently exclude P. rex from the mainstem Smith River from the dam to about 4 km downstream of the mouth of Town Creek (Krause, Newcomb & Orth, 2005). This theoretically would deter dispersal between Town Creek and Smith River during all but the coldest months, when stream temperatures are similar across these reaches. Nevertheless, fish from the two streams were genetically indistinguishable, suggesting that P. rex either disperses between streams during winter or tolerates extreme between-stream temperature differences (i.e. >10 °C) during non-winter dispersal. Further research on the influences of thermal barriers on dispersal of warmwater stream fishes is needed to help distinguish these explanations.
Another important determinant of genetic differentiation in P. rex was genetic drift via its effect on genetic diversity within sites. Within-site genetic diversity (HE) ranged from 0.52 to 0.85, which, assuming a stepwise mutation model (Ohta & Kimura, 1973), amounts to a nearly 13-fold range in relative population sizes. Detailed demographic histories for these populations are lacking, but rank genetic diversities are consistent with expert opinion about the anthropogenic impact that populations have experienced (Rosenberger, 2007). For example, the lowest gene diversities were observed at sites in populations occupying the middle Piedmont physiographic province (i.e. Pigg, Goose and Otter). These areas have been chronically impacted by anthropogenic sedimentation associated with agricultural and silvicultural runoff since the 1700s (Jenkins & Burkhead, 1994). Furthermore, the Pigg population was probably bottlenecked by a chemical discharge in 1975 that killed all fish within a 36-km segment of the Pigg River (Jenkins & Burkhead, 1994). Isolated populations in Goose and Otter were discovered only recently (i.e. since 2004), suggesting that these populations persist at low abundances. In contrast, the highest gene diversities were observed at sites in the two most montane populations, Roanoke and upper Smith. Both of these areas exhibit higher channel gradient than other occupied river systems, which may inhibit the accumulation of silt on the stream benthos; both areas also contain extensive reaches of low human impact (Rosenberger, 2007). Regardless, high extant gene diversity in these two populations results in surprisingly low genetic divergence between them (Fig. 3), given their hydrological separation. George, Neely & Mayden (2010) found a similar pattern based on a survey of mitochondrial DNA variation in P. rex. We interpret these findings as evidence of historically higher pre-dam connectivity between the Roanoke and Dan basins, the signatures of which have been lost in most other populations that have lost much of their genetic diversity.
Stream-dwelling species often are considered ‘textbook’ examples of the one-dimensional IBD evolutionary model. However, we found that spatial distance between P. rex sites had less influence on pairwise FST than fragmentation or genetic drift. The optimal BGLMM predicted that, holding the effects of barriers and genetic diversity constant, FST would increase by only 0.01 for every 100 km of spatial distance. Thus, the most distant sites in the study would exhibit an FST value of only 0.09. By comparison, the presence of a dam between sites was predicted to inflate FST to a value of 0.12, equivalent to a between-site distance of over 1200 km of unimpounded river. Interestingly, the presence of a barrier increased the intercept of the IBD relationship, but did not affect the slope. The relatively weak relationship between differentiation and distance in P. rex, regardless of whether or not a barrier is present, suggests that P. rex is highly mobile and capable of gene flow over large spatial extents, and that prior to the construction of barriers connectivity was substantially higher throughout the range of P. rex. Our study thus indicates the danger of failing to account for barriers and interpopulation variation in genetic drift when testing for IBD. Had we failed to do so, we may have interpreted the contemporary strong differentiation of populations as evidence of long-term isolation, and recommended a management strategy of maintained isolation. Instead, available evidence indicates that isolation is recent, resulting from anthropogenic fragmentation. A prudent management strategy therefore may be to counteract rapid contemporary divergence by restoring connectivity, either through barrier removal or intentional translocation among populations (Tallmon, Luikart & Waples, 2004; Frankham et al., 2011). This strategy could complement ongoing strategies of habitat enhancement via sediment control in catchments harbouring P. rex (Rosenberger, 2007).
Implications for ecology and conservation
An understanding of landscape connectivity and population structure is central to the conservation of stream fishes, yet existing knowledge comes overwhelmingly from studies of salmonids, which may poorly represent other life-history types, and from biased studies of fish movement. Many salmonids are migratory (i.e. anadromous or potamodromous), undergoing extensive movements to meet changing habitat needs over ontogeny (Northcote, 1978). Yet despite this great potential for mobility, salmonids tend to exhibit strong fidelity to and low dispersal (‘straying’) from natal habitats (Quinn, 1993), which results in small average lifetime dispersal distances (e.g. Koizumi et al., 2006) and fine-scaled genetic structure (e.g. Neville et al., 2006; Primmer et al., 2006; Kanno, Vokoun & Letcher, 2011). In contrast, many small-bodied, benthic warm-water fishes undergo comparably minor ontogenetic shifts in habitat needs, which can be accommodated via localized movements (Winn, 1958; Hall, 1972; Rosenberger & Angermeier, 2003; Roberts & Angermeier, 2007), seemingly obviating extensive migration or dispersal. This observation, combined with the observation that small-bodied benthic fishes are poor swimmers, has led to the general presumption that such species are sedentary (Radinger & Wolter, 2013). Unfortunately, mark–recapture data seldom are useful for testing this assumption, due to the limited spatiotemporal scope of such studies (Fausch et al., 2002). Further, indirect estimates of mobility from studies of catchment-scale gene flow often are confounded by the presence of movement barriers between sampling sites (e.g. Hänfling & Weetman, 2006; Beneteau et al., 2009; Lamphere & Blum, 2012; Sterling et al., 2012).
Our study of P. rex suggests that, in the absence of hydrological barriers, benthic, non-migratory species can undertake surprisingly extensive gene flow. Conceptual models presuming restricted movement of such species need to be critically examined and further tested, and the spatial scale of monitoring and management activities adjusted accordingly. We also found that hydroelectric dams drastically accelerated genetic differentiation relative to historical, riverine connections. Given the global ubiquity of hydroelectric projects, this finding has profound implications for fish conservation. We encourage others to conduct analogous analyses of population structure, to help: a) assess general patterns within and among taxa (including salmonid and non-salmonid species), migratory strategies and habitat types, b) sort out influences of fragmentation agents such as dams, reservoirs and tailwaters and c) assess consequences for persistence and evolution of stream fishes.
Acknowledgments
This research was funded by the Virginia Department of Game and Inland Fisheries and the U.S. Fish and Wildlife Service. Additional support was provided by the U.S. Army Corps of Engineers, U.S. Geological Survey and Virginia Transportation Research Council. We thank W. Hester, M. Pinder, K. Smith and S. Smith in particular for logistical help. D. Dutton and J. Printz provided invaluable expertise and assistance with laboratory work. M. McKinney, R. Nichols, M. Raley and S. Smith kindly supplied additional genetic material. A. Dolloff, P. Grobler, J. Jones and M. Kelly provided helpful reviews of the manuscript. This work was carried out under the auspices of Institutional Animal Care and Use Committee protocols 08-106FIW and 11-035-FIW at Virginia Tech. The Virginia Cooperative Fish and Wildlife Research Unit is jointly supported by U.S. Geological Survey, Virginia Polytechnic Institute and State University, Virginia Department of Game and Inland Fisheries and Wildlife Management Institute. Any use of trade, product or firm names does not imply endorsement by the U.S. government.




