Funding: Prof. Alfredo Cuesta-Infante was supported by R&D project TED2021-129162B-C22, funded by MICIU/AEI/ 10.13039/501100011033/and the European Union NextGenerationEU/PRTR, and R&D project PID2021-128362OB-I00, funded by MICIU/AEI/ 10.13039/501100011033/and FEDER/UE.

About

Sections

PDF

Tools

Share a link

Email
Wechat
Bluesky

ABSTRACT

In text classification, creating an adversarial example means subtly perturbing a few words in a sentence without changing its meaning, causing it to be misclassified by a classifier. A concerning observation is that a significant portion of adversarial examples generated by existing methods change only one word. This single-word perturbation vulnerability represents a significant weakness in classifiers, which malicious users can exploit to efficiently create a multitude of adversarial examples. This paper studies this problem and makes the following key contributions: (1) We introduce a novel metric $\rho$ to quantitatively assess a classifier's robustness against single-word perturbation. (2) We present the SP-Attack, designed to exploit the single-word perturbation vulnerability, achieving a higher attack success rate, better preserving sentence meaning, while reducing computation costs compared to state-of-the-art adversarial methods. (3) We propose SP-Defence, which aims to improve $\rho$ by applying data augmentation in learning. Experimental results on 4 datasets and 2 masked language models show that SP-Defence improves $\rho$ by 14.6% and 13.9% and decreases the attack success rate of SP-Attack by 30.4% and 21.2% on two classifiers respectively, and decreases the attack success rate of existing attack methods that involve multiple-word perturbations.

1 Introduction

With proliferation of generative AI based applications, text classifiers have become mission critical. These classifiers are designed to be guardrails for outputs of an application that uses a large language model underneath. A text classifier can be used to detect if a chatbot is accidentally giving financial advise; or leaking sensitive information, or in the past they are frequently used in security-critical applications such as misinformation detection (Wu et al. 2019; Torabi Asr and Taboada 2019; Zhou et al. 2019). At the same time, there has been a steady stream of work showing that these classifiers are vulnerable to perturbations. That is, simple perturbations—subtly modified sentences that, while practically indistinguishable from the original sentences, nonetheless change the output label of a classifier resulting in failure modes of these classifiers. Deploying these classifiers alongside generative AI applications have brought up the question of whether the failure modes of these classifiers can be identified before the classifiers are deployed—and, if they can be identified, whether they can also be updated to overcome these failure modes. One promising solution is to synthetically construct these “subtly modified” sentences in order to test the classifiers, and also to create sentences we can add to the training data to make the classifiers more robust in the first place. Not surprisingly, synthetic data generation is also possible with large language models. In this paper, we propose and demonstrate the use of use large language models to construct synthetic sentences that are practically indistinguishable from the real sentences. In classical literature, sentences that can trick these classifiers are known as “adversarial examples”. The process of trying to find these examples for a given classifier (or in general) is called an “adversarial attack” and training the classifier to be robust to these attacks is called “defense”. We will use these terms here, as they enable us to compare our method with other well-known methods using similar notations and language. A common metric for assessing the vulnerability of a classifier to such attacks is the Attack Success Rate (ASR), defined as the percentage of labelled sentences for which an adversarial sentence could be successfully designed. Recent proposed methods can achieve an ASR of over 80% (Jin et al. 2020; Li, Zhang, et al. 2021), making adversarial vulnerability a severe issue.

These attacks work through black box methods, accessing only the output of a classifier. They tweak sentences in an iterative fashion, changing one or multiple words and then querying the classifier for its output until an adversarial example is achieved. When we examined the adversarial sentences generated by these methods, we were surprised to find that in a significant portion of them, just one word had been changed. In Table 1 we show results of three existing methods, their attack success rates and the percentage of adversarial examples they generated that had only single-world changes (SP). For example, 66% of adversarial examples generated by CLARE attacks (Li, Zhang, et al. 2021) on a movie review (MR) dataset (Pang and Lee 2005) changed only one word. Furthermore, many different adversarial sentences used the same word, albeit placed in different positions. For example, inserting the word “online” into a sentence repeatedly caused business news articles to be misclassified as technology news articles.

TABLE 1. The ASR and percentage of adversarial examples with single-word perturbation (denoted as SP%).

	ASR	SP%	ASR	SP%	ASR	SP%	ASR	SP%
	TextFooler		BAE		CLARE		SP-Attack
AG	65.2	17.0	19.3	35.8	84.4	38.6	82.7	100
MR	72.4	49.2	41.3	66.6	90.0	66.2	93.5	100

Note: We attack a vanilla BERT classifier on AG and MR, the datasets used in our experiments, using TextFooler (Jin et al. 2020), BAE (Garg and Ramakrishnan 2020), CLARE (Li, Zhang, et al. 2021) and our SP-Attack.

Directly modelling this vulnerability is crucial, as both of these properties are beneficial to attackers. First, the fewer words that are changed, the more semantically similar the adversarial example will be to the original, making it look more “innocent” and running the risk that it will not be detected by other methods. Second, knowing that a particular word can reliably change the classification will enable an attacker to reduce the number of queries to the classifier in a black box attack, which is usually $l$ queries, where $l$ is the sentence length.

Despite the attractive properties of direct methods for attackers, to the best of our knowledge, no existing work has been done to design a single-word perturbation- based attack—nor is there a specific metric to quantify the robustness of a classifier against single-word perturbations. We approach this problem in a comprehensive way.

First, we define a measure—the single-word flip capability, denoted as $\kappa$ – for each word in the classifier's vocabulary. This measure, presented in Section 2, is the percentage of sentences whose classification can be successfully changed by replacing that word at one of the positions. A subset of such sentences that are fluent enough and similar enough to the original sentence would comprise legitimate attacks. $\kappa$ allows us to measure a text classifier's robustness against single-word perturbations, denoted as $\rho$ . $\rho$ is the percentage of sentence-word pairs in the Cartesian product of the dataset and the vocabulary where the classifier will not flip regardless of the word's position, meaning a successful attack is not possible.

The vocabulary size of the classifiers and datasets we are working with are too large for us to compute these metrics through brute force (30 k words in the classifier's vocabulary, and datasets with 10 k sentences of 30 words on average). Therefore, in Section 3, we propose an efficient upper bound algorithm (EUBA) for $\rho$ , which works by finding as many successful attacks as possible within a given time budget. We use first-order Taylor approximation to estimate the potential for each single-word substitution to lead to a successful attack. By prioritising substitutions with high potential, we can find most of the successful attacks through verifying a subset of word substitutions rather than all of them, reducing the number of queries to the classifier.

With these two measures, we next design an efficient algorithm, SP-Attack, to attack a classifier using single-word perturbations while still maintaining fluency and semantic similarity (Section 4). SP-Attack pre-computes $\kappa$ for all words using EUBA, then performs an attack by changing only one word in a sentence, switching it to another high-capacity word (i.e., high $\kappa$ ) to trigger a misclassification. We show that SP-Attack is more efficient than existing attack methods due to pre-computing $\kappa$ and flipping only one word.

To overcome this type of attack, in Section 5, we design SP-Defence, which leverages the first-order approximation to find single-word perturbations and augment the training set. We retrain the classifier to become more robust—not only against single-word perturbation attacks, but also against attacks involving multiple word changes.

We also carry out extensive experiments on masked language models, specifically BERT classifiers, in Section 6 to show that: (1) $\kappa$ and $\rho$ are necessary robustness metrics; (2) EUBA is an efficient way to avoid brute force when computing the robustness metric $\rho$ ; (3) SP-Attack can match or improve ASR compared to existing attacks that change multiple words, and better preserve the semantic meanings; (4) SP-Defence is effective in defending against baseline attacks as well as against SP-Attack, thus improving classifier robustness.

2 Quantifying Classifier Robustness Against Single-Word Perturbations

In this section, we formulate the single-word perturbation adversarial attack problem, and define two novel and useful metrics: $\kappa$ , which represents how capable a particular word is at flipping a prediction, and $\rho$ , which represents the robustness of a text classifier against single-word perturbation. We also refer the reader to Table 2 for other notations used throughout the paper.

TABLE 2. Our notations.

Notation	Description
$f\left(\cdot \right)$	A text classifier
$V$	The vocabulary used by $f$
$D$	A text classification training set
${D}^{+}$	A subset of $D$ where $f$ can correctly classify
${D}^{\ast }$	The Cartesian product of ${D}^{+}$ and $V$
$S\left(\mathbf{x},w\right)$	A set of sentences constructed by replacing one word in $\mathbf{x}$ with $w$
${\kappa}_f(w)$	The single-word adversarial capability of $w$
$\rho (f)$	The robustness against single-word perturbation measured on the training set
${\rho}^{\ast }(f)$	The robustness against single-word perturbation measured on the test set
ASR	Attack success rate

2.1 Single-Word Perturbation Attack Setup

We consider a restricted adversarial attack scenario where the attacker can substitute only one word. The attack is considered successful if the classifier's prediction differs from the label.

Let

D={\left({\mathbf{x}}_i,{y}_i\right)}_{i=1\dots \mid D\mid }

be a text classification dataset, where

{\mathbf{x}}_i

is a sentence composed of words,

{y}_i

is the label of the sentence and

\mid D\mid

denotes the cardinality of

D

. A classifier

f\left(\cdot \right)

is trained on

D

to predict

{y}_i

with input

{\mathbf{x}}_i

. Additionally,

V

is the vocabulary associated with

f\left(\cdot \right)

. The goal of the single-word perturbation attack is to construct an

{\mathbf{x}}^{\prime }

for a sentence-label pair

\left(\mathbf{x},y\right)

by replacing one word so that

the prediction is flipped, i.e., $f\left({\mathbf{x}}^{\prime}\right)\ne y$ ;
${\mathbf{x}}^{\prime }$ is a fluent sentence;
${\mathbf{x}}^{\prime }$ is semantically similar to $\mathbf{x}$ .

Fluency of the sentence is measured by perplexity, while the similarity is measured by the cosine similarity of a Universal Sentence Encoder (USE) (Cer et al. 2018) and human annotators.

2.2 Two Useful Metrics for Robustness

To see how robust a given classifier

f\left(\cdot \right)

is against single-word perturbation, we take the training set

D

, and find the subset

{D}^{+}

where

f

can correctly predict the label. We want to find out whether each word

{w}_j\in V

can flip the prediction of each example sentence

\left({\mathbf{x}}_i,{y}_i\right)\in {D}^{+}

. Therefore, we define a matrix

A\in {\left[0,1\right]}^{\mid {D}^{+}\mid \times \mid V\mid }

indicating whether a word can successfully flip the classifier's prediction of a sentence, specifically

{A}_{i,j}=\left\{\begin{array}{ll}1& \mathrm{if}\kern0.5em \exists {\mathbf{x}}^{\prime}\in S\left({\mathbf{x}}_i,{w}_j\right)\kern0.5em \mathrm{s}.\mathrm{t}.\kern0.5em f\left({\mathbf{x}}^{\prime}\right)\ne {y}_i\\ {}0& \mathrm{otherwise}\end{array}\right.

(1)

where

S\left(\mathbf{x},w\right)

is a set of sentences constructed by replacing one word in

\mathbf{x}

with

w

. Note that

A

only indicates that the prediction was flipped, and does not take into account similarity or fluency.

With this matrix, we can find the single-word flip capability for each word in the classifier's vocabulary, denoted as

\kappa

and defined as the percentage of sentences whose prediction can be successfully flipped using that word. It can be computed as

\kappa \left({w}_j\right)=\frac{1}{\mid {D}^{+}\mid}\sum \limits_i\;{A}_{i,j}

Second, we can find the robustness against single-word perturbations, for a text classifier, denoted as

\rho

and defined as the percentage of sentence-word pairs in the Cartesian product of the dataset and the vocabulary where the classifier prediction cannot be successfully flipped. It can be computed as

\rho (f)=\frac{1}{\mid {D}^{+}\mid \cdot \mid V\mid}\sum \limits_{i,j}\left(1-{A}_{i,j}\right)

2.3 Definitions and Theorem

We then give formal definitions and a theorem.

Definition 1.The single-word flip capability of word $w$ on a classifier $f$ is

{\kappa}_f(w)=\frac{\mid \left\{\left(\mathbf{x},y\right)\in {D}^{+}\mid \exists {\mathbf{x}}^{\prime}\in S\left(\mathbf{x},w\right)\kern0.5em s.t.\kern0.5em f\left({\mathbf{x}}^{\prime}\right)\ne y\right\}\mid }{\mid {D}^{+}\mid }

where

{D}^{+}=\left\{\left(\mathbf{x},y\right)\in D\mid f\left(\mathbf{x}\right)=y\right\}

is a subset of

D

that is correctly classified by

f

, and

S\left(\mathbf{x},w\right)

is a set of sentences constructed by replacing one word in

\mathbf{x}

with

w

. We omit

f

and use notation

\kappa (w)

in the rest of the paper.

Definition 2.The robustness against single-word perturbation is

\rho (f)=\frac{\mid \left\{\left(\left(\mathbf{x},y\right),w\right)\in {D}^{\ast}\mid \forall {\mathbf{x}}^{\prime}\in S\left(\mathbf{x},w\right):f\left({\mathbf{x}}^{\prime}\right)=y\right\}\mid }{\mid {D}^{\ast}\mid }

where

{D}^{\ast }={D}^{+}\times V

is the Cartesian product of

{D}^{+}

and vocabulary

V

$\rho (f)$ can be interpreted as the accuracy of $f$ on ${D}^{\ast }$ , where $f$ is considered correct on $\left(\left(\mathbf{x},y\right),w\right)$ if all sentences in $S\left(\mathbf{x},w\right)$ are predicted as $y$ .

Theorem 1. $\kappa$ and $\rho$ have the following relation:

\rho (f)=1-\frac{1}{\mid V\mid}\sum \limits_{w\in V}\;{\kappa}_f(w)

Proof.

\begin{array}{c}\rho (f)=\frac{\sum_{i,j}1-{A}_{i,j}}{\mid {D}^{+}\mid \times \mid V\mid}\\ {}=1-\frac{1}{\mid V\mid}\sum \limits_{j=1}^{\mid V\mid}\frac{\sum_{i=1}^{\mid {D}^{+}\mid }{A}_{i,j}}{\mid {D}^{+}\mid}\\ {}\begin{array}{c}=1-\frac{1}{\mid V\mid}\sum \limits_{j=1}^{\mid V\mid}\;\kappa \left({w}_j\right)\end{array}\end{array}

3 Efficient Estimation of the Metrics

Directly computing $\kappa$ and $\rho$ metrics is time-consuming, because each word in the vocabulary needs to be placed in all sentences at all positions and then verified on the classifier. To overcome this issue, we instead estimate the lower bound of $\kappa$ (and thus the upper bound of $\rho$ ). In this section, we first give an overview of the efficient upper bound algorithm (EUBA), then detail our first-order approximation. Figure 1 depicts the algorithm and the pseudocode is presented in Appendix B.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

The EUBA algorithm can efficiently find prediction flip by using first-order Taylor approximations.

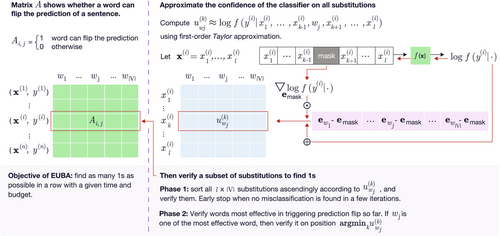
3.1 Overview

To find the lower bound of $\kappa (w)$ , we want to find as many $\left(\mathbf{x},y\right)\in {D}^{+}$ such that $w$ can successfully flip the prediction. Since we want to compute $\kappa$ for all words, we can convert it to the symmetric task of finding as many $w\in V$ as we can for each $\left(\mathbf{x},y\right)\in {D}^{+}$ such that the sentence can be successfully flipped by the word. This conversion enables a more efficient algorithm.

For each example

\left(\mathbf{x},y\right)

, where

\mathbf{x}={x}_1,\dots, {x}_l

, each word can be substituted with any

w\in V

, leading to a total of

l\times \mid V\mid

substitutions. For a substitution

{x}_k\to w

, we compute

{u}_w^{(k)}\approx \log f\left(y|{x}_1,\dots, {x}_{k-1},w,{x}_{k+1},\dots, {x}_l\right)

(2)

where

f\left(y|\cdot \right)

is the classifier's probability of predicting

y

. We will show the computation of

{u}_w^{(k)}

in Section 3.2. We assume substitutions with lower

{u}_w^{(k)}

are more likely to flip predictions and verify them in two phases.

Phase 1: We sort all substitutions in ascending order by ${u}_w^{(k)}$ , and verify them on the classifier. We stop the verification after $m$ consecutive unsuccessful attempts and assume all remaining substitutions are unsuccessful, where $m$ is a hyper-parameter.

Phase 2: If a word can successfully flip many other sentences in the class $y$ , it is more likely to succeed on $\mathbf{x}$ . Therefore, we keep track of how many successful flips each word can trigger on each category. We sort all words in descending order by the number of their successful flips, and verify them. For each word $w$ , we only verify the position where it is most likely to succeed (i.e., $\arg\;{\min}_k\;{u}_w^{(k)}$ ). Similarly, phase 2 stops after $m$ consecutive unsuccessful attempts.

By using ${u}_w^{(k)}$ , we can skip a lot of substitutions that are unlikely to succeed, improving efficiency. The hyper-parameter $m$ controls the trade-off between efficiency and the gap between the lower bound and the exact $\kappa$ . When setting $m\to \infty$ , EUBA can find the exact $\kappa$ and $\rho$ . In Section 6.5, we show that efficiency can be improved a lot if a relatively small $m$ is used, at the small cost of neglecting some successful flips. We also compare EUBA with two alternative designs.

3.2 First-Order Approximation

We then show how to efficiently compute

{u}_w^{(i)}

using first-order approximation. We construct the following structure

S\left(\mathbf{x},<\mathtt{mask}>\right)=

\left\{\begin{array}{cc}{\mathbf{s}}_1:& <\mathtt{mask}>,{x}_2,{x}_3,\dots, {x}_l;\\ {}{\mathbf{s}}_2:& {x}_1,<\mathtt{mask}>,{x}_3,\dots, {x}_l;\\ {}& \dots \\ {}{\mathbf{s}}_l:& {x}_1,{x}_2,\dots, {x}_{l-1},<\mathtt{mask}>;\end{array}\right..

In a typical classifier, the input sentence will be converted to a sequence of embeddings noted

{\mathbf{e}}_{\cdot }

; thus we convert

S\left(\mathbf{x},<\mathtt{mask}>\right)

\left\{\begin{array}{cc}{E}_{{\mathbf{s}}_1}:& {\mathbf{e}}_{<\mathtt{mask}>},{\mathbf{e}}_{x_2},{\mathbf{e}}_{x_3},\dots, {\mathbf{e}}_{x_l};\\ {}{E}_{{\mathbf{s}}_2}:& {\mathbf{e}}_{x_1},{\mathbf{e}}_{<\mathtt{mask}>},{\mathbf{e}}_{x_3},\dots, {\mathbf{e}}_{x_l};\\ {}& \dots \\ {}{E}_{{\mathbf{s}}_l}:& {\mathbf{e}}_{x_1},{\mathbf{e}}_{x_2},\dots, {\mathbf{e}}_{x_{l-1}},{\mathbf{e}}_{<\mathtt{mask}>};\end{array}\right..

We input

{\mathbf{s}}_k

into the classifier, then compute the gradient of

\log f\left(y|{\mathbf{s}}_k\right)

with respect to

{\mathbf{e}}_{<\mathtt{mask}>}

at the

k

-th position. We then approximate the log probability by substituting

{\mathbf{e}}_{<\mathtt{mask}>}

with

{\mathbf{e}}_w

. The log probability change can be approximated by the inner product of

{\nabla}_{{\mathbf{e}}_{<\mathtt{mask}>}}\log f\left(y|{\mathbf{s}}_k\right)

and

{\mathbf{e}}_w-{\mathbf{e}}_{<\mathtt{mask}>}

. Formally,

\begin{array}{l}{u}_w^{(k)}=\left\langle {\nabla}_{{\mathbf{e}}_{<\mathtt{mask}>}}\log f\left(y|{\mathbf{s}}_k\right),{\mathbf{e}}_w-{\mathbf{e}}_{<\mathtt{mask}>}\right\rangle \\ {}\kern2.36em +\log f\left(y|{\mathbf{s}}_k\right)\end{array}

(3)

f\left(y|{\mathbf{s}}_k\right)

and

{\nabla}_{{\mathbf{e}}_{<\mathtt{mask}>}}\log f\left(y|{\mathbf{s}}_k\right)

needs to be computed only once for each masked sentence

{\mathbf{s}}_k

, and does not have to repeat for every word-and-sentence combo.

{\mathbf{e}}_w

and

{\mathbf{e}}_{<\mathtt{mask}>}

are fixed vectors. Equation (3) is an inner product, and thus very efficient to compute.

4 Single-Word Perturbation Attack

For attackers who try to find fluent and semantically similar adversarial examples, words with high $\kappa$ provide the potential for low-cost attacks. We propose SP-Attack, which first uses our algorithm, EUBA to estimate $\kappa$ , then use the top $M$ words with highest $\kappa$ to craft an attack. Figure 2 shows the attack pipeline.

To conduct an attack on a sentence

\mathbf{x}

of length

l

, we try to put these words at all possible positions to create a pool of

l\times M

candidate sentences. Then, we draw samples from the pool and verify them on the classifier. We stop when we either exhaust the pool or find

k

candidates that change the prediction. To ensure similarity and fluency, we employ Universal Sentence Encoder (USE) (Cer et al. 2018) and BERT language models. For each

{\mathbf{x}}^{\prime }

that can change the prediction, we compute a joint criteria score

\alpha \cos \left(H\left({\mathbf{x}}^{\prime}\right),H\left(\mathbf{x}\right)\right)-\beta \frac{\mathrm{PPL}\left({\mathbf{x}}^{\prime}\right)}{\mathrm{PPL}\left(\mathbf{x}\right)}

(4)

where

H\left(\cdot \right)

is the USE sentence embedding, and

\mathrm{PPL}\left(\cdot \right)

is the perplexity of a sentence measured by BERT. We then pick the sentence with the highest score as output. We set

M=50,k=50,\alpha =3,\beta =20

in our experiments.

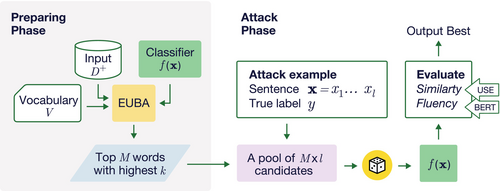
There are two differences between SP-Attack and conventional black-box adversarial attacks. (1) SP-Attack substitutes only one word with one of the $M=50$ words, whereas conventional methods can change multiple words and can use any word. As a result, SP-Attack is much more efficient. (2) Estimating $\kappa$ using EUBA requires computing the gradient of the classifier, while black-box adversarial attack methods do not. Even so, our attack method can be applied to real-world scenarios—for example, an insider attack where someone with access to the classifier calculates the flip capacity and leaks high-capacity words to other malicious users, who use them to conduct attacks.

5 Single-Word Perturbation Defence

We present a data augmentation strategy, SP-Defence, to improve the robustness of the classifier in a single-word perturbation scenario. Specifically, we design three augmentations.

Random augmentation randomly picks one word in a sentence, then replaces it with another random word in $V$ . Since $95\%$ words have at least 6.5% $\kappa$ according to our experimental results, even pure randomness can sometimes alter the classifier's prediction.

Gradient-based augmentation uses gradient information to find a single-word substitution that is more likely to cause misclassification. We approximate the log probability of correct prediction after substituting

{x}_i

with

w

{v}_w^{(i)}=\left\langle {\nabla}_{{\mathbf{e}}_{x_i}}\log f\left(y|\mathbf{x}\right),{\mathbf{e}}_w-{\mathbf{e}}_{x_i}\right\rangle +\log f\left(y|\mathbf{x}\right)

(5)

Then we apply the substitution with the minimum ${v}_w^{(i)}$ . Equation (5) is more efficient because it only needs one forward and backward pass on $f\left(y|\mathbf{x}\right)$ to compute ${\nabla}_{{\mathbf{e}}_{x_i}}\log f\left(y|\mathbf{x}\right)$ , comparing to $l$ forward and backward passes on ${\nabla}_{<\mathtt{mask}>}\log f\left(y|{\mathbf{s}}_i\right)$ in Equation (3). Therefore it is more suitable for data augmentation, which usually involves large-scale training data.

Some attack methods use a vocabulary different from

V

. They can substitute

{x}_i

with a word

t\cancel{\in }V

. Neither gradient-based nor random augmentation can defend against adversarial examples caused by

t

. Special word augmentation is designed to address this issue. For each class

y

, we find a set of words that occurs much more frequently in other classes

{y}^{\prime }

, formally

\begin{array}{l}T(y)=\Big\{t\mid \underset{y^{\prime}\ne y}{\max}\log {\mathrm{freq}}_D\left(t,{y}^{\prime}\right)\\ {}\kern4.12em -\log {\mathrm{freq}}_D\left(t,y\right)>1\Big\}\end{array}

(6)

where

{\mathrm{freq}}_D\left(t,y\right)

is the frequency of the word

t

in all the training examples with the label

y

. To augment an example

\left(\mathbf{x},y\right)

, we randomly sample a position in

\mathbf{x}

and replace it with a random word

t\in T(y)

In each training iteration, we apply gradient-based augmentation on half of the batch. For the other half, we randomly choose from original training data, random augmentation, or special word augmentation.

6 Experiments

In this section, we conduct comprehensive experiments to support the following claims: $\kappa$ and $\rho$ metrics are necessary in showing the classifier robustness against single-word perturbation (Section 6.2); SP-Attack is as effective as conventional adversarial attacks that change multiple words (Section 6.3); SP-Defence can improve any classifier's robustness in both single-word and multiple-word perturbation setups (Section 6.4); EUBA is well-designed and configured to achieve a tighter bound than alternative designs (Section 6.5).

6.1 Setup

Datasets. We conduct our experiments on four datasets: (1) AG—news topic classification, (2) MR—movie review sentiment classification (Pang and Lee 2005), (3) SST2—Binary Sentiment Treebank (Wang et al. 2019), and (4) Hate speech detection dataset (Kurita et al. 2020). Dataset details are shown in Table 3.

TABLE 3. Dataset details. #C is the number of classes, Len is the average number of words in a sentence.

Name	#C	Len	Description
AG	4	43	News topic classification.
MR	2	32	Movie review dataset by Pang and Lee (2005).
SST2	2	20	Binary Sentiment Treebank (Wang et al. 2019).
HATE	2	23	Hate speech detection dataset by Kurita et al. (2020).

Classifiers. We evaluate our method on two classifiers, the BERT-base classifier (Devlin et al. 2019) and the distilBERT-base classifier (Sanh et al. 2019). We select BERT models, which are masked language models, because they are trained to predict the masked token. The vanilla classifiers are trained with the full training set for 20 k batches with batch size 32 using the AdamW (Loshchilov and Hutter 2019) optimizer and learning rate 2e-5. We also include results for the RoBERTa-base classifier (Liu et al. 2019) in Appendix E.3.

Metrics. We use several metrics to show the quality and robustness of a classifier.

(CAcc $\uparrow$ ): clean accuracy, the accuracy of the classifier measured on the original test set.
$\rho$ : quantifies classifier robustness in a single-word perturbation scenario.
- –
  $\rho$ ( $\uparrow$ ) is measured on 1000 examples sampled from the training set.
- –
  ${\rho}^{\ast }$ ( $\uparrow$ ) is measured on the test set.
(ASR $\downarrow$ ): attack success rate that shows how robust the classifier is against an adversarial attack method. This is defined as

ASR=\frac{\#\kern0.5em \mathrm{successful}\kern0.5em \mathrm{attacks}}{\#\kern0.5em \mathrm{correct}\kern0.5em \mathrm{prediction}\kern0.5em \mathrm{in}\kern0.5em \mathrm{testset}}

A lower ASR means the classifier is more robust. We consider an attack to be successful if the similarity measured by the cosine of USE embeddings is greater than 0.8.

(ASR1 $\downarrow$ ): Since we are interested in single-word perturbations, we constrain other attack methods and use adversarial examples from them that have only one word perturbed and evaluate ASR.

Note that ASR also shows the efficacy of attack methods. A higher ASR means the attack method is more effective. We use ASR $\left(\uparrow \right)$ , and similarly ASR1 $\left(\uparrow \right)$ , in the context of comparing attacks.

Human evaluation. We collect human annotation to further verify the similarity and fluency of adversarial sentences. We ask human annotators to rate sentence similarity and sentence fluency in 5-likert. In addition, we ask humans to check if the adversarial sentence preserves the original label. See Appendix E.2 for detailed settings.

Adversarial attack SOTA. We compare SP-Attack against three state-of-the-art methods, namely: TextFooler (Jin et al. 2020), BAE (Garg and Ramakrishnan 2020) and CLARE (Li, Zhang, et al. 2021). When reporting ASR, any adversarial example generated with one (or more) word changes is considered a successful attack. While in ASR1, we consider the subset of adversarial sentences with only a single-word change as a successful attack.

Data augmentation and adversarial training. We compare SP-Defence with several baselines.

Rand: We conduct random perturbations to augment training data in all steps of training.
A2T (Yoo and Qi 2021) is an efficient gradient-based adversarial attack method designed for adversarial training.

For Rand and SP-Defence, we tune the classifier with another 20 k batches. For A2T, we tune the classifier with 3 additional epochs as recommended by the authors.

6.2 Necessity of $\kappa$ and $\rho$ Metrics

We measure the exact $\kappa$ using brute force for the BERT-base classifier on AG and MR. The measurement takes 197 and 115 GPU hours respectively on a single Nvidia V100 GPU. Figure 3 shows the histogram of $\kappa$ . We find that 95% of words in the vocabulary can successfully attack at least 6.5% and 12.4% of examples, while the top 0.1% of words can change as much as 38.7% and 49.4% examples on the two datasets respectively. This shows that classifiers are extremely vulnerable to single-word perturbations. The distributions of $\kappa$ for the two tasks are different, showing $\kappa$ is task-dependent. Words have lower average $\kappa$ on AG than on MR. We compute the $\rho (f)$ as $90.9$ and $83.8$ for the two datasets respectively. See additional analysis of words with high $\kappa$ in Appendix D.

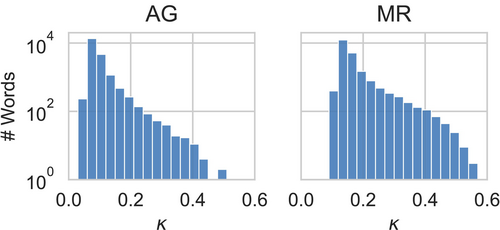
We highlight the necessity of $\kappa$ and $\rho$ metrics. $\kappa$ can show the flip capability of each individual word. It precisely reveals all vulnerabilities of the classifier under single-word perturbation. $\rho$ is derived from $\kappa$ and factors in the number of different single-word perturbations that can successfully attack each sentence. It quantifies classifier robustness to single-word perturbation scenarios more effectively than ASR, which only shows whether each sentence could be successfully attacked.

6.3 SP-Attack Performance

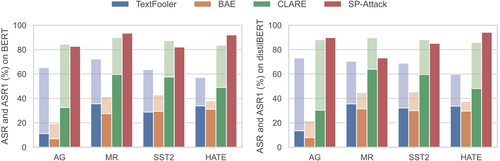
Figure 4 shows the ASR and ASR1 for all datasets, two different classifiers (left and right) and multiple attack methods. We make a few noteworthy observations. SP-Attack is the most effective method for finding adversarial examples based on single-word perturbations. ASR1's for SP-Attack are at least 73%, and over 80% in 7 out of 8 cases, demonstrating the significant vulnerability of these classifiers. A second observation is that other methods, even those with a notable number of single word perturbation-based adversarial examples, have significantly lower ASR1's (where only single-word adversarial examples are included) than ASR's (where multi-word adversarial examples are included). For TextFooler across the 8 experiments, the difference between ASR and ASR1 is 38.3%. An obvious next question we examine is whether multi-word substitutions are essential for achieving higher attack success rates. Our experiments also show that SP-Attack achieves comparable ASR with single-word perturbations, and even beats the best multi-word substitution in 4 out of 8 cases.

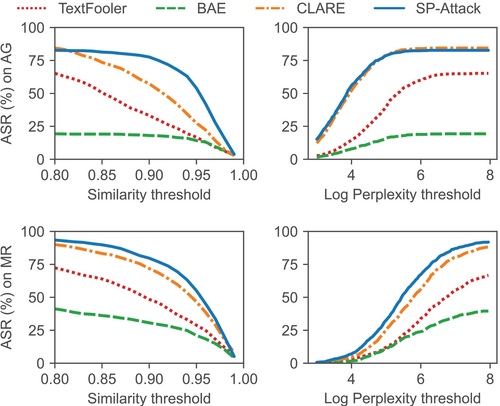
Single-word perturbation may cause poor fluency and/or low semantic similarity. To show SP-Attack is comparable with multi-word attacks in terms of fluency and similarity, we plot the ASR under different similarity and perplexity thresholds. We measure similarity using USE and perplexity using a BERT language model fine-tuned on the dataset. Figure 5 shows the results on AG and MR datasets. It shows that, at the same threshold, SP-Attack achieves comparable or better ASR than those attack baselines. Table 4 shows the human evaluation. The similarity and fluency scores are similar for all methods, but SP-Attack outperforms baselines by 5% and 10% in preserving the original label on AG and MR datasets respectively. We show inter-annotator agreement in Appendix E.2.

TABLE 4. Similarity scores, fluency scores and the percentage of sentences which preserve the original label by human annotators.

Dataset	Attack	Similarity	Fluency	Preserve label
AG	TextFooler	3.40	3.41	80%
	Clare	3.37	3.33	82%
	SP-Attack	3.47	3.39	87%
MR	TextFooler	3.93	3.47	69%
	Clare	3.96	3.41	83%
	SP-Attack	4.02	3.48	93%

6.4 SP-Defence Performance

6.4.1 Can Our SP-Defence Overcome Our Attack?

We measure the accuracy and robustness of the vanilla and improved classifiers. The complete results are available in Appendix E.3.

Table 5 shows the CAcc, $\rho$ , ${\rho}^{\ast }$ and ASR of SP-Attack. We observe that all data augmentation or adversarial training methods have small impacts on CAcc; in most cases, the decrease is less than 1%. However, $\rho$ and ${\rho}^{\ast }$ differ a lot, showing that classifiers with similar accuracy can be very different in terms of robustness to single-word attacks (both in training and testing). We found that SP-Defence outperforms Rand and A2T on ${\rho}^{\ast }$ in all cases. This shows that SP-Defence can effectively improve a classifier's robustness in a single-word perturbation scenario. Averaged over 4 datasets, SP-Defence achieves 14.6% and 13.9% increases on $\rho$ ; 8.7% and 8.4% increases on ${\rho}^{\ast }$ ; and 30.4% and 21.2% decreases on ASR of SP-Attack on BERT and distilBERT classifiers respectively.

TABLE 5. CAcc(

\uparrow

\rho

(

\uparrow

) and ASR(

\downarrow

) of SP-Attack on vanilla and improved classifiers.

	Defence	CAcc	$\rho$	${\rho}^{\ast }$	ASR	CAcc	$\rho$	${\rho}^{\ast }$	ASR	CAcc	$\rho$	${\rho}^{\ast }$	ASR	CAcc	$\rho$	${\rho}^{\ast }$	ASR
	Defence	AG				MR				SST2				HATE
BERT	NA	93.7	91.5	90.1	82.7	87.7	86.4	77.2	93.5	80.6	74.7	76.6	82.1	94.5	72.6	71.4	92.1
	Rand	92.0	96.3	93.1	66.2	87.5	98.2	80.7	84.2	79.8	82.1	79.7	77.9	94.3	86.3	83.2	89.2
	A2T	93.4	96.2	92.9	62.7	88.3	90.4	76.2	69.3	80.4	76.5	74.9	69.5	93.4	87.1	82.1	87.3
	SP-D	94.3	97.4	94.1	33.7.	87.5	99.8	83.1	61.8	79.3	90.0	80.5	68.8	93.7	96.6	92.5	64.4
distilBERT	NA	94.0	91.7	91.6	89.9	85.9	85.6	72.7	73.2	78.7	75.8	74.3	85.1	93.3	73.8	72.9	94.2
	Rand	94.2	95.4	92.0	69.5	86.0	96.5	78.1	92.2	78.0	81.1	78.3	87.2	93.1	85.6	82.6	91.3
	A2T	94.0	95.3	92.6	64.8	85.0	85.1	73.4	88.8	78.3	77.7	76.1	80.5	93.2	86.1	82.0	89.5
	SP-D	94.3	97.6	93.6	43.1	85.1	99.8	79.6	73.4	78.2	88.3	80.2	73.0	92.0	96.9	91.6	68.4

Note: NA denotes the vanilla classifier. Bold values are the best results of each column according to the up/down arrows in the caption.
Abbreviation: SP-D, SP-defence.

6.4.2 Can Our SP-Defence Overcome Other SOTA Attacks Constrained to Single-Word Adversarial Examples?

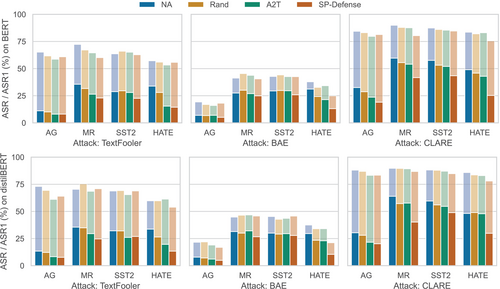
Figure 6 shows the ASR and ASR1 on vanilla and improved classifiers for different SOTA attacks (left to right). The ASR1 decreases by a large margin after the application of SP-Defence, which is consistent with the improvement on ${\rho}^{\ast }$ . The ASR also decreases in 20 out of 24 cases, showing the improvement of classifier robustness against a conventional multi-word adversarial attack setup.

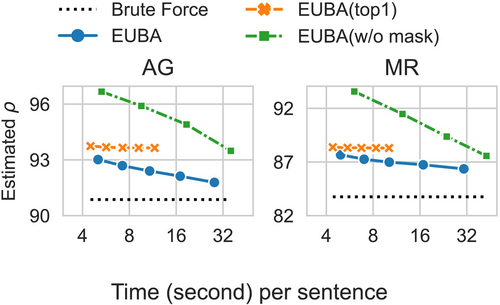
6.5 Justifying Design Decisions of EUBA

We show the gap between the

\rho

upper bound and its true value when setting different early stop criteria. We set

m=\left\{\mathrm{128,256,512,1024,2048}\right\}

. We also changed phase 1 in EUBA to form two alternative designs:

EUBA (top 1): We use the same gradient-based approximation. But for each word, we only verify the top position, that is, $\arg {\min}_i\;{u}_w^{(i)}$ .
EUBA (w/o mask): We do not replace each position with masks. Instead, we use the original sentence to directly compute a first-order approximation like Equation (5).

Figure 7 shows the estimated

\rho

with respect to average time consumption for each example in

{D}^{+}

. We observe that our proposed design is the closest to brute force. EUBA outperforms alternative methods given the same time budget, and is very close to the true

\rho

7 Related Work

The widespread deployment of text classifiers has exposed several vulnerabilities. Backdoors can be injected during training that can later be used to manipulate the classifier output (Li, Song, et al. 2021; Zhang, Xiao, et al. 2023; Jia et al. 2022; Yan et al. 2023; You et al. 2023; Du et al. 2024). The use cases of backdoor attacks are limited because they involve interfering with the training. Universal adversarial triggers can be found for classifiers (Wallace et al. 2019), wherein triggers, usually involving multiple-word perturbations, change the classifier prediction for most sentences. Adversarial attack methods (Jin et al. 2020; Garg and Ramakrishnan 2020; Li et al. 2020; Li, Zhang, et al. 2021; Zhan et al. 2024; Zhan et al. 2023; Zhang, Huang, et al. 2023; Li et al. 2023; Ye et al. 2022) change a classifier's prediction by perturbing a few words or characters in the sentence. They maintain high semantic similarity and fluency, but are computationally expensive. SP-Attack attacks the classifier by trying just a few single-word perturbations, making it an efficient attack that maintains the high similarity and effective fluency of conventional adversarial attacks.

To defend against attacks, adversarial training can be applied. Adversarial training is often used to help the classifier resist the types of attacks described above. A2T (Yoo and Qi 2021) is an efficient attack designed specifically for adversarial training. There are other defence methods including perplexity filtering (Qi et al. 2021), and synonym substitution (Wang et al. 2021), which increase the inference time complexity of the classifier. Our SP-Defence does not add overhead to inference and can effectively defend against adversarial attacks.

8 Conclusion

In this paper, we comprehensively analyse a restricted adversarial attack setup with single-word perturbation. We define two useful metrics—ρ, the quantification of a text classifier's robustness against single-word perturbation attacks, and $\kappa$ , the adversarial capability of a word—and show that these metrics are useful to measure classifier robustness. Furthermore, we propose SP-Attack, a single-word perturbation attack which achieves a comparable or better attack success rate than existing and more complicated attack methods on vanilla classifiers, and significantly reduces the effort necessary to construct adversarial examples. Finally, we propose SP-Defence to improve classifier robustness in a single-word perturbation scenario, and show that it also improves robustness against multi-word perturbation attacks.

Acknowledgements

Prof. Cuesta-Infante was supported by R&D project TED2021-129162B-C22, funded by MICIU/AEI/10.13039/501100011033/ and the European Union NextGenerationEU/PRTR, and R&D project PID2021-128362OB-I00, funded by MICIU/AEI/10.13039/501100011033/ and FEDER/UE.

Open Research

Data Availability Statement

The data that support the findings of this study are openly available in Movie Review Data at https://www.cs.cornell.edu/people/pabo/movie-review-data/.

Supporting Information

References

Cer, D., Y. Yang, S.-y. Kong, et al. 2018. “Universal Sentence Encoder for English. In Proceedings of the Conference on Empirical Methods in Natural Language Processing: System Demonstrations”.
Google Scholar
Devlin, J., M.-W. Chang, K. Lee, and K. Toutanova. 2019. “Bert: Pre-Training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the Annual Conference of the North American Chapter of the Association for Computational Linguistics”.
Google Scholar
Du, W., T. Ju, G. Ren, G. L. Li, and G. Liu. 2024. “Backdoor NLP Models via AI-Generated Text. In Proceedings of the 2024 Joint International Conference on Computational Linguistics, Language Resources and Evaluation (LREC-COLING 2024), 2067–2079, Torino, Italia. ELRA and ICCL”.
Google Scholar
Garg, S., and G. Ramakrishnan. 2020. “Bae: Bert-Based Adversarial Examples for Text Classification. In Proceedings of the Conference on Empirical Methods in Natural Language Processing and the International Joint Conference on Natural Language Processing”.
Google Scholar
Jia, J., Y. Liu, and N. Z. Gong. 2022. “Badencoder: Backdoor Attacks to Pre-Trained Encoders in Self-Supervised Learning. In 2022 IEEE Symposium on Security and Privacy (SP), 2043–2059”.
Google Scholar
Jin, D., Z. Jin, J. T. Zhou, and P. Szolovits. 2020. “Is Bert Really Robust? Natural Language Attack on Text Classification and Entailment. In Proceedings of the AAAI Conference on Artificial Intelligence”.
Google Scholar
Kurita, K., P. Michel, and G. Neubig. 2020. “Weight Poisoning Attacks on Pretrained Models. In ACL”.
Google Scholar
Li, D., Y. Zhang, H. Peng, et al. 2021. “Contextualized Perturbation for Textual Adversarial Attack. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics”.
Google Scholar
Li, G., B. Shi, Z. Liu, et al. 2023. “ Adversarial Text Generation by Search and Learning.” In Findings of the Association for Computational Linguistics: EMNLP 2023, 15722–15738. Association for Computational Linguistics.
10.18653/v1/2023.findings-emnlp.1053
Google Scholar
Li, L., R. Ma, Q. Guo, X. Xue, and X. Qiu. 2020. “Bert-Attack: Adversarial Attack Against Bert Using Bert. In Proceedings of the Conference on Empirical Methods in Natural Language Processing and the International Joint Conference on Natural Language Processing”.
Google Scholar
Li, L., D. Song, X. Li, J. Zeng, R. Ma, and X. Qiu. 2021. “Backdoor Attacks on Pre-Trained Models by Layerwise Weight Poisoning. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, 3023–3032, Online and Punta Cana, Dominican Republic. Association for Computational Linguistics”.
Google Scholar
Liu, Y., M. Ott, N. Goyal, et al. 2019. Roberta: A Robustly Optimized Bert Pretraining Approach. arXiv Preprint arXiv:1907.11692.
Google Scholar
Loshchilov, I., and F. Hutter. 2019. “Decoupled Weight Decay Regularization. In Proceedings of the International Conference on Learning Representations”.
Google Scholar
Pang, B., and L. Lee. 2005. “Seeing Stars: Exploiting Class Relationships for Sentiment Categorization With Respect to Rating Scales. In Proceedings of the Annual Meeting of the Association for Computational Linguistics”.
Google Scholar
Qi, F., Y. Chen, M. Li, Y. Yao, Z. Liu, and M. Sun. 2021. “Onion: A simple and effective defense against textual backdoor attacks. In EMNLP”.
Google Scholar
Sanh, V., L. Debut, J. Chaumond, and T. Wolf. 2019. “Distilbert, a Distilled Version of Bert: Smaller, Faster, Cheaper and Lighter. 5th NeurIPS Workshop on Energy Efficient Machine Learning and Cognitive Computing (2019), ArXiv Preprint arXiv:1910.01108”.
Google Scholar
Torabi Asr, F., and M. Taboada. 2019. “Big Data and Quality Data for Fake News and Misinformation Detection.” Big Data & Society 6, no. 1: 2053951719843310.
10.1177/2053951719843310
Google Scholar
Wallace, E., S. Feng, N. Kandpal, M. Gardner, and S. Singh. 2019. “Universal adversarial triggers for attacking and analyzing NLP. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), 2153–2162, Hong Kong, China. Association for Computational Linguistics”.
Google Scholar
Wang, A., A. Singh, J. Michael, F. Hill, O. Levy, and S. R. Bowman. 2019. “Glue: A Multi-Task Benchmark and Analysis Platform for Natural Language Understanding. In Proceedings of the International Conference on Learning Representations”.
Google Scholar
Wang, X., H. Jin, Y. Yang, and K. He. 2021. “Natural Language Adversarial Defense Through Synonym Encoding. In the Conference on Uncertainty in Artificial Intelligence”.
Google Scholar
Wu, L., F. Morstatter, K. M. Carley, and H. Liu. 2019. “Misinformation in Social Media: Definition, Manipulation, and Detection. ACM SIGKDD Explorations Newsletter”.
Google Scholar
Yan, J., V. Gupta, and X. Ren. 2023. “BITE: Textual Backdoor Attacks With Iterative Trigger Injection. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 12951–12968, Toronto, Canada. Association for Computational Linguistics”.
Google Scholar
Ye, M., C. Miao, T. Wang, and F. Ma. 2022. “Texthoaxer: Budgeted Hard-Label Adversarial Attacks on Text.” Proceedings of the AAAI Conference on Artificial Intelligence 36, no. 4: 3877–3884.
10.1609/aaai.v36i4.20303
Google Scholar
Yoo, J. Y., and Y. Qi. 2021. “Towards Improving Adversarial Training of nlp Models. In Findings of EMNLP”.
Google Scholar
You, W., Z. Hammoudeh, and D. Lowd. 2023. “Large Language Models Are Better Adversaries: Exploring Generative Clean-Label Backdoor Attacks Against Text Classifiers. In Findings of the Association for Computational Linguistics: EMNLP 2023, pages 12499–12527, Singapore. Association for Computational Linguistics”.
Google Scholar
Zhan, P., J. Yang, W. He, C. Zheng, and L. Wang. 2024. “Rethinking Word-Level Adversarial Attack: The Trade-Off Between Efficiency, Effectiveness, and Imperceptibility. In Proceedings of the 2024 Joint International Conference on Computational Linguistics, Language Resources and Evaluation (LREC-COLING 2024), 14037–14052, Torino, Italia. ELRA and ICCL”.
Google Scholar
Zhan, P., J. Yang, H. Wang, C. Zheng, X. Huang, and L. Wang. 2023. “ Similarizing the Influence of Words With Contrastive Learning to Defend Word-Level Adversarial Text Attack.” In Findings of the Association for Computational Linguistics: ACL 2023, 7891–7906. Association for Computational Linguistics.
10.18653/v1/2023.findings-acl.500
Google Scholar
Zhang, J., Y.-C. Huang, W. Wu, and M. R. Lyu. 2023. “Towards Semantics- and Domain-Aware Adversarial Attacks. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-23, Pages 536–544. International Joint Conferences on Artificial Intelligence Organization. Main Track”.
Google Scholar
Zhang, Z., G. Xiao, Y. Li, et al. 2023. “Red Alarm for Pre-Trained Models: Universal Vulnerability to Neuron-Level Backdoor Attacks.” Machine Intelligence Research 20, no. 2: 180–193.
10.1007/s11633-022-1377-5
Web of Science® Google Scholar
Zhou, Z., H. Guan, M. M. Bhat, and J. Hsu. 2019. “Fake News Detection via NLP is Vulnerable to Adversarial Attacks. In Proceedings of the 11th International Conference on Agents and Artificial Intelligence, ICAART'19, 794–800”.
Google Scholar

Volume42, Issue8

August 2025

e70079

Single Word Change Is All You Need: Using LLMs to Create Synthetic Training Examples for Text Classifiers

ABSTRACT

1 Introduction

2 Quantifying Classifier Robustness Against Single-Word Perturbations

2.1 Single-Word Perturbation Attack Setup

2.2 Two Useful Metrics for Robustness

2.3 Definitions and Theorem

3 Efficient Estimation of the Metrics

3.1 Overview

3.2 First-Order Approximation

4 Single-Word Perturbation Attack

5 Single-Word Perturbation Defence

6 Experiments

6.1 Setup

6.2 Necessity of $\kappa$ and $\rho$ Metrics

6.3 SP-Attack Performance

6.4 SP-Defence Performance

6.4.1 Can Our SP-Defence Overcome Our Attack?

6.4.2 Can Our SP-Defence Overcome Other SOTA Attacks Constrained to Single-Word Adversarial Examples?

6.5 Justifying Design Decisions of EUBA

7 Related Work

8 Conclusion

Acknowledgements

Open Research

Data Availability Statement

Supporting Information

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Single Word Change Is All You Need: Using LLMs to Create Synthetic Training Examples for Text Classifiers

ABSTRACT

1 Introduction

2 Quantifying Classifier Robustness Against Single-Word Perturbations

2.1 Single-Word Perturbation Attack Setup

2.2 Two Useful Metrics for Robustness

2.3 Definitions and Theorem

3 Efficient Estimation of the Metrics

3.1 Overview

3.2 First-Order Approximation

4 Single-Word Perturbation Attack

5 Single-Word Perturbation Defence

6 Experiments

6.1 Setup

6.2 Necessity of κ $$ \kappa $$ and ρ $$ \rho $$ Metrics

6.3 SP-Attack Performance

6.4 SP-Defence Performance

6.4.1 Can Our SP-Defence Overcome Our Attack?

6.4.2 Can Our SP-Defence Overcome Other SOTA Attacks Constrained to Single-Word Adversarial Examples?

6.5 Justifying Design Decisions of EUBA

7 Related Work

8 Conclusion

Acknowledgements

Open Research

Data Availability Statement

Supporting Information

References

Figures

References

Related

Information

6.2 Necessity of $\kappa$ and $\rho$ Metrics