Resisting annihilation: relationships between functional trait dissimilarity, assemblage competitive power and allelopathy
Abstract
Allelopathic species can alter biodiversity. Using simulated assemblages that are characterised by neutrality, lumpy coexistence and intransitivity, we explore relationships between within-assemblage competitive dissimilarities and resistance to allelopathic species. An emergent behaviour from our models is that assemblages are more resistant to allelopathy when members strongly compete exploitatively (high competitive power). We found that neutral assemblages were the most vulnerable to allelopathic species, followed by lumpy and then by intransitive assemblages. We find support for our modeling in real-world time-series data from eight lakes of varied morphometry and trophic state. Our analysis of this data shows that a lake's history of allelopathic phytoplankton species biovolume density and dominance is related to the number of species clusters occurring in the plankton assemblages of those lakes, an emergent trend similar to that of our modeling. We suggest that an assemblage's competitive power determines its allelopathy resistance.
Introduction
Superior competitors exploit resources better than inferior competitors (Tilman 1977, 1982; Keddy 1989). Yet, species that are poor exploiters may persist by employing interference strategies to gain access to resources (Case & Gilpin 1974). In phytoplankton, where resources are commonly nutrients, an active behaviour to enhance nutrient acquisition employed by some species is allelopathy (Smayda 1997; Legrand et al. 2003; Thornton 2014), a process where exuded chemicals of a species negatively affect the fitness of competing species of the same trophic level (Legrand et al. 2003; Hattenrath-Lehmann & Gobler 2011). Negative effects could involve lysis, and subsequent phagotrophy of cell fragments by the allelopathic species or uptake of liberated cellular compounds through osmotrophy, or the allelopathic species might simply benefit from microbial regeneration of nutrients from lysed cells that then become available for reuse (Uronen et al. 2007). Note, for our purposes ‘allelopathy’ is different from ‘toxicity’ (see Supporting Information).
While the prima facie cornerstone of allelopathic ecological understanding is that allelopathy facilitates bloom formation by reducing competitor density and subsequently increasing nutrient availability (Lewis 1986; Smayda 1997; Fistarol et al. 2003; Legrand et al. 2003; Jonsson et al. 2009), experimental and field observations of exuded chemical impacts within phytoplankton assemblages reveal a wide spectrum of effects (Hattenrath-Lehmann & Gobler 2011). For example, pairwise interactions of species exposed to exudate of the dinoflagellate Karenia brevis reveal differential effects among assemblage members (Poulson et al. 2010). Similarly, stimulatory effects of exudates to other phytoplankters have been observed with cyanobacteria and dinoflagellates that otherwise are considered allelopathic groups (Suikkanen et al. 2005; Poulson et al. 2010; Neisch et al. 2012). Succession during some allelopathic blooms is complex, with observed co-dominance of species (Lindholm et al. 1999; Redalje et al. 2008) and persistence of multiple sub-dominant species (West et al. 1996; de Figueiredo et al. 2006). This variation of exuded chemical effects spotlights our limited understanding of allelopathic functioning in ecosystems.
Further understanding of allelopathic functioning in plankton systems may arise from insights into phytoplankton assemblage structure, and how this structure relates to the degree of exploitative competition occurring within assemblages, which we now refer to as the ‘competitive power’ of the assemblage. For our purposes here, ‘structure’ refers to the competitive abilities of assemblage members to exploit resources relative to each other, which is typically depicted by the distribution of R* values through the resource trade-off space (sensu Tilman, discussed further below). In theory, this type of structure characterisation is related to biodiversity, succession dynamics, productivity and stability (Tilman 2004; Chase & Leibold 2014). Here, we explore whether assemblage structure influences allelopathy efficacy with a focus on assemblages whose structure derives from generalised ecological concepts relating to competition, which are neutrality, lumpy coexistence and intransitivity (see Supporting Information).
As mentioned before, effects of allelopathy on phytoplankton are diverse, and our limited understanding of underpinning mechanisms might be, in part, a function of our lack of knowledge of distinctive assemblage structures occurring in natural environments. Researchers acknowledge that methodologies for study of sensitivities of individual phytoplankton species to allelopathic compounds overlook assemblage dynamics (Kubanek et al. 2005), and experiments exploring allelopathic influence on natural assemblages do not directly relate allelopathy and assemblage state (Poulson et al. 2010; Tang & Gobler 2010; Poulson-Ellestad et al. 2014). We address that here by employing mathematical models to explore the interaction of allelochemical production rate and target species sensitivity on diversity in assemblages governed by neutrality, lumpy coexistence and intransitivity. Emergent behaviour of our combined models is then tested using phytoplankton time-series data from several lakes of varied morphometry and trophic state.
Methods
Mathematical model
We started with a well-known numerical model that depicts multiple phytoplankton species competing for multiple growth-limiting resources (Leon & Tumpson 1975; Tilman 1982; Grover 1997). The model structure and its parameterisation and initialisation follows closely with Roelke & Eldridge (2008) (see Supporting Information). Briefly, the model is dimensionless, employing time-dependent ordinary differential equations. To the phytoplankton equations of this model, we added a factor depicting allelopathy, affecting species that were non-allelochemical producing. We added a differential equation that depicted the concentration of the allelochemicals where increases in concentrations came about through production by the allelochemical species and decreases in concentration were through a fixed rate of decay (Martines et al. 2009). We considered only the effect of one allelopathic species on multiple non-allelopathic species.
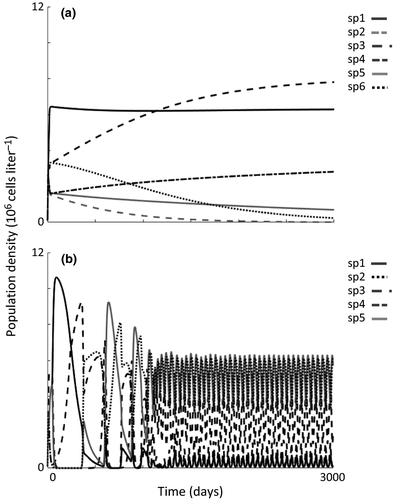
We explored how the structure of phytoplankton assemblages influenced allelopathy efficacy. We used biodiversity collapse (richness reducing to one, where the sole surviving species was the allelopathic species) to define scenarios under which allelopathy led to blooms. The scenarios explored here were based on the sensitivity of assemblage members to allelochemicals and the rate of allelochemical production. Assemblages used in these analyses (reported in Roelke & Eldridge 2008), in the absence of allelopathy, were species supersaturated, meaning the number of co-existing species at steady-state exceeded the number of limiting resources (Schippers et al. 2001). Species supersaturation (ranging between 5 and 8 species co-existing on three resources) was sustained by either neutrality, lumpy coexistence, or intransitivity. A detailed description of the self-organisation process used to generate supersaturated phytoplankton assemblages can be found in Roelke & Eldridge (2008). Population dynamics for these assemblage types in the absence of allelopathy either asymptotically approached a steady state when sustained by either neutrality or lumpy coexistence (Fig. 1a), or showed recurrent and out-of-phase species oscillations when sustained by intransitivity (Fig. 1b).
Conceptual framework
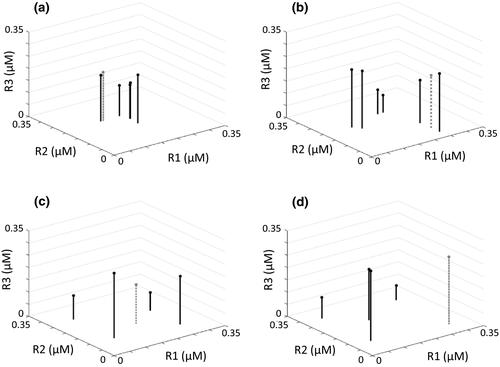
Competitive abilities of species in each assemblage type are demonstrated with a three-dimensional resource trade-off space using the R* for each species for each of the three resources (see Roelke & Eldridge 2008). The distribution of species’ R*s through the three-dimensional resource trade-off space is used to define the assemblage structure. For example, all species in neutral assemblages show close clustering in the resource trade-off space (Fig. 2a). Species in assemblages characteristic of lumpy coexistence also show close clustering, but with co-occurrence of multiple species clusters (Fig. 2b). Species in intransitive assemblages were characteristic of a recognizable geometric species distribution with assemblage members being near-equidistant to a centrally located species in the three-dimensional trade-off space (Fig. 2c,d).
Sensitivity analysis of model
We explored the resistance of phytoplankton assemblages to allelopathy by looking at how an allelopathic species influences assemblage diversity over a gradient of allelopathic effect. We varied the allelochemical production rate value (‘εc’ in the equations presented in Supporting Information), and the growth-inhibition coefficient (‘KI’ in the equations presented in Supporting Information), for which low values of KI represented extreme growth-inhibition of the non-allelopathic species, and high values of KI represented less inhibition. This resulted in varying levels of sensitivity to the allelochemical by the non-allelochemical producers. A gradient of 12 values used for εc ranged from 0 to 0.055, which spanned allelochemical production rates observed previously for cyanobacteria (Grover et al. 2010). A gradient of 100 values was used for KI, ranging from 0 to 1. During preliminary simulations we observed that values > 1 for the growth inhibition coefficient showed no effect of allelopathy. So those simulations are not reported here.
Each simulation started with all species in the assemblage and ran for 5000 days. For neutral and lumpy assemblages, starting species richness was between six and eight species, whereas for the intransitive assemblages, five species were used. Because the number of species in these assemblage types varied initially, we analysed the relative diversity instead of diversity (see more below). Using the relative diversity calculations, biodiversity maps showing changes in relative diversity in response to allelopathy were created. These maps displayed the resulting relative diversity of each assemblage at all possible combinations of εc and KI (1212 model simulations for each map).
Assemblage characteristics of interest and emergent behaviour
Relative species diversity (Shannon & Weaver 1949), relative assemblage cell density, assemblage resistance and the averaged distance of each species from the allelopathic species in the resource trade-off space were determined for the thirty assemblages (i.e. 10 neutral, 10 lumpy and 10 intransitive). These factors provide a context for ecological study at different levels of interspecific competition, although assemblage response to allelopathy will involve multiple factors in natural systems.
The assemblage resistance is given by the slopes of the boundary between allelopathic monoculture to a multispecies assemblage in the biodiversity maps (in early explorations of the model we discovered this transition to be abrupt, as we will show in our figures). The slope values were calculated by averaging the changes in εc over the changes in KI along the bloom transition boundary.
One way to characterise the competitive power of resource exploitation between species within an assemblage is through evaluation of the distance between species–specific R* values through the three-dimensional resource trade-off space (Roelke & Spatharis 2015). Here, we take that approach further by characterising the competitive similarity of the allelopathic species to all other members of the assemblage. For this, the three-dimensional distance between each species and the allelopathic species was calculated using the Pythagorean Theorem and orthogonal triangles. These distances were averaged, giving one value for each assemblage. We now refer to this calculation as the allelopathy R* composite distance.
An emergent behaviour of the model is then explored by plotting the allelopathy R* composite distance for each of the assemblages against the resistance of each assemblage to allelopathy. In this way, we were able to explore theoretical relationships between assemblage types (i.e. neutral, lumpy and intransitive) and allelopathy functioning.
Phytoplankton time-series data
For our analysis of plankton time-series, we relied on records collected from several lakes, most of which experienced harmful algal blooms at some point in their recent history and the harmful bloom-forming species were known allelochemical producers. The lake data comprised taxa mostly identified to the species level and cellular size information (Table S1). The data did not include information on the same life-history traits used in the numerical modeling that defined species competitive abilities. Instead, competitive abilities within lake assemblages were surmised by us based on the size distribution of phytoplankton species with a specific focus on the incidence and number of co-occurring species clusters (explained further below). Insights into mechanisms that link assemblage structure to efficacy of allelopathy were then achieved through comparisons of emergent behaviour of the model and emergent behaviour of the assemblages observed in the lakes.
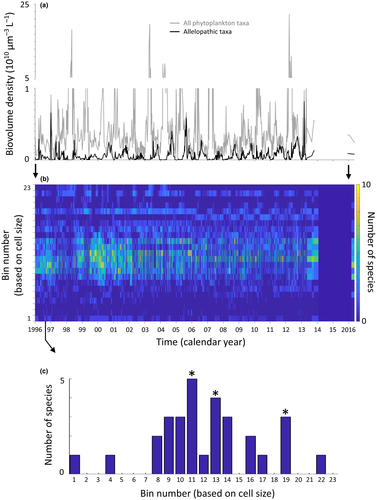
We analysed multiyear time-series data (ranging from weekly to monthly sampling frequency) of phytoplankton composition and biovolume density from eight freshwater lakes. These were Lake Mikri Prespa (2½ years) bordered by Greece and Albania; Lakes Volvi (2 years) and Koronia (1½ years) in Greece; Lake Kinneret (19 years) in Israel; Lake Constance (15 years) bordered by Switzerland, Austria and Germany; and Lakes Fancsika 1 (19 years), Fancsika 2 (19 years) and Mézeshegyi-tó (19 years) in Hungary. The lakes vary in morphometry and trophic state. Lakes Constance and Kinneret are of large area and greater depth, while being oligotrophic and mesotrophic to eutrophic, respectively. Lakes Volvi and Mikri Prespa are of intermediate area and depth, both being eutrophic. Lakes Fancsika 1, Fancsika 2 and Mézeshegyi-tó are small and shallow, all being eutrophic to hypereutrophic. Lake Koronia is a heavily modified hypereutrophic system of large area and shallow depth. Details of the collection methods for the eight lakes, including sampling and microscopy analyses for cellular size measurements can be found in those studies (Gaedke & Schweizer 1993; Gaedke 1998; Borics et al. 2000, 2013; Michaloudi et al. 2009; Zohary et al. 2012; Moustaka-Gouni et al. 2014). Time-series data for Lakes Mikri Prespa, Volvi, Koronia, and Kinneret included temporal variation in species-specific cellular size. Time-series data for Lakes Fancsika 1-es tározó, Fancsika 2-es tározó, Mézeshegyi-tó and Constance employed an averaged cellular size.
Time-series data were processed as species–specific biovolume density (μm3 L−1) and species-specific cellular biovolume (μm3 cell−1). To determine the assemblage cellular size distribution for each sampling date, we first log10 transformed cellular biovolume values and parsed the transformed data into pre-defined size classes. The pre-defined size classes were based on the largest species from all eight lakes and an optimal number of size classes. We identified the number of size classes by exploring multiple pre-defined size classes until a number was found that optimised the tradeoff between number of size classes and the size range over which each size class spanned. This optimisation process resulted in 23 size classes being selected, which spanned the range from the smallest to largest sized taxa found in all eight lakes. Following this procedure meant that size classes applied to each lake's assemblages were the same, thus enabling a comparison of assemblages across lakes. We note that the results reported here were robust over a large range of predetermined size classes.
To determine the incidence and number of species clusters occurring within assemblages, we summed the number of species occurring within each of the 23 size classes at each sampling date. The presence or absence of a species was registered once, independent of its biovolume density. In other words, we created size-frequency histograms. We then developed an algorithm to quantify the number of species clusters for each sampling date using a slope criteria applied to the size-frequency histograms. The algorithm identified ‘peaks’ in the size-frequency histograms that were only considered as central locations of species clusters if the slope from the preceding minima, or ‘valley’ (moving from smaller size taxa to larger) was ≥ 3, and the slope to the following minima, or the next ‘valley’ (still moving from smaller size taxa to larger) was ≤ −3. In this way, the number of species clusters in the assemblage was identified for each sampling date from each lake where the minimum number of species comprising a cluster was three.
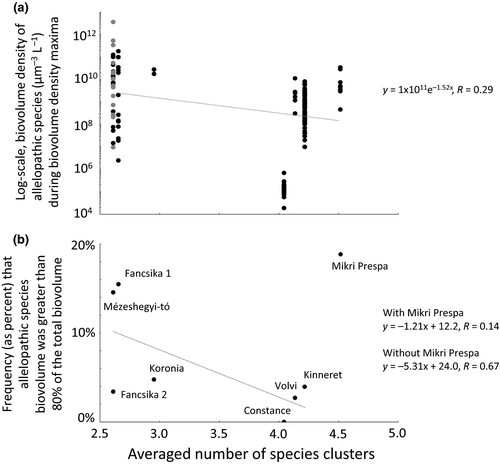
An emergent behaviour of these lake systems was then explored. For this, we first calculated the average number of species clusters occurring on any given day of sampling in each of the lakes. We plotted this against the biovolume density of allelopathic bloom-forming taxa occurring during periods when the summed biovolume densities of allelopathic species reached seasonal peaks. We fitted an exponential regression line through this data. We then calculated the frequency of allelochemical-producing species dominance, where we defined ‘dominance’ as a condition where > 80% of the total phytoplankton biovolume was comprised of allelochemical-producing species. We then plotted the average number of species clusters occurring on any given day of sampling in each of the lakes against the lakes’ frequency of allelochemical-producing species dominance. We fitted linear regression lines through this data, the first regression line using data from all eight lakes and the second regression line using only seven of the lakes (Lake Mikri Prespa excluded). We excluded Lake Mikri Prespa from the second regression because of its position as an outlier in this second plot and the known extreme weather condition the lake experienced during the time of sampling collection (discussed further below). This procedure enabled exploration of relationships between assemblage structure (here, the average number of species clusters) and allelopathy functioning (the magnitude of biovolume density maxima of allelopathic species and the frequency of dominance).
During the periods included in our analysis, there were direct measurements of allelochemicals during times of blooms of allelochemical-producing species (i.e. microcystins detected in Lake Koronia during a mixed bloom Prymnesium parvum and cyanobacteria, Michaloudi et al. 2009), and from cultures isolated from blooms of allelochemical-producing species (i.e. microcystins and cylindrospermopsins in Lake Kinneret, Sukenik et al. 2014), and observations of toxic and allelopathic impacts (i.e. fish kills and bird mortalities, copepod mortality, and rapid demise of diatoms in Lake Koronia, Michaloudi et al. 2009) that possess chemicals identified as both allelopathic and toxic (Pflugmacher 2002; Gross 2003; Mitrovic et al. 2004; Leão et al. 2009; James et al. 2011; Svercel 2013). There were also direct measurements of allelochemicals during blooms of allelochemical-producing species outside periods in our analysis (i.e. microcystins measured in Lakes Volvi and Mikri Prespa, Papadimitriou et al. 2010). From this evidence, we are confident that allelopathic interactions occur in our study lakes where allelochemical-producing species are present.
Results
Expectantly, population dynamics and assemblage composition changed with increasing effect of allelopathy in our simulations. For assemblages characteristic of neutrality and lumpy coexistence, assemblages asymptotically approached a species-rich steady state when allelopathic effects were low (similar to what is shown in Fig. 1a). As the allelopathic effect increased, either by increasing the sensitivity to allelochemicals (decreasing KI values) or increasing the allelochemical production rate (εc), the allelopathic species increased in dominance until eventually high allelopathic effects led to monospecific blooms of the allelopathic species. For assemblages characteristic of intransitivity, oscillating and out-of-phase population dynamics occurred when allelopathic effects were low, resulting in assemblages of three species (similar to what is shown in Fig. 1b). With an allelopathic effect, sometimes a condition of alternating states emerged where the assemblages were comprised of five species oscillating out-of-phase or sometimes a steady-state emerged with co-existence of the allelopathic species with another species. But as the allelopathy effect increased further, a monospecific bloom always resulted.
Biodiversity maps were all similar in that they showed a trend of high relative diversity rapidly transitioning to low relative diversity (monospecific bloom of the allelopathic species) as allelopathic effects increased (Fig. 3). When viewing a biodiversity map from right to left, transition from a stable multispecies assemblage when KI values were large to an allelopathic monoculture when KI values were small is seen. When viewing a map from bottom to top, transition from a stable multispecies assemblage when εc values were low to an allelopathic monoculture when εc values were large is seen. The biodiversity maps differed, however, with regard to the positioning of this transition boundary along the allelochemical production and competitor sensitivity gradients. Because the transition boundaries were mostly linear over the range of εc and KI values explored here, the differing positions of the transition boundaries between assemblages could be quantified based on their slopes. This enabled a comparison between assemblages characteristic of neutrality, lumpy coexistence and intransitivity.
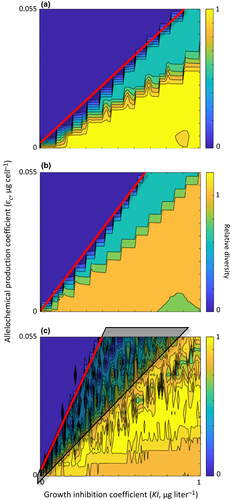
Neutral assemblages had low transitional boundary slopes indicating a low resistance to allelopathy (representative assemblage shown in Fig. 3a). Lumpy assemblage maps had steeper bloom transition slopes than neutral maps, indicating greater resistance to allelopathic effects than neutral assemblages (Fig. 3b). Both neutral and lumpy assemblages always showed a monotonic change from high diversity to low diversity as allelopathic effect increased. Intransitive assemblages showed the steepest slopes of the bloom transition boundaries, indicating even greater resistance to allelopathic effect. With these assemblages, however, the change from high to low relative diversity as allelopathic influence increased was not monotonic, as relative diversity values sometimes increased with strengthening allelopathic effect (Fig. 3c). With intransitive assemblages, collapses in relative diversity that occurred in regions of the biodiversity maps to the right of the monospecific bloom transition boundaries were not associated with emergence of the allelochemical producing species (shaded region in Fig. 3c).
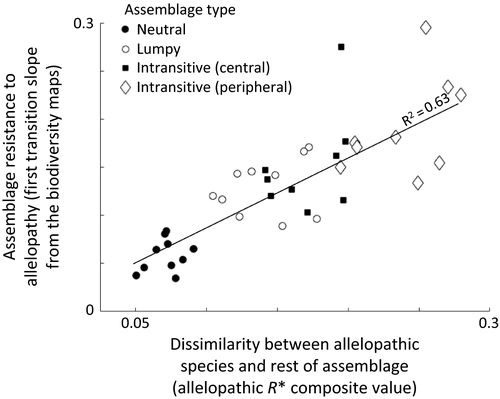
Our characterisation of resistance to allelopathy, based on the slope of the bloom transition boundary, was positively correlated (r2 = 0.63) to the allelopathic R* composite distance, the average distance between all non-allelopathic species of the assemblage and the allelopathic species (Fig. 4). This relationship was observed within and across assemblage type. Neutral assemblages fared worst in this regard with allelopathic influence, followed by lumpy assemblages, then by intransitive assemblages where the allelopathic species was centrally-located among competitor's R*s, and finally by intransitive assemblages where the allelopathic species was peripherally located with competitor's R*s.
Allelopathic species biovolume density and dominance, and assemblage size structure from lake data
Biovolume density (μm3 L−1) of all allelopathic species combined typically showed seasonal maxima (representative example for Lake Kinneret, Fig. 5a). The biovolume density of these summed allelopathic species maxima varied between lakes, with Lakes Mézeshegyi-tó, Fancsika 1, and Fancsika 2 showing the highest values, Lake Constance showing the lowest values, and the other lakes showing intermediate values (Fig. 6a).
The frequency of allelopathic species dominance also varied between lakes, with Lakes Mézeshegyi-tó, Fancsika 1, and Mikri Prespa having higher frequencies, Lake Constance having the lowest frequency, and the other lakes having intermediate frequencies (Fig. 6b).
The size structure of assemblages varied over time, as did the number of species clusters (representative example for Lake Kinneret, Fig. 5b,c). The average number of species clusters observed on a sampling day for each lake varied between lakes, with Lakes Mikri Prespa, Kinneret, Volvi and Constance having higher values, followed by Lakes Koronia, Fancsika 1, Fancsika 2 and Mézeshegyi-tó (Fig. 6).
A negative relationship between the number of averaged species clusters in lake assemblages and allelopathic species biovolume densities was observed. An exponential curve fit regression model suggested a c. 10-fold decrease in allelopathic species biovolume density over the c. 2.5 to c. 4.5 assemblage species cluster range (Fig. 6a). Allelopathic species biovolume density showed greater variance from the regression model prediction when the number of species clusters was lower.
Negative relationships between the number of averaged species clusters in lake assemblages and frequency of dominance were also observed. Linear fit regression models suggest a c. 5-fold decrease in frequency of dominance of allelopathic species over the c. 2.5–4.5 species cluster range (Fig. 6b). A stronger regression model (i.e. higher R-value) was obtained when Lake Mikri Prespa was omitted.
Discussion
In our model, transitions were abrupt between non-bloom states of higher biodiversity and monospecific bloom states of the allelopathic species. The bloom states were monospecific because of the suppressing effect by interference competition from the allelopathic species on exploitative competition. The transitions were abrupt because of the positive feedback resulting from increased toxin concentration by increasing densities of the allelopathic species, leading to a stronger suppression of their non-allelopathic competitors and a further reduced exploitative competitive effect by the non-allelopathic species. Positive feedbacks leading to rapid bloom formation, such as this, have been surmised from field observations and experiments (Sunda et al. 2006; Granéli et al. 2012). In addition, near-monospecific blooms are commonly observed in nature (Keating 1978; Michaloudi et al. 2009; Hattenrath-Lehmann & Gobler 2011). Through our modeling here, we mechanistically demonstrate the functioning of one such positive feedback.
The emergent behaviour of our model suggests that an assemblage's resistance to monospecific bloom formation of the allelopathic species may be tied to the degree of competitive interactions between assemblage members. In our simulations, the more dissimilar assemblage members were from the allelopathic species in their ability to exploit resources, the more resistant the assemblages became to monospecific blooms of the allelopathic species. In other words, stronger allelochemical effects (through εc and KI) were required to overcome assemblages with greater competitive power. This observation of our model's emergent behaviour is similar to what has been observed in plant systems that have experienced invasions, where invasion success and impact on residents were a function of the invaders life history traits relative to the life history traits of the residents (Von Holle et al. 2003; Ortega & Pearson 2005; Gruntman et al. 2014).
For some simulations, assemblage states other than the dichotomous biodiverse and monospecific bloom states occurred. Specifically, for some of the intransitive assemblages non-allelopathic species with dissimilar traits from the allelopathic species were able to survive in monoculture or persist with the allelopathic species under high allelopathic effect. In these instances, the population losses arising from allelochemical exposure did not completely mask the advantage gained by being competitively dissimilar. Though the combinations of εc and KI where this was observed were few, it occurred several times for some intransitive assemblages. Perhaps this is why sometimes near-monospecific blooms of allelopathic species are observed in nature, as referenced above, and other times non allelopathic species are able to co-exist with allelopathic species during blooms (West et al. 1996; Lindholm et al. 1999; Redalje et al. 2008; de Figueiredo et al. 2006).
Our model results also showed that the incidence of monospecific blooms of the allelopathic species was a function of the assemblage type. For example, neutral assemblages occupied the smallest volume of the three-dimensional resource tradeoff space. Consequently, these allelopathic R* composite distances were the least. The neutral assemblages were also the most vulnerable to monospecific blooms of the allelopathic species. An explanation for this may be that an allelopathic species can be expected to affect the population dynamics of all functionally equivalent members in the same way. Conversely, assemblages characteristic of lumpy coexistence and intransitivity occupied larger volumes of the three-dimensional resource tradeoff space, had greater allelopathic R* composite distances and exhibited stronger resistance to monospecific blooms of the allelopathic species. An explanation for this may be that an allelopathic species can be expected to affect the population dynamics of assemblage members differentially when they are competitively dissimilar. Interestingly, other modeling studies comparing the resistance and resilience of neutral, lumpy and intransitive assemblages to various other processes common in aquatic environments showed that intransitive assemblages were generally much more vulnerable to biodiversity collapses than neutral and lumpy assemblages, suggesting incidence of intransitivity in plankton systems might be rare (Roelke & Eldridge 2008; Bhattacharyya et al. 2018; Withrow et al. 2018). Here, we show that when allelopathic interactions are considered, intransitive assemblages are more resistant, which suggests intransitivity in plankton systems might not be as rare as previously suggested.
Observations from the eight lakes used in this study are consistent with our model findings. Lake Mézeshegyi-tó had among the highest biovolume densities of allelopathic species. It also had the least number of assemblage species clusters. Relatively high biovolume densities and low average species clusters are also observed with Lakes Fancsika 1, Fancsika 2 and Koronia. Contrastingly, high average number of species clusters and generally lower biovolume densities of allelopathic species were observed with Lakes Kinneret, Constance, Volvi and Mikri Prespa. Similarly, Lakes Mézeshegyi-tó and Lakes Fancsika 1 had higher frequencies of dominance of allelopathic species, while Lakes Kinneret, Constance, and Volvi had lower frequencies of allelopathic species dominance. If we assume that the biovolume density and frequency of allelopathic species dominance are, in part, influenced by the resistance of the phytoplankton assemblage to monospecific blooms of allelopathic species (which our model shows); and if we assume that an assemblage characteristic of species clustering is more resistant to allelopathic species than assemblages without species clusters (which our model shows); then an inverse relationship should exist between biovolume density of allelopathic species and species clustering, and also the frequency of allelopathic species dominance and species clustering, which is indeed the case with the lakes analysed here.
However, other processes may also influence biovolume density and frequency of allelopathic species dominance. Other biological processes, such as disruption of grazing (Caron et al. 1989) and adaptation to low light environments (Jöhnk et al. 2008), can influence algal bloom density. Other factors also play roles in determining algal bloom biomass, such as lake trophic state (Smith 2003) and morphometry as it influences mixing depth (Huisman & Sommeijer 2002). River discharges also influence the frequency of blooms (Mitrovic et al. 2011; Roelke et al. 2011). Indeed, in both our regression models there is variance from the model predictions, suggesting that other processes were at play.
Regarding allelopathic species biovolume density, for fewer species clusters the allelopathic species biovolume is c. 10-fold higher and the variance is greater. Lakes Mézeshegyi-tó, Fancsika 1, Fancsika 2 and Koronia are all nutrient rich and of shallow depth. While enriched waters certainly allow for phytoplankton assemblages to reach higher biovolume density (whether comprised of allelopathic species or not), it is also likely that population dynamics of greater magnitude occur. That is, larger and more rapid changes in population densities might lead to greater prevalence of ‘boom and bust’ cycles (Rosenzweig 1971). In addition, the shallow depths of these lakes also likely lead to greater dynamics in nitrogen to phosphorus ratios and ammonium to nitrate ratios as aperiodic winds drive upward mixing of nutrient-rich and possibly oxygen-depleted bottom waters. Taken together, this would suggest that at the time of resource replenishment following a mixing event, the composition of the phytoplankton and the stoichiometry of the nutrients would be highly variable. Given that succession dynamics and resulting assemblage composition can be sensitive to initial conditions (Roelke 2000; Huisman & Weissing 2001), the large variance observed in our regression model at low numbers of species clusters is not surprising.
Conversely, when lakes are deeper and less eutrophic, allelopathic species biovolume variance is lessened. The exception is our largest and deepest lake, Lake Constance, which has much lower allelopathic species biomass than the regression model predicts. This system has undergone a high rate of oligotrophication with implementation of nutrient loading reduction strategies (Sommer et al. 1993; Murphy et al. 2018). It may be that over time the phytoplankton assemblage of this lake will continue to change towards a state where there are even more species clusters, or it might change towards a state where the biomass of allelopathic species becomes greater. An investigation of changing number of species clusters and allelopathic species over time is left for future research.
The frequency of dominance of allelopathic species is c. 5-fold higher when assemblages have fewer species clusters, as predicted by our regression model with Lake Mikri Prespa excluded. Again, variance from the model prediction is greater when there are fewer species clusters. For example, Lakes Mézeshegyi-tó and Fancsika 1, which have extremely high levels of nutrients, have higher frequencies of allelopathic species dominance than predicted by the regression model, while Lakes Fancsika 2 and Koronia, also with high nutrients, but not as high as the previous two lakes (Borics et al. 2016; Michaloudi et al. 2009, although this study measures soluble reactive phosphorus in the lake while the other lakes were measured for total phosphorus), have lower frequencies of allelopathic species dominance than predicted by the regression model. It may be that with extreme eutrophication the incidence of light limitation is greater, likely selecting for species able to form and maintain surface scums, like many allelopathic species of cyanobacteria are able to do. This notion is also left for future research. Regarding our exclusion of Lake Mikri Prespa from this latter regression model, an extreme drought condition persisted at the time of sampling for this lake, which likely led to an uncommon condition of allelopathic species persistence.
Conclusions
Central to niche theory is the idea that tradeoffs in competitive abilities for multiple resources promote coexistence among species, a cornerstone of widely embraced theory of resource competition (Tilman 1982). We showed that the relative magnitude of the tradeoffs may lead to differential effects of exploitative and interference competition on individual species. Even small changes in the R* values can strongly influence fitness of assemblage members confronted with allelopathy. While many factors contribute to the development of allelopathic blooms, with our research we show for the first time that differences in assemblage competitive power can affect an assemblage's resistance to allelopathy. This hard-to-measure characteristic of natural phytoplankton assemblages may help explain why some blooms appear suddenly when other environmental factors seem stable. This research represents a first step in characterising another mechanism, assemblage competitive power, to explain the incidence of allelopathic blooms in natural assemblages.
Acknowledgements
This was unfunded research. The authors are grateful to anonymous reviewers for their constructive comments on a previous iteration of this manuscript.
Authorship
RM and DLR conceived the idea and designed the study. RM, DLR, JB and FGW performed the numerical modeling and analysis of time-series data. All authors (RM, DLR, TZ, MMG, US, GB, UG, FGW and JB) contributed to the ecological interpretation of the research. RM and DLR wrote the first iteration of the manuscript. All authors revised and edited the manuscript.
Data Accessibility
Data available from the Dryad Digital Repository: http://doi.org/10.5061/dryad.3vk16fq
Conflict of Interest
The authors have no conflicts of interest.




