Effects of host heterogeneity on pathogen diversity and evolution
Abstract
Phenotypic variation is common in most pathogens, yet the mechanisms that maintain this diversity are still poorly understood. We asked whether continuous host variation in susceptibility helps maintain phenotypic variation, using experiments conducted with a baculovirus that infects gypsy moth (Lymantria dispar) larvae. We found that an empirically observed tradeoff between mean transmission rate and variation in transmission, which results from host heterogeneity, promotes long-term coexistence of two pathogen types in simulations of a population model. This tradeoff introduces an alternative strategy for the pathogen: a low-transmission, low-variability type can coexist with the high-transmission type favoured by classical non-heterogeneity models. In addition, this tradeoff can help explain the extensive phenotypic variation we observed in field-collected pathogen isolates, in traits affecting virus fitness including transmission and environmental persistence. Similar heterogeneity tradeoffs might be a general mechanism promoting phenotypic variation in any pathogen for which hosts vary continuously in susceptibility.
Introduction
Phenotypic variation within a pathogen species is very common in nature, with multiple pathogen strains existing within a population or even a single host (Hodgson et al. 2001; Pedersen & Fenton 2007; Rigaud et al. 2010). This variation can affect the population dynamics of hosts and pathogens (Gupta et al. 1994), the emergence of new diseases (Musser 1996) and the evolution of increased virulence in existing diseases (Musser 1996; Alizon et al. 2013).
Phenotypic variation in a pathogen can arise from neutral evolutionary processes or alternatively through processes involving selection. The tradeoff theory of the evolution of virulence proposes that pathogen traits with opposite effects on fitness (often transmission and removal rates) are likely to be positively correlated, leading to a peak in fitness at intermediate virulence (Levin & Pimentel 1981; Anderson & May 1982). If tradeoffs are present, strains collected from geographically distinct populations can have the same fitness even though they differ in measured traits (de Roode et al. 2008; Chapuis et al. 2012). This is similar to community ecology theory, where the ability to use different resources can lead to the coexistence of competing species (Tilman 1977). However, classical tradeoff theory does not allow for multiple pathogen strains in a single host population. Classical pathogen competition models, assuming a homogeneous host population, predict that the strain which is able to invade at a lower host population size should always competitively exclude the other (Bremermann & Thieme 1989; Keeling & Rohani 2008). In this study, we extend tradeoff theory to develop a mechanism by which host heterogeneity in the form of continuous or quantitative resistance promotes phenotypic variation in a pathogen.
Host heterogeneity in susceptibility can lead to pathogen polymorphism if fitness of different pathogen types varies across different hosts (Regoes et al. 2000; Kirchner & Roy 2002; Osnas & Dobson 2012). If hosts vary continuously in their susceptibility to a pathogen, transmission rate will drop during an epidemic as the more susceptible individuals are removed first. This decrease in instantaneous transmission is affected by a trait we call ‘variation in transmission’. Different host populations might have different values of variation in transmission if they are more or less variable in susceptibility. Less intuitively, different values of variation in transmission might also be observed for different pathogens in a single host population. This would occur if a host population varied in its susceptibility to one pathogen, but had a more consistent response to a second pathogen. In a pathogen with low variation in transmission, instantaneous transmission decreases more slowly (and thus is less variable); with high variation in transmission, it changes more rapidly. Variation in transmission therefore has both the potential to vary among pathogens as well as a strong effect on infection rate and thus pathogen fitness. In this study, we consider variation in transmission as a trait that might vary among different pathogen types and be subject to tradeoffs.
Transmission models that allow for continuous host variation in susceptibility predict that changes in the level of host variation can alter the curvature of the infection rate response when plotted against pathogen density (Figs 1 and S1). We have repeatedly confirmed this prediction in the gypsy moth baculovirus system, observing this host heterogeneity effect in field experiments comparing high- and low-variability host strains (Dwyer et al. 1997) or half-sibling families (Elderd et al. 2008). In contrast, small-scale spatial structure and insect feeding behaviour appear to only weakly influence the curvature in these plots (Eakin et al. 2015). A more gradual increase in infection rate with pathogen density is consistent with high variation in host susceptibility: highly susceptible individuals can be infected even at very low pathogen densities (causing a sharp initial increase in infections), while the last individuals left uninfected in the population will likely be highly resistant, thus causing infection rates to slow their increase at the highest pathogen densities. The observed heterogeneity can be incorporated into host-pathogen population models as the coefficient of variation (CV = SD/mean) of transmission rate (Dwyer et al. 1997, 2000), a unitless quantity that accounts for the tendency of variance to increase with the mean. This term also determines how quickly transmission will decrease during an epidemic, and is thus the ‘variation in transmission’ mentioned above. Note that the curvature of the infection plots also depends on the pathogen isolate identity (Fig. 1), consistent with the idea that variation in transmission can be treated as a pathogen trait.
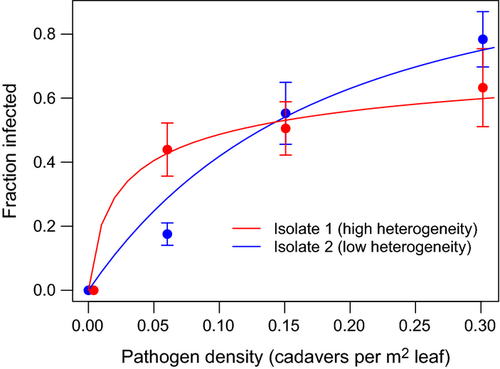
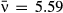 and variation in transmission C = 2.08 for isolate 1 (red), and
and variation in transmission C = 2.08 for isolate 1 (red), and 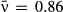 and C = 0.6 for isolate 2 (blue).
and C = 0.6 for isolate 2 (blue).We present evidence that host heterogeneity helps maintain pathogen diversity in a baculovirus that infects gypsy moth (Lymantria dispar) larvae. Field-collected pathogen isolates were found to differ in how much their transmission varies over time during an outbreak, which results from host heterogeneity. A tradeoff between mean transmission rate and variation in transmission promotes pathogen polymorphism by introducing two alternative strategies for the pathogen: a low-mean-transmission, low-variability pathogen can coexist with a high-mean-transmission, high-variability pathogen. Simulations of a population model incorporating this empirically observed tradeoff predict long-term coexistence of two pathogen types, and thus help to explain the extensive phenotypic variation we found in 16 field-collected pathogen isolates.
Materials and Methods
To ask whether a tradeoff between mean transmission rate and variation in transmission could promote pathogen coexistence, we first estimated parameters for 16 field-collected virus isolates using field and laboratory data. Next, we fit linear and nonlinear models to look for tradeoffs between those parameters, using each isolate as a separate data point. We then incorporated the estimated tradeoffs into a two-pathogen differential equation model, and used numerical simulations of this model to ask under what conditions pathogen coexistence is predicted.
The host-pathogen population model was parameterised from empirical data collected in this study. These data come primarily from two sources: a laboratory experiment to estimate speed of kill, and a field experiment to estimate mean transmission rates, variation in transmission (heterogeneity) and environmental decay rates. In the following sections, we first present the study system and the population model, and then describe the data collection, statistical analysis and model fitting. See Table 1 for data sources of all model parameters.
Study system
We used the baculovirus that infects gypsy moth (Lymantria dispar) caterpillars as our experimental system. Baculovirus outbreaks begin when gypsy moth larvae hatch in the spring and consume contaminated egg material. Infected neonates die on leaves of host trees, contaminating leaf material that is consumed by later-instar larvae (Woods & Elkinton 1987). Transmission occurs only after death of the infected larva, when the host cuticle dissolves and infectious particles (occlusion bodies) are released onto leaves (Miller 1997). The baculovirus is unable to infect adults or pupae, and gypsy moths have only one generation per year. Thus hosts are only available from approximately early May until mid-August, when larvae pupate. The virus overwinters on tree bark, sheltered by gypsy moth egg masses, and a new epizootic begins the following spring when the next generation hatches (Woods & Elkinton 1987).
| Parameter | Description | Value/range | Source of estimate(s) |
|---|---|---|---|
|
Mean transmission rate1 | 0.86–10.15 | Field experiment |
| C | CV of transmission rate1 | 0.6–2.21 | Field experiment |
| μ | Pathogen within-season decay rate1 | 0.24–1.03 | Field experiment |
| δ | Transition between exposed classes1 | 0.057–0.069 | Speed of kill lab experiment |
| k | Number of exposed classes1 | 22–35 | Speed of kill lab experiment |
| ρ | Correlation of transmission between isolates | −1 to 1 | Full range considered |
| ϕ | Pathogen overwintering rate | 4 | Murray & Elkinton 1989,Dwyer et al. 2000 |
| λN | Host annual growth rate | 10 | Dwyer et al. 2000 |
- 1Varies by isolate; parameter estimates fit for each isolate separately.
Population model
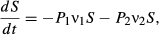 (1)
(1)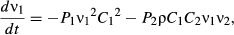 (2)
(2)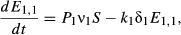 (3)
(3)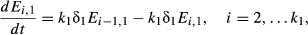 (4)
(4)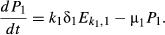 (5)
(5)We show here equations for the first isolate from a two-pathogen model (see eqns A36–A44, Appendix A, for the complete model and its derivation). Uninfected hosts (S) vary continuously in their susceptibilities. This variation (described by Cj, the coefficient of variation of transmission) causes the instantaneous transmission rate of pathogen j, ν(t)j,j = 1,2, to drop throughout the epizootic as the more susceptible individuals are removed (Fig. 2, eqn 2). When the instantaneous transmission rate νj(t) is large, 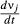 declines more steeply, as can be seen by taking the partial derivative of eqn 2 with respect to νj(t). This occurs because with large νj(t) hosts are infected and thus removed from the susceptible population more quickly, causing a more rapid decrease. The mean transmission rate
declines more steeply, as can be seen by taking the partial derivative of eqn 2 with respect to νj(t). This occurs because with large νj(t) hosts are infected and thus removed from the susceptible population more quickly, causing a more rapid decrease. The mean transmission rate  estimated for individual isolates is the population mean for an uninfected population, and thus
estimated for individual isolates is the population mean for an uninfected population, and thus  .
.
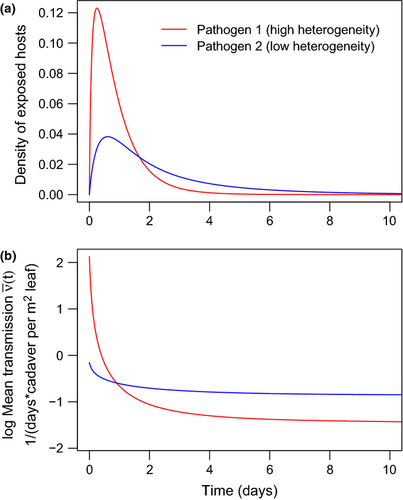
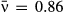 , C = 0.6) compared to a high-variation isolate that starts at a higher mean transmission (red line (b),
, C = 0.6) compared to a high-variation isolate that starts at a higher mean transmission (red line (b), 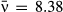 , C = 2.21). Time is plotted over only the first 10 days of the epizootic to show the initial wave of infection.
, C = 2.21). Time is plotted over only the first 10 days of the epizootic to show the initial wave of infection.Increasing Cj, the variation among hosts in their susceptibilities to pathogen j, also causes the transmission rate to drop off more steeply (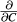 of eqn 2), because individuals removed at the beginning of the epizootic are much more susceptible than those removed later (Fig. 2). In the case of homogeneous hosts, Cj = 0 and transmission rate does not change (eqn 2 becomes zero). Lower variation of transmission C gives a higher fraction of individuals infected within a season (eqn 9, see also Appendix B) and therefore lower values of C are favourable for the pathogen. In general, lower variation of transmission is associated with more rapid spread of infection (Hethcote & VanArk 1987; Diekmann et al. 1990) and lower extinction risk (Lloyd-Smith et al. 2005).
of eqn 2), because individuals removed at the beginning of the epizootic are much more susceptible than those removed later (Fig. 2). In the case of homogeneous hosts, Cj = 0 and transmission rate does not change (eqn 2 becomes zero). Lower variation of transmission C gives a higher fraction of individuals infected within a season (eqn 9, see also Appendix B) and therefore lower values of C are favourable for the pathogen. In general, lower variation of transmission is associated with more rapid spread of infection (Hethcote & VanArk 1987; Diekmann et al. 1990) and lower extinction risk (Lloyd-Smith et al. 2005).
Because both pathogens remove hosts from the same variable population, instantaneous transmission for one pathogen depends on the density of the other, according to ρ, the between-isolate Pearson's correlation in their transmission. A positive value of ρ indicates that individuals highly susceptible to pathogen 1 are also more susceptible to pathogen 2. ρ is thus a measure of host-pathogen specificity, with negative values indicating specialisation. We varied the correlation of transmission ρ over its full range (−1 to 1), but present results for ρ = 1, as this is the case in which coexistence is least likely (i.e. no host-pathogen specialisation). If ρ < 0, the instantaneous transmission rate 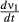 (eqn 2) can actually increase over the course of the epizootic: removal of hosts susceptible to pathogen 2 will increase the mean susceptibility of the population to pathogen 1, because those individuals removed by pathogen 2 had low susceptibility to pathogen 1. However, note that even if the instantaneous transmission rate ν1 increases, the total transmission term P1ν1S must still eventually decrease as susceptible hosts are removed, and can even decrease while the instantaneous transmission rate increases.
(eqn 2) can actually increase over the course of the epizootic: removal of hosts susceptible to pathogen 2 will increase the mean susceptibility of the population to pathogen 1, because those individuals removed by pathogen 2 had low susceptibility to pathogen 1. However, note that even if the instantaneous transmission rate ν1 increases, the total transmission term P1ν1S must still eventually decrease as susceptible hosts are removed, and can even decrease while the instantaneous transmission rate increases.
The delay between consumption of virus and transmission after death is modeled with a series of k exposed (E) classes, with individuals moving from class to class at rate kδ, and k and δ describing a gamma distribution of kill times. Infectious particles are only produced if the host dies (Miller 1997), and therefore we model only those infections that lead to death, and all individuals entering the E1 class progress to the pathogen (P) class. Pathogen decays on foliage at rate μ. Unlike the classic Anderson & May (1981) insect-virus model, where pathogen density decreases through contact with susceptible hosts, there is evidence that this assumption is incorrect for this system (Appendix D), most likely because larvae consume uncontaminated foliage at a higher rate than contaminated foliage (Eakin et al. 2015). Adding pathogen removal through consumption produces similar qualitative results in model simulations (Appendix D).
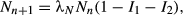 (6)
(6) (7)
(7) (8)
(8)At the end of the season, surviving hosts Nn(1−I1−I2) reproduce at rate λN, to give the host population the following year, Nn+1. The fraction surviving is given by 1 − I1 − I2, where I1 is the fraction of larvae infected with pathogen 1, and I2 the fraction with pathogen 2. Pathogen j, (Zj), is produced at rate NnIj and overwinters on host egg masses at rate ϕ.
Following standard practices, we assume that host evolution is slower than pathogen evolution, and therefore do not model host evolution. Assuming no coevolution and a single overwintering rate for both isolates is also the most conservative case, in which pathogen polymorphism is least likely. For simplicity, coinfections are not modelled. Although a moderate rate of coinfection has been observed in this system (Kennedy 2012), adding coinfections tends to increase the likelihood of coexistence (May & Nowak 1995), and thus excluding coinfections is also conservative.
Field experiment
We used controlled epizootic experiments in the field to estimate population model parameters for 16 field-collected virus isolates, including mean transmission rates, variation in transmission, and environmental decay rates. Experiments were conducted with each of the 16 virus isolates separately, and isolate-specific parameters were estimated for each isolate in isolation. See ‘Collection of virus isolates’ in Supporting Information for more details on isolate collection.
Our experimental design replicates the natural infection process; outbreak data from naturally occurring populations indicate that transmission peaks in the field when infected neonates infect larger 3rd and 4th instar larvae (Woods & Elkinton 1987). First instar larvae (neonates) were infected in the lab with each of the virus isolates and then allowed to die in the field on red oak branches with 40 leaves contained in Reemay fabric bags. Viral decay within these bags is close to zero (Fuller et al. 2012). In order to estimate environmental decay rates, we varied the length of time for which cadavers were exposed to the environment, by removing bags for 3, 1, or 0 days. Three densities of infectious cadavers were used: 10, 25 and 50 cadavers/branch. First instar cadavers contain approximately 1.5 × 107 infectious particles (data from necropsies). Cadaver size and thus number of infectious particles varies to some extent within and among virus isolates, and this variation is captured by the isolate-specific mean transmission and variation in transmission parameters. After death of the infected first instar larvae, branches were exposed to the environment according to their exposure treatment, and then 25 healthy lab-raised 4th instar larvae were added to each bag. Infection occurs when susceptible larvae consume leaf material that has been contaminated with virus-killed cadavers. Healthy larvae were allowed to feed for one week, and then raised in the laboratory in individual cups of artificial diet in order to determine infection status. Infected larvae display a typical ‘melted’ phenotype, due to dissolution of the cuticle (Miller 1997). Infection state was determined by visual inspection and confirmed with necropsies under a light microscope at 400× magnification. Virus particles are contained in large protein-coated occlusion bodies that are visible at 400× (Miller 1997).
It is crucial to conduct these experiments in the field, because virus decay and variation in transmission both depend on environmental conditions that cannot be accurately replicated in the lab (Fuller et al. 2012). Variation in transmission is also affected by larval feeding behaviour and the distribution of virus-killed cadavers on leaves (Eakin et al. 2015), and our field experiments allow for these processes. In July 2011, we used two densities of infectious cadavers (25 and 50 cadavers/branch) crossed with three exposure treatments, replicated three times. In June 2012, we repeated the experiment with a single exposure treatment (0 days exposed) and all three densities of infectious cadavers, replicated three times. This gave a total of 10 800 susceptible larvae over both years. All field experiments were conducted at MSU's Kellogg Biological Station, Hickory Corners, MI, USA (Fig. S2).
All gypsy moth larvae used in the field and laboratory experiments were the New Jersey Standard Strain, from the USDA-APHIS colony at Otis Air Force Base, Buzzard Bay, MA, USA. These larvae have been bred in the laboratory for over 40 generations, but are not a clonal or inbred line. Larvae from different egg masses (full-sib families) were combined and randomised before assignment to different treatments, to ensure that a mix of genetic families was used. Egg masses were surface sterilised by soaking in a 4% formaldehyde solution for 90 minutes to prevent infection upon hatching in case of contamination (Dwyer et al. 1997). To control for any effects of artificial diet, body size or developmental stage on infection risk, larvae used in experiments were selected just prior to molting to 4th instar at the point when the head capsule had slipped forward, and starved for 24 h during molting (Grove & Hoover 2007).
Speed of kill laboratory experiment
To estimate the distribution of kill times and size of larvae at death, we infected 100 recently molted 4th instar larvae per isolate with a dose of virus intended to kill 95% of individuals. Each individual was fed a dose of 6750 occlusion bodies in 3 μL of solution placed on a small cube of artificial diet (3 mm3). Larvae were given 24 h to consume the infected cubes, and those that did not ingest the entire dose were discarded. They were then raised separately in cups of artificial diet at 22 ∘C (mean daily temperature in June at the site of field experiments) and checked daily after infection until all had died or pupated. To estimate size at death, we took photographs of larvae at infection and after death, and estimated larval area (mm2) using the software ImageJ.
Model fitting
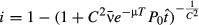 (9)
(9)As in the population model (eqns 1-5), 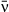 and C are the mean and coefficient of variation of transmission rate, and μ is the environmental decay rate. The remaining parameters were set by the experimental design. P0 is the initial virus density, which is approximately constant over time in experimental bags (Fuller et al. 2012). Bags were removed to expose virus-killed cadavers to the environment for T days, and thus pathogen density after decay is given by P0exp(−μT). Healthy larvae were allowed to feed on contaminated leaf material for
and C are the mean and coefficient of variation of transmission rate, and μ is the environmental decay rate. The remaining parameters were set by the experimental design. P0 is the initial virus density, which is approximately constant over time in experimental bags (Fuller et al. 2012). Bags were removed to expose virus-killed cadavers to the environment for T days, and thus pathogen density after decay is given by P0exp(−μT). Healthy larvae were allowed to feed on contaminated leaf material for  days.
days.
Previous work using this method of controlled epizootic experiments has shown that data from these field experiments are not variance-inflated (Dwyer et al. 2005; Elderd et al. 2008) and thus a binomial likelihood is appropriate. We used Bayesian MCMC methods to fit model parameters to data (see Supporting Information for details) and to compare penalised goodness of fit of two sets of model types: (1) models with host heterogeneity described by variation in transmission (eqn 9) vs. models with linear transmission and no heterogeneity (eqn B8, Appendix B) and (2) models with isolate-specific parameters vs. models in which some or all parameters are the same for all virus isolates (see Table S1 in Supporting Information for a complete list of models considered).
The expected distribution of kill times (described by k and δ in the population model, eqns 3-5) was fit separately from the other model parameters, using the mean and variance of time of death from the laboratory experiment and assuming a gamma distribution of death times. It is not possible to use the field data to fit these parameters, as ingestion of virus could occur at any time within a one-week window and thus exact time of infection is not known.
Tradeoff analysis
After fitting the model and obtaining the posterior distribution of all parameters, we looked for tradeoffs between different model parameters affecting pathogen fitness. To do so, we fit linear and nonlinear regression models using each isolate as a separate data point. We compared linear models regressing environmental decay μ and the coefficient of variation of transmission C against mean transmission 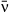 to nonlinear models of the form y = kxα traditionally used in tradeoff theory, where x is typically transmission and y is typically host mortality or pathogen decay (Anderson & May 1982; Keeling & Rohani 2008). For the regression of variation in transmission C against mean transmission
to nonlinear models of the form y = kxα traditionally used in tradeoff theory, where x is typically transmission and y is typically host mortality or pathogen decay (Anderson & May 1982; Keeling & Rohani 2008). For the regression of variation in transmission C against mean transmission 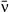 we also fit a nonlinear logistic function of the form
we also fit a nonlinear logistic function of the form 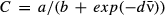 . This function takes only positive values and is thus appropriate for the CV, which has a lower limit of zero. Both independent and dependent variables in all tradeoff regressions were parameter estimates fit to data and thus contain error. To account for this error, we propagated the posterior parameter distributions into the tradeoff regression models. We used Monte Carlo sampling of the posterior distributions and resampled the posteriors of each parameters 10 000 times, refitting the regression model each time. This produced 95% credible intervals around the regression lines that account for the error in both dependent (C or μ) and independent (
. This function takes only positive values and is thus appropriate for the CV, which has a lower limit of zero. Both independent and dependent variables in all tradeoff regressions were parameter estimates fit to data and thus contain error. To account for this error, we propagated the posterior parameter distributions into the tradeoff regression models. We used Monte Carlo sampling of the posterior distributions and resampled the posteriors of each parameters 10 000 times, refitting the regression model each time. This produced 95% credible intervals around the regression lines that account for the error in both dependent (C or μ) and independent ( ) variables.
) variables.
Positive correlations between these model parameters are consistent with the presence of tradeoffs between them. Lower environmental decay rates are associated with increased pathogen fitness, and thus increasing decay rate with increasing mean transmission would indicate a tradeoff. Likewise, lower variation of transmission C is advantageous to a pathogen; lower values of C give a higher fraction of individuals infected in a season (see Population Model above).
Estimating pathogen fitness
In the case of a heterogeneous population in which hosts vary continuously in their susceptibilities, the basic reproductive ratio R0 is not the most informative measure of pathogen fitness (Diekmann et al. 1990; Dieckmann 2002). We therefore used two other more appropriate measures of pathogen fitness: (1) initial annual population growth rate λZ of a pathogen invading a mostly susceptible host population and (2) invasion success of a new mutant into a population with a resident pathogen, an adaptive dynamics approach using pairwise invasibility plots (Geritz et al. 1997). We found qualitatively similar results from both measures.
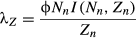 (10)
(10)The growth rate depends on the host density in the previous year, Nn, and thus we estimated the annual growth rate at several different host densities. It also depends on the pathogen overwinter persistence, ϕ, and the fraction infected I(Nn,Zn), which can be found by solving the epizootic burnout approximation equation (Appendix B).
The second measure of pathogen fitness was the invasion success of a new mutant into a population with a resident pathogen present at equilibrium densities (Geritz et al. 1997). In the gypsy moth-baculovirus system, transmission depends on the densities of both host and pathogen populations, and the optimal transmission rate (that which maximises pathogen growth rate) varies with host density. When transmission rates depend on host density, adaptive dynamics that can take into account density-dependent behaviour are a more appropriate analysis (Dieckmann 2002). Simulations to estimate success of an invading pathogen were also used to determine regions of two-pathogen coexistence in pairwise invasibility plots (Appendix B).
Overall invasion success of a new mutant of a given mean transmission rate was computed by summing the cases in which the invader was able to persist over the range of resident mean transmission values, then dividing by the total number of resident mean transmission values tested, to give a proportion between 0 and 1 that we call ‘invasion success’.
Results
Field-collected virus isolates showed a high level of polymorphism in field experiments (Fig. 3), and the best-fitting model had isolate-specific parameters for mean transmission rates, variation (CV) of transmission, and environmental decay (Table S1). Isolates also varied in their speed of kill in laboratory experiments (Fig. S5, parametric survival regression with Weibull distribution, W = 87.3, d.f. = 15, P < 0.001).
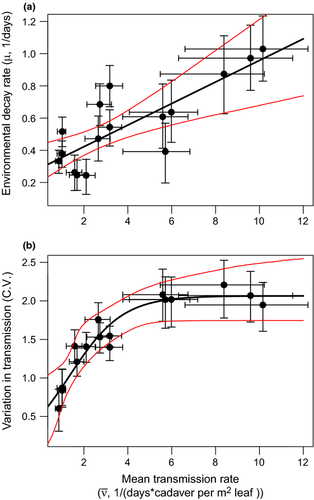
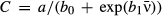 , R2 = 0.80, P < 0.001), consistent with tradeoffs between those traits. Each point gives the mean ± 1 SE parameter value for one virus isolate, where the SE was estimated from the highest posterior density (HPD) intervals (see ‘Model fitting methods’ in Supporting Information for details). Red lines give bootstrapped 95%CI for the regression line, computed by propagating the posterior parameter distributions. Variation in transmission is the coefficient of variation (CV) and by definition is unitless.
, R2 = 0.80, P < 0.001), consistent with tradeoffs between those traits. Each point gives the mean ± 1 SE parameter value for one virus isolate, where the SE was estimated from the highest posterior density (HPD) intervals (see ‘Model fitting methods’ in Supporting Information for details). Red lines give bootstrapped 95%CI for the regression line, computed by propagating the posterior parameter distributions. Variation in transmission is the coefficient of variation (CV) and by definition is unitless.Mean transmission rates correlated positively with environmental decay, consistent with a tradeoff between these traits (Fig. 3a). However, this tradeoff alone is insufficient to explain coexistence of multiple isolates (Table 2). A second tradeoff between mean transmission and variation in transmission (Fig. 3b) is more important in allowing pathogen polymorphism. This tradeoff creates a second fitness peak at low values of mean transmission (pathogen fitness measured as initial growth rate in a susceptible population; Fig. S6). This introduces an alternative to a high mean transmission strategy: an isolate with low mean transmission rate has high fitness because it is also less variable in its transmission. An intermediate transmission rate is never favoured (Fig. S7).
| Mean transmission | Decay rate | CV of transmission | Coexistence (years) | |||||
|---|---|---|---|---|---|---|---|---|
| Model | Tradeoffs |
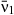
|
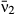
|
μ1 | μ2 | C 1 | C 2 | |
| Homogeneous pop | None | 10.5 | 0.5 | 0.65 | 0.65 | 0 | 0 | 0 |
| Decay | 10.5 | 0.5 | 0.99 | 0.32 | 0 | 0 | 0 | |
| Heterogeneous pop | None | 10.5 | 0.5 | 0.65 | 0.65 | 1.53 | 1.53 | 4 |
| Decay | 10.5 | 0.5 | 0.99 | 0.32 | 1.53 | 1.53 | 5 | |
| Variation of transmission | 10.5 | 0.5 | 0.65 | 0.65 | 2.06 | 0.68 | > 150 | |
| Decay & variation of transmission | 10.5 | 0.5 | 0.99 | 0.32 | 2.06 | 0.68 | > 150 | |
Another measure of fitness, the proportion of phenotype space over which a pathogen is able to invade a population with a resident pathogen already present (‘invasion success’), follows a similar pattern, with highest invasion success at either low or high invader mean transmission rates (Fig. 4). The values of invasion success for high-transmission pathogens depend on the range of phenotype space considered; at high values of mean transmission, invasion success increases linearly with mean transmission rate. However, the low-mean-transmission peak in invasion success persists even when an expanded upper range of mean transmission rates is considered, and does not depend on the range (Fig. S8).
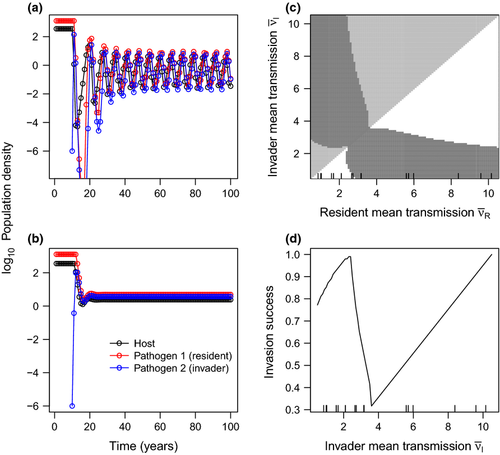
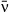 was incremented by 0.1, and variation in transmission and environmental decay were computed as functions of
was incremented by 0.1, and variation in transmission and environmental decay were computed as functions of 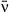 (c,d). Vertical ticks on the x-axis mark values observed for 16 field-collected virus isolates (c,d).
(c,d). Vertical ticks on the x-axis mark values observed for 16 field-collected virus isolates (c,d).Coexistence of multiple pathogen isolates results from the empirically observed tradeoff between mean transmission rate and variation (CV) of transmission (Fig. 4a,b); merely adding host heterogeneity to the model is not sufficient (Table 2). Pairwise invasibility plots (PIPs) incorporating the observed tradeoffs predict pathogen polymorphism in a single host population over a wide range of transmission values (Figs 4c and S8a). Isolates are more likely to coexist if they differ in their transmission rates: a low-variability, low-mean-transmission pathogen is able to coexist with a more variable, high-mean-transmission pathogen.
Discussion
We found evidence of a tradeoff arising from host heterogeneity that promotes long-term coexistence of two pathogen types in a single host population. This tradeoff helps to explain the observed range of mean transmission rates in field-collected baculovirus isolates: those isolates with low mean transmission rates tended to also have favourable low variation (CV) of transmission rates, which could explain their persistence in the population.
Variation in transmission arises in our model from host heterogeneity, and yet we found that estimates of this variation differed when the same group of hosts was infected by different virus isolates. Among-isolate differences do not appear to be due to genetic polymorphism within isolates (see ‘Collection of virus isolates’, Supporting Information), suggesting that variation of transmission is truly a phenotypic trait of the virus, not merely the result of variation within isolates. These differences might arise because added stochasticity of within-host processes in high-transmission isolates might lead to increased variation of transmission. As time to death increases, larval size at death (and thus viral load) increases but variation in size at death also increases, due to an intermediate peak in size at death with increasing time to death (Fig. S9). Alternatively, interactions between pathogen and host genotypes (G × G) could lead to different distributions of host susceptibilities and thus different variation of transmission C among isolates. Moderate host-pathogen G × G effects were observed in laboratory infections using the baculovirus isolates from the current study (A. Hudson, unpublished data).
Our tradeoff between mean transmission and variation in transmission predicts the coexistence of two pathogen types, while the 16 field-collected isolates exhibit more variation than merely two types. In the following paragraphs, we consider other evolutionary processes that might also contribute to maintaining variation: tradeoffs between other pathogen traits, within-host dynamics and coinfection, mutation-selection balance, host-pathogen specialisation, local adaptation and frequency-dependent selection.
We tested for the presence of two tradeoffs: the classical transmission-removal tradeoff (Anderson & May 1982), which was insufficient for coexistence, and the tradeoff between mean transmission rate and variation in transmission. However, it is likely that other tradeoffs are also acting to maintain variation here. For example, larvae can detect and avoid virus particles on leaves to some extent (Eakin et al. 2015). Variation in detectability could trade off with other traits such as decay rate, if qualities such as larger size of virus particles ensure persistence on leaves but also increase detectability. Variation in detectability among isolates could also lead to differences in variation in transmission C, as feeding behaviour is known to contribute to variation in transmission (Eakin et al. 2015). In addition, transmission of the virus occurs at two different stages: within-season transmission, measured in this study, and overwinter transmission (Woods & Elkinton 1987). Tradeoffs might also occur between pathogen traits that affect overwinter transmission.
Tradeoffs in traits affecting within-host competition among pathogens are also likely to be important, as coinfections have been previously observed in this system (Kennedy 2012). For example, a slow-growing isolate might avoid detection by the host immune system, but be at a disadvantage in competition with other isolates in that host (Bremermann & Pickering 1983). More generally, tradeoffs between competition and colonisation abilities, similar to the classic community ecology tradeoff (Levins & Culver 1971), have been empirically observed in pathogen within-host dynamics (e.g. Ojosnegros et al. 2010). Coinfections generally increase the likelihood of pathogen coexistence (May & Nowak 1995; Keeling & Rohani 2008), although if there is strong or hierarchical competition between strains within a host, polymorphism might actually become less likely (Bonhoeffer & Nowak 1994; Nowak & May 1994).
Mutation-selection balance is another alternative explanation for the observed variation among isolates: random mutation introduces genetic variation, while selection tends to reduce it (Gillespie 1991). However, the phenotypic differences among isolates have quite large effects on fitness; in the absence of a tradeoff with variation in transmission, low-mean-transmission isolates are predicted to rapidly go extinct (Table 2). Given this strong selection to eliminate inferior isolates, the mutation rate would have to be quite high if mutation-selection balance is the sole mechanism maintaining phenotypic diversity. Mutation rates for double-stranded DNA viruses with similarly sized genomes (160 kb) are relatively low, ∼ 10−7-10−8 substitutions per nucleotide per generation (Sanjuán et al. 2010). Many viral generations occur during one infection, but transmission bottlenecks severely reduce genetic diversity (Bergstrom et al. 1999), making it difficult to predict the rate of genetic change expected in the pathogen in one host generation. While random mutation might contribute to maintenance of genetic diversity in this system, with such large phenotypic differences it seems likely that selection is also acting. The tradeoff we observe here provides a mechanism for selection to maintain pathogen polymorphism.
Most prior theoretical (Regoes et al. 2000) and empirical work (Lively & Dybdahl 2000; Barrett et al. 2009) on host heterogeneity has focused on gene-for-gene resistance, where pathogen polymorphism arises from hosts and pathogens belonging to discrete specialised types (Flor 1971). In models with discrete host types, different host and pathogen types are often structured geographically, consistent with local adaptation (Lively & Dybdahl 2000). They might also fluctuate over time due to frequency-dependent selection (Bensch et al. 2007; Tack et al. 2012). We find no evidence for geographic structure here (Figs S3 and S4), but it might be present at larger spatial scales, or at very small scales, due to limitations on dispersal of older larvae between groves of trees. Temporal fluctuations in isolate densities might also contribute to polymorphism. The isolates used in this study were collected over two months (see ‘Collection of virus isolates’, Supporting Information), and thus our current data are not appropriate to test this hypothesis. However, host and pathogen densities fluctuate in nature, and mean transmission rates also appear to vary over time due to fluctuating selection for host resistance (Elderd et al. 2008). The fitness of different isolates varies with host and pathogen density (Figs S6 and S7; Appendix B), suggesting that temporal fluctuations in isolate densities might also occur.
In this and other pathogens, it is likely that many different mechanisms are acting simultaneously to maintain polymorphism. There is clear evidence that the isolates used in this study were truly coexisting. Isolates within a collection site show polymorphism as well as evidence of following the observed tradeoff between mean transmission and variation of transmission (Fig. S3b), suggesting that this tradeoff could be an important mechanism maintaining the observed coexistence.
In contrast to prior work, our mechanism for pathogen coexistence depends only on continuous variation in host susceptibility. In our model, coexistence is possible over the whole range of correlation of transmission values, from a perfect correlation between isolates (ρ = 1) to complete local adaptation, where susceptibility to one pathogen perfectly predicts resistance to the other (ρ = −1). This makes our model flexible enough to predict coexistence in systems with different degrees of host-pathogen specialisation. Although the discrete generation model is specific to this system (as well as to many other annual plant and animal species such as outbreaking forest insects (Hunter 1991)), the within-season epidemic model is quite general. The result that pathogen polymorphism can be maintained by a tradeoff arising from host heterogeneity should apply to any system with a continuous distribution of host susceptibilities and density-dependent transmission, including many human diseases (Hill 1998).
Acknowledgements
This study was supported by the NIH grant R01GM096655 to G. Dwyer, V. Dukic and B. Rehill, and conducted under USDA-APHIS permit P526P-12-01466 to G. Dwyer. Computing resources were provided in part by the University of Chicago Research Computing Center. We thank J. Armagost, P. Brandt, S. Carpenter, C. Gilroy, D. Howard, T. O'Halloran, C. Maguire, Y. Ren, E. Rouse, I. Rouse, A. Saad, K. Sirianni, K. Smith, J. Tyrell, K. Vavra-Musser and S. Xie for their help with field and laboratory experiments. Comments from S. Cobey, D.A. Kennedy, D.J. Páez, A. Read, K. Lafferty and three anonymous reviewers substantially improved this manuscript.
Authorship
AFD and GD collected data, designed experiments and wrote the code for simulations and model fitting; GD, VA and AFD derived the mathematical model; and AFD and VD conducted statistical analyses. AFD wrote the initial draft, and all authors revised the manuscript.




