1 INTRODUCTION

There is ample empirical evidence showing that the brain tracks temporal regularities in the acoustic input, perhaps by synchronizing slow rhythmic brain activity to the temporal regularities in stimuli (Ahissar et al., 2001; Arnal et al., 2015; Doelling et al., 2014; Howard & Poeppel, 2010; Peelle, 2012; Peelle et al., 2013). It has been proposed that neural oscillations, which reflect rhythmic fluctuations of local neuronal excitability (Buzsáki & Draguhn, 2004; Lakatos et al., 2005), play an instrumental role in capturing rhythmic structures in the acoustic input (Schroeder & Lakatos, 2009; Zion Golumbic et al., 2013). Such synchronization, otherwise referred to as ‘entrainment’, involves the temporal adjustment of the period and/or the phase of neural oscillations to dominant rhythms in the acoustic input (Poeppel & Teng, 2020; Thut et al., 2011), such that the high-excitability phase of the oscillations is temporally aligned with critical acoustic events in the input signal (Giraud & Poeppel, 2012; Kayser et al., 2009; Lakatos et al., 2005, 2008; Schroeder & Lakatos, 2009). Furthermore, it has been demonstrated that entrained oscillatory activity can be sustained for a brief time after the termination of the rhythmic stimulation (Lakatos et al., 2013). Cumulatively, the findings suggest a mechanism through which rhythmicity in the preceding acoustic input is internalized by the human brain to optimize auditory processing of upcoming signals (Lakatos et al., 2019).

Recent behavioural and neural studies have provided evidence for the impact of oscillatory entrainment after rhythmic stimulation (e.g., Hickok et al., 2015; Kösem et al., 2018). For instance, several studies show that the rate of a preceding acoustic rhythm regulates the ‘sampling rate’ of the auditory system and thereby alters participants' perception of upcoming ambiguous stimuli (Bosker & Ghitza, 2018; Dilley & Pitt, 2010; Kösem et al., 2018). Other studies have tested whether the phase of entrained oscillations influences the processing of upcoming signals (e.g., Hickok et al., 2015; Jones et al., 2002). These studies typically used a paradigm in which they presented an acoustic target with equal probabilities across a range of time points after the offset of a rhythmic stimulus. If oscillatory entrainment to an acoustic rhythm outlasts the stimulation period and influences the perception of a following target, one should expect to observe the same type of rhythmicity in the temporal fluctuation of participants' performance on the target. For instance, in a series of studies, Jones et al. showed that exposure to a sequence of periodically presented pure tones facilitated participants' processing of an upcoming target tone that occurred at the time predicted by the rhythm of the preceding sequence (Barnes & Jones, 2000; Jones et al., 2002, 2006). These findings demonstrated a specific form of the entrainment effect wherein the rhythmic carrier provides a direct prediction for the timing of an upcoming auditory event and thereby facilitates processing of target stimuli that occur at the predicted timing (in phase) as opposed to those out of phase. Other forms of the entrainment effect have been revealed by studies that did not use the approach of direct temporal probing (Farahbod et al., 2020; Hickok et al., 2015). For instance, Hickok et al. (2015) exposed participants to a broadband noise stimulus whose amplitude was sinusoidally modulated at 3 Hz. This exposure period was followed by a target period during which a brief 1-kHz tone target was presented with equal probability across nine temporal positions covering two cycles of the preceding amplitude modulation. They showed that participants' detection of the tonal target at different temporal positions fluctuated cyclically at the same rate as the noise modulation. Interestingly, the cyclic pattern of target detectability showed an anti-phase relation with the noise modulation, with detection accuracy reaching local maxima when the noise signal would have approached the minimum amplitude if the modulation had continued. The authors argued that the observed entrainment effect cannot be explained by a direct temporal prediction mechanism but reflects the impact of specific phase of the slow neural oscillations on perception of the upcoming stimuli. 1

These studies provide evidence for the impact of oscillatory entrainment to a preceding rhythmic signal on upcoming perceptual processes, but the robustness of these effects remains an active topic of debate (see Haegens & Zion Golumbic, 2018, for a review; Lin et al., 2021, for an empirical challenge). One critical issue concerns the degree of variability of entrainment effects across participants and studies. For instance, in revisiting the paradigm used in Jones et al. (2002), Bauer et al. (2015) failed to replicate the entrainment effect at the group level that was observed in the original study. Crucially, after assessing individual data, the authors found that only 40 of 140 tested participants exhibited the original effect. The authors suggested that the specific pitch comparison task used in the original paradigm may contribute to this variability, as the task can induce mixed listening strategies among participants regarding their treatment of the entraining signal. Behavioural differences also exist among participants who have exhibited a positive entrainment effect. These differences concern the temporal alignment between the phase of the entraining signal and the effect of perceptual facilitation on acoustic targets, which has been mostly demonstrated in studies using rhythmic carriers that undergo continuous acoustic modulations (Farahbod et al., 2020; Forseth et al., 2020; Henry et al., 2014; Henry & Obleser, 2012; Hickok et al., 2015). For instance, Henry et al. (2014) and Henry and Obleser (2012) observed that while an ongoing frequency modulation of a background noise impacted most participants' detection of a short acoustic gap embedded at different locations of the noise, there was little convergence across participants regarding the exact phase of the modulation that induced facilitation of target detection. In the case of perceptual facilitations from post stimulation entrainment, Hickok et al. (2015) found an anti-phase effect that was consistent across the tested participants. However, in a subsequent study using the same paradigm (Forseth et al., 2020), the authors observed that the perceptual facilitation for target detection seemed to occur in-phase with the preceding modulation, with an increase of target detectability during the rising portion of the amplitude modulation. 2 The conflicting findings from the two studies cast doubt on the robustness with which perceptual facilitation is mechanistically associated with entrainment to a specific phase of amplitude modulation in the acoustic signal.

Here, we aim to address the issue of individual variability in the effect of neural entrainment on the processing of post-stimulation targets. Specifically, we revisit the study of Hickok et al. (2015), as it provides an opportunity to examine both aspects of the variability mentioned above. One particular aspect of that study that is of significance is the small sample size (N = 5), which by itself is not necessarily problematic (the authors argue that the small sample size is justified by the large number of trials each participant performed for each experimental condition). Moreover, the individual results showed substantial convergence across the participants in terms of both the existence and the phase alignment of the entrainment effect. However, several studies incorporating entrainment phenomena indeed reveal population-level differences in the existence of effects at the individual level (Assaneo et al., 2019; Assaneo, Rimmele et al., 2021; Bauer et al., 2015). The findings from these studies motivate a reassessment of the nature of the entrainment effect from Hickok et al. (2015) across a larger number of participants. A second unique feature of Hickok et al. (2015) is the way the authors presented target stimuli during the experiment and the way in which they selected trials for analysis. In fact, one common design across previous studies is to present the task-related property of the target stimuli at a near-threshold level, which decreases the likelihood of ceiling performance and enhances the sensitivity of the paradigm to reveal the effect of the experimental manipulation. In order to achieve this goal, a common practice has been to measure the level of the acoustic property that corresponds to threshold-level performance for each participant and to present the target stimuli at this level during the main experiment (Henry et al., 2014; Henry & Obleser, 2012; Ng et al., 2012). In contrast, Hickok et al. (2015) used a different approach: they presented the tone target at five levels of intensity during the main experiment, orthogonal to the manipulation of the target's temporal position. They observed that targets at a specific intensity level yielded—across all the five participants—a response accuracy that was closest to their detection threshold and thus included trials only from this level in the analysis on the impact of temporal position on target detectability. One downside of this design choice is the substantial number of unanalyzed trials, corresponding to ~80% of the total trials. The authors argue, building on findings from a later study, that the inclusion of intensity variation during the experiment is crucial for the observation of the entrainment effect (Farahbod et al., 2020). In the current study, we will also examine whether the original entrainment effect can be reproduced with a shortened experimental procedure. Altogether, the current study assesses the robustness of the entrainment effect from Hickok et al. (2015) using both a larger sample size and a procedural modification, on the basis of two experiments: one is a shortened experimental procedure (i.e., conceptual replication) and the other is the same procedure as the original study (i.e., exact replication).

2 MATERIALS AND METHODS

2.2 Stimuli

In both experiments, we used the same stimulus design as Hickok et al. (2015). Each trial consisted of a broadband Gaussian noise that lasted for 4 s (Figure 1). The amplitude of the first 3.167 s of noise was sinusoidally modulated at 3 Hz with 80% modulation depth. This portion of the noise corresponds to 9.5 cycles of modulation, starting with the lowest amplitude and ending at maximum amplitude. The final 0.833 s of the noise were unmodulated, with the amplitude remaining at the maximum level. In half of the trials, a 50-ms duration 1-kHz pure tone target (with 5-ms rise-and-decay time) was presented at one of nine temporal positions. These positions started at the offset of the amplitude modulation (3.167 s from the onset of the noise) and were successively spaced 83.3 ms apart. The interval between two successive target positions corresponded to one-quarter of a modulation cycle, such that the nine temporal positions covered the time period equivalent to two full cycles of the amplitude modulation if the modulation had continued. In Hickok et al. (2015), the authors presented the tonal targets at five different levels of signal-to-noise ratio (SNR) with respect to the unmodulated part of the broadband noise. The two experiments in the current study differ in this feature of the stimulus design.

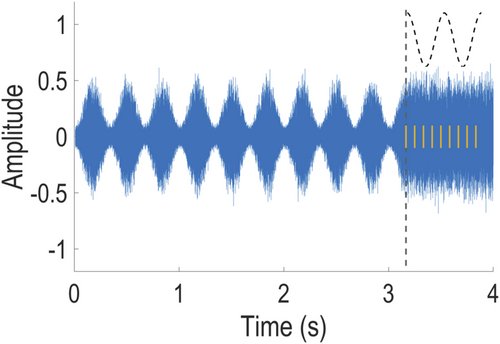
2.2.1 Experiment 1

In Experiment 1, we presented the tonal target at two SNR levels only. The two levels corresponded to (a) the near-threshold level, which was determined for each participant using a staircase procedure prior to the experiment and (b) the above-threshold level, which was fixed at 6 dB above the threshold level for each participant. Note that this design preserves the presence of intensity uncertainty in auditory targets, which was argued to be critical for the entrainment effect to take place (Farahbod et al., 2020).

2.2.2 Experiment 2

In Experiment 2, we adopted the same design as the original Hickok et al. (2015) study, which presented the tonal targets at five SNR levels covering a range of 12 dB. Specifically, the five levels were composed of one below-threshold level (Level 1), one near-threshold level (Level 2) and three above-threshold levels (Levels 3–5). Note that the same SNR levels were used for all participants, such that the near-threshold level (Level 2) in the original study was not determined for each participant. In the current experiment, we aimed to recreate the same correspondence between SNR levels and overall detection accuracy as in the original study. The key was to assure that targets at Level 2 resulted in near-threshold performance at the group level. In order to achieve this goal, we estimated the group level detection threshold by averaging individual threshold SNRs across all participants from Experiment 1 and used this level as SNR Level 2 in Experiment 2. Finally, the SNR of the other four levels were spaced such that the five levels covered 12 dB with equal distance.

3 RESULTS

3.1 Reanalysis of data from the original study: Hickok et al. (2015)

We first analysed the data from the original study of Hickok et al. (2015), using the modified analysis pipeline. The objective of this reanalysis was twofold. First, we sought to provide a more fine-grained quantitative description of the strength of 3-Hz modulation observed in the accuracy curves of the original study. Second, we wanted to compare the strength of 3-Hz modulation between accuracy curves and hit rate curves in order to test to what extent the entrainment effect presented in the original study persisted after the removal of random response noise from non-target trials. Recall that, due to the arbitrary assignment of experimental conditions to non-target trials, participants' performance on these trials cannot be objectively associated with any temporal position (see Section 2.4.1 for a detailed explanation). Modulation strength from hit rate curves then serves as a reference to which results of the current study will be compared. We used the preprocessed data from the original study, which were made public by the authors (Saberi et al., 2020).

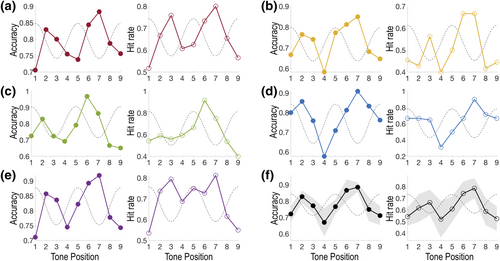
We first computed mean hit rates for targets at five SNR levels across different participants (Table 1). Our results confirmed that the detectability of targets at SNR Level 2 is closest to participants' detection threshold (Mean = 0.61; standard deviation [SD] = 0.07). We then examined the impact of temporal position on target detectability at SNR Level 2. Accuracy and hit rate curves from the five participants are presented in Figure 2. For accuracy curves, both PCA and the analysis of normalized 2.67-Hz power confirmed strong evidence for near-3-Hz modulation in all five participants' performance. Results from the PCA revealed a dominant bi-cyclic, M-shape, pattern that accounted for 80.97% of the variance across the five participants' performance curves (Figure 3a). Moreover, analysis of the normalized 2.67-Hz power in accuracy curves showed positive modulation strength in all the five participants (Mean = 1.14; SD = 0.39). For hit rate curves, our results also showed evidence for near-3-Hz modulation, although the strength of the effect manifested at a lower level than in the case of accuracy. Specifically, PCA analysis showed that the dominant pattern, which had a similar bi-cyclic shape as the one for accuracy curves, provided less explanatory power for the variance cross participants' performance (70.55%; Figure 3b). In a similar vein, analysis of the normalized 2.67-Hz power showed a decreased average modulation strength (Mean = 0.75; SD = 0.56). In fact, decreases in the modulation strength were observed in four out of five participants (Figure 3c), which is in line with the less apparent cyclic pattern in hit rate curves of these participants compared to accuracy curves (For instance, Figure 2c and 2e).

TABLE 1. Average hit rate for target tones at the five SNR levels across the five participants in Hickok et al. (2015)

	1	2	3	4	5
Mean	0.22	0.61	0.95	0.99	0.99
SD	0.04	0.07	0.01	0.02	0.01

• Abbreviations: SD, standard deviation; SNR, signal-to-noise ratio.

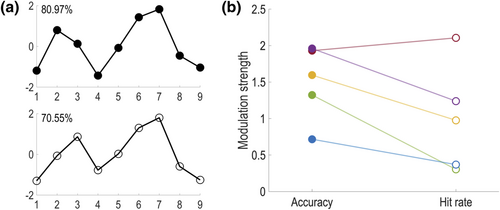
In summary, reanalysis of the data from the original study using our quantitative methods confirmed the observation of a positive entrainment effect (normalized 2.67-Hz power) in all participants' hit rate curves. Meanwhile, our results also showed that the strength of the effect decreased in most participants, after the removal of their performance in non-target trials, which cannot be objectively associated with any temporal position (see Section 2.4.1 for a detailed explanation).

3.2 Modulation of target detectability by position: Current study

Having established a new quantitative description of the entrainment effect observed in Hickok et al. (2015), we applied the same analyses to hit rate results from the two experiments of the current study. We first assessed the average hit rate for near-threshold targets in both new experiments. Our results showed comparable hit rates between our experiments (Experiment 1: N = 24, Mean = 0.61, SD = 0.14; Experiment 2: N = 23, Mean = 0.59, SD = 0.16) and the original study (N = 5; Mean = 0.61; SD = 0.07). In addition to the average hit rate for near-threshold targets, we also checked whether participants from our experiments exhibited similar performance in non-target trials as those from the original study. This assessment showed similar false alarm rate across all non-target trials between our experiments (Experiment 1: N = 24; Mean = 0.047; SD = 0.055; Experiment 2: N = 23; Mean = 0.048; SD = 0.042) and the original study (N = 5; Mean = 0.050; SD = 0.011). 4

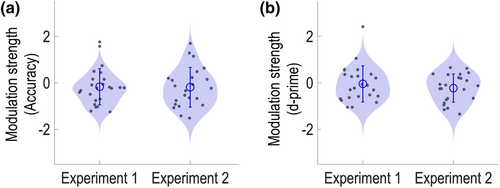
We then examined the impact of temporal position on detectability of the near-threshold targets. Interestingly, visual inspection revealed no sign of a bi-cyclic pattern in the average hit rate curves across participants for either experiment (Figure 4a; see Figures S1 and S2 for an inspection of individual hit rate curves of each experiment). Results from our analyses quantitatively confirmed this observation. For Experiment 1, the dominant PCA component presented a non-cyclic pattern across the nine temporal positions (Figure 4b). This component accounted for 41.62% of the variance in hit rate curves across participants and indicated best target detectability at the Positions 5 and 6. Analysis of the normalized 2.67-Hz power revealed that the average modulation strength across participants was not significantly different from 0 (Mean = −0.15; SD = 0.78; t[23] = −0.96; p > .1). Assessment of individual results showed that only 9 out of 24 participants had a positive modulation strength (Figure 5a). For Experiment 2, the dominant PCA component did not show the bi-cyclic, M-shape, pattern either (Figure 4b). Instead, it also revealed a non-cyclic pattern, where target detectability was low at initial and final positions and peaked around Positions 6–8. In addition, analysis of the normalized 2.67-Hz power revealed that the average modulation strength was not significantly different from zero (Mean = −0.20, SD = 0.72, t[22] = −1.32, p > .1). Assessment of individual results showed 8 out of 23 participants with a positive modulation strength (Figure 5a). Finally, the comparison between the two experiments (Experiment 1 vs. Experiment 2) revealed no significant difference in average modulation strength (t[45] = .21, p > .1).

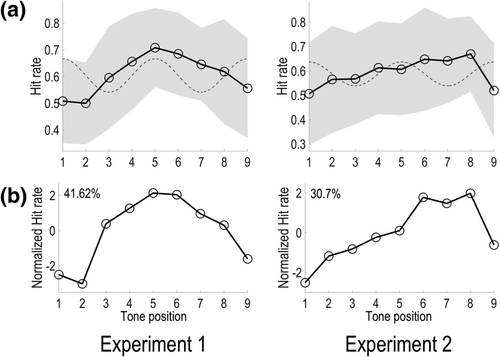
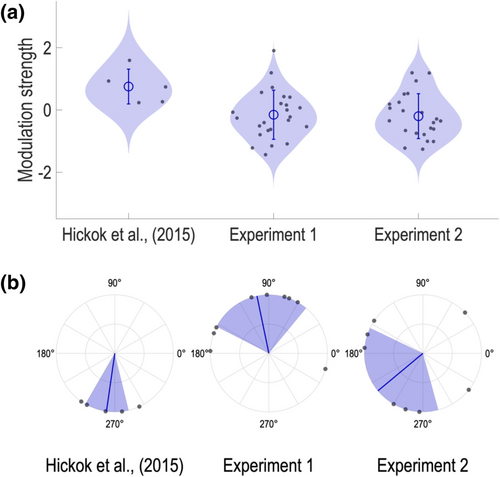
It is noteworthy that both of our experiments showed larger cross-participant variability in overall hit rate for near-threshold targets than the original study does. We next examined whether the absence of the entrainment effect at the group level in our experiments was due to this larger variability. One might argue that when participants' overall hit rate is too high (clearly above threshold) or too low (clearly below threshold), it reduces the likelihood of observing fluctuations across different temporal positions and hence decreases the sensitivity of the measurement in revealing potential modulation effects from the entraining signal. If there was any truth in this conjecture, one would expect to observe a clearer presence of the entrainment effect across participants whose overall hit rate is confined within a narrower range, similar to the one reported in the original study. In order to test this hypothesis, we computed a range of interest, using the mean and SD of overall hit rates for near-threshold targets across participants of Hickok et al. (2015). Specifically, this range of interest corresponded to the 95% confidence interval of a normal distribution defined with that mean and SD ([0.47, 0.75]). We then selected, for each of our experiments, participants whose overall hit rate for near-threshold targets was enclosed in this range (Experiment 1: 15 out of 24 participants; Experiment 2: 16 out of 23 participants). In order to further increase the level of comparability in terms of overall performance between our experiments and the original study, we also excluded participants whose overall false alarm rate is higher than 95th percentile of the distribution estimated from the false alarm rate of the five participants of the original study (0.069). This procedure additionally excluded six participants from Experiment 1 and three participants from Experiment 2. We then compared the average modulation strength across the selected participants of each experiment against 0 using t tests. Results from this more restricted analysis showed that the average modulation strength of selected data is not significantly above 0 (Experiment 1: Mean = −0.29; SD = 0.52; t(8) = −1.70, p > .1; Experiment 2: Mean = −0.21; SD = 0.72; t(12) = −1.04, p > .1; Figure 6).

Another important finding from Hickok et al. (2015) was the anti-phase relation between target detectability and the pattern of the preceding amplitude modulation of the background noise. Specifically, detection accuracy often reached a local maximum at temporal positions where the phase of preceding amplitude modulation would have approached the minimum. In the original study, this observation was confirmed by a narrow distribution of starting phase of 3 Hz power near −π/2 (−90° or 270°), which is the opposite phase of noise modulation (90°) at the same time instant (see fig. 4 from Hickok et al., 2015, for details). Here, we first re-examined this phenomenon using the hit rate data from Hickok et al. (2015). For each participant, we computed the phase of 2.67 Hz from the FFT of the hit rate curve. Mean and SD of the 2.67-Hz phase were calculated using the CircStat toolbox in MATLAB (Berens, 2009). Our results confirmed the original observation, with the starting phase of 2.67-Hz modulation being around 270° in all five participants (Mean = 261.80°; SD = 21.88°; Figure 5b). Although our own experiments did not provide any evidence for near-3-Hz modulation in target detectability at the group level, some participants did exhibit positive modulation strength in their results. Thus, we examined the distribution of 2.67-Hz phase in hit rate curves across these participants (Experiment 1: n = 9; Experiment 2: n = 8). Overall, our results did not show an anti-phase relation between target detectability and noise modulation in either experiment (Experiment 1: Mean = 101.71°; SD = 51.23°; Experiment 2: Mean = 219.80°; SD = 65.50°; Figure 5b). In terms of individual results, for Experiment 1, no participant showed a starting phase within a range of ±30° from 270°. For Experiment 2, only three participants showed a starting phase within that range.

3.3 Additional analysis of participants' accuracy and d-prime data

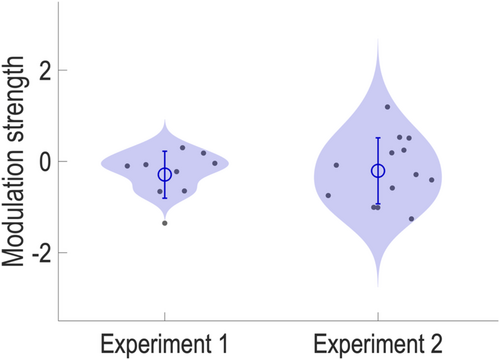
Due to the arbitrary pairing of non-target trials with experimental conditions, participants' performances in these trials cannot be objectively assigned to any specific temporal position (see Section 2.4.1 for a detailed explanation). We thus did not include non-target trials in our previous analyses. Meanwhile, we deem it necessary to address potential criticism related to the exclusion of non-target trials. We therefore conducted the same analyses on the normalized 2.67-Hz power using two measurements that take into account participants' performance in non-target trials, namely, accuracy and d-prime. 5 If the labelling of non-target trials with temporal position is indeed fully arbitrary, then the distribution of participants' correction rejection and false alarm responses across the nine temporal positions should be random. Thus, the inclusion of participants' performance from the non-target trials in the analysis, although would introduce random noise in participants' performance across different temporal positions, should not affect the statistical outcome of the entrainment effect observed in participants' hit rate curves at the group level.

Results from these analyses are presented in Figure 7. For both accuracy (Figure 7a) and d-prime (Figure 7b), the average modulation strength across participants was not significantly different from zero in Experiment 1 (accuracy data: Mean = −0.17, SD = 0.77, t(23) = −1.07, p > .1; d-prime data: Mean = −0.04, SD = 0.78, t(23) = −0.26, p > .1) or Experiment 2 (accuracy data: Mean = −0.19, SD = 0.85, t(22) = −1.06, p > .1; d-prime data: Mean = −0.23, SD = 0.60, t(22) = −1.80, p = .09). This finding supports the non-significance of the entrainment effect at the group level in both of our experiments, even when participants' performances in non-target trials were taken into account (see Figures S3–S6 for visual inspections of accuracy and d-prime curves of individual participants from the two experiments).

3.4 Non-cyclic modulation of detectability across temporal positions

Although the main objective of the current study was to examine the presence of bi-cyclic modulation patterns in target detectability across temporal positions, results from our PCA analyses revealed the existence of a non-cyclic pattern in participants' performance from both experiments of the current study (Figure 4b). This pattern resembles an inverted U-shape, where target detectability is low at initial and final temporal positions and reaches the maximum around the positions in the middle. These observations invited an examination of the presence of a non-cyclic pattern in the individual data of our participants. For this purpose, we conducted an analysis similar to the one used to investigate the strength of bi-cyclic modulation. Specifically, we calculated the goodness of fit (i.e., R²) of the hit rate curve of each participant to an inverted U-shape curve that was generated using a generic polynomial function. 6 This goodness of fit indicates the degree of presence of an inverted U-shape pattern in the hit rate curve of each participant. We then normalized the observed goodness of fit with a baseline level, which was computed from a permutated dataset created using the same permutation approach as for the analysis of 2.67-Hz power. Specifically, the baseline goodness of fit consisted of the averaged goodness of fit to the inverted U-shape function across hit rate curves from the permutated dataset, which indicates the average degree of presence of an inverted U-shape pattern that could arise from random fluctuations of participants' detection performance across the nine temporal positions. Finally, we computed the normalized goodness of fit by subtracting the baseline goodness of fit from the one observed in the real hit rate curve of each participant. Our hypothesis was that if participants' target detection across the nine temporal positions was resembling an inverted U-shape and this was not due to chance, then participants' real hit rate curves should show significantly stronger goodness of fit than the baseline level. Accordingly, the normalized goodness of fit should be significantly higher than 0 at the group level.

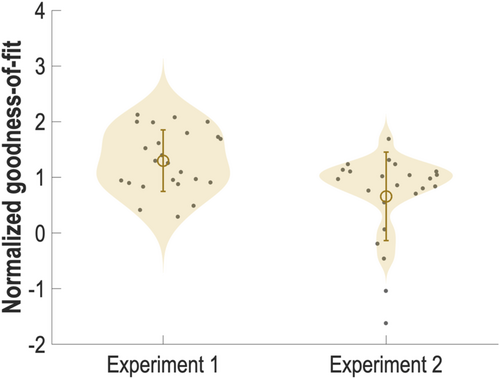
Results of our analysis showed a consistent presence of this non-cyclic pattern in participants' hit rate curves in both experiments (Figure 8). In Experiment 1, our results revealed that the normalized goodness of fit is significantly higher than 0 at the group level (Mean = 1.30; SD = 0.55; t(23) = 11.51; p < .001). Specifically, the normalized goodness of fit in every participant is higher than 0. In Experiment 2, our results showed that the normalized goodness of fit was also significantly higher than 0 at the group level (Mean = 0.66, SD = 0.80, t(22) = 3.97, p < .001). Assessment of individual results revealed that the normalized goodness of fit in 19 of the 23 participants is positive. Meanwhile, comparison between the two experiments revealed that normalized goodness of fit in Experiment 2 is significantly lower than those in Experiment 1 (t[45] = 3.22; p < .01).

4 DISCUSSION

The study was designed to replicate and extend the findings of Hickok et al. (2015) in order to understand the robustness of the paradigm and investigate the impact of oscillatory entrainment to a rhythmic signal on subsequent auditory processing. Specifically, we examined to what extent the entrainment effect observed in the original study can be reproduced with an increased sample size and with simplifications in the experimental procedure. The results from two new experiments reveal that only a subset of participants (~36%) exhibited the entrainment effect in behavioural performance. Consequently, neither of our experiments showed a significant entrainment effect at the group level. 7 Importantly, for both experiments, the failure to observe a significant entrainment effect at the group level was revealed with three different measures quantifying participants' performance across the nine temporal positions: hit rate, accuracy and d-prime. Second, further analysis focusing on subset of participants who did show the entrainment effect provided little evidence for a systematic anti-phase alignment between temporal fluctuations of target detectability and the pattern of the preceding entraining modulation. The current study does not demonstrate a consistent impact of a preceding rhythmically modulated background noise on the detection of upcoming near-threshold tone targets. It highlights substantial variability across subjects. The variable or absent entrainment effect held true in results from both the conceptual replication (Experiment 1) and the exact replication (Experiment 2).

In trying to understand the factors that underlie why our effects differ from Hickok et al. (2015), we first address methodological differences between the studies (which mostly concern modifications introduced in Experiment 1). First, in Experiment 1, we used individually measured detection thresholds to determine the SNR level of near-threshold tone targets for each participant, which contrasts with the use of a common near-threshold SNR level for all the participants in the original study. Despite this methodological difference, the average hit rate for near-threshold targets from Experiment 1 was at the same level as (i) that from the original study and (ii) our own exact replication (Experiment 2). Participants from both of our experiments also exhibited false alarm rates similar to the original study, which further confirmed a good level of comparability in terms of participants' overall performance between our experiments and the original study. Although the overall hit rates and false alarm rates from both of our experiments exhibited larger variability across participants than in the original study, our restricted analysis showed that this enlarged variability in participants' overall performance cannot account for the absence of the entrainment effect at the group level.

Second, in Experiment 1, we presented tone targets at two SNR levels instead of five in the original study. This modification not only shortened the duration of the experiment but also reduced the degree of uncertainty regarding the intensity of the targets. One might argue that this design difference potentially contributes to the disappearance of the entrainment effect in the experiment. However, that speculation is not supported empirically, as the results from Experiment 1 on modulation strength did not differ from those from Experiment 2, with the latter being an exact replication of the original study. In summary, the robust similarity between the results across our two experiments makes it unlikely that the methodological modifications in Experiment 1 played a major role to the absence of the entrainment effect at the group level.

Third, arguably the biggest difference between the current study and Hickok et al. (2015) concerns the sample size, with each of our experiments having data from four times more participants than the original study. Results from both of our experiments showed substantial cross-participant variability in the strength of near-3-Hz modulation compared to the level observed in the original study. Importantly, unlike the original study that showed a ubiquitous presence of positive modulation for all five participants, both of our experiments revealed a large proportion of participants who exhibited negative modulation strengths, which indicates the absence of a bi-cyclic pattern in hit rates. Consequently, our results reveal a decrease of average modulation strength from the level observed the original study to near 0. Although larger cross-participant variability could be expected with an increased sample size, the disappearance of the entrainment effect at the group level in both our experiments is surprising and could have multiple explanations. On the one hand, the overall higher modulation strength from Hickok et al. (2015) could result from certain contingent details of the experimental environment of the original study that implicitly facilitated the observation of entrainment effect across the tested participants. On this interpretation, one might expect stability of average modulation strength at a positive level, if more participants are tested in the same experimental environment despite a potential overall increase of cross-participant variability. On the other hand, it is also possible that the overall positive modulation strength observed in the study is due to an accidental underrepresentation of participants within the pool of tested participants who do not exhibit the entrainment effect. According to this interpretation, one should expect a decrease of the overall modulation strength at the group level, if more participants are tested in the same experimental environment.

Next, one characteristic of the original study is the consistent anti-phase alignment between the fluctuation of target detectability and the amplitude modulation in the preceding noise across participants. Our results did not reveal an anti-phase relation between participants' performance and noise modulation. In all participants who exhibited a positive entrainment effect, we observed sizeable variations in phase alignment within each experiment as well as between the two experiments.

Variable phase alignment between the rhythmic signal and perceptual facilitation could be due to multiple mechanisms. One possibility is that, given the continuous nature of acoustic modulation, the auditory system of different participants could phase lock to different parts of the entraining signal, which consequently induces perceptual facilitation at variable temporal positions. Although this explanation may account for the widely distributed phase alignment between rhythmic stimulation and performance facilitation when participants were entrained to frequency-modulated noise (Henry et al., 2014; Henry & Obleser, 2012), it is most likely not the case for the entrainment to amplitude modulation. Indeed, existing neurobiological findings have demonstrated converging phase alignment of slow cortical oscillations across participants in response to the amplitude envelope of auditory input (Doelling et al., 2019; Forseth et al., 2020; Simon & Wallace, 2017). Moreover, in a recent study using electrocorticography (ECoG) (Oganian & Chang, 2019), the authors found that auditory neuronal populations in the superior temporal gyrus (STG) exhibit maximum firing rate during the rising portion of the amplitude envelope of the acoustic input.

As suggested by the above-mentioned neurobiological studies, consistent neural responses to specific amplitude changes in the acoustic input should reduce the chance for jittered phase alignment. However, it is not straightforward to assume that a converging phase correspondence between the input signal and auditory neural activity should definitely induce better target detection at the same temporal position for every participant. A crucial question, which these previous investigations did not address, is to what extent the temporally aligned neural excitability would specifically facilitate sensory processing of the target stimulus. For instance, Bauer et al. (2015) addressed this question in explaining the lack of consistent perceptual facilitation for in-phase targets in their study. Note that, in that study, participants were asked to perform a task on the pitch of a target tone that was preceded by a sequence regularly paced distractor tones with a different pitch. They argued that, although attending to the preceding rhythmic signal should induce stronger temporal expectation for target tones that occurred in-phase with the preceding rhythm, it could be the case that a strong association could be instantiated between in-phase positions and the pitch value of the distractor tones and consequently hinder the perception of target tones that occur at these positions. Therefore, the conflicting benefits of temporal and spectral information carried by the entraining signal could contribute to the lack of consistent observation of behavioural facilitation of in-phase targets. As for the current paradigm, note that there is no direct correspondence between the spectral content of the entraining signal (broadband noise) and the target stimulus (1-kHz pure tone). Therefore, it is not clear to what extent a specific part of amplitude envelope of a broadband noise would trigger neural responses that specifically facilitate the detection of a 1-kHz tone. Recent neurobiological studies demonstrated that neurons in primary auditory cortex phase lock to rhythmic acoustic stimulation in a frequency specific manner (Lakatos et al., 2013; O'Connell et al., 2011). That is, when being stimulated with a sequence of pure tones, A1 neurons align their high excitability phase to the input signal only if the frequency of pure tones correspond to the preferred frequency of these neurons. These findings suggest that one could increase the sensitivity of the paradigm used in Hickok et al. (2015) in order to observe an entrainment effect by applying a stronger spectral correspondence between the entrainment signal and the target stimulus.

Finally, despite the failure to find a consistent bi-cyclic pattern in participants' performance, our results based on the PCA analysis reveal a non-cyclic pattern that is present in both of our experiments. This pattern is characterized by an increase of target detectability from the initial temporal positions towards the ones in the middle, which is followed by a decrease of target detectability towards the final temporal positions. Although the extracted pattern of the two experiments differ with regard to the exact location where detectability reaches the maximum, both patterns exhibit lower detectability at positions near the borders of the target window. Our analysis of the normalized goodness of fit to an inverted U-shape function shows more consistent presence of this non-cyclic pattern across our participants than of a bi-cyclic pattern. Interestingly, the hit rate curves of two participants from Hickok et al. (2015) also resemble the form of this non-cyclic pattern. The presence of this pattern in all three datasets invites speculations regarding an alternative behavioural phenomenon induced by the paradigm. In fact, a previous study, in which target stimuli were uniformly distributed within a time range, also found better target detection towards the middle of the time range than that towards the borders (Ng et al., 2012).

One possible explanation for this phenomenon could be that participants, after noticing that the target could occur across a certain time range, preferentially focused their attention on the centre of the time range. This performance pattern could result from a form of statistical learning of the temporal distribution of the target stimulus based on local temporal cues, sometimes known as a foreperiod effect (see Hoehl et al., 2021, for a review). A foreperiod is referred to as the time interval between the target stimulus and the final stimulus of a preceding entraining sequence. In the current study, one could consider the beginning of the unmodulated noise as a reference stimulus. Then, each temporal position for the target stimulus presents a specific foreperiod with respect to the reference stimulus, with the shortest foreperiod for the first position and the longest for the last position. Previous investigations have shown that when various foreperiods were mixed within an experimental block, target stimuli with different foreperiods would be processed with different efficiency (e.g., Ellis & Jones, 2010; Schirmer et al., 2021). In particular, it has been shown that participants were better at perceiving stimuli presented with the middle range foreperiod compared to those presented with foreperiods at the shortest and the longest ends (Ellis & Jones, 2010). Our finding is in line with these observations.

Given that the observed non-cyclic pattern manifests across the full time range for target occurrence, it should arise independently from the rhythmicity presented in the preceding stimulation. Meanwhile, studies have also shown that the shape of the performance pattern due to the foreperiod effect can be modulated by the presence of rhythmicity in a preceding entraining sequence (Ellis & Jones, 2010; Schirmer et al., 2021). Although it is uncontroversial to assume that the human brain integrates temporal information from different sources when predicting the timing of upcoming sensory stimuli (Hoehl et al., 2021), our findings suggests that the current paradigm allows more robust inferences about the impact of the foreperiod effect than that of the entrainment effect on the detection of tonal targets.

5 CONCLUSION

The primary goal of the current study was to replicate the entrainment effect observed in Hickok et al. (2015). Our findings raise questions about the robustness of the paradigm used in the original study, in revealing the impact of oscillatory entrainment on subsequent auditory processing. Specifically, based on findings from two experiments with increased sample sizes, no significant bicyclic modulation in target detection was observed at the group level. We suggest that the real effect size is substantially lower than originally estimated. Interestingly, while existing neurobiological studies have provided converging evidence for brain's ability to entrain to external rhythmicity (e.g., Lakatos et al., 2013), the lack of consistency in the demonstration of an entrainment effect at the behavioural level raises an issue of generalizability of the entrainment phenomenon across different cognitive levels. Therefore, designing and testing behavioural paradigms that allow for robust evidence of the entrainment effect at the behavioural level would be an essential requirement for understanding the complicated pathway from regulated fluctuations of local neural activities to potential modulations of efficiency in perceiving auditory events.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

AUTHOR CONTRIBUTIONS

Y. Sun and D. Poeppel designed research. Y. Sun collected experimental data. Y. Sun and G. Michalareas performed data analyses. Y. Sun wrote the initial draft. Y. Sun, G. Michalareas and D. Poeppel edited the final draft.