2.1 Why this matters

Neural field recordings are characterised not only by oscillatory activity, but also aperiodic ‘1/f’ or ‘1/f-like’ activity, in which signal power decreases exponentially as a function of frequency (Freeman et al., 2003; He, 2014). This is usually formalised as 1/f^χ where χ represents the decay of power across frequencies. In neural data, χ often ranges between 0 and 4, where a signal with χ = 0 is white noise, with equal power across all frequencies, and higher values of χ indicate increasingly ‘steeper’ spectra. Aperiodic neural activity has been linked to the underlying activity of postsynaptic potentials and is a ubiquitous and sometimes dominant feature of neural field data (Gao et al., 2017; Miller et al., 2009).

The fact that aperiodic activity is omnipresent together with the large observable variability of neural oscillations (Donoghue, Haller, et al., 2020; Frauscher et al., 2018; Groppe et al., 2013) requires care in how band-limited power obtained by spectral analysis is measured and interpreted. Due to the presence of aperiodic activity, there is always non-zero power at all frequency bands. This means that any spectral measure—including computing a power spectrum, narrowband filtering, and average band-power measures—will always return a numerical value for power for a given frequency band, even if there is no oscillatory activity present. That is, just because there is power in a frequency band does not imply that there is an oscillation in that same frequency band (Bullock et al., 2003). It is a fallacy to presume that an analysis of a predefined narrowband frequency range necessarily reflects physiological oscillatory activity.

To introduce how transient and aperiodic signals are represented in the spectral domain, the Dirac delta can be used, whereby a single non-zero value in the time domain is represented by constant power across all frequencies in the frequency domain (Figure 1a). This illustrates that power in a specific frequency band does not generally correspond to a present oscillation in the time domain. Similarly, 1/f-like aperiodic activity, which is common in neural data, shows power across all frequencies, with decreasing power for higher frequencies (Figure 1b). Despite the lack of periodic activity in aperiodic time series, narrowband filtering, which imposes a sinusoidal basis, extracts components that appear to be oscillatory, when filtered into canonical band ranges (Figure 1c). By comparison, rhythmic signals, such as a pure sinusoid, exhibit as a frequency specific peak in the power spectrum (Figure 1d). Neural field recordings can be simulated as a summation of oscillatory and aperiodic components, resulting in a power spectrum that exhibits a spectral peak exceeding the aperiodic component, reflecting a high amount of band-specific power (Figure 1e). In this case, the presence of the spectral peak is indicative of oscillatory power. In general, since different signal components can contribute to spectral power across different frequency ranges, power in a frequency band may not reflect oscillatory activity.

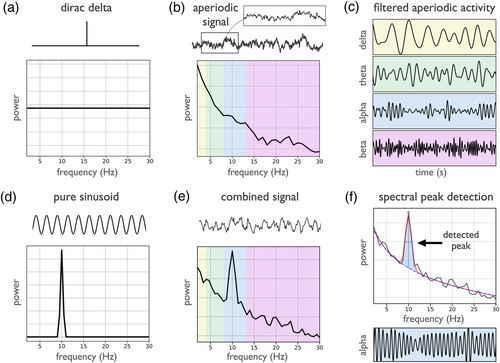
2.2 Recommendations

Investigations of oscillations should start with a detection step, verifying the presence of oscillations of interest. This verification step can be done in both the frequency and time domains. In the time domain, visualising the data allows for examining if there are clear rhythmic segments in the data. In the frequency domain, oscillations manifest as peaks of power over and above the aperiodic signal (Buzsáki et al., 2013). As an initial check, visually inspecting power spectra can help to verify the presence of prominent oscillations. Including figures of power spectra in manuscripts is recommended, as it provides supporting evidence to the reader that there is oscillatory activity in the data under study.

Numerous quantitative methods also exist to detect oscillatory activity in neural field data, such as automated methods that detect narrowband spectral peaks (Pascual-Marqui et al., 1988). This can be systematically done by parameterizing the power spectrum, in which a mathematical model that quantifies periodic and aperiodic activity is applied to detect any putative oscillatory peaks above the measured aperiodic component (Donoghue, Haller, et al., 2020) (see Figure 1f). Similarly, both the ‘multiple oscillation detection algorithm’ (MODAL) method (Watrous et al., 2018) and the ‘extended better oscillation detection’ (eBOSC) method (Kosciessa et al., 2020), which is itself an extension of prior methods (Caplan et al., 2015; Whitten et al., 2011), use a fit of the aperiodic activity to detect frequency specific activity.

It may also be useful to examine rhythmic properties of the data, to search for putative oscillatory activity in situations in which a spectral peak may be difficult to observe (Pesaran et al., 2018). For example, oscillations may be present in the form of rare or infrequent bursts, which will not appear as clear spectral peaks when the spectrum is calculated across the whole time interval. In such situations, examining shorter time ranges, and selecting time windows with higher band power and/or around events of interest may be required to resolve peaks in the frequency domain. Alternatively, time domain and burst detection methods, further described in Sections 4 and 5, may be more applicable. Another potential approach for addressing this is lagged coherence (Fransen et al., 2015), which explicitly quantifies the rhythmicity in time series, in contrast to measuring solely spectral power and can also be used to differentiate between oscillatory signals and transients (see Figure 1a).

Because oscillations can vary in their presence within and between participants, and across different frequency bands (Donoghue, Haller, et al., 2020; Frauscher et al., 2018) oscillation detection should be performed for each frequency band of interest, participant and analysed region. If oscillations are not detected, this may preclude further analyses. Group-level analyses may obscure variation in oscillatory presence in individual participants. For example, if not all participants display a clear rhythm, effect size estimates of oscillatory changes at the group level may be confounded by including the subset of participants without any clear oscillatory activity. Alternatively, a comparison of oscillatory power between regions without doing oscillation detection may conflate a change in oscillatory power with a difference in oscillatory presence. Analyses that include filtering or band-specific measures without first examining if an oscillation is present can provide ambiguous results that may reflect aperiodic activity, in which case it is a misinterpretation to describe physiological oscillatory activity. Applying analyses to detect oscillatory presence can assure that measures reflect oscillatory activity.

3.1 Why this matters

Neural oscillations display significant variations in their peak frequencies, including variation across age (Lindsley, 1939), within and between participants (Haegens et al., 2014), and across cortical locations (Mahjoory et al., 2020). Alpha peak frequency, for example, is considered a stable trait marker (Grandy et al., 2013), and is also associated with some clinical disorders, displaying, for example, a slower frequency in attention-deficit hyperactivity disorder (ADHD) (Lansbergen et al., 2011). The frequency of neural oscillations can also vary within participants within a task (Benwell et al., 2019), including in task relevant ways (Wutz et al., 2018).

Due to frequency variation, even if the presence of oscillations is verified, the use of canonically defined frequency ranges may still fail to accurately reflect the data, as this may misestimate power of an oscillation if the spectral peak is not well captured in the canonical range. For example, in Figure 2, a canonically defined alpha range of 8–12 Hz captures the peak of a 10-Hz oscillation (Figure 2a), but fails to accurately capture an 8-Hz peak (Figure 2b). Despite the signals being simulated with the same amount of oscillatory power, estimated alpha power using a canonical frequency range differs between the signals (Figure 2c), due to an underestimate of the power in the signal with an idiosyncratic peak frequency. This issue also impacts the result of band-pass filtering, as a canonical filter range underestimates the amount of alpha power present, as compared to an individualized band in which the filter range is made to reflect the oscillation in the data (Figure 2d). Using individualized frequency band ranges to control for frequency differences accurately captures the alpha power in each signal (Figure 2e). Overall, predefined frequency band definitions may fail to address variation in peak frequencies, and lead to misestimations.

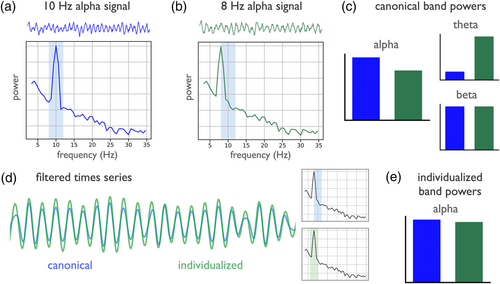
Potential differences in peak frequency are important for analyses that compute an estimate within a specific frequency range, such as calculating band power, or narrowband filtering to a frequency range of interest. Applying a fixed frequency range may lead to information loss when the individual peak frequency lies near the border or outside of the defined range; it can also be non-specific if the range captures an adjacent oscillation or aperiodic activity. These issues apply both to analyses of individual frequency bands, as well as to composite measures such as ratios computed between the power of different frequency bands, since variation in the peak frequency or bandwidth of peaks can impact measured results (Donoghue, Dominguez, & Voytek, 2020). For example, what had previously been reported as a difference in the theta/beta ratio of participants with ADHD was found to be partially driven by a slowed alpha peak in the ADHD group, changing the interpretation of the data (Lansbergen et al., 2011).

3.2 Recommendations

In order to address the variability of peak frequencies, any analyses that employ narrowband frequency ranges should assess how well the chosen ranges match the data. Visual inspection can help determine how well the defined frequency boundaries reflect actual peaks in the power spectra. This should be done for all analysed frequency bands at the level of individual participants, because individual participants may have idiosyncratic peak frequencies that could influence group level results if they are misestimated. For within-subject analyses, changes in peak frequency over time or between tasks should also be considered in order to address whether a measured change in power could reflect a change in peak frequency, in which frequencies may ‘drift’ outside defined ranges of interest. Including power spectra in manuscripts also enables readers to observe that applied band ranges match the peaks observed in the data.

If canonically defined frequency ranges do appropriately match the data, then they can safely be used for subsequent analyses. However, if chosen band ranges of interest do not appropriately reflect the data, then individualized frequency bands may be applied (Klimesch, 1999). Methods for computing individualized frequency bands often do so by measuring spectral peaks (Haegens et al., 2014; Pascual-Marqui et al., 1988). Automated approaches have also been developed, that include spectral smoothing to improve performance (Corcoran et al., 2018). Such approaches do not always generalise to multiple peaks or bands, though some approaches use ‘anchor frequencies’ (Klimesch, 1999), defining, for example, theta as a range below the identified range of alpha. This approach has the limitation of not considering the oscillation detection step. Peak detection for multiple putative peaks, without predefining frequency ranges, can also be done with spectral parameterization (Donoghue, Haller, et al., 2020), after which peaks can be grouped into observed bands of interest.

Beyond spectral peak detection, methods for detecting oscillations can be used to detect frequencies with peak rhythmicity, for example, by applying lagged coherence across frequencies (Fransen et al., 2015). Some methods also allow for jointly learning multiple band definitions. For example, the Oscillation ReConstruction Algorithm (ORCA) evaluates multiple band definitions in terms of how well each definition is able to reconstruct the data (Watrous & Buchanan, 2020), and the gedBounds method identifies frequency boundaries by clustering similarities across frequencies (Cohen, 2021). These methods, which examine all analysed frequencies together, may help to obtain more consistent groups of frequency ranges within and across participants. Collectively, some form of evaluation needs to be done to verify frequency bands, in order to ensure that applied measures accurately capture the intended oscillatory activity.

4.1 Why this matters

As previously introduced, neural field recordings contain aperiodic activity (B. J. He, 2014). This activity is not only ubiquitously present, but is also variable and dynamic within and between subjects (Freeman & Zhai, 2009; Podvalny et al., 2015). Between subject variability of aperiodic activity can relate to age (He et al., 2019; Voytek et al., 2015), and clinical diagnoses (Robertson et al., 2019), whereas within subjects, aperiodic activity varies with state, such as sleep (Lendner et al., 2020), relates to behavioural tasks (Podvalny et al., 2015) and can be influenced by exogenous stimuli and cognitive demands (Waschke et al., 2021). This dynamic aperiodic activity has different putative generators, physiological interpretations, and task related dynamics (Gao et al., 2017, 2020; Miller et al., 2009, 2014), as compared to oscillations, making it an interesting feature of interest in itself. Altogether, aperiodic neural activity is dynamic in many contexts in which neural oscillations are usually the focus of inquiry.

This dynamic quality of aperiodic activity is an important consideration for detecting neural oscillations, as previously discussed (see Section 2), as well as for interpreting measured changes in the data. With multiple dynamic components, analyses must adjudicate which aspects of the data are changing, and how, in order to allow for appropriate interpretations. Since aperiodic activity has power at all frequencies, changes or differences in aperiodic activity can induce patterns of differential activity across all frequencies. This can be seen by comparing white (χ = 0) and pink (χ = 1) noise 1/f^χ signals, which have different amounts of power in a canonically defined alpha-band (Figure 3a). Even with a validated spectral peak and frequency range, a difference in band-power between two conditions within a given frequency range may not be specific to oscillatory changes, as it may reflect a global change in aperiodic activity. For example, in Figure 3b, a measured difference in alpha-band power between two conditions reflects a change in the aperiodic exponent, not changes relating to a spectral peak in the alpha-band, since the periodic activity is the same in the two signals.

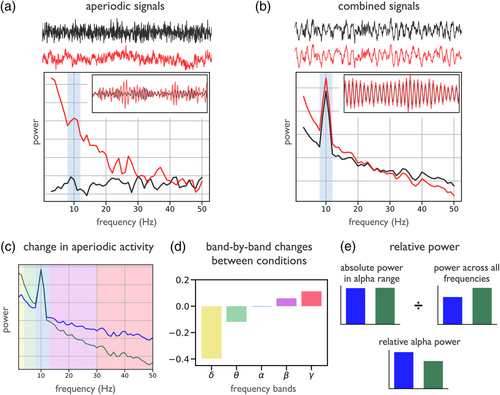
Considering aperiodic activity is particularly important for analyses that investigate band-power across a series of frequency bands, since systematic patterns of measured changes across bands may not reflect any changes in oscillatory activity. For example, in Figure 3c, the band-power of two conditions is compared across five different frequency bands. Despite this analysis suggesting a pattern of changes in band power across a series of canonically defined frequency bands (Figure 3d), the changes are actually driven by a change in aperiodic activity. Patterns of correlated changes across frequency bands can therefore sometimes be more parsimoniously explained by a change in aperiodic activity, rather than as multiple distinct oscillatory changes, as has been shown to be the case in development (He et al., 2019).

Changes in global power, due to aperiodic changes, can also impact relative or normalised measures of oscillatory activity. In the spectra in Figure 3c, there is a visible spectral peak in the alpha-band. Even though there is no change in peak power, a relative power measure suggests a change in alpha power, due to a change in the power across all frequencies, that is driven by a change in aperiodic activity (Figure 3e). This issue also impacts other compound measures, such as ratios of band-power, including the theta/beta-ratio, often investigated as a potential biomarker for ADHD (Lansbergen et al., 2011; Robertson et al., 2019), as it has been shown that band ratio measures often reflect a change of the aperiodic activity (Donoghue, Dominguez, & Voytek, 2020), and that the putative relationship between ADHD and theta/beta-ratio appears to be driven by aperiodic activity (Robertson et al., 2019).

4.2 Recommendations

As both oscillatory and aperiodic components are dynamic, it is important for analyses to validate which elements of the data are specifically changing, in order to appropriately interpret results. This is relevant for any analysis investigating putative narrowband power, including investigations that examine multiple oscillation bands. Aperiodic activity should be explicitly measured to evaluate whether it explains the band-specific changes, including whether correlated patterns of changes across frequency bands may be more parsimoniously explained as a change in the broadband aperiodic activity. Approaches that assume oscillations exist upon a stationary ‘background’, such as relative power measures that divide by power across all frequencies, or band ratio measures, should be avoided, as they conflate changes in oscillatory and aperiodic components (Donoghue, Dominguez, & Voytek, 2020). For example, a change in a relative power measure could arise from a change in band-specific power of interest, or be due to a change in aperiodic component that changes the measured power across all frequencies that is used as the denominator.

Explicitly measuring aperiodic activity requires methods that explicitly conceptualise both aperiodic and periodic activity, to avoid erroneously attributing aperiodic activity as oscillatory changes. Methods that define and measure oscillatory activity relative to aperiodic activity, including previously introduced methods such as spectral parameterization (Donoghue, Haller, et al., 2020) and eBOSC (Kosciessa et al., 2020), are designed to measure and control for aperiodic activity, and so address this issue. There are also dedicated methods for measuring aperiodic activity. For example, the irregular-resampling auto-spectral analysis (IRASA) method leverages the scale-free nature of aperiodic activity by proposing a resampling procedure to isolate aperiodic activity (Wen & Liu, 2016). IRASA can be used to separate and measure aperiodic neural activity, after which analyses can evaluate each component to examine whether measures of interest specifically reflect the intended component. Overall, controlling for aperiodic activity requires employing an oscillation detection step and evaluating oscillatory power relative to the aperiodic component in order to assess whether measured changes are capturing oscillatory or aperiodic activity.

5.1 Why this matters

Neural oscillations often display burst-like temporal dynamics (Lundqvist et al., 2016; Sherman et al., 2016) and are rarely, if ever, completely consistent and continuous. These temporal dynamics of neural oscillations are a potentially important feature; for example, the rate of burst events has been found to be predictive of behaviour across tasks and species (Shin et al., 2017), including in investigations of working memory (Lundqvist et al., 2016) and motor activity (Wessel, 2020). Some generative models of oscillations predict non-continuous events in a way that is consistent with what is seen in empirical data (Sherman et al., 2016).

Despite this, many methods implicitly assume stationarity of the signal under study, when analysing, for example, average band power across time or trials. In such cases, variability of oscillation presence or temporal dynamics can be misinterpreted as differences in power. For example, in simulations with stochastic onset and offset of oscillatory activity, signals can display different proportions of the data with oscillatory activity present, with the oscillatory power when present being equivalent (Figure 4a). Measured power in such cases reports a different amount of band specific power, typically interpreted as reflecting a change in the overall amplitude of the oscillation, however, measured differences can be due to temporal variability (Figure 4b). These kinds of averaging effects are also important in scenarios such as time-frequency analyses that average across trials, which may create an illusion of sustained activity in averaged data (Feingold et al., 2015; Jones, 2016). This can happen if individual trials have burst-like temporal dynamics that occur at different times across different trials, which can average together in a way as to suggest a sustained response in average data, despite such continuity not occurring in any individual trial (Figure 4c). The temporal variability of neural oscillations motivates the importance of considering single trial dynamics (Kosciessa et al., 2020; Rey et al., 2015; Stokes & Spaak, 2016).

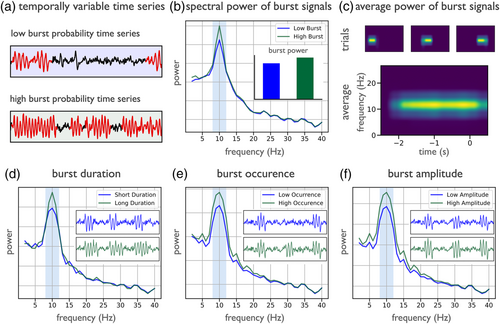
Oscillatory bursts can vary in multiple ways that can lead to similar measured changes in band power, which may be misinterpreted as reflecting changes in tonic band power. This includes changes in burst duration (Figure 4d), burst occurrence (Figure 4e), or burst amplitude (Figure 4f), each of which can vary within or between analysed time periods (Quinn et al., 2019; Zich et al., 2020). Understanding the different sources of variability has implications on how these signals should be interpreted, as a change in the length, number, or size of bursts each likely reflect different circuit mechanisms and putative relationships to neural function. However, this cannot be appropriately evaluated unless methods acknowledge oscillations as potentially transient, with potential variability in rate, timing, and duration as well as amplitude (van Ede et al., 2018).

5.2 Recommendations

Analyses of neural oscillations must therefore evaluate whether temporal variability, rather than overall power, may be driving measured changes. In order to address temporal variability, both the spectral and temporal domain have to be considered together (Zich et al., 2020). Time-frequency analyses, such as spectrograms, can be used to examine spectral properties across time in order to adjudicate between changes in the average power of oscillations and changes in their temporal dynamics. In doing so, it is important to analyse single-trials (Rey et al., 2015; Stokes & Spaak, 2016), to avoid misinterpreting averaged power. If reporting spectrograms, single-trial examples should be included in order to evaluate whether apparent sustained activity is truly sustained, or arises as a result of averaging many short bursts.

Burst detection methods can also be applied to identify segments of the signal in which oscillations are present, which can then be characterised in terms of the durations of the bursts, the number of bursts, and/or the amplitude of the bursts. A common approach for burst detection is to use an amplitude threshold, detecting segments of power in which frequency specific power is greater than a chosen threshold level (Feingold et al., 2015). The previously described eBOSC algorithm (Kosciessa et al., 2020) can be considered to be a threshold based burst detection, in which the threshold is based on the aperiodic component, and can be used for burst detection.

Other algorithms for burst detection include matching pursuit, in which a dictionary of atoms, which can include oscillatory bursts, is fit to the data, providing potentially more accurate estimates of burst onset and duration (Chandran KS et al., 2018). Alternatively, methods such as hidden Markov modelling can be used, which seek to characterise state transitions, and can be used to model transitions into and out of oscillatory states in a probabilistic way (Quinn et al., 2019; Vidaurre et al., 2016). Time-domain measures that identify oscillations by characterising individual cycles, further described in Section 6, can also be used to detect and analyse the number and duration of bursts, and their cycle-by-cycle properties (Cole & Voytek, 2019; Schaworonkow & Nikulin, 2019). After detection, analyses of burst-like neural activity typically involve subsequent analysis of the identified bursts, in order to evaluate whether they are changing in their duration, occurrence, and/or amplitude.

6.1 Why this matters

The waveform shape of neural oscillations is often non-sinusoidal (Cole & Voytek, 2017; Jones, 2016), as seen, for example, in the arc-shaped sensorimotor mu-rhythm, visual alpha, which can be triangular, and the sawtooth-shaped hippocampal theta-rhythm. These waveform properties of neural oscillations may reflect physiological properties, for example the synchronisation of neural activity (Schaworonkow & Nikulin, 2019), spiking patterns of underlying neurons (Cole & Voytek, 2018), or behavioural correlates such as running speed (Ghosh et al., 2020). Waveform shape can therefore be an important feature of interest, with potential to impose constraints on generative circuit models of oscillations (Sherman et al., 2016) as well as time constants of involved synaptic currents.

The variable waveform shape of oscillations also creates substantial methodological and interpretation hurdles, due to the assumed sinusoidal basis underlying most methods. For instance, estimating instantaneous phase typically involves narrowband filtering the signal before applying a Hilbert transform. Applying a narrowband filter on data with variations in waveform shape can be problematic, as the phases of sinusoidal outputs of narrowband filtering will not correspond to phases of a non-sinusoidal signal (Figure 5a). This occurs because in the spectral domain, nonsinusoidal shapes are represented by power across multiple frequencies, and if the signal content in the harmonic frequencies is removed, the resulting filtered signal will have shifted peaks and troughs compared to the original non-sinusoidal signal (Figure 5a). This is an important consideration for any analyses that examine cycle properties, such as the location of signal peaks and troughs, as putatively corresponding to specific physiological states. For analyses that rely on exact temporal characteristics (e.g., investigating the effects of pre-stimulus phase on behavioural measures), controlling for waveform shape may be beneficial.

In spectral analysis, non-sinusoidal waveforms are reflected in the power spectrum as harmonics occurring at multiples of the dominant frequency, as illustrated in Figure 5b. This can result in interpreting these separate peaks as independent physiological rhythms. In the case of an arc-shaped mu-rhythm, for example, the waveform shape of the oscillation will create peaks in both the alpha- and beta-frequency ranges. This may be interpreted as separate alpha- and beta-rhythms with an assumed phase- and amplitude-coupled relationship, when in reality only one non-sinusoidal rhythm is present. Differentiating between those situations is complicated by the fact that several types of rhythms can be found across the cortex (see Section 7). Figure 5c shows how the degree of non-sinusoidality is reflected in the power of harmonic frequencies, with higher power in the harmonic frequency range for increasing non-sinusoidality. This should be considered when evaluating differences in spectral power between conditions, to control for potential changes in waveform shape.

The spurious coupling that waveform shape can induce between frequencies (Kramer et al., 2008) is especially important when considering measures such as phase-amplitude coupling that are greatly influenced by waveform shape (Cole et al., 2017; Lozano-Soldevilla et al., 2016). Waveform shape can result in systematic changes in the amplitude at harmonic frequencies, as seen in Figure 5d, which can depend on the phase of the base oscillation, as quantified in Figure 5e. This results in significant measures of cross-frequency phase-amplitude coupling. Numerically, these values are not objectionable, as they reflect a relationship between frequencies in the spectral domain. However, there is possible fallacy in the interpretation, if this relationship is taken to reflect significant coupling between independent rhythms, when in fact no such interaction between multiple rhythms need exist. Because of these methodological limitations, careful work needs to be done to adjudicate between phase amplitude coupling measures that reflect waveform shape versus those that truly reflect nested oscillations (Giehl et al., 2021; Vaz et al., 2017).

6.2 Recommendations

In order to evaluate and control for waveform shape, explicit measurement of waveform and cycle properties should be done. Time domain measures of individual cycles can be used to characterise waveform shape by, for example, calculating measures such as the rise/decay symmetry or peak sharpness (Cole & Voytek, 2019; Schaworonkow & Nikulin, 2019). Other methods aim at learning and grouping waveforms into observed categories, for example through attempting to learn recurring patterns in the data by sliding-window matching (Gips et al., 2017) or by attempting to learn a dictionary of observed shapes in the data and finding occurrences of particular waveforms in the data based on templates (Barthélemy et al., 2013; Brockmeier & Principe, 2016; Jas & Dupré, 2017).

In the frequency domain, specific waveforms can create stereotypical patterns in power spectra and time-frequency representations, which can complicate the detection of oscillations (see Section 2). If spectral peaks are present at exact multiples of slower frequencies, quantifying waveform shape may help to distinguish between an independent oscillation at that particular frequency or harmonic spectral peaks induced by waveform shape. Since different waveform shapes may exhibit similar time-frequency representations (Jones, 2016), time-domain analyses may be required to evaluate if and how waveform shape is contributing to spectral representations.

For cross-frequency coupling analysis, the frequency extent of local coupling within a region (e.g., for phase amplitude coupling, the range of higher frequencies that are coupled to the low frequency phase) can suggest whether it is likely to be genuine oscillatory coupling or a shape effect (Cole et al., 2017; Vaz et al., 2017), with narrow ranges at exactly multiples of the base frequencies indicative of possible coupling caused by waveform shape. Applying and comparing multiple measures of cross-frequency coupling can dissociate harmonic and non-harmonic phase-amplitude coupling (Giehl et al., 2021). More generally, frequency domain methods such as bicoherence, a measure of non-linear interactions between frequencies, can also be used to investigate waveform shape in the frequency domain (Bartz et al., 2019).

7.1 Why this matters

Non-invasive recordings of neural oscillations reflect aggregate activity across relatively large cortical areas. Through volume conduction, a term used to describe the propagation of electrical fields from their original source across tissues to recording sensors, recording electrodes can reflect activity from multiple local sources, as well contributions from more distant sources that overlap both spatially as well as temporally (Buzsáki et al., 2012; Nunez & Srinivasan, 2006). For instance, in the context of MEG/EEG, there are several alpha-rhythm sources, with locations in somatosensory, occipital, parietal and temporal cortex (Hindriks et al., 2017), which can be co-active at the same time. In many studies, recordings are analysed in sensor space, by directly analysing activity from recording sensors. In such cases, the aggregate signal may appear markedly different from the underlying sources of interest due to the spatial and temporal overlap of multiple distinct sources. Measures applied to these combined signals may therefore not accurately reflect the underlying sources, with distortions in measures of temporal dynamics or waveform shape (Schaworonkow & Nikulin, 2019).

Examining how spectral and time domain measures can be affected by overlapping sources is shown in an example in which sensor space activity from a single electrode is composed of activity from two underlying sources in the parietal and visual cortices (Figure 6a). In the spectral domain, this configuration can result in two peaks in the alpha-frequency range (Figure 6b), when the two sources have slightly different peak frequencies. This has been observed in empirical data as ‘double alpha’ or ‘split alpha’ peaks (Chiang et al., 2008). Analyses in sensor space may lead to the interpretation that a specific circuit generates signals with two simultaneously present peak frequencies, which in turn will influence theories of generating mechanisms. Spatial summation of multiple underlying rhythms of similar peak frequencies can also mask temporal features of interest of the underlying rhythms, as seen in Figure 6c, due to constructive and destructive interference effects (Schaworonkow & Nikulin, 2019). Phase differences between sources of similar frequencies can attenuate the oscillation in sensor space, due to interference, even though oscillatory power has not changed in the underlying sources. This may lead to erroneous interpretations regarding changing oscillatory power of the sources, when it may be that only their relative temporal relationship has changed.

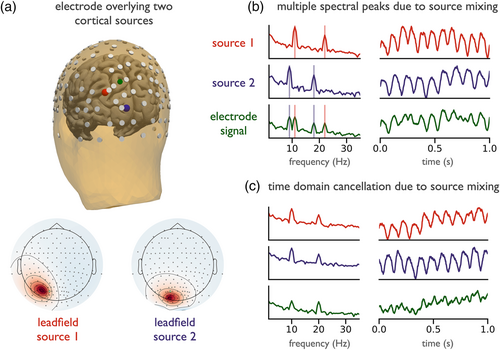
Inter-regional connectivity measures are also impacted by the simultaneous presence of multiple sources. Computing connectivity measures using sensor space signals can lead to spurious findings, because volume conduction influences these measures (Haufe et al., 2013; Palva et al., 2018; Palva & Palva, 2012; Schoffelen & Gross, 2009). Because individual sources propagate to multiple sensors, regularities in amplitude and phase will be present across multiple sensors. This can yield highly significant statistical relationships between electrodes, reflecting signal content that is present due to a common source rather than genuine interregional coupling, which may lead to erroneous interpretation of connectivity between oscillatory sources.

7.2 Recommendations

Due to overlapping sources, analysing sensor level time series or power spectra can be misleading regarding which aspects of the oscillation are present and/or are changing. Whenever possible, sensor space analysis should be complemented by source-level analysis. Source separation methods can be applied to attempt to separate different narrowband periodic components in the signal, which can help to reveal features that are not visible in sensor space data, as well as helping to localise sources. There are many possible approaches for source separation. Because inferring the activity of many more sources than channels is not possible, constraints are needed to arrive at a specific decomposition. The choice of the appropriate method also depends on the specific goals of source separation, including, for example, localising activity to specific regions and/or decomposing time series into components based on statistical properties.

Based on these goals, two main approaches with different optimisation criteria can be used for estimating source activity from sensor space activity. The first main type of methods use anatomical information to constrain the inverse solution based on individual or template structural MRI, in combination with methods such as beamformer or minimum norm estimation techniques (Hauk et al., 2019). The second main type of methods are agnostic to anatomical information and rely solely on the statistical structure of signals across channels. In this approach, channel activity is assumed to be a linear mixture of multiple underlying sources, defined by a leadfield matrix, which describes how individual sources map onto sensors (Parra et al., 2005). By assuming specific statistical properties of the source time series as well as mixing properties, demixing can be attempted. Methods in this realm include joint decorrelation (de Cheveigné & Parra, 2014) or independent component analysis (Hyvärinen & Oja, 2000). In the context of investigating neural oscillations, there are variants that specifically maximise signal-to-noise ratio (SNR) of narrowband oscillatory components, while minimising SNR in flanking bands or in comparison to broadband activity. For enhancing oscillatory SNR, spatial-spectral decomposition (Nikulin et al., 2011) or generalised eigendecomposition (Cohen, 2017b) can be used. The Common Spatial Patterns algorithm (Koles, 1991) and its variants (Lotte & Guan, 2011) can be used for maximising differences in narrowband activity between task conditions. For investigating relationships between narrowband activity and a continuous variable, Source Power Correlation analysis (Dähne et al., 2014) may be of interest. Spatial filtering methods can also be used as a preprocessing step for dimensionality reduction (Haufe, Dähne, & Nikulin, 2014), easing statistical comparisons and computational needs.

Components that result from source separation need validation, since different methods or parameter settings can yield highly different results, and solutions are not guaranteed to reflect physiologically meaningful activity. As such, source separation can be non-trivial and has its own set of methodological considerations as well as reporting guidelines (Cohen & Gulbinaite, 2014; Haufe, Meinecke, et al., 2014; Mahjoory et al., 2017). These guidelines can be used to evaluate robustness of the solution, such as with goodness of fit and/or localisation error metrics, and to adequately convey reconstruction quality and method details to the reader.

8.1 Why this matters

Neural oscillations are embedded in complex recordings containing multiple rhythmic signals, aperiodic activity, and transient events. Analysing oscillatory signals of interest requires defining features of interest (signal), and extracting this signal from the rest of the data (noise). As with all measures, methods for analysing oscillations require an adequate signal to noise ratio (SNR). Indeed, ubiquitous processing steps such as filtering are used largely in order to increase the SNR (Widmann et al., 2015). Many of the considerations thus far (detecting oscillations, adjusting frequency ranges, controlling for aperiodic activity, burst detection, and source separation) can all be conceptualised as aiming to increase SNR by tuning analyses to specific properties of the data. Beyond these specific properties, applied measures can still be inaccurately estimated if SNR is low or variable.

The SNR of oscillatory activity relates to the ratio of oscillatory power to noise, typically the aperiodic background. Oscillatory power is a dynamic property, which can be seen by the variable height of oscillatory peaks over and above the aperiodic component (Figure 7a). Many experimental paradigms will change oscillatory power, as presentation of stimuli may result in event-related attenuation of oscillations (Pfurtscheller & Lopes da Silva, 1999). This change in oscillatory power changes SNR, which in turn may influence accuracy and stability of other oscillatory measures such as instantaneous phase and frequency. When SNR is high, estimations of phase and frequency can be reliably estimated (Figure 7b). However, when SNR is low, estimation can be very noisy (Sameni & Seraj, 2017) as can be seen in Figure 7c, leading to artefactual large variations, often referred to as phase slips.

Changes in oscillatory power which change SNR and corrupt phase estimations can lead to inaccurate estimates of derived measures, such as the phase-locking value (Muthukumaraswamy & Singh, 2011) or inter-trial coherence (van Diepen & Mazaheri, 2018). Low SNR makes it difficult to reliably extract oscillations of interest (Figure 7d), leading to variable phase estimates (Figure 7e). When computing coupling measures on such estimates, differences in SNR, absent any true changes in phase alignment, can erode the detection of phase-locking between two signals (Figure 7f). Unstable estimation of oscillatory measures can also propagate to multivariate analysis, such as cross-frequency coupling, whereby oscillatory power changes that influence SNR can lead to a change in measured cross-frequency coupling (Aru et al., 2015). Time domain analyses, such as those designed for analysing waveform shape, are also strongly dependent on their being adequate SNR to meaningfully measure the properties of interest.

In cases of low SNR, unreliable estimates could, for example, lead to false-negatives due to noisy estimations that are not able to adequately capture measures of interest. Conversely, certain analyses may return false positive results, if the measured variability of the signal is mis-interpreted as a feature of interest, and/or leads to an artefactual measured change between conditions due to variable SNR. This may be an issue when comparing between groups who are known to have differences in relative power of oscillations, and/or when comparing within participants across conditions that may have different SNR.

8.2 Recommendations

Considering the SNR required for stable estimation of measures of oscillations starts by choosing appropriate experimental designs. When designing the protocol and tasks, experimenters should consider what is known about the reliability and effect size of effects of interest, and consider doing a power analysis to design well powered studies. This includes considering recording modalities, as different modalities have different sensitivities to different source locations (Piastra et al., 2020), as well as the different temporal, spatial, and frequency resolutions they offer. When recording the data, best practices should be employed to minimise non-neuronal noise, and use appropriate preprocessing in order to increase the quality of the data with the respect to desired analyses (Keil et al., 2014; Pernet et al., 2020).

Once recordings have been collected, or if considering existing datasets for potential re-analysis, SNR has to be considered to validate if the dataset is appropriate for the desired analyses. This requires explicitly measuring SNR to verify that applied measures are robust in the SNR regime of the data. If the SNR is too low to provide accurate measurements, the analyses may be non-viable, as any measurements will be uninterpretable. If the analysis can be run, then SNR should still be continuously verified, to evaluate whether potential changes of SNR across time or between conditions may explain measured changes in results (van Diepen & Mazaheri, 2018).

General approaches for optimising SNR include good filter design (de Cheveigné & Nelken, 2019; Widmann et al., 2015), and using information about spectral estimators and signals of interest to select the most appropriate methods to improve the accuracy and stability of estimates (Chavez et al., 2006; Lepage et al., 2013). There are also specific methods for more robust estimations of phase in low power situations, including Monte Carlo estimation (Sameni & Seraj, 2017) and applying a Kalman smoother (Mortezapouraghdam et al., 2018). Many of the previously described methods such as detecting oscillatory peaks, using individualized frequency ranges, and using burst detection can all improve SNR. Source separation techniques, including those that explicitly optimise SNR (de Cheveigné & Arzounian, 2015; Nikulin et al., 2011) can be used to extract oscillatory components with higher SNR.