1 INTRODUCTION

In our everyday life, we continually encounter more visual stimuli than our brain is able to process. Visuospatial attention allows us to spatially select behaviourally relevant stimuli from cluttered visual environments. Classical interpretations of visuospatial attention, such as the spotlight analogy (Cave & Bichot, 1999; Eriksen & St James, 1986; Posner et al., 1980), have largely ignored the temporal dynamics of spatial attention. Visuospatial attention is often studied using spatial cueing paradigms (Egly et al., 1994; Fan et al., 2002; Posner, 1980). These paradigms assume that visuospatial attention uninterruptedly monitors a certain behaviourally relevant location.

The conception that sustained attention is a continuous process, however, has been challenged in recent years (Fiebelkorn et al., 2013; Landau & Fries, 2012; VanRullen et al., 2007). Visual attentional performance has been shown to fluctuate, whereby the likelihood of detecting a given stimulus increases and decreases over time (Fiebelkorn et al., 2013; Fiebelkorn & Kastner, 2019). This waxing-and-waning of attentional performance follows a rhythmic pattern, predominantly at the theta (7–8 Hz) frequency (VanRullen, 2018). These rhythmic attention cycles seem to operationalise a rhythmic sampling of the visual environment. Hence, a sequential sampling of visual stimuli or spatial locations is possible during periods of heightened perceptual sensitivity (Fiebelkorn & Kastner, 2019). This phenomenon has been found in different types of attention (e.g. covert attention and overt attention; Fiebelkorn et al., 2013; Helfrich et al., 2018; Landau & Fries, 2012; Re et al., 2019; Song et al., 2014) using a variety of study designs. Furthermore, evidence from neurophysiological studies indicates a tight link between rhythmic sampling during attentional fluctuations and neuronal oscillations, both in humans and in non-human primates (Fiebelkorn et al., 2018, 2019; Spyropoulos et al., 2018). Electroencephalography (EEG) studies show that detection performance of attended stimuli is predicted by both alpha and theta oscillations in the visual cortex (Busch & VanRullen, 2010; Mathewson et al., 2009). These findings have been further corroborated by studies employing MEG (Landau et al., 2015) and TMS (Dugué et al., 2016) showing further evidence of the role theta-rhythmic modulations of visual attention. Studies on non-human primates have found that rhythmic neural activity in higher order cortical areas such as the FEF (Fiebelkorn et al., 2018, 2019; Gaillard et al., 2020) and in visual areas (Spyropoulos et al., 2018) relates to rhythmic attentional behaviour. For a recent full review on converging neurophysiological evidence of rhythmic attention sampling, see Gaillard and Ben Hamed (2020).

The variable landscape of study designs does not easily allow to compare results across studies. Indeed, studies show strong discrepancies in their results. Some studies have found rhythmic sampling effects at locations that were probed by a spatial cue (Helfrich et al., 2018; Landau & Fries, 2012), some studies only found effects at non-cued locations (Peters et al., 2020; Senoussi et al., 2019), and some found effects at both cued and non-cued locations (Fiebelkorn et al., 2013). Also, the reported frequency of rhythmic sampling is not consistent across studies, with frequencies ranging from 2 to 12 Hz (Landau & Fries, 2012; Song et al., 2014). Thus, although evidence of rhythmic sampling can be found across multiple behavioural paradigms, there is no broad consensus. Therefore, there is a strong need for consistent study designs and results, and the replication of key findings within this field is necessary, especially considering that many results obtained in this field of research might go unnoticed due to the so-called ‘file drawer’ effect, where negative results remain unpublished (VanRullen, 2013).

Two seminal studies have demonstrated the existence of rhythmic fluctuations in attentional performance using a modified version of the Egly–Driver task (Fiebelkorn et al., 2013; Helfrich et al., 2018). This task involves detecting a target that can appear at one end of one bar (i.e. the cued location), or at the other end of that same bar (i.e. space-based, non-cued location), or at the equidistant end of another bar (object-based, non-cued location) (Egly et al., 1994). Fiebelkorn et al. (2013) found evidence of rhythmic sampling at the cued and non-cued locations (Fiebelkorn et al., 2013). Although rhythmic sampling at the cued location occurred at 8 Hz (with another non-significant peak found at 4 Hz), the attentional sampling frequency at the non-cued location depended on the location of the target. Namely, sampling of the non-cued target within the same object, the other end of the bar, occurred at a frequency of 8 Hz, whereas sampling between objects, the non-cued target at the other bar, happened at a lower rate of 4 Hz (Fiebelkorn et al., 2013). From this study, it appears that attention samples the cued location at approximately 8 Hz, but also periodically samples other locations where a target could appear. Helfrich et al. (2018) followed up on this study. Using a similar task design, they showed that behavioural oscillations in detection accuracy on the Egly–Driver task tightly map onto neural oscillations in the frontoparietal dorsal attention network (Helfrich et al., 2018). With respect to the specific nature of the found behavioural oscillations, they did not find an 8-Hz peak at the validly cued location. Instead, they found that rhythmic sampling occurred within a broad frequency range around 4 Hz (the peak was only visible after alignment of all subjects' individual spectral peaks). Rhythmic sampling at the non-cued locations was not examined in their study. In summary, there is a discrepancy between the exact frequency range of the effect at the cued location. Moreover, both studies show low effect sizes for this effect at the cued location. Another study, investigating rhythmic sampling in working memory, did not find any effect at the cued location (Peters et al., 2020). Given the importance of these studies and the relevance for the field, it is crucial to understand whether, and at what frequency, the effects occur at the cued location.

Within the behavioural rhythmic sampling literature, it has repeatedly been found that the frequency of behavioural oscillations depends on the amount of behaviourally relevant locations in the visual field (Holcombe & Chen, 2013; VanRullen, 2016). Namely, attention seems to sample one object after the other at an ~8-Hz frequency, resulting in a split of this ~8-Hz sampling frequency over the total amount of behaviourally relevant locations (Fiebelkorn et al., 2013; Jans et al., 2010; VanRullen, 2016). For instance, Landau et al. (2012) found that two locations were each visually tracked at a ~4-Hz rhythm, where the fluctuating pattern of detection accuracy at one location was the anti-phase pattern of that of the other location. This suggests that attention samples the two locations one after the other, where each location is attended to at every second sampling moment. Furthermore, when tracking two moving objects, each object is sampled at ~3–4 Hz, but when tracking three objects, the sampling frequency declines to ~2.3 Hz (Holcombe & Chen, 2013). However, none of these studies contain a probabilistic cue, which renders one location more relevant than another. This cue is key in the Egly–Driver task to modulate endogenous attention, but it could potentially modulate the exact frequency of the rhythmic pattern at which attentional sampling occurs.

In endogenous attentional paradigms, spatial cues often function as a means to render spatial locations behaviourally relevant. The informativeness of the spatial cue, the cue validity, is the likelihood that the cue correctly predicts an upcoming stimulus. A spatial cue dictates the behavioural relevance of a certain location, that is, the extent of attentional resources devoted to that location. A very informative cue promotes sustained attention at one location, whereas a non-informative cue promotes the direction of attention towards multiple locations (Chou & Yeh, 2018). Cue informativeness can be regulated by changing the number of trials where a cue validly predicts an upcoming stimulus. A fully informative cue should prompt all attentional deployment towards the cued location and leave little to no attentional resources to sample away towards other locations. If 8 Hz is the fundamental rhythmic sampling frequency, then this should lead to sampling only at the cued location, at approximately 8 Hz. A less informative cue, on the other hand, would lower the behaviour sampling frequency (Gaillard et al., 2020). We hypothesise that a low cue informativeness (validity) would motivate observers to adopt a strategy where attentional resources are equally divided over locations, leading to more occasional switches from the cued object to the non-cued object. We therefore expect a predominant 4-Hz component in the power spectrum, indicating a regular and frequent sampling back and forth between the cued and non-cued locations (which is then also effectively sampled at 4 Hz). Note that we expect a 4-Hz and not a ~2-Hz sampling frequency even though in the Egly–Driver task three locations have to be sampled, because the results in Fiebelkorn et al. (2013) clearly indicate that the frequency split in the Egly–Driver task was only based on objects, and not locations. The notion that attentional switches away from the cued object to the non-cued object occur more frequently after non-informative cues than after informative cues has been discussed by Fiebelkorn and Kastner (2019).

In this study, we investigated rhythmic sampling of attention using a modified Egly–Driver task (after Fiebelkorn et al., 2013; Helfrich et al., 2018). Firstly, we aimed to investigate whether there is evidence of rhythmic sampling, and at what frequency, at the cued location. We expect to demonstrate evidence of rhythmic sampling around either 4 Hz or 8 Hz (or both), as reported in Fiebelkorn et al. (2013) and Helfrich et al. (2018). Secondly, we investigated whether the frequency of rhythmic sampling at the cued and non-cued locations depends on the informativeness of the cue. If behavioural relevance of spatial locations, manipulated by cue informativeness, indeed influences rhythmic attentional sampling, we should see a predominant ~4-Hz cued-location sampling at low cue informativeness and predominant ~8-Hz sampling at high cue informativeness.

2 METHODS

2.2 Procedure and experimental design

Participants performed a variant of the Egly–Driver task, modified to investigate detection performance across different cue-to-target interval bins (Egly et al., 1994; Fiebelkorn et al., 2013; Helfrich et al., 2018). Participants were seated in front of a PC monitor in a lightly dimmed room. Viewing distance was kept stable at 57 cm from the monitor by means of a chin rest. We performed video-based monocular eye tracking at 1000 Hz with the EyeLink 1000 system (SR Research, Mississauga, Ontario, Canada). A standard 9-point calibration and validation procedure was used to calibrate the eye tracker. After calibration of the eye tracker, participants were familiarised with the task using a practice block (60 trials, on 80% cue informativeness). Participants were asked to maintain fixation on a centralised fixation dot throughout each trial and to blink only after their response.

Trials started with a 300-ms fixation period, after which two peripheral white bars (size 4.4 × 22°, at 8.8° eccentricity) appeared on the screen, oriented either horizontally or vertically (Figure 1a). After a variable delay of 400–800 ms, a spatial cue (a black line around the one end of one bar, thickness 0.5°, area of coverage 4.4 × 4.4) appeared for a duration of 100 ms. The spatial cue predicted with varying probabilities (depending on the cue informativeness condition; see below) where the target would appear. The target was a small change in luminance on one end of one bar (size 4.4 × 4.4°), which appeared for a duration of 100 ms. Cue-to-target intervals were binned between 500 and 1683 ms in steps of ~16.7 ms (equivalent to display refresh rate). The trial distributions were pseudorandomly constructed so that each interval bin contained four validly cued trials. Cue-to-target intervals were randomly distributed across the experiment. Participants were asked to press a button on a response box (with the right hand) if they detected the target and to refrain from responding if no target was detected. There was a window of 1500 ms where responses were recorded. Target detection performance was titrated at 80% (similar to Helfrich et al., 2018 by adjusting the target luminance every 15 trials in steps of 1 RGB value (max. 255 [white])—thus, when performance was below 80%, the RGB value was increased by 1 and vice versa. The starting RGB value was 250. Task stimuli were presented on a gamma-corrected Iiyama ProLite monitor with an aspect ratio of 1920 × 1080 and a refresh rate of 60 Hz. Stimuli were programmed using the Psychophysics Toolbox (PsychToolbox; Brainard, 1997) in MATLAB (MathWorks, Version 2018b).

Our task consisted of three different cue informativeness conditions (see Figure 1b). The moderately informative cue condition involved identical cue parameters as in Helfrich et al. (2018). Here, the cue indicated the correct location of the target in 80% of the cued trials. During invalid trials (20%), targets could either appear at the other end of the cued location on the same bar (10%) or at the other bar at a location equidistant from the cued location (10%). Next to this, we introduced two other conditions. First, we added a non-informative condition in which the cue correctly predicted the location of the target in 33% of the cued trials. The probability that the target would appear at the cued location or either of the other two non-cued locations was, thus, equal. Second, we added a fully informative condition in which the cue always predicted the location of the target in cued trials; thus, the distribution was 100% validly cued trials versus no invalidly cued trials. In each condition, we added a small number of catch trials (10%) on top of these valid–invalid trial distributions. Catch trials, in which a cue was shown but no target appeared, were meant to keep the participants engaged. We divided the session into six blocks—two blocks for each cue informativeness type. The order of the cue informativeness conditions was counterbalanced across participants. Each condition consisted of 288 valid trials, so the number of invalid (non-cued) trials differed in each condition (non-informative cue: 864 trials, moderately informative cue: 72 trials), as well as the total number of trials (non-informative cue: 950 trials; moderately informative cue: 396 trials; fully informative cue: 317 trials). Valid (cued) trials were equally divided over the 72 cue-to-target interval bins, which resulted in four valid trials per bin. Invalid (non-cued) trials were randomly divided over the cue-to-target interval bins (thus, on average, there were eight trials per bin in the non-informative cue condition and one trial per bin in the moderately informative condition). Before each block and in every small break (after 50 trials), participants were informed about the current cue informativeness percentage to encourage them to adopt an appropriate attentional strategy.

To allow us to directly replicate the behavioural findings of Helfrich and colleagues, our moderately informative cue condition involved nearly identical task parameters and data preprocessing and analysis (see next section), apart from the following: (1) Trials started automatically, and not at button press, in order to increase the flow of the experiment, (2) we used an eye tracker to filter out and discard saccades and eye blinks, (3) participants were informed about the cue informativeness percentage, and (4) we vastly increased the number of trials and the number of participants (originally seven participants [main experiment] or 14 participants [control experiment], mean of 190 trials) (Helfrich et al., 2018). Note, however, that the number of trials is substantially lower than reported in an earlier study with a similar paradigm by Fiebelkorn et al. (2013).

2.4 Data analysis

To recreate the course of hit rates (Egly–Driver task) over the entire cue-to-target interval, we followed the preprocessing steps by Helfrich et al. (2018). First, we calculated the average hit rates over a window of 50 ms. We then slid this window forward over the entire cue-to-target interval, in steps of 1 ms. We smoothed the raw time course using a boxcar rolling average with a window size of 25 ms. A representational time course can be found in Figure 1c. Next, we applied a Hanning window and zero-padded the time course to a length of 10 s. In order to analyse the power across the frequency spectrum, we applied a fast Fourier transform (FFT) over these preprocessed time courses.

For our first aim, we examined whether there is rhythmic sampling at the cued location and at which frequencies. Power spectra were first tested for significant peaks using non-parametric permutation testing at subject and group levels. We constructed a surrogate distribution of power spectra. To that aim, we first randomised the hits and misses in each time bin across the cue-to-target interval for each participant. Then, for 1000 iterations, we conducted the same steps as described above. At subject level (for each participant individually), we determined the p-value per frequency, represented by the proportion of values of the surrogate distribution that exceeds the power at that particular frequency. The frequency with the highest p-value above the confidence level (P < 0.05) between 2 and 10 Hz served as the peak frequency for that participant. At group level, we took two approaches to compare the observed data against the surrogate distribution. First, we constructed a group distribution of surrogate data by averaging the individual surrogate data by each permutation. We then determined the proportion of values of the group-averaged surrogate distribution that exceeds the group-averaged power spectrum (i.e. the p-value). Second, we ran a paired-samples t-test between the observed data and the medians of the power spectrum of the individual surrogate distributions. All p-values were corrected for multiple comparisons using the false discovery rate (FDR) procedure (Benjamini & Hochberg, 1995).

Furthermore, we used two additional spectral analysis methods as per Helfrich et al. (2018). Both of these analyses include a group alignment of individual spectral peaks to account for the fact that the exact spectral peak frequency potentially could not be consistent over participants. First, we z-scored the power spectrum relative to the median and the SD of the surrogate distribution and selected the frequency with highest z-value, in the range of 2–10 Hz, as individual peak frequency (IPF). Second, we used Irregular Resampling Auto-Spectral Analysis (IRASA; Wen & Liu, 2016) to separate the oscillatory component from the fractal component (1/f activity) in the signal. We used a time window of 75% of the total signal and a step size of 50 ms. We applied IRASA to both the observed time series and permuted time series. We then selected the frequency where the oscillatory component maximally exceeded the fractal component. For both of these analysis methods, we aligned the individual power spectra according to the found peak frequencies. Subsequently, we compared the aligned observed data against the median aligned surrogate data using a paired-samples t-test.

For our second aim, we examined whether cue informativeness altered rhythmic sampling behaviour. Firstly, to determine whether cue informativeness significantly affected overall perceptual accuracy, a 2 × 3 repeated measures analysis of variance (RM ANOVA) was conducted with factors LOCATION (cued, same-object non-cued and different-object non-cued) and CONDITION (moderately informative and non-informative). The fully informative condition could not be included in this analysis, because it lacks non-cued trials. To analyse the other two cue informativeness conditions (fully informative and non-informative cues), we repeated the above-mentioned spectral peak identification analyses (i.e. subject-level permutation testing, group-level permutation testing, paired samples of observed data vs. the surrogate distribution, group alignments based on z-scoring and IRASA).

As an extra analytical step, in order to provide more evidence for specific null or alternative hypotheses, we used the Bayesian framework for t-tests, as proposed by Rouder et al. (2009). Using JASP (JASP Team, 2020), we conducted Bayesian paired-samples t-tests between the observed power spectra and the medians of the surrogate power spectra for each cue validity condition and at each target location separately. We first averaged the power at predetermined peaks, namely, at 4 Hz (between 3.5 and 4.5 Hz) and at 8 Hz (between 7.5 and 8.5 Hz), which we based on previous studies (Fiebelkorn et al., 2013; Helfrich et al., 2018). The null hypothesis (H₀) poses that around those predetermined peaks, there is no difference between the observed power and the power of the surrogate distribution; the alternative hypothesis (H_A) states that the observed power is higher than the power of the surrogate distribution. The Bayesian analysis compares the likelihood of the data fitting under H_A (Hypothesis 1) versus H₀ (Hypothesis 1), resulting in the Bayes factor (BF). A BF₁₀ of 3, for example, indicates that the data are three times more likely to fit under H_A than under H₀ (Wagenmakers et al., 2018). A BF₁₀ of 1 indicates no evidence, 1–3 anecdotal evidence, 3–10 moderate evidence and 10–30 strong evidence for H_A (for a full overview, see Wagenmakers et al., 2018). We always assigned a Cauchy prior distribution with r = 1/√2 to our analyses.

We also determined the effects of rhythmic sampling at the non-cued locations (i.e. same-object and different-object locations) and compared these effects across the moderately informative and non-informative conditions. This comparison was not possible in the fully informative condition due to a lack of non-cued trials. We constructed time series for the non-cued location in the same manner as the cued location (see above), except that we used a longer sliding window of 100 ms, to accommodate for the scarcity of trials. In the moderately informative cue condition, there were more trials (i.e. 288) in the cued than in the non-cued locations (i.e. 36 at each location), impeding direct comparison across locations. To overcome this, we took 10 samples of 36 hits and misses amongst the validly cued trials, created a time series for each sample (see above) and averaged these into one time series. Within each condition, for each location separately, we compared the observed data against the surrogate data using the two non-parametric testing analyses described above ([1] score the group-averaged power spectrum against a group-averaged surrogate distribution, and [2] perform a paired-samples t-test of individual power spectra vs. the medians of individual surrogate distributions). We also investigated whether the significant effects at the pooled non-cued locations in the moderated informative cue condition could not be explained by an autocorrelation in the behavioural time course (Brookshire, 2021). We used the Monte Carlo singular spectrum analysis (SSA) method, originally proposed by Allen and Smith (1996), to differentiate the signal from aperiodic background activity. In this analysis, Monte Carlo simulations are used to estimate the expected spectral signal based on coloured AR(1) (autoregressive model with 1 positive coefficient) noise. To reduce our spectral resolution (unnecessary for this analysis), we down-sampled our time course to 50 Hz. SSA was performed with a sliding window of 20 samples using the Broomhead and King estimation (Broomhead & King, 1986). We used source code for the python implementation of the SSA available at https://github.com/VSainteuf/mcssa.

Finally, as a robustness check, we ran simulations to see what effect we would be able to statistically reveal using the current trial amount of four trials per bin. To this aim, we simulated data of 26 participants and a range of 1–10 trials per bin in steps of one trial per bin. We simulated trials with hits or misses and cue–target interval bins (72 in total, ranging stepwise between 500 and 1700 ms). Per trial, we randomly sampled between hit (1) and miss (0), where the probability of sampling a hit (P_hit) was defined by a 4-Hz sinusoid with the following formula:

where b is the effect size (amplitude) ranging from 0.0 to 0.2, in steps of 0.02, and where i denotes the cue–target interval. We introduced interindividual variability β, based on the results that we found at the cued location in the moderately informative cue condition. The coefficient of variation at 4 Hz in the power spectrum was ~0.5 (0.54 precisely). For each participant, we randomly drew β from a distribution where mean = 1 and SD = 0.5. The probability of a miss (P_miss) is P_hit − 1. Individual variability in underlying frequency (4 Hz) is not taken into account in these simulations. We created 500 distributions of hits and misses and one surrogate distribution of 500 permutations per participant. Then, we ran these distributions through our analysis pipeline: construction of behavioural time series, zero padding, applying a Hanning window and performing an FFT. For each effect size, trial per bin and each of our 500 simulations, we scored the group-averaged simulated data against a surrogate distribution. The surrogate distribution was created by analysing, in the same pipeline, 500 distributions of 80% hits (1) and 20% misses (0).

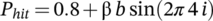
3 RESULTS

3.1 No evidence of rhythmic attention at the cued location

For our first aim, we investigated if there is evidence of rhythmic sampling at the cued location, and at which frequency, in an Egly–Driver task. Overall reaction time for this condition was 467 ± 45 ms (mean ± SD). In our experiment, detection accuracy was aimed to be titrated at ~80%, using an adaptive staircase procedure, as per Helfrich et al. (2018). The actual observed detection accuracy at moderate cue informativeness was 78.52% (±2.89%), which is only slightly but significantly lower than 80% (t₂₅ = −2.56, P = 0.014).

On a subject level, we assessed whether the individual spectral power exceeded the 95th percentile of the surrogate distribution, at any frequency in the range between 2 and 10 Hz (see Figure 2a for a representational power spectrum). This was the case for only four participants, where the mean peak frequency lied outside the theta band (at 9.1 Hz). On average, the highest spectral peak was found at the ~85th percentile (84.96%) of the surrogate distribution, at a frequency of 4.64 ± 2.79 Hz (see Figure S2).

At group level, we scored the mean spectral power against the group-averaged surrogate distribution (see Figure 2b). The spectral power did not exceed the 95th percentile at any frequency (P_min,uncorr. = 0.44 at 2.0 Hz). As a second means of comparing against the surrogate distribution, we ran a paired-samples t-test against the median of the individual surrogate distributions. Here, we found no significant spectral peaks either (P_min,uncorr. = 0.52 at 2.0 Hz). In order to investigate the extent of evidence for the null hypothesis, we ran a paired-samples t-test under the Bayesian framework for spectral peaks at 4 and 8 Hz. Based on Fiebelkorn et al. (2013), who found a significant peak around 8 Hz, and Helfrich et al. (2018), who found a significant peak around 4 Hz, our H_A at both of these peaks stated that the observed data are greater than the median surrogate distribution. We found a BF₀₁ of 7.20 at 4 Hz (i.e. the data are 7.20 times more likely to fall under H₀ than H_A) and a BF₀₁ of 17.35 at 8 Hz, indicating moderate and strong evidence for H₀, respectively.

Furthermore, we used two peak alignment methods as per Helfrich et al. (2018). First, we z-scored the power against the median and SD of the permutations and selected the highest z-scores for each participant between 2 and 10 Hz (see Figure S1 for individual plots). Using this method, we found a mean peak frequency of ~5 Hz (4.67 ± 2.81 Hz). This peak was not significant, with a z-score of 1.28 ± 0.56 (Figure 2c). Second, we used irregular resampling (IRASA) to filter out the fractal (1/f) component of the signal. Between 2 and 10 Hz, the power spectrum exceeded the fractal component maximally at an average frequency of 4.64 ± 2.07 Hz. Once again, we constructed an aligned power spectrum around the IPF (see Figure 2d). As any peak will naturally arise due to the alignment to the maximum peak frequency over subjects, we need to correct for this in our statistical test. Therefore, we ran each permutated time series (see Section 2) through the IRASA procedure and identified peaks for each permutation. Subsequently, we compared the aligned observed data against the median aligned surrogate data (peak at 5.24 ± 0.08 Hz) using a paired-samples t-test (see Figure 2d). At the spectral peak, the aligned observed power spectrum was significantly lower than the aligned surrogate power spectrum (t₂₅ = −2.81, P = 0.009).

3.2 No influence of cue informativeness on rhythmic attention at the cued location

As our second aim, we investigated whether the existence and extent of rhythmic attentional sampling depend on the informativeness of the cue. First, we assessed whether overall detection accuracy at each (cued and non-cued) location was dependent on the informativeness of the cue using a 2 × 3 RM ANOVA (Condition × Location). Data were normally distributed, as assessed by a Shapiro–Wilk test (P > 0.05 for all combinations). A Greenhouse–Geisser correction was applied due to violation of the sphericity assumption. Detection accuracy was significantly different across both LOCATION (F_1.91,0.05 = 12.43, P < 0.001) and CONDITION (F_1,0.06 = 24.33, P < 0.001), as well as the LOCATION × CONDITION interaction term (F_1.62,0.05 = 11.56, P < 0.001). See Figure 3a. Post hoc analyses revealed that detection accuracy did not differ significantly across target locations within the non-informative cue condition. In contrast, within the moderately informative (80%) cue condition, detection accuracy at both the same object (0.73, 95% CI [0.04, 0.11], P = 0.001) and the different object (0.11, 95% CI [0.08, 0.14], P < 0.001) was significantly lower than at the cued location. There was no significant difference in detection accuracy at the same object versus at the different object (0.37, 95% CI [−0.02, 0.09], P = 0.17). These results indicate that we successfully altered behavioural performance by altering the informativeness of the cue. Note that there was no significant difference at the cued location between the cue informativeness conditions, as expected, because detection accuracy was always titrated at ~80%.

We repeated the above-mentioned spectral peak identification methods to assess attentional rhythmicity at the cued location across our different cue informativeness conditions (for fully informative cue and non-informative cue, see Figure 3b,c). Scoring subject by subject against the surrogate distribution yielded no significant spectral peaks (fully informative cue: 87.36% at 5.09 ± 2.55 Hz; non-informative cue:82.78% at 6.43 ± 2.58 Hz). There were also no significant spectral peaks on a group level, neither according to a paired-samples t-test of the observed power spectrum against the medians of the permutations (fully informative cue: P_min,uncorr. = 0.14 at 3.5 Hz; non-informative cue: P_min,uncorr. = 0.77 at 6.6 Hz) nor when scoring the observed data against a group-averaged surrogate distribution spectral peaks (fully informative cue: P_min,uncorr. = 0.14 at 3.6 Hz; non-informative cue: P_min,uncorr. = 0.62 at 6.6 Hz). In order to assess the evidence for the null hypothesis, we also ran a Bayesian paired-samples t-test to compare the spectral power of the observed data to the median of the surrogate distribution. As mentioned in the introduction, we have a directional H_A for the fully informative cue condition at 8 Hz, stating that the observed data are greater than the median surrogate distribution, and a non-directional H_A at 4 Hz, stating that the observed data are different than the median surrogate distribution. We found a BF₀₁ of 2.94 at 4 Hz and a BF₀₁ of 4.61 at 8 Hz, indicating anecdotal and moderate evidence for H₀, respectively. For the fully informative cue condition, our hypotheses are reversed: H_A at 8 Hz states that the observed data are different than the median surrogate distribution, whereas H_A at 4 Hz states that the observed data are greater than the median surrogate distribution. Here, we found a BF₀₁ of 13.16 at 4 Hz (i.e. the data are 13.16 times more likely to fall under H₀ [no difference] than H_A) and a BF₀₁ of 2.72 at 8 Hz, indicating strong and anecdotal evidence for H₀, respectively.

We also did not find evidence for attentional rhythmicity using the two spectral peak alignment methods after Helfrich et al. (2018). We z-scored against the mean and SD of the permutations (fully informative cue: a z-score of 1.56 ± 0.15 [mean ± SEM] at a mean peak frequency of 5.09 ± 2.55 Hz [mean ± SD]; non-informative cue: a z-score of 1.31 ± 0.16 [mean ± SEM] at a mean peak frequency of 6.43 ± 2.61 Hz [mean ± SD]). See Figures S3 and S4 for power spectra aligned around the identified spectral peaks for both additional conditions. Using IRASA, we found spectral peaks around ~5 Hz for both conditions (fully informative: 5.25 ± 0.48 Hz; non-informative: 5.69 ± 0.49 Hz), but the power at the subsequently aligned peaks was not significantly higher than the median of the surrogate aligned peaks (fully informative cue: t₂₅ = 0.34, P = 0.74) or was even significantly lower (non-informative cue: t₂₅ = −2.47, P = 0.02; see Figures S3 and S4).

Our simulation showed that from four trials per cue–target interval bin onwards (the number of trials per bin used in our study) and a P-value cut-off of 0.001, the power would be 80% for effect sizes as low as 0.04, corresponding to a sinusoidal function of detection accuracy varying between 0.78 and 0.82. With 10 trials per bin, we would have reached a power of >80% (i.e. 100%) with an effect size as low as 0.04. A heatmap of the proportion of significant tests for each effect size and trial per bin combination, for different cut-off values, (P < 0.05, P < 0.01 and P < 0.001) can be found in Figure S5.

3.3 Characteristics of rhythmic attention at non-cued locations

We were also interested in whether the effects of cue informativeness might become visible at the non-cued locations, instead of the cued locations. Therefore, we decided to analyse time course and spectral power at the non-cued locations using location-specific permutation testing, after Fiebelkorn et al. (2013). Note that the data can only be considered for exploratory analysis. Due to the low number of trials per bin at the non-cued locations in the moderately informative cue condition (our focus was on the cued conditions), we cannot construct a time course that is similarly reliable as is the original study by Fiebelkorn and colleagues. Descriptively, there is no phase opposition visible as was the case in Fiebelkorn et al. (2013) (see the blue and yellow time courses in Figure 4b). To investigate whether the power spectra of these time courses contained any spectral peaks, we scored the group-level spectral power between 2 and 10 Hz against the group-averaged surrogate distribution within each cue informativeness condition and for each location separately. We did not observe any significant spectral peaks (i.e. spectral power exceeding the 95th percentile of the surrogate distribution) at any location within the non-informative cue condition (cued: P_min,uncorr. = 0.527 at 9.3 Hz; same object: P_min,uncorr. = 0.10 at 5.4 Hz; different object: P_min,uncorr. = 0.60 at 6.00 Hz). In contrast, the indication for attentional rhythmicity at the non-cued locations was higher when the cue was moderately informative. Namely, in the moderately informative condition, we observed a spectral peak around ~3 Hz at the different-object location, which was not significant after corrections for multiple comparisons (2.7–3.5 Hz, P_min,uncorr. = 0.02 at 3.2 Hz, P_min,FDR = 0.42). Moreover, although a spectral peak at ~7–8 Hz is visible at the same-object location, it is not significant either (P_min,uncorr. = 0.10 at 7.6 Hz). There was no distinctive spectral peak at the cued location (P_min,uncorr. = 0.40 at 4 Hz). We repeated our analysis after first averaging the time series at each location and constructing one power spectrum of this averaged time course. We did not find any significant peaks after scoring this power spectrum against a surrogate distribution (all P_min,uncorr. > 0.8). Thus, although the insufficient number of non-cued trials and the low statistical power as a result of it hamper adequate interpretation of the results, these results seem, descriptively, consistent with the most prominent result of Fiebelkorn and colleagues (2013).

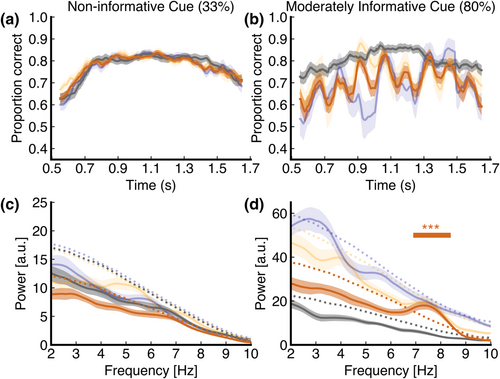
The behavioural time courses showed a phase-consistent pattern for the two non-cued locations in the moderately informative cue condition. Thus, we pooled the time courses across these two locations (see Figure 4). Once again, we scored the data against the against the group-averaged surrogate distribution of hits and misses at the pooled, non-cued locations. We found a distinct, significant spectral peak at 7–8 Hz (P_min,FDR < 0.001), specifically between 7 and 8.3 Hz. Our effects were still significant after correcting for autocorrelated (AR(1)) noise (P < 0.001 for 7.2–7.5 Hz) (see Figure S6). When we repeated the same analysis for the non-informative cue, we did not find any significant effects (all P > 0.05). Finally, to verify that we did not have evidence of opposing phase effects for both non-cued locations (same-object vs. different-object locations) as previously found by Fiebelkorn et al. (2013), we again pooled across the non-cued locations but changed the polarity of the different-item location. Any phase opposition should enlarge any sinusoidal modulation by this subtraction. No significant effects were found (all P > 0.05).

4 DISCUSSION

Recent studies have suggested that visuospatial attentional performance is not continuous, but rhythmically fluctuates, reflected by a heightening and lessening of perceptual sensitivity. It is thought that these heightened periods of perceptual sensitivity allow for attentional shifts from one spatial location to another. This rhythmic attentional sampling mechanism expresses itself as a rhythmic pattern of behavioural performance (e.g. detection accuracy) at each separate spatial location. Here, we investigated rhythmic attention at the validly cued location in a modified Egly–Driver task. As previously reported in studies employing this task (Fiebelkorn et al., 2013; Fiebelkorn et al., 2018; Helfrich et al., 2018), and a similar task version in monkeys (Fiebelkorn et al., 2018, 2019), we expected to demonstrate evidence of rhythmic attention around either 4 or 8 Hz, or both. In addition, we also tested for a possible effect of the behavioural relevance of the sampled location, comparing three conditions: a fully informative cue, a moderately informative cue and a non-informative cue. Using several different peak identification methods, we found no significant rhythmic attentional sampling at the cued location. Our null results are further corroborated by hypothesis testing in the Bayesian framework that unilaterally point towards evidence for the absence of an effect. Our manipulation of cue type did show a main effect of cue informativeness on overall behavioural accuracy (see Figure 3). However, we found no differences in spectral power at the cued location across cue informativeness conditions as a result of this modification. The spectral patterns of detection accuracy at the non-cued (i.e. same-object and different-object) locations, in the moderately informative cue condition, bear similarities with Fiebelkorn et al. (2013) although the low number of trials in this condition and the absence of a specific a priori hypothesis impeded us from drawing robust conclusions. Interestingly, however, when inspecting behavioural performance pooled across both non-cued locations, a highly significant and distinct 7- to 8-Hz pattern of rhythmic attentional sampling was revealed for the moderately informative cue condition. These patterns were not present for the non-informative cue condition.

In an earlier study using a modified Egly–Driver task, Fiebelkorn et al. (2013) found effects at the cued location (at ~8 Hz), but the most prominent effects were found at the non-cued locations. In a similar paradigm, Helfrich et al. (2018) found significant rhythmicity in attention (at ~4 Hz) at the cued location. They focused only on the cued location, because a sufficient number of trials to analyse non-cued locations were not feasible in their (ECoG) study. In contrast to these two studies, our study failed to find pronounced effects at the cued location but did found significant effects at the non-cued location. Another recent study assessing behavioural rhythmicity in an object-based versus space-based paradigm also found no significant performance fluctuations at the cued location (Peters et al., 2020). In this study, it was suggested that attention clearly prioritises the cued location when the cue renders a location behaviourally relevant. As a result of this, attention never fully switches away from the cued location so that, consequently, no rhythmicity in behaviour can be found there (Lou et al., 2020; Peters et al., 2020). In certain moments, the authors argue, attention swiftly sweeps across the object towards the non-cued location on the same object; in other moments, it is distributed across the cued and the non-cued location on the different object. It could be that rhythmicity in attention becomes visible only when attention needs to swiftly reorient to lesser relevant locations and back to the most relevant location, as has been previously found (Senoussi et al., 2019). This notion seems consistent with our results at non-cued locations, suggesting that following an informative cue, attention seems to rhythmically monitor the two non-cued locations at 7–8 Hz. It is also consistent with our results in the non-informative cue condition, in which there seem to be no rhythmic sampling effects at any (cued or non-cued) location. We speculate that, in that case, no reorienting of attention is necessary, as each location bears similar behavioural relevance or attentional weight as the other location. Note that this is in the absence of a very salient cue, such as a flash stimulus (as used in Landau et al., 2012), which could serve as a sampling starting point, even though it is non-informative.

Our results of an attentional sampling at non-cued locations in the behaviourally relevant cue condition fits well with findings reporting that the 7- to 8-Hz frequency is most often found when attention is undivided and directed to one location only, as found in electrophysiological studies (Busch et al., 2009; Busch & VanRullen, 2010). Curiously, whereas earlier studies found that non-cued locations on the same object and the different object were sampled in an anti-phasic pattern (Fiebelkorn et al., 2013; Peters et al., 2020), we rather found a phase-consistent pattern in this study.

We expected to see a shift of the rhythmic sampling frequency at the cued location when the behavioural relevance of the cue disappears. Namely, once the informative value of the cue disappears, non-cued locations should be given more attentional weight. This would result in a loss of the detection accuracy benefit at the cued location, which normally occurs when the cue is behaviourally relevant (Chou & Yeh, 2018; He et al., 2004). Indeed, our overall behavioural results clearly show that the benefit of the cue dissipates when the cue becomes non-informative. There is a clear detection accuracy gain at the cued location compared with the non-cued location in circumstances where the cue carries information. This performance benefit disappears completely after a non-informative cue, where detection accuracy at each location is equal. It is proposed that the less relevant a cue is, the more attentional saccades there are to be expected towards other locations (Fiebelkorn & Kastner, 2019). A completely non-informative cue renders all locations equally relevant for attention, resulting in a systematic one-by-one rhythmic sampling of all possible locations (Jia et al., 2017). Indeed, in a task that requires monitoring two equally relevant locations, each location seems to be sampled in alternation, each at a ~4-Hz rhythm (Landau & Fries, 2012; Re et al., 2019; VanRullen, 2016). We successfully managed to manipulate attentional weight that is allocated to the cued versus non-cued locations, as shown by the significant difference between the average accuracy at the non-cued locations versus the cued location in the moderately informative condition and no difference in the informative cue condition. However, attentional rhythmicity at the cued location seems to be unaffected by the informativeness of the cue. The differential effect of a location's attentional weight on rhythmic attention towards that location may play a role in the vast dispersion of reported frequencies in rhythmic attention paradigms.

Several methodological factors should be discussed in light of our null results at the cued location. First, by losing its informative character, a cue might fail to structurally reset the brain's rhythmic sampling pattern. A non-informative cue could still be salient enough to reset spatial sampling, for example, when it is a bright flash (Landau & Fries, 2012), but when it is not, it might not be enough to reset spatial sampling when it bears no attentional weight. This could explain the absence of evidence for attentional rhythmicity at any (cued or non-cued) location during the non-informative condition. The ability of the cue to reset the brain's overt attentional sampling is a necessary prerequisite for reliably evaluating fluctuations in detection accuracy in a behavioural paradigm (VanRullen, 2016). Indeed, it is established that salient stimuli, such as a loud noise, reset ongoing neuronal oscillations (Lakatos et al., 2008). A ‘flash’ event that is salient enough clearly initiates a reliable object-to-object attentional sampling pattern that always starts at the flashed location (Landau & Fries, 2012). In line with this notion, in the present study, we could have used a more salient, briefly flashing exogenous cue to increase our confidence that we reliably reset the attentional sampling phase in each trial. Another option would have been to use an auditory stimulus concurrently with the visual cue (Fiebelkorn et al., 2011; Lakatos et al., 2007).

Second, detection accuracy was titrated at ~80% in the present study, after Helfrich et al. (2018). We wonder whether this percentage was sensitive enough in our sample, as other studies tend to use lower thresholds (Busch & VanRullen, 2010; Fiebelkorn et al., 2013). Even though Helfrich et al. (2018) adjusted the detection threshold to ~80% (to keep subjects engaged), they found similar effects when running an identical task in a control sample. The main issue with a high detection threshold is a ceiling effect of detection performance, compromising the exposure of the highest potential amplitude of attentional fluctuations. This would result in behavioural oscillations that are lower in amplitude or that are capped, which would hamper adequate inspection of power-frequency components in the behavioural time courses.

Third, rhythmic attentional sampling paradigms need a vast number of trials in order to construct time-resolved behavioural estimates of detection performance across cue–target intervals. We were able to reliably estimate effects at the cued location, as we had 288 validly cued trials to perform this analysis. This number is considerably higher than the study by Helfrich et al. (2018), which had ~137 validly cued trials on average. To gain additional insight into this matter, we ran simulations across combinations of different trials per bin and effect sizes. Here, we found that with an effect size (amplitude of underlying sinusoidal function) of down to 0.04, we found a statistical power of 95% at P < 0.05. Even though these simulations assume that fluctuating patterns of performance are equally present and equally measurable in all participants, they indicate that the current number of cued trials could detect an effect size that we deem relevant (a sinusoidal accuracy modulation between 0.78 and 0.82). Nevertheless, a higher number of trials would have contributed to more robust results for two main reasons. Firstly, the lower the trial number, the more noise emerges into the data, arising from momentary lapses in attention and responses that are unrelated to the rhythmic fluctuations in attention that is subject to the main measurement. Secondly, if we had aimed at doing a comprehensive and reliable analysis of the results of all factors and conditions, it would have been necessary to consider adjusting the study to contain sufficient number of cued and non-cued trials. For example, Fiebelkorn et al. (2013), where analysis of effects at the non-cued locations was included, used ~388 non-cued trials, compared with 72 in this study. Thus, though the number of trials in this study was sufficient to draw conclusions on rhythmic attention at cued locations, it was likely not sufficient to confidently draw conclusions about rhythmic attention at non-cued locations for the moderately informative condition. Adding more trials would furthermore have allowed us to determine hemifield-specific effects, which have been found in other paradigms (Landau & Fries, 2012).

Fourth, a related issue that could have brought more noise into the data is caused by the fact that trials were not self-initiated. Self-initiated trials would have allowed for more frequent breaks by the participant, for example, when they feel fatigued or overwhelmed by the task. The automatically induced trials in this study might have introduced more noise due to decreased attentional performance caused by fatigue. However, we did introduce very frequent breaks, after every 50 trials (around 2.5 min), allowing the participant to take as long a break as desired.

Fifth, the addition of an electrophysiological technique would have provided more insight and evidence in the phenomenon of rhythmic attention in this study. Using electrophysiology, it is possible to directly link behavioural performance (e.g. detection accuracy) with neuronal processes, as has been shown before (Fiebelkorn et al., 2018; Helfrich et al., 2018). This not only sheds more light on the neural correlates of rhythmic attentional sample but additionally allows for a trial-by-trial analysis of the data (as opposed to relying on across-trial, aggregated performance).

There is no clear consensus on methods to analyse the spectral dynamics of behavioural oscillations (Helfrich et al., 2018; Zoefel et al., 2019; Zoefel & Sokoliuk, 2014). In this study, we used several approaches to find meaningful spectral peaks. We used permutation-based approaches, where the observed power on each frequency is compared to a surrogate distribution (Fiebelkorn et al., 2013; Helfrich et al., 2018). We also used an approach where we separated the oscillatory activity from the 1/f background activity using IRASA and subsequent alignment of the highest oscillatory power above the 1/f background (Helfrich et al., 2018; Wen & Liu, 2016). The 1/f signal, also called pink noise, is a widely occurring phenomenon in natural and biological systems, where power tends to fall off with increasing frequency. As such, it is a known component of neurophysiological signals (He, 2014). The behavioural time series in this study are an aggregation of averaged performance at time points; therefore, it does not resemble a naturally occurring, continuous measurement. However, 1/f noise has been previously found in similar artificially constructed time series of cognitive performance (Gilden et al., 1995; Kello et al., 2010; Wagenmakers et al., 2004). Thus, there is still good reason to believe that there is a distinct 1/f component present in our behavioural signal. However, it could still be fruitful to explore other means of quantitatively analysing spectral peaks based on the 1/f component. One of these other methods, FOOOF (Fitting Oscillations & One-Over-F), allows more elaborate modelling of the 1/f signal through more extensive parameter setting (Donoghue et al., 2020). It proposedly overcomes a problem that occurs using IRASA, where oscillations with a large amplitude are difficult to separate from the signal (Donoghue et al., 2020). Thus, in studies into behavioural oscillations, it is necessary to carefully consider the suitability of the spectral peak detection method.

Behavioural or electrophysiological spectral group data can be attractively displayed using spectral peak alignment (as in Helfrich et al., 2018; see also Holt et al., 2019; Richter et al., 2017). In our study, even though we did not find effects at the individual level, aligned peaks still provided a strong visual impression that spectral peaks were present (Figure 2c,d). However, statistical analyses suggest the opposite. We showed that peak alignment after z-scoring the observed data against the surrogate data, and the IRASA procedure, in both cases did not resulted in a statistically significant peak. Performing the IRASA procedure over randomised data yielded an aligned peak that was higher than the aligned peak of the observed data. This shows that whereas peak alignment is a visually attractive means of presenting group data, it might result in a false impression that spectral peaks are present in the data. Therefore, it is necessary to conduct and report statistical evidence of the relevance of the group-aligned spectral peak in question.

Above all, the current study illustrates that a robust method of evaluating rhythmic attentional sampling in behavioural paradigms still ought to be found. There is a strong need to deduct the vast variability in paradigms and move towards more standardised ways of collecting data of rhythmic behavioural studies. For example, a systematic way (i.e. salient flash) to reset the ongoing attentional sampling phase could be implemented in most behavioural paradigms. The effect of this phase-resetting event could be further warranted by electrophysiological findings. Another question is whether dichotomous data (e.g. detection accuracy) or continuous data (e.g. reaction times) better capture rhythmic variability in behaviour. Both types have been used in rhythmic attention paradigms (Fiebelkorn et al., 2013; Landau & Fries, 2012; Peters et al., 2020). Furthermore, there is still no consensus on the best way to identify peaks in power spectra that result from behavioural time courses.

In conclusion, we found no effect of rhythmic attention, nor effects of behavioural relevance of a cue on rhythmic attention, at the cued location. We did find indications of periodic attentional sampling towards non-cued locations, with effects occurring specifically when the cue renders one location behaviourally relevant (i.e. it is informative). These attentional switches seem to occur systematically, in a theta-rhythmic fashion. However, these results are not suitable for drawing robust conclusions due to the absence of a priori expectations and the low number of trials in this condition.

The attentional weight of an object or location that is required in the wide landscape of rhythmic attention paradigms might play a role in the vast differences that are observed in rhythmic sampling frequency. However, more research needs to be conducted to the exact role of a spatial location's attentional weight on rhythmic sampling. Other open questions concern the causes of interindividual variability in sampling frequency and what role rhythmic attention serves amongst other attentional processes.

CONFLICT OF INTEREST

No conflict of interest to declare.

AUTHOR CONTRIBUTIONS

O.W. designed the experiment, performed the measurements, analysed the data and wrote the manuscript; S.O. designed the experiment and contributed to data analysis and writing; T.S. designed the experiment and contributed to data interpretation and writing; A.S. facilitated the research and contributed to experimental design, data interpretation and writing. All authors gave feedback on the manuscript.

DATA ACCESSIBILITY STATEMENT

Data and code are available through the following link: https://doi.org/10.34894/7VP5OA