1 INTRODUCTION

Alpha oscillations (α, 8–12 Hz) in the occipito-parietal cortex reflect ongoing fluctuations in cortical excitability (Adrian & Matthews, 1934; Bishop, 1932; Kelly, Lalor, Reilly, & Foxe, 2006; Worden, Foxe, Wang, & Simpson, 2000). It follows that the perceptual fate of a visual stimulus would depend upon the instant it evokes neural activity within the ongoing α-cycle, leading to cyclic alternations between more and less favourable phases for perceptual processing (Jensen, Gips, Bergmann, & Bonnefond, 2014; Jensen & Mazaheri, 2010; Klimesch, 2012; Klimesch, Sauseng, & Hanslmayr, 2007; VanRullen, 2016a). This hypothesis has been entertained for nearly a hundred years (since Bishop, 1932), and it has revived recently (see VanRullen, 2016a). The fact that α-fluctuations can be picked up extra-cranially via magnetic or electrical encephalography (M/EEG) makes α an optimal candidate to study human perception non-invasively. Specifically, both the power (Babiloni, Vecchio, Bultrini, Romani, & Rossini, 2006; Ergenoglu et al., 2004; Foxe & Snyder, 2011; Kelly et al., 2006; Klimesch et al., 2007; Palva & Palva, 2007; Thut, Nietzel, Brandt, & Pascual-Leone, 2006; Worden et al., 2000) and the phase of the occipito-parietal α (Jensen et al., 2014; Klimesch, 2012; Klimesch et al., 2007; Mathewson, Gratton, Fabiani, Beck, & Ro, 2009; Palva & Palva, 2007; VanRullen, 2016b) have been linked to performance in visual perception (Jensen et al., 2011; Jensen & Mazaheri, 2010; Samaha & Postle, 2015; van Dijk, Schoffelen, Oostenveld, & Jensen, 2008; VanRullen, 2016a). However, while the evidence for the role of α-power in perceptual judgements seems well-established (Bompas, Sumner, Muthumumaraswamy, Singh, & Gilchrist, 2015; Jensen et al., 2011; Lansing, Schwartz, & Lindsley, 1959; Walsh, 1952; but see Benwell et al., 2017), the role of the α-phase is still not clearly settled (Benwell et al., 2017; O’Hare, 1954; Ruzzoli, Torralba, Fernández, & Soto-Faraco, 2019; Walsh, 1952).

So far, most studies have used an offline approach to study changes in perception based on the α-phase. In these studies, stimuli that demand a behavioural response are presented at random (or pseudo-random) intervals while EEG is recorded, and at a later time, trials are separated in terms of the behavioural outcome (hit vs. miss; fast vs. slow reaction times—RTs) and sorted post hoc based on which phase within the pre-target α-cycle, the stimuli happened to fall. Average responses are then statistically compared across phase bins to conclude on a phase-behavioural relationship (see Busch, Dubois, & VanRullen, 2009 for an example). A significant correlation between phase and behaviour, when found, provides support for the theory.

However, the possibility to link α-fluctuations to behaviour via non-invasive methods, such as EEG, is also attractive given the potential applications in brain–computer interfaces (BCIs; Jensen et al., 2011; Zrenner, Belardinelli, Müller-Dahlhaus, & Ziemann, 2016). For example, one could design closed-loop BCI systems that deliver information at favourable brain states for perceptual encoding to improve alerting, learning or memory (Brunner et al., 2015; see Zrenner et al., 2016 for examples in the motor domain).

To harness on the α-theories to develop BCI systems, one must use an online approach, which should be efficient even at the single-subject level. Real-time EEG analysis allows BCI settings to trigger stimuli at precise phase angles during the ongoing fluctuations in the individual α-rhythm that are thought to be associated with specific outcomes (hit/miss, fast/slow RTs). This approach exploits a specific brain–behaviour relationship (e.g., α-phase and perception) to augment encoding of information with millisecond precision. The efficiency of closed-loop BCI must rely on predictable brain–behaviour relationships, in which the relevant parameters at play must be known beforehand. Hence, in turn, the attempt at using a closed-loop BCI approach is a test bench of neurocognitive theories such as the α-theories.

Interestingly, a good number of studies in the sixties already capitalized on the idea of time-locking stimulus presentation to the α-phase in real time. Such attempts were popular enough by the middle of the decade as to prompt Callaway & Layne to write “The idea of presenting photic stimuli at various phases of the spontaneous alpha rhythm to alter degrees of photic driving has occurred to many investigators” (Callaway & Layne, 1964, pp 421). In one pre-eminent study published in the journal Science in 1960, Callaway and Yeager (1960) endeavoured a closed-loop BCI addressing the relationship between the α-phase and RTs to visual events. They found that RTs were modulated as a function of the instant within the α-cycle the target flash was presented (see Dustman & Beck, 1965; Lansing, 1957 for similar results also in a real-time setting). Despite the substantial potential impact such as closed-loop BCI on both theory and application, to the best of our knowledge, no modern study has implemented and reported a similar real-time protocol harnessing on occipital α-phase. The 60-year hiatus is remarkable, especially considering the α-theories are still entirely current up to this date.

Here, we capitalized on the putative relationship between the phase of ongoing α-oscillations and visual perception adopting a closed-loop BCI approach to provide new evidence for the α-theories, which opened enduring questions a long time ago. At the same time, the present study aimed at providing a proof of concept for the use of the phase of ongoing α-oscillations as a control signal in a closed-loop BCI system for practical applications. This experiment is a modern replication of Callaway and Yeager’ study (1960). We employed a visual speeded detection task in which the visual target was triggered in real time as a function of the phase of the participant's α-cycle. We expected that visual RTs would fluctuate along the α-cycle, or at least, that it should be possible to find two distinct phases associated with fast and slow RTs, respectively. The hypothesis, the procedure and the pipeline of the analysis were pre-registered before data collection (https://osf.io/nfdsv/). Deviations from the pre-registered procedure and exploratory analyses are clearly stated in the manuscript. All experimental data can be accessed from the Open Science Foundation (https://osf.io/84nfq/).

2 METHODS

2.2 Experimental procedure

The experimental protocol started with a screening, followed by a training and two consecutive experimental stages (explained below). In the training and experimental stages, participants performed a speeded visual detection task in which stimuli were presented according to the phase of the individual spontaneous α-activity in real time (see Figure 1).

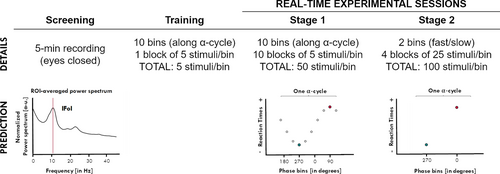
2.2.1 Task

Participants sat on a comfortable chair wearing an EEG cap, and a pair of opaque sunglasses, with twoLEDs, mounted on each lens. The LEDs were controlled through the parallel port (both LEDs switched on and offsimultaneously; luminance 0.076 cd/m² at an approximate distance to participants’ eye of 1 cm). 2 Participants were asked to keep their eyes closed throughout the experiment to maintain α-activity high and to limit eye movements. We instructed the participants to remain attentive and to respond to the visual flashes as fast as possible by pressing a button in a response box using their right index finger. After the response (or after 1 s time out), the LEDs were switched off. An inter-trial interval (ITI), randomly chosen between 1,500 and 2,500 ms, was introduced between the button response (or 1-s time out) and the beginning of the next trial. RTs were measured from the onset of the visual target until a button press was detected.

2.2.2 Training stage

Before the real-time experimental stages, participants were familiarised with the task in a training block (50 trials), identical to Stage 1 (see below).

2.2.3 Experimental stages

After training, participants went on to Stage 1, where visual targets were aimed at 10 equally spaced phase bins covering the whole α-cycle (see Real-time stimulus presentation). This experimental stage was divided into 10 blocks, each ending after the acquisition of at least five valid RTs per phase bin, for a total of 50 RTs per phase bin across blocks. Once Stage 1 had been completed, the phase bins corresponding to the fastest and slowest mean RTs were selected and used for Stage 2 (at the individual level). No statistical test was performed at Stage 1. Stage 2 started right after Stage 1. In Stage 2, visual targets were aimed only at the “fast”-phase and the “slow”-phase bins, estimated from Stage 1. Participants ran 4 blocks, each block ended after the collection of at least 25 valid trials for each of the two-phase bins, for a minimum total of 100 trials per bin.

2.2.4 EEG recording

Continuous EEG data were recorded at 500 Hz using the ENOBIO 20 5G system (Neuroelectrics, Barcelona, Spain) from 14 channels (F3, Fz, F4, C3, Cz, C4, P7, P3, Pz, P4, P8, O1, Oz and O2) with Cl-Ag electrodes placed according to the 10–20 international system. Impedance was kept below 10 kOhm, according to the Enobio-coded system. Additional external electrodes were used to record vertical and horizontal eye movements. Electrode AFz was used as online reference and the right mastoid as ground. Activity from the left mastoid was recorded for offline re-referencing.

2.2.5 Screening and estimation of the individual frequency of interest

We recorded 5 min of resting EEG with the eyes closed, which we used to determine the specific frequency of interest within the α-band for the real-time stages of the experiment. We estimated the power spectrum density (PSD) within the α-band (5–15 Hz) over occipito-parietal electrodes (OP cluster: P7, P3, Pz, P4, P8, O1, Oz, O2) using the Welch method (window = 500 ms; overlap = 10%; resolution = 0.25 Hz). For each participant, the power spectrum was averaged across the electrodes of interest and normalized by the mean power spectrum from 1 to 40 Hz. We verified the strength of the peak—power at the local maximum within the 5- to 15-Hz window—is greater than average power in the 1- to 40-Hz window—and its uniqueness—the peak is a single local maximum within a ±5 Hz band. If a single frequency peak existed, it was considered as the individual frequency of interest (IFoI) 3 and used later as a parameter for real-time analyses (Figure 1). If a unique frequency peak could not be detected, the participant was excluded from the study (see Exclusion Criterion 1).

2.2.6 Real-time stimulus presentation

We developed a BCI setting to trigger flashes (LEDs) at a specific α-phase based on real-time data from electrode O1 (as in Callaway & Yeager, 1960) through custom-built code in MATLAB (MathWorks, R2015.b). We used the Lab Streaming Layer (LSL) library (Swartz Center for Computational Neuroscience, UCSD, January 2018) to acquire EEG data with the ENOBIO acquisition software (NIC V2.0). Given that synchronization between the EEG time acquisition and local PC time is not supported for online streams by ENOBIO, we used an external signal (a parallel port pin connected to one of the ENOBIO electrodes) as time reference. In each iteration, we randomly pre-selected, among the bins available (10 bins in Stage 1, or 2 bins in Stage 2), a phase bin when to send the stimulus trigger. Ten seconds of EEG data from the O1 electrode was continuously buffered, demeaned, and band-pass-filtered (Butterworth forward filter, order 2, IFoI ±5 Hz). Amplitude and phase were estimated at each time point using the Hilbert transform. When the average amplitude in the last second of the buffer was above 30% of the median value of the buffered data, a reference time point was set at the peak (90°) of the last α-cycle. Then, the moment at which the phase of interest in a given trial would occur was forecasted by extending a sine wave (frequency = IFoI) from the reference point. We targeted one of the 10 phase bins (36º each) within the next α-cycle starting after a safety buffer of 72° (~20 ms) for computation time. The stimulus trigger switched on the LEDs at the latency corresponding to the centre of the targeted phase bin (error ≤2 ms).

2.2.7 Responses and trial selection

Responses were collected from a button press via a response box connected to the parallel port. There was a response time out of 1 s after the stimulus, following which the next trial iteration began. If a response was registered before time out, we stored the RT and checked the accuracy of the real-time phase estimation by calculating the difference between the empirical phase at which the stimulus was delivered (according to the recorded EEG) and the intended one, using the Circular Statistics Toolbox in MATLAB (Berens, 2009). In Stage 1, if the stimulus had been triggered in an unintended phase, the trial was relocated to the actual (empirically measured) phase bin. In Stage 2, we only targeted two phases and set a tolerance of ±1 phase bin to reduce the testing time, and we did not relocate trials. A trial was excluded if the empirical phase did not fall within the tolerance zone, or it fell in an overlapping bin between the slow bin and the fast bin (this could happen if the fast/slow bins were less than 72º apart).

Only trials that satisfied all the following criteria were accepted as valid: (a) reaction time criterion: RTs within 50 and 300 ms (as in Callaway & Yeager, 1960) and (b) amplitude criterion: the amplitude of the IFoI-cycle window centred at stimulus onset had to be above the 30% of the median amplitude in the last 10s (this threshold criterion facilitated reliable phase estimation at stimulus presentation).

A block stopped when the intended number of trials per phase bin was reached (N = 5 in Stage 1 or N = 25 in Stage 2). In between blocks, participants took a break before starting a new one. Excess trials (which could happen due to trial relocation) were discarded.

3 RESULTS

Here, we present the results obtained from the pre-registered analyses as explained above, which replicated the conditions of the seminal study by Callaway and Yeager (1960), followed by reality checks and a set of exploratory analyses.

3.1 Results of the pre-registered analyses

3.1.1 Stage 1: Selection of the fast/slow-phase bins along α-cycle

We collected an average of 1,034 (SD = 219) responses per participant. An average of 77 (SD = 53; 7.41%) trials were excluded because the RTs fell out of the 50–300 ms range and 341 (SD = 190; 33%) trials were excluded because the amplitude threshold criterion was not met, leaving an average of 617 (SD = 36; 60%) valid trials per participant. Among the valid trials, 280 (SD = 35; 45.33%) trials hit the target phase bin of interest, whereas 337 (SD = 61; 54.67%) trials had to be relocated to the intended phase bin offline (most of them fell on neighbouring bins, see Section 3.2.1, below). Therefore, we reached the intended 50 valid trials per bin for each participant (following the elimination of excess trials). 4 RTs for valid trials were on average 206 ms (SD = 9 ms). We calculated the mean RT for each phase bin along the α-cycle for each participant (see Figure 2 and Table S1; see Table S2 for information about the number of trials at the individual level), and selected the phase bins associated with the slowest and fastest mean RTs, to be used in Stage 2. Overall, the mean RT difference between slow- and fast-phase bins in Stage 1 was 12 ms (SD = 4; Max = 17 ms; Min = 8 ms).

At this point, if the distribution of slow and fast RTs meets the expectations of the α-theory, the corresponding slow- and fast-phase bins should fall on roughly opposite angles (approximately 180°). However, what we observed is that for most of the participants, slow- and fast-phase bins were closer than 180°, being the mean difference 90° (SD = 51°).

3.1.2 Stage 2: Validation of the α-phase relation to RT speed

In Stage 2, we collected an average of 408 (SD = 103) trials per participant. Among these, 31 (SD = 14; 7.65%) trials were excluded because they fell outside the RT criterion, 144 (SD = 84; 35.30%) trials were excluded for not satisfying the amplitude threshold criterion and 33 (SD = 24; 8.09%) trials for not falling in the bin acceptance zone. After trial exclusion, we were left with a total of 200 valid trials each participant (100 trials per bin), as intended. Among these, an average of 107 (SD = 24; 54%) trials hit the target phase bin of interest (±1 bin), whereas 93 (SD = 24; 46%) trials were relocated. Note that from the valid trials, we discarded those trials that shared a common phase bin in the phase bin acceptance zone, leaving 79 (SD = 15) and 86 (SD = 13) trials on average for predicted slow and predicted fast trials, respectively. For information on the number of trials in Stage 2 at individual level, see Table S3.

The mean RT difference across participants between slow- and fast-phase bins in Stage 2 was −0.439 ms (SD = 4), which was not significant according to a group t test (t(7) = −0.2977, p = .6127, d_z = −0.1052). Individually, none of the participants presented a significant difference in RTs between the visual targets presented in the predicted slow- and fast-phase bins of the α-cycle (all ps > .1; Table 1).

TABLE 1. Individual data for fast/slow-phase bins including phase bin acceptance zone in Stage 2

Part.	Slow-phase bin			Fast-phase bin			RT diff. phases (in ms)	Statistics
	No. of trials	Phase bin	Mean (SD) RTs (in ms)	No. of trials	Phase bin	Mean (SD) RTs (in ms)
								t	dof	p	dz	RT diff. 95% CI
1	88	162°	198 (34)	85	234°	200 (37)	−2	−0.30	171	.62	−0.05	−10.43, 7.24
2	100	162°	196 (39)	100	18°	202 (30)	−6	−1.26	198	.90	−0.18	−14.24, 1.90
3	74	90°	203 (32)	59	126°	206 (39)	−3	−0.54	131	.71	−0.10	−11.70, 5.88
4	66	306°	202 (36)	86	234°	195 (39)	8	1.24	150	.11	0.20	−2.53, 17.83
5	100	54°	194 (29)	100	306°	191 (33)	3	0.69	198	.24	0.10	−4.18, 10.27
6	62	54°	207 (34)	87	18°	207 (32)	0	−0.02	147	.51	−0.00	−9.05, 8.85
7	75	306°	200 (32)	78	270°	201 (40)	−1	−0.21	151	.58	−0.03	−10.97, 8.50
8	68	306°	191 (39)	90	54°	193 (37)	−2	−0.36	156	.64	−0.06	−12.07, 7.68
Mean (SD)	79 (15)	—	199 (5)	86 (13)	—	199 (6)	0 (4)	—	—	—	—	—
Group level	633	—	199 (5)	685	—	199 (6)	0	−0.30	7	.61	−0.11	−5.66, 4.78

Not<del author="Salvador Soto-Faraco" command="Delete" timestamp="1603472884963" title="Deleted by Salvador Soto-Faraco on 23/10/2020 19:08:04" class="reU3">e</del>

• For each participant, the number of trials (max = 100), the tested angular points (degrees) and the mean RTs (ms) are reported for the fast- and slow-phase bins tested in Stage 2. Statistics indicate the results (t value, degrees of freedom, p-value, Cohen's d_z and 95% confidence intervals (CIs)) of an unpaired t test (right-tailed, p < .05) comparing slow vs. fast RTs individually. Group-level data and statistics are also reported.

3.2 Interim discussion and reality checks

The analyses according to the pre-registered pipeline adapted from Callaway and Yeager (1960) did not return a consistent relation between the phase of individual ongoing α-oscillations and the speed of responses to visual targets at the individual level or group level. Compared to offline experimental approaches, where analyses can be adjusted retrospectively, real-time settings imply a priori parameter choices that can affect the outcome. Therefore, we proceeded to exclude the possibility that the null results from the main analyses may have originated from a priori choices in the real-time setting. We focused on three aspects: first, we checked the accuracy of the closed-loop BCI system in sending the stimulus trigger at the intended phases along the α-cycle; second, we questioned whether the choice of the IFoI based on resting EEG data was representative of the dominant α-frequency during the task; and finally, we checked that the electrode choice (O1) for the real-time α-phase estimation was representative of α-activity of interest in the occipito-parietal cluster of electrodes.

3.2.1 Reality check 1: Accuracy of phase estimation during the real-time experiment

The question here was how precisely the closed-loop BCI triggered visual stimuli at the desired phases along the α-cycle. We therefore selected all valid trials for each stage and extracted the phase at which the stimulus was presented from the empirical EEG offline and computed the absolute difference between the desired phase and the actual phase using the Circular Statistics Toolbox (Berens, 2009). On average, across phase bins and participants, our BCI system hit +1.21° (SD = 33.70°) off the intended phase in Stage 1 and +3.79° (SD = 25.43°) in Stage 2 (see Figure 3 and Figures S2 and S3 for individual results on phase accuracy in Stage 1 and Stage 2, respectively). The phase estimation accuracy of our real-time BCI setting seems comparable to previous attempts at phase-triggered events, like for example targeting the α-frequency in the motor cortex (Hougaard et al., 2019; Zrenner, Desideri, Belardinelli, & Ziemann, 2018) which typically achieved an accuracy within −12º to 5º off of the desired phase, with SDs between 48º and 55º.

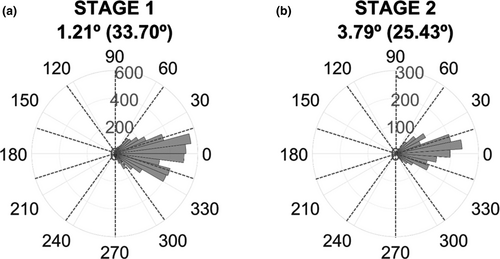
We also decided to check the reasonable expectation of whether the accuracy of the phase estimation depended on the latencies from the reference point of the EEG signal (i.e., phase bins) and whether it was worse at increasing latencies. We rearranged phase accuracy values based on the phase bins and found, as expected, that both the mean and standard deviation of phase accuracy are worse at increasing latencies (see Figure S4 and Table S4 for individual and group data). When subtracting the accuracy of the last-first latencies, the average mean varies −5.42º (SD = 9.38º) and the variability increases 32.20º (SD = 10.64º).

Finally, we calculated the cumulative percentage of trials as a function of the phase bin difference between target and hit phases. Table S5 shows the results at the individual and group levels. Overall, 45% of trials felt in the target phase bin, 88% of trials within ±1 bin and nearly all trials within ±2 bins.

These overall results show a reliable alignment at each of the targeted phases of the α-cycle. Although extrapolating approximately over one α-cycle has led to more unreliable phase accuracy at increasing latencies, the accuracies are still within safe limits in terms of our purposes. Note that the accuracy of phase estimation was checked against real data as part of the BCI setting, so that trials with erroneous estimations that satisfied the trial validity criteria (i.e., RT and amplitude) were eventually relocated if necessary to the hit phase bin in Stage 1 or discarded if did not fall within the acceptance zone in Stage 2. We therefore think that the possibility that null results in the α-phase–RT relationship might be explained by an inaccurate triggering of targets is minimal.

3.2.2 Reality check 2: Frequency of interest during the real-time experiment

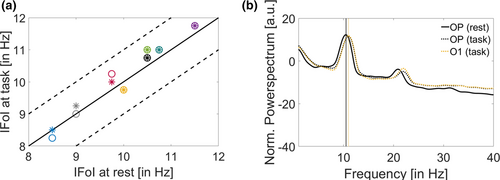
The real-time stages of the experiment used the IFoI, which was estimated in a 5-min pre-experiment screening session from a cluster of occipito-parietal electrodes (see Screening and estimation of the IFoI for more details). This pre-screening is a common practice in order to customize the EEG analysis in terms of individual frequency, especially in the α-band. One potential problem, however, is that the frequency measured in the screening session was not representative of the relevant frequency during the task. Small deviations between the relevant α-frequency during task execution and the one actually used might be mitigated in our protocol because we used a relatively large spectral window (IFoI ± 5 Hz). However, large deviations might affect the subsequent steps of the online protocol, such as filtering and forward prediction. To estimate whether such deviations took place, we compared the IFoI used in the real-time experiment stages (i.e., the one estimated from the screening stage) against the actual dominant α frequency recorded during task execution. IFoI during task execution was computed following the same procedure as for the IFoI in the screening stage. To avoid potential contamination from visual and motor-evoked responses, we used EEG epochs from +500 ms after button press to stimulus onset of the next trial (duration about 2 s, depending on inter-trial jitter). We computed the power spectrum density (PSD) within the α-band (5–15 Hz) for O1 electrode (the electrode in the BCI setting) and for the OP cluster (the same as used in the screening session for the selection of the IFoI: P7, P3, Pz, P4, P8, O1, Oz, O2) using the Welch method (window = 500 ms; overlap = 10%; resolution = 0.25 Hz). For each participant, the power spectrum was normalized by the mean power in the 1- to 40-Hz window. Figure 4a illustrates the single frequency peak within the α-band during task execution, plotted against the IFoI at rest used in the real-time experiment. Overall, the mean peak difference between rest (OP cluster) and task (O1 electrode) IFoIs was 0.16 Hz (SD = 0.23), with a maximum absolute mean difference of 0.50 Hz in participant 8 (see Table S6 for individual results). IFoI at rest in OP cluster was very close to the dominant α-frequency during task execution from the same electrode, with deviations of the central frequency of less than 1 Hz.

Moreover, we decided to check whether the instantaneous frequency differed from the IFoI on a trial-by-trial basis. We calculated the instantaneous frequency for each trial using the Hilbert transform. We band-pass-filtered the data from O1 electrode within 5–15 Hz (Butterworth filter order 2, one-pass), epoched from –2 to 2 s (from stimulus onset), demeaned and detrended. We computed the instantaneous frequency using the MATLAB function “instfreq.” We selected the pre-stimulus window of interest of −1 to 0 s from stimulus onset (same time window as the one-second buffer in the real-time experiment) to average the instantaneous frequency within the selected window. Figure S5 shows a heat map chart of the variation of the phase accuracy as a function of the frequency difference from IFoI for each participant, in which colour denotes the number of trials. All the participants show a mean frequency deviation from IFoI lower than 1 Hz. Participant P08 shows the smaller variability in frequency deviation (mean SD = 0.32 Hz), whereas participants P03 and P05 show the larger variability (mean SD = 0.73 Hz; see Table S5). At group level, the average mean frequency across participants is 0.73 (SD = 0.24) Hz.

Note that we were extrapolating approximately one α-cycle from a reference point at the peak of the EEG signal. Therefore, we would expect to see that if the error in the frequency estimation is negative (i.e., actual instantaneous frequency is slower than the estimated IFoI), then there will be a positive error in the phase estimation (i.e., the stimuli would reach an earlier hit phase and the target phase would happen afterwards in time). Hence, we expected the direction of the correlation to be negative. To check for this hypothesis, we decided to compute a linear correlation between the frequency difference from IFoI and the phase accuracy for each participant by adopting a directional one-tailed hypothesis testing. Table S6 shows the results, including Pearson's coefficient with its p-value. Overall, we see that 5 out of eight participants present a negative correlation, as expected, and only participants P01 (p = .04), P02 (p = .001) and P07 (p < .001) show a significant negative correlation.

We can therefore conclude that the BCI setting employed here was successful in centring the spectral analysis around the desired relevant frequency of interest and variation in frequency from the IFoI at a single-trial level might have influenced the phase accuracy of the BCI setting. However, as stated in the previous section, if there was a deviation in the frequency from the IFoI in a given trial, we took that into account by checking the empirical phase at stimulus presentation and reallocate it if necessary to the hit phase bin in Stage 1 or discarded if did not fall within the acceptance zone in Stage 2.

3.2.3 Reality check 3: Electrode of interest used in the real-time experiment

As for the frequency of interest, we had to a priori decide about the electrode of interest to be used in the BCI system. Following Callaway and Yeager (1960), we chose O1 electrode. This choice appeared convenient to limit real-time computational delays due to clustering over a larger set of electrodes. However, it is perhaps important to check that the signal picked up from O1 electrode in the real-time stages was representative of the α-frequency dominant in a wider occipito-parietal cluster. Therefore, we compared the activity in O1 electrode to that of a cluster of occipito-parietal electrodes (OP clusters: P7, P3, Pz, P4, P8, O1, Oz, O2). The spectral comparison was analogous to the one described for the reality check 2 (IFoI rest vs. IFoI task). The results, illustrated in Figure 4b (see Figure S6 and Table S6 for individual data), show that the two α estimates were within 0.20 Hz. In five out of the eight participants, the relevant frequency peak using the occipito-parietal cluster was the same as in O1 electrode. We can therefore confirm that the α-fluctuations picked up from O1 electrode as our IFoI during the real-time experiment were closely representative of the occipito-parietal activity.

4 EXPLORATORY ANALYSES

In the present study, we aimed at employing a closed-loop BCI approach to show that the phase of ongoing α-oscillations measured with EEG can be harnessed to expedite RTs. This proof of concept can not only open avenues for neurodevices but also help to test the relevance of the α-theories. To do so, we sought to achieve a conceptual replication of a seminal study where such effects had been reported in the past (Callaway & Yeager, 1960). Although our setting included some corrective measures and online checks, we ensured that the system successfully phase-locked visual stimulation to ongoing occipital α-oscillations, the pre-registered analyses returned null results. We decided to explore the data further to find out whether phase effects on RTs could be found using other approaches.

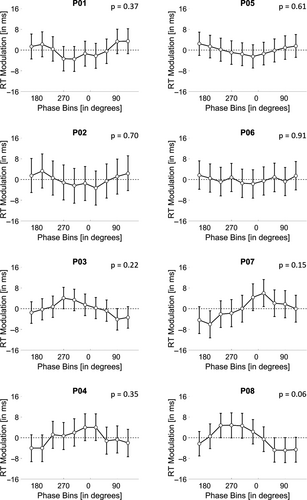
4.2 Smoothing the RT-phase modulation

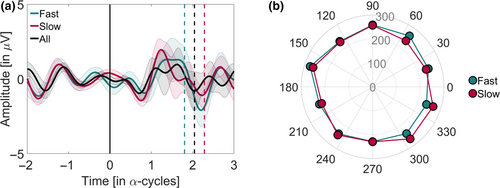
The main purpose of Stage 1 was to estimate the phase bins with fastest and slowest RTs for later use in Stage 2. However, given that we collected a minimum of 50 RTs for each of the 10 bins distributed throughout the α-cycle, one could search for a possible phase-ordered pattern in the RTs in that data set. As described in Section 3, plotting the mean RTs for each phase bin (Figure 1, 2) did not seem to highlight any discernible oscillatory pattern. However, we did not perform a formal statistical analysis at that stage. In this follow-up analysis, we adapted an analytical approach used by Fiebelkorn et al. (2013) to test statistically for an oscillatory pattern in Stage 1 data. The logic behind this approach is that if a phase-dependent modulation of RTs exists, then RTs should vary significantly around opposite phases of α (as in the idealized example in Figure 1). Therefore, we looked for pairs of phases 180° apart that could result in a larger difference between RTs. We calculated the average RT over the trials lumped within −90° and +90° around each phase bin to obtain 10 phase-centred RT averages. Then, we normalized each phase-centred RT average by the average RT across all trials. If RTs were modulated by phase, the normalized phase-centred RTs would resemble a sine wave. To test the statistical significance of possible phase modulation, we transformed these phase-centred RT averages to the frequency domain through a fast Fourier transform (FFT). We tested the significance (α-level = 0.05) of the peak in the FFT for one cycle using a Monte Carlo randomization procedure (10,000 randomizations). The statistical tests showed that none of the participants displayed a significant RT modulation (p-values ranged from .11 to .92; Figure 5). This outcome confirmed the results from the pre-registered analysis on phase effects, described above.

4.3 Searching for phase opposition at stimulus onset

If the response to a stimulus is related to the phase of the α-activity, we should expect a pattern of opposition within the α-frequency (the narrow band EEG) when comparing between slow and fast RT trials at stimulus onset (time = 0; Mathewson et al., 2009). We checked for this possibility by offline band-pass filtering data from electrode O1 using a Butterworth filter (order 2, two-pass) around the IFoI ± 5 Hz band. No re-referencing was applied. All valid trials from Stage 1 were used for the analysis. EEG data were epoched from −200 to 300 ms (t = 0 being the stimulus onset time), and then demeaned and baseline-corrected (−200 to 0 ms). To average across subjects with different IFoI, the time dimension of the EEG was transformed into α-cycle units (the time vector multiplied by the IFoI; data resampled by linear interpolation). RTs were median-split into slow and fast categories. The inter-participants average RT was 231 ms (SD = 9) for slow trials and 182 ms (SD = 8) for fast trials. Figure 6 shows the narrow-band activity for the slow and fast RTs, and for all trials pooled together (see, Figure S7, for individual plots). Although visual inspection suggests an opposition pattern in the narrow-band activity between slow and fast trials at stimulus onset, this pattern is not statistically significant. This can be appreciated by comparing the apparent difference with the large overlap in the confidence intervals (fast trial mean = −0.4454 µV, 95% CI = −1.5599, 0.6691 µV; slow trial mean = 0.3901 µV, 95% CI = −0.6210, 1.4012 µV). However, to test for phase opposition beyond visual inspection, we used the phase opposition sum (POS) method (VanRullen, 2016b). We forward-filtered the data from electrode O1 using a Butterworth filter (order 2, one-pass) around the IFoI ± 5 Hz band and computed the phase by means of the Hilbert transform. We applied the POS on phase values at stimulus onset for fast versus slow trials, at both individual and group levels. The statistical significance was assessed using non-parametric permutations tests (10,000 iterations) using random shuffles of trial assignment to slow/fast bins to compute the distributions of POS values to be expected by chance for each subject. For the group, the distribution of POS values to be expected by chance corresponded to the average of individual POS values to be expected by chance. The p-value associated with measured POS at individual (group) level corresponded to the proportion of times that individual (group-averaged) POS obtained in the permutation exceeded measured individual (group-averaged) POS. In line with the results of the pre-registered analyses, we did not observe a significant group-level effect of POS between slow and fast RTs (p = .932) nor at individual-level effect.

5 DISCUSSION

The present study aimed at providing a proof of concept for harnessing on the phase of ongoing α-oscillations recorded non-invasively with EEG for real-time BCI, and to garner support for the role of such occipito-parietal α-oscillations in visual perception. Evidence of this kind is valuable because it can help achieve a better understanding of the relation between the occipito-parietal α-phase and behavioural outcome (i.e., speed of reaction times to visual events), and lay the groundwork for possible BCI applications. Our study was a modern replication of Callaway and Yeager's study (1960), where participants performed a speeded detection on visual targets triggered in real time at different angles of a participant's α-cycle. First, we sampled RTs to visual targets presented at 10 different phase bins throughout the α-cycle (Stage 1) to select the phases associated with slowest/fastest RTs. Second, we measured RTs to visual targets presented at these two pre-selected phase bins (Stage 2). If a consistent phase-RT relation exists in the expected direction, it follows that, in Stage 2, stimuli presented at the slow phase would have led to slower RTs compared with stimuli presented at the fast phase.

Contrary to what was expected, the analyses did not return a consistent relation between the phase of ongoing α-oscillations and RTs neither at the group level nor at the individual level. Because this experiment was run in real time, most analytical choices had been made a priori, based on the previous literature (Callaway & Yeager, 1960). Note that, obtaining the expected results using a priori set analytical pipeline would implicitly corroborate the brain-behaviour theory behind the decisions for the closed loop. In this sense, closed-loop BCI can be considered a test bench for brain-behaviour theories. However, because some of the prior choices might have been decisive in producing a null result in the present study, we performed a few reality checks a posteriori. First, we verified that the intended phase of visual stimulation and the actual one were in alignment by comparing the time of stimulus delivery with the empirical EEG measurements, offline. Real-time phase estimation was less than 5º off the intended phase (+1.21 ± 33.70° and +3.79 ± 25.43°, in Stages 1 and 2, respectively), which compares well with estimation accuracy in other modern phase-based closed-loop BCIs (Hougaard et al., 2019; Zrenner et al., 2018). We also demonstrated that the accuracy of the phase estimation depended on the latencies along the α-cycle. We found an average mean variation of −5.42º (SD = 9.38º) and an increase in variability of 32.20º (SD = 10.64º) between the last and the first latencies. Second, we double-confirmed that the initial choice of the frequency of interest was representative of the predominant α-frequency during task execution by analysing the data at both single-trial and stage-data levels. Third, we validated our choice of the electrode (O1) for the real-time analysis as representative of the central frequency of interest in the occipito-parietal cluster, the most common for the α-rhythm in visual perception (Benwell et al., 2017; Harris, Dux, & Mattingley, 2018; Myers, Stokes, Walther, & Nobre, 2014; Ruzzoli et al., 2019; Samaha, Bauer, Cimaroli, & Postle, 2015). Taking the results altogether, we reckon two possible reasons why phase estimation accuracy varied over latencies. One is that the estimation was made along almost one full α-cycle, and the other that the IFoI may have varied slightly on a trial-by-trial basis. This is also probably the reason why we had to reallocate trials in Stage 1 and widen the phase acceptance zone to ±1 bin in Stage 2. However, we would like to highlight that, in practical terms, nearly an average of 88% of the trials felt within ±1 bin, which we do not consider to be a poor phase estimation for a BCI setting given the resolution of our EEG system and the method we implemented to estimate the phase by extending a sinus using the IFoI from a reference point in the EEG signal.

It is important to note that even if the data we obtained were variable across participants, the focus of our analysis was on the individual effects because one of the interests in this study was BCI application. The cross-validation protocol implemented in our design (selection and validation of phase bins from Stage 1 to Stage 2 within the same individual) also highlighted a substantial within-participant variability, in many cases leading to opposite trends from Stage 1 to Stage 2 (e.g., the expected fast-phase bin returned, on average, the slowest RTs).

As we mentioned in the introduction, the relation between the posterior pre-stimulus α-phase and behaviour has been (and it still is) based on a popular hypothesis, leading to several sister theories (see Ellingson, 1956, for an overview). For example, the α-phase has been interpreted as a sensory gateway (Bartley & Bishop, 1932); a sensory gateway with a functional inhibitory role (Jensen & Mazaheri, 2010); as a scanning mechanism (Walter, 1950); and as evidence for excitability cycles (Bishop, 1932; Lindsley, 1952; see VanRullen, 2016a, for a similar version). The main point in common among these theories is that reactions (accuracy or RTs) to visual stimuli correlate with (and can be predicted by) the oscillatory activity from the occipito-parietal cortex in the α-band. A critical analysis of the literature shows that this hypothesis has not been free of controversy: Early studies reported no (O’Hare, 1954; Walsh, 1952) or weakly significant effects (Callaway, 1962a, 1962b; Callaway & Yeager, 1960; Dustman & Beck, 1965; Lansing, 1957). Null evidence is also reported in modern times with respect to accuracy (Benwell et al., 2017; Ruzzoli et al., 2019). The present study adds to the previous literature showing that the α-phase/RT relationship is variable and not reliable when targeted in real time, at least using extra-cranial EEG.

It is worth mentioning that we focused on human non-invasive studies (i.e., EEG or MEG) on the role of the α-phase on perception because one of our goals was to provide evidence for the possibility to capitalize on this well-studied relationship for BCI settings. We acknowledge, indeed, that prior studies have frequently found a reliable relationship between α-power and spatial attention (for example Kelly et al., 2006; Thut et al., 2006; Worden et al., 2000) or visual memory (see Palva & Palva, 2007); however, the main focus here was narrowed to visual detection performance (Benwell et al., 2017; Bompas et al., 2015; Lansing et al., 1959; Ruzzoli et al., 2019; Walsh, 1952). In this specific case, despite the α-power/behaviour correlation has been established in the literature, the present study was not optimized to reveal power/behaviour relationships. Indeed, we introduced measures to achieve a consistently high α-power to facilitate reliable phase estimations for stimulus presentation, resulting in a small variability in α-power. 5

Returning to the putative impact of α-phase on reactions to visual events, we should consider three critical aspects of our design that might have influenced the negative outcome. First, we asked the participants to perform the task with their eyes closed. The eyes-closed strategy, also implemented in Callaway & Yeager's study (1960), induces higher α-power at occipito-parietal locations which is convenient for reliable phase estimation. However, whether and how performing a perceptual task with the eyes closed jeopardized the outcome is unknown. Excluding the possibility that an eyes-closed condition could also involve subcortical generators of the α-activity (Lopes da Silva, van Lierop, Schrijer, & Storm van Leeuwen, 1973, but see Bollimunta, Mo, Schroeder, & Ding, 2011; Sokoliuk et al., 2019), we did not find any theoretical caveat against the eyes-closed strategy, which was instead technically convenient. Note that others have successfully used eyes-closed preparations in the past (Callaway & Yeager, 1960; Lansing et al., 1959) and more recently (Hwang et al., 2015; Lim, Hwang, Han, Jung, & Im, 2013). Based on this, we doubt that the eyes-closed condition may have been critical to producing a null result. The second aspect of our design was to use speeded detection, therefore adopting RTs instead of accuracy as the measure of interest. Even if the α-theories have been related to both (RTs: Callaway & Yeager, 1960; Lansing, 1957; Lansing et al., 1959; Walsh, 1952; Accuracy: Busch et al., 2009; van Dijk et al., 2008), no explicit claims have been made on possible differences between the two measures regarding their sensitivity to pre-stimulus oscillations. One would believe that if the temporal structure of α-oscillations is important to parse sensory information into perception, then it should be relevant for both RTs and accuracy. Furthermore, unlike accuracy, RT is a continuous measure potentially more sensitive to moment-to-moment variation in excitability than the dichotomic responses in a detection task. Another aspect of our design that merits discussion was that stimulus intensity was supra-threshold and fixed across participants. This is often the approach in experiments measuring RT. Yet, one could perhaps argue that the stimulus was so strong that possibly subtle phase-dependent variations in sensory responses were saturated, thereby having a negligible impact on behaviour. It is difficult to answer this question examining previous literature because luminance levels have been rarely reported in a precise fashion. Callaway (1962a) published the results of a study examining the RT–α-phase relationship with dim and bright visual stimuli (although the actual luminance was not reported) and stated that the depth of such modulation did not vary consistently as a function of brightness. To the best of our knowledge, the only study measuring the RT–α-phase relationship where stimulus intensity was reported clearly is Dustman and Beck (1965). The authors found a consistent effect of RT to α-phase with stimuli of 0.7 lum/m² (i.e., 0.128 cd/m²) at 40 cm distance to the subject's (closed) eyes. This is brighter than our stimulus intensity (0.076 cd/m²). In the absence of reliable information about the stimulus intensity in past studies, one can also look at the response latencies as a proxy. The average RT in our study was 206 ms (SD = 9) in Stage 1 and 199 ms (SD = 6) in Stage 2. Past studies where a significant RT–α-phase relationship was reported range from faster responses than ours (167 ± 22 ms, Dustman & Beckman, 1965) to slower (245 ± 15 and 236 ± 12 ms respectively for slow and fast RTs in Callaway & Yeager, 1960; 295 ± 51 and 348 ± 64 ms for bright and dim stimuli, respectively in Callaway, 1962a). Therefore, even if one cannot be certain of a possible saturation in neural responses following our stimuli, the stimulus strength and the speed of ensuing latencies were within the range of past studies reporting positive effects.

Finally, a fair question to ask is whether the occipito-parietal α-phase is a critical parameter for perception, but difficult to be extracted from EEG-based closed-loop BCI, or whether it is not critical at all. Fluctuations in neuronal excitability giving way to the oscillatory patterns observable with EEG (and MEG) are ubiquitous in the brain, and the relationship between these fluctuations and neural responses to stimuli is well-established in physiology (Bishop, 1932; Buzsáki & Draguhn, 2004). This makes oscillations seen in the EEG appealing candidates to explain and predict behaviour. However, the outcomes of tests regarding the role of occipito-parietal α-phase in the organization of the visual flow of information have been positive (Callaway & Yeager, 1960; Lansing, 1957; Lansing et al., 1959; Mathewson et al., 2009) as well as negative (Benwell et al., 2017; O’Hare, 1954; Ruzzoli et al., 2019; Walsh, 1952). One could argue that a relationship between phase and visual detectability (and hence, response latencies) may exist, but it was obscured by the signal-to-noise variability when recoding from scalp electrodes in EEG. This is, in fact, likely given by the oscillatory patterns in neural excitability so frequently observed in intra-cranial recordings (Bishop, 1932; Lakatos, Karmos, Mehta, Ulbert, & Schroeder, 2008; Lopes Da Silva & Storm Van Leeuwen, 1977) or animal studies (Fiebelkorn, Pinsk, & Kastner, 2018, 2019; Haegens, Nácher, Luna, Romo, & Jensen, 2011; Spaak, Bonnefond, Maier, Leopold, & Jensen, 2012). Based on this, one would have to conclude that despite the results from the present study are far from significant, they are also not conclusive as to disproof an effect and challenge the α-theories meaningfully.

Apart from theoretical considerations, we also had a second main goal in mind running this experiment: to provide a proof of concept for the use of oscillatory phase as a real-time control signal in a BCI. We estimated that a minimum RT difference between slow/fast phases of 2.681 ms could be expected (33% of the effects in Callaway &Yeager, 1960). However, from a more practical perspective, we wonder whether such a small (and variable) effect can be efficiently picked up by scalp EEG and, if so, whether it can be considered meaningful in a BCI application. Saving less than 3 ms in, for example, the efficiency of warning signals would seem close to nothing in most applied contexts.

6 CONCLUSIONS

Taken together, we must infer that our data do not support a relationship between the phase of α-fluctuations measured extra-cranially and response latencies to visual events. A prudent conclusion is that theoretical and empirical knowledge regarding this relationship may need to progress further to generate enough confidence to attempt the application of the α-theory to neurodevices. Further research might investigate the influence of parameters such as the eyes-closed strategy, the different sensitivity of discrimination performance versus reaction times as the dependent variable or the impact of stimulus intensity. We believe that, at present, the effort to implement a closed-loop BCI application based on the relationship of occipito-parietal α-phase measured with EEG and reactions to visual events might not pay off. In addition, we encourage other scientists and BCI practitioners to use BCI for hypothesis testing, setting methods a priori. Incognitive neuroscience this can be a test bench for brain-behavioural theories, and a way to explore the feasibility of EEG-based BCI applications.

CONFLICT OF INTEREST

The authors have no conflict of interest to declare.

AUTHOR CONTRIBUTIONS

IVG: Methodology, software, validation, formal analysis, investigation, data curation, writing original draft & editing, visualization. LMF: Conceptualization, methodology, software, validation, formal analysis, visualization, writing – review & editing. MTC: Conceptualization, validation, formal analysis, visualization, writing – review & editing. MR: Conceptualization, investigation, writing original draft & editing, supervision, funding acquisition. SSF: Conceptualization, writing original draft & editing, supervision, resources, project administration, funding acquisition.