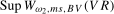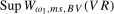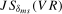Robust tests for deterministic seasonality and seasonal mean shifts
Summary
We develop tests for the presence of deterministic seasonal behaviour and seasonal mean shifts in a seasonally observed univariate time series. These tests are designed to be asymptotically robust to the order of integration of the series at both the zero and seasonal frequencies. Motivated by the approach of Hylleberg, Engle, Granger and Yoo, we base our approach on linear filters of the data that remove any potential unit roots at the frequencies not associated with the deterministic component(s) under test. Test statistics are constructed using the filtered data such that they have well defined limiting null distributions regardless of whether the data are either integrated or stationary at the frequency associated with the deterministic component(s) under test. In the same manner as Vogelsang, Bunzel and Vogelsang and Sayginsoy and Vogelsang, we scale these statistics by a function of an auxiliary seasonal unit root statistic. This allows us to construct tests that are asymptotically robust to the order of integration of the data at both the zero and seasonal frequencies. Monte Carlo evidence suggests that our proposed tests have good finite sample size and power properties. An empirical application to UK gross domestic product indicates the presence of seasonal mean shifts in the data.
1 Introduction
The ability to correctly specify the deterministic component in the econometric analysis of time series processes is crucial for delivering reliable policy modelling, prediction and forecasting. It is also important in the context of unit root testing; in particular, omitting deterministic components present in the underlying data generating process (DGP) can lead to non-similar and inconsistent unit root tests, while the inclusion of irrelevant deterministic components can effect significant efficiency losses, even in large samples.
Perron (
1989) showed that an unmodelled broken trend in the DGP can bias standard (zero frequency) unit root tests toward non-rejection of the unit root null, while allowing for an unnecessary broken trend leads to a loss of power to reject the unit root null when the data are stochastically stationary (denoted, following standard convention, 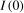 ). One could therefore envisage pre-testing for the presence of deterministic components prior to performing a unit root test. This is not straightforward, however. As discussed in Harvey et al. (
2007), if the data are
). One could therefore envisage pre-testing for the presence of deterministic components prior to performing a unit root test. This is not straightforward, however. As discussed in Harvey et al. (
2007), if the data are 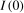 , then an optimal test for the presence of a linear time trend can be performed on the levels data, whereas if the data admit a zero frequency autoregressive unit root (denoted
, then an optimal test for the presence of a linear time trend can be performed on the levels data, whereas if the data admit a zero frequency autoregressive unit root (denoted 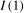 ), an optimal test involves testing for a nonzero mean in the first difference of the series. However, tests based on the first differences of the data exhibit poor power properties if the data are, in fact,
), an optimal test involves testing for a nonzero mean in the first difference of the series. However, tests based on the first differences of the data exhibit poor power properties if the data are, in fact, 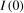 , and the form of the limiting null distributions of tests based on levels data depend on whether the series is
, and the form of the limiting null distributions of tests based on levels data depend on whether the series is 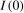 or
or 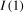 . A circular testing problem therefore exists. There have accordingly been a number of papers that look to break this circularity by deriving tests for the presence of deterministic linear and broken linear trend components that are robust to whether the series contains a zero frequency unit root or not; see inter alia Vogelsang (
1998), Bunzel and Vogelsang (
2005), Harvey et al. (
2007), Perron and Yabu (
2009) and Sayginsoy and Vogelsang (
2011).
. A circular testing problem therefore exists. There have accordingly been a number of papers that look to break this circularity by deriving tests for the presence of deterministic linear and broken linear trend components that are robust to whether the series contains a zero frequency unit root or not; see inter alia Vogelsang (
1998), Bunzel and Vogelsang (
2005), Harvey et al. (
2007), Perron and Yabu (
2009) and Sayginsoy and Vogelsang (
2011).
The assumption that a time series can admit a unit root and deterministic components at only the zero frequency is likely to be too restrictive when we are dealing with seasonally observed data. Here it is natural to allow the deterministic component to vary across the seasons and also to allow autoregressive unit roots to potentially occur at both the zero and seasonal frequencies. Testing for the presence of deterministic components in seasonally observed data is considerably complicated by the fact that the performance of any test using the levels data will depend on the order of integration of the data at all of the zero and seasonal frequencies. Moreover, there is currently no test procedure available to practitioners that allows them to test for the presence of deterministic components in seasonally unadjusted data in such a way as to yield inference that is robust to whether the series contains unit roots at the zero and seasonal frequencies or not. In the absence of such tests, practitioners wishing to perform (zero and/or seasonal frequency) unit root tests on seasonally observed data need to make an ad hoc decision on what form of deterministic seasonality to allow for in their testing procedures, and where an incorrect choice is made, qualitatively similar problems to those seen in the non-seasonal case occur; see, for example, Franses and Vogelsang ( 1998) and Harvey et al. ( 2006).
One of the most common adjustments made to seasonally observed macroeconomic data is seasonal adjustment. Seasonal adjustment tends to be motivated by the desire to give a clearer picture of the underlying growth rate in the data. The quality and reliability of the resulting seasonally adjusted data are, therefore, heavily dependent on whether the underlying deterministic seasonal component is well specified, or at least well approximated. In relation to this point, the Office for National Statistics (ONS), one of the leading providers of seasonally adjusted data, specifically notes that the quality of its seasonally adjusted data can be negatively impacted by abrupt changes in the seasonal patterns. 1 Even when working with data that are not seasonally adjusted, the presence of deterministic seasonality is of interest in its own right, with deterministic seasonality and any shifts in deterministic seasonality important for both the identification of seasonal effects and the ability to correctly forecast a seasonally observed series; see, in particular, the extensive discussion on these issues in Miron ( 1996). Clearly, if a time series is subject to structural change in deterministic seasonality, then any forecasts produced from a model that does not account for such a break will be unreliable.
In the non-seasonal context, Vogelsang ( 1998) and Bunzel and Vogelsang ( 2005) show that an appropriately constructed test statistic for the presence of zero frequency deterministic trend components has a limiting distribution that depends on the order of integration of the data at the zero frequency. Based on this result, they apply a scaling factor that is a function of an auxiliary zero frequency unit root test statistic that ensures that, for a given significance level, the asymptotic size of the test procedure is controlled when the data are either integrated or stationary at the zero frequency. Likewise, Sayginsoy and Vogelsang ( 2011) employ a similar approach to test for breaks in the deterministic component at the zero frequency. We extend the approach of Vogelsang ( 1998), Bunzel and Vogelsang ( 2005) and Sayginsoy and Vogelsang ( 2011) to the seasonal context. Specifically, we propose tests based on data that have been filtered to remove potential unit roots at all but the frequency of the deterministic component(s) under test. We show that appropriate test statistics can be constructed from the filtered data such that they have well defined limiting distributions whose form depends only on the order of integration at the frequency corresponding to the deterministic component(s) under test. Consequently, and paralleling the approach taken in the non-seasonal case, we suggest modifying these statistics by the use of a scaling factor that is a function of an appropriate auxiliary seasonal unit root test statistic. This allows the asymptotic size of the modified tests to be controlled for a given significance level, irrespective of the order of integration of the data at each of the zero and seasonal frequencies.
The remainder of the paper is organized as follows. Section 2 outlines the seasonal model and the underlying assumptions we will work under. Our proposed test statistics for deterministic seasonality and for seasonal mean shifts are outlined in Section 3. Section 4 provides asymptotic critical values and scaling constants for implementing the proposed tests and discusses issues relating to optimal bandwidth choice when using kernel-based variance estimates. Section 5 discusses issues relating to the practical implementation of the proposed tests. Section 6 reports the results of an empirical application of the proposed tests to seasonally unadjusted quarterly UK gross domestic product (GDP) data. Section 7 concludes. The online Appendix details the results of a Monte Carlo study into local asymptotic power and finite sample properties of our proposed tests, and provides representations for their limiting distributions under both the null and the local alternatives.
2 The model and assumptions
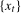 , observed with constant seasonal periodicity, S, formed as the sum of a purely deterministic component,
, observed with constant seasonal periodicity, S, formed as the sum of a purely deterministic component, 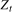 , and a purely stochastic process,
, and a purely stochastic process, 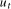 ; viz.,
; viz.,
 (2.1)
(2.1) (2.2)
(2.2)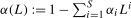 is an Sth order autoregressive polynomial in the usual lag operator, L. For the purposes of this paper we will concentrate on the quarterly case,
is an Sth order autoregressive polynomial in the usual lag operator, L. For the purposes of this paper we will concentrate on the quarterly case, 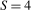 ; generalisations to an arbitrary S are entirely straightforward and only introduce additional notational complexity. Again to simplify notation, but with no loss of generality, we assume that
; generalisations to an arbitrary S are entirely straightforward and only introduce additional notational complexity. Again to simplify notation, but with no loss of generality, we assume that 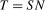 , where N is the number of complete seasonal cycles within the data span. The initial conditions,
, where N is the number of complete seasonal cycles within the data span. The initial conditions,  , are taken to be of
, are taken to be of 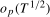 .
.The shocks  in (
2.2) are taken to follow a zero-mean linear process driven by the innovations
in (
2.2) are taken to follow a zero-mean linear process driven by the innovations  . Precise conditions are now detailed in Assumption
2.1.
. Precise conditions are now detailed in Assumption
2.1.
Assumption 2.1.Let 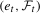 be a martingale difference sequence, with filtration
be a martingale difference sequence, with filtration 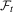 , where
, where 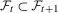 for all t and such that (a)
for all t and such that (a) 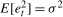 , (b)
, (b) 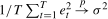 and (c)
and (c) 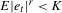 with
with 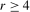 , where K is some constant depending only upon r. The polynomial
, where K is some constant depending only upon r. The polynomial 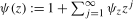 is such that (d)
is such that (d) 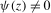 for all
for all 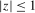 and (e)
and (e) 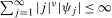 for some
for some 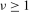 .
.
Remark 2.1.Under Assumption
2.1 the spectral density (and, hence, long run variance) of  in (
2.2) is bounded at both the zero frequency,
in (
2.2) is bounded at both the zero frequency, 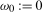 , and the seasonal spectral frequencies,
, and the seasonal spectral frequencies, 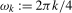 ,
, 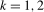 , and is everywhere nonzero. A leading special case of Assumption
2.1 is where
, and is everywhere nonzero. A leading special case of Assumption
2.1 is where  is a stationary and invertible autoregressive moving average,
is a stationary and invertible autoregressive moving average, 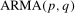 , process.
, process.
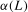 in (
2.1) can be factorized as
in (
2.1) can be factorized as
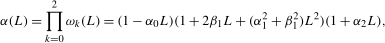 (2.3)
(2.3) associates the parameter
associates the parameter 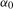 with the zero frequency
with the zero frequency 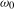 ,
, 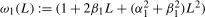 corresponds to the harmonic (annual) seasonal frequency and
corresponds to the harmonic (annual) seasonal frequency and 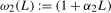 associates the parameter
associates the parameter  with the Nyquist (biannual) seasonal frequency
with the Nyquist (biannual) seasonal frequency 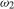 . We can therefore permit
. We can therefore permit 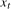 to be either (stochastically) stationary or (near-) integrated at the zero and seasonal frequencies through the parameters
to be either (stochastically) stationary or (near-) integrated at the zero and seasonal frequencies through the parameters 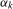 ,
, 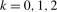 , and
, and 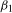 . When
. When 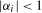 ,
, 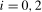 ,
, 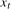 is stationary at the zero frequency and the Nyquist frequency, respectively, and when
is stationary at the zero frequency and the Nyquist frequency, respectively, and when 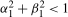 ,
, 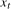 is stationary at the annual frequency. Setting
is stationary at the annual frequency. Setting 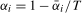 ,
, 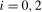 , with
, with 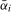 finite constants,
finite constants, 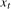 is (near-) integrated at the zero and Nyquist frequencies, respectively, with
is (near-) integrated at the zero and Nyquist frequencies, respectively, with 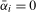 ,
, 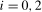 , yielding an exact unit root at the zero and Nyquist frequencies, respectively. When
, yielding an exact unit root at the zero and Nyquist frequencies, respectively. When  , with
, with 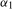 a finite constant, and
a finite constant, and 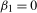 , the process is (near-) integrated at the annual frequency. Here
, the process is (near-) integrated at the annual frequency. Here 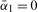 yields a pair of complex conjugate exact unit roots at the annual frequency. As shorthand notation, in what follows we will denote a process that is stationary at frequency
yields a pair of complex conjugate exact unit roots at the annual frequency. As shorthand notation, in what follows we will denote a process that is stationary at frequency 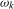 as
as 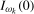 , and a process that is (near-) integrated at frequency
, and a process that is (near-) integrated at frequency 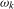 as
as 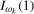 ,
, 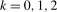 . In what follows, and where no confusion arises, the terms ‘near-integrated’ and ‘integrated’, the latter denoting the exact unit root case, will be used synonymously.
. In what follows, and where no confusion arises, the terms ‘near-integrated’ and ‘integrated’, the latter denoting the exact unit root case, will be used synonymously.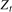 in (
2.1) using the frequency-based representation
in (
2.1) using the frequency-based representation
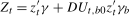 (2.4)
(2.4)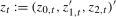 , where
, where 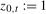 is a (standard) zero frequency intercept,
is a (standard) zero frequency intercept, 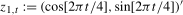 is a pair of annual frequency spectral intercepts and
is a pair of annual frequency spectral intercepts and 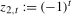 is a Nyquist frequency intercept. Moreover,
is a Nyquist frequency intercept. Moreover, 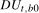 in (
2.4) is a level break dummy variable that takes the value 1 after some (deterministic) break date,
in (
2.4) is a level break dummy variable that takes the value 1 after some (deterministic) break date, 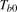 . The vectors of associated spectral intercept and spectral level break coefficients are given by
. The vectors of associated spectral intercept and spectral level break coefficients are given by 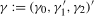 , where
, where 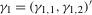 , and
, and 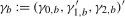 , where
, where 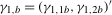 , respectively. The break fraction associated with the latter will be denoted
, respectively. The break fraction associated with the latter will be denoted 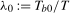 . We assume throughout this paper that the putative break date,
. We assume throughout this paper that the putative break date, 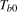 , is unknown to the practitioner but that it lies within the set
, is unknown to the practitioner but that it lies within the set 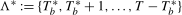 , with the convention that
, with the convention that 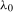 and
and 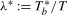 remain fixed constants as the sample size increases.
remain fixed constants as the sample size increases.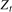 in (
2.4) can be equivalently written in terms of standard seasonal indicator variables as
in (
2.4) can be equivalently written in terms of standard seasonal indicator variables as
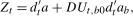 (2.5)
(2.5) , with
, with 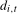 a conventional seasonal indicator variable that takes the value 1 if t lies in season i and 0 otherwise,
a conventional seasonal indicator variable that takes the value 1 if t lies in season i and 0 otherwise, 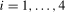 . Defining
. Defining  , the intercept (prior to any seasonal level breaks occurring) in season i is therefore given by
, the intercept (prior to any seasonal level breaks occurring) in season i is therefore given by 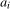 ,
, 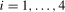 . The vector of break magnitudes,
. The vector of break magnitudes, 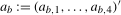 , entails that the intercept in season i switches from
, entails that the intercept in season i switches from 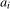 to
to 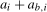 at time
at time 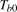 , a break occurring in the level for season i if
, a break occurring in the level for season i if 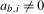 ,
, 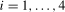 . The representations in (
2.5) and (
2.4) are mathematically equivalent with
. The representations in (
2.5) and (
2.4) are mathematically equivalent with 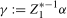 and
and 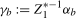 , where the
, where the 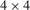 matrix
matrix  and where
and where 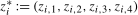 ,
, 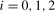 . Notice that the columns of the matrix
. Notice that the columns of the matrix 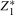 are mutually orthogonal.
are mutually orthogonal.
Remark 2.2.To simplify the outline of the test statistics that follow, we have not included either a zero frequency linear trend or a broken zero frequency linear trend in the deterministic component, 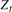 , in (
2.4). However, we will discuss in Section
5.2 how such components could be dealt with when applying the tests in practice.
, in (
2.4). However, we will discuss in Section
5.2 how such components could be dealt with when applying the tests in practice.
Remark 2.3.Although the seasonal intercepts and seasonal level breaks, 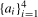 and
and 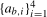 , respectively, in (
2.5) may be nonzero, this does not necessarily mean that there are nonzero spectral means or spectral level shifts at a particular spectral frequency in (
2.4). As a simple example, if the magnitude of the seasonal mean shifts average out to zero over a calendar year, such that
, respectively, in (
2.5) may be nonzero, this does not necessarily mean that there are nonzero spectral means or spectral level shifts at a particular spectral frequency in (
2.4). As a simple example, if the magnitude of the seasonal mean shifts average out to zero over a calendar year, such that  , then so
, then so 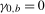 , regardless of the level break magnitudes in each season in (
2.5), and, hence, no level break occurs at the zero frequency. More generally, a zero spectral intercept (zero spectral level break) at frequency
, regardless of the level break magnitudes in each season in (
2.5), and, hence, no level break occurs at the zero frequency. More generally, a zero spectral intercept (zero spectral level break) at frequency 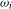 ,
, 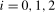 , occurs where
, occurs where 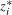 and α (
and α (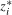 and
and 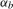 ) are orthogonal to each other.
) are orthogonal to each other.
Remark 2.4.The specification we have adopted for  in (
2.4) results in the restriction of a common level break date for the deterministic components across all frequencies. While this might appear restrictive, under a more general model where level breaks can occur at different dates at each frequency, the asymptotic theory provided in this paper based on the assumption of a common break date remains valid. This holds because when performing a test at, say, the Nyquist frequency, any level breaks present at other points in the sample at either the zero or annual frequency of the data will manifest in the filtered data as a finite number of impulse dummy terms. These are of asymptotically negligible magnitude and, hence, the omission of these from the deterministic component being modelled has no impact in large samples.
in (
2.4) results in the restriction of a common level break date for the deterministic components across all frequencies. While this might appear restrictive, under a more general model where level breaks can occur at different dates at each frequency, the asymptotic theory provided in this paper based on the assumption of a common break date remains valid. This holds because when performing a test at, say, the Nyquist frequency, any level breaks present at other points in the sample at either the zero or annual frequency of the data will manifest in the filtered data as a finite number of impulse dummy terms. These are of asymptotically negligible magnitude and, hence, the omission of these from the deterministic component being modelled has no impact in large samples.
3 Tests for deterministic seasonality and seasonal mean shifts
3.1 Preliminaries
Tests for the presence of deterministic seasonality or a shift in deterministic seasonality at a given seasonal frequency (or frequencies) cannot be based on the levels data, 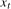 . This is because the form of the limiting null distribution of the resulting test statistics would depend on the order of integration of the data at both the zero and all of the seasonal frequencies. As we shall see, this problem can be circumvented by following an approach first used in Hylleberg et al. (
1990) (HEGY, hereafter) and applying test procedures to transformations of the levels data that reduce the order of integration by 1 at all but the frequency under test. This reduces the problem down to the need to develop tests that are robust to whether or not the data are integrated at the particular seasonal frequency (or frequencies) at which one is testing, which can be readily solved by using a scale factor approach in the manner of Vogelsang (
1998).
. This is because the form of the limiting null distribution of the resulting test statistics would depend on the order of integration of the data at both the zero and all of the seasonal frequencies. As we shall see, this problem can be circumvented by following an approach first used in Hylleberg et al. (
1990) (HEGY, hereafter) and applying test procedures to transformations of the levels data that reduce the order of integration by 1 at all but the frequency under test. This reduces the problem down to the need to develop tests that are robust to whether or not the data are integrated at the particular seasonal frequency (or frequencies) at which one is testing, which can be readily solved by using a scale factor approach in the manner of Vogelsang (
1998).
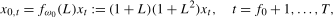 (3.1)
(3.1)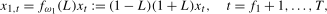 (3.2)
(3.2)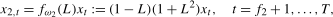 (3.3)
(3.3)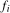 denotes the order of
denotes the order of 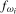 ,
, 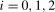 . We will show that the filtered data
. We will show that the filtered data 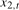 can be used for testing hypotheses concerning the Nyquist frequency deterministic component of
can be used for testing hypotheses concerning the Nyquist frequency deterministic component of 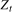 , while
, while 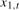 is the relevant filtered data to use for testing hypotheses concerning the annual frequency deterministic component. One could also use the filtered data
is the relevant filtered data to use for testing hypotheses concerning the annual frequency deterministic component. One could also use the filtered data 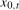 to construct tests relating to the deterministic component at the zero frequency. We will not pursue this further here because the limiting distributions of test statistics constructed from
to construct tests relating to the deterministic component at the zero frequency. We will not pursue this further here because the limiting distributions of test statistics constructed from 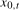 would only depend on the order of integration of
would only depend on the order of integration of 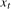 at the zero frequency, so one could, for example, simply apply test procedures of the form proposed in Vogelsang (
1998) and Bunzel and Vogelsang (
2005) to test for a zero frequency mean, and in Sayginsoy and Vogelsang (
2011) to test for the presence of a zero frequency mean shift.
at the zero frequency, so one could, for example, simply apply test procedures of the form proposed in Vogelsang (
1998) and Bunzel and Vogelsang (
2005) to test for a zero frequency mean, and in Sayginsoy and Vogelsang (
2011) to test for the presence of a zero frequency mean shift.We will be able to base our tests on these filtered data because the transformations 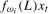 ,
, 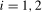 , reduce the order of integration by 1 at each frequency
, reduce the order of integration by 1 at each frequency 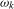 ,
, 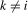 . From (
2.1) and (
2.2), for
. From (
2.1) and (
2.2), for 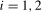 , we have that
, we have that 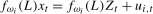 ,
, 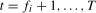 , where
, where 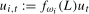 . Consequently,
. Consequently, 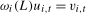 , where
, where 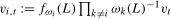 ,
, 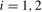 . The filtered error process
. The filtered error process 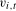 ,
, 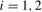 , might therefore contain moving average unit roots (equivalently, spectral zeroes), but only at the frequencies at which the order of integration has been reduced. For example, the filtered data appropriate for testing hypotheses concerning the Nyquist frequency deterministic component,
, might therefore contain moving average unit roots (equivalently, spectral zeroes), but only at the frequencies at which the order of integration has been reduced. For example, the filtered data appropriate for testing hypotheses concerning the Nyquist frequency deterministic component, 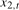 , would contain moving average unit roots in
, would contain moving average unit roots in 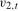 at the zero (
at the zero (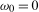 ) frequency if
) frequency if 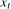 was
was 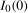 , and at the annual (
, and at the annual (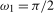 ) frequency if
) frequency if 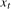 was
was 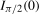 , but would not contain moving average unit roots in
, but would not contain moving average unit roots in 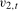 at the Nyquist (
at the Nyquist (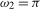 ) frequency.
) frequency.
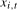 ,
, 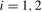 , will only contain deterministic components associated with frequency
, will only contain deterministic components associated with frequency 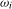 . However, where a level break occurs, the filtered series
. However, where a level break occurs, the filtered series 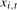 ,
, 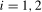 , will also contain
, will also contain 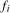 additional impulse dummy terms occurring at the dates
additional impulse dummy terms occurring at the dates 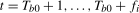 immediately following the level shift. Specifically, the filtered series
immediately following the level shift. Specifically, the filtered series 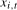 ,
, 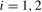 , satisfy
, satisfy
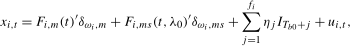 (3.4)
(3.4)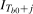 is an impulse dummy variable that takes the value 1 if
is an impulse dummy variable that takes the value 1 if 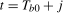 and 0 otherwise, and where
and 0 otherwise, and where 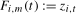 is the vector formed of those regressors that do not depend on the break date and
is the vector formed of those regressors that do not depend on the break date and 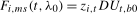 is the vector formed of those regressors (other than the impulse dummies) whose form depends on the break date. In (
3.4),
is the vector formed of those regressors (other than the impulse dummies) whose form depends on the break date. In (
3.4), 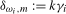 and
and 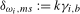 , where
, where 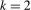 when
when 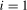 and
and 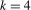 when
when  ; that is, the filter applied to the data magnifies the coefficient on any deterministic components at the frequency under test. The coefficients on the impulse dummies are functions of the break magnitudes on any level breaks present at the zero and all of the seasonal frequencies. They are, therefore, uninformative in practice about the break magnitude(s) at any proper subset of the zero and seasonal frequencies.
; that is, the filter applied to the data magnifies the coefficient on any deterministic components at the frequency under test. The coefficients on the impulse dummies are functions of the break magnitudes on any level breaks present at the zero and all of the seasonal frequencies. They are, therefore, uninformative in practice about the break magnitude(s) at any proper subset of the zero and seasonal frequencies.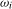 ,
,  . We do so by considering the filtered data
. We do so by considering the filtered data 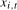 and testing for the presence of the deterministic components contained in
and testing for the presence of the deterministic components contained in 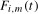 in (
3.4). These tests will, therefore, be based on estimating the regression by ordinary least squares (OLS),
in (
3.4). These tests will, therefore, be based on estimating the regression by ordinary least squares (OLS),
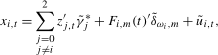 (3.5)
(3.5)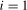 and
and  for the annual (
for the annual (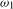 ) and Nyquist (
) and Nyquist (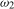 ) frequencies, respectively.
) frequencies, respectively.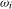 ,
, 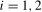 , by testing for the presence of the deterministic components contained in
, by testing for the presence of the deterministic components contained in 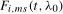 in (
3.4). For a generic putative break date,
in (
3.4). For a generic putative break date, 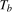 , and associated break fraction,
, and associated break fraction, 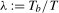 , these would be based on the estimated OLS regression
, these would be based on the estimated OLS regression
 (3.6)
(3.6)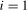 for tests at the annual frequency and
for tests at the annual frequency and  for tests at the Nyquist frequency. However, because the true break date
for tests at the Nyquist frequency. However, because the true break date 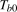 is assumed unknown, we will construct estimates of the form in (
3.6) over all possible break dates
is assumed unknown, we will construct estimates of the form in (
3.6) over all possible break dates 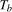 within the set
within the set  .
2
.
23.2 Tests for seasonal spectral means
We first consider tests of the separate null hypotheses 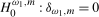 and
and 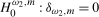 in (
3.4) (equivalently,
in (
3.4) (equivalently, 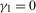 and
and 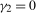 , respectively, in (
2.4)). In each case we will work under the maintained hypothesis that no seasonal level break is present in
, respectively, in (
2.4)). In each case we will work under the maintained hypothesis that no seasonal level break is present in 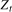 ; that is,
; that is, 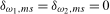 (equivalently, that
(equivalently, that 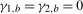 in (
2.4)). However, it should be clear that such tests would also be consistent against series that display level breaks at the seasonal frequency under test, and indeed many other more general deterministic seasonal patterns at that frequency. The first of these null hypotheses involves two linear restrictions (other than those imposed by the maintained hypothesis) that together entail there being no deterministic seasonal component present at the annual frequency. The second involves one linear restriction that entails there being no deterministic seasonal component present at the Nyquist frequency. Tests of the joint null hypothesis of no deterministic seasonal component, such that
in (
2.4)). However, it should be clear that such tests would also be consistent against series that display level breaks at the seasonal frequency under test, and indeed many other more general deterministic seasonal patterns at that frequency. The first of these null hypotheses involves two linear restrictions (other than those imposed by the maintained hypothesis) that together entail there being no deterministic seasonal component present at the annual frequency. The second involves one linear restriction that entails there being no deterministic seasonal component present at the Nyquist frequency. Tests of the joint null hypothesis of no deterministic seasonal component, such that 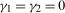 in (
2.4), will be subsequently discussed in Section
3.5.
in (
2.4), will be subsequently discussed in Section
3.5.
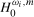 ,
, 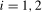 , using the heteroskedasticity autocorrelation (HAC) robust Wald-type statistics
, using the heteroskedasticity autocorrelation (HAC) robust Wald-type statistics
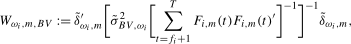 (3.7)
(3.7)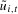 and
and 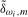 are the OLS residuals and OLS estimator of
are the OLS residuals and OLS estimator of 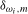 , respectively, from (
3.5), and where
, respectively, from (
3.5), and where
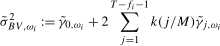 (3.8)
(3.8)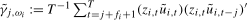 are the sample autocovariances. We make the following assumptions on the kernel,
are the sample autocovariances. We make the following assumptions on the kernel, 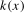 and bandwidth, M.
and bandwidth, M.
Assumption 3.1.The kernel function  is continuous at
is continuous at 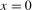 and satisfies
and satisfies 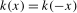 ,
, 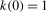 ,
, 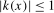 and
and 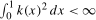 . The function
. The function 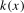 is also twice continuously differentiable everywhere with associated second derivative
is also twice continuously differentiable everywhere with associated second derivative 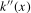 . We also define
. We also define 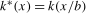 , where the bandwidth M is such that
, where the bandwidth M is such that 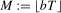 ,
,  denoting the integer part of its argument, with bandwidth fraction
denoting the integer part of its argument, with bandwidth fraction 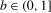 .
.
Remark 3.1.The kernel function 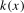 is therefore assumed to satisfy the conditions given for a type 1 kernel in Sayginsoy and Vogelsang (
2011). Like Sayginsoy and Vogelsang (
2011), we found that among a range of popularly applied kernel functions, tests based on the Daniell kernel delivered the best finite sample performance. As a result, all of the numerical results reported in this paper pertain to the use of the Daniell kernel.
is therefore assumed to satisfy the conditions given for a type 1 kernel in Sayginsoy and Vogelsang (
2011). Like Sayginsoy and Vogelsang (
2011), we found that among a range of popularly applied kernel functions, tests based on the Daniell kernel delivered the best finite sample performance. As a result, all of the numerical results reported in this paper pertain to the use of the Daniell kernel.
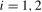 , an alternative and closely related test statistic can be formed by replacing the HAC estimator
, an alternative and closely related test statistic can be formed by replacing the HAC estimator 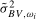 in (
3.7) with
in (
3.7) with 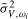 , where
, where 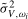 is a seasonal variance estimator, corresponding to frequency
is a seasonal variance estimator, corresponding to frequency 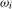 , based on the spectrally (at frequency
, based on the spectrally (at frequency 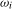 ) cumulated OLS residuals
) cumulated OLS residuals 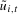 from (
3.5):
from (
3.5):
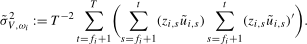 (3.9)
(3.9) ,
, 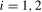 , can be viewed as the seasonal frequency analogues (aside from the scale factor, which we will subsequently discuss in Section
3.4) of the PSW test statistic outlined on p.131 of Vogelsang (
1998) for the present testing problem.
3 Notice that in Vogelsang (
1998), because the hypotheses being tested relate to a zero frequency deterministic component and robustness is required to the order of integration of the data at the zero frequency, the equivalent of
, can be viewed as the seasonal frequency analogues (aside from the scale factor, which we will subsequently discuss in Section
3.4) of the PSW test statistic outlined on p.131 of Vogelsang (
1998) for the present testing problem.
3 Notice that in Vogelsang (
1998), because the hypotheses being tested relate to a zero frequency deterministic component and robustness is required to the order of integration of the data at the zero frequency, the equivalent of 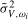 would be calculated from standard (rather than spectrally) cumulated residuals; that is, standard partial sums of the residuals would be taken, not the seasonal partial sums required here.
would be calculated from standard (rather than spectrally) cumulated residuals; that is, standard partial sums of the residuals would be taken, not the seasonal partial sums required here.3.3 Tests for seasonal spectral mean shifts
We next develop tests of the null hypotheses  and
and 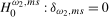 in (
3.4). The former involves two linear restrictions, and entails that there is no seasonal level break present at the annual frequency,
in (
3.4). The former involves two linear restrictions, and entails that there is no seasonal level break present at the annual frequency, 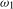 . The latter imposes one linear restriction that entails there is no level break in the seasonal component at the Nyquist frequency,
. The latter imposes one linear restriction that entails there is no level break in the seasonal component at the Nyquist frequency, 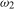 .
4 Joint frequency tests will again be discussed in Section
3.5.
.
4 Joint frequency tests will again be discussed in Section
3.5.
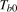 , were known, then
, were known, then  ,
, 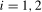 , could be tested along the same lines considered for the tests for deterministic seasonality in Section
3.2 by using the HAC robust Wald statistics,
, could be tested along the same lines considered for the tests for deterministic seasonality in Section
3.2 by using the HAC robust Wald statistics,
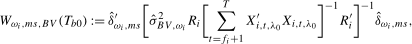 (3.10)
(3.10)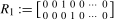 ,
, 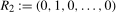 and, in each case for
and, in each case for 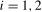 ,
, 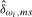 is the OLS estimate of
is the OLS estimate of 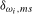 from (
3.6) and
from (
3.6) and 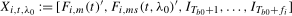 . The HAC variance estimator
. The HAC variance estimator 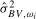 is constructed exactly as for the
is constructed exactly as for the 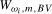 statistic in Section
3.2 but using the OLS residuals,
statistic in Section
3.2 but using the OLS residuals, 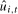 , from estimating (
3.6) rather than
, from estimating (
3.6) rather than 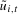 . Again, an alternative statistic can be formed using the OLS-type variance estimator of the form given in (
3.9), but again with
. Again, an alternative statistic can be formed using the OLS-type variance estimator of the form given in (
3.9), but again with 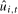 replacing
replacing 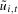 ; we will denote this estimator by
; we will denote this estimator by 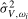 and the resulting test statistic by
and the resulting test statistic by 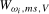 .
. , is taken to be unknown to the practitioner, we follow the approach of Sayginsoy and Vogelsang (
2011) and base our tests on the supremum of the sequences of Wald statistics of the form given in (
3.10), evaluated across all possible break dates
, is taken to be unknown to the practitioner, we follow the approach of Sayginsoy and Vogelsang (
2011) and base our tests on the supremum of the sequences of Wald statistics of the form given in (
3.10), evaluated across all possible break dates 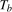 in the search set
in the search set 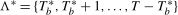 . Our proposed test statistics for testing for a seasonal mean shift at frequency
. Our proposed test statistics for testing for a seasonal mean shift at frequency 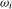 ,
, 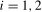 (where we again recall that
(where we again recall that 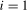 corresponds to the annual frequency,
corresponds to the annual frequency, 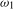 , and
, and  to the Nyquist frequency,
to the Nyquist frequency, 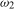 ), are, therefore, given by
), are, therefore, given by
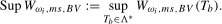 (3.11)
(3.11)
Remark 3.2.In addition to the supremum-based statistics in (
3.11), we also considered the corresponding statistics based on taking the average across the sequence of Wald statistics, 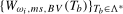 . However, and in accordance with the findings in Sayginsoy and Vogelsang (
2011) for the problem of testing for a zero frequency mean shift, we found that tests based on supremum-based statistic delivered superior power properties to the corresponding average-based tests. Therefore, we only report results for tests based on the supremum statistic in what follows. Corresponding results for tests based on the average statistic can be obtained from the authors on request.
. However, and in accordance with the findings in Sayginsoy and Vogelsang (
2011) for the problem of testing for a zero frequency mean shift, we found that tests based on supremum-based statistic delivered superior power properties to the corresponding average-based tests. Therefore, we only report results for tests based on the supremum statistic in what follows. Corresponding results for tests based on the average statistic can be obtained from the authors on request.
3.4 Scaled statistics
Although, as the results presented in Section 4 will show, the Wald-type statistics proposed in Sections 3.2 and 3.3 have well defined limiting null distributions, both when the data are stationary and when the data are integrated at the frequency under test, crucially these limiting distributions do not coincide. In particular, for a given statistic, the limiting null distribution in the integrated case is right-skewed relative to the corresponding limiting null distribution in the stationary case. Therefore, and in the same manner as is done in, inter alia, Vogelsang ( 1998), Bunzel and Vogelsang ( 2005) and Sayginsoy and Vogelsang ( 2011), we propose scaling the aforementioned Wald-type statistics for seasonal means and seasonal mean shifts by an exponential function of an auxiliary seasonal unit root test statistic such that, for a chosen significance level, the tests have asymptotically controlled size regardless of whether the data are stationary or integrated at the seasonal frequency under test (as well as to the order of integration of the data at the other spectral frequencies).
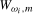 to generically denote either
to generically denote either  or
or 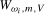 and use
and use 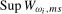 to generically denote either
to generically denote either 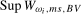 or
or 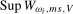 , in each case for
, in each case for  (recall that
(recall that 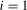 relates to the annual frequency,
relates to the annual frequency, 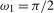 , and
, and  relates to the Nyquist frequency,
relates to the Nyquist frequency, 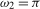 ). We will also use the notation UR to generically denote the unit root statistic used in the scale factor approach. The scaled statistics can, thus, be written in corresponding generic form as
). We will also use the notation UR to generically denote the unit root statistic used in the scale factor approach. The scaled statistics can, thus, be written in corresponding generic form as
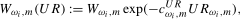 (3.12)
(3.12)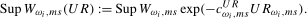 (3.13)
(3.13)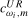 and
and 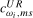 are scaling constants while
are scaling constants while 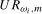 and
and 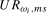 are seasonal unit root test statistics that, respectively, allow for either spectral means or spectral means and spectral mean shifts in their modelled deterministic component. These unit root statistics will need to possess the properties that where
are seasonal unit root test statistics that, respectively, allow for either spectral means or spectral means and spectral mean shifts in their modelled deterministic component. These unit root statistics will need to possess the properties that where 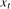 is
is 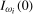 (i.e., stationary at the frequency under test), they converge to zero, and where
(i.e., stationary at the frequency under test), they converge to zero, and where 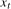 is
is  (i.e., integrated at the frequency under test), they have a well defined limiting distribution that does not depend on any unknown nuisance parameters, other than
(i.e., integrated at the frequency under test), they have a well defined limiting distribution that does not depend on any unknown nuisance parameters, other than 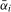 , under the null hypothesis being tested. As a result, where
, under the null hypothesis being tested. As a result, where 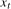 is
is 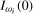 , the exponential scaling factors in (
3.12) and (
3.13) will converge to unity as the sample size diverges, leaving the asymptotic distribution of the statistics unaffected. In the case where
, the exponential scaling factors in (
3.12) and (
3.13) will converge to unity as the sample size diverges, leaving the asymptotic distribution of the statistics unaffected. In the case where 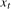 is
is 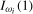 , and selecting the ξ level critical value from the asymptotic null distribution of
, and selecting the ξ level critical value from the asymptotic null distribution of 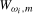 or
or 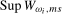 appropriate for the stationary case, we can, therefore, for any candidate seasonal unit root test statistic, choose values of the scaling constants
appropriate for the stationary case, we can, therefore, for any candidate seasonal unit root test statistic, choose values of the scaling constants 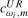 or
or 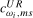 such that the asymptotic sizes of the tests based on the resulting scaled statistics and this critical value do not exceed ξ% across a range of values of
such that the asymptotic sizes of the tests based on the resulting scaled statistics and this critical value do not exceed ξ% across a range of values of 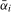 .
.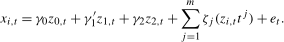 (3.14)
(3.14)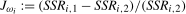 , where
, where 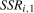 denotes the sum of squared residuals from estimating (
3.14) and
denotes the sum of squared residuals from estimating (
3.14) and 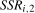 denotes the sum of squared residuals from the OLS estimation of
denotes the sum of squared residuals from the OLS estimation of 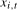 onto
onto 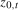 ,
, 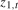 and
and 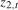 . We set
. We set  for the Nyquist frequency unit root test statistic,
for the Nyquist frequency unit root test statistic, 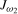 , and set
, and set  for the annual frequency unit root test statistic,
for the annual frequency unit root test statistic, 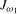 , as we found these choices of m gave the best asymptotic power performance for the resulting tests for seasonal means at the Nyquist and annual frequencies, respectively. The scaled statistics in (
3.12) based on
, as we found these choices of m gave the best asymptotic power performance for the resulting tests for seasonal means at the Nyquist and annual frequencies, respectively. The scaled statistics in (
3.12) based on 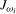 will be denoted
will be denoted 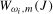 with the associated scaling constant denoted as
with the associated scaling constant denoted as 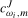 ,
, 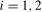 , in what follows.
, in what follows.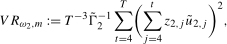 (3.15)
(3.15) (3.16)
(3.16)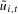 ,
, 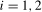 , the OLS residuals from (
3.5) and where
, the OLS residuals from (
3.5) and where 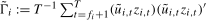 . The scaled statistics in (
3.12) based on
. The scaled statistics in (
3.12) based on 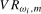 will be denoted
will be denoted 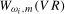 , with the associated scaling constant denoted as
, with the associated scaling constant denoted as  ,
, 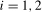 , in what follows.
, in what follows.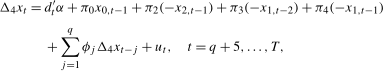 (3.17)
(3.17)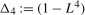 and the lag length, q, satisfies the usual rate condition that
and the lag length, q, satisfies the usual rate condition that 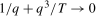 as
as 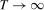 . The HEGY test statistic for a Nyquist frequency unit root is given by the standard regression t-ratio for
. The HEGY test statistic for a Nyquist frequency unit root is given by the standard regression t-ratio for 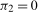 , say
, say 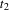 , in (
3.17) and that for the (complex pair of) annual frequency unit roots is given by the regression F-statistic for
, in (
3.17) and that for the (complex pair of) annual frequency unit roots is given by the regression F-statistic for 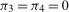 in (
3.17), say
in (
3.17), say 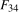 . In each case our candidate unit root statistic will be based on the reciprocal of the absolute value of the statistic. The scaled statistics in (
3.12) using the appropriate frequency HEGY statistic will be denoted
. In each case our candidate unit root statistic will be based on the reciprocal of the absolute value of the statistic. The scaled statistics in (
3.12) using the appropriate frequency HEGY statistic will be denoted 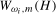 with the associated scaling constant denoted as
with the associated scaling constant denoted as 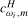 ,
, 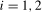 , in what follows.
, in what follows.Consider next the scaling factor used in connection with the seasonal spectral level shift tests in (
3.13). The seasonal unit root statistics outlined above can be straightforwardly adapted to the case where a level break may occur at a known break date 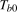 . For the
. For the 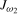 and
and 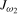 statistics one simply augments the test regression in (
3.14) with the additional regressors
statistics one simply augments the test regression in (
3.14) with the additional regressors 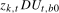 ,
, 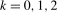 , and
, and 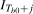 ,
, 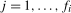 . For tests based on HEGY statistics, we may use the reciprocals of HEGY-type test statistics obtained from the two-step procedure embodied in (4)–(6) of Franses and Vogelsang (
1998), whereby the broken deterministic components of
. For tests based on HEGY statistics, we may use the reciprocals of HEGY-type test statistics obtained from the two-step procedure embodied in (4)–(6) of Franses and Vogelsang (
1998), whereby the broken deterministic components of 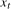 are first estimated, and a HEGY regression, using appropriate dummy variables, is applied to the residuals from this first-step regression. For tests based on the variance ratio statistics, these would be computed as in (
3.15) and (
3.16) but now using the OLS residuals
are first estimated, and a HEGY regression, using appropriate dummy variables, is applied to the residuals from this first-step regression. For tests based on the variance ratio statistics, these would be computed as in (
3.15) and (
3.16) but now using the OLS residuals 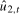 and
and 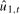 , respectively, from (
3.6); we denote the resulting statistics as
, respectively, from (
3.6); we denote the resulting statistics as 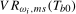 ,
, 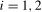 .
.
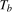 , and do so across all values of
, and do so across all values of 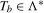 . As we treat the true break date as unknown, we then select the infimum of unit root statistics in the resulting sequence following Sayginsoy and Vogelsang (
2011). Specifically, denoting a generic unit root test statistic at frequency
. As we treat the true break date as unknown, we then select the infimum of unit root statistics in the resulting sequence following Sayginsoy and Vogelsang (
2011). Specifically, denoting a generic unit root test statistic at frequency 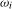 ,
, 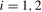 , which allows for a level break at time
, which allows for a level break at time 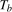 as
as 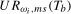 , we would calculate
, we would calculate 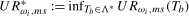 for
for 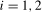 . In what follows we will consider level break tests based on the infimum of the sequence of
. In what follows we will consider level break tests based on the infimum of the sequence of 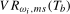 statistics when testing for a seasonal mean shift at frequency
statistics when testing for a seasonal mean shift at frequency 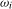 ; that is,
; that is,
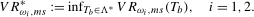 (3.18)
(3.18)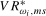 will be denoted
will be denoted 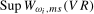 , with the associated scaling constant denoted as
, with the associated scaling constant denoted as 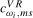 ,
, 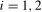 , in what follows. Tests based on the Park and Choi (
1988)-type statistics and the HEGY-type statistics were found to deliver very poor finite sample behaviour and so will not be discussed further here.
, in what follows. Tests based on the Park and Choi (
1988)-type statistics and the HEGY-type statistics were found to deliver very poor finite sample behaviour and so will not be discussed further here.3.5 Joint frequency tests
The test procedures outlined thus far are designed to test for a seasonal spectral mean or a shift in seasonal spectral mean at either the annual frequency, 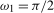 , or the Nyquist frequency,
, or the Nyquist frequency, 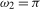 . In practice, one might wish to also consider joint tests for the presence of seasonal spectral means or level shifts in seasonal spectral means occurring at either or both frequencies, thereby yielding size controlled tests for deterministic seasonality in the former case and for a shift in deterministic seasonality in the latter case.
. In practice, one might wish to also consider joint tests for the presence of seasonal spectral means or level shifts in seasonal spectral means occurring at either or both frequencies, thereby yielding size controlled tests for deterministic seasonality in the former case and for a shift in deterministic seasonality in the latter case.
Joint tests are straightforward to develop because the limiting distributions of the test statistics constructed at frequency 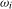 will turn out to be independent of the limit distributions of the statistics constructed at frequency
will turn out to be independent of the limit distributions of the statistics constructed at frequency 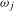 ,
, 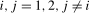 . Simulation results in the online Appendix show that the best overall performance when testing for individual frequency spectral means and spectral mean shifts are obtained using the
. Simulation results in the online Appendix show that the best overall performance when testing for individual frequency spectral means and spectral mean shifts are obtained using the 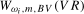 and the
and the 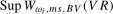 statistics, respectively, and so we will focus attention in what follows on how joint tests for spectral means and spectral mean shifts can be constructed from these individual frequency statistics; however, the same principles could be applied to any of the individual frequency statistics discussed previously.
statistics, respectively, and so we will focus attention in what follows on how joint tests for spectral means and spectral mean shifts can be constructed from these individual frequency statistics; however, the same principles could be applied to any of the individual frequency statistics discussed previously.
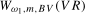 and
and 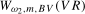 , respectively; that is,
, respectively; that is,
 (3.19)
(3.19)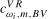 ,
, 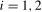 , are the scaling constants appropriate for the individual frequency
, are the scaling constants appropriate for the individual frequency 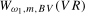 and
and 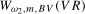 tests
tests 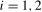 that will be detailed in Section
4.1.
5 Note that if we took a simple average of the two individual frequency
that will be detailed in Section
4.1.
5 Note that if we took a simple average of the two individual frequency 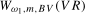 and
and 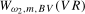 test statistics, there would be many possible combinations of
test statistics, there would be many possible combinations of 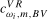 ,
, 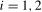 , that would yield a robust joint test. As such, the appropriate scaling constants for the individual frequency tests are both multiplied by a further scaling constant
, that would yield a robust joint test. As such, the appropriate scaling constants for the individual frequency tests are both multiplied by a further scaling constant 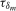 , where
, where 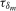 can be chosen such that the asymptotic size of the resulting test does not exceed ξ% when the data are
can be chosen such that the asymptotic size of the resulting test does not exceed ξ% when the data are 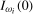 or
or 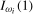 ,
,  . This has the practical advantage of reducing the problem from choosing between multiple pairs of
. This has the practical advantage of reducing the problem from choosing between multiple pairs of 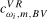 ,
, 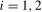 , to selecting a single value of
, to selecting a single value of  .
.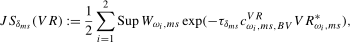 (3.20)
(3.20)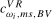 ,
, 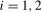 , are the scaling constants appropriate for the individual frequency
, are the scaling constants appropriate for the individual frequency 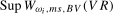 statistics
statistics 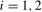 .
.Relevant values of 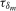 and
and 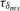 that yield robust tests will be given in Section S.1.2 in the online Appendix.
that yield robust tests will be given in Section S.1.2 in the online Appendix.
4 Large sample results
The online Appendix provides representations for the limiting distributions of the 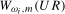 and
and 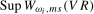 ,
, 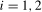 , statistics proposed in Section
3, together with the corresponding joint frequency test statistics from Section
3.5, under both the null and local alternative hypotheses. The form of the latter depend on whether the data are stationary or integrated at the frequency (or frequencies in the case of the joint frequency tests) of interest. We first define these local alternatives formally. The relevant local alternatives when testing for seasonal spectral means or for seasonal spectral mean shifts are now given in Definitions
4.1 and
4.2, respectively.
, statistics proposed in Section
3, together with the corresponding joint frequency test statistics from Section
3.5, under both the null and local alternative hypotheses. The form of the latter depend on whether the data are stationary or integrated at the frequency (or frequencies in the case of the joint frequency tests) of interest. We first define these local alternatives formally. The relevant local alternatives when testing for seasonal spectral means or for seasonal spectral mean shifts are now given in Definitions
4.1 and
4.2, respectively.
Definition 4.1.Let the filtered data 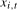 ,
, 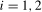 , be generated according to (
3.4). Then (a) if the data are
, be generated according to (
3.4). Then (a) if the data are 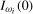 ,
, 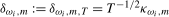 and
and 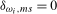 , and (b) if the data are
, and (b) if the data are 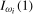 ,
, 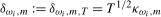 and
and 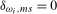 . In each case
. In each case 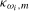 is a finite constant.
is a finite constant.
Remark 4.1.The scaling of the 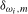 coefficients in (
3.4) by powers of
coefficients in (
3.4) by powers of 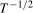 in (a) and by
in (a) and by 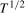 in (b) provide the appropriate Pitman localization rates when the data are
in (b) provide the appropriate Pitman localization rates when the data are 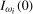 and
and 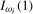 , respectively, with the Pitman drift parameters in each case given by
, respectively, with the Pitman drift parameters in each case given by 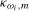 . Notice that we have set
. Notice that we have set 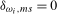 in Definition
4.1 because the seasonal spectral mean tests outlined in this paper are constructed under the maintained assumption that no level break is present in the seasonal deterministic component.
in Definition
4.1 because the seasonal spectral mean tests outlined in this paper are constructed under the maintained assumption that no level break is present in the seasonal deterministic component.
Definition 4.2.Let the filtered data 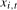 ,
, 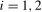 , be generated according to (
3.4). Then (a) if the data are
, be generated according to (
3.4). Then (a) if the data are 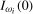 ,
, 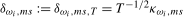 , and (b) if the data are
, and (b) if the data are 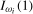 ,
, 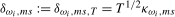 . In each case
. In each case 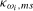 is a finite constant.
is a finite constant.
Remark 4.2.Notice that no restrictions are placed on the parameters 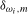 in (
3.4) by Definition
4.2 because the inclusion of
in (
3.4) by Definition
4.2 because the inclusion of 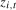 in regression (
3.6) renders the seasonal spectral mean shift tests exact invariant to these parameters.
in regression (
3.6) renders the seasonal spectral mean shift tests exact invariant to these parameters.
Remark 4.3.Notice that the local alternatives given for 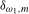 and
and 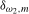 in Definition
4.1 reduce, respectively, to the null hypothesis
in Definition
4.1 reduce, respectively, to the null hypothesis 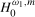 when
when 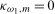 and to
and to 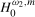 when
when 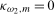 . Similarly, the local alternatives for
. Similarly, the local alternatives for 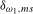 and
and 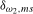 in Definition
4.2 reduce to
in Definition
4.2 reduce to 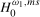 when
when 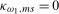 and
and 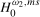 when
when 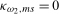 , respectively.
, respectively.
Representations for the limiting distributions under the relevant local alternative for the annual frequency spectral mean statistics, 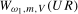 and
and 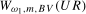 , are given in Theorems S.2 and S.3 for the case where the data are
, are given in Theorems S.2 and S.3 for the case where the data are 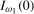 and
and 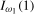 , respectively. Corresponding results for the Nyquist frequency statistics,
, respectively. Corresponding results for the Nyquist frequency statistics, 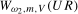 and
and 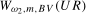 , are given in Theorems S.4 and S.5 for the case where the data are
, are given in Theorems S.4 and S.5 for the case where the data are 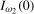 and
and  , respectively. The corresponding limiting distributions for the annual frequency mean shift statistics,
, respectively. The corresponding limiting distributions for the annual frequency mean shift statistics, 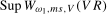 and
and 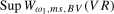 , are given in Theorems S.7 and S.8 for the case where the data are
, are given in Theorems S.7 and S.8 for the case where the data are 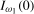 and
and 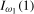 , respectively. Finally, corresponding results for the Nyquist frequency mean shift statistics,
, respectively. Finally, corresponding results for the Nyquist frequency mean shift statistics, 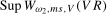 and
and 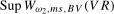 , are given in Theorems S.9 and S.10 for the case where the data are
, are given in Theorems S.9 and S.10 for the case where the data are 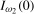 and
and 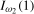 , respectively.
, respectively.
The results in Theorems S.2–S.5 and S.7–S.10 show that for all of the statistics, where the data are stationary at the frequency under test, then so the limiting distributions of the statistics are unaffected by the choice of unit root statistic employed in the scale factor used in their construction. This is because, the unit root statistics converge in probability to zero in large samples, such that the multiplicative exponential functions used in the scale factors converges in probability to unity. Where the data are integrated at the frequency of interest, the limiting distributions of the statistics now also involve the limiting distribution of the seasonal unit root statistic used in their construction. In Section 4.1 we will discuss how appropriate values of the scaling factor constants can be chosen to yield tests that are robust to whether the data are stationary or integrated at the frequency under test.
The results in Theorems S.2–S.5 and S.7–S.10 also show that the limiting distributions of each of the annual frequency test statistics, either for spectral means or for spectral mean shifts, are independent of the limiting distributions of each of the corresponding Nyquist frequency test statistics. This is because the terms that feature in the limiting distributions of the statistics at the annual and Nyquist frequencies are formed from independent Brownian motions. An implication of this is that the limiting distributions of the joint frequency statistics in Section 3.5 are simply the averages of the limiting distributions of their two constituent statistics.
4.1 Asymptotic null distributions
The limiting null distributions of the 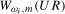 and
and 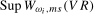 ,
, 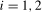 , statistics under their respective null hypotheses,
, statistics under their respective null hypotheses, 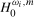 and
and  ,
, 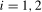 , are obtained from the limiting distributions given in Theorems S.2–S.5 and Theorems S.7–S.10 by setting the relevant Pitman drift parameter from Definitions
4.1 and
4.2, respectively, to zero.
, are obtained from the limiting distributions given in Theorems S.2–S.5 and Theorems S.7–S.10 by setting the relevant Pitman drift parameter from Definitions
4.1 and
4.2, respectively, to zero.
The limiting null distributions of all of the test statistics conducted at frequency 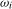 ,
, 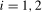 , are seen to be asymptotically free of nuisance parameters when the data are
, are seen to be asymptotically free of nuisance parameters when the data are 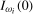 . For the
. For the 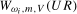 and
and 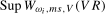 test statistics, these distributions depend on
test statistics, these distributions depend on 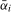 and
and 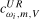 and
and 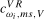 , respectively, when the data are
, respectively, when the data are 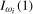 . Denoting the ξ% critical value from the limiting null distribution of any individual frequency
. Denoting the ξ% critical value from the limiting null distribution of any individual frequency 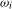 statistic when the data are
statistic when the data are 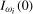 as
as 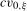 , a robust test can be performed by selecting a value of the scaling constant
, a robust test can be performed by selecting a value of the scaling constant 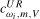 or
or 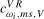 such that when the test statistic is compared to
such that when the test statistic is compared to 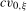 , the asymptotic size of the test procedure does not exceed ξ% when the data are
, the asymptotic size of the test procedure does not exceed ξ% when the data are 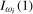 for a range of values of
for a range of values of 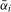 . The asymptotic null distributions of the
. The asymptotic null distributions of the 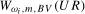 and
and 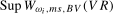 statistics additionally depend on the bandwidth fraction, b, and kernel,
statistics additionally depend on the bandwidth fraction, b, and kernel, 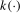 , associated with the long run variance estimator. Thus, for given b and
, associated with the long run variance estimator. Thus, for given b and 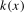 , if we denote the ξ% critical value from the limiting null distribution of an individual frequency
, if we denote the ξ% critical value from the limiting null distribution of an individual frequency 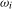 statistic when the data are
statistic when the data are 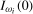 as
as 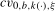 , we can again choose a value of the scaling constant
, we can again choose a value of the scaling constant 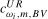 or
or 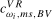 such that, when compared to
such that, when compared to 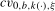 , the test has size that does not exceed ξ% when the data are
, the test has size that does not exceed ξ% when the data are 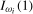 for a range of values of
for a range of values of 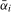 when using a bandwidth b and kernel
when using a bandwidth b and kernel 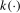 .
.
So as to determine the critical values and scaling constant for the tests, the asymptotic null distributions of the test statistics outlined in Theorems S.2–S.5 and Theorems S.7–S.10 were simulated using Monte Carlo methods. The Brownian motion processes appearing in the asymptotic distributions were approximated using independent and identically distributed (i.i.d.) standard normal random variates discretized over 1,000 steps. All simulations were carried out using 10,000 replications and with the trimming parameter set to 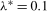 . The range of values of
. The range of values of 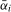 considered when determining the scaling constants was set to
considered when determining the scaling constants was set to 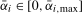 , where
, where  was chosen such that the (asymptotic) size of all of the tests considered was maximized at 5% for some
was chosen such that the (asymptotic) size of all of the tests considered was maximized at 5% for some 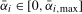 . The asymptotic 5% critical values and appropriate scaling constants for the tests when using the Daniell kernel are reported in Tables S.1–S.4 in Section S.1.2 in the online Appendix.
6
. The asymptotic 5% critical values and appropriate scaling constants for the tests when using the Daniell kernel are reported in Tables S.1–S.4 in Section S.1.2 in the online Appendix.
6
For the joint frequency tests discussed in Section
3.5, we require values of the joint scaling constants 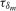 and
and 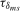 , such that when using the scaling constants
, such that when using the scaling constants 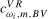 or
or 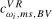 ,
,  , appropriate for the individual statistics, the asymptotic sizes of the joint
, appropriate for the individual statistics, the asymptotic sizes of the joint 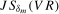 and
and 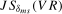 tests do not exceed ξ% for a large range of
tests do not exceed ξ% for a large range of 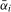 ,
, 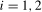 , when the data are, potentially,
, when the data are, potentially, 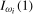 ,
, 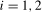 . Asymptotic critical values and appropriate values of
. Asymptotic critical values and appropriate values of 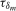 and
and 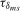 for nominal 5% tests when constructing the
for nominal 5% tests when constructing the 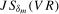 and
and 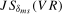 tests are reported in Tables S.5 and S.6, respectively, in Section S.1.2 in the online Appendix. Notice that these are functions of the bandwidth fractions
tests are reported in Tables S.5 and S.6, respectively, in Section S.1.2 in the online Appendix. Notice that these are functions of the bandwidth fractions  and
and 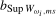 ,
, 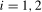 , used to construct the individual
, used to construct the individual 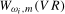 and
and 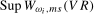 statistics.
statistics.
4.2 Asymptotic local power
We next explore how the asymptotic local power of the test statistics that use the 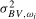 variance estimate can be used to determine the optimal bandwidth to use for a given value of
variance estimate can be used to determine the optimal bandwidth to use for a given value of 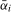 . The asymptotic distributions of the test statistics were simulated using the same Monte Carlo methods used for simulating the limiting null distributions and power for various local alternatives was computed. In all simulations we set
. The asymptotic distributions of the test statistics were simulated using the same Monte Carlo methods used for simulating the limiting null distributions and power for various local alternatives was computed. In all simulations we set 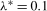 and
and 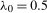 . We restricted our attention to this one parameter setting because of the intensive computational requirements when simulating the limiting distributions under local alternatives.
7 Using the 5% asymptotic critical values and scaling factors reported in Section S.1.2, asymptotic local power was computed for the case where the data were
. We restricted our attention to this one parameter setting because of the intensive computational requirements when simulating the limiting distributions under local alternatives.
7 Using the 5% asymptotic critical values and scaling factors reported in Section S.1.2, asymptotic local power was computed for the case where the data were 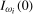 and
and 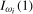 for a range of values of
for a range of values of 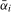 .
.
For individual frequency 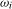 ,
, 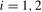 , tests using the
, tests using the 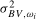 variance estimator, local power depends on the bandwidth, b, and the kernel,
variance estimator, local power depends on the bandwidth, b, and the kernel, 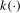 , used to construct this variance estimator when the series is
, used to construct this variance estimator when the series is 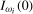 or
or 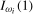 , and additionally depends on
, and additionally depends on 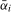 when the series is
when the series is 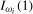 . It is also the case that no single bandwidth maximizes asymptotic local power uniformly for all local alternatives for any individual test; in particular, the asymptotic local power curves for tests constructed using different values of the bandwidth fraction b for a given kernel
. It is also the case that no single bandwidth maximizes asymptotic local power uniformly for all local alternatives for any individual test; in particular, the asymptotic local power curves for tests constructed using different values of the bandwidth fraction b for a given kernel 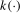 cross one another. Consequently, we proceed in the same manner as Sayginsoy and Vogelsang (
2011) to determine the optimal bandwidth fraction, b, to use both when the series are
cross one another. Consequently, we proceed in the same manner as Sayginsoy and Vogelsang (
2011) to determine the optimal bandwidth fraction, b, to use both when the series are 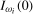 or
or 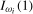 by evaluating integrated asymptotic power.
by evaluating integrated asymptotic power.
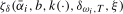 denote the limiting distribution of an individual frequency
denote the limiting distribution of an individual frequency 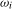 statistic constructed using the appropriate scaling constant for a ξ level test under the local alternative
statistic constructed using the appropriate scaling constant for a ξ level test under the local alternative 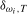 and where the kernel function and bandwidth fraction in (
3.8) are given by
and where the kernel function and bandwidth fraction in (
3.8) are given by 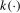 and b, respectively. Asymptotic local power is given by
and b, respectively. Asymptotic local power is given by 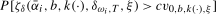 , where
, where 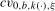 is the ξ% asymptotic critical value of the test statistic when the data are
is the ξ% asymptotic critical value of the test statistic when the data are 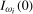 . Consequently, the integrated asymptotic local power of the test is given by
. Consequently, the integrated asymptotic local power of the test is given by
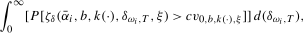 (4.1)
(4.1)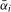 , the maximum value of
, the maximum value of 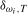 is chosen such that the asymptotic local power of any given test is equal to at least 0.99 for at least one bandwidth fraction b. Using this method we find values of b, when using the Daniell kernel, such that integrated power is maximized for a given
is chosen such that the asymptotic local power of any given test is equal to at least 0.99 for at least one bandwidth fraction b. Using this method we find values of b, when using the Daniell kernel, such that integrated power is maximized for a given 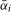 over a grid of values of
over a grid of values of 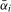 selected such that the optimal bandwidth fraction for the largest value of
selected such that the optimal bandwidth fraction for the largest value of 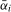 is equal to the lowest bandwidth fraction considered of
is equal to the lowest bandwidth fraction considered of 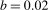 . The optimal bandwidth fraction for each test is larger for smaller values of
. The optimal bandwidth fraction for each test is larger for smaller values of 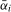 , declining to 0.02 as
, declining to 0.02 as 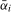 increases. A similar analysis when the process is
increases. A similar analysis when the process is 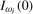 confirmed that
confirmed that 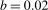 is also optimal in this instance. Optimal bandwidth fractions for all test statistics using the
is also optimal in this instance. Optimal bandwidth fractions for all test statistics using the 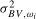 variance estimate are given in Section S.1.1 in the online Appendix.
8
variance estimate are given in Section S.1.1 in the online Appendix.
85 Additional practical implementation issues
5.1 Bandwidth selection
In the previous section we derived optimal bandwidth functions for tests based on the 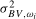 variance estimator using the Daniell kernel. These involve the non-centrality parameters
variance estimator using the Daniell kernel. These involve the non-centrality parameters 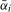 ,
, 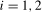 , which are unknown in practice and cannot be consistently estimated. We can, however, use a feasible data-dependent bandwidth rule to select the bandwidth.
, which are unknown in practice and cannot be consistently estimated. We can, however, use a feasible data-dependent bandwidth rule to select the bandwidth.
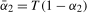 we can propose a similar method to that used by Bunzel and Vogelsang (
2005) and Sayginsoy and Vogelsang (
2011) to obtain an estimate of
we can propose a similar method to that used by Bunzel and Vogelsang (
2005) and Sayginsoy and Vogelsang (
2011) to obtain an estimate of 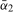 . Specifically, estimate by OLS
. Specifically, estimate by OLS
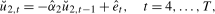 (5.1)
(5.1)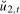 are the residuals from the OLS regression in (
3.5) when testing for a Nyquist frequency mean, or in the case of the tests for a level break at the Nyquist frequency, the residuals from regression (
3.6) evaluated at the break date
are the residuals from the OLS regression in (
3.5) when testing for a Nyquist frequency mean, or in the case of the tests for a level break at the Nyquist frequency, the residuals from regression (
3.6) evaluated at the break date  , where
, where 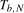 is chosen such that it minimizes the sum of squared residuals
is chosen such that it minimizes the sum of squared residuals 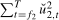 . We then compute
. We then compute 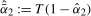 . The test can then be performed using the optimal bandwidth corresponding to the estimated value of
. The test can then be performed using the optimal bandwidth corresponding to the estimated value of 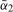 .
.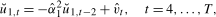 (5.2)
(5.2)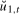 are the residuals from the OLS regression in (
3.5) when testing for an annual frequency mean, or for the annual frequency level break test, the residuals from regression (
3.6) evaluated at the break date
are the residuals from the OLS regression in (
3.5) when testing for an annual frequency mean, or for the annual frequency level break test, the residuals from regression (
3.6) evaluated at the break date 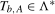 , where
, where 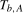 is chosen such that it minimizes the sum of squared residuals
is chosen such that it minimizes the sum of squared residuals 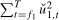 . If
. If 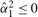 , we perform the test using the optimal bandwidth for when the data are stationary at the annual frequency; otherwise we compute
, we perform the test using the optimal bandwidth for when the data are stationary at the annual frequency; otherwise we compute 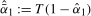 . The test can then be performed using the optimal bandwidth for the estimated value of
. The test can then be performed using the optimal bandwidth for the estimated value of  .
9
.
95.2 Allowing for zero frequency linear and broken linear trends
Although the specification of  in (
2.4) does not include a zero frequency linear trend, the filters applied to the data in (
3.2) and (
3.3) would reduce a zero frequency linear trend, should one be present in
in (
2.4) does not include a zero frequency linear trend, the filters applied to the data in (
3.2) and (
3.3) would reduce a zero frequency linear trend, should one be present in 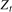 , to a zero frequency intercept in the filtered data,
, to a zero frequency intercept in the filtered data,  ,
, 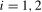 . Consequently, because (
3.5) and (
3.6) both include a zero frequency intercept, a linear trend in
. Consequently, because (
3.5) and (
3.6) both include a zero frequency intercept, a linear trend in 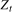 is already allowed for in our proposed seasonal frequency test procedures.
is already allowed for in our proposed seasonal frequency test procedures.
If one were concerned about the possibility of a single break in the zero frequency trend function, two choices could be made. First, the zero frequency trend break test of Sayginsoy and Vogelsang (
2011) could be performed on 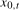 of (
3.1) as a pre-test, and the data de-trended accordingly if a broken trend was signalled. Alternatively, the tests outlined in this paper could be constructed using the filtered data
of (
3.1) as a pre-test, and the data de-trended accordingly if a broken trend was signalled. Alternatively, the tests outlined in this paper could be constructed using the filtered data 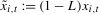 ,
,  . This transforms the zero frequency trend break to a single outlier that would have no impact on the large sample properties of the seasonal frequency tests. Notice that one does not need to know or estimate the location of any zero frequency trend break in this latter approach, which is also asymptotically valid for a more general segmented zero frequency trend function, provided the number of breaks is fixed.
. This transforms the zero frequency trend break to a single outlier that would have no impact on the large sample properties of the seasonal frequency tests. Notice that one does not need to know or estimate the location of any zero frequency trend break in this latter approach, which is also asymptotically valid for a more general segmented zero frequency trend function, provided the number of breaks is fixed.
5.3 Practical recommendations
In the online Appendix, we report results from a Monte Carlo study examining the finite sample size and power properties of the tests proposed in this paper. These results suggest that when testing for seasonal spectral means, the 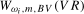 ,
, 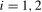 , tests display the best size and power performance across the tests for spectral means at the annual and Nyquist frequencies, respectively. Likewise, when testing for seasonal spectral mean shifts, the results suggest that the
, tests display the best size and power performance across the tests for spectral means at the annual and Nyquist frequencies, respectively. Likewise, when testing for seasonal spectral mean shifts, the results suggest that the  ,
,  , tests display the best size and power performance when testing for spectral mean shifts at the annual and Nyquist frequencies, respectively. We therefore recommend the use of
, tests display the best size and power performance when testing for spectral mean shifts at the annual and Nyquist frequencies, respectively. We therefore recommend the use of  ,
, 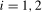 , and the associated joint seasonal frequency test for deterministic seasonality,
, and the associated joint seasonal frequency test for deterministic seasonality, 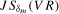 when testing for seasonal means, and when testing for seasonal mean shifts, we recommend the use of the
when testing for seasonal means, and when testing for seasonal mean shifts, we recommend the use of the 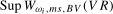 ,
,  , tests and the associated joint seasonal frequency test,
, tests and the associated joint seasonal frequency test, 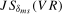 . In each case these tests should be constructed using the Daniell kernel and using the bandwidth selection rules outlined in Section
5.1.
. In each case these tests should be constructed using the Daniell kernel and using the bandwidth selection rules outlined in Section
5.1.
6 An empirical application to UK GDP
We now provide an empirical example using quarterly unadjusted real GDP data from 1997Q1–2015Q4 taken from the ONS website. Our aim is to investigate whether or not the deterministic seasonal pattern in these data is constant across the sample period. Visual inspection of the data in Figure 1 is suggestive of the presence of a segmented zero frequency linear trend in the data, characterized by a negative growth rate in real GDP during the financial crisis of 2007–2009 in a series otherwise exhibiting positive long run growth. A segmented zero frequency trend of this form would lead to zero frequency level shifts in the filtered data used to construct the seasonal frequency tests outlined in this paper. We therefore first detrend the data to allow for two trend breaks, with the break dates chosen so as to minimize the residual sum of squares from the detrending regression. The fitted zero frequency segmented trend is also graphed in Figure 1.
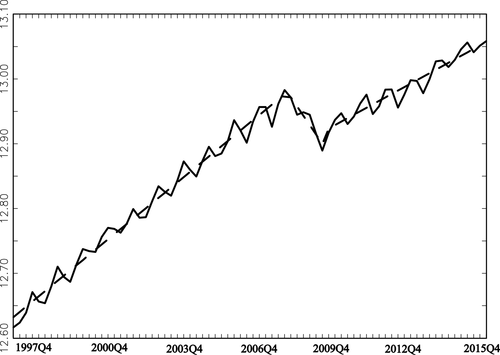
Fitted segmented trend. Series: ------, fitted segmented trend: - - - - -.
In Table
1 we report the results of applying the tests for the presence of a seasonal mean shift at the annual and Nyquist frequencies, 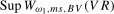 and
and 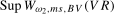 , respectively, together with the joint frequency seasonal mean shift test,
, respectively, together with the joint frequency seasonal mean shift test, 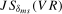 , to the detrended data. All tests are run at the nominal asymptotic 5% level in each case using the Daniell kernel and the bandwidth selection rules outlined in Section
5.1. All of the tests reject the null hypothesis of no level break. The timing of the break, identified by the estimated break date that led to the largest Wald statistic in the construction of the
, to the detrended data. All tests are run at the nominal asymptotic 5% level in each case using the Daniell kernel and the bandwidth selection rules outlined in Section
5.1. All of the tests reject the null hypothesis of no level break. The timing of the break, identified by the estimated break date that led to the largest Wald statistic in the construction of the 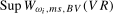 test statistic, is estimated to be 2006Q4 for the Nyquist frequency deterministic component and 2009Q2 for the annual frequency deterministic component. Although these estimated break dates are at different points in the sample, they do, however, straddle the onset of the financial crisis in 2007–2008.
10
test statistic, is estimated to be 2006Q4 for the Nyquist frequency deterministic component and 2009Q2 for the annual frequency deterministic component. Although these estimated break dates are at different points in the sample, they do, however, straddle the onset of the financial crisis in 2007–2008.
10
|
Test |
Test statistic |
Critical value |
Break date identified |
|---|---|---|---|
|
|
16.63 |
14.45 |
2006Q4 |
|
|
30.76 |
28.77 |
2009Q2 |
|
|
27.93 |
21.61 |
NA |
We next estimate the deterministic component in the detrended GDP series both for the case where we allow for the broken deterministic seasonal components identified by our test procedures, and for the case where it is assumed that there are no seasonal mean shifts. In the former case we include the 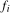 impulse dummies after the break identified at frequency
impulse dummies after the break identified at frequency 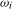 to eliminate the effect of any outliers in the filtered data caused by the break; cf. (
3.4). Figure
2 plots the detrended GDP series against the fitted seasonal deterministic components for both cases. This graph suggests that both fitted series appear to track the detrended data reasonably well for the majority of the sample. However, the impact of failing to model the identified seasonal level breaks can be more clearly seen in Figure
3, which graphs the squared deviations of each fitted deterministic component from the detrended series. The model that does not allow for a break in deterministic seasonality at the time of the financial crisis is prone to making very large errors in the post-crisis period. For the period 2010Q1–2015Q4 (chosen such that the sample contains no indicator dummies to ensure a fair comparison) the mean square error (MSE) for the model where the seasonal level breaks are accounted for is 0.0000401, which is around 40% lower than the MSE of 0.0000658 for the model that does not allow for seasonal level breaks. It therefore seems likely that not allowing for the seasonal mean shifts identified by our proposed tests would have had an adverse affect on the quality of the seasonally adjusted data and any forecasts made in the post-crisis period.
to eliminate the effect of any outliers in the filtered data caused by the break; cf. (
3.4). Figure
2 plots the detrended GDP series against the fitted seasonal deterministic components for both cases. This graph suggests that both fitted series appear to track the detrended data reasonably well for the majority of the sample. However, the impact of failing to model the identified seasonal level breaks can be more clearly seen in Figure
3, which graphs the squared deviations of each fitted deterministic component from the detrended series. The model that does not allow for a break in deterministic seasonality at the time of the financial crisis is prone to making very large errors in the post-crisis period. For the period 2010Q1–2015Q4 (chosen such that the sample contains no indicator dummies to ensure a fair comparison) the mean square error (MSE) for the model where the seasonal level breaks are accounted for is 0.0000401, which is around 40% lower than the MSE of 0.0000658 for the model that does not allow for seasonal level breaks. It therefore seems likely that not allowing for the seasonal mean shifts identified by our proposed tests would have had an adverse affect on the quality of the seasonally adjusted data and any forecasts made in the post-crisis period.

Fitted deterministic component. Series: ------, modelled break: - - - - -, unmodelled break: ⋅ ⋅ ⋅ ⋅ ⋅.
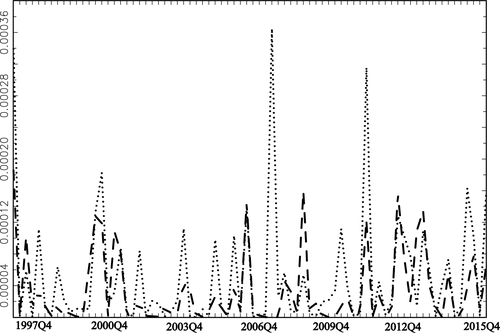
Squared estimation errors in detrended data. Series: ------, modelled break: - - - - -, unmodelled break: ⋅ ⋅ ⋅ ⋅ ⋅.
7 Conclusions
We have proposed tests for the presence of deterministic seasonality and breaks in deterministic seasonality in seasonally observed time series that are designed to be asymptotically robust to the order of integration of the data at both the zero and the seasonal frequencies. Simulation results in the online Appendix show that our proposed tests have good size control in finite samples. Recommendations have been provided for how to perform these tests in practice. In an empirical example, we have shown that quarterly seasonally unadjusted UK GDP appears to have been subject to a significant shift in its deterministic seasonal pattern around the time of the financial crisis.
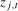 ,
, 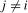 , in (
3.5) and (
3.6) to ensure that the statistics we develop for testing hypotheses on
, in (
3.5) and (
3.6) to ensure that the statistics we develop for testing hypotheses on 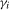 ,
, 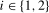 , are exact invariant to the
, are exact invariant to the 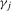 ,
, 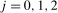 ,
, 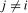 , parameters in (
2.4).
, parameters in (
2.4).
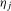 ,
, 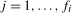 , coefficients in (
3.6) when testing for level shifts because these coefficients could be nonzero in cases where a level break is not present at frequency
, coefficients in (
3.6) when testing for level shifts because these coefficients could be nonzero in cases where a level break is not present at frequency 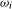 , but a level break is present at frequency
, but a level break is present at frequency 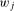 ,
, 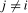 .
.
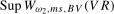 , is seen to be identical to that of the zero frequency mean shift test based on Model (1) of Sayginsoy and Vogelsang (
2011) under both the null and the local alternative hypotheses. As such, critical values and the appropriate scaling constant used to construct the
, is seen to be identical to that of the zero frequency mean shift test based on Model (1) of Sayginsoy and Vogelsang (
2011) under both the null and the local alternative hypotheses. As such, critical values and the appropriate scaling constant used to construct the 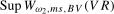 test statistic, again for the case of the Daniell kernel, can be taken directly from Table 1.1.1 of Sayginsoy and Vogelsang (
2008).
test statistic, again for the case of the Daniell kernel, can be taken directly from Table 1.1.1 of Sayginsoy and Vogelsang (
2008).
 using the Daniell kernel, is again identical to the optimal bandwidth rule for Model (1) of Sayginsoy and Vogelsang (
2011) reported in Figure 1.1 of Sayginsoy and Vogelsang (
2008).
using the Daniell kernel, is again identical to the optimal bandwidth rule for Model (1) of Sayginsoy and Vogelsang (
2011) reported in Figure 1.1 of Sayginsoy and Vogelsang (
2008).
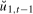 as a regressor in (
5.2), consistent with the definition of near-integration at the annual frequency that sets
as a regressor in (
5.2), consistent with the definition of near-integration at the annual frequency that sets 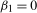 in (
2.3).
in (
2.3).
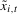 ,
, 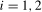 . This yielded similar results to those reported above for the detrended data, although the
. This yielded similar results to those reported above for the detrended data, although the 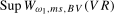 test failed to reject the null of no shift in mean at the annual frequency. The break dates identified using this approach only differed from those found using the de-trended data by one quarter at each frequency, with a mean shift at the Nyquist frequency detected in 2007Q1 and a mean shift at the annual frequency most likely to have occurred in 2009Q3.
test failed to reject the null of no shift in mean at the annual frequency. The break dates identified using this approach only differed from those found using the de-trended data by one quarter at each frequency, with a mean shift at the Nyquist frequency detected in 2007Q1 and a mean shift at the annual frequency most likely to have occurred in 2009Q3.