Non-parametric inference on the number of equilibria
Summary
This paper proposes an estimator and develops an inference procedure for the number of roots of functions that are non-parametrically identified by conditional moment restrictions. It is shown that a smoothed plug-in estimator of the number of roots is superconsistent under i.i.d. asymptotics, but asymptotically normal under non-standard asymptotics. The smoothed estimator is furthermore asymptotically efficient relative to a simple plug-in estimator. The procedure proposed is used to construct confidence sets for the number of equilibria of static games of incomplete information and of stochastic difference equations. In an application to panel data on neighbourhood composition in the United States, no evidence of multiple equilibria is found.
1. INTRODUCTION
Some economic systems show large and persistent differences in outcomes even though the observable exogenous factors influencing these systems differ little.1 One explanation for such persistent differences in outcomes is multiplicity of equilibria. If a system does have multiple equilibria, then temporary, large interventions might have a permanent effect, by shifting the equilibrium attained, while long-lasting, small interventions might not have a permanent effect.
Knowing the number of equilibria, and in particular whether there are multiple equilibria, is of interest in many economic contexts. Multiple equilibria and poverty traps are discussed by Dasgupta and Ray (1986), Azariadis and Stachurski (2005) and Bowles et al. (2006). Poverty traps can arise, for instance, if an individual's productivity is a function of their income and if wage income reflects productivity, as in models of efficiency wages. Productivity might depend on wages because nutrition and health are improving with income. If this feedback mechanism is strong enough, there might be multiple equilibria, and extreme poverty might be self-perpetuating. In that case, public investments in nutrition and health can permanently lift families out of poverty. Multiple equilibria and urban segregation are discussed by Becker and Murphy (2000) and Card et al. (2008). Urban segregation, along ethnic or sociodemographic dimensions, might arise because households' location choices reflect a preference over neighbourhood composition. If this preference is strong enough, different compositions of a neighbourhood can be stable, given constant exogenous neighbourhood properties. Transition between different stable compositions might lead to rapid composition change, or ‘tipping’, as in the case of gentrification of a neighbourhood. Interest in such tipping behaviour motivated Card et al. (2008), and is the focus of the application discussed in Section 4. of this paper. Multiple equilibria and the market entry of firms are discussed by Bresnahan and Reiss (1991) and Berry (1992). Entering a market might only be profitable for a firm if its competitors do not enter that same market. As a consequence, different configurations of which firms serve which markets might be stable. In sociology, finally, multiple equilibria are of interest in the context of social norms. If the incentives to conform to prevailing behaviours are strong enough, different behavioural patterns might be stable norms (i.e. equilibria); see Young (2008). Transitions between such stable norms correspond to social change. One instance where this has been discussed is the assimilation of immigrant communities into the mainstream culture of a country.
This paper develops an estimator and an inference procedure for the number of equilibria of economic systems. It will be assumed that the equilibria of a system can be represented as solutions to the equation 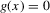 . It will furthermore be assumed that g can be identified by some conditional moment restriction. The procedure proposed here provides confidence sets for the number
. It will furthermore be assumed that g can be identified by some conditional moment restriction. The procedure proposed here provides confidence sets for the number 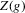 of solutions to the equation
of solutions to the equation 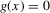 .
.
This procedure can be summarized as follows. In a first stage, g and its derivative 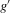 are non-parametrically estimated. These first-stage estimates of g and
are non-parametrically estimated. These first-stage estimates of g and 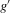 are then plugged into a smooth functional
are then plugged into a smooth functional 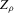 , as defined in 2.4. We show that under standard i.i.d. asymptotics, and for the bandwidth parameter ρ small enough, the continuously distributed
, as defined in 2.4. We show that under standard i.i.d. asymptotics, and for the bandwidth parameter ρ small enough, the continuously distributed 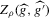 is equal to
is equal to 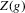 with probability converging to 1. A superconsistent estimator of
with probability converging to 1. A superconsistent estimator of 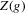 can thus be formed by projecting
can thus be formed by projecting 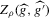 on the closest integer.2
on the closest integer.2
We then show that a rescaled version of 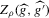 converges to a normal distribution under a non-standard sequence of experiments. This non-standard sequence of experiments is constructed using increasing levels of noise and shrinking bandwidth as sample size increases. Under this same sequence of experiments, the bootstrap provides consistent estimates of the bias and standard deviation of
converges to a normal distribution under a non-standard sequence of experiments. This non-standard sequence of experiments is constructed using increasing levels of noise and shrinking bandwidth as sample size increases. Under this same sequence of experiments, the bootstrap provides consistent estimates of the bias and standard deviation of 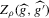 relative to
relative to  . We can thus construct confidence sets for
. We can thus construct confidence sets for 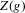 using t-tests. These confidence sets are sets of integers containing the true number of roots with a pre-specified asymptotic probability of
using t-tests. These confidence sets are sets of integers containing the true number of roots with a pre-specified asymptotic probability of 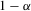 . An alternative to the procedure proposed here would be to use the simple plug-in estimator
. An alternative to the procedure proposed here would be to use the simple plug-in estimator  . This estimator just counts the roots of the first-stage estimate of g. We show, however, that the simple plug-in estimator is asymptotically inefficient relative to the smoothed estimator
. This estimator just counts the roots of the first-stage estimate of g. We show, however, that the simple plug-in estimator is asymptotically inefficient relative to the smoothed estimator 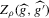 under the non-standard sequence of experiments considered.
under the non-standard sequence of experiments considered.
Sections 3.4. and 3.5. discuss two general set-ups that allow us to translate the hypothesis of multiple equilibria into a hypothesis on the number of roots of some identifiable function g; these set-ups are static games of incomplete information and stochastic difference equations. Section 3.4. discusses a non-parametric model of static games of incomplete information, similar to the one analysed by Bajari et al. (2010).3 Under the assumptions detailed in Section 3.4., we can non-parametrically identify the average best response functions (averaging over private information) of the players in a static incomplete information game. This allows us to represent the Bayesian Nash equilibria of this game as roots of an estimable function. Section 3.4. discusses how to perform inference on the number of such Bayesian Nash equilibria.
Section 3.5. considers panel data of observations of some variable X, where X is generated by a general non-linear stochastic difference equation. This is motivated by the study of neighbourhood composition dynamics in Card et al. (2008). Section 3.5. argues that we can construct tests for the null hypothesis of equilibrium multiplicity of such non-linear difference equations by testing whether non-parametric quantile regressions of 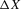 on X have multiple roots.
on X have multiple roots.
The rest of this paper is structured as follows. Section 2. presents the inference procedure and its asymptotic justification for the baseline case. Section 3. discusses generalizations, as well as identification and inference in static games of incomplete information and in stochastic difference equations. Section 4. applies the inference procedure to the data on neighbourhood composition studied by Card et al. (2008). In contrast to their results, no evidence of ‘tipping’ (equilibrium multiplicity) is found here. Section 5. concludes. Appendix A presents some Monte Carlo evidence. All proofs are relegated to Appendix B. Additional figures and tables are given in the online Appendix, which also contains a second application of the inference procedure to data on economic growth, similar to those discussed by Azariadis and Stachurski (2005), in their Section 4.1, and by Quah (1996).
2. INFERENCE IN THE BASELINE CASE
2.1. Set-up
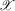 of its support:
of its support:
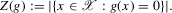 (2.1)
(2.1)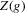 follows from identification of g on
follows from identification of g on 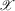 . In this section, inference on
. In this section, inference on 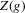 is discussed for functions g with one-dimensional and compact domain and range. Throughout, the following assumption will be maintained.
is discussed for functions g with one-dimensional and compact domain and range. Throughout, the following assumption will be maintained.
Assumption 2.1.(a) The observable data are i.i.d. draws of 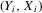 , where each draw has the same distribution as
, where each draw has the same distribution as 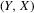 ; (b) the set
; (b) the set  is compact, and the density of X is bounded away from 0 on
is compact, and the density of X is bounded away from 0 on 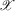 ; (c) the function g is identified by a conditional moment restriction of the form
; (c) the function g is identified by a conditional moment restriction of the form
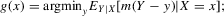 (2.2)
(2.2)Examples of functions characterized by conditional moment restrictions as in 2.2 are conditional mean regressions, for which 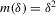 , and conditional qth quantile regressions, for which
, and conditional qth quantile regressions, for which 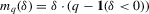 .
.
Definition 2.1. (Genericity)A continuously differentiable function g is called generic if 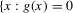 and
and 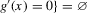 , and if all roots of g are in the interior of
, and if all roots of g are in the interior of 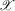 .
.
Genericity of g implies that g has only a finite number of roots.4 Genericity in the sense of Definition 2.1 is commonly assumed in microeconomic theory; see the discussion in Mas-Colell et al. (1995, p. 593ff).
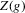 . First, estimate
. First, estimate  and
and  using local linear m-regression:
using local linear m-regression:
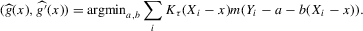 (2.3)
(2.3)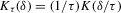 for some (symmetric, positive) kernel function K integrating to one with bandwidth τ. Equation 2.3 is a sample analogue of 2.2, where a kernel weighted local average is replacing the conditional expectation. Next, calculate
for some (symmetric, positive) kernel function K integrating to one with bandwidth τ. Equation 2.3 is a sample analogue of 2.2, where a kernel weighted local average is replacing the conditional expectation. Next, calculate 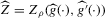 , where
, where 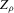 is defined as
is defined as
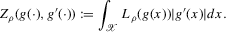 (2.4)
(2.4)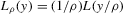 for a Lipschitz continuous, positive symmetric kernel L integrating to one with bandwidth 1 and support [ − 1, 1]. The intuition for this expression will be discussed in detail below. Estimate the variance and bias of
for a Lipschitz continuous, positive symmetric kernel L integrating to one with bandwidth 1 and support [ − 1, 1]. The intuition for this expression will be discussed in detail below. Estimate the variance and bias of 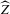 relative to Z using bootstrap. Finally, construct integer valued confidence sets for Z using t-statistics based on
relative to Z using bootstrap. Finally, construct integer valued confidence sets for Z using t-statistics based on 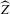 and the bootstrapped variance and bias.
and the bootstrapped variance and bias.2.2. Basic properties and consistency
The rest of this section will motivate and justify this procedure. First, we see that 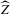 is a superconsistent estimator of Z, in the sense that
is a superconsistent estimator of Z, in the sense that 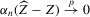 for any diverging sequence
for any diverging sequence 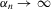 , under i.i.d. sampling and conditions to be stated. Then, we present the central result of this paper, which establishes asymptotic normality of
, under i.i.d. sampling and conditions to be stated. Then, we present the central result of this paper, which establishes asymptotic normality of 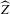 under a non-standard sequence of experiments. From this result, it follows that inference based on t-statistics, using bootstrapped standard errors and bias corrections, provides asymptotically valid confidence sets for Z. We also show that
under a non-standard sequence of experiments. From this result, it follows that inference based on t-statistics, using bootstrapped standard errors and bias corrections, provides asymptotically valid confidence sets for Z. We also show that 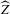 is an efficient estimator relative to the simple plug-in estimator
is an efficient estimator relative to the simple plug-in estimator 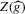 under the non-standard asymptotic sequence.
under the non-standard asymptotic sequence.
We are mainly concerned with constructing confidence sets for Z, rather than a point estimator. A point estimator could be formed by projecting 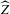 on the closest integer. While
on the closest integer. While 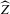 will be called an estimator of
will be called an estimator of 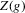 , it should be kept in mind that its primary role is as an intermediate statistic in the construction of confidence sets.
, it should be kept in mind that its primary role is as an intermediate statistic in the construction of confidence sets.
The following proposition states that 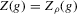 for generic g and ρ small enough. The two functionals only differ around non-generic g, or ‘bifurcation points’ (i.e. g where Z jumps). The functional
for generic g and ρ small enough. The two functionals only differ around non-generic g, or ‘bifurcation points’ (i.e. g where Z jumps). The functional 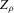 is a smooth approximation of Z which varies continuously around such jumps.
is a smooth approximation of Z which varies continuously around such jumps.
Proposition 2.1.For g continuously differentiable and generic, if 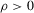 is small enough, then
is small enough, then
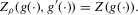
The intuition underlying Proposition 2.1 is as follows. Given a generic function g, consider the subset of 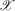 where
where 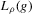 is not zero. If ρ is small enough, this subset is partitioned into disjoint neighbourhoods of the roots of g, and g is monotonic in each of these neighbourhoods. A change of variables, setting
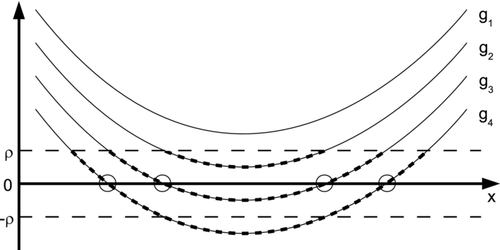
is not zero. If ρ is small enough, this subset is partitioned into disjoint neighbourhoods of the roots of g, and g is monotonic in each of these neighbourhoods. A change of variables, setting 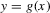 , shows that the integral over each of these neighbourhoods equals one. Figure 1 illustrates the relationship between Z and
, shows that the integral over each of these neighbourhoods equals one. Figure 1 illustrates the relationship between Z and 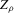 . For the functions g depicted,
. For the functions g depicted, 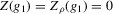 ,
, 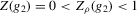 ,
,  and
and 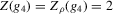 . The two functionals are equal if g does not peak within the range
. The two functionals are equal if g does not peak within the range 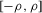 , but if g does peak within the range
, but if g does peak within the range 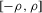 , they are different and
, they are different and 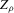 is not integer valued.
is not integer valued.
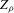 .
.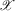 ,
, 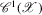 , with the following norm:
, with the following norm:
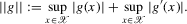 (2.5)
(2.5)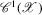 . Given this norm, we have the following proposition.
. Given this norm, we have the following proposition.
Proposition 2.2. (Local constancy)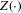 is constant in a neighbourhood, with respect to the norm
is constant in a neighbourhood, with respect to the norm 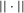 , of any generic function
, of any generic function 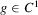 , and so is
, and so is 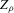 if ρ is small enough.
if ρ is small enough.
Using a neighbourhood of g with respect to the sup norm in levels only, instead of 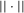 , is not enough for the assertion of Proposition 2.2 to hold. For any function g1 that has at least one root, we can find a function g2 arbitrarily close to g1 in the uniform sense, which has more roots than g1, by adding a ‘wiggle’ around a root of g1. Figure 2 illustrates. This figure shows two functions that are uniformly close in levels but not in derivatives, and which have different numbers of roots. However, if one additionally restricts the first derivative of g2 to be uniformly close to the the derivative of g1, additional wiggles are precluded around generic roots, because around these g1 has a non-zero derivative. Because derivatives are ‘harder’ to estimate than levels, variation in the estimated derivatives dominates the asymptotic distribution of estimators for
, is not enough for the assertion of Proposition 2.2 to hold. For any function g1 that has at least one root, we can find a function g2 arbitrarily close to g1 in the uniform sense, which has more roots than g1, by adding a ‘wiggle’ around a root of g1. Figure 2 illustrates. This figure shows two functions that are uniformly close in levels but not in derivatives, and which have different numbers of roots. However, if one additionally restricts the first derivative of g2 to be uniformly close to the the derivative of g1, additional wiggles are precluded around generic roots, because around these g1 has a non-zero derivative. Because derivatives are ‘harder’ to estimate than levels, variation in the estimated derivatives dominates the asymptotic distribution of estimators for 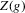 , as will be shown. Proposition 2.2 immediately implies the following theorem as a corollary. This theorem states that the plug-in estimator
, as will be shown. Proposition 2.2 immediately implies the following theorem as a corollary. This theorem states that the plug-in estimator 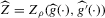 converges to a degenerate limiting distribution at an ‘infinite’ rate, if
converges to a degenerate limiting distribution at an ‘infinite’ rate, if 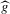 converges with respect to the norm
converges with respect to the norm 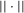 (i.e.
(i.e. 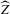 is equal to the true number of roots with probability converging to 1).5
is equal to the true number of roots with probability converging to 1).5
Theorem 2.1. (Superconsistency)If 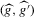 converges uniformly in probability to
converges uniformly in probability to 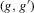 , if g is generic and if
, if g is generic and if 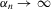 is some arbitrary diverging sequence, then
is some arbitrary diverging sequence, then
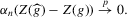
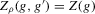 holds, then
holds, then
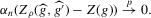

This result implies that 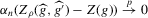 if
if 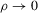 as
as 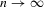 .
.
2.3. Asymptotic normality and relative efficiency
We have shown our first claim, superconsistency of 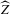 given uniform convergence of
given uniform convergence of 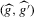 . Next, we show our second claim, asymptotic normality of
. Next, we show our second claim, asymptotic normality of 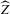 under a non-standard sequence of experiments. This section then concludes by formally stating the efficiency of
under a non-standard sequence of experiments. This section then concludes by formally stating the efficiency of 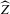 relative to the simple plug-in estimator
relative to the simple plug-in estimator 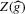 . To further characterize the asymptotic distribution of
. To further characterize the asymptotic distribution of 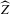 , we need a suitable approximation for the distribution of the first-stage estimator
, we need a suitable approximation for the distribution of the first-stage estimator 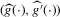 . Kong et al. (2010) provide uniform Bahadur representations for local polynomial estimators of m-regressions. We state their result, for the special case of local linear m-regression, as an assumption.
. Kong et al. (2010) provide uniform Bahadur representations for local polynomial estimators of m-regressions. We state their result, for the special case of local linear m-regression, as an assumption.
Assumption 2.2. (Bahadur expansion)The estimation error of the estimator 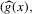
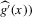 defined by 2.3 can be approximated by a local average as follows:
defined by 2.3 can be approximated by a local average as follows:
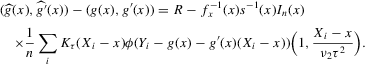 (2.6)
(2.6)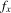 is the density of X,
is the density of X, 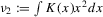 ,
, 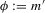 (in a piecewise derivative sense; m is assumed to be piecewise differentiable),
(in a piecewise derivative sense; m is assumed to be piecewise differentiable), 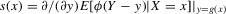 ,
, 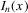 is a non-random matrix converging uniformly to the identity matrix, and
is a non-random matrix converging uniformly to the identity matrix, and 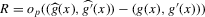 uniformly in x.
uniformly in x.
The crucial part of Assumption 2.2 is the assumption that the remainder R is asymptotically negligible relative to the linear (sample mean) component of  . This assumption is only well defined in the context of a specific sequence of experiments.6 In Theorem 2.2, this assumption will be understood to hold relative to the sequence of experiments defined in Assumption 2.3. In the case of qth quantile regression,
. This assumption is only well defined in the context of a specific sequence of experiments.6 In Theorem 2.2, this assumption will be understood to hold relative to the sequence of experiments defined in Assumption 2.3. In the case of qth quantile regression, 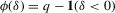 and
and 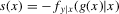 . In the case of mean regression,
. In the case of mean regression, 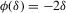 and
and 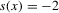 .
.
The asymptotic results in the remainder of this section depend on the availability of an expansion in the form of expansion 2.6 and the relative negligibility of the remainder, but not on any other specifics of local linear m-regression. This will allow for fairly straightforward generalizations of the baseline case considered here to the cases discussed in Section 3., as well as to other cases that are beyond the scope of this paper, once we have appropriate expansions for the first-stage estimators.
By Proposition 2.2, consistency of any plug-in estimator follows from uniform convergence of 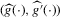 . Such uniform convergence follows from Assumption 2.2, combined with a Glivenko–Cantelli theorem on uniform convergence of averages, assuming i.i.d. draws from the joint distribution of
. Such uniform convergence follows from Assumption 2.2, combined with a Glivenko–Cantelli theorem on uniform convergence of averages, assuming i.i.d. draws from the joint distribution of 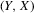 as
as 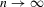 ; see van der Vaart (1998), Chapter 19. Superconsistency of
; see van der Vaart (1998), Chapter 19. Superconsistency of 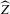 therefore follows, which implies that standard i.i.d. asymptotics with rescaling of the estimator yield only degenerate distributional approximations. This is because
therefore follows, which implies that standard i.i.d. asymptotics with rescaling of the estimator yield only degenerate distributional approximations. This is because 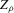 and Z are constant in a C1 neighbourhood of any generic g, even though they jump at bifurcation points (i.e. non-generic g). As a consequence, all terms in a functional Taylor expansion of
and Z are constant in a C1 neighbourhood of any generic g, even though they jump at bifurcation points (i.e. non-generic g). As a consequence, all terms in a functional Taylor expansion of 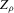 , as a function of g, vanish, except for the remainder. The application of ‘delta method’ type arguments, as in Newey (1994), gives only the degenerate limit distribution.
, as a function of g, vanish, except for the remainder. The application of ‘delta method’ type arguments, as in Newey (1994), gives only the degenerate limit distribution.
In finite samples, however, the sampling variation of 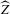 is, in general, not negligible, as the simulations of Appendix A confirm, which makes the distributional approximation of the degenerate limit useless for inference. Asymptotic statistical theory approximates the finite sample distribution of interest by a limiting distribution of a sequence of experiments, of which our actual experiment is an element. The choice of sequence is to some extent arbitrary; the standard sequence where observations are i.i.d. draws from a distribution, which does not change as n increases, is just one possibility. In econometrics, non-standard asymptotics are used, for instance, in the literature on weak instruments; see, e.g. Staiger and Stock (1997), Imbens and Wooldridge (2007) and Andrews and Cheng (2012). In the present set-up, a non-degenerate distributional limit of
is, in general, not negligible, as the simulations of Appendix A confirm, which makes the distributional approximation of the degenerate limit useless for inference. Asymptotic statistical theory approximates the finite sample distribution of interest by a limiting distribution of a sequence of experiments, of which our actual experiment is an element. The choice of sequence is to some extent arbitrary; the standard sequence where observations are i.i.d. draws from a distribution, which does not change as n increases, is just one possibility. In econometrics, non-standard asymptotics are used, for instance, in the literature on weak instruments; see, e.g. Staiger and Stock (1997), Imbens and Wooldridge (2007) and Andrews and Cheng (2012). In the present set-up, a non-degenerate distributional limit of 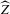 can only be obtained under a sequence of experiments, which yields a non-degenerate limiting distribution of the first-stage estimator
can only be obtained under a sequence of experiments, which yields a non-degenerate limiting distribution of the first-stage estimator 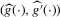 .7 We now consider asymptotics under such a sequence of experiments. The sequence we consider has increasing amounts of noise relative to signal as sample size increases.8
.7 We now consider asymptotics under such a sequence of experiments. The sequence we consider has increasing amounts of noise relative to signal as sample size increases.8
Assumption 2.3.Experiments are indexed by n, and for the nth experiment we observe 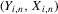 for
for 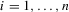 . The observations
. The observations 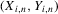 are i.i.d. given n, and
are i.i.d. given n, and
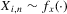 (2.7)
(2.7)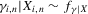 (2.8)
(2.8)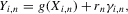 (2.9)
(2.9)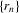 is a real-valued sequence and
is a real-valued sequence and
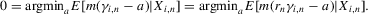
The last equality requires the criterion function m to be scale neutral. This holds for quantiles and the mean, in particular. For a given sample size n, this is the same model as before. As n changes, the function g identified by 2.2 is held constant. If 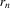 grows in n, the estimation problem in this sequence of models becomes increasingly difficult relative to i.i.d. sampling. Note that 2.9 does not describe an additive structural model, which would allow us to predict counterfactual outcomes. Instead,
grows in n, the estimation problem in this sequence of models becomes increasingly difficult relative to i.i.d. sampling. Note that 2.9 does not describe an additive structural model, which would allow us to predict counterfactual outcomes. Instead, 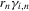 is simply the statistical residual, given by the difference of Y and
is simply the statistical residual, given by the difference of Y and 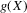 , which is also well defined for non-additive structural models.
, which is also well defined for non-additive structural models.
Our next result, Theorem 2.2, assumes that the approximation of Assumption 2.2 holds under the non-standard sequence of experiments described by Assumption 2.3. Theorem 1 in Kong et al. (2010) implies that Assumption 2.2 holds under standard asymptotics and weak regularity conditions. Their result extends to our setting in a fairly straightforward way, however. This is most easily seen in the case of mean regression. We can write 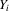 as a sum of two terms: (a)
as a sum of two terms: (a) 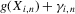 ; (b)
; (b) 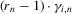 . We can then apply the result of Kong et al. (2010) to local linear regression on
. We can then apply the result of Kong et al. (2010) to local linear regression on 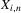 of each of these terms separately. Both the Bahadur expansion and the local linear mean regression estimator are linear in Y. As a consequence, the remainder R for a regression of
of each of these terms separately. Both the Bahadur expansion and the local linear mean regression estimator are linear in Y. As a consequence, the remainder R for a regression of 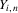 on
on 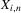 is given by the sum of the two remainders corresponding to regression of terms (a) and (b) on
is given by the sum of the two remainders corresponding to regression of terms (a) and (b) on 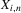 . Whichever of the two Bahadur expansions corresponding to (a) and (b) dominates the asymptotic distribution is thereby guaranteed to be of larger order than the sum of the two remainder terms. A similar logic applies more generally, for instance to the case of local linear quantile regression; a complete proof is beyond the scope of the present paper.
. Whichever of the two Bahadur expansions corresponding to (a) and (b) dominates the asymptotic distribution is thereby guaranteed to be of larger order than the sum of the two remainder terms. A similar logic applies more generally, for instance to the case of local linear quantile regression; a complete proof is beyond the scope of the present paper.
By Corollary 2.1, a necessary condition for a non-degenerate limit of 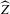 is that
is that 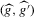 converges to a non-degenerate limiting distribution. As is well known, and also follows from Assumption 2.2,
converges to a non-degenerate limiting distribution. As is well known, and also follows from Assumption 2.2, 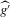 converges at a slower rate than
converges at a slower rate than  , so that asymptotically variation in
, so that asymptotically variation in 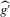 will dominate, namely by adding ‘wiggles’ around the actual roots. If
will dominate, namely by adding ‘wiggles’ around the actual roots. If 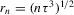 in the sequence of experiments defined in Assumption 2.3,
in the sequence of experiments defined in Assumption 2.3, 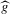 converges uniformly in probability to g, whereas
converges uniformly in probability to g, whereas 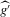 converges pointwise to a non-degenerate limit. This is the basis for the following theorem.9
converges pointwise to a non-degenerate limit. This is the basis for the following theorem.9
Theorem 2.2. (Asymptotic normality)Under Assumptions 2.1, 2.2 and 2.3, and if 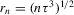 ,
,  ,
, 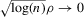 and
and 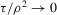 , then there exist
, then there exist 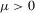 and V such that
and V such that
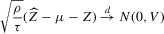
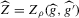 . Both μ and V depend on the data-generating process only via the asymptotic mean and variance of
. Both μ and V depend on the data-generating process only via the asymptotic mean and variance of 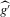 at the roots of g, which in turn depend upon
at the roots of g, which in turn depend upon 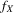 ,
, 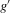 , s and Var
, s and Var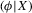 evaluated at the roots of g.
evaluated at the roots of g.
This theorem justifies the use of t-tests based on 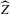 for null hypotheses of the form
for null hypotheses of the form 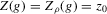 . The construction of a t-statistic requires a consistent estimator of V and an estimator of μ converging at a rate faster than
. The construction of a t-statistic requires a consistent estimator of V and an estimator of μ converging at a rate faster than 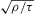 . Based on the last part of Theorem 2.2, we can construct such estimators as follows. Any plug-in estimator that consistently estimates the (co)variances of
. Based on the last part of Theorem 2.2, we can construct such estimators as follows. Any plug-in estimator that consistently estimates the (co)variances of 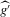 under the given sequence of experiments consistently estimates μ and V. One such plug-in estimator is standard bootstrap (i.e. resampling from the empirical distribution function). The Bahadur expansion in Assumption 2.2, which approximates
under the given sequence of experiments consistently estimates μ and V. One such plug-in estimator is standard bootstrap (i.e. resampling from the empirical distribution function). The Bahadur expansion in Assumption 2.2, which approximates 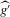 by sample averages, implies that the bootstrap gives a resampling distribution with the asymptotically correct covariance structure for
by sample averages, implies that the bootstrap gives a resampling distribution with the asymptotically correct covariance structure for 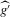 . From this and Theorem 2.2, it then follows that the bootstrap gives consistent variance and bias estimates for
. From this and Theorem 2.2, it then follows that the bootstrap gives consistent variance and bias estimates for 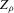 , where the bias is estimated from the difference of the resampling estimates relative to
, where the bias is estimated from the difference of the resampling estimates relative to 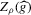 . If sample size grows fast enough relative to
. If sample size grows fast enough relative to 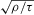 and τ, the asymptotic validity of a standard normal approximation for the pivot follows.
and τ, the asymptotic validity of a standard normal approximation for the pivot follows.
It would be interesting to develop distributional refinements for this statistic using higher-order bootstrapping, along the lines discussed by Horowitz (2001). However, higher-order bootstrapping might be very computationally demanding in the present case, in particular if criteria such as quantile regression are used to identify g.
Theorem 2.2 also implies that increasing the bandwidth parameter ρ reduces the variance without affecting the bias in the limiting normal distribution. Asymptotically, the difficulty in estimating Z is driven entirely by fluctuations in 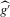 . These fluctuations lead both to upward bias and to variance in plug-in estimators. When ρ is larger, these fluctuations are averaged over a larger range of X, thereby reducing variance. Theorem 2.2 implies that
. These fluctuations lead both to upward bias and to variance in plug-in estimators. When ρ is larger, these fluctuations are averaged over a larger range of X, thereby reducing variance. Theorem 2.2 implies that 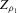 is asymptotically inefficient relative to
is asymptotically inefficient relative to 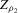 for
for 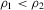 . Furthermore, by Proposition 2.1,
. Furthermore, by Proposition 2.1, 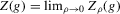 for all generic g. If the relative inefficiency carries over to the limit as
for all generic g. If the relative inefficiency carries over to the limit as 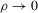 , it follows that the simple plug-in estimator
, it follows that the simple plug-in estimator 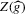 is asymptotically inefficient relative to
is asymptotically inefficient relative to 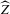 . Note, however, that this is only a heuristic argument. We cannot exchange the limits with respect to ρ and with respect to n to obtain the limit distribution of
. Note, however, that this is only a heuristic argument. We cannot exchange the limits with respect to ρ and with respect to n to obtain the limit distribution of 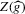 . The following theorem, which is fairly easy to show, states a formally correct version of this argument.
. The following theorem, which is fairly easy to show, states a formally correct version of this argument.
Theorem 2.3. (Asymptotic inefficiency of the naive plug-in estimator)Consider the set-up of Theorem 2.2, and assume 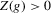 . Then, as
. Then, as 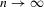 ,
,
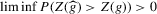
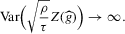
From this theorem, it follows in particular that tests based on 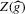 will, in general, not be consistent under the sequence of experiments considered (i.e. the probability of false acceptances does not go to zero). This stands in contrast to tests based on
will, in general, not be consistent under the sequence of experiments considered (i.e. the probability of false acceptances does not go to zero). This stands in contrast to tests based on 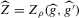 .
.
2.4. Alternative approaches
The reader might wonder rightly whether there are alternative estimators that, like our 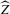 , avoid the issues of the naive estimator (overestimating the number of roots, in particular), and that possibly beat
, avoid the issues of the naive estimator (overestimating the number of roots, in particular), and that possibly beat 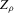 in terms of some notion of relative efficiency.10 One possible estimator that comes to mind is the ϱ-packing number of the set of roots of
in terms of some notion of relative efficiency.10 One possible estimator that comes to mind is the ϱ-packing number of the set of roots of 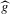 , where
, where 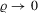 slowly. The packing number is the largest integer z such that there are z disjoint balls of radius ϱ centred at roots of
slowly. The packing number is the largest integer z such that there are z disjoint balls of radius ϱ centred at roots of 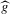 .
.
The packing number is in fact closely related to our estimator  . For an appropriate scaling of ϱ, we can think of
. For an appropriate scaling of ϱ, we can think of 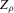 as smoothly interpolating the packing number. The following numerical illustration helps to make the point. Consider
as smoothly interpolating the packing number. The following numerical illustration helps to make the point. Consider 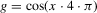 , and
, and 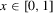 . This function has four roots at a distance of 1/4 from each other, and has a maximum absolute value of 1. For this function g, consider both
. This function has four roots at a distance of 1/4 from each other, and has a maximum absolute value of 1. For this function g, consider both 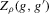 and the packing number of g as a function of ρ (or ϱ). The result is plotted in Figure 3, which illustrates the relationship between
and the packing number of g as a function of ρ (or ϱ). The result is plotted in Figure 3, which illustrates the relationship between 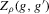 and the packing number of the set of roots of g for the function
and the packing number of the set of roots of g for the function 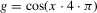 , by plotting both as a function of bandwidth. For comparability, we have scaled
, by plotting both as a function of bandwidth. For comparability, we have scaled 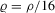 . As can be seen from this figure, both estimators behave similarly, with
. As can be seen from this figure, both estimators behave similarly, with 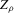 interpolating the jumps of the packing number. To the extent that smoother estimators are preferable in many contexts (see the literature on model selection versus shrinkage), it might be that
interpolating the jumps of the packing number. To the extent that smoother estimators are preferable in many contexts (see the literature on model selection versus shrinkage), it might be that 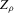 is better behaved. A formalization of this heuristic argument, and a full development of the asymptotic theory of packing numbers, is beyond the scope of the present paper. One advantage of considering
is better behaved. A formalization of this heuristic argument, and a full development of the asymptotic theory of packing numbers, is beyond the scope of the present paper. One advantage of considering 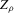 , which motivates our focus on this estimator rather than, for instance, the packing number, is that it allows for an easier development of asymptotic theory and of corresponding inference procedures, which are the main object of the present paper.
, which motivates our focus on this estimator rather than, for instance, the packing number, is that it allows for an easier development of asymptotic theory and of corresponding inference procedures, which are the main object of the present paper.
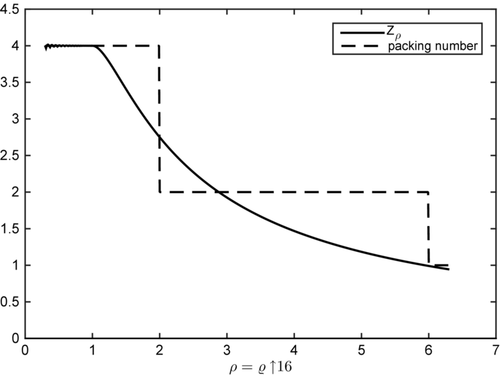
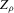 and the packing number.
and the packing number.The reader might further wonder, rightly again, whether the sequence of experiments we chose in Assumption 2.3 is peculiar, and whether another sequence might give different answers. The problem of estimating 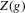 might be made more difficult not only by increasing the variance of the regression residuals, but also by letting the roots of g move closer to each other. Formally, we might consider
might be made more difficult not only by increasing the variance of the regression residuals, but also by letting the roots of g move closer to each other. Formally, we might consider 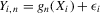 where
where 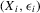 are i.i.d. and
are i.i.d. and 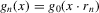 for a diverging sequence
for a diverging sequence 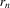 . Such a sequence of experiments, however, effectively reduces to the setting of standard asymptotics once we substitute the bandwidth ρ by
. Such a sequence of experiments, however, effectively reduces to the setting of standard asymptotics once we substitute the bandwidth ρ by 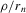 , and account for the fact that effective sample size grows only at rate
, and account for the fact that effective sample size grows only at rate 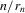 . This implies, in particular, that the superconsistency result of Theorem 2.1 also applies to this alternative sequence of experiments, which makes it unsuitable for inference.
. This implies, in particular, that the superconsistency result of Theorem 2.1 also applies to this alternative sequence of experiments, which makes it unsuitable for inference.
3. EXTENSIONS AND APPLICATIONS
In this section, several extensions and applications of the results of Section 2. are presented. Sections 3.1.–3.3. discuss, respectively, inference on Z if g is identified by more general moment conditions, inference on Z if the domain and range of g are multidimensional and inference on the number of stable and unstable roots. Sections 3.4. and 3.5. discuss identification and inference for the two applications mentioned in the introduction: static games of incomplete information and stochastic difference equations.
3.1. Conditioning on covariates
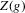 was discussed for functions g identified by the moment condition
was discussed for functions g identified by the moment condition
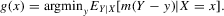
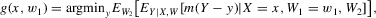 (3.1)
(3.1)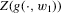 , the number of roots of g in x given w1. The conditional moment restriction 3.1 can be rationalized by a structural model of the form
, the number of roots of g in x given w1. The conditional moment restriction 3.1 can be rationalized by a structural model of the form 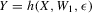 , where
, where 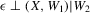 and g is defined by
and g is defined by
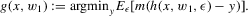
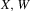 is bounded away from zero on the set
is bounded away from zero on the set 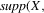
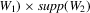 , where supp denotes the compact support of either random vector.
, where supp denotes the compact support of either random vector.The vector W2 serves as a vector of control variables. The conditional independence assumption 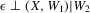 is also known as ‘selection on observables’. The function g is equal to the average structural function if
is also known as ‘selection on observables’. The function g is equal to the average structural function if 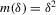 , and equal to a quantile structural function if
, and equal to a quantile structural function if 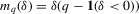 . The average structural function will be of importance in the context of games of incomplete information, as discussed in Section 3.4.; quantile structural functions will be used to characterize stochastic difference equations in Section 3.5.. When games of incomplete information are discussed in Section 3.4.,
. The average structural function will be of importance in the context of games of incomplete information, as discussed in Section 3.4.; quantile structural functions will be used to characterize stochastic difference equations in Section 3.5.. When games of incomplete information are discussed in Section 3.4.,  will correspond to the component of public information, which is not excluded from either player's response function.
will correspond to the component of public information, which is not excluded from either player's response function.
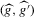 is plugged into the functional
is plugged into the functional 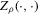 , which is a smooth approximation of the functional
, which is a smooth approximation of the functional 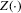 . We can generalize this approach by maintaining the same second step while using more general first-stage estimators
. We can generalize this approach by maintaining the same second step while using more general first-stage estimators 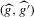 . Equation 3.1 suggests estimating g by a non-parametric sample analogue, replacing the conditional expectation with a local linear kernel estimator of it, and the expectation over W2 with a sample average. Formally, let
. Equation 3.1 suggests estimating g by a non-parametric sample analogue, replacing the conditional expectation with a local linear kernel estimator of it, and the expectation over W2 with a sample average. Formally, let 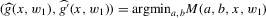 , where
, where
 (3.2)
(3.2)An asymptotic normality result can be shown in this context, which generalizes Theorem 2.2. In light of the proof of Theorem 2.2, the crucial step is to obtain a sequence of experiments such that 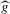 converges uniformly to g while
converges uniformly to g while 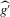 has a non-degenerate limiting distribution. If we obtain an approximation of
has a non-degenerate limiting distribution. If we obtain an approximation of 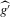 equivalent to the approximation in Assumption 2.2, all further steps of the proof apply immediately. This can be done, using the results of Newey (1994), for the following sequence of experiments.
equivalent to the approximation in Assumption 2.2, all further steps of the proof apply immediately. This can be done, using the results of Newey (1994), for the following sequence of experiments.
Assumption 3.1.Experiments are indexed by n, and for the nth experiment we observe 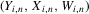 for
for  . The observations
. The observations 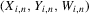 are i.i.d. given n, and
are i.i.d. given n, and
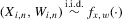 (3.3)
(3.3)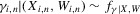 (3.4)
(3.4)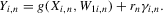 (3.5)
(3.5)
3.2. Higher-dimensional systems
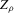 integrates. All results of Section 2. are easily extended to a higher-dimensional set-up. In particular, assume we are interested in the number of roots of a function g from
integrates. All results of Section 2. are easily extended to a higher-dimensional set-up. In particular, assume we are interested in the number of roots of a function g from  to
to 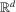 . Generalizing 2.4, we can define
. Generalizing 2.4, we can define 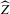 as
as
 (3.6)
(3.6)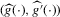 are again estimated by local linear m regression,
are again estimated by local linear m regression, 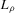 is a kernel with support
is a kernel with support 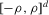 , and the integral is taken over the set
, and the integral is taken over the set 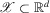 in the support of g. As in the one-dimensional case, superconsistency follows from uniform convergence of
in the support of g. As in the one-dimensional case, superconsistency follows from uniform convergence of 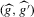 . The following theorem, generalizing Theorem 2.2, holds for arbitrary d.
. The following theorem, generalizing Theorem 2.2, holds for arbitrary d.
3.3. Stable and unstable roots
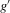 is negative, and unstable roots are those where
is negative, and unstable roots are those where 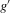 is positive:
is positive:
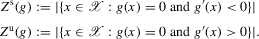 (3.7)
(3.7)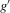 . We can define smooth approximations of the parameters Zs and Zu as follows:
. We can define smooth approximations of the parameters Zs and Zu as follows:
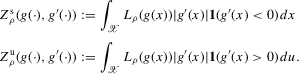 (3.8)
(3.8)Again, all arguments of Section 2. go through essentially unchanged for these parameters. In particular, Theorem 2.2 applies literally, replacing Z with Zs or Zu.
More generally, functionals that are smooth approximations of the number of roots with various stability properties can be constructed in the multidimensional case by multiplying the integrand with an indicator function depending on the signs of the eigenvalues of 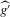 .
.
3.4. Static games of incomplete information
This section and Section 3.5. discuss how to apply the inference procedure proposed to test for equilibrium multiplicity in economic models. The discussion in this subsection builds on Bajari et al. (2010).
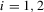 , who both have to choose between one of two actions,
, who both have to choose between one of two actions, 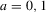 . Player i makes her choice based on public information s, as well as private information
. Player i makes her choice based on public information s, as well as private information  . The public information s is observed by the econometrician, and
. The public information s is observed by the econometrician, and  is independent of s. It is assumed that
is independent of s. It is assumed that  does not enter player i's utility.11 Denote the probability that player i plays strategy
does not enter player i's utility.11 Denote the probability that player i plays strategy 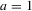 given the public information s by
given the public information s by 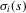 . Player i's expected utility given her information, and hence her optimal action
. Player i's expected utility given her information, and hence her optimal action 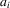 , depends on s and
, depends on s and  , as well as player
, as well as player 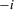 's probability of choosing
's probability of choosing 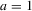 ,
, 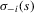 . Let us denote the average best response of player i, integrating over the distribution of
. Let us denote the average best response of player i, integrating over the distribution of  , by
, by
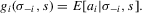 (3.9)
(3.9)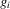 for a given s. The functions
for a given s. The functions 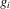 are the (average) best response functions, Bayesian Nash equilibrium requires
are the (average) best response functions, Bayesian Nash equilibrium requires 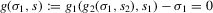 , and we observe one equilibrium
, and we observe one equilibrium 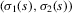 in the data. In this figure, there are two further equilibria that are not directly observable. In Bayesian Nash equilibrium, the probability of player i choosing
in the data. In this figure, there are two further equilibria that are not directly observable. In Bayesian Nash equilibrium, the probability of player i choosing 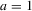 ,
, 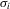 , equals the average best response of player i,
, equals the average best response of player i, 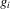 . This implies the two equilibrium conditions
. This implies the two equilibrium conditions
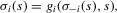
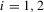 . In Figure 4, the Bayesian Nash equilibria correspond to the intersections of the graphs of the two
. In Figure 4, the Bayesian Nash equilibria correspond to the intersections of the graphs of the two 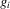 . The condition for Bayesian Nash equilibrium in this game can be restated as
. The condition for Bayesian Nash equilibrium in this game can be restated as 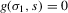 , where
, where
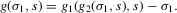 (3.10)
(3.10)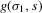 in σ1 is the number of Bayesian Nash equilibria in this game, given s.
in σ1 is the number of Bayesian Nash equilibria in this game, given s.
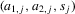 , the players' realized actions and the public information of the game, where
, the players' realized actions and the public information of the game, where 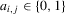 for
for 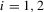 and
and 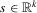 . In this subsection, i indexes players and j indexes observations. Rational expectation beliefs of player
. In this subsection, i indexes players and j indexes observations. Rational expectation beliefs of player 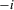 about the expected action of player i are given by
about the expected action of player i are given by 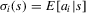 . The following two-stage estimation procedure is a non-parametric variant of the procedure proposed by Bajari et al. (2010). We can get an estimate of the beliefs,
. The following two-stage estimation procedure is a non-parametric variant of the procedure proposed by Bajari et al. (2010). We can get an estimate of the beliefs, 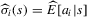 , by local linear mean regression.
, by local linear mean regression.
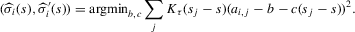 (3.11)
(3.11)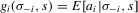 . Without further restrictions,
. Without further restrictions, 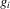 is not identified, because by definition σ is functionally dependent on s. If, however, exclusion restrictions of the form
is not identified, because by definition σ is functionally dependent on s. If, however, exclusion restrictions of the form
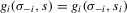 (3.12)
(3.12)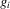 can be identified. In particular, assume that exclusion restriction 3.12 holds, with
can be identified. In particular, assume that exclusion restriction 3.12 holds, with 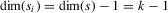 . There is one excluded component of s for each player, the remaining
. There is one excluded component of s for each player, the remaining 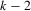 components are not excluded from either response function
components are not excluded from either response function 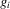 . Assume furthermore that
. Assume furthermore that 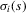 has full support [0, 1] given
has full support [0, 1] given 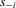 , for
, for 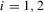 . Under these assumptions, we can estimate the best response functions,
. Under these assumptions, we can estimate the best response functions, 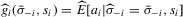 , again using local linear mean regression:
, again using local linear mean regression:
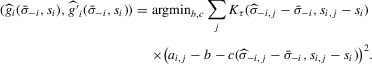 (3.13)
(3.13) . This stands in contrast to Bajari et al. (2010), who need to impose such restrictions in order to be able to identify the underlying preferences. Recall that the condition for Bayesian Nash equilibrium in this game is given by
. This stands in contrast to Bajari et al. (2010), who need to impose such restrictions in order to be able to identify the underlying preferences. Recall that the condition for Bayesian Nash equilibrium in this game is given by 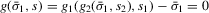 . Inserting
. Inserting 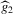 into
into 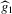 , both estimated by 3.13, yields an estimator of g, which can be written as
, both estimated by 3.13, yields an estimator of g, which can be written as
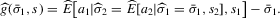 (3.14)
(3.14)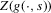 . In particular, let
. In particular, let
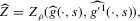 (3.15)
(3.15)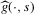 is given by 3.14. The term
is given by 3.14. The term 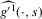 refers to the estimated derivative of g w.r.t.
refers to the estimated derivative of g w.r.t. 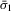 , and similarly for
, and similarly for 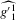 and
and 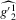 , so that
, so that
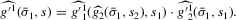 (3.16)
(3.16)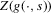 can now proceed as before, if an asymptotic normality result similar to Theorem 2.2 can be shown. In the proof of Theorem 2.2, three properties of
can now proceed as before, if an asymptotic normality result similar to Theorem 2.2 can be shown. In the proof of Theorem 2.2, three properties of 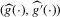 needed to be proven for the statement of the theorem to follow. First, under the given sequence of experiments,
needed to be proven for the statement of the theorem to follow. First, under the given sequence of experiments, 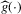 converges uniformly in probability to a degenerate limit. Second,
converges uniformly in probability to a degenerate limit. Second, 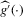 converges in distribution to a non-degenerate limit. Third,
converges in distribution to a non-degenerate limit. Third, 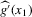 and
and 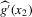 are asymptotically independent for
are asymptotically independent for 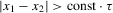 . These properties can be shown for
. These properties can be shown for 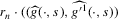 in the present case, with
in the present case, with  replacing x, for an appropriate choice of sequence of experiments, where
replacing x, for an appropriate choice of sequence of experiments, where 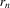 is a scale parameter as before.
is a scale parameter as before.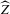 , in the baseline model, is invariant to a proportional rescaling of Y, g and ρ. We can therefore define a sequence of experiments that is equivalent to the one defined by 2.7–2.9 if we replace 2.9 by
, in the baseline model, is invariant to a proportional rescaling of Y, g and ρ. We can therefore define a sequence of experiments that is equivalent to the one defined by 2.7–2.9 if we replace 2.9 by

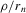 . Intuitively, shrinking the signal g is equivalent to increasing the noise
. Intuitively, shrinking the signal g is equivalent to increasing the noise 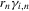 . Returning to games of incomplete information, consider the following sequence of experiments.
. Returning to games of incomplete information, consider the following sequence of experiments.
Assumption 3.2.For 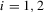 ,
, 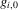 is continuously differentiable and monotonic in
is continuously differentiable and monotonic in 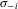 , and
, and 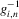 denotes the inverse of
denotes the inverse of 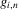 with respect to the
with respect to the 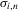 argument, given
argument, given  . Experiments are indexed by n, and for the nth experiment we observe
. Experiments are indexed by n, and for the nth experiment we observe 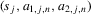 for
for 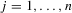 . The observations
. The observations 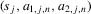 are i.i.d. given n and
are i.i.d. given n and
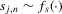 (3.17)
(3.17)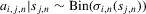 (3.18)
(3.18)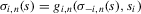 (3.19)
(3.19)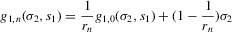 (3.20)
(3.20)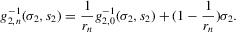 (3.21)
(3.21)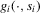 towards the
towards the 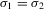 line (compare Figure 4), parallel to the σ1 axis. Denote
line (compare Figure 4), parallel to the σ1 axis. Denote 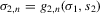 . We obtain
. We obtain
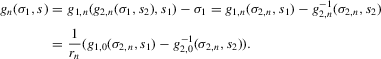
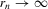 , then
, then 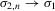 , and hence
, and hence
 (3.22)
(3.22)Using this sequence of experiments, we can now state an asymptotic normality result, similar to Theorem 2.2, for static games of incomplete information. The statement of the theorem differs in two respects from the baseline case. First, ρ is replaced by 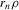 in all expressions. Because this sequence of experiments shrinks g rather than expanding the error, the bandwidth ρ must also shrink correspondingly. Second, the rate of growth of
in all expressions. Because this sequence of experiments shrinks g rather than expanding the error, the bandwidth ρ must also shrink correspondingly. Second, the rate of growth of 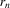 is smaller. Because all regressions are controlling for s1 or s2, rates of convergence are slower. In particular,
is smaller. Because all regressions are controlling for s1 or s2, rates of convergence are slower. In particular, 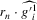 converges to a non-degenerate limit iff
converges to a non-degenerate limit iff 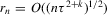 , where k is the dimensionality of the support of the response functions
, where k is the dimensionality of the support of the response functions 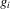 ,
, 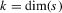 .
.
Theorem 3.3. (Asymptotic normality, static games of incomplete information)Under the sequence of experiments defined by Assumption 3.2, if 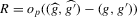 uniformly in the Bahadur expansions as
uniformly in the Bahadur expansions as 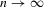 , and if
, and if 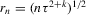 ,
,  ,
, 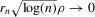 and
and 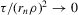 , then there exist
, then there exist 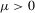 and V such that
and V such that
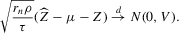
3.5. Stochastic difference equations
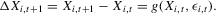 (3.23)
(3.23)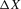 on X. The notion of multiple equilibria here has to be generalized to the notion of multiple equilibrium regions.
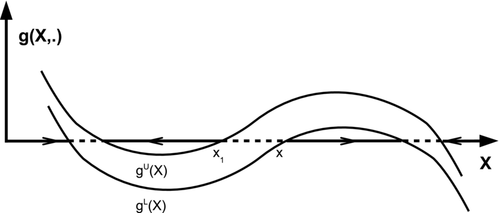
on X. The notion of multiple equilibria here has to be generalized to the notion of multiple equilibrium regions.The intuition for this claim is as follows. Holding ε constant, the number of roots of g in X is the number of equilibria of the difference equation 3.23. If ε is stochastic, then the number of roots can still serve to characterize qualitative dynamics in terms of equilibrium regions. This is shown in Figure 5, which illustrates the characterization of dynamics derived in this section. In this figure, gU and gL are upper and lower envelopes of g for a sequence of realizations of ε. There are ranges of X in which the sign of 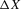 does not depend on ε. This implies that in these ranges X moves towards the equilibrium regions, which are the regions in which the roots of
does not depend on ε. This implies that in these ranges X moves towards the equilibrium regions, which are the regions in which the roots of 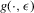 lie. Equilibrium regions correspond to the dashed segments of the X-axis, the basin of attraction of the lower equilibrium region is given by
lie. Equilibrium regions correspond to the dashed segments of the X-axis, the basin of attraction of the lower equilibrium region is given by 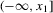 and the basin of attraction of the upper equilibrium region is
and the basin of attraction of the upper equilibrium region is 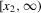 .
.
How is the joint distribution of 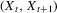 related to the transition function g? Unobserved heterogeneity, which is positively related over time, leads to an upward bias in quantile regression slopes relative to the corresponding structural slopes. To show this, denote the qth conditional quantile of
related to the transition function g? Unobserved heterogeneity, which is positively related over time, leads to an upward bias in quantile regression slopes relative to the corresponding structural slopes. To show this, denote the qth conditional quantile of 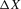 given X by
given X by 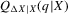 , the conditional cumulative distribution function at Q by
, the conditional cumulative distribution function at Q by  , and the conditional probability density by
, and the conditional probability density by 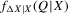 . The following lemma shows that quantile regressions of
. The following lemma shows that quantile regressions of 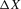 on X yield biased slopes relative to the structural slope
on X yield biased slopes relative to the structural slope 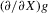 , if X is not exogenous. The second term in 3.24 reflects the bias due to statistical dependence between X and ε.
, if X is not exogenous. The second term in 3.24 reflects the bias due to statistical dependence between X and ε.
Lemma 3.1. (Bias in quantile regression slopes)If 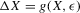 , and if Q and F are differentiable with respect to the conditioning argument X, then
, and if Q and F are differentiable with respect to the conditioning argument X, then
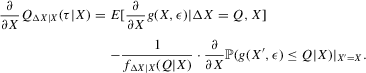 (3.24)
(3.24)The following assumption of first-order stochastic dominance states that there is no negative dependence between current 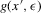 , evaluated at fixed
, evaluated at fixed 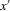 , and current X.
, and current X.
Assumption 3.3. (First-order stochastic dominance)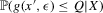 is non-increasing as a function of X, holding
is non-increasing as a function of X, holding 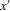 constant.
constant.
Violation of this assumption would require some underlying cyclical dynamics, in continuous time, with a frequency close enough to half the frequency of observation, or more generally with a ratio of frequencies that is an odd number divided by two. It seems safe to discard this possibility in most applications. This assumption might not hold, for instance, if outcomes were influenced by seasonal factors and observations were semi-annual.
We can now formally state the claim that, if there are unstable equilibria structurally, then quantile regressions should exhibit multiple roots.
Proposition 3.1. (Unstable equilibria in dynamics and quantile regressions)Assume that 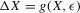 and that
and that 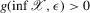 , and
, and 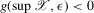 for all ε. If Assumption 3.3 holds and
for all ε. If Assumption 3.3 holds and 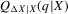 has only one root X for all q, then the conditional average structural functions
has only one root X for all q, then the conditional average structural functions 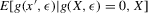 , as functions of
, as functions of 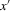 , are stable at the roots m:
, are stable at the roots m:
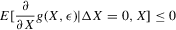
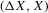 .
.
This proposition assumes global stability of g (i.e. X does not diverge to infinity). Under such global stability, if there is only one root of g, then this root is stable. According to this proposition, if quantile regressions only have one stable root, then the same is true for the conditional average structural functions. This is not conclusive, but it is suggestive that 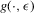 themselves have only one root.
themselves have only one root.
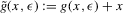 . If g describes a structural relationship, the counterfactual time path under ‘manipulated’ initial condition
. If g describes a structural relationship, the counterfactual time path under ‘manipulated’ initial condition 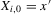 is given by
is given by
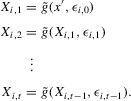 (3.25)
(3.25)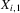 and shocks
and shocks  , 3.23 describes a time inhomogeneous deterministic difference equation. The following argument makes statements about the qualitative behaviour of this difference equation based on properties of the function g, in particular based on the number of roots in x of
, 3.23 describes a time inhomogeneous deterministic difference equation. The following argument makes statements about the qualitative behaviour of this difference equation based on properties of the function g, in particular based on the number of roots in x of 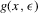 for given unobservables
for given unobservables  . Consider Figure 5, which shows gU and gL defined by
. Consider Figure 5, which shows gU and gL defined by
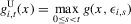 (3.26)
(3.26)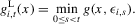 (3.27)
(3.27)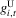 and
and 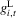 are the upper and lower envelopes of the family of functions
are the upper and lower envelopes of the family of functions 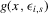 for
for 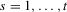 . The direction of movement of X over time does not depend on s in the ranges where
. The direction of movement of X over time does not depend on s in the ranges where 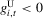 or
or 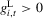 (which is where the horizontal axis is drawn solid in Figure 5), because the sign of
(which is where the horizontal axis is drawn solid in Figure 5), because the sign of 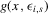 does not depend on s in these ranges. In other words, suppose we start off with an initial value below x1 in the picture. If that is the case,
does not depend on s in these ranges. In other words, suppose we start off with an initial value below x1 in the picture. If that is the case, 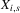 will converge monotonically toward the left-hand dashed range and then remain within that range for all
will converge monotonically toward the left-hand dashed range and then remain within that range for all 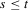 . Similarly, for
. Similarly, for 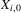 in the upper ‘basin of attraction’ beyond x2,
in the upper ‘basin of attraction’ beyond x2, 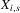 will converge to the upper ‘equilibrium range’ given by the right-hand dashed range. Hence, small changes of initial conditions (from x1 to x2) can have large and persistent effects on X in this case, in contrast to the case where
will converge to the upper ‘equilibrium range’ given by the right-hand dashed range. Hence, small changes of initial conditions (from x1 to x2) can have large and persistent effects on X in this case, in contrast to the case where 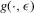 only has one stable root for all ε. These arguments are summarized in the following proposition.
only has one stable root for all ε. These arguments are summarized in the following proposition.
Proposition 3.2. (Characterizing dynamics of stochastic difference equations)Assume that 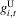 and
and 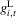 , defined by (3.26) and (3.27), are smooth and generic, positive for sufficiently small x and negative for sufficiently large x, and have the same number z of roots,
, defined by (3.26) and (3.27), are smooth and generic, positive for sufficiently small x and negative for sufficiently large x, and have the same number z of roots,  and
and  , and let
, and let 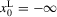 ,
, 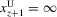 . Define the following mutually disjoint ranges:
. Define the following mutually disjoint ranges:
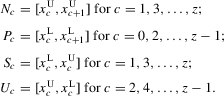
 are negative on the
are negative on the 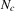 , and positive on the
, and positive on the 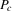 . Furthermore, all
. Furthermore, all 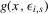 are negative in a neighbourhood to the right of the maximum of the
are negative in a neighbourhood to the right of the maximum of the 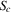 and positive to the left of the minimum, and the reverse holds for the
and positive to the left of the minimum, and the reverse holds for the 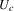 . Therefore, if
. Therefore, if 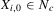 and
and 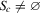 , then
, then 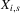 will converge monotonically toward
will converge monotonically toward 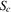 and then remain within
and then remain within 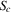 . If
. If 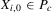 and
and 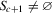 , then
, then 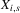 will converge monotonically toward
will converge monotonically toward 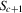 and then remain within
and then remain within 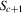 .
.
Assuming non-emptiness of these ranges, the interval 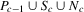 is a basin of attraction for
is a basin of attraction for 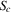 (i.e. X in this interval converges monotonically to
(i.e. X in this interval converges monotonically to 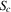 and then remains there). The main difference relative to the deterministic, time homogenous case is the blurring of the stable equilibrium to a stable set
and then remains there). The main difference relative to the deterministic, time homogenous case is the blurring of the stable equilibrium to a stable set 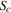 .
.
We did not make any assumptions on the joint distribution of the unobserved factors  . The whole argument of the preceding theorem is conditional on these factors. However, the predictions of the theorem will be sharper (given g) if serial dependence of unobserved factors is stronger, increasing the number of units i to which the assertion is applicable and reducing the size of the intervals
. The whole argument of the preceding theorem is conditional on these factors. However, the predictions of the theorem will be sharper (given g) if serial dependence of unobserved factors is stronger, increasing the number of units i to which the assertion is applicable and reducing the size of the intervals 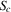 and
and 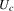 , because
, because 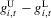 is going to be smaller on average.
is going to be smaller on average.
In summary, Proposition 3.1 implies that, if we do not find multiple roots in quantile regressions, then the conditional average structural functions 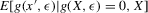 do not have multiple roots. Proposition 3.2 implies that, if upper and lower envelopes of
do not have multiple roots. Proposition 3.2 implies that, if upper and lower envelopes of 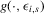 do not have multiple roots, then the dynamics of the system are stable and initial conditions do not matter in the long run.
do not have multiple roots, then the dynamics of the system are stable and initial conditions do not matter in the long run.
4. APPLICATION TO THE DYNAMICS OF NEIGHBOURHOOD COMPOSITION
This section analyses the dynamics of minority share in a neighbourhood, applying the methods developed in the last two sections to the data used for analysis of neighbourhood composition dynamics by Card et al. (2008). They study whether preferences over neighbourhood composition lead to a ‘white flight’, once the minority share in a neighbourhood exceeds a certain level. They argue that such ‘tipping’ behaviour implies discontinuities in the change of neighbourhood composition over time as a function of initial composition, and they test for the presence of such discontinuities in cross-sectional regressions over different neighbourhoods in a given city. This argument is based on the theoretical models of Becker and Murphy (2000), which do not allow for individual heterogeneity and consider infinite time horizons. The present paper argues that, if we allow for heterogeneity and finite time, and if tipping does take place, then we should expect multiple roots rather than discontinuities. Kasy (2015) discusses a search-matching model of the housing market with social externalites, which has this implication.
Card et al. (2008) provided full access to their datasets, which allows us to use identical samples and variable definitions as in their work. The dataset is an extract from the Neighbourhood Change Database (NCDB), which aggregates US census variables to the level of census tracts. Tract definitions are changing between census waves but the NCDB matches observations from the same geographic area over time, thus allowing observation of the development over several decades of the universe of US neighbourhoods. In the dataset used by Card et al. (2008), all rural tracts are dropped, as well as all tracts with population below 200 and tracts that grew by more than five standard deviations above the metropolitan statistical area (MSA) mean. The definition of MSA used is the MSAPMA from the NCDB, which is equal to a ‘primary metropolitan statistical area’ if the tract lies in one of those, and equal to the MSA it lies otherwise. For further details on sample selection and variable definition, see Card et al. (2008).
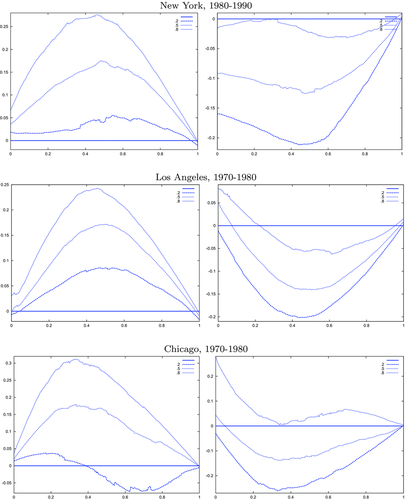
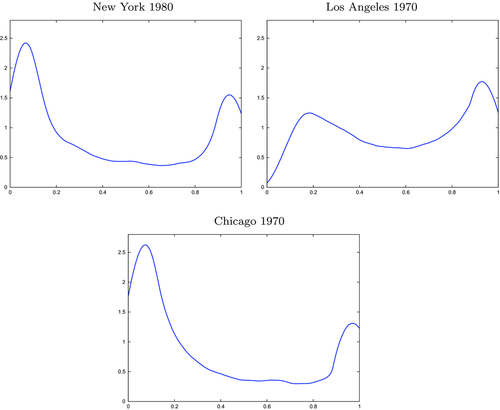
The graphs and tables to be discussed are constructed as follows. For each of the MSAs and each of the decades separately, we run local linear quantile regressions of the change in minority share of a neighbourhood (tract) on minority share at the beginning of the decade. This is done for the quantiles 0.2, 0.5 and 0.8, with a bandwidth τ of 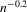 , where n is the sample size.12 Figure 6 shows local linear quantile regressions of the change in minority share (left column) and of the change in white population relative to initial population (right column) on initial minority share for the quantiles 0.2, 0.5 and 0.8. The figures do not show confidence bands. The figure plots these quantile regressions for the three largest MSAs. For each of the regressions,
, where n is the sample size.12 Figure 6 shows local linear quantile regressions of the change in minority share (left column) and of the change in white population relative to initial population (right column) on initial minority share for the quantiles 0.2, 0.5 and 0.8. The figures do not show confidence bands. The figure plots these quantile regressions for the three largest MSAs. For each of the regressions, 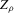 is calculated, where ρ is chosen as 0.04. The integral in the expression for
is calculated, where ρ is chosen as 0.04. The integral in the expression for 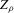 is taken over the interval [0, 1], intersected with the support of initial minority share if the latter is smaller. Note that it is possible to find no (stable) equilibrium for an MSA (i.e.
is taken over the interval [0, 1], intersected with the support of initial minority share if the latter is smaller. Note that it is possible to find no (stable) equilibrium for an MSA (i.e. 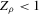 ), if high initial minority shares do not occur in that MSA and most neighbourhoods experienced growing minority shares. Figure 7 shows kernel density plots of the regressor, the initial minority share across neighbourhoods, which suggest that support problems are not an issue, at least for the largest MSAs. For each
), if high initial minority shares do not occur in that MSA and most neighbourhoods experienced growing minority shares. Figure 7 shows kernel density plots of the regressor, the initial minority share across neighbourhoods, which suggest that support problems are not an issue, at least for the largest MSAs. For each 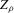 , bootstrap standard errors and bias are calculated, as well as the corresponding t-test statistics for the null hypothesis
, bootstrap standard errors and bias are calculated, as well as the corresponding t-test statistics for the null hypothesis 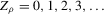 , implying an integer-valued confidence set (of level 0.05) for z. By the results of Section 2., these confidence sets have an asymptotic coverage probability of 95%. By the Monte Carlo evidence of Appendix A, they are likely to be conservative (i.e. have a larger coverage probability). If the confidence sets thus obtained are empty, the two neighbouring integers of
, implying an integer-valued confidence set (of level 0.05) for z. By the results of Section 2., these confidence sets have an asymptotic coverage probability of 95%. By the Monte Carlo evidence of Appendix A, they are likely to be conservative (i.e. have a larger coverage probability). If the confidence sets thus obtained are empty, the two neighbouring integers of 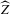 are included in the intervals shown. This makes inference even more conservative. Table 1 shows the resulting confidence sets for the 12 largest MSAs in the United States (by 2009 population), for all quantiles and decades under consideration.13
are included in the intervals shown. This makes inference even more conservative. Table 1 shows the resulting confidence sets for the 12 largest MSAs in the United States (by 2009 population), for all quantiles and decades under consideration.13
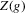 by decade and quantile, change in minority share
by decade and quantile, change in minority share| 1970s | 1980s | 1990s | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSA | 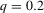 |
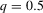 |
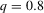 |
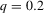 |
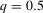 |
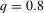 |
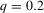 |
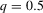 |
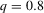 |
| New York, NY PMSA | [0,1] | [0,1] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] |
| Los Angeles-Long Beach, CA PMSA | [1,1] | [1,1] | [0,1] | [0,1] | [0,1] | [0,1] | [1,1] | [1,1] | [0,0] |
| Chicago, IL PMSA | [0,1] | [0,1] | [0,1] | [2,2] | [0,1] | [0,1] | [1,1] | [0,1] | [0,0] |
| Dallas, TX PMSA | [1,2] | [1,1] | [0,0] | [0,1] | [0,0] | [0,0] | [0,1] | [0,1] | [0,0] |
| Philadelphia, PA-NJ PMSA | [1,2] | [0,1] | [0,1] | [1,1] | [0,1] | [0,1] | [1,1] | [0,1] | [0,0] |
| Houston, TX PMSA | [1,1] | [0,0] | [0,0] | [1,2] | [0,1] | [0,0] | [0,1] | [0,0] | [0,0] |
| Miami, FL PMSA | [0,1] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] |
| Washington, DC-MD-VA-WV PMSA | [0,1] | [0,0] | [0,0] | [1,1] | [0,1] | [0,0] | [1,1] | [0,1] | [0,0] |
| Atlanta, GA MSA | [1,1] | [1,1] | [0,0] | [2,3] | [0,0] | [0,0] | [0,0] | [0,0] | [0,0] |
| Boston, MA-NH PMSA | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,0] | [1,1] | [0,0] | [0,1] |
| Detroit, MI PMSA | [1,2] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,0] |
| Phoenix-Mesa, AZ MSA | [1,1] | [0,0] | [0,0] | [1,1] | [0,1] | [0,0] | [1,1] | [0,1] | [0,0] |
| San Francisco, CA PMSA | [1,1] | [0,1] | [0,1] | [0,0] | [0,1] | [0,0] | [1,1] | [0,0] | [0,0] |
Note
- The table shows confidence intervals in the integers for
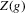 for the 12 largest MSAs of the United States, ordered by population, where g is estimated by quantile regression of the change in minority share over a decade on the initial minority share for the quantiles 0.2, 0.5 and 0.8. Regression bandwidth
for the 12 largest MSAs of the United States, ordered by population, where g is estimated by quantile regression of the change in minority share over a decade on the initial minority share for the quantiles 0.2, 0.5 and 0.8. Regression bandwidth 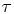 is
is 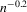 , and σ is chosen as 0.04. Confidence sets are based on t-statistics using bootstrapped bias and standard errors.
, and σ is chosen as 0.04. Confidence sets are based on t-statistics using bootstrapped bias and standard errors.
As can be seen from the table, in very few cases there is evidence of Z exceeding 1. In all cases shown, except for the 0.2 quantile for Atlanta in the 1980s, we can reject the null 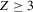 . Similar patterns hold for almost all of the 118 cities in the dataset. Rather than exhibiting multiple equilibria, the data indicate a general rise in minority share that is largest for neighbourhoods with intermediate initial share, but not to the extent of leading to tipping behaviour. Proposition 3.1 suggests that, if we do not find multiple roots in quantile regressions, we can reject multiple equilibria in the underlying structural relationship. I take these results as indicative that tipping is not a widespread phenomenon in US ethnic neighbourhood composition over the decades under consideration. This stands in contrast to the conclusion of Card et al. (2008), who do find evidence of tipping.
. Similar patterns hold for almost all of the 118 cities in the dataset. Rather than exhibiting multiple equilibria, the data indicate a general rise in minority share that is largest for neighbourhoods with intermediate initial share, but not to the extent of leading to tipping behaviour. Proposition 3.1 suggests that, if we do not find multiple roots in quantile regressions, we can reject multiple equilibria in the underlying structural relationship. I take these results as indicative that tipping is not a widespread phenomenon in US ethnic neighbourhood composition over the decades under consideration. This stands in contrast to the conclusion of Card et al. (2008), who do find evidence of tipping.
The approach used here differs from the main analysis in Card et al. (2008) in a number of ways. Card et al. (2008) (a) use polynomial least-squares regression with a discontinuity. They (b) use a split sample method to test for the presence of a discontinuity, and they (c) regress the change in the non-Hispanic, white population, divided by initial neighbourhood population, on initial minority share. We (a) use local linear quantile regression without a discontinuity, we (b) run the regressions on full samples for each MSA and test for the number of roots, and we (c) regress the change in minority share on initial minority share.
To check whether the differing results are due to variable choice (c) rather than testing procedure, the left column of Figure 6 and Table 1 are replicated using the change in the non-Hispanic, white population relative to initial population as the dependent variable, as did Card et al. (2008). The right column of Figure 6 shows such quantile regressions. These figures correspond to the ones in Card et al. (2008, p. 190), using the same variables but a different regression method and the full samples. Table 2 shows confidence sets for the number of roots of these regressions for the 12 largest MSAs. In comparing Tables 1 and 2, note that there is a correspondence between the lower quantiles of the first (low increase in minority share) and the upper quantiles of the latter (higher increase/lower decrease of white population). The two tables show fairly similar results. Again, no systematic evidence of multiple roots is found.
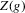 by decade and quantile, change in white population
by decade and quantile, change in white population| 1970s | 1980s | 1990s | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSA | 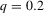 |
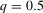 |
 |
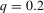 |
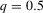 |
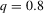 |
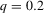 |
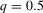 |
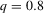 |
| New York, NY PMSA | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] |
| Los Angeles-Long Beach, CA PMSA | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] |
| Chicago, IL PMSA | [0,1] | [0,1] | [0,1] | [0,0] | [0,1] | [1,1] | [0,1] | [0,1] | [0,1] |
| Dallas, TX PMSA | [0,1] | [0,1] | [0,1] | [0,0] | [1,1] | [0,2] | [0,1] | [1,1] | [0,1] |
| Philadelphia, PA-NJ PMSA | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [0,1] | [1,1] |
| Houston, TX PMSA | [0,1] | [0,1] | [0,1] | [1,1] | [1,1] | [1,1] | [0,1] | [0,1] | [0,1] |
| Miami, FL PMSA | [0,1] | [0,1] | [0,1] | [0,0] | [0,0] | [1,1] | [1,1] | [1,1] | [1,1] |
| Washington, DC-MD-VA-WV PMSA | [0,1] | [0,0] | [0,1] | [0,0] | [1,1] | [0,0] | [0,1] | [0,1] | [0,1] |
| Atlanta, GA MSA | [0,1] | [1,1] | [0,1] | [1,1] | [1,1] | [1,1] | [1,1] | [1,2] | [0,1] |
| Boston, MA-NH PMSA | [0,1] | [0,1] | [0,1] | [0,0] | [0,0] | [1,1] | [0,0] | [0,1] | [0,1] |
| Detroit, MI PMSA | [0,1] | [0,1] | [0,1] | [0,0] | [0,0] | [1,1] | [0,1] | [0,1] | [0,1] |
| Phoenix-Mesa, AZ MSA | [0,1] | [0,1] | [0,1] | [0,0] | [1,1] | [0,0] | [0,1] | [0,1] | [0,1] |
| San Francisco, CA PMSA | [0,1] | [0,1] | [0,1] | [0,0] | [0,0] | [0,0] | [0,0] | [1,1] | [0,0] |
Note
- The table shows confidence intervals in the integers for
 for the 12 largest MSAs of the United States, ordered by population, where g is estimated by quantile regression of the change in the non-Hispanic, white population over a decade, divided by initial total population, on the initial minority share for the quantiles 0.2, 0.5 and 0.8. Regression bandwidth
for the 12 largest MSAs of the United States, ordered by population, where g is estimated by quantile regression of the change in the non-Hispanic, white population over a decade, divided by initial total population, on the initial minority share for the quantiles 0.2, 0.5 and 0.8. Regression bandwidth 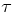 is
is 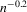 , and σ is chosen as 0.05 times the maximal change. Confidence sets are based on t-statistics using bootstrapped bias and standard errors.
, and σ is chosen as 0.05 times the maximal change. Confidence sets are based on t-statistics using bootstrapped bias and standard errors.
Some factors might lead to a bias in the estimated number of equilibria, using the methods developed here. First, the test might be sensitive to the chosen range of integration if there are roots near the boundary. If a root lies right on the boundary of the chosen range of integration, it enters 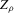 as 1/2 only. Extending the range of integration beyond the unit interval, however, might also lead to an upward bias in the estimated number of roots, if extrapolated regression functions intersect with the horizontal axis. Second, choosing a bandwidth parameter ρ that is too large might bias the estimated number of equilibria downwards, if the function g peaks within the range
as 1/2 only. Extending the range of integration beyond the unit interval, however, might also lead to an upward bias in the estimated number of roots, if extrapolated regression functions intersect with the horizontal axis. Second, choosing a bandwidth parameter ρ that is too large might bias the estimated number of equilibria downwards, if the function g peaks within the range 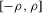 . Third, there might be roots of g in the unit interval but beyond the support of the data.
. Third, there might be roots of g in the unit interval but beyond the support of the data.
5. SUMMARY AND CONCLUSION
This paper proposes an inference procedure for the number of roots of functions non-parametrically identified using conditional moment restrictions, and develops the corresponding asymptotic theory. In particular, it is shown that a smoothed plug-in estimator of the number of roots is superconsistent under i.i.d. asymptotics, but asymptotically normal under non-standard asymptotics, and asymptotically efficient relative to a simple plug-in estimator. In Section 3., these results are extended to cover various more general cases, allowing for covariates as controls, higher-dimensional domain and range, and for inference on the number of equilibria with various stability properties. This section also discusses how to apply the results to static games of incomplete information and to stochastic difference equations. In an application of the methods developed here to data on neighbourhood composition dynamics in the United States, no evidence of multiple of equilibria is found.
The inference procedure can also be used to test for bifurcations (i.e. (dis)appearing equilibria as a function of changing exogenous covariates). It is easy to test the hypothesis 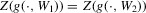 , because the corresponding estimators
, because the corresponding estimators 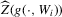 are independent for W1 and W2 further apart than twice the bandwidth τ. If there are bifurcations, small exogenous shifts might have a large (discontinuous) effect on the equilibrium attained, if the ‘old’ equilibrium disappears.
are independent for W1 and W2 further apart than twice the bandwidth τ. If there are bifurcations, small exogenous shifts might have a large (discontinuous) effect on the equilibrium attained, if the ‘old’ equilibrium disappears.
In the dynamic set-up, one might furthermore consider to apply the procedure to detrended data (e.g. by demeaning  ). It seems likely that regressions of detrended data have a higher number of roots. The rationale of such an approach could be found in underlying models in which the dynamics of a detrended variable are stationary. This is, in particular, the case in Solow-type growth models, in which GDP or capital stock is stationary after normalizing by a technological growth factor.
). It seems likely that regressions of detrended data have a higher number of roots. The rationale of such an approach could be found in underlying models in which the dynamics of a detrended variable are stationary. This is, in particular, the case in Solow-type growth models, in which GDP or capital stock is stationary after normalizing by a technological growth factor.
Finally, it might also be interesting to extend the results obtained here to cover further cases where g cannot be directly estimated using conditional moment restrictions. The crucial step for such extensions, as illustrated by the various cases discussed in Section 3., is to find a sequence of experiments such that the first-stage estimator 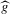 converges in probability to a degenerate limit whereas
converges in probability to a degenerate limit whereas 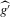 converges in distribution to a non-degenerate limit. Furthermore,
converges in distribution to a non-degenerate limit. Furthermore, 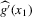 needs to be asymptotically independent of
needs to be asymptotically independent of 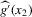 for all
for all 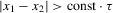 . There are many potential applications of the results obtained here, where it might be interesting to know whether the underlying dynamics or strategic interactions imply multiple equilibria. Examples include household level poverty traps, intergenerational mobility, efficiency wages, macro models of economic growth (as analysed in the online Appendix), financial market bubbles (herding), market entry and social norms.
. There are many potential applications of the results obtained here, where it might be interesting to know whether the underlying dynamics or strategic interactions imply multiple equilibria. Examples include household level poverty traps, intergenerational mobility, efficiency wages, macro models of economic growth (as analysed in the online Appendix), financial market bubbles (herding), market entry and social norms.
ACKNOWLEDGEMENTS
I thank seminar participants at UC Berkeley, UCLA, USC, Brown, NYU, UPenn, LSE, UCL, Sciences Po, TSE, Mannheim and IHS Vienna for their helpful comments and suggestions. I particularly thank Tim Armstrong, David Card, Kiril Datchev, Victor Chernozhukov, Jinyong Hahn, Michael Jansson, Bryan Graham, Susanne Kimm, Patrick Kline, Rosa Matzkin, Enrico Moretti, Denis Nekipelov, James Powell, Alexander Rothenberg, Jesse Rothstein, James Stock and Mark van der Laan for many valuable discussions, and David Card, Alexander Mas and Jesse Rothstein for the access provided to their data. This work was supported by a DOC fellowship from the Austrian Academy of Sciences at the Department of Economics, UC Berkeley.
Appendix A: MONTE CARLO EVIDENCE
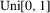 random variables, and the additive errors γ are either uniformly or normally distributed,
random variables, and the additive errors γ are either uniformly or normally distributed,
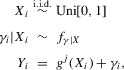 (A.1)
(A.1)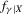 is an appropriately centred and scaled uniform or normal distribution. Two functions
is an appropriately centred and scaled uniform or normal distribution. Two functions 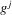 are considered, the first with one root and the second with three roots:
are considered, the first with one root and the second with three roots:
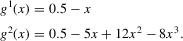
The function g is estimated by median regression, mean regression and 0.9 quantile regression, where the γ in the simulations are shifted appropriately to have median, mean or 0.9 quantile at the respective g. Figures A.1–A.3 and Table A.1 show sequences of four experiments with 400, 800, 1,600 and 3,200 observations. These models are chosen to be comparable to the empirical application discussed in Section 4.. The variance of γ in each experiment is chosen to yield the same variance for 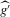 , as implied by the asymptotic approximation of the Bahadur expansion, in all experiments for a given g. By the proof of Theorem 2.2, we should therefore obtain similar simulation results across all set-ups. Furthermore, the variance of
, as implied by the asymptotic approximation of the Bahadur expansion, in all experiments for a given g. By the proof of Theorem 2.2, we should therefore obtain similar simulation results across all set-ups. Furthermore, the variance of 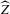 should be constant up to a factor
should be constant up to a factor 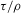 . The parameters of these simulations are chosen to lie in an intermediate range where variation in
. The parameters of these simulations are chosen to lie in an intermediate range where variation in 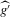 is existent but moderate.
is existent but moderate.
Figure A.1 shows density plots for 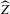 from the sequences of Monte Carlo experiments with uniform errors and g identified by median regression, as described in this appendix; in the online Appendix, similar figures are presented for the other experiments. The upper graph shows the distribution from four experiments with increasing sample size n and correspondingly growing variance of the residual γ, where the true parameter Z equals one. The same holds for the lower graph, except that
from the sequences of Monte Carlo experiments with uniform errors and g identified by median regression, as described in this appendix; in the online Appendix, similar figures are presented for the other experiments. The upper graph shows the distribution from four experiments with increasing sample size n and correspondingly growing variance of the residual γ, where the true parameter Z equals one. The same holds for the lower graph, except that  . As predicted by Theorem 2.2, biases are positive, and both bias and variance are decreasing in n. Figure A.2 shows the distribution of the naive plug-in estimator
. As predicted by Theorem 2.2, biases are positive, and both bias and variance are decreasing in n. Figure A.2 shows the distribution of the naive plug-in estimator 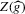 , from the same simulations as in Figure A.1. It was shown in Section 2. that this estimator is asymptotically inefficient relative to the smoothed plug-in estimator. This relative inefficiency is reflected in a larger dispersion in the simulations, as can be seen by comparing Figures A.1 and A.2. Figure A.3 shows density plots for
, from the same simulations as in Figure A.1. It was shown in Section 2. that this estimator is asymptotically inefficient relative to the smoothed plug-in estimator. This relative inefficiency is reflected in a larger dispersion in the simulations, as can be seen by comparing Figures A.1 and A.2. Figure A.3 shows density plots for 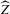 , normalized by its sample mean and standard deviation, from the same simulations as in Figure A.1. It also shows, as a reference, the density of a standard normal. These plots suggest that the sample distribution of
, normalized by its sample mean and standard deviation, from the same simulations as in Figure A.1. It also shows, as a reference, the density of a standard normal. These plots suggest that the sample distribution of 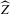 is somewhat right-skewed relative to a normal distribution.
is somewhat right-skewed relative to a normal distribution.
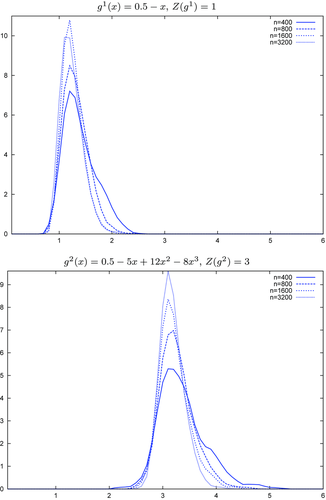
 in Monte Carlo experiments.
in Monte Carlo experiments.
 in Monte Carlo experiments.
in Monte Carlo experiments.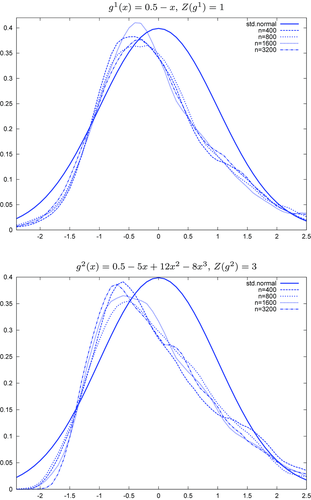
 in Monte Carlo experiments.
in Monte Carlo experiments.Table 3 shows the results of simulations using bootstrapped standard deviations and biases, for mean regression with uniform errors. The results show, for the range of experiments considered, that rejection frequencies are lower than the 0.05 value implied by asymptotic theory. If this pattern generalizes, inference based upon the t-statistic proposed in this paper is conservative in finite samples. In particular, it seems that bootstrapped standard errors are too large.
| n | τ | r | 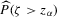 |
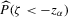 |
|---|---|---|---|---|
| 400 | 0.065 | 0.179 | 0.05 | 0.01 |
| 800 | 0.059 | 0.194 | 0.03 | 0.02 |
| 1,600 | 0.055 | 0.231 | 0.02 | 0.01 |
| 3,200 | 0.052 | 0.290 | 0.02 | 0.01 |
| 400 | 0.065 | 0.268 | 0.03 | 0.02 |
| 800 | 0.059 | 0.292 | 0.01 | 0.02 |
| 1,600 | 0.055 | 0.347 | 0.01 | 0.01 |
| 3,200 | 0.052 | 0.434 | 0.01 | 0.02 |
Note
- This table shows the frequency of rejection of the null under a test of asymptotic level 5%, for the sequences of Monte Carlo experiments described in Appendix A. The g are estimated by mean regression, the errors are uniformly distributed, and the first four experiments are generated using g1 with one root, the next four using g2 with three roots. The columns show sample size, regression bandwidth, error standard deviation and the rejection probabilities of one-sided tests, respectively.
Appendix B: PROOFS
Proof of Proposition 2.1.By continuity of 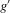 as well as genericity of g, we can choose ρ small enough such that
as well as genericity of g, we can choose ρ small enough such that 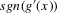 is constantly equal to
is constantly equal to 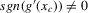 in each of the neighbourhoods of the
in each of the neighbourhoods of the 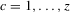 roots of g,
roots of g, 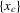 , defined by
, defined by 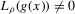 . Hence, we can write the integral
. Hence, we can write the integral 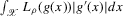 as a sum of integrals over these neighbourhoods, in each of which there is exactly one root. Assume w.l.o.g. that
as a sum of integrals over these neighbourhoods, in each of which there is exactly one root. Assume w.l.o.g. that 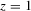 and
and 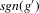 is constant in the range of x where
is constant in the range of x where 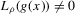 . Then, by a change of variables setting
. Then, by a change of variables setting 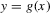 ,
,
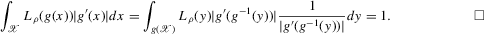
Proof of Proposition 2.2.We need to find ε such that 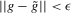 implies
implies  . By genericity of g, each root
. By genericity of g, each root  of g is such that
of g is such that 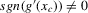 . By continuous first derivatives, we can then find δ such that
. By continuous first derivatives, we can then find δ such that 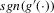 is constant in the neighbourhood
is constant in the neighbourhood 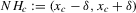 of each of the finitely many roots
of each of the finitely many roots 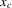 and the
and the 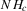 are mutually disjoint. By continuity of g,
are mutually disjoint. By continuity of g,
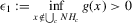 (B.1)
(B.1)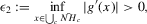 (B.2)
(B.2)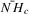 is the closure of
is the closure of 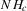 . Choosing
. Choosing 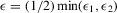 fulfils our purpose. To see this, choose
fulfils our purpose. To see this, choose 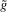 such that
such that 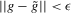 . For
. For 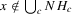 ,
, 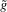 is bounded away from zero by B.1. In
is bounded away from zero by B.1. In 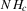 , there must be exactly one x such that
, there must be exactly one x such that 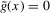 : Because
: Because 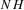 are mutually disjoint,
are mutually disjoint, 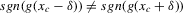 , by B.1 again
, by B.1 again 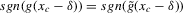 and
and 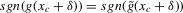 , and finally the sign of
, and finally the sign of 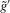 is constantly equal to
is constantly equal to 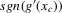 in
in 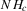 by B.2.
by B.2.The assertion for 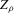 follows now from the first part of this proof, combined with Proposition 2.1, if we can choose ρ independent of
follows now from the first part of this proof, combined with Proposition 2.1, if we can choose ρ independent of 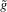 such that Proposition 2.1 applies. Sufficient for this is ρ that separates roots. Choosing
such that Proposition 2.1 applies. Sufficient for this is ρ that separates roots. Choosing  accomplishes this. By B.1,
accomplishes this. By B.1,  will separate the
will separate the 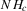 , and by the previous argument each of the
, and by the previous argument each of the  will contain exactly one root of
will contain exactly one root of 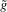 .
.
Proof of Theorem 2.2.We use 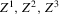 to denote a sequence of approximations to
to denote a sequence of approximations to 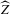 . Write
. Write 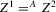 , if
, if 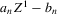 and
and 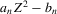 have the same non-degenerate distributional limit for some non-random sequences
have the same non-degenerate distributional limit for some non-random sequences 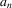 and
and 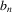 . In particular, as long as such sequences exist that guarantee convergence to a non-degenerate limit, this is implied by equality up to a remainder, which is asymptotically negligible under the given sequence of experiments (i.e.
. In particular, as long as such sequences exist that guarantee convergence to a non-degenerate limit, this is implied by equality up to a remainder, which is asymptotically negligible under the given sequence of experiments (i.e. 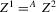 if
if 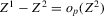 ).
).
1. Approximation of 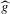 with g
with g
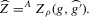
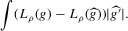
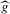 at a rate faster than ρ under our sequence of experiments. Under the given sequence of experiments, the variance of
at a rate faster than ρ under our sequence of experiments. Under the given sequence of experiments, the variance of 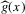 is of order
is of order 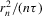 – this follows from the Bahadur expansion. Because we have assumed
– this follows from the Bahadur expansion. Because we have assumed 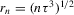 , we obtain
, we obtain 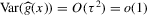 , which implies pointwise convergence. Pointwise convergence at rate τ implies uniform convergence at the slightly slower rate
, which implies pointwise convergence. Pointwise convergence at rate τ implies uniform convergence at the slightly slower rate 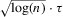 , which is faster than ρ by our assumptions on τ and ρ; for background on uniform convergence of kernel estimators, see, e.g. Appendix A.1 of Armstrong (2014).
, which is faster than ρ by our assumptions on τ and ρ; for background on uniform convergence of kernel estimators, see, e.g. Appendix A.1 of Armstrong (2014).The fact that 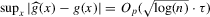 implies that the remainder
implies that the remainder 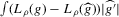 is of the same order. To see this, note that
is of the same order. To see this, note that 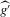 is
is 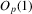 , so that the remainder is of the same order as
, so that the remainder is of the same order as 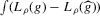 . The integrand of this expression is non-zero only in a neighbourhood of size of order ρ of the roots of g; the difference
. The integrand of this expression is non-zero only in a neighbourhood of size of order ρ of the roots of g; the difference 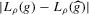 is of order
is of order 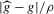 because
because 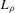 is Lipschitz with constant
is Lipschitz with constant 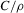 , so that the claim follows.
, so that the claim follows.
Thus, we have shown that the remainder 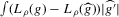 is of order
is of order 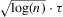 ; this is smaller than the order of the leading term of
; this is smaller than the order of the leading term of 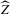 , which we show to be
, which we show to be 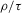 . The remainder is thus asymptotically negligible.
. The remainder is thus asymptotically negligible.
From the approximation 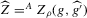 we immediately obtain
we immediately obtain 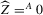 if
if 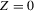 , because in that case
, because in that case 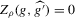 for ρ small enough. The claim of Theorem 2.2 is thus trivially satisfied for the case
for ρ small enough. The claim of Theorem 2.2 is thus trivially satisfied for the case 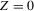 , and we assume
, and we assume 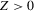 for the rest of this proof.
for the rest of this proof.
2. Approximation of 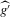 by the Bahadur expansion.
by the Bahadur expansion.
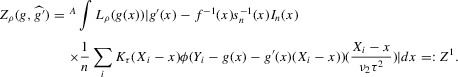
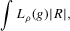
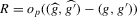 uniformly in x).
uniformly in x).3. Restriction to one root at 0 and Taylor approximations
Assume that 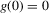 and
and 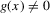 for
for 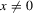 (i.e.
(i.e.  ). This is without loss of generality, because the integral for the general case is simply a sum of the independent integrals in a neighbourhood of each root.
). This is without loss of generality, because the integral for the general case is simply a sum of the independent integrals in a neighbourhood of each root.
Now define 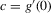 ,
, 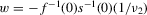 ,
, 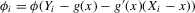 and
and 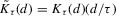 .
.
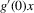 in
in 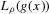 and replacing
and replacing 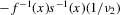 with w, both justified by smoothness and
with w, both justified by smoothness and 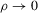 , as well as
, as well as 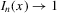 uniformly, we obtain
uniformly, we obtain
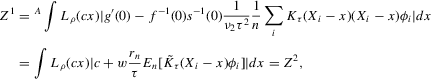
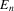 to denote the sample average. The absolute value of the remainder of this approximation is less than or equal to
to denote the sample average. The absolute value of the remainder of this approximation is less than or equal to
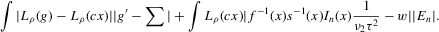
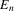 as shorthand for the sum and sample average of the previous display. Both terms in this expression go to 0 as
as shorthand for the sum and sample average of the previous display. Both terms in this expression go to 0 as 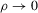 . We can assume furthermore that
. We can assume furthermore that
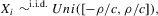
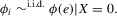
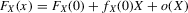 and
and 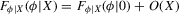 , assuming both distribution functions to be differentiable at 0. To see that this approximation is justified, note that distributional convergence to the same limit is equivalent to convergence of the expectations of any Lipschitz continuous bounded function of the statistics to the same limit. The difference in expectations between a function h of Z2 and of its approximation using conditionally uniform X and i.i.d. ϕ is given by
, assuming both distribution functions to be differentiable at 0. To see that this approximation is justified, note that distributional convergence to the same limit is equivalent to convergence of the expectations of any Lipschitz continuous bounded function of the statistics to the same limit. The difference in expectations between a function h of Z2 and of its approximation using conditionally uniform X and i.i.d. ϕ is given by
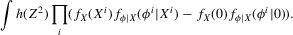
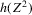 in X is a neighbourhood of 0 shrinking to 0.
in X is a neighbourhood of 0 shrinking to 0.4. Partitioning the range of integration
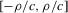 into subintervals
into subintervals 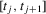 ,
,  with
with 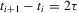 . Then
. Then
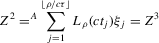
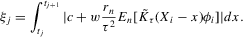
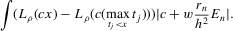
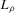 with a Lipschitz constant of order
with a Lipschitz constant of order 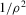 , and by
, and by  .
.5. Poisson approximation
The following argument essentially replaces the number of X falling into the interval 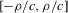 , which is approximately distributed
, which is approximately distributed 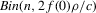 , with a Poisson random variable with parameter
, with a Poisson random variable with parameter 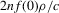 ; the distribution of everything else conditional on this number remains the same.
; the distribution of everything else conditional on this number remains the same.
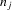 be distributed i.i.d.
be distributed i.i.d. 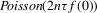 for
for  . This is an approximation to the number of X falling into the bin
. This is an approximation to the number of X falling into the bin 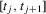 . Draw
. Draw 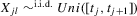 and
and 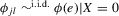 for
for  and
and  . Now define
. Now define
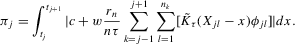
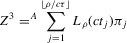
 are identically distributed and
are identically distributed and  is independent of
is independent of 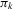 for
for 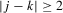 .
.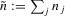 , the equality is exact. The exact distribution of the number of observations falling in the interval
, the equality is exact. The exact distribution of the number of observations falling in the interval 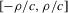 , corresponding to
, corresponding to  , would be given by
, would be given by
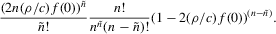
 . This is justified by the usual arguments deriving the Poisson distribution as a limit of Binomial distributions. The approximation of Z3 follows by an argument similar to the second part of step 3 in this proof, once we note that the multinomial probability mass function converges uniformly.
. This is justified by the usual arguments deriving the Poisson distribution as a limit of Binomial distributions. The approximation of Z3 follows by an argument similar to the second part of step 3 in this proof, once we note that the multinomial probability mass function converges uniformly.6. Moments of the integrals over the subintervals
- (a)
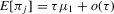 .
. - (b)
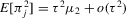 .
. - (c)
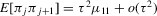 .
. - (d)
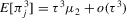 .
.
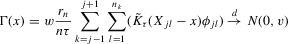
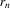 matters:
matters:
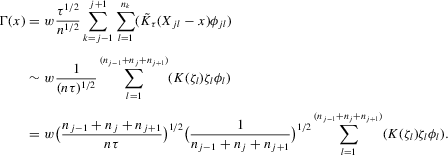
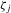 are i.i.d.
are i.i.d.  . Now asymptotic normality follows by noting
. Now asymptotic normality follows by noting
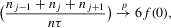
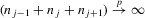 and
and 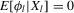 . Similarly
. Similarly
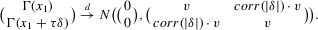
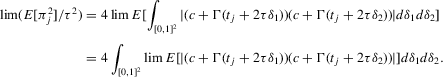
7. Central limit theorem applied to the sum of integrals over the subintervals
 is an m-dependent sequence with
is an m-dependent sequence with  . We have
. We have
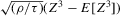 follows, and by
follows, and by 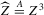 , the same holds for
, the same holds for  . Furthermore,
. Furthermore, 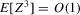 , and hence so is
, and hence so is 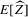 .
.
Proof of Theorem 2.3.Fix one of the roots x0 of g. By the arguments of the proof of Theorem 2.2, 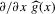 (not to be confused with
(not to be confused with 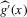 ) converges to a non-degenerate normal distribution for all x. In particular,
) converges to a non-degenerate normal distribution for all x. In particular,
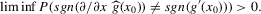
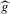 and the intermediate value theorem (compare also Figure 2),
and the intermediate value theorem (compare also Figure 2),
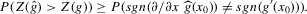
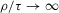 .
.
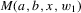 by a criterion function that has the form of 2.3 (i.e. a local weighted average over the empirical distribution of some objective function). Based on this approximation, we can then again apply the results of Kong et al. (2010). Newey (1994) provides a set of results that facilitate such approximations of partial means. In particular, Lemma 5.4 in Newey (1994) allows derivation of the required approximation by replacing the outer sum over j in 3.2 with an expectation, and by linearizing the fraction inside. The first replacement is asymptotically warranted because the variation created by averaging over the empirical distribution is of order
by a criterion function that has the form of 2.3 (i.e. a local weighted average over the empirical distribution of some objective function). Based on this approximation, we can then again apply the results of Kong et al. (2010). Newey (1994) provides a set of results that facilitate such approximations of partial means. In particular, Lemma 5.4 in Newey (1994) allows derivation of the required approximation by replacing the outer sum over j in 3.2 with an expectation, and by linearizing the fraction inside. The first replacement is asymptotically warranted because the variation created by averaging over the empirical distribution is of order 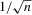 and is hence dominated by the variation in the non-parametric component. The second replacement follows from differentiability and requires, in particular, that the denominator of the fraction be asymptotically bounded away from zero. This is guaranteed by the requirement that W2 has full conditional support given
and is hence dominated by the variation in the non-parametric component. The second replacement follows from differentiability and requires, in particular, that the denominator of the fraction be asymptotically bounded away from zero. This is guaranteed by the requirement that W2 has full conditional support given 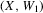 . Formally, Lemma 5.4 in Newey (1994) gives
. Formally, Lemma 5.4 in Newey (1994) gives
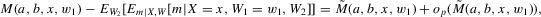
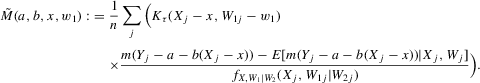 (B.3)
(B.3)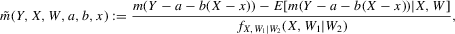 (B.4)
(B.4)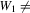 const, the rates have to be adapted as follows. The number of observations within each rectangle of size
const, the rates have to be adapted as follows. The number of observations within each rectangle of size 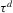 goes to ∞ if
goes to ∞ if 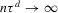 . Finally, the variance of
. Finally, the variance of 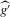 converges iff
converges iff 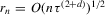 .
.
Proof of Theorem 3.2.The proof requires the following modifications relative to the one-dimensional case. Assumption 2.2 is still applicable, where the only difference in the d-dimensional case is that 2.6 has to be multiplied by 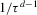 . For
. For 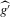 to have a pointwise non-degenerate distributional limit, we have to choose the rate
to have a pointwise non-degenerate distributional limit, we have to choose the rate 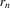 to equal
to equal 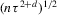 , which is slower for higher d. To see this, note that Var
, which is slower for higher d. To see this, note that Var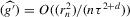 . Here,
. Here,  is Lipschitz continuous of order
is Lipschitz continuous of order  , so that we require
, so that we require 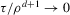 for step 4 of the proof of Theorem 2.2. The range of integration has to be partitioned into rectangular subranges of area
for step 4 of the proof of Theorem 2.2. The range of integration has to be partitioned into rectangular subranges of area 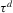 instead of intervals of length τ. There will be approximately const
instead of intervals of length τ. There will be approximately const 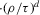 such subintegrals. The variance of the integral of
such subintegrals. The variance of the integral of 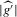 over each of these subranges will be of order
over each of these subranges will be of order 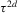 , similarly for expectations and covariances. This yields a variance of
, similarly for expectations and covariances. This yields a variance of 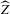 of
of 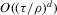 ; see step 7 of the proof of Theorem 2.2.
; see step 7 of the proof of Theorem 2.2.
Proof of Theorem 3.3.By 3.14 and 3.16, it is sufficient to show that 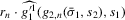 and
and 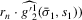 converge jointly in distribution, while
converge jointly in distribution, while 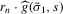 , as well as
, as well as 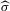 , converge in probability. These claims follow as before if we combine the convergence of
, converge in probability. These claims follow as before if we combine the convergence of 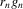 from display 3.22 with Bahadur expansion 2.6 for
from display 3.22 with Bahadur expansion 2.6 for 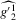 and
and 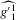 , where the latter are evaluated at
, where the latter are evaluated at 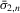 , which is not constant but converges.
, which is not constant but converges.
Proof of Lemma 3.1.By definition of conditional quantiles, 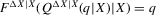 . Differentiating this with respect to X gives
. Differentiating this with respect to X gives
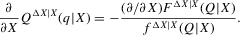 (B.5)
(B.5)The differential in the numerator has two components, one due to the structural relation between 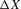 and X (i.e. the derivative with respect to the argument X of
and X (i.e. the derivative with respect to the argument X of 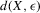 ), and one due to the stochastic dependence of X and ε:
), and one due to the stochastic dependence of X and ε:

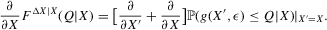
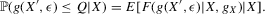
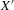 gives
gives
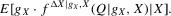

Proof of Proposition 3.1.Because X and  have their support in the interval [0, 1],
have their support in the interval [0, 1], 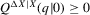 and
and 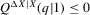 . Therefore, the unique root X of
. Therefore, the unique root X of 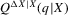 must be stable,
must be stable, 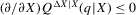 . By Lemma 3.1 and Assumption 3.3, this implies that
. By Lemma 3.1 and Assumption 3.3, this implies that 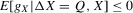 .
.
Finally, note that for all X where (0, X) is in the support of 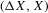 , there exists a q such that
, there exists a q such that 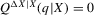 .
.
Proof of Proposition 3.2.The claims are immediate, noting that 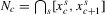 and similarly for
and similarly for 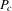 . Furthermore,
. Furthermore, 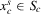 for all s,
for all s, 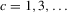 and
and 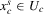 for all s,
for all s, 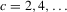 . Next,
. Next, 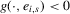 on
on  ,
,  from which negativity on
from which negativity on  follows, similarly for
follows, similarly for 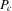 .
.
Finally, under monotonicity of potential outcomes, assuming for simplicity differentiability of g,

The numerator is always positive by assumption, the denominator is negative for 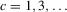 and positive for
and positive for 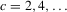 because we had assumed g positive for sufficiently small x. Hence,
because we had assumed g positive for sufficiently small x. Hence, 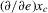 is positive for
is positive for 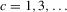 and negative for
and negative for 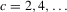 .
.
REFERENCES
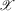 . Then, the set of x such that
. Then, the set of x such that 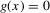 has an accumulation point in
has an accumulation point in 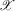 . At this accumulation point, genericity is violated.
. At this accumulation point, genericity is violated.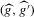 to
to 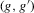 . Note that this is a slightly different condition from convergence of
. Note that this is a slightly different condition from convergence of 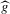 w.r.t. the norm
w.r.t. the norm 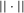 because
because 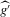 need not equal
need not equal 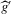 .
.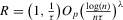 uniformly in X, for some
uniformly in X, for some 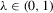 as
as 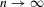 for stationary mixing processes.
for stationary mixing processes.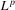 norm) of kernel density estimators.
norm) of kernel density estimators.


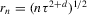 , where
, where 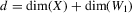 ,
, 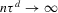 ,
, 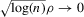 and
and 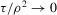 , then there exist
, then there exist  and V such that
and V such that
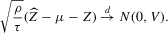
 and
and  defined by
defined by 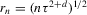 ,
, 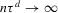 ,
, 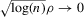 and
and 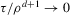 , then there exist
, then there exist 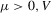 such that
such that
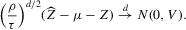
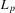 -norms of multivariate density estimators
-norms of multivariate density estimators
