Robust hypothesis tests for M-estimators with possibly non-differentiable estimating functions
Summary
We propose a new robust hypothesis test for (possibly non-linear) constraints on M-estimators with possibly non-differentiable estimating functions. The proposed test employs a random normalizing matrix computed from recursive M-estimators to eliminate the nuisance parameters arising from the asymptotic covariance matrix. It does not require consistent estimation of any nuisance parameters, in contrast with the conventional heteroscedasticity-autocorrelation consistent (HAC)-type test and the Kiefer–Vogelsang–Bunzel (KVB)-type test. Our test reduces to the KVB-type test in simple location models with ordinary least-squares estimation, so the error in the rejection probability of our test in a Gaussian location model is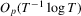 
. We discuss robust testing in quantile regression, and censored regression models in detail. In simulation studies, we find that our test has better size control and better finite sample power than the HAC-type and KVB-type tests.
1. INTRODUCTION
Conventional hypothesis testing rests on consistent estimation of the asymptotic covariance matrix. In time series econometrics, the non-parametric kernel estimator originating from the spectral estimation of Priestley (1981) is a leading example; see also Newey and West (1987, 1994), Andrews (1991) and den Haan and Levin (1997) for econometric contributions. This estimator, which is also known as a heteroscedasticity-autocorrelation consistent (HAC) estimator, leads to asymptotic chi-squared tests that are robust to heteroscedasticity and serial correlations of unknown form, but the testing results can vary with the choices of the kernel function and its bandwidth.
In view of this, Kiefer et al. (2000, KVB hereafter) propose to replace the HAC estimator with a random normalizing matrix to avoid the selection of the bandwidth in the non-parametric kernel estimation in linear regression models. This approach is extended to robust testing in non-linear regression and generalized method of moments (GMM) models; see Bunzel et al. (2001) and Vogelsang (2003) for more details. As for specification testing, Lobato (2001) develops a portmanteau test for serial correlations, and Kuan and Lee (2006) propose general M-tests of moment conditions that are robust not only in the KVB sense but also in the presence of an estimation effect. For robust overidentifying restrictions (OIR) tests, see Sun and Kim (2012) and Lee et al. (2014).
As we will see later, to test for (possibly non-linear) constraints on the class of M-estimators of Huber (1967), a consistent estimator for the derivative of the expectation of the estimating function is needed. When the estimating function is differentiable with respect to the parameter vector, a consistent estimator for this is simply the sample average of the derivative of the estimating function. However, when the estimating function is not differentiable, the estimation is less straightforward; a leading example is the quantile regression (QR) estimator of Koenker and Basset (1978). Although an explicit form of the derivative of the expectation of the estimating function is available in this case, the conditional density of model errors is in the expression. Therefore, a consistent estimator for this matrix involves non-parametric kernel estimation of the conditional density. As such, user-chosen bandwidth is needed and the performance of the HAC-type and KVB-type tests can be sensitive to this choice. However, one may appeal to the bootstrap method to circumvent consistent estimation of any nuisance matrix – see, e.g., Buchinsky (1995) and Fitzenberger (1997) – but the resulting tests are computationally demanding. Moreover, tests based on the moving blocks bootstrap (MBB), as suggested by Fitzenberger (1997), can be sensitive to the selection of block length and the number of bootstrap samples. Subsampling may also be applied, but it suffers from a problem similar to MBB.
In this paper, we propose a new robust hypothesis test for possibly non-linear constraints on M-estimators with possibly non-differentiable estimating functions. The proposed test employs a normalizing matrix computed from recursive M-estimators to eliminate the nuisance parameters in the limit and hence does not require consistent estimation of any nuisance parameters, in contrast with the HAC-type and KVB-type tests. This feature makes the proposed test appealing because consistent estimators for such nuisance parameters may not only be difficult to obtain but also sensitive to user-chosen parameters, which in turn lead to poor finite sample performance of the test. The null limit of the proposed test is shown to be the same as that of Lobato (2001) and hence the asymptotic critical values are already available. Moreover, we show that the proposed test reduces to the KVB-type test in simple location models with ordinary least-squares (OLS) estimation so the error in rejection probability of the proposed test in a Gaussian location model is thus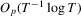 
, in contrast with the conventional tests for which the error in rejection probability is typically no better than 
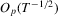. We consider robust testing in QR and censored regression models in detail. In simulation studies, we find that our test can have better size control and better finite sample power than the HAC-type and KVB-type tests.
Our method is also known as the self-normalization method in the statistics literature.1 Note that, while Shao (2010) constructs confidence intervals for the parameters that are functionals of the marginal or joint distribution of stationary time series (e.g. mean or normalized spectral means), we consider hypothesis testing on parameters defined in a more general class of econometric models that include these parameters as special cases. Shao (2012) later constructs confidence intervals for the parameters in stationary time series models based on the frequency domain maximum likelihood estimator that can be applied to a large class of long/short memory time series models with weakly dependent innovations; see also Zhou and Shao (2013) and Huang et al. (2015) for the inference for parameters in different context.
This paper proceeds as follows. In Section 2., we introduce M-estimation and related asymptotic results. Then, in Section 3., we present the proposed test as well as the HAC-type and KVB-type tests. As examples, we discuss robust testing in QR and censored regression models in Section 4.. We report simulation results in Section 5., and we conclude in Section 6.. All proofs are deferred to the Appendix.
2. M-ESTIMATION AND ASYMPTOTIC RESULTS
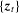be a sequence of 
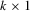random vectors and let θ be a 
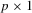unknown parameter vector with the true value 
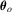. In the context of M-estimation, an M-estimator 
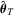for 
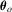can be defined as the one satisfying the following estimating equation,
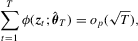(2.1)
-valued estimating function with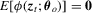 
. Clearly, the class of M-estimators includes many estimators as special cases. For example, consider the linear regression model: 
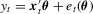. The OLS estimator 
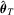satisfies 
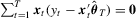, the asymmetric least-squares estimator 
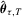of Newey and Powell (1987) and Kuan et al. (2009) for the τth conditional expectile of 
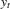satisfies 
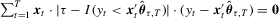, where I is the indicator function, and the QR estimator 
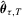for the τth conditional quantile of 
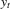is such that
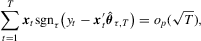
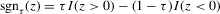; see Fitzenberger (1997) for more details. The symmetrically trimmed least-squares estimator 
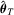proposed by Powell (1986b) is also an M-estimator because, for truncated data, it satisfies
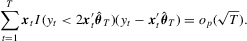
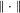denotes the sup norm for a vector, 
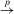denotes convergence in probability, 
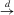denotes convergence in distribution, 
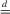denotes equality in distribution and ⇒ denotes weak convergence of associated probability measures. We also let Wq be a vector of q independent, standard Wiener processes and we let Bq be the Brownian bridge with 
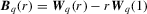for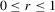 
.2.1. Asymptotic normality of M-estimators
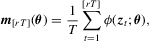
; for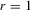 
, we simply write 
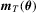, which is the sample average of 
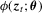. To derive the limiting distribution of 
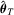, we impose the following ‘high-level’ assumptions that 
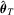is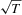 
consistent and 
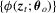obeys a multivariate functional central limit theorem (FCLT).
Assumption 2.1.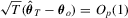
.
Assumption 2.2.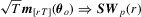
, where 
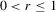and S is the matrix square root of 
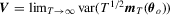; (i.e. 
).
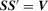Assumption 2.1 holds under various sets of primitive regularity conditions. These conditions typically require that some stochastic properties (such as memory, heterogeneity and moment restrictions) of 
and some smoothness and domination conditions on ϕ so that 
obeys a weak uniform law of large numbers,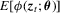 
is continuous in θ, and that 
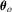is identifiably unique. The discussion for consistency of M-estimation can be found, for example, in Huber (1981, Chapter 6), Tauchen (1985, pp. 422–24) and White (1994, pp. 33–35). Assumption 2.2 is more than enough to establish the asymptotic normality of M-estimators but is required to derive the weak limit of recursive M-estimators. Note that the conditions that ensure multivariate FCLT are sufficient for Assumption 2.2; see, e.g., Corollary 4.2 of Wooldridge and White (1988) or Theorem 7.30 of White (2001). By Assumption 2.2, 
.
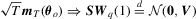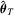can be easily derived using the first-order Taylor expansion. By expanding the estimating equation 2.1 about 
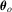, we immediately have under Assumption 2.1 that
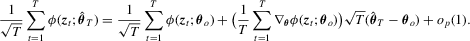
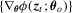, a Bahadur representation for 
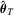can then be given by
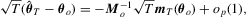(2.2)
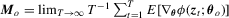, a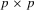 
non-singular matrix of constants. Under Assumption 2.2, 
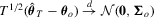, where 
.
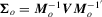using the technique above, but a Bahadur representation as in 2.2 is still available for such M-estimators. To see this, define
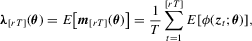
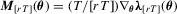; for 
, we simply write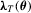 
and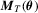 
. We now impose the following two assumptions; see also Weiss (1991) for primitive conditions.
Assumption 2.3.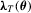
is twice continuously differentiable with a bounded second derivative and satisfies the following property: 
.
Assumption 2.4.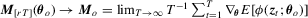
uniformly in 
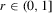and Mo is non-singular.
Given these two assumptions and by a first-order Taylor expansion of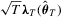 
around 
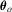, we obtain an expression as in 2.2, and hence the asymptotic normality for such M-estimators follows immediately from Assumption 2.2.
2.2. Weak convergence of recursive M-estimators
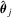be the recursive M-estimator using the subsample of first j observations; that is, 
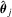is the one such that
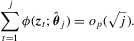
Assumption 2.1′.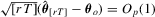
, uniformly in 
.
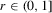Assumption 2.3′.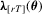
is twice continuously differentiable with a bounded second derivative and satisfies 
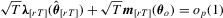, uniformly in 
.
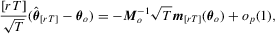
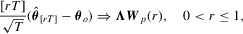
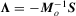. By replacing 
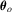with the full-sample M-estimator 
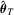, we can apply the continuous mapping theorem to obtain that
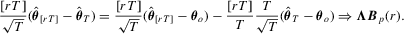(2.3)3. TESTS FOR GENERAL HYPOTHESES
possibly non-linear restrictions on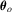 
,
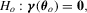(3.1)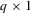
vector of continuously differentiable functions with 
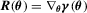that is of full row rank in a neighbourhood of 
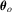. Under the assumptions above and using a delta method, we can show that 
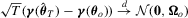, where 
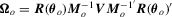.3.1. The HAC-type test
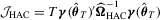, in which 
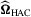is the HAC estimator for the asymptotic covariance matrix of 
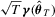such that 
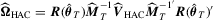, where 
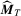is a consistent estimator of Mo and 
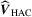is a non-parametric kernel estimator of V given by
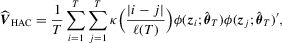
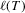denotes the truncation lag or bandwidth. As 
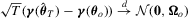, where 
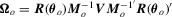, and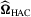 
is consistent for 
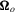. The null distribution of 
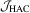is a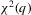 
distribution. In this paper, a test based on test statistic 
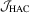will be called the 
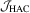test.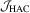
has a standard null limit and is robust to heteroscedasticity and serial correlations of unknown form, its finite sample performance will depend on choices of the kernel function and its bandwidth. To implement the 
test, it also requires a consistent estimator for Mo. If ϕ is continuously differentiable, then
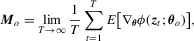
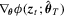is a natural consistent estimator for Mo. However, when ϕ is not differentiable, the estimation is less straightforward. For example, in the QR regression models, the Mo involves the conditional density of the error terms. Although kernel-based estimators for Mo are available (see Weiss, 1991), the resulting 
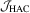test would suffer from the problems arising from non-parametric kernel estimation. For more details and more examples, see Section 4.. In addition, if the constraints are non-linear, we will need to estimate 
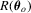by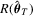 
. Even it is straightforward to obtain 
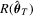, the finite sample performance of the tests may be adversely affected by this estimator.3.2. The KVB-type test
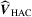to avoid the problems arising from non-parametric kernel estimation. Following this approach, we construct 
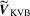as
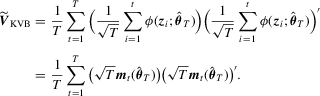
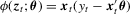with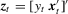 
. Given 
, a KVB-type test statistic is defined as
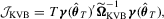
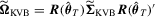with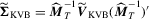 
.It is easy to derive the weak limit of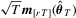 
(and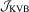 
) when ϕ is smooth (see Kuan and Lee, 2006), and it is less straightforward when ϕ is non-smooth. To allow for non-smooth ϕ, we impose the following assumption, which is similar to the condition (v) of Theorem 7.2 in Newey and McFadden (1994).
Assumption 3.1.Define
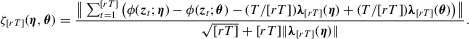
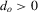such that 
.
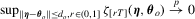This assumption should not be restrictive because sufficient conditions for Assumption 2.3′ are also sufficient for Assumption 3.1; see, e.g. Huber (1967, p. 227) and Weiss (1991, p. 62).
Lemma 3.1.Suppose that Assumptions 2.1, 2.2, 2.3′, 2.4 and 3.1 hold. Then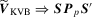 
, where 
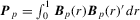and S is the matrix square root of V.
As shown in Lemma 3.1,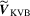 
remains random in the limit so the null distribution of 
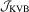will not be a 
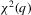distribution. However, the following theorem shows that 
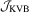is asymptotically pivotal under the null and its weak limit is the same as that of Lobato (2001). Therefore, the corresponding critical values can be found in Lobato (2001, p. 1067).
Theorem 3.1.Suppose that Assumptions 2.1, 2.2, 2.3′, 2.4 and 3.1 hold. Then under the null,
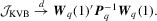
Although the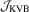 
test does not require consistent estimation of V, it still requires consistent estimation of Mo and 
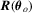. In particular, as we have discussed previously, it can be hard to obtain Mo and there might be an additional smoothing parameter to pick when ϕ is not differentiable. In view of this, in the next subsection, we propose a new way to construct robust tests without consistent estimation of Mo and 
.
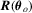3.3. The proposed test
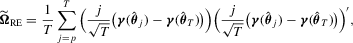(3.2)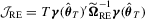
. Note that we do not need to estimate Mo and 
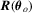to obtain 
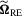, and this makes our test appealing. Under the assumptions above, we can show that
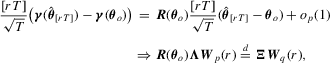(3.3)
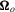and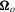 
is the asymptotic variance of 
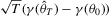. It follows that
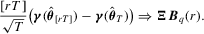(3.4)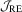
which is summarized in the following theorem.
Theorem 3.2.Suppose that Assumptions 2.1′, 2.2, 2.3′ and 2.4 hold. Then,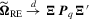 
. Moreover,
.
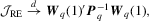
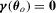Remark 3.1.In 3.2 the summation starts with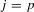 
where p is the number of unknown parameters. When the criterion function is not smooth, it may not be easy to compute the M-estimators. In addition, if the sample size is small, the optimization might not be stable and the global minimization or maximization may not be easy to guarantee. Therefore, one might want to start with a larger subsample size to avoid these problems. In fact, the theory would still hold as long as the summation starts with 
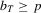and the sequence 
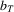satisfies 
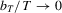such that if 
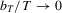, then
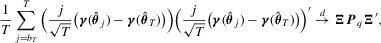
Remark 3.2.To shed more insight on the difference and similarity between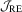 
and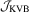 
, we consider the linear model 
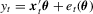and the null hypothesis 3.1 with 
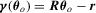. Based on the OLS estimator 
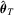, the KVB normalizing matrix can be expressed as
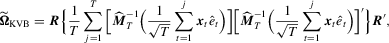
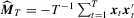and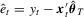 
. As for 
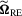, we first show that for 
,
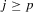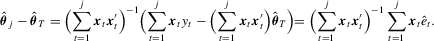
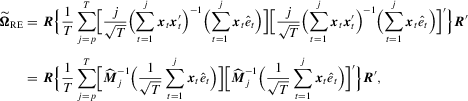
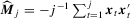. The result above shows that 
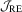and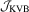 
employ different but similar normalizing matrices in the context of linear regression with OLS estimation. Of particular interest is that in a simple location model (i.e. 
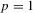and 
for all t), these two tests are algebraically equivalent because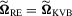 
in this case. Therefore, the error in rejection probability of the proposed 
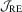test is also 
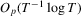in a Gaussian location model, as shown in Jansson (2004).
3.4. Asymptotic local power
, 
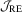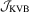and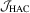 
tests under local alternatives defined as
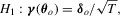(3.5)
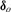is a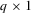 
vector of non-zero constants. Under the local alternatives, the limiting distributions of these tests are summarized in the following theorem. Let 
.
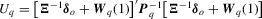Theorem 3.3.Suppose that Assumptions 2.1′, 2.2, 2.3′, 2.4 and 3.1 hold. Then under the local alternatives defined in 3.5,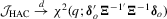 
, 
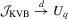and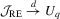 
.
Given Theorem 3.3, we can derive the asymptotic local power for these tests now. Let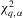 
and 
be the critical values at α significance level taken from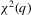 
and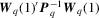 
, respectively. Also, let 
, 
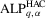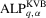and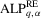 
be the asymptotic local powers of the 
, 
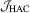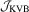and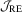 
tests, respectively.
Corollary 3.1.Suppose that Assumptions 2.1′, 2.2, 2.3′, 2.4 and 3.1 hold. Then, under the local alternatives,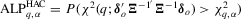 
and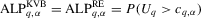 
.
It is obvious that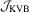 
and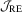 
have the same asymptotic local power because their limiting distributions are identical. The local power curves of these tests are the same as those in Figure 1 of Kuan and Lee (2006), so we omit them here. As we can see from Figure 1 of Kuan and Lee (2006), 
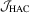has better local power than the other two tests. However, 
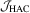may not outperform the other two tests in finite samples because its performance would depend on user-chosen parameters as well.
4. EXAMPLES
In this section, we illustrate the application of the proposed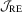 
test in QR and in censored regression models. QR is a leading example for a non-differentiable ϕ. In the second example, whether the corresponding ϕ is differentiable or not and whether consistent estimation of Mo is easy or not depend on the estimation method used.
4.1. QR models
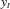given a vector of explanatory variables xt is typically specified as
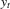given xt, 
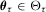is a 
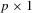vector of unknown parameters with the true value 
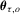and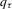 
is a real-valued function that is continuously differentiable in the neighbourhood of 
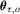. Similar to the mean regression model, the QR model can also be written as
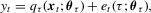(4.1)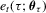
is the error term with the τth conditional quantile being zero under the true value 
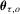, a condition ensuring the correct specification for the model 4.1. Note that the model 4.1 with 
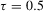is also known as a median regression model.
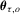, Koenker and Bassett (1978) propose the QR estimator 
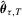that minimizes the following criterion function:
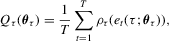
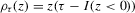is known as a check function. An analytic form for 
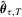is generally not available; nonetheless, many algorithms for obtaining 
have been proposed in the literature; see, e.g. Koenker and d'Orey (1987) and Koenker and Park (1996). Note also that the LAD estimator corresponds to the QR estimator with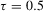 
.Note that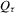 
is not differentiable, so the limiting distribution of 
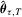is relatively difficult to derive. Nonetheless, under suitable conditions, the asymptotic normality result remains valid for the QR estimator (or LAD estimator); see Powell (1986a), Weiss (1991) and Fitzenberger (1997), among many others. Consider the linear quantile regression (i.e. 
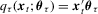). The linear QR estimator 
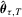is an M-estimator satisfying 
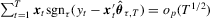. For more general non-linear models, we can follow Weiss (1991) and Fitzenberger (1997), and show that 
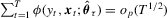, where 
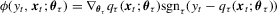; see also Koenker (2005, p. 124). Therefore, 
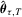is an M-estimator with a non-differentiable ϕ.
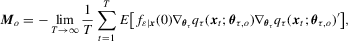
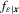is the conditional density of 
. 
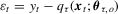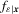can be estimated by a non-parametric kernel method, but the test performance will depend on the choices of kernel and bandwidth. To circumvent consistent estimation of Mo, one may appeal to MBB or subsampling, but the testing results can be sensitive to the selection of block length instead. Therefore, the proposed 
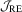test seems to be practically useful for testing in QR models because it avoids consistent estimation of Mo and is thus free from user-chosen parameters.4.2. Censored regression models
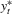be the dependent variable generated according to 
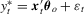. If we only observe data points 
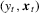with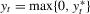 
, then 
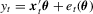forms a censored regression model and the OLS estimator by regression 
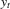on xt is not consistent for 
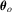; see Amemiya (1984) for an early review. Most studies rely on maximum likelihood (ML) estimation. Let 
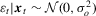and let 
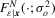and 
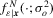be the corresponding conditional distribution and density functions. Under the assumption of independence, the log likelihood function can then be written as 
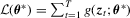, where 
, 
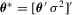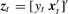and
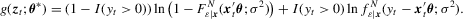
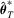is an M-estimator that solves 
.
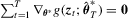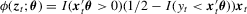. Although such an estimator is robust to conditional heteroscedasticity and non-normality, hypothesis tests based on this estimator are not easy to implement because
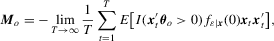(4.2)
is the true conditional density of 
. Therefore, the censored LAD-based test would suffer from the same problems as in QR models.
is symmetric about 
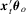, the symmetrically trimmed least-squares estimator introduced by Powell (1986b) is also consistent for 
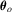and robust to conditional heteroscedasticity and non-normality. Moreover, tests based on this estimator are easier to implement. To see this, from equation (2.9) in Powell (1986b), this estimator is an M-estimator with 
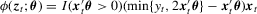. Although ϕ is non-differentiable, the corresponding Mo can be expressed as
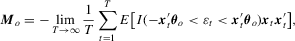
The censored regression model can be applied not only to cross-sectional data but also to time series data. For time series data, the assumption of serial independence may not be appropriate, but Robinson (1982) show that the Gaussian ML estimator remains consistent and asymptotically normal with a complicated asymptotic covariance matrix. Therefore, the test developed in this paper can also be useful.
5. MONTE CARLO SIMULATIONS
In this section, the finite sample performance of the proposed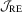 
test is evaluated via Monte Carlo simulations. We consider three sample sizes (
, 100 and 500) and two different nominal sizes (5% and 10%). The number of replications is 5,000 for size simulations and 1,000 for power simulations. Because the results for different nominal sizes are qualitatively similar, we report only the results for 5% nominal size.
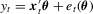, where xt is a 5 × 1 vector of regressors, with the first element equal to 1 for all t and where other elements are mutually independent AR(1) processes. The last four elements are generated in the same way as the AR(1)-HOMO errors introduced below. In the same simulation design, the correlation coefficients and the distributions of the regressors are the same as those of the error terms. θ is an unknown parameter vector with the true value 
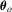, and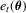 
is an error term. The null hypothesis is given by
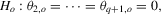
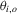is the ith element of 
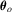and q denotes the number of restrictions on 
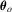. We consider 
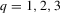for size simulations and 
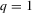for power simulations. To test these hypotheses, we apply the OLS and LAD methods for estimating 
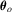. It is well known that the OLS estimator enjoys optimality under (i.i.d.) normal errors, but the LAD estimator may be better for leptokurtic errors.In size simulations, we set 
and 
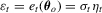, where 
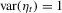and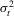 
represents the conditional variance of 
. The data-generating processes (DGPs) for 
are AR(1)-HOMO and AR(1)-HET. AR(1) indicates that 
is governed by the AR(1) model,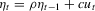 
, where ρ is set to be either 0.5 or 0.8, 
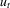is a white noise with unit variance and 
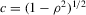, which is a scaling factor such that 
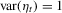. While HOMO stands for conditional homoscedasticity of 
(we set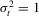 
for all t), HET denotes that 
is conditionally heteroscedastic with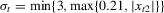 
as considered in Fitzenberger (1997, p. 255). We generate 
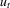from i.i.d. 
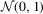and standardized Student's t(4). This enables us to examine if LAD-based tests are more appropriate for leptokurtic data. As for the regressors, they follow the AR(1) model specified as that for 
.
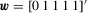and two preliminary truncation lags, 
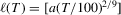, where 
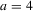and 12. Unlike the 
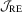test, these two tests require consistent estimation of Mo. Thus, we employ the estimator 
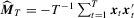for OLS and the following kernel-based estimator for LAD:
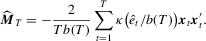
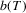is the bandwidth that vanishes in the limit and 
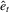are LAD residuals. Although optimal selection of bandwidth has been extensively discussed in the literature on density estimation, it is not clear how the value of 
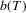should be selected such that 
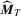enjoys optimality in some sense. We thus examine the effect of selecting 
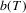by employing the two bandwidths: (a) 
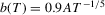; (b)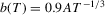 
. Here, 
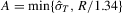with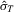 
and R being the sample standard deviation and interquartile range of the LADresiduals, respectively. The first is suggested by Silverman (1986, p. 48) to obtain an optimal rate for density estimation, but the second goes to zero at the same rate as in Koenker (2005, p. 81). Given these choices, the OLS-based tests read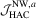 
and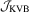 
, and the LAD-based tests are denoted as 
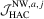and 
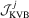, where 
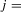(a) and (b).
The empirical sizes for the OLS-based tests are reported in Tables 1 and 2. Clearly, these tests are all oversized in small samples (e.g. 
) and the distortions deteriorate when q or ρ becomes larger. We also observe that leptokurtosis has little effect on the size performance, but heteroscedasticity does result in more size distortions especially for leptokurtic data and smaller q. Among these tests, the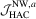 
test has the largest size distortions, regardless of the values of a. In particular, its size distortions are much larger for 
and remain even when 
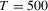. The other tests are clearly less oversized and a quite encouraging result is that the proposed 
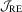test dominates the 
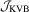test in terms of finite sample size. It is also found that when data become more persistent (i.e. ρ becomes larger), the size distortion of the former increases slightly, yet the size distortion of the latter increases dramatically.
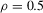)| AR(1)-HOMO | AR(1)-HET | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
t(4) |  |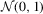
t(4) | ||||||||||
| q |  |
100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | |
 |
1 | 6.3 | 5.3 | 5.0 | 5.7 | 5.8 | 4.8 | 9.9 | 8.2 | 5.9 | 11.6 | 8.9 | 5.8 |
| 2 | 7.8 | 6.3 | 5.3 | 7.8 | 6.3 | 5.5 | 10.5 | 8.2 | 5.2 | 11.6 | 8.4 | 6.6 | |
| 3 | 10.4 | 7.7 | 5.8 | 9.7 | 7.6 | 6.2 | 12.6 | 9.2 | 5.9 | 13.1 | 9.5 | 6.8 | |
 |
1 | 9.9 | 7.3 | 5.6 | 9.7 | 7.9 | 5.5 | 11.7 | 8.6 | 6.1 | 14.0 | 10.3 | 5.9 |
| 2 | 11.3 | 8.2 | 5.8 | 11.8 | 8.7 | 6.1 | 12.7 | 8.7 | 5.5 | 13.9 | 10.0 | 7.0 | |
| 3 | 14.5 | 9.5 | 6.2 | 14.3 | 10.5 | 6.8 | 14.0 | 9.4 | 6.0 | 15.7 | 10.7 | 7.0 | |
 |
1 | 16.2 | 12.2 | 8.3 | 17.3 | 13.1 | 7.6 | 19.4 | 13.7 | 8.4 | 23.6 | 16.9 | 8.2 |
| 2 | 23.7 | 17.9 | 9.9 | 25.3 | 17.7 | 10.5 | 25.7 | 18.8 | 9.6 | 29.1 | 19.8 | 10.1 | |
| 3 | 33.4 | 22.9 | 10.5 | 32.5 | 21.1 | 11.7 | 32.8 | 22.6 | 10.4 | 34.5 | 22.3 | 11.6 | |
 |
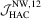1 | 23.4 | 16.6 | 8.1 | 25.1 | 17.5 | 7.0 | 27.8 | 18.3 | 8.3 | 31.1 | 21.3 | 8.7 |
| 2 | 37.9 | 25.3 | 10.3 | 40.0 | 25.9 | 10.7 | 40.4 | 27.4 | 10.3 | 43.1 | 28.0 | 11.0 | |
| 3 | 52.1 | 34.9 | 11.6 | 51.0 | 34.5 | 12.6 | 53.1 | 34.9 | 12.4 | 53.1 | 35.7 | 12.8 | |
Note
- The entries are rejection frequencies in percentages; the nominal size is 5%.
)| AR(1)-HOMO | AR(1)-HET | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
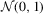t(4) |  |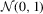
t(4) | ||||||||||
| q |  |
100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | |
 |
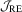1 | 7.5 | 5.9 | 5.6 | 7.1 | 6.3 | 5.3 | 11.9 | 10.4 | 6.5 | 13.3 | 10.6 | 6.7 |
| 2 | 10.2 | 8.7 | 5.5 | 9.6 | 8.3 | 5.7 | 14.2 | 10.8 | 5.6 | 14.6 | 12.1 | 6.8 | |
| 3 | 14.6 | 11.4 | 7.9 | 13.5 | 11.7 | 7.1 | 17.9 | 13.7 | 7.9 | 17.8 | 13.9 | 7.5 | |
 |
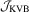1 | 17.8 | 12.2 | 6.9 | 17.4 | 12.4 | 7.1 | 21.0 | 14.6 | 7.1 | 22.7 | 15.5 | 7.3 |
| 2 | 23.1 | 16.4 | 7.6 | 22.9 | 16.7 | 8.1 | 24.7 | 17.3 | 7.0 | 27.3 | 18.8 | 8.8 | |
| 3 | 32.3 | 20.6 | 9.4 | 30.6 | 20.8 | 9.4 | 31.4 | 20.2 | 9.1 | 31.9 | 20.9 | 8.9 | |
 |
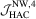1 | 28.9 | 23.2 | 10.7 | 30.5 | 23.5 | 10.5 | 35.1 | 27.0 | 11.7 | 39.0 | 29.5 | 12.7 |
| 2 | 45.4 | 35.1 | 13.6 | 46.9 | 34.6 | 14.8 | 47.7 | 37.2 | 14.9 | 51.1 | 37.2 | 16.1 | |
| 3 | 60.7 | 46.0 | 18.3 | 60.4 | 44.3 | 18.5 | 59.5 | 45.4 | 18.2 | 60.4 | 44.9 | 18.5 | |
 |
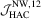1 | 34.1 | 24.6 | 11.8 | 35.7 | 24.9 | 11.5 | 40.2 | 29.4 | 12.7 | 43.8 | 31.7 | 13.9 |
| 2 | 53.7 | 38.6 | 15.6 | 55.7 | 39.2 | 16.6 | 56.9 | 41.4 | 16.6 | 59.0 | 42.0 | 17.6 | |
| 3 | 70.8 | 51.6 | 20.9 | 69.9 | 51.3 | 20.6 | 70.0 | 52.5 | 20.5 | 71.1 | 52.1 | 20.9 | |
Note
- The entries are rejection frequencies in percentage; the nominal size is 5%.
The empirical sizes for LAD are summarized in Tables 3 and 4. Generally, the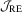 
test is still the best test and the HAC-type test is the worst. Compared with the preceding tables, we observe that the OLS-based and LAD-based tests have similar patterns regarding size performance. It is also found that the LAD-based 
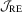test has empirical sizes closer to the nominal size of 5%, but this is not necessary for the other tests. These results suggest that, as far as an accurate finite sample size is concerned, the LAD-based 
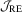test is preferred for testing in linear regressions.
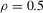)| AR(1)-HOMO | AR(1)-HET | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
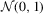t(4) |  |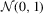
t(4) | ||||||||||
| q |  |
100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | |
 |
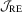1 | 4.4 | 3.5 | 4.2 | 4.1 | 3.8 | 4.1 | 7.1 | 5.9 | 5.2 | 8.4 | 7.2 | 5.7 |
| 2 | 5.0 | 4.2 | 4.3 | 4.7 | 4.1 | 4.0 | 6.4 | 4.7 | 4.1 | 6.6 | 4.5 | 5.0 | |
| 3 | 7.1 | 5.4 | 4.2 | 6.2 | 4.9 | 4.3 | 6.6 | 4.7 | 3.8 | 7.0 | 5.4 | 4.2 | |
 |
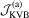1 | 6.6 | 5.5 | 4.9 | 6.0 | 5.7 | 5.4 | 9.3 | 7.4 | 5.5 | 12.1 | 10.0 | 6.4 |
| 2 | 7.7 | 7.0 | 5.2 | 8.8 | 7.0 | 5.7 | 9.3 | 6.6 | 4.4 | 11.9 | 7.9 | 5.9 | |
| 3 | 11.2 | 8.2 | 5.9 | 10.1 | 8.5 | 6.4 | 9.3 | 6.2 | 4.5 | 12.4 | 8.8 | 5.9 | |
 |
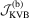1 | 9.3 | 7.4 | 5.5 | 8.8 | 8.8 | 7.5 | 12.3 | 10.2 | 6.6 | 15.9 | 13.5 | 8.9 |
| 2 | 12.8 | 9.9 | 6.7 | 14.3 | 11.8 | 8.4 | 14.9 | 10.5 | 6.7 | 17.6 | 14.6 | 9.1 | |
| 3 | 19.4 | 13.5 | 8.5 | 19.2 | 16.2 | 10.4 | 17.0 | 12.1 | 8.1 | 20.0 | 15.8 | 10.1 | |
 |
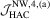1 | 13.6 | 9.8 | 6.8 | 13.3 | 10.8 | 7.6 | 17.5 | 11.9 | 7.9 | 21.0 | 16.0 | 9.1 |
| 2 | 20.0 | 14.0 | 8.0 | 21.4 | 15.4 | 8.8 | 20.2 | 13.7 | 6.8 | 24.4 | 16.8 | 9.0 | |
| 3 | 28.8 | 20.3 | 9.7 | 27.6 | 20.6 | 10.5 | 25.7 | 15.9 | 7.4 | 27.6 | 19.7 | 8.9 | |
 |
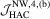1 | 17.5 | 13.2 | 8.2 | 17.9 | 15.0 | 10.0 | 21.6 | 15.5 | 10.4 | 25.8 | 19.9 | 11.6 |
| 2 | 28.1 | 19.7 | 11.3 | 30.6 | 23.0 | 14.8 | 28.0 | 20.0 | 11.3 | 33.1 | 25.0 | 14.5 | |
| 3 | 41.7 | 30.3 | 14.8 | 42.6 | 33.5 | 18.5 | 37.7 | 26.2 | 14.1 | 40.7 | 29.8 | 17.4 | |
 |
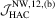1 | 23.7 | 17.2 | 8.2 | 23.6 | 18.2 | 9.8 | 27.7 | 19.0 | 10.2 | 30.7 | 23.1 | 11.4 |
| 2 | 39.1 | 27.8 | 11.8 | 41.2 | 30.1 | 15.8 | 39.0 | 27.5 | 11.8 | 41.9 | 32.0 | 14.9 | |
| 3 | 55.8 | 41.6 | 16.6 | 55.0 | 44.0 | 20.0 | 51.6 | 37.4 | 15.3 | 54.2 | 40.6 | 18.9 | |
Note
- The entries are rejection frequencies in percentage; the nominal size is 5%.
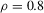)| AR(1)-HOMO | AR(1)-HET | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
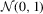t(4) |  |
t(4) | ||||||||||
| q |  |
100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | 50 | 100 | 500 | |
 |
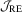1 | 5.3 | 4.9 | 4.2 | 4.6 | 4.3 | 4.6 | 8.9 | 8.1 | 5.9 | 10.0 | 7.7 | 5.7 |
| 2 | 7.1 | 6.3 | 5.0 | 6.8 | 5.7 | 4.7 | 7.8 | 6.6 | 4.6 | 8.3 | 6.9 | 4.6 | |
| 3 | 9.2 | 7.6 | 6.0 | 9.1 | 8.2 | 5.9 | 10.3 | 6.2 | 5.1 | 9.2 | 7.2 | 4.7 | |
 |
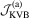1 | 12.3 | 8.9 | 5.7 | 12.0 | 8.9 | 6.1 | 14.1 | 10.3 | 6.1 | 16.1 | 11.3 | 6.6 |
| 2 | 18.3 | 12.8 | 7.2 | 18.1 | 13.9 | 7.0 | 17.0 | 11.2 | 5.5 | 20.2 | 13.7 | 6.2 | |
| 3 | 25.8 | 17.7 | 8.4 | 26.1 | 17.9 | 8.0 | 21.3 | 13.2 | 6.7 | 22.9 | 15.7 | 6.4 | |
 |
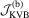1 | 15.7 | 11.5 | 6.1 | 15.2 | 12.3 | 7.5 | 17.9 | 12.9 | 7.1 | 20.0 | 14.6 | 8.6 |
| 2 | 24.3 | 16.7 | 9.1 | 25.2 | 17.9 | 9.5 | 23.6 | 16.1 | 9.1 | 27.1 | 17.7 | 9.1 | |
| 3 | 36.1 | 26.0 | 11.0 | 36.2 | 27.0 | 12.0 | 30.4 | 21.0 | 9.5 | 32.8 | 24.0 | 10.3 | |
 |
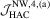1 | 24.5 | 18.0 | 9.1 | 23.6 | 18.2 | 9.6 | 27.9 | 20.3 | 10.1 | 29.8 | 21.4 | 10.9 |
| 2 | 37.2 | 28.2 | 12.6 | 38.4 | 30.4 | 13.5 | 35.8 | 25.0 | 9.9 | 38.4 | 29.8 | 12.1 | |
| 3 | 51.5 | 39.6 | 17.1 | 51.9 | 39.5 | 16.7 | 44.3 | 32.5 | 13.4 | 46.6 | 34.7 | 13.4 | |
 |
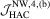1 | 28.8 | 21.1 | 10.7 | 28.0 | 22.9 | 12.6 | 32.2 | 23.4 | 11.8 | 34.1 | 27.3 | 13.3 |
| 2 | 44.6 | 34.4 | 16.9 | 46.6 | 36.4 | 17.2 | 44.3 | 33.1 | 15.8 | 46.9 | 35.4 | 16.4 | |
| 3 | 62.4 | 50.5 | 22.7 | 62.7 | 50.9 | 23.2 | 55.7 | 43.2 | 19.1 | 57.6 | 46.5 | 20.0 | |
 |
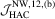1 | 33.1 | 23.0 | 11.0 | 32.7 | 24.1 | 12.9 | 35.7 | 24.7 | 11.9 | 37.0 | 27.9 | 13.6 |
| 2 | 52.6 | 38.1 | 18.0 | 54.1 | 39.8 | 18.1 | 52.0 | 37.3 | 17.2 | 54.0 | 38.9 | 17.9 | |
| 3 | 70.3 | 55.6 | 24.6 | 71.7 | 56.1 | 25.1 | 65.5 | 49.1 | 20.7 | 65.6 | 52.3 | 21.6 | |
Note
- The entries are rejection frequencies in percentage; the nominal size is 5%.
For power simulations, we consider 
and 100 and the null hypothesis 
against the alternatives for which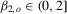 
. The DGPs considered are AR(1)-HOMO and AR(1)-HET with 
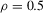and two error terms: 
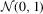and (standardized) Student's t errors. As shown in the preceding results, the 
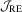test is slightly oversized for these DGPs, but other tests have substantial size distortions, especially when 
and when inappropriate user-chosen parameters are used. To provide a proper power comparison, we thus simulate the size-adjusted powers. However, it should be stressed that, while size adjustment enables us to compare the power performance of tests with different finite sample sizes, it is generally infeasible in practical applications.
The power curves for the OLS-based and LAD-based tests are plotted in Figures 1 and 2, respectively, with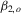 
on the horizonal axis. The different panels show the following: AR(1)-HOMO with (a) normal errors and 
, (b) normal errors and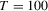 
, (c) t(4) errors and 
and (d) t(4) errors and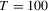 
; AR(1)-HET with normal errors and (e) 
and (f)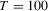 
. Clearly, their powers grow with 
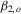and T, but are adversely affected by leptokurtosis or heteroscedasticity. Comparing the OLS-based 
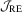and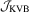 
tests, we find that although the latter delivers slightly higher power when 
, they perform quite similarly when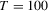 
, which shows that their power differences disappear very quickly. In the LAD case, the KVB-type test is no longer free from user-chosen parameters and it is of interest to see that 
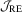performs similarly to 
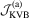and outperforms 
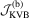in both samples. Note that 
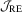may be even more powerful than 
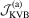in a larger sample, in contrast with the OLS case. Comparing 
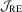with the HAC-type test, 
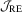does suffer from power loss in the OLS case, but it still performs similarly to 
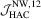when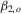 
is small. For LAD, the HAC-type test depends on more user-chosen parameters and it is clear that 
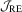performs better than 
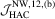in a smaller sample.
These simulation results together suggest that the proposed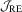 
test is practically useful because it dominates the other tests in terms of finite sample size and can enjoy power advantage when the other tests are computed using inappropriate user-chosen parameters. Finally, by comparing Figures 1 and 2 we also find that although the LAD-based 
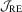test is dominated by the OLS-based 
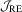test for AR(1)-HOMO with normal errors, the former may perform better when data are leptokurtic (resulting from either heteroscedasticity or leptokurtic errors).
6. CONCLUSIONS
In this paper, we propose new robust hypothesis tests for non-linear constraints on M-estimators with possibly non-differentiable estimating functions. The proposed approach may serve as a good alternative to hypothesis testing because it does not require consistent estimation of any nuisance parameters in the asymptotic covariance matrix. Hence, it circumvents the problems arising from such consistent estimation, a sharp contrast with the HAC-type and KVB-type tests. Our simulations also suggest that the proposed test is practically useful because it performs better than the HAC-type and KVB-type tests in terms of finite sample size, and it has a power advantage when the latter tests are computed with inappropriate user-chosen parameters.
ACKNOWLEDGEMENTS
We thank the editor Michael Jansson, Anil Bera, Joon Park, Werner Ploberger, Jeffrey Racine, two anonymous referees, and the participants at the 2006 Far Eastern Meeting of the Econometric Society in Beijing for helpful suggestions and comments. All errors are our responsibility. The research support from the National Science Council of the Republic of China (NSC94-2415-H-194-009 for W-M. Lee) is also gratefully acknowledged.
Appendix A A
Proof of Lemma 3.1.Let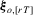 
and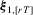 
be defined as
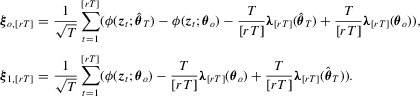
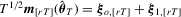with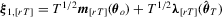 
. We first consider the term 
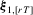. By the first-order Taylor expansion about 
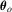, we have under Assumptions 2.1 and 2.4 that
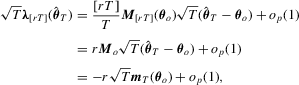(A.1)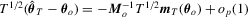
(as shown in Section 2.1.). As a result,
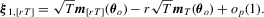
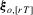, its sup norm can be expressed as
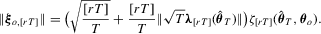
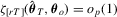. Moreover, 
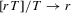and, as shown in equation A.1, 
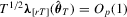. These results together imply 
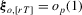. As such
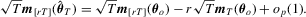
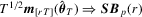. Applying again the continuous mapping theorem yields the weak limit of 
.
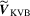Proof of Theorem 3.1.As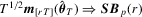
, we immediately have
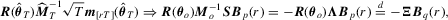
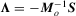and Ξ is a non-singular 
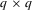matrix square root of 
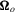. It then follows from Lemma 3.1 that 
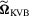has the following weak limit:
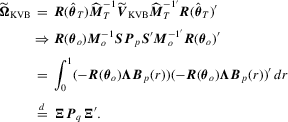
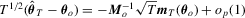and applying the delta method,
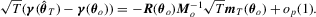
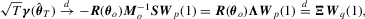
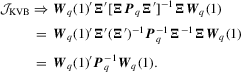
Proof of Theorem 3.3.Under the local alternative 3.5, we have
, 
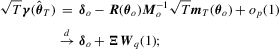
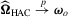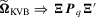and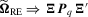 
regardless of the values of 
, the weak limits for the three tests immediately follow.
Proof of Corollary 3.1.The results follows directly from Theorem 3.3.
