A Head-count Measure of Rank Mobility and its Directional Decomposition
Abstract
We propose and characterize a new measure of rank mobility. The index is given by the head count of those whose positions change in the move from one period to the next divided by population size. The interpretation of this head-count ratio is straightforward and intuitive. In addition, we illustrate how the measure can be decomposed into an index of upwards mobility and an index of downwards mobility. The axioms used in our characterization results are appealing and easy to justify. We conclude with an application to the Human Development Index, a summary measure of average achievement in key dimensions of human development: a long and healthy life, being knowledgeable and having a decent standard of living.
Introduction
The measurement of mobility is an issue that is, by now, well-established in the area of economic and social index numbers. The fundamental issue to be addressed is the design of measures that reflect the extent to which members of a society (or, at a more aggregate level, population subgroups or countries) move across social or economic boundaries from one period to the next. A crucial aspect that distinguishes mobility from most other criteria that are used to assess the performance of a society (such as income inequality or poverty) is that mobility is difficult—if not impossible—to define without any reference to intertemporal considerations. Of course, intertemporal approaches to the measurement of inequality, poverty and other social phenomena have been explored, but they can also be defined without any difficulties in a single-period setting; in contrast, there is no mobility without movement. As a consequence, the arguments of a mobility measure are pairs of indicators of economic or social status—one indicator for each of the time periods under consideration.
According to Fields (2008), six aspects of mobility can be identified in the literature. These are time-independence, positional movement, share movement, non-directional income movement, directional income movement, and equalizer of longer-term incomes. See, for instance, Maasoumi (1998), Fields and Ok (1999), and Jäntti and Jenkins (2014) for comprehensive surveys.
While the majority of earlier contributions deal with mobility in the context of income distributions, there has been an increasing interest in the notion of rank mobility—that is, the positional movement of individuals, households or countries in economic or social hierarchies. Rank-based measures are widely applied in empirical research (see, for example, Dickens 1999), but as far as we are aware, only a few contributions, such as D'Agostino and Dardanoni (2009), Cowell and Flachaire (2011) and Bossert et al. (2016), investigate them from a theoretical perspective.
The notion of rank mobility plays a role in Cowell and Flachaire (2011), but its axiomatic analysis is not the focus of that paper. They propose a flexible approach that is based on a general measure of distance between individual statuses. Absolute status levels may or may not be directly observable—much of their notion is based on the status of individuals relative to the position of others.
Rank correlation measures are nowadays widely used to assess the intergenerational mobility of societies. For example, Chetty et al. (2014) examine the extent of intergenerational mobility in the USA. Using a comprehensive dataset, they show that this type of mobility can vary substantially across different geographical regions. Moreover, they identify variables that correlate with upwards mobility. Venator and Reeves (2015) provide a comparison of rank mobility measures and the more traditional intergenerational elasticity coefficient. In a recent contribution, Nybom and Stuhler (2017) analyze the biases that can be associated with the use of intergenerational elasticities as well as other indicators, including log-linear and rank correlation measures.
Focusing on measures of rank mobility is particularly relevant in the framework of indicators of progress of countries beyond GDP. Notable examples of the latter are the Human Development Index of the United Nations and the more recent Better Life Index of the OECD. What attracts the attention of policymakers and the media is not the value of these composite indicators but the positions of the countries and the changes in the rankings over time. We use the Human Development Index to provide an empirical application of our new measures later in the paper.
D'Agostino and Dardanoni (2009) and Bossert et al. (2016) propose rank mobility measures that are based on two dominant measures of non-parametric rank correlation, namely, Spearman's (1904) ρ index and Kendall's (1938) τ index. D'Agostino and Dardanoni (2009) characterize rank mobility pre-orders that are linked to Spearman's ρ index; Bossert et al. (2016), on the other hand, focus on mobility measures that have their foundation in Kendall's τ index. The latter is at the core of the Kemeny distance, which is one of the most prominent distance measures for orderings; see Kemeny (1959) and Kemeny and Snell (1962), where the Kemeny distance is characterized. As pointed out by Can and Storcken (2013), this axiomatization involves a redundant axiom, an observation that allows Can and Storcken (2013) to substantially improve on Kemeny and Snell's (1962) result.
In this paper, we depart from the approach based on measures of rank correlation followed by D'Agostino and Dardanoni (2009) and Bossert et al. (2016). We develop an axiomatic framework from first principles rather than confining ourselves to tools that have their origins in a different (but, of course, closely related) subfield of statistical analysis.
Our central result is a characterization of what we refer to as the head-count ratio. It is a simple and intuitively appealing measure that conveys the basic principles of rank mobility in a transparent manner. The index calculates the rank mobility value by counting the number of individuals who change position in the move from period zero to period one, and divides the resulting value by the size of the population under consideration. The axioms employed in our characterization are plausible and not difficult to justify. We then proceed to a decomposition of the head-count ratio into an upwards head-count ratio and a downwards head-count ratio. As their labels suggest, these measures are obtained by dividing the number of those who move up (respectively, down) by the population size. The benefit of such a decomposition into two opposing measures is the ability to compare the number of individuals who move down with the number of those who move up (at the expense of the former). Our characterizations of these directional mobility measures are achieved by formulating suitable adaptations of the overall mobility axioms to the respective directional case. Again, the resulting properties are easily justifiable and intuitively appealing. We conclude that our new index, along with its directional components, provides an attractive alternative to measures that are currently in use. It has a simple and transparent structure, it is straightforward to calculate and to interpret, and it allows policymakers to access the relevant mobility information by means of a tool that is easy to use while resting on a solid theoretical foundation.
The next section introduces the basic notion of rank mobility. Our new rank mobility measure—the head-count ratio—is presented, discussed and characterized in Section 3. A natural decomposition into upwards rank mobility and downwards rank mobility, along with the requisite characterization results, follows in Section 4. Section 4 also discusses some conceptual difficulties when considering weighted means of upwards and downwards rank mobility. Section 5 concludes, with a discussion of our results and an application of the indices that we propose to the most well-known multidimensional measure of wellbeing and indicator of progress of countries beyond GDP, the Human Development Index.
1 Rank Mobility
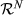 . For convenience, we sometimes express strict orderings in line notation, that is, we list the elements of N in decreasing order of rank. For instance, if N = {a, b, c}, then R = abc is the strict ordering that ranks a above b, and b above c. For a ∈ N and
. For convenience, we sometimes express strict orderings in line notation, that is, we list the elements of N in decreasing order of rank. For instance, if N = {a, b, c}, then R = abc is the strict ordering that ranks a above b, and b above c. For a ∈ N and 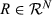 , the rank of individual a in R is denoted by r(a, R), that is,
, the rank of individual a in R is denoted by r(a, R), that is,
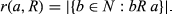
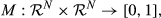
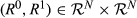 , we denote the set of agents whose ranking improved when moving from period zero to period one by
, we denote the set of agents whose ranking improved when moving from period zero to period one by
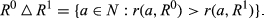
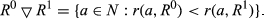
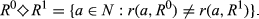
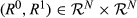 ,
,
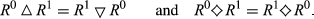
For k ∈ {2, …, n}, we say that a pair 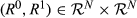 is of degree k if |R0 ◇ R1| = k. Analogously, for k ∈ {1,…,n−1}, the pair
is of degree k if |R0 ◇ R1| = k. Analogously, for k ∈ {1,…,n−1}, the pair 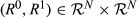 is of upwards (respectively, downwards) degree k if |R0 △ R1| = k (respectively, |R0▽R1|=k).
is of upwards (respectively, downwards) degree k if |R0 △ R1| = k (respectively, |R0▽R1|=k).
2 The Head-count Ratio
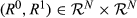 ,
,
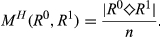
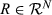 , we define the relation Rπ by letting, for all a,b ∈ N,
, we define the relation Rπ by letting, for all a,b ∈ N,

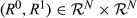 and for all permutations π:N→N,
and for all permutations π:N→N,
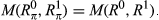
Next, we normalize the maximal possible value of M to the number 1. Normalization. 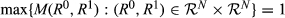 .
.
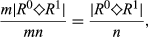
To reflect the feature that our measure depends only on those individuals who experience a change in their respective rank, we employ an invariance axiom. We require the rank mobility values associated with two pairs of strict orderings 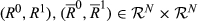 to coincide whenever the sets of individuals whose position changes are the same.
to coincide whenever the sets of individuals whose position changes are the same.
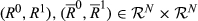 , if
, if  , then
, then
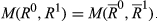
Finally, we introduce an additivity property with an intuitive interpretation. Consider a situation in which the rank mobility associated with a move from period zero to period one is determined and, analogously, the rank mobility corresponding to a move from period one to period two is calculated (we can think of the time periods under consideration as years, for instance). Now suppose that we want to measure the mobility associated with the move from period zero to period two (that is, consider a biannual setting). If the set of individuals whose rank changed in the move from period zero to period one and the set of those whose rank changed in the move from period one to period two are disjoint, then it seems natural to combine these distinct (annual) moves in an additive manner (as a biannual move). That is, if it so happens that the rank changes from period zero to period one and from period one to period two are distinct in the sense that they involve different individuals, then the rank mobility associated with a move from period zero to period two is given by the sum of the rank mobility for the two moves from zero to one and from one to two. Thus we impose the following property.
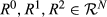 , if (R0◇R1)∩(R1◇R2) = ∅, then
, if (R0◇R1)∩(R1◇R2) = ∅, then
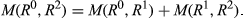
We can now state and prove our first characterization result. As will become clear once we go through the proof, the result is valid only for societies with at least six members.
Theorem 1.Given any N with n ≥ 6, a rank mobility measure M satisfies anonymity, normalization, change invariance and change additivity if and only if M = MH.
Proof.It is straightforward to verify that MH satisfies the axioms of the theorem statement. Now suppose that M is a rank mobility measure that satisfies the axioms. Let k ∈ {2, …, n}, and consider any pair 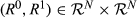 that is of degree k, that is, |R0
that is of degree k, that is, |R0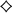 R1| = k. Let
R1| = k. Let 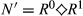 , and define
, and define 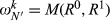 . Now consider any N ⊆ N and
. Now consider any N ⊆ N and 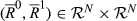 such that
such that
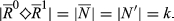
If N = N′, then 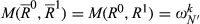 follows from change invariance.
follows from change invariance.
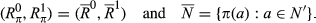
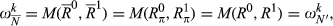
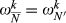 for all pairs of degree k. Thus
for all pairs of degree k. Thus 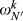 cannot depend on N′, and we write it as ωk. It therefore follows that M(R0,R1) = ωk for all pairs (R0,R1) of degree k.
cannot depend on N′, and we write it as ωk. It therefore follows that M(R0,R1) = ωk for all pairs (R0,R1) of degree k.Next, we establish a relationship between the ωk values. Let 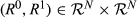 be of degree k. Without loss of generality, suppose that R0◇R1 = {a1, …, ak}.
be of degree k. Without loss of generality, suppose that R0◇R1 = {a1, …, ak}.
Case 1.k is even. Let 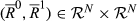 be such that
be such that 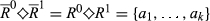 and
and
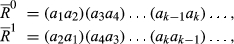
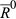 to
to 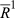 . By change invariance, it follows that
. By change invariance, it follows that 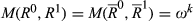 because
because 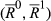 is of degree k. The move from
is of degree k. The move from 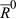 to
to 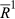 can be decomposed into k/2 pairs of degree 2, where the sets of individuals whose positions change in each of these moves are given by {a1, a2},…,{ak−1, ak}. These sets are pairwise disjoint, and change additivity can be applied repeatedly to conclude that
can be decomposed into k/2 pairs of degree 2, where the sets of individuals whose positions change in each of these moves are given by {a1, a2},…,{ak−1, ak}. These sets are pairwise disjoint, and change additivity can be applied repeatedly to conclude that
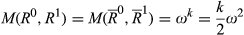 (1)
(1)
Case 2.k is odd. Let 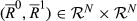 be such that
be such that 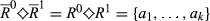 and
and
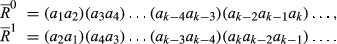
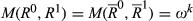 because
because 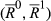 is of degree k. The move from
is of degree k. The move from 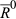 to
to 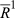 can be decomposed into (k−3)/2 pairs of degree 2 and one pair of degree 3. The sets of individuals whose positions change in each of these moves are {a1, a2}, …, {ak−4, ak−3} and {ak−2, ak−1, ak}. Again, these sets are pairwise disjoint, and invoking change additivity repeatedly, it follows that
can be decomposed into (k−3)/2 pairs of degree 2 and one pair of degree 3. The sets of individuals whose positions change in each of these moves are {a1, a2}, …, {ak−4, ak−3} and {ak−2, ak−1, ak}. Again, these sets are pairwise disjoint, and invoking change additivity repeatedly, it follows that
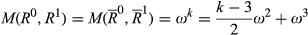 (2)
(2)Because n ≥ 6, there exist 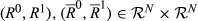 such that
such that
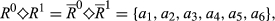
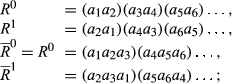
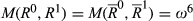 . Using change additivity, we obtain
. Using change additivity, we obtain

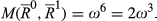
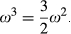
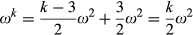
By normalization, there exists a pair 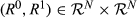 such that M assumes its maximal value of 1 at (R0, R1). Because ωk is increasing in k, this maximal value is obtained for k = n. Using (1), it follows that ωn = (n/2)ω2 = 1 and hence ω2 = 2/n. Thus for any
such that M assumes its maximal value of 1 at (R0, R1). Because ωk is increasing in k, this maximal value is obtained for k = n. Using (1), it follows that ωn = (n/2)ω2 = 1 and hence ω2 = 2/n. Thus for any 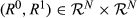 of degree k, it follows that
of degree k, it follows that
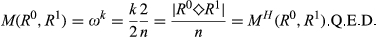
The assumption that N consists of at least six members is essential in the above proof. The ωk values are determined by considering multiples of degree-two situations and degree-three situations, and the combination of the two yields the desired values. But this method can be applied only if there are at least six individuals to begin with: six is the smallest number that can be expressed as a multiple of two and as a multiple of three. It is straightforward to see that if N has fewer than six members, then other measures become available, and thus this minimal-cardinality assumption cannot be dispensed with in the above theorem.
3 Upwards and Downwards Mobility Ratios
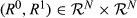 ,
,
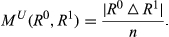
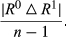 (3)
(3)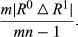
Directional normalization. 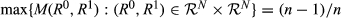 .
.
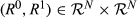 ,
,
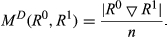
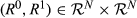 ,
,
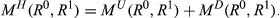
We now provide characterizations of MU and of MD. To do so, the two axioms of change invariance and change additivity can be rephrased in a natural way to capture upwards and downwards rank mobility. Instead of focusing on the set of agents whose positions change in the move from R0 to R1, we restrict attention to those whose positions improve (respectively, worsen) so that we obtain the following properties.
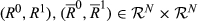 , if
, if  , then
, then
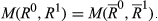
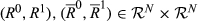 , if
, if  , then
, then
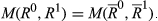
 , if (R0△R1)∩(R1△R2) = ∅, then
, if (R0△R1)∩(R1△R2) = ∅, then
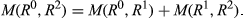
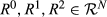 , if (R0▽R1)∩(R1▽R2) = ∅, then
, if (R0▽R1)∩(R1▽R2) = ∅, then
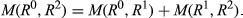
The property of anonymity need not be changed; it is just as natural and plausible in the directional case. We can now state and prove two theorems that parallel Theorem 1. However, their proofs differ somewhat from that of our first theorem. In particular, it is now no longer necessary to require that there be at least six agents—any society with at least two members is covered by these results.
Theorem 2.Given any N with n ≥ 2, a rank mobility measure M satisfies anonymity, directional normalization, upwards invariance and upwards additivity if and only if M = MU.
Proof.Again, it is straightforward to verify that MU satisfies all of the axioms. Now suppose that M is a rank mobility measure that satisfies the four axioms. Let k ∈ {1, …, n−1} and consider any pair 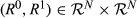 that is of upwards degree k, that is, |R0 △ R1| = k. Replacing change invariance with upwards invariance and R0
that is of upwards degree k, that is, |R0 △ R1| = k. Replacing change invariance with upwards invariance and R0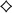 R1 with R0 △ R1 in the corresponding part of the proof of Theorem 1, we conclude that there exists ωk such that M(R0, R1) = ωk for all pairs
R1 with R0 △ R1 in the corresponding part of the proof of Theorem 1, we conclude that there exists ωk such that M(R0, R1) = ωk for all pairs 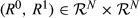 that are of upwards degree k.
that are of upwards degree k.
Now consider the following three rankings:
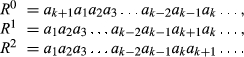
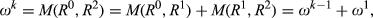

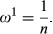
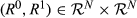 that are of upwards degree k, it follows that
that are of upwards degree k, it follows that
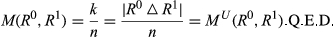
Clearly, the above proof works in the same way if upwards invariance and upwards additivity are replaced with downwards invariance and downwards additivity. Thus we immediately obtain the following characterization of our measure of downwards rank mobility MD.
Theorem 3.Given any N with n ≥ 2, a rank mobility measure M satisfies anonymity, directional normalization, downwards invariance and downwards additivity if and only if M = MD.
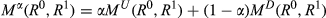 (4)
(4) . The interpretation of (4) it straightforward: the higher the value of α, the higher the relative importance of upwards movements. In general, the maximal value of Mα is
. The interpretation of (4) it straightforward: the higher the value of α, the higher the relative importance of upwards movements. In general, the maximal value of Mα is
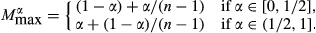
4 Discussion and an Empirical Application
The measures proposed in this paper are simple and intuitive indices of rank mobility based on the count of individuals or countries who change their position from one period to the next. However, our approach can serve as the basis of more complex aggregation procedures. For example, one may want to capture the intensity of period-to-period movements by incorporating information on the number of positions involved in each individual change. Another interesting aspect of mobility not explored here is the likelihood of expected changes, and weighted counts may be performed, where different weights are given to changes occurring in different positions of the ranking.
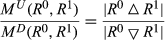
From an applied perspective, note that the proposed measures are defined on strict rankings. But ties occur frequently in data such as those relating to household incomes, for instance. The measure of income that is usually attributed to individuals is equivalent household income, thus all household members have the same income level and hence the same rank. Of course, this issue can be dealt with by considering households to be the relevant units rather than individuals. An additional potential problem arises in self-reported income data: individuals tend to report rounded values such as $3500 rather than $3473.84, say. The resulting clustering gives rise to further ties in the ranking. One way in which our measures can be applied in such cases is to consider all possible ways of breaking ties in these rankings, then calculate the index values for each of the resulting strict rankings, and finally perform an averaging operation.
Ties in rankings are unlikely to occur in many settings where the mobility of groups or countries is considered. The average income of a group (such as teachers, physicians, and so on) can be used as a proxy of the social status of these groups in a society. Analogously, countries are frequently ranked according to GDP per capita or to indices beyond GDP such as the Human Development Index or the Better Life Index—and ties are extremely rare in these contexts. What matters in public debates on these issues is the relative ranking of countries derived from these indices rather than the values of the indicators per se. Thus this is another area in which our results can be applied successfully and to which we turn next.
The remainder of the paper is devoted to an application of the proposed measure to the first and most well-known multidimensional measure of wellbeing: the Human Development Index (henceforth HDI), introduced in the first Human Development Report (henceforth HDR) by the United Nations Development Programme in 1990. The HDI is an extremely popular measure among policymakers and the general public because of its intuitive character and the large number of countries entering the evaluation. It measures human development with the three key dimensions of leading a long and healthy life, being knowledgeable, and having a decent standard of living.
The current version of the HDI was introduced on the occasion of the twentieth anniversary of the HDR in 2010. According to the definition available in United Nations Development Programme (2017a):
The health dimension is assessed by life expectancy at birth, the education dimension is measured by mean of years of schooling for adults aged 25 years and more and expected years of schooling for children of school entering age. The standard of living dimension is measured by gross national income [GNI] per capita. The HDI uses the logarithm of income, to reflect the diminishing importance of income with increasing GNI. The scores for the three HDI dimension indices are then aggregated into a composite index using [the] geometric mean.
To maximize the number of countries included in our study, we focus on the years between 2010 and 2015, the latter being the most recent available year at the time of our analysis. Before 2014, data for Sudan include South Sudan, which renders the analysis for the two countries inconsistent, and for this reason we exclude both. See United Nations Development Programme (2017b) for the list of included countries. It is standard practice in the HDR to report values of the HDI only up to the third decimal place, accepting a few ties in the ranking. When no such approximation is performed, ties are very unlikely, and indeed we do not observe any two countries among the 186 considered with the same annual HDI. We compute the head-count ratio MH along with its two directional components MU and MD for yearly mobility profiles. Moreover, the values of the ratio of upwards and downwards mobility are included because this statistic provides a clear and intuitive indication of positional improvements versus deteriorations.
The results, summarized in Table 1, are presented for the entire set of 186 countries but also separately for the 35 countries belonging to the OECD and the remaining 151 who are not members of this entity. The head-count ratio oscillates over the period under consideration, reaching its minimum value of 0.785 in the move from 2014 to 2015. When we distinguish between OECD and non-OECD countries, we notice that the head-count ratio for the former decreases over time from its highest value of 0.943 to its lowest level of 0.686 in the period between 2013 and 2014, to move back up to 0.80 in the move from 2014 to 2015. The picture for the non-OECD countries, the great majority of the observations, mimics the path of the entire sample where we observe an increase in persistence in the positions from 2012 onwards. Among the countries primarily responsible for the overall decrease in the head-count ratio are the Czech Republic (which remains in the same position starting in 2012), Côte d'Ivoire, Greece (in the same position since 2011), Norway (in the same position since 2011), Palau, Poland and Slovenia (in the same position since 2013).
| 2010–11 | 2011–12 | 2012–13 | 2013–14 | 2014–15 | |
|---|---|---|---|---|---|
| Head-count | |||||
| Entire sample | 0.919 | 0.806 | 0.898 | 0.849 | 0.785 |
| Non-OECD | 0.914 | 0.801 | 0.921 | 0.887 | 0.781 |
| OECD | 0.943 | 0.829 | 0.800 | 0.686 | 0.800 |
| Upwards | |||||
| Entire sample | 0.495 | 0.382 | 0.371 | 0.398 | 0.382 |
| Non-OECD | 0.503 | 0.364 | 0.391 | 0.430 | 0.384 |
| OECD | 0.457 | 0.457 | 0.286 | 0.257 | 0.371 |
| Downwards | |||||
| Entire sample | 0.425 | 0.425 | 0.527 | 0.452 | 0.403 |
| Non-OECD | 0.411 | 0.437 | 0.530 | 0.457 | 0.397 |
| OECD | 0.486 | 0.371 | 0.514 | 0.429 | 0.429 |
| Upwards/downwards ratio | |||||
| Entire sample | 1.165 | 0.899 | 0.704 | 0.881 | 0.947 |
| Non-OECD | 1.226 | 0.833 | 0.738 | 0.942 | 0.967 |
| OECD | 0.941 | 1.231 | 0.556 | 0.600 | 0.867 |
The upwards head-count ratio reaches its highest value during the first two years and then oscillates around 0.38. The declining trend in the move towards better positions is especially due to the OECD countries. The downwards head-count ratio for the entire sample and the non-OECD countries follows a reversed-V path, while for the OECD member states the picture more resembles a W. In all cases, MD reaches its highest value for the move from 2012 to 2013.
The last three rows of Table 1 report the values of the ratio of upwards and downwards mobility. Values greater than 1 indicate that there are relatively more countries whose human development is improving, which is a result that we observe only once and in different years: for the entire sample and for the non-OECD countries in the move from 2010 to 2011, and for the OECD countries in the transition from 2011 to 2012. For the entire sample and the non-OECD countries, the ratio is U-shaped over time, with the lowest value of 0.704 (respectively, 0.738) reached in the period between 2012 and 2013. For the OECD member states, the peak observed in the change from 2011 to 2012 is followed by a trough that reaches a value as low as 0.556 between 2012 and 2013, indicating that there are almost twice as many OECD countries whose ranks deteriorate as compared to those who move up. This observation provides some cause for concern among international bodies: the countries that move downwards significantly outnumber those that move up, a feature that appears to be rather undesirable. Note that, on the other hand, the requisite ratios increased in each of the two most recent moves. If this is the beginning of an upwards trend, then the international community may be on the right track; it may, however, be too soon to come to an overly optimistic conclusion, and continued close monitoring of these developments seems to be called for.
Acknowledgments
We thank the editor Stephen Machin and two anonymous referees for comments. Financial support from the Fonds de Recherche sur la Société et la Culture of Québec, the Social Sciences and Humanities Research Council of Canada, the Netherlands Organisation for Scientific Research (NWO) under the grants Open Competitie (OC: 400-09-354) and Innovational Research Incentives Scheme (VENI 2013: 451-13-017), and the Fonds National de la Recherche Luxembourg, is gratefully acknowledged.




