Predicting cetacean distributions in data-poor marine ecosystems
Abstract
Aim
Human activities are creating conservation challenges for cetaceans. Spatially explicit risk assessments can be used to address these challenges, but require species distribution data, which are limited for many cetacean species. This study explores methods to overcome this limitation. Blue whales (Balaenoptera musculus) are used as a case study because they are an example of a species that have well-defined habitat and are subject to anthropogenic threats.
Location
Eastern Pacific Ocean, including the California Current (CC) and eastern tropical Pacific (ETP), and northern Indian Ocean (NIO).
Methods
We used 12 years of survey data (377 blue whale sightings and c. 225,400 km of effort) collected in the CC and ETP to assess the transferability of blue whale habitat models. We used the models built with CC and ETP data to create predictions of blue whale distributions in the data-poor NIO because key aspects of blue whale ecology are expected to be similar in these ecosystems.
Results
We found that the ecosystem-specific blue whale models performed well in their respective ecosystems, but were not transferable. For example, models built with CC data could accurately predict distributions in the CC, but could not accurately predict distributions in the ETP. However, the accuracy of models built with combined CC and ETP data was similar to the accuracy of the ecosystem-specific models in both ecosystems. Our predictions of blue whale habitat in the NIO from the models built with combined CC and ETP data compare favourably to hypotheses about NIO blue whale distributions, provide new insights into blue whale habitat, and can be used to prioritize research and monitoring efforts.
Main conclusions
Predicting cetacean distributions in data-poor ecosystems using habitat models built with data from multiple ecosystems is potentially a powerful marine conservation tool and should be examined for other species and regions.
Introduction
All of the world's oceans are affected by human activities, and over 40% of the oceans are influenced by multiple activities (Halpern et al., 2008). The impacts of these activities can result in significant conservation challenges for cetaceans. Spatially explicit risk assessments can be used to address these conservation challenges because they link species distributions to the potential effects and distribution of human activities (Stelzenmüller et al., 2010; Grech et al., 2011). For example, Redfern et al. (2013) used species distribution models to assess the risk of ships striking blue, humpback, and fin whales in alternative shipping lanes for the Southern California Bight, which includes the two largest ports on the west coast of the United States. Spatially explicit risk assessments require quantitative representations of species distributions, which do not exist for many cetacean species. Consequently, in addition to investing in data collection, one of the most pressing marine conservation needs is to develop tools to predict cetacean distributions in data-poor ecosystems.
Species distribution models are a powerful tool for predicting species distributions within surveyed regions (Redfern et al., 2006; Forney et al., 2012). The ability of these models to predict distributions in novel ecosystems (i.e. extrapolation outside surveyed areas) is variable. For example, Vanreusel et al. (2007) found high levels of transferability among study sites located in the same ecoregion (sites were a maximum of 53 km apart and had similar climates, topography, soil types, and vegetation) for resource-based models of two butterfly species. In contrast, Randin et al. (2006) found weak transferability between study sites spanning subalpine and alpine belts in Switzerland and Austria for 54 plant distribution models. An assessment of model transferability between eastern and western Finland for birds, butterflies, and plants using 10 modelling techniques found good prediction accuracy and transferability for three modelling techniques (MaxEnt, generalized additive models (GAMs), and generalized boosting methods) and that plant distribution models showed lower transferability than bird and butterfly models (Heikkinen et al., 2012).
Few studies have assessed model transferability in marine ecosystems. Mannocci et al. (2015) developed a habitat modelling approach to extrapolate cetacean densities outside of surveyed areas; however, they did not have the data needed to quantitatively evaluate their predictions. The first comprehensive test of transferability for a marine predator (grey petrels) showed that models identified potential distributions (where a species could live) but failed to identify realized distributions (where a species actually occurs relative to available habitat) in novel ecosystems (Torres et al., 2015). We use data from two large, well-surveyed regions in the eastern Pacific Ocean to assess the transferability of blue whale (Balaenoptera musculus) distribution models. Blue whales are an example of a cetacean species that have well-defined habitats (i.e. they associate closely with upwelling conditions in both temperate and tropical ecosystems; Reilly & Thayer, 1990; Ballance & Pitman, 1998; Croll et al., 2005) and are subject to anthropogenic threats (e.g. ship strikes and bycatch) in data-poor regions, such as the northern Indian Ocean (NIO) (de Vos et al., 2016). Very little information is available about blue whale abundance and distribution in the NIO, but they have been observed in areas where there is high shipping traffic, seismic exploration, and commercial whale watching (Ilangakoon, 2012; Randage et al., 2014) and ship strikes have been documented off Sri Lanka (de Vos et al., 2013).
We built blue whale distribution models using systematic line-transect survey data collected by NOAA Fisheries’ Southwest Fisheries Science Center between 1991 and 2009 in two ecosystems within the eastern Pacific Ocean: the California Current (CC) and eastern tropical Pacific (ETP). The CC and ETP contain some of the most extensive cetacean line-transect survey effort in the world (Kaschner et al., 2012). Together they cover a large spatial extent that includes a diversity of habitats. The 12 marine mammal and ecosystem assessment surveys conducted in these regions span a 19-year period and cover a broad range of interannual variability. Models were built using data from the CC, ETP, and both ecosystems combined. Throughout the world oceans, blue whales forage on krill in upwelling areas associated with the shelf edge and are also found in areas of oceanic upwelling (Reilly & Thayer, 1990; Fiedler et al., 1998; Palacios, 1999; Gill et al., 2011; Torres, 2013). We derived habitat variables that indicate upwelling and processes that concentrate krill from a global ocean reanalysis data set and a map of seafloor geomorphic features. The models were used to predict blue whale distributions in the CC, ETP, and NIO. Model predictions were assessed using sightings data (CC, ETP, and NIO) and whaling data (NIO).
Methods
Blue whale ecology and data
Blue whale distributions have been extensively studied in temperate and tropical ecosystems within the eastern Pacific Ocean (15° S to 45° N) (e.g. Reilly & Thayer, 1990; Fiedler et al., 1998). The highest blue whale densities in these ecosystems are associated with upwelling-modified waters that are highly productive and support dense aggregations of euphausiids (e.g. krill). In the temperate CC, blue whales feed on krill patches associated with the shelf edge (Fiedler et al., 1998). When topographic breaks in the shelf edge are located down-current from upwelling centres, they may provide foraging blue whales with an opportunity for high energy gains (Croll et al., 2005). In the ETP, upwelling is associated with the shelf edge (near the Galápagos Islands and at the equatorward extremes of the California and Peru Currents) and oceanic upwelling occurs along the equator and at the Costa Rica Dome (Kessler, 2006).
We used distance to the shelf edge from a global, seafloor geomorphic features map (Harris et al., 2014) to represent the importance of this topographic feature in concentrating krill. We used wind speed (WSPD) and sea surface temperature (SST), salinity (SSS), and height (SSH) to identify variations in upwelling, circulation, and water column stratification that may affect forage availability. These four dynamic variables were selected because upwelling is generally expected to be stronger in coastal and equatorial areas where strong winds can drive offshore transport or divergence of surface waters. Upwelled waters are also expected to be colder and have higher salinity concentrations than adjacent surface waters. The higher density of upwelled waters in the surface layer is expected to result in lower sea surface heights (Talley et al., 2011).
Interactions between these variables can also be important indicators of upwelling and other oceanographic processes. For example, interactions between distance to shelf and the dynamic variables may indicate local areas of coastal upwelling and interactions between SSH and other dynamic variables may provide a better representation of stratification and upwelling than SSH alone. The interaction between SST and SSS can differentiate surface water masses and interactions between WSPD and the other dynamic variables may reflect the influence of winds on sea surface heat exchange and evaporation (Talley et al., 2011). The four dynamic variables were extracted from a Simple Ocean Data Assimilation reanalysis data set (SODA; Carton & Giese, 2008). These data are available as monthly fields for the global ocean at 0.5-degree resolution from 1871 through 2010 (SODA 2.2.4, http://apdrc.soest.hawaii.edu/dods/public_data/SODA). We extracted SST and SSS values at 5.01 m, which is the shallowest depth available in the SODA data. We derived WSPD from zonal and meridional wind stress. The monthly 0.5-degree fields were interpolated using a two-dimensional cubic spline to a 0.1-degree resolution using the MATLAB routine interp2 (MATLAB, 2016).
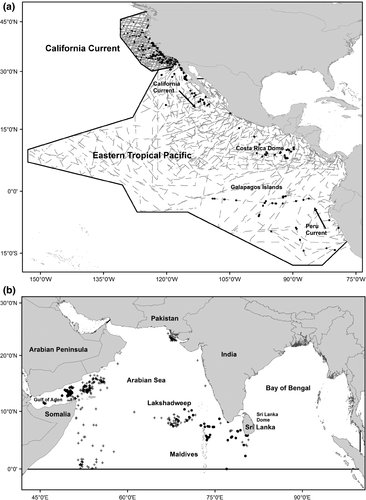
We used 377 sightings of one or more blue whales (c. 441 individuals in the CC and 226 individuals in the ETP) and c. 225,400 km of effort (Fig. 1a) from surveys conducted by NOAA Fisheries’ Southwest Fisheries Science Center from August through November (CC: 1991, 1993, 1996, 2001, 2005, 2008, and 2009; ETP: 1998, 1999, 2000, 2003, and 2006). Line-transect surveys were conducted in both ecosystems using large research vessels (i.e. observations were made from a flying bridge located between 10 and 15 m above the sea surface). Survey effort consisted of two observers using pedestal-mounted 25 × 150 binoculars to search for marine mammals during daylight hours; a third observer searched by eye or with 7× handheld binoculars and recorded both sightings data and survey conditions. When marine mammals were detected, the vessel approached the group as needed to identify species and estimate group size (see Kinzey et al., 2000 for detailed survey protocols). We obtained a single group size estimate by averaging the best estimates from all observers. If no observers provided a best estimate, we averaged the minimum estimates.
We divided transects into continuous effort segments of c. 10 km using the approach described by Becker et al. (2010). Distance to the shelf edge was calculated at the midpoint of each segment using the Near tool in ArcGIS (version 10.2.2; Esri, Redlands, CA, USA). Monthly SODA habitat variables were averaged over the calendar year to represent the full upwelling cycle (Kessler, 2006; Bograd et al., 2009) and to facilitate transferability to regions that have been surveyed in different seasons (i.e. the NIO). We used bilinear interpolation to extract WSPD, SST, SSS, and SSH from the averaged SODA grids at the segment midpoint.
The number of blue whales was predicted in each cell of a 10 km × 10 km grid spanning the study areas. For predictions in the CC and ETP, monthly SODA habitat variables were averaged from July to December to capture the upwelling conditions associated with the surveys. Predictions were made for each year of survey data using distance to shelf calculated at the centre of each grid cell and the averaged SODA variables extracted at the centre of each grid cell by bilinear interpolation. The predictions for each year were averaged to summarize the predicted number of blue whales across multiple years. The average predictions represent expected long-term patterns in blue whale distributions between July and December; they do not account for within-year variation in distributions.
Blue whale data in our NIO study area (defined as north of the equator) are extremely limited (Fig. 1b). They consist of Soviet whaling data (n = 833) that were collected primarily in November (other months include October and December) between 1963 and 1966 (Mikhalev, 2000). A small number of more recent sightings (n = 17) were available from a survey of the western tropical Indian Ocean conducted from March to June in 1995 (Ballance & Pitman, 1998). Sightings were also available from a study conducted around the Maldives in April of 1998 (n = 4; Ballance et al., 2001) and studies conducted on the southern coast of Sri Lanka in January and March of 2012 (n = 533; A. de Vos unpublished data and de Vos et al., 2014b).
Blue whale distribution models cannot be built using the NIO data because of their limited spatial and temporal resolution. However, multiple studies have suggested that blue whale ecology may be similar in the NIO and eastern Pacific Ocean. For example, blue whales have been observed feeding off the southern and northeastern coasts of Sri Lanka in upwelling areas associated with the shelf edge and topographic breaks in the shelf edge (e.g. submarine canyons and sloping bathymetry) (Alling et al., 1991; Randage et al., 2014). The characteristics of these feeding areas are similar to the characteristics of their feeding areas in the CC. Ballance & Pitman (1998) found that blue whale sightings were highly localized and that many of the whales were likely feeding during a survey of the western tropical Indian Ocean. Consequently, they hypothesized that blue whales in the Indian Ocean may be associated with localized, productive areas, similar to blue whale distributions in the ETP. Additionally, interannual variability in blue whale distributions off the southern coast of Sri Lanka has been hypothesized to correspond to changes in productivity (de Vos et al., 2014b).
We use our models that capture the full upwelling cycle in the eastern Pacific Ocean to predict blue whale distributions in the NIO because of the potential similarity of blue whale ecology in both regions. Upwelling in the NIO is strongly influenced by seasonally reversing monsoon winds that can be divided into four periods: Northeast Monsoon (December–April), first inter-monsoon (May), Southwest Monsoon (June–October), and second inter-monsoon (November) (Tomczak & Godfrey, 2005). During the Southwest Monsoon, wind and current patterns create strong upwelling off the coasts of Somalia and the Arabian Peninsula (Schott & McCreary, 2001); upwelling also occurs off southwest India and Sri Lanka (Schott & McCreary, 2001). Consequently, we expect lower SST, higher SSS, and lower SSH in these regions. Upwelling is generally weaker and more localized during the Northeast Monsoon (Schott & McCreary, 2001; de Vos et al., 2014a). An example of a local, productive area occurs off the southern coast of Sri Lanka. Monsoon winds result in coastal upwelling and, concomitantly, increased productivity in this area (de Vos et al., 2014a). We predict blue whale distributions in the NIO using monthly SODA habitat variables averaged from January to March and July to September to capture the upwelling patterns associated with each monsoon season. Predictions were made in each cell of a 10 km × 10 km grid for both monsoon seasons in each year within the two decades that span the CC and ETP time series (i.e. 1991–2010); the predictions in each monsoon season were averaged to summarize the predicted number of blue whales.
Habitat models
We used GAMs (Wood, 2006) to relate the number of blue whales in each transect segment to the habitat variables, largely following the methods of Becker et al. (2016). We fit GAMs in the R (version 3.1.1; R Core Team, 2014) package mgcv (version 1.8-4; Wood, 2011). We used a Tweedie distribution (Miller et al., 2013) to account for overdispersion and restricted maximum likelihood (REML) to optimize the parameter estimates. Marra & Wood (2011) found that REML allows for better smoothing parameter estimation than generalized cross-validation.
One model was built using a thin plate regression spline for each of the five habitat variables. Variables were selected for exclusion from the model using a shrinkage approach that modifies the smoothing penalty (Marra & Wood, 2011). Unmodified smoothing penalties do not typically remove a smooth from a model because they only shrink functions in the penalty range space and do not shrink functions in the penalty null space. The shrinkage approach adds a shrinkage term to the penalty null space, which allows the smooth to become identically zero and be removed from the model (Marra & Wood, 2011). Additionally, we removed variables from the model that had approximate P-values > 0.05. Models were refit after removing non-significant variables to ensure all remaining variables had an approximate P-value < 0.05.
Ten additional models were built by replacing each pair of habitat variables with a tensor product interaction term and using a thin plate regression spline for each of the three remaining habitat variables. Variable selection for the models with interactions followed the same approach as used for the model with no interactions. Models were built using data from the CC, ETP, and both ecosystems combined. Models built using only the CC or ETP data are referred to as ecosystem-specific models. The area searched on each segment was included as an offset in all models because the amount of effort varied among segments. The area searched was calculated as 2 × ESW × g(0) × distance travelled on effort, where ESW is the effective strip width and g(0) is a correction for missing animals on the transect. We use ESW and g(0) estimates derived from some of the same surveys in the CC (Barlow, 2003) and similar surveys in the ETP (survey data were collected using the same methods and some of the same vessels; Ferguson & Barlow, 2001), but did not truncate the most distant sightings because we wanted to maximize the sample sizes for our models. Using all sightings might introduce a small bias in predictions of the absolute number of whales, but would not affect spatial patterns of relative whale abundance.
Model assessment
We created presence and absence data points using the midpoint of the transect segments (i.e. segments with no sightings were assigned an absence and segments with one or more sightings were assigned a presence) to evaluate model performance in the CC and ETP. The NIO blue whale data are comprised primarily of presence-only data. We evaluated model performance for each monsoon period in the NIO using the data collected within the monsoon period (December to April for the Northeast Monsoon and June to October for the Southwest Monsoon) and data from monsoon transition periods (data were only collected during the November inter-monsoon). We also randomly generated 500 sets of pseudo-absences for each monsoon period; the number of generated absences was equal to the number of presences. Absences were generated throughout the study area because presences and absences can occur close together in the eastern Pacific Ocean across a range of time scales (i.e. within a single survey period and between survey periods). We used the same approach to generate pseudo-absence data for eastern Pacific Ocean ecosystems and compared the results of model assessment conducted with absence versus pseudo-absence data.
We assess the models using the area under the receiver operating characteristic curve (AUC) (Fawcett, 2006) and the true skill statistic (TSS) (Allouche et al., 2006). While the reliability of AUC has been questioned, it can be used to compare models for a single species and study extent (Lobo et al., 2008). Consequently, we use AUCs to compare model predictions within each ecosystem. The TSS is a threshold-dependent measure of model performance that has been shown to be independent of species prevalence (Allouche et al., 2006). We used the sensitivity-specificity sum maximization approach (Liu et al., 2005) to obtain thresholds for species presence when calculating TSS.
Golicher et al. (2012) show that the interpretation of AUC can be compromised when using pseudo-absence data. Both AUC and TSS must be calculated using pseudo-absences in the NIO because very few absence data are available. Consequently, we also evaluate models by the percentage of sightings contained in the highest 2% of predicted blue whale densities. The highest 2% of predicted densities was selected because biologically important feeding areas (BIAs) cover c. 1.4% of the CC study area. The CC BIAs were primarily identified using non-systematic, coastal surveys conducted by small boat to maximize encounters with blue whales for photo-identification and tagging studies (Calambokidis et al., 2015). They provide an independent estimate of the prevalence of important areas for blue whales in the CC. No independent estimates of prevalence are available in the ETP and NIO. Consequently, we evaluate the percentage of sightings in the highest 2% of predicted densities in all ecosystems. We also use the percentage of sightings in the highest 10% of predicted blue whale densities to ensure that an increasing percentage of sightings is included as we expand the area deemed to be good habitat.
All four measures of model performance were used to assess how well the ecosystem-specific models predicted within ecosystem distributions (e.g. predictions of blue whale distributions in the CC made by models built with CC data) and how well they predicted a novel ecosystem (e.g. predictions of blue whale distributions in the ETP made by models built with CC data). All four measures were also used to assess how well models built with data from the CC and ETP predicted within ecosystem distributions (e.g. predictions of blue whale distributions in the CC made by models built with combined CC and ETP data). Each model was assigned four ranks based on the measures of model performance: AUC, TSS, and the percentage of sightings contained in the highest 2% and 10% of predicted densities. The mean of the four ranks was used to select the best model in each ecosystem. We used a chi-square statistic to test whether sightings in the NIO occurred in the highest 2% and 10% of predicted blue whale densities more often than expected by random chance.
Results
Are the models transferable in the eastern Pacific Ocean?
The functional forms of the relationships between the number of blue whales and each habitat variable, as characterized by the thin plate regression splines, were similar across models with and without interaction terms. Consequently, the primary habitat relationships are shown in Fig. 2 using the models developed without interactions for all three data sets (CC, ETP, and both ecosystems combined). In the CC, blue whales were associated with the shelf and upwelling conditions. The strongest relationship was between increased blue whale numbers and increased SSS. Blue whale numbers also decreased in waters that had the lowest and highest SSH values. A similar and strong association was also seen between blue whale numbers and SSH in the ETP. However, the relationship with SSS was much weaker in the ETP and this variable was excluded from the model built without interactions. Instead, increased numbers of blue whales were found from the shelf edge out to a distance of c. 1,000 km. Models built with the combined CC and ETP data were characterized by the strongest habitat relationships in the ecosystem-specific models (i.e. the models built with only the CC data or only the ETP data).
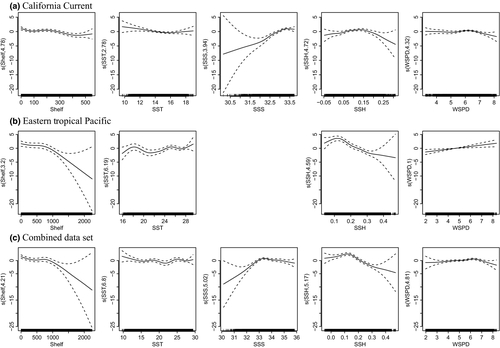
All four measures of model performance suggest that the ecosystem-specific models accurately predict within ecosystem blue whale distributions, but they do not accurately predict blue whale distributions in a novel ecosystem (Tables 1 & 2). Specifically, there is a large drop in the AUCs and TSSs when models built with data from one ecosystem are used to predict distributions in the other ecosystem (Tables 1 & 2). Additionally, larger numbers of sightings are contained in the highest 2% and 10% of predicted blue whale densities when the ecosystem-specific models are used to make predictions within their respective ecosystems (e.g. 15% and 50% of sightings in the CC, respectively, and 41% and 64% of sightings in the ETP, respectively), compared to making predictions in novel ecosystems (Tables 1 & 2).
| Model | Data set | Percentage of sightings | AUC | TSS | Mean rank | |
|---|---|---|---|---|---|---|
| Highest 2% of predictions | Highest 10% of predictions | |||||
| Shelf + SSS + SSH × WSPD | CC | 15.38 | 45.73 | 0.760 | 0.431 | 1.5 |
| Shelf × SSH + SSS + WSPD | CC | 14.53 | 50.00 | 0.758 | 0.427 | 2.75 |
| Shelf + SST × SSH + SSS + WSPD | CC | 15.38 | 44.02 | 0.756 | 0.416 | 4.75 |
| Shelf × SSS + SST + SSH + WSPD | CC + ETP | 15.38 | 44.87 | 0.751 | 0.412 | 6.75 |
| Shelf + SST × WSPD + SSS + SSH | CC + ETP | 14.96 | 41.88 | 0.752 | 0.412 | 8.75 |
| Shelf + SST + SSS + SSH + WSPD | CC | 11.97 | 43.16 | 0.746 | 0.425 | 9.25 |
| Shelf × SSH + SSS + WSPD | CC + ETP | 14.10 | 44.02 | 0.752 | 0.411 | 9.25 |
| Shelf × SSS + SST + SSH + WSPD | CC | 11.11 | 43.16 | 0.746 | 0.424 | 11 |
| Shelf × SST + SSS + SSH + WSPD | CC + ETP | 14.53 | 41.88 | 0.749 | 0.403 | 11.25 |
| Shelf + SST × SSS + SSH + WSPD | CC + ETP | 11.97 | 40.17 | 0.749 | 0.413 | 11.75 |
| Shelf × WSPD + SST + SSS + SSH | CC + ETP | 11.97 | 40.17 | 0.749 | 0.413 | 12.25 |
| Shelf + SST + SSS × WSPD + SSH | CC + ETP | 12.39 | 40.60 | 0.745 | 0.413 | 12.75 |
| Shelf + SST × SSH + SSS + WSPD | CC + ETP | 14.53 | 38.03 | 0.753 | 0.410 | 12.75 |
| Shelf × WSPD + SST + SSS + SSH | CC | 12.39 | 38.46 | 0.743 | 0.426 | 13 |
| Shelf + SST × WSPD + SSS + SSH | CC | 9.40 | 44.44 | 0.744 | 0.417 | 13 |
| Shelf × SST + SSS + WSPD | CC | 11.54 | 44.02 | 0.739 | 0.412 | 13.75 |
| Shelf + SST + SSS × SSH + WSPD | CC | 11.54 | 39.32 | 0.739 | 0.426 | 14 |
| Shelf + SST + SSS + SSH + WSPD | CC + ETP | 9.83 | 41.88 | 0.747 | 0.413 | 14 |
| Shelf + SST + SSS × WSPD + SSH | CC | 9.83 | 38.89 | 0.742 | 0.431 | 15 |
| Shelf + SST + SSS + SSH × WSPD | CC + ETP | 11.11 | 40.60 | 0.745 | 0.412 | 15.5 |
| Shelf + SST × SSS + SSH + WSPD | CC | 10.68 | 39.32 | 0.736 | 0.422 | 16.5 |
| Shelf + SST + SSS × SSH + WSPD | CC + ETP | 8.55 | 41.03 | 0.736 | 0.408 | 20 |
| Shelf × WSPD + SST + SSH | ETP | 10.68 | 35.47 | 0.618 | 0.275 | 22.25 |
| Shelf + SST + SSS + SSH × WSPD | ETP | 10.26 | 29.06 | 0.581 | 0.210 | 24.25 |
| Shelf + SST + SSH + WSPD | ETP | 2.14 | 31.62 | 0.581 | 0.216 | 25.25 |
| Shelf × SST + SSH | ETP | 0.00 | 22.65 | 0.663 | 0.286 | 26 |
| Shelf × SSS + SST + SSH | ETP | 8.97 | 26.92 | 0.566 | 0.123 | 26.5 |
| Shelf × SSH + SST + SSS + WSPD | ETP | 7.69 | 23.50 | 0.564 | 0.162 | 27 |
| Shelf + SST + SSS × WSPD + SSH | ETP | 0.85 | 20.09 | 0.540 | 0.151 | 28.5 |
| Shelf + SST + SSS × SSH + WSPD | ETP | 0.43 | 16.67 | 0.511 | 0.098 | 30 |
| Shelf + SST × WSPD + SSH | ETP | 0.00 | 5.98 | 0.527 | 0.080 | 30.75 |
| Shelf + SST × SSH + WSPD | ETP | 0.00 | 2.56 | 0.474 | 0.079 | 31.75 |
| Shelf + SST × SSS + SSH + WSPD | ETP | 0.00 | 0.43 | 0.408 | 0.084 | 31.75 |
| Model | Data set | Percentage of sightings | AUC | TSS | Mean Rank | |
|---|---|---|---|---|---|---|
| Highest 2% of predictions | Highest 10% of predictions | |||||
| Shelf + SST × SSH + WSPD | ETP | 40.78 | 64.08 | 0.883 | 0.675 | 3.5 |
| Shelf × SSS + SST + SSH | ETP | 33.98 | 53.40 | 0.890 | 0.711 | 4 |
| Shelf + SST × SSH + SSS + WSPD | CC + ETP | 30.10 | 75.73 | 0.887 | 0.666 | 4.5 |
| Shelf × WSPD + SST + SSH | ETP | 25.24 | 58.25 | 0.883 | 0.690 | 5.75 |
| Shelf + SST × SSS + SSH + WSPD | CC + ETP | 25.24 | 60.19 | 0.869 | 0.670 | 8.75 |
| Shelf + SST + SSH + WSPD | ETP | 25.24 | 59.22 | 0.874 | 0.669 | 8.75 |
| Shelf + SST + SSS × SSH + WSPD | ETP | 36.89 | 61.17 | 0.874 | 0.639 | 9 |
| Shelf × SSS + SST + SSH + WSPD | CC + ETP | 25.24 | 40.78 | 0.877 | 0.699 | 9.75 |
| Shelf × SSH + SST + SSS + WSPD | ETP | 26.21 | 62.14 | 0.874 | 0.635 | 9.75 |
| Shelf + SST + SSS × WSPD + SSH | ETP | 26.21 | 57.28 | 0.876 | 0.644 | 9.75 |
| Shelf × SST + SSS + SSH + WSPD | CC + ETP | 25.24 | 45.63 | 0.871 | 0.679 | 11.5 |
| Shelf + SST × SSS + SSH + WSPD | ETP | 25.24 | 57.28 | 0.867 | 0.661 | 11.75 |
| Shelf × SST + SSH | ETP | 26.21 | 55.34 | 0.868 | 0.648 | 12 |
| Shelf + SST + SSS + SSH × WSPD | CC + ETP | 25.24 | 50.49 | 0.868 | 0.655 | 13.5 |
| Shelf + SST + SSS + SSH + WSPD | CC + ETP | 25.24 | 50.49 | 0.864 | 0.669 | 13.75 |
| Shelf + SST + SSS × WSPD + SSH | CC + ETP | 25.24 | 51.46 | 0.866 | 0.657 | 14 |
| Shelf × SSH + SSS + WSPD | CC + ETP | 27.18 | 47.57 | 0.865 | 0.659 | 14.25 |
| Shelf × WSPD + SST + SSS + SSH | CC + ETP | 24.27 | 48.54 | 0.867 | 0.684 | 14.5 |
| Shelf + SST × WSPD + SSS + SSH | CC + ETP | 25.24 | 48.54 | 0.859 | 0.660 | 15.25 |
| Shelf + SST + SSS + SSH × WSPD | ETP | 23.30 | 53.40 | 0.875 | 0.641 | 15.25 |
| Shelf + SST × WSPD + SSH | ETP | 24.27 | 36.89 | 0.868 | 0.675 | 16 |
| Shelf × SSS + SST + SSH + WSPD | CC | 26.21 | 51.46 | 0.731 | 0.368 | 17.25 |
| Shelf + SST + SSS × SSH + WSPD | CC + ETP | 25.24 | 45.63 | 0.857 | 0.645 | 17.5 |
| Shelf + SST × SSH + SSS + WSPD | CC | 0.00 | 1.94 | 0.758 | 0.523 | 24.25 |
| Shelf + SSS + SSH × WSPD | CC | 0.00 | 0.00 | 0.716 | 0.466 | 25.75 |
| Shelf + SST + SSS + SSH + WSPD | CC | 0.00 | 0.00 | 0.692 | 0.427 | 26.25 |
| Shelf × SST + SSS + WSPD | CC | 1.94 | 36.89 | 0.625 | 0.227 | 26.25 |
| Shelf × WSPD + SST + SSS + SSH | CC | 0.00 | 0.97 | 0.680 | 0.304 | 27 |
| Shelf + SST + SSS × SSH + WSPD | CC | 0.00 | 0.97 | 0.604 | 0.351 | 27 |
| Shelf + SST + SSS × WSPD + SSH | CC | 0.00 | 2.91 | 0.600 | 0.334 | 27 |
| Shelf + SST × WSPD + SSS + SSH | CC | 0.00 | 0.00 | 0.569 | 0.202 | 29 |
| Shelf + SST × SSS + SSH + WSPD | CC | 0.00 | 0.00 | 0.537 | 0.188 | 29.5 |
| Shelf × SSH + SSS + WSPD | CC | 0.00 | 0.00 | 0.482 | 0.175 | 30 |
The four measures of model performance also show that the accuracy of predictions from the ecosystem-specific models within their respective ecosystems is similar to the accuracy of predictions from models built with data from both ecosystems combined (Tables 1 & 2). In particular, the AUCs and TSSs for models built with data from both ecosystems combined are similar to the AUCs and TSSs for the ecosystem-specific models within their respective ecosystems. A large percentage of sightings are also contained in the highest 2% and 10% of blue whale densities predicted by the models built with data from both ecosystems combined (15% and 44% of sightings in the CC, respectively, and 30% and 76% of sightings in the ETP, respectively). For the ecosystem-specific models and the models built with data from both ecosystems combined, the overall model assessment results were similar for the absence and pseudo-absence data. In particular, the same models were selected as the best models in both the CC and ETP. Although the mean model ranks were not identical when using pseudo-absences, there was a high correlation between the mean ranks calculated using absence and pseudo-absence data in both ecosystems (> 0.95).
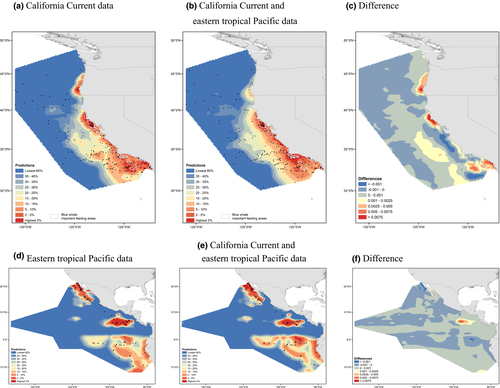
Predictions of blue whale distributions in the CC from the best model built with CC data and the best model built with data from both ecosystems combined (Fig. 3a,b) show higher blue whale densities close to shore and that higher densities occur farther offshore in the south. The largest differences in the maps occur in the areas of the highest predicted densities near the coast (Fig. 3c). Predictions of blue whale distributions in the ETP from the best model built with ETP data and the best model built with data from both ecosystems combined reflect upwelling areas: near the Galápagos Islands, in the California and Peru Currents, along the equator, and at the Costa Rica Dome (Fig. 3d,e). Differences between the predictions (Fig. 3f) are smaller than the differences in the CC (Fig. 3c) and occur primarily in the Costa Rica Dome.
Can the models predict distributions in a novel, data-poor ecosystem?
We used the models built with CC and ETP data to predict blue whale distributions in the NIO because these models were able to accurately capture blue whale distributions in both eastern Pacific Ocean ecosystems. The four measures of model performance identify a single model that provides the best match to the NIO blue whale data for the Northeast Monsoon (i.e. January–March). In particular, the model that contains sea surface salinity, wind speed, and an interaction between distance to the shelf edge and sea surface height was ranked as the best model by all four measures (Table 3). The chi-square statistic shows that this model contains significantly (P < 0.0001) more sightings in the highest 2% and 10% of predicted blue whale densities (11% and 18% of sightings, respectively) than expected by random chance.
| Model | Data set | Percentage of sightings | AUC | TSS | Mean rank | |
|---|---|---|---|---|---|---|
| Highest 2% of predictions | Highest 10% of predictions | |||||
| Northeast Monsoon | ||||||
| Shelf × SSH + SSS + WSPD | CC + ETP | 11.25 | 18.49 | 0.732 | 0.447 | 1 |
| Shelf + SST × SSH + SSS + WSPD | CC + ETP | 9.36 | 17.21 | 0.640 | 0.348 | 3.75 |
| Shelf + SST + SSS + SSH × WSPD | CC + ETP | 6.04 | 16.38 | 0.666 | 0.398 | 4.5 |
| Shelf + SST × SSS + SSH + WSPD | CC + ETP | 8.91 | 18.11 | 0.518 | 0.258 | 5 |
| Shelf × WSPD + SST + SSS + SSH | CC + ETP | 5.28 | 18.49 | 0.505 | 0.285 | 5.5 |
| Shelf + SST × WSPD + SSS + SSH | CC + ETP | 9.43 | 18.34 | 0.505 | 0.169 | 5.75 |
| Shelf + SST + SSS + SSH + WSPD | CC + ETP | 7.85 | 18.19 | 0.472 | 0.202 | 7 |
| Shelf + SST + SSS × WSPD + SSH | CC + ETP | 1.28 | 8.83 | 0.521 | 0.235 | 7.5 |
| Shelf + SST + SSS × SSH + WSPD | CC + ETP | 0.68 | 0.68 | 0.551 | 0.233 | 8.25 |
| Shelf × SSS + SST + SSH + WSPD | CC + ETP | 0.08 | 4.15 | 0.505 | 0.238 | 8.5 |
| Shelf × SST + SSS + SSH + WSPD | CC + ETP | 6.64 | 13.21 | 0.410 | 0.095 | 9 |
| Southwest Monsoon | ||||||
| Shelf × SSS + SST + SSH + WSPD | CC + ETP | 18.96 | 32.72 | 0.799 | 0.501 | 3.25 |
| Shelf + SST × SSS + SSH + WSPD | CC + ETP | 15.31 | 33.57 | 0.778 | 0.525 | 3.75 |
| Shelf + SST + SSS + SSH + WSPD | CC + ETP | 14.75 | 37.78 | 0.768 | 0.490 | 4 |
| Shelf × SST + SSS + SSH + WSPD | CC + ETP | 6.74 | 37.22 | 0.796 | 0.512 | 4.5 |
| Shelf + SST + SSS × WSPD + SSH | CC + ETP | 12.22 | 36.94 | 0.756 | 0.436 | 5.5 |
| Shelf × SSH + SSS + WSPD | CC + ETP | 10.81 | 34.27 | 0.757 | 0.433 | 6 |
| Shelf + SST × SSH + SSS + WSPD | CC + ETP | 16.43 | 40.87 | 0.606 | 0.321 | 6 |
| Shelf + SST × WSPD + SSS + SSH | CC + ETP | 8.57 | 47.05 | 0.637 | 0.374 | 6.25 |
| Shelf × WSPD + SST + SSS + SSH | CC + ETP | 17.56 | 27.67 | 0.630 | 0.229 | 7.75 |
| Shelf + SST + SSS + SSH × WSPD | CC + ETP | 9.27 | 31.74 | 0.668 | 0.332 | 8 |
| Shelf + SST + SSS × SSH + WSPD | CC + ETP | 0.00 | 13.90 | 0.529 | 0.175 | 11 |
In the Southwest Monsoon (i.e. July–September), the model with the best mean rank did not have the best rank for all four measures of model performance. This model, which contains sea surface temperature and height, wind speed, and an interaction between distance to the shelf edge and sea surface salinity, had the best rank for the percentage of sightings contained in the highest 2% of predicted densities and AUC, but ranked lower for the percentage of sightings contained in the highest 10% of predicted densities and TSS (Table 3). However, the chi-square statistic shows that this model contains significantly (P < 0.0001) more sightings in the highest 2% and 10% of predicted blue whale densities (19% and 33% of sightings, respectively) than expected by random chance.
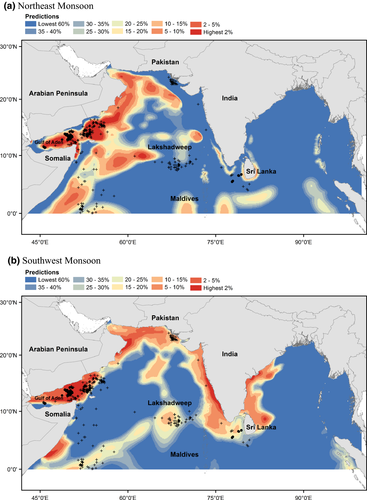
Blue whale habitat was predicted off the Arabian Peninsula and in the Gulf of Aden during both monsoon seasons, although there is a shift towards more coastal habitat during the Southwest Monsoon season (Fig. 4). Blue whale habitat was also predicted around southwestern India and Sri Lanka in both seasons, although there is a shift towards more offshore habitat during the Southwest Monsoon, including the Sri Lanka Dome, an oceanic upwelling feature off the east coast of Sri Lanka. The biggest change between seasons was an increase in predicted habitat along the coast of Pakistan, to the west of the Maldives and Lakshadweep, and on the eastern and western coasts of India during the Southwest Monsoon. Whaling data collected in waters on the Pakistan–India border and west of the Maldives and Lakshadweep during the November inter-monsoon occur in areas predicted to contain few blues whales during the Northeast Monsoon (Fig. 4). However, these areas are predicted to contain habitat (i.e. higher numbers of blue whales) during the Southwest Monsoon.
Discussion
Are the models transferable in the eastern Pacific Ocean?
In the eastern Pacific Ocean, blue whales are associated with upwelling-modified waters that are highly productive and support dense aggregations of euphausiids. Intermediate SSH was an important indicator of the upwelling-modified waters associated with blue whale habitat in our models for both eastern Pacific Ocean ecosystems (i.e. the CC and ETP). Pardo et al. (2015) also found higher blue whale densities in waters with intermediate values of absolute dynamic topography (SSH is one of the variables used to calculate absolute dynamic topography). They suggested that blue whales may be found in waters with intermediate values because biomass aggregations tend to be found downstream from upwelling centres.
Although SSH was an important variable in both ecosystem-specific models, the models were not transferable. Consequently, the models suggest that other variables are also needed to identify blue whale habitat and that these variables are unique in each ecosystem. In the CC, there is a large difference between the higher salinity upwelling-modified waters and the lower salinity surface waters flowing from the north (Auad et al., 2011). Consequently, salinity was an important indicator of upwelling-modified waters in blue whale habitat models for the CC. The ETP is oceanographically more diverse and contains regions with little to no near-surface salinity gradients and extreme thermal stratification (Fiedler & Talley, 2006), reducing the importance of salinity as an indicator of upwelling-modified waters in blue whale habitat models. However, the range of distances to the shelf edge is much larger in the ETP than the CC and blue whales occur closer to the shelf edge in both regions. Consequently, distance to the shelf edge was an important variable in blue whale habitat models for the ETP and indicates that blue whales are not found in the most offshore waters.
Models built with the combined CC and ETP data were characterized by the strongest habitat relationships in the ecosystem-specific models. The accuracy of predictions from these models was similar to the accuracy of the ecosystem-specific models within their respective ecosystems. However, the best model built with data from both ecosystems combined was unique in each ecosystem. Specifically, the best CC model contained an interaction between distance to the shelf edge and salinity, indicating the importance of upwelling-modified waters close to the shelf edge. The best ETP model contained an interaction between SST and SSH, indicating the importance of water column stratification. The flexibility in our modelling framework (developing a suite of models using the combined data sets and independently selecting the best model for each ecosystem, rather than selecting a single best model for both ecosystems) resulted in accurate predictions of blue whale distributions throughout the entire region (the eastern Pacific Ocean).
Can the models predict distributions in a novel, data-poor ecosystem?
We used the models built with CC and ETP data to predict blue whale distributions in the NIO because these models were able to accurately capture blue whale distributions in both eastern Pacific Ocean ecosystems and studies have suggested that blue whale ecology is likely similar in the eastern Pacific Ocean and the NIO. We selected the best models for both eastern Pacific Ocean ecosystems using the mean rank of four measures of model performance. Model ranks calculated using presence and absence data were similar to model ranks calculated using presence and pseudo-absence data and the same models were selected as the best models in both eastern Pacific Ocean ecosystems. Consequently, we selected the best models for each monsoon season in the NIO using the mean rank of the four measures of model performance. Predictions from the best models for both monsoon seasons compare favourably to hypotheses about NIO blue whale distributions and provide new insights into blue whale habitat.
Anderson et al. (2012) described blue whale distribution and movement patterns in the NIO from a comprehensive synthesis of available data, including the data used in our study, other sightings data, strandings, and acoustic detections. They hypothesize that blue whales feed in areas associated with strong upwelling during the Southwest Monsoon and seek out localized, highly productive areas during the Northeast Monsoon, when upwelling is weaker. Ilangakoon & Sathasivam's (2012) review of sightings and strandings from Sri Lanka and India suggests that blue whales are present in this small, highly productive feeding area throughout the year. They suggest that blue whales make localized movements within this area, including potentially moving farther off the east coast of Sri Lanka during the Southwest Monsoon to feed in the Sri Lanka Dome.
Our models predict blue whale habitat in the upwelling areas suggested by Anderson et al. (2012) during the Southwest Monsoon (i.e. off the Arabian Peninsula, southwestern India, and western Sri Lanka). However, our models also predict that blue whale habitat occurs in these areas during the Northeast Monsoon. The habitat predicted in the western NIO during the Northeast Monsoon occurs farther offshore than the habitat predicted during the Southwest Monsoon, suggesting that localized movements may occur in this region. A narrow band of habitat is predicted on the shelf edge off southwestern India and around eastern, western, and southern Sri Lanka during the Northeast Monsoon. During the Southwest Monsoon, the habitat expands offshore and covers a much larger area, including the Sri Lanka Dome. This expansion is consistent with the localized movements suggested by Ilangakoon & Sathasivam (2012).
Our models predict blue whale habitat along the coast of Pakistan and to the west of the Maldives and Lakshadweep during the Southwest Monsoon; our models predict low numbers of blue whales in these areas during the Northeast Monsoon. Anderson et al. (2012) hypothesized that whales would be present in these areas during the Northeast Monsoon. Whaling data were primarily collected in these areas during the November inter-monsoon, resulting in a correspondence between our predictions and these data in the Southwest Monsoon and a mismatch between our predictions and these data in the Northeast Monsoon. Time lags between upwelling and biomass accumulation may suggest that the habitat predicted by our models in these regions during the Southwest Monsoon (July–September) continues to support blue whales during the November inter-monsoon.
Our predictions can be used to prioritize blue whale research and monitoring efforts in the NIO. In particular, future research and monitoring efforts should be directed to collect distribution data in the areas predicted to be good blue whale habitat: the western Arabian Sea during all seasons, off southwestern India and Sri Lanka in all seasons, off Pakistan and western India during the Southwest Monsoon, off eastern India during the Southwest Monsoon, and west of the Maldives and Lakshadweep during the Southwest Monsoon. Research and monitoring in these areas are critically important because these areas overlap with some of the busiest shipping routes in the world (Tournadre, 2014). For example, the major shipping route linking the Arabian Sea and Europe goes through the Gulf of Aden before entering the Red Sea and Suez Canal. Shipping traffic is also high off southwestern India and Priyadarshana et al. (2016) found consistently high densities of blue whales off Sri Lanka in one of the world's busiest shipping routes.
Our predictions should be reassessed and refined as more data become available in the NIO. We used whaling data to assess our models because limited recent sightings data are available. Use of the whaling data assumes that habitat has not changed since the data were collected in the 1960s. Regime shifts and interdecadal variability have been identified in all ocean basins, although most studies show stronger variability in the Pacific Ocean than the Indian Ocean (e.g. Messié & Chavez, 2011) and the mid-1970s shift may have been particularly weak in the Indian Ocean (Powell & Xu, 2015). There is also an overlap between recent sightings (Ballance & Pitman, 1998; Ballance et al., 2001) and whaling data in the eastern Arabian Sea (between the Maldives and Sri Lanka). Observations of blue whales at the mouth of the Gulf of Aden on the coast of Somalia in 1985 by Small & Small (1991) overlap with whaling data in the western NIO.
The habitat data used in our models should also be reassessed and refined as more data become available. We used the distance to the shelf edge and physical oceanographic data in our models because more direct measures of productivity (e.g. chlorophyll concentrations) are not currently available for our full time series of data in the eastern Pacific Ocean. However, the uncertainty in our predictions may be reduced by incorporating these more direct measures of productivity in the models. Finally, our predictions identify areas with relatively good and poor blue whale habitat over long time scales; the predictions do not capture interannual variability in blue whale distributions. Previous studies have found interannual variability in blue whale distributions in the NIO (Ballance et al., 2001; de Vos et al., 2014b). For example, Ballance et al. (2001) found few blue whales in a previously occupied area near the Maldives during the 1998 El Niño; one of the observed whales was thin (the dorsal processes of the vertebral column were clearly visible along the back anterior to the dorsal fin), suggesting that El Niño may influence their distribution and feeding success. The uncertainty in our predictions caused by this interannual variability can be reduced as more blue whale distribution data become available and models are refined.
Conclusion
The ecosystem-specific models that we developed for blue whales were not transferable to novel ecosystems, even though we selected blue whales because they are an example of a cetacean species with well-defined habitat and we used data from two large ecosystems that have some of the most extensive cetacean survey effort in the world. We were able to identify areas of potential habitat in a novel, data-poor marine ecosystem where the species ecology is expected to be similar using models built with data from both ecosystems. Using data sets from multiple ecosystems improved transferability by expanding the range of spatial and temporal habitat variability included in the models. This approach represents a potentially powerful tool for addressing a pressing marine conservation need and should be examined for other species and regions.
Acknowledgements
This study would not have been possible without the tireless efforts of the scientists, coordinator, and crew for each survey. We also wish to thank J. Barlow, S. Chivers, D. Croll, R. Heikkinen, K. Kaschner, D. Palacios, M. Pardo, B. Tershy, and two anonymous reviewers for insightful comments on this project or manuscript. The world country boundaries used in all maps were downloaded from Esri ArcGIS Online (http://www.arcgis.com; last modified May 13, 2015; Esri, DeLorme Publishing Company, Inc.).
References
Biosketch
Dr. Jessica V. Redfern leads the Marine Mammal Spatial Habitat and Risk Program in the Marine Mammal and Turtle Division at the Southwest Fisheries Science Center in La Jolla, California. This group of modellers, ecologists, and oceanographers uses ecosystem data to predict the location of marine mammals, identify priority habitat, and conduct spatially explicit risk assessments. Jessica's current projects include assessing the risk of ships striking whales in areas with high shipping traffic around the world and identification of priority habitat for large whales in the eastern Pacific Ocean.
Author contributions: J.V.R., A.D.V., R.L.B., and L.T.B. conceived the ideas; J.V.R., T.J.M., P.C.F., K.A.F., and E.A.B. conducted the analyses; and all authors contributed to writing the manuscript.




