Learning to Be (In)variant: Combining Prior Knowledge and Experience to Infer Orientation Invariance in Object Recognition
Abstract
How does the visual system recognize images of a novel object after a single observation despite possible variations in the viewpoint of that object relative to the observer? One possibility is comparing the image with a prototype for invariance over a relevant transformation set (e.g., translations and dilations). However, invariance over rotations (i.e., orientation invariance) has proven difficult to analyze, because it applies to some objects but not others. We propose that the invariant transformations of an object are learned by incorporating prior expectations with real-world evidence. We test this proposal by developing an ideal learner model for learning invariance that predicts better learning of orientation dependence when prior expectations about orientation are weak. This prediction was supported in two behavioral experiments, where participants learned the orientation dependence of novel images using feedback from solving arithmetic problems.
1 Introduction
How are people so successful at perceiving, reasoning, and acting given limited information? Solving these problems successfully is generally attributed to people's ability to encode useful information from observations using representations. A representation is an abstraction, “something that stands in place for something else” (Palmer, 1978, p. 282), reflecting relevant structure in the world. For example, the sensory image of the arithmetic symbol (“+”) may be represented as a plus sign with a perceived orientation of 0° or as a multiplication sign with a perceived orientation of 45°. The images produced by addition and multiplication symbols can thus be perceived as upright or oblique. So, given only an image consisting of two short line segments intersecting at roughly 90°, it is ambiguous whether it should be represented as a plus sign or a multiplication sign. This ambiguity highlights the “inverse problem” that underlies inferring representations for images: Any retinal image is potentially consistent with an arbitrary number of objects1 observed at different orientations. How does the mind infer which object from which viewpoint produced a particular image?2
From a computational perspective, a solution to this inverse problem is to choose the representation that is consistent with observations, (implicit or explicit) constraints, and/or prior expectations (e.g., von Helmholtz, 1866/1962; Rumelhart & McClelland, 1986; Tenenbaum, Kemp, Griffiths, & Goodman, 2011). If the mind knew a priori the set of possible objects and the set of possible viewpoints from which each object could be observed, solutions (i.e., recognizing an object in an image) would be relatively straightforward. For example, a Bayesian agent might choose the object from the set of objects capable of producing the observed retinal image that maximizes the product of the probability of the object in a corresponding viewpoint producing the observed image and the prior probability of the object in that viewpoint.
People do not know the set of objects they might observe a priori, however, and so novel objects (and novel object representations) must be learned from experience. Converging behavioral, neural, and developmental evidence suggests that people construct novel representations from interacting with the world (e.g., Austerweil & Griffiths, 2013; op de Beeck & Baker, 2010; Czerwinski, Lightfoot, & Shiffrin, 1992; Goldstone, Son, & Byrge, 2011). Thus, a mechanism to construct representations must be included in explanations of object recognition. Incorporating a mechanism to learn representations necessarily complicates the computational problem in at least two ways. First, the mind must decide whether an observation is a valid image of a pre-existing representation or requires forming a new representation (i.e., whether it is a valid projection of a stored object representation or not). Second, if a new representation is needed, which additional images should be considered consistent with it?3
How does the mind learn which transformations are permissible for a novel object representation (i.e., over which transformations is it invariant)? As depicted in Fig. 1, many transformations do not change the identity of an object (e.g., translations and/or dilations that simply change the position and/or size of the image). However, rotating the image of some objects preserves its identity (e.g., “5”), but rotating the image of other objects changes its identity (e.g., “+” and “×”) (Mach, 1886/1959; Palmer, 1989; Rock, 1973). This is problematic because it makes it difficult to determine whether recognition of a newly constructed object representation should be orientation-invariant (OI) or orientation-dependent (OD).
1.1 Orientation in object recognition
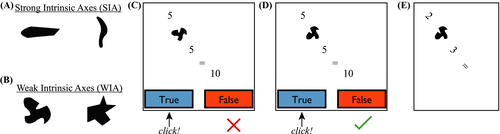
One cue the mind uses to determine whether an object representation should be orientation-invariant versus orientation-dependent is the intrinsic axes (IA) of the object's image (Wiser, 1981). Some images (e.g., “5” in Fig. 2A) have strong IA (Wiser, 1981) because they are represented with respect to the same image-determined coordinate axes (Palmer, 1983, 1989; Rock, 1973), regardless of their orientation with respect to the retina or gravity. More precisely, the image-determined coordinate axes of an object is the object's reference frame in the image, which is a set of coordinate axes that define the scale, location, and orientation of the object's image within the retinal image. Images with strong IA tend to be orientation-invariant—they are recognizable as instances of the same object at any orientation. Note that the intrinsic axes and reference frame of an object's image are not part of the sensory input and must be inferred by the visual system using cues, such as elongation and symmetry, to determine whether an image has strong IAs and, if so, what the orientation of its reference frame is (Humphreys, 1983; Palmer, 1980, 1983, 1989; Quinlan & Humphreys, 1993; Sekuler & Swimmer, 2000; Wiser, 1981). Other images (e.g., the blob in Fig. 2B) have weak intrinsic axes (IAs)—the image is consistent with multiple reference frames. The reference frame used for images with weak IAs in a given situation depends on the gravitational axis and other contextual factors (Palmer, 1989; Rock, 1973). The mind therefore has weaker expectations about how OI images with weak IAs will be represented and recognized than those with strong IAs.
Recognizing objects in images at different orientations depends on the intrinsic-axis strength, where recognition is faster for images with strong IAs (Humphreys, 1983; Quinlan, 1988). Thus, when the mind constructs a representation for a novel image, one source of information it uses to determine the set of invariant transformations is whether the image has weak IAs or strong IAs, which is estimated from the properties of its image. But this estimate is fallible and can conflict with observed information. Consider the first time a child observes images of numbers. Based on elongation or symmetry cues, she should have similar prior expectations for the images of “5” and “6” (both of which are elongated, suggesting strong IAs). Because she only hears one label with the image of the object “5” regardless of its orientation, her experience with the image and its rotational variants is consistent with a single reference frame signaling OI. In contrast, she hears different labels for the object “6” depending on whether the closed portion of the image is nearer the bottom (“6”) or the top (“9”), consistent with “6” having two different reference frames and OD. This analysis suggests people can learn OD for images with strong IAs. Conversely, when the child first sees the image of a “G,” its lack of symmetry or elongation suggests weak intrinsic axes and that the “G” should be OD. Because she only hears one label with the object “G” regardless of its image's orientation, she ultimately learns that the object “G” is OI. How do people combine their prior expectations about the object's OI with the current evidence about that object being OD or OI?
1.2 How prior beliefs and evidence contribute to transformation invariance in object recognition
Previous work has focused on cases in which prior expectations based on the image of an object suggest recognition should be OD due to its weak IAs, but experience in an experiment suggests it should be OI. For example, many researchers have explored how OI develops by investigating how an object with initially OD recognition develops OI when participants observe the object from several orientations (Jolicoeur, 1985; Tarr & Pinker, 1989; Tarr, Williams, Hayward, & Gauthier, 1998). Neuroscientists have found that orientation invariance develops when particular neural regions selectively activate to different observed orientations of each novel object (Andersen, Vinberg, & Grill-Spector, 2009; Logothetis, Pauls, & Poggio, 1995). Thus, most modern theories of object recognition explain learned orientation invariance as interpolation between and extrapolation from stored views of the object (e.g., Bülthoff & Edelman, 1992; Riesenhuber & Poggio, 1999). This is a compelling explanation of how orientation invariance develops for a novel object that is expected to be OD, but experience is consistent with it being OI. It does not explain how orientation dependence might develop for the images of objects with strong IAs, which are expected to be OI. So, this explanation might only be a partial account of how OI and OD are learned in object recognition.3 How people learn when the recognition of a novel object should be OD remains unknown.
This article contributes two main findings to the study of invariance in object recognition. First, we analyze how an ideal learner would learn whether recognition of a novel object should be OI or OD. The ideal learner predicts that learning OI should be easy for objects with images containing strong IAs and weak IAs, but that people should learn OD more easily for images with weak IAs than images with strong IAs. Second, we find empirical support for this prediction in two behavioral experiments, which provide the first experimental demonstration that people can learn to recognize novel objects as OD given images that only differ in their orientation.
2 Learning invariance: An ideal learner model
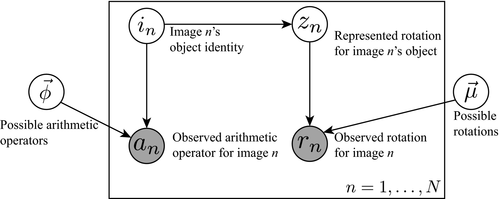
To determine how people might optimally infer the degree to which a given object should be represented as OI, based on both prior expectations and experiences, we derive an ideal learner model by formulating it as the solution to a computational-level problem4 (Marr, 1982). We simplify the problem as follows. We assume (a) that an ideal learner is given images that only differ with respect to the transformation of interest (e.g., rotation), (b) that the set of possible transformations is parameterizable (e.g., transforming an image by a central rotation can be parameterized by a single number that specifies the size of the angle through which the image is rotated about its center), and (c) that, for each image, the ideal learner is given some noisy contextual information regarding the object to which it corresponds (e.g., which arithmetic operation should be applied). The learner's goal is to infer a set of (one or more) object representations that correspond to the given images and contextual information, where each object representation includes its canonical image (the image of the object from an ideal viewpoint; Palmer, Rosch, & Chase, 1981), its associated information (e.g., its function), and a probability distribution over what transformations are permissible. For the following experiments, the “associated contextual information” for each novel object will be the arithmetic operator to which it corresponds. We chose to apply the model to arithmetic as a domain because solving arithmetic problems is a non-trivial decision-making process in which the recognition of some arithmetic operators is clearly OD (e.g., “+” vs. “×”), whereas the recognition of others is clearly OI (e.g., “÷”). In particular, we will examine how information learned through solving addition and multiplication operators with novel operator images can affect the degree to which the recognition of novel objects associated with those images is OI or OD.
To complete the model, we need to specify the generative processes for how the environment creates objects and contextual information associated with the object, and how objects correspond to images. With knowledge of these generative processes, and after observing a set of images and their contextual information, the ideal learner can invert the process optimally using Bayes’ rule to infer object representations, where each object is associated with a set of permissible transformations. We assume that the environment is populated with objects according to a process satisfying two properties: the order in which a learner observes the objects does not matter (i.e., they are exchangeable), and that objects are present in the environment with probability proportional to how often they have been observed previously (given that there is always some chance of encountering a novel object).
The Chinese Restaurant Process (CRP; Aldous, 1985) is a process satisfying these two properties (Pitman, 1996, 2002) and is frequently used in ideal learner models (e.g., categorization and classical conditioning; Anderson, 1991; Gershman, Blei, & Niv, 2010). The CRP sequentially assigns observations (images) to groups (object representations) without knowing how many groups there are ahead of time. It proceeds as follows. The first observation is given a new group. Successive observations are assigned to each pre-existing group with probability  , where mk is the number of observations assigned to group k, or they are assigned to a new group with probability
, where mk is the number of observations assigned to group k, or they are assigned to a new group with probability  , where parameter α controls the expected number of groups and N is the number of observations. Models using the CRP are Bayesian nonparametric models whose representations adapt to match the complexity of the observed data (see Austerweil, Gershman, Tenenbaum, & Griffiths, 2015, for an introduction).
, where parameter α controls the expected number of groups and N is the number of observations. Models using the CRP are Bayesian nonparametric models whose representations adapt to match the complexity of the observed data (see Austerweil, Gershman, Tenenbaum, & Griffiths, 2015, for an introduction).
To develop the generative process further, we need to define an object representation. We assume objects are encoded by a simple representation containing three components: (a) its template or canonical image, (b) the contextual information associated with it, and (c) a probability distribution over permissible transformations that defines the set of possible observable images of the object. Because we have restricted the problem to the case where the observed images only differ according to the transformation of interest, all of the objects have the same canonical image. We therefore do not include assumptions about how images are split into subsets that all contain the canonical image as part of our ideal learner model, although we note that this is an interesting direction for future inquiry. In the present case of learning to discriminate OI and OD objects, we assume that the input provided by observed image n is its perceived rotation rn (based on the retinal image and contextual cues). The perceived rotation is generated from the distribution over possible rotations for object n.
What should be the distribution over possible rotations of an object? Based on prior work, we know that people have prior expectations about how OI a novel object representation should be based on its image: People expect objects with weak IAs to be OD and those with strong IAs to be OI. We also know that OI representations can be learned for novel objects whose recognition is initially OD. Thus, we use the following two-step generative process to produce perceived rotations that satisfy these psychological constraints. The orientation of the object-centered reference frame is generated (zn), and then the perceived orientation (rn) is a noisy copy of this orientation. The orientation of an object's reference frame is a previously observed orientation with probability proportional to the number of times it has been observed and a new orientation with probability proportional to the prior expectations associated with the object's image (i.e., strong IAs or weak IAs). Thus, as in the case of generating the identity of the object associated with an image, the reference frame orientation of an image is generated by assigning image n to group zn of object images that share the same reference orientation according to a CRP. In this case “groups” are images of the object whose object-centered reference frame shares the same orientation and each group k is associated with a continuous value (μk), which encodes the true orientation of images associated with that group. The orientation of group k, μk, is generated from a Normal distribution centered at the canonical orientation of the object (μ0, assumed to be 0 degrees) with variance 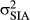 or
or 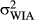 depending on whether the object has strong IAs (SIA) or weak IAs (WIAs), respectively. To capture the expectation that the orientations of reference frames for objects with strong IAs are the same, we assume that
depending on whether the object has strong IAs (SIA) or weak IAs (WIAs), respectively. To capture the expectation that the orientations of reference frames for objects with strong IAs are the same, we assume that 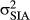 is small. Conversely, people have weak expectations as to the orientations of reference frames for objects with weak IAs, and so we assume
is small. Conversely, people have weak expectations as to the orientations of reference frames for objects with weak IAs, and so we assume 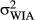 is large. Thus, the assumed constraint (
is large. Thus, the assumed constraint (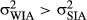 ) incorporates the psychological expectation of intrinsic axis strength into the model. Given the reference frame orientation of the object's image, its perceived orientation is sampled from a Normal distribution centered at the reference frame orientation (μ0, where k = zn) and with variance
) incorporates the psychological expectation of intrinsic axis strength into the model. Given the reference frame orientation of the object's image, its perceived orientation is sampled from a Normal distribution centered at the reference frame orientation (μ0, where k = zn) and with variance 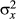 . We assume that the variance in producing the perceived orientation of images,
. We assume that the variance in producing the perceived orientation of images, 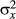 , is greater than the variance in orientation of reference frames of images with strong IAs,
, is greater than the variance in orientation of reference frames of images with strong IAs, 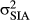 (because reference frame orientation is inferred through image cues for images with strong IAs), but less than the variance in orientation of reference frames for images with weak IAs,
(because reference frame orientation is inferred through image cues for images with strong IAs), but less than the variance in orientation of reference frames for images with weak IAs, 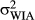 (because reference frame orientation is not inferred through image cues for images with weak IAs). Formally, these psychological factors impose the following constraint on the variances:
(because reference frame orientation is not inferred through image cues for images with weak IAs). Formally, these psychological factors impose the following constraint on the variances: 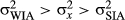 .
.
 (1)
(1)
3 Simulations: Learning orientation invariance from prior expectations and experience
The model infers the number of objects, the arithmetic operator assigned to each object, and the possible orientations of images of each object from observing rotations of novel images and associated arithmetic operations. In this simulation, we explore model predictions varying prior expectations of whether the new object should be OI based on its image structure (strong IAs vs. weak IAs) and whether the model's experience with the image in different orientations is OI or OD (i.e., is the arithmetic operator the same or different when the image is rotated?). Prior expectations were varied by changing the variance of the distribution generating possible rotations to reflect whether the image has weak IAs (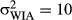 ) or strong IAs (
) or strong IAs (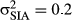 ). There were two properties of the evidence that we manipulated: the strength of the evidence and whether it was consistent with OI or OD. Evidence strength was manipulated by changing the number of images observed by the model (N = 2, 4, 16, and 32). Orientations of 0° and 45° were encoded as 0 and 1 and each observation of an orientation was perturbed by normally distributed noise with data variance
). There were two properties of the evidence that we manipulated: the strength of the evidence and whether it was consistent with OI or OD. Evidence strength was manipulated by changing the number of images observed by the model (N = 2, 4, 16, and 32). Orientations of 0° and 45° were encoded as 0 and 1 and each observation of an orientation was perturbed by normally distributed noise with data variance  .5 Each orientation was given to both simulations an equal number of times (so each was observed N/2 times). In OI simulations, the same operator was associated with each orientation. In OD simulations, different operators were associated with each orientation. This bimodal distribution for orientations was motivated by + and × as well the Mach square/diamond (Mach, 1886/1959). For both OI and OD simulations, we assumed the operator retrieval error rate was 10% (λ = 0.1). We also assumed a form of simplicity bias for the number of objects, so the model preferred fewer objects when possible (α0 = 0.01). We assumed a relatively neutral prior for the number of components to the distribution of permissible rotations (α1 = 1) and that the expected orientation of the canonical image of an object was zero (μ0 = 0). The discussed model results—that OD is learned faster for weak IAs than for strong IAs—are robust over reasonable changes to parameter values as long as the constraints over the variances are maintained, λ is relatively small (smaller values improve performance and produce smaller differences between strong IAs-OD and weak IAs-OD), α0 is small (the model learns orientation dependence faster with smaller values and faster with larger values), and α1 is close to 1 (the model learns orientation dependence slower with smaller values and faster with larger values).
.5 Each orientation was given to both simulations an equal number of times (so each was observed N/2 times). In OI simulations, the same operator was associated with each orientation. In OD simulations, different operators were associated with each orientation. This bimodal distribution for orientations was motivated by + and × as well the Mach square/diamond (Mach, 1886/1959). For both OI and OD simulations, we assumed the operator retrieval error rate was 10% (λ = 0.1). We also assumed a form of simplicity bias for the number of objects, so the model preferred fewer objects when possible (α0 = 0.01). We assumed a relatively neutral prior for the number of components to the distribution of permissible rotations (α1 = 1) and that the expected orientation of the canonical image of an object was zero (μ0 = 0). The discussed model results—that OD is learned faster for weak IAs than for strong IAs—are robust over reasonable changes to parameter values as long as the constraints over the variances are maintained, λ is relatively small (smaller values improve performance and produce smaller differences between strong IAs-OD and weak IAs-OD), α0 is small (the model learns orientation dependence faster with smaller values and faster with larger values), and α1 is close to 1 (the model learns orientation dependence slower with smaller values and faster with larger values).
To elicit predictions from the model, we performed inference using Gibbs sampling (Geman & Geman, 1984) with 30 chains, running each chain for 4,000 sweeps, using a burn-in of 50 sweeps (discarding the first 50 sweeps), and performing thinning by only using one out of every four sweeps. An image was considered OI on a given sweep if it was only associated with a single operator (and OD otherwise). Accuracy was calculated as the percentage of used sweeps where the inferred invariance of the image matched the evidence (e.g., accuracy given OI evidence was the percentage of used sweeps where the image was considered OI).
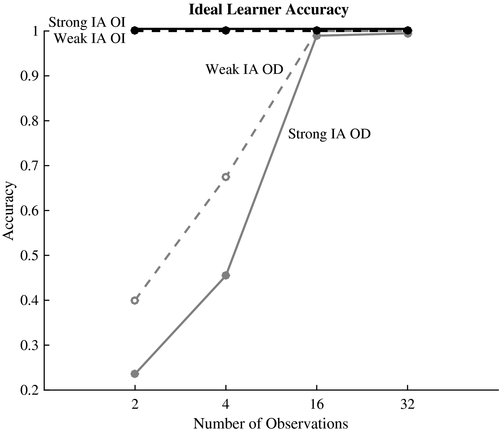
Fig. 4 plots the results of how an ideal observer would integrate prior expectations and experience to learn orientation invariance. First, regardless of prior expectations, the ideal observer quickly learns that object recognition of an image should be OI given OI evidence. This is consistent with previous results showing that OI recognition can be learned for objects with weak IAs images. Furthermore, it predicts that people should learn OI in our task given little evidence regardless of the intrinsic axis strength. Second, regardless of prior expectations, the ideal observer can learn that object recognition of an image should be OD given OD evidence. Furthermore, it predicts that learning OD should be faster for weak IAs images than strong IAs images, but in both cases slower than learning OI. Next, we test these predictions in two behavioral experiments.
4 Experiment 1: Learning orientation (in)variance through feedback
In this experiment, we tested the model predictions by giving participants novel images with either strong IAs or weak IAs (differing prior expectations) and evidence consistent with object recognition being either OI or OD. To do so, we adapted an implicit method developed by Austerweil, Friesen, and Griffiths (2011) in which the perceived orientation and recognized object of an image are inferred indirectly through arithmetic problems (see Fig. 5).
4.1 Methods
4.1.1 Participants
Sixty-four participants were recruited through Amazon Mechanical Turk and received a small monetary reward. Nine were excluded for having a training accuracy lower than 75% at the end of the experiment, leaving 55 participants for analysis.
4.1.2 Stimuli and procedure
There were four operator images, two with strong IAs and two with weak IAs (see Fig. 5A,B). They were divided into two sets (between-subjects), each containing one strong IA image and one weak IA image. Images were presented in two orientations (upright and oblique). The operators assigned to one image were OD (i.e., addition was correct for one orientation and multiplication was correct for the other orientation). The operator associated with the other image was OI (i.e., addition or multiplication was correct regardless of orientation). The assignment of operation, images, and intrinsic-axis strength of the OD image were counterbalanced across participants.
Participants were told that they would be given single-digit addition or multiplication problems from an alien planet. They were told the number of symbols representing each operation, that multiple symbols could represent an operation (e.g., × and • both represent multiplication), and that the same symbol in different orientations could represent different operations (using + and × as an analogy). Trials alternated between training (16 trials) and testing blocks (32 trials). During training, participants were shown an arithmetic problem with a potential answer (Fig. 5C,D), guessed whether the answer was true or false, and were given feedback about whether they were correct (a “✓”) or not (an “✕”). Each digit was randomly sampled from {1,2,3,4,5,7,8}. Each operator image was used eight times per training block (half upright and half oblique), and the provided answer was correct on half of those trials. When the provided answer was incorrect, the other operator was always the correct answer. The test trials were the same as training trials except that participants provided answers to the arithmetic problems and were not given feedback (Fig. 5E). During testing, each image was presented sixteen times (eight at each orientation). Within-block trials were randomly ordered. Participants alternated blocks until achieving 90% accuracy on a training block or having completed four testing blocks.
4.2 Results
On average, participants were accurate on 75% of the trials. When participants made errors, 91% were due to performing the opposite operation (the rest were some other arithmetic error). Fig. 6 presents the accuracy of participants on test trials per block, depending on the image's intrinsic-axis strength (strong IAs or weak IAs), amount of evidence (block number), and evidence type (OI or OD). Test accuracy for OD images was not above chance in test block 1 (Binomial exact tests: 212/432, p = .74 and 214/448, p = .37 for weak IAs and strong IAs, respectively). Accuracy was otherwise significantly above chance. To investigate the results, we estimated best-fit lines for each participant's accuracy results (one line for the strong IA operator and another line for the weak IA operator) and analyzed two mixed-effects models, where each coefficient of the best-fit line (Intercept and Slope) was the dependent measure. So the best-fitting intercepts and slopes for each participant were analyzed using the mixed-effects models. For each model, intrinsic-axis strength and evidence type were coded as within-subject and between-subject factors, respectively.
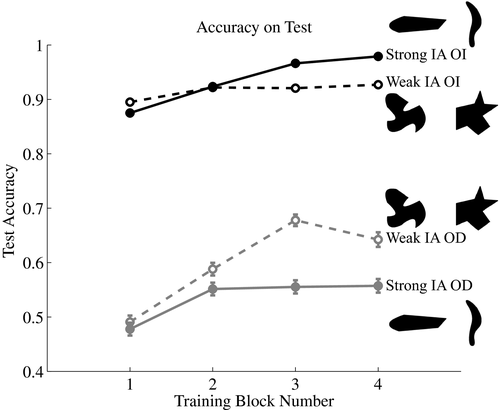
First, we consider the intercepts of the best-fit lines to accuracy, which encode participant accuracy at the first test block (after only the first training block). The main effects of both factors were not significant (F(1, 53) < 0.36, p = .55 and F(1, 53) < 0.72, p = .40 for intrinsic-axis strength and evidence type, respectively). However, the interaction of intrinsic-axis strength and evidence type was highly significant (F(1, 53) = 200.14, p < .001). The interaction is driven by a large intercept when the evidence type was OI (median intercept is 0.97 and 0.94 for strong IAs and weak IAs, respectively) versus a low intercept when the evidence type was OD (median intercept is 0.45 and 0.44 for strong IAs and weak IAs, respectively). So participants were close to ceiling in their accuracy for images assigned to have OI evidence type and approximately at chance in their accuracy for images assigned to have OD evidence type after one training block. Thus, any differences in learning may be explored by analyzing any differences in the slope of the accuracy for images assigned to have OD evidence type depending on the image's intrinsic-axis strength.
Next, we consider the slopes (learning rate) of the best-fit lines to accuracy, which encode the change in accuracy of participants over the experiment (i.e., their learning). Neither factor had a significant main effect on the learning rate (F(1, 53) < 1, p = .83 and F(1, 53) = 2.16, p = .15 for intrinsic-axis strength and evidence type, respectively). Conversely, the interaction of intrinsic-axis strength and evidence type was significant (F(1, 53) = 10.68, p < .005). The interaction is driven by a faster learning rate for weak IAs (median slope = 0.10) than for strong IAs (median slope = 0.01) when the evidence type for the image is OD. This result supports that prior knowledge of weak IAs versus strong IAs influences learning of OD.
The ideal learner model predicted better learning in the weak IA-OD condition than the strong IA-OD condition. To investigate this prediction further, we compared the slopes of the best-fit lines in the weak IA-OD condition to the strong IA-OD condition (between-subjects). Because the slopes were not Normally distributed (Shapiro–Wilk Normality tests: W = 0.91, p < .05, N = 27, and W = 0.75, p < .0001, N = 28 for weak IA-OD and strong IA-OD, respectively),6 we used a robust version of the t test, the trimmed mean t test with bootstrapping. According to a bootstrapped trimmed mean t test (20% trim with 2,000 bootstrap samples), the slopes of the weak IA-OD condition were significantly larger than the strong IA-OD condition (t = 1.66, p < .05, with N = 27 and 28 for weak IA-OD and strong IA-OD, respectively). Although participant accuracy was not as extreme as the model predictions (as discussed below), the results provide quantitative support for the model's predictions as well (the rank correlation between model predictions and average participant accuracy was close to one: Spearman's ρ = 0.93, p < .005, N = 8 constrained to accuracy on OD, and ρ = 0.90, p < .001, N = 16 for all accuracy results).
5 Experiment 2: Lab replication
In this experiment, we replicate Experiment 1 in a traditional laboratory setting.
5.1 Methods
5.1.1 Participants
The participants were 111 psychology undergraduates at University of California, Berkeley, who volunteered to participate in the experiment for course credit. The number of participants was the result of running the experiment for one semester through the University of California, Berkeley, participant pool rather than a planned sample size. Twenty were excluded for failing to answer at least 75% of the training trials correctly (on the last training block), leaving 91 participants for analysis.
5.1.2 Stimuli and procedure
The stimuli and procedures were the same as in Experiment 1.
5.2 Results
On average, participants were accurate on 74% of the trials. When participants made errors, 90% were due to performing the opposite operation (the rest were some other arithmetic error). Fig. 7 shows the results of Experiment 2. They replicate those of Experiment 1 and further support the model predictions. Test accuracy for OD images was not above chance in test block 1 (Binomial exact tests: 348/720, p = .39 and 352/736, p = .25 for weak IAs and strong IAs, respectively). Otherwise accuracy was significantly above chance (except OD accuracy for strong IAs images at test block 2 was trending; Binomial exact test: 393/736, p = .07). With respect to the best-fit line mixed-effect analyses, neither factor had a significant main effect on the intercept (F(1, 88) < 1, p = .39 and F(1, 88) < 1, p = .37 for intrinsic-axis strength and evidence type, respectively). The interaction of intrinsic-axis strength and evidence type was highly significant (F(1, 88) = 242.71, p < .001). It is driven by a large intercept when the evidence type was OI (median intercept is 0.94 and 1.00 for strong IAs and weak IAs, respectively) versus a low intercept when the evidence type was OD (median intercept is 0.47 and 0.43 for strong IAs and weak IAs, respectively). Neither factor had a significant main effect on the slope or learning rate (F(1, 88) < 1, p = .99 and F(1, 88) = 1.74, p = .19 for intrinsic-axis strength and evidence type, respectively). Critically, the interaction of intrinsic-axis strength and evidence type was significant (F(1, 88) = 5.44, p < .05). As in Experiment 1, the interaction is driven by a larger learning rate for weak IAs (median slope = 0.04) than for strong IAs (median slope = 0.02) when the evidence type was OD.
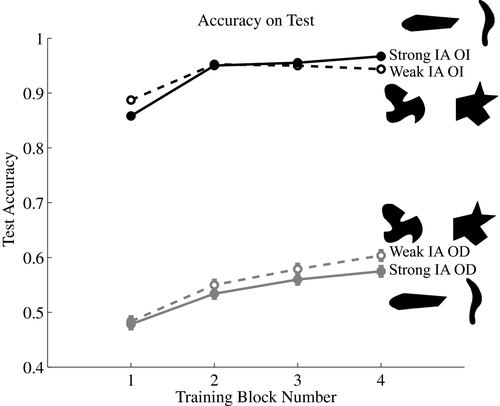
As in Experiment 1, we further investigated the model prediction of better learning of weak IA-OD than strong IA-OD by comparing the slopes of the best-fit lines in the weak IA-OD condition to the strong IA-OD condition (between-subjects). Because the slopes were not Normally distributed (Shapiro–Wilk Normality tests: W = 0.93, p < .01, N = 44 and W = 0.90, p < .001, N = 46 for weak IA-OD and strong IA-OD, respectively),7 we used a robust version of the t test, the trimmed mean t test with bootstrapping. According to a bootstrapped trimmed mean t test (20% trim with 2,000 bootstrap samples), the slopes of the weak IA-OD condition were not significantly larger than the strong IA-OD condition, but there was a trend in the predicted direction (t = 1.20, p = .10, N = 44 and 46 for the weak IA-OD and strong IA-OD, respectively). Although the corresponding results are a bit weaker, Experiment 2 replicates the most important findings of Experiment 1. The results quantitatively support the model's predictions as well (Spearman's ρ = 0.98, p = .001, N = 8 constrained to accuracy on OD, and ρ = 0.89, p = .001, N = 16 for all accuracy results).
6 Discussion and conclusions
When constructing a novel representation for an image, an observer must determine the set of transformations over which the representation is invariant. We derived an ideal learner model of how prior expectations and evidence should be integrated to learn invariance. The analysis predicted that orientation invariance should be easy to learn regardless of prior expectations, but orientation dependence should be easier to learn when there are weak expectations than strong expectations based on intrinsic axes. Supporting these predictions, people learned orientation dependence faster when an image had weak IAs. We demonstrated that people learn the set of transformations over which a representation is invariant by combining their prior expectations with relatively abstract information: feedback from solving arithmetic problems.
It is worth emphasizing that these are not trivial predictions in two different senses. First, previous results have shown that strong intrinsic-axis images are better recognized (Wiser, 1981) and so, one might hypothesize that it would be easier to remember them in each orientation and link each of these with an operator. This hypothesis would predict that orientation dependence is easier to learn for strong intrinsic-axis than weak intrinsic-axis images. However, our results contradict this hypothesis. Second, the prevailing stored-views account of learning OI does not predict any differences because each image is observed in each orientation an equal number of times and it does not consider prior expectations based on image cues (e.g., Riesenhuber & Poggio, 1999, 2000). Thus, the stored-views account of how orientation invariance is learned should be modified to incorporate higher-order feedback and prior expectations based on image factors.
Although the experimental results were consistent with the model predictions, the model incorrectly predicted that orientation-dependent accuracy should reach the same level as orientation-invariant accuracy. Participants learned whether the recognition of latent objects producing novel images should be orientation-dependent or orientation-invariant based on a few training blocks with 20 trials of feedback from responding to a solved arithmetic problem with the image as an operator consistent with either orientation-dependent or orientation-invariant recognition. It is possible that with more direct feedback, explicit training, and/or additional training participants would reach the same level of accuracy for orientation dependence as they achieve for orientation invariance. Anecdotally, this seems plausible given that human accuracy for recognizing + and × seems to be as good as their accuracy for recognizing orientation-invariant objects. An additional possibility is that the human mind has an additional bias toward transformation invariance.8 Our experimental results and computational model provide a framework for investigating these future questions. For example, a bias for orientation invariance occurs naturally in our ideal observer model, which can be used as a baseline in future investigations of whether an additional bias is necessary to capture human learning of orientation invariance.
There are limitations to the experimental results and computational model as an explanation of how people learn which transformations are invariant for recognizing a given object. First, our experiments used simple black-and-white images for 2-D shapes, which are less naturalistic than color images of real-world objects (although the experiments closely resemble one real-world problem that literate individuals have to solve: which characters should have orientation-invariant or orientation-dependent recognition). Second, we investigated an information-preserving transformation (planar rotations) in the sense that two images of the same object can be transformed into each other without needing to add or remove any parts of the image. People also face recognizing the same object in two images where the transformation to make one image equivalent to the other is not information-preserving (e.g., a 3-D object occludes itself as an observer rotates around it). Our model can be extended to handle this more general case by including in it an explicit model of how images are generated by objects under different transformations (including those that do not preserve information). The model developed in this article provides a foundation on which to build this extended model.
The present results provide further evidence to a growing literature suggesting that higher-level cognition and perception are intertwined, and that conceptual information can directly affect perceptual representations (Goldstone, Gerganov, Landy, & Roberts, 2008; Schyns, Goldstone, & Thibaut, 1998). In particular, our results demonstrate that feedback from arithmetic problems can influence an object's representation in terms of the transformations over which its recognition is invariant. Clearly, higher-level cognition and perception influence each other, but few computational models provide formal accounts of their interaction (see Austerweil & Griffiths, 2013; Goldstone et al., 2008 for preliminary computational frameworks). We hope that the present findings will inspire future work on computational models that provide an integrated framework for understanding the interaction between perceptual and conceptual processing.
Acknowledgments
We thank Karen Schloss, Tania Lombrozo, David Whitney, Bill Prinzmetal, the Berkeley Computational Cognitive Science Lab, and the Configural Processing Consortium for insightful discussions, and Christina Vu, Benj Shaprio, and Julia Ying for help running participants. We also thank Rick Cooper, Drew Hendrickson, and two anonymous reviewers for their insightful comments on previous drafts of the article.




