Dealing with Big Numbers: Representation and Understanding of Magnitudes Outside of Human Experience
Abstract
Being able to estimate quantity is important in everyday life and for success in the STEM disciplines. However, people have difficulty reasoning about magnitudes outside of human perception (e.g., nanoseconds, geologic time). This study examines patterns of estimation errors across temporal and spatial magnitudes at large scales. We evaluated the effectiveness of hierarchical alignment in improving estimations, and transfer across dimensions. The activity was successful in increasing accuracy for temporal and spatial magnitudes, and learning transferred to the estimation of numeric magnitudes associated with events and objects. However, there were also a number of informative differences in performance on temporal, spatial, and numeric magnitude measures, suggesting that participants possess different categorical information for these scales. Educational implications are discussed.
1 Introduction
Being able to estimate quantity is central to everyday life, as when someone cooking dinner estimates how much food is required to serve four guests and how much time dinner will take to prepare. Estimation is also important for success in science, technology, engineering, and mathematics (STEM). For example, accurate estimation of the position of numerals on a number line is strongly predictive of mathematical achievement (Booth & Siegler, 2006; Siegler & Booth, 2004), as well as causally related to arithmetic learning (Booth & Siegler, 2008).
Unfortunately, students consistently have difficulty understanding and comparing the magnitudes of scientific phenomena at very small scales (e.g., Swarat, Light, Park, & Drane, 2011) and at very large scales (e.g., Jones, Tretter, Taylor, & Oppewal, 2008; Libarkin, Anderson, Dahl, Beilfuss, & Boone, 2005; Tretter, Jones, Andre, Negishi, & Minogue, 2006). Even students in STEM majors have difficulty reasoning about magnitudes outside of human perception (Drane, Swarat, Hersam, Light, & Mason, 2009). In particular, students have difficulty in identifying and comparing absolute magnitudes (Jones et al., 2008; Tretter et al., 2006). For example, while most students are able to place major geologic events in the correct order, they do not understand the magnitude of time between these events (Libarkin, Kurdziel, & Anderson, 2007).
Developing a clear understanding of how people reason about magnitudes outside human perception is both theoretically and practically important. Many scientific concepts (e.g., geologic time), technologies (e.g., nanotechnology), and global issues (e.g., global warming) occur at scales that cannot be directly perceived by humans. In fact, “size and scale” have been identified as fundamental to science education (e.g., Hawkins, 1978; Peterson & Parker, 1998; Schneider, 1994; Tretter et al., 2006), and are especially relevant for understanding many of the pressing global environmental issues of today (Buizer, Arts, & Kok, 2011). Size and scale have been proposed as a unifying theme in science education by the NRC Framework for K-12 Science Education (National Research Council, 2011), the Benchmarks for Science Literacy (American Association for the Advancement of Science (AAAS), 2008), and the Next Generation Science Standards (NGSS Lead States, 2013).
Most research investigating how people reason about magnitude has focused on magnitudes at scales within the range of human experience. For example, studies of magnitude representation along a mental number line have concentrated on estimations of numbers less than 1,000 (e.g., Ebersbach, Luwel, Frick, Onghena, & Verschaffel, 2008; Izard & Dehaene, 2008; Opfer, Siegler, & Young, 2011). More recently, research is beginning to examine reasoning about larger scales. Thompson and Opfer (2010) found that students as young as sixth grade are accurate at estimating numbers on a number line from zero to 100,000, and second graders can be trained to be just as accurate. In larger ranges, however, even adults may have difficulties. Approximately 50% of undergraduate students were inaccurate when estimating numbers on a 1,000–1 billion number line (Landy, Silbert, & Goldin, 2013). Resnick, Davatzes, Newcombe, and Shipley (in press) suggest that people use categorical information when making estimations, including at the billion scale, and that variation in estimation at large magnitudes is due to imprecision of categories. However, given the limited number of studies, more research is needed to characterize how people reason about magnitudes outside human perception.
A review of how people reason about magnitudes within human scales may be useful in thinking about how one might reason about larger magnitudes. Converging evidence from cognitive, neurocognitive, developmental, and comparative fields suggest that reasoning about any type of magnitude (e.g., temporal, spatial, abstract) uses the same neural and conceptual resources (e.g., Bueti & Walsh, 2009; Cantlon, Platt, & Brannon, 2009; Lourenco & Longo, 2011; Walsh, 2003; for a review, see Cohen Kadosh, Lammertyn, & Izard, 2008). This view is formalized as a general magnitude system (Lourenco & Longo, 2011) or a theory of magnitude (Walsh, 2003), and argues that the inferior parietal cortex is responsible for processing all more/less judgments required for action. Processing involves the automatic extraction of magnitude information, which is spatially organized (e.g., Dehaene, Bossini, & Giraux, 1993; Ishihara, Keller, Rossetti, & Prinz, 2008; Moyer & Landauer, 1967).
The spatial organization of magnitude is often characterized as being structured along a mental number line (e.g., Hubbard, Pinel, Piazza, & Dehaene, 2005; Izard & Dehaene, 2008; Moyer & Landauer, 1967). The exact distribution pattern of magnitude along the mental number line is debated (see Barth and Paladino (2011) and Opfer et al. (2011) for a discussion on mental models of magnitude representation). However, all theories suggest people possess compressed representations of the relatively larger, unfamiliar magnitudes. Compression refers to the observed pattern of overestimation of relatively smaller magnitudes and underestimation of relatively larger magnitudes. For example, on a number line from 0 to 1 billion, people may overestimate one million to be located roughly at midpoint (which is actually 500,000,000) and underestimate 750,000,000 to be closer to the midpoint than the end of the number line.
Resnick, Shipley, Newcombe, Massey, and Wills (2012) hypothesize that compression of the mental number line can be accounted for by the category adjustment model (e.g., Huttenlocher, Hedges, & Prohaska, 1988; Huttenlocher, Hedges, Vevea, 2000). The category adjustment model argues that magnitude is stored as a hierarchical combination of metric and categorical information. In the absence of lower level information (e.g., precise metric information), people use higher level categories to aide in estimation. Variation in estimation therefore occurs due to imprecision of category boundaries (Shipley & Zacks, 2008; Zacks & Tversky, 2001). Recall is biased toward the “prototype” of the respective category. With regards to the mental number line, smaller and more familiar magnitudes may constitute individual categories, populating much of the mental number line; whereas a wide range of larger unfamiliar numbers may be encompassed by a few categories, such as “big” and “really big,” thus making these larger numbers harder to discriminate.
The integrated theory of numerical development suggests that number learning involves continually expanding the size and type of number whose magnitudes can be accurately represented (Siegler & Lortie-Forgues, 2014). While this may be a continuous process for magnitudes within human perception (Matthews, Lewis, & Hubbard, 2015; Siegler & Lortie-Forgues, 2014; Siegler, Thompson, & Schneider, 2011), there is some evidence that for magnitudes outside of human perception, resources from small number processing are recycled, as opposed to extended (Landy, Charlesworth, & Ottmar., 2014). At these larger scales, people divide numerical magnitudes into categories, apply linear responses to each subscale, and then connect each subscale to form one continuous range (Landy et al., 2014).
With regards to reasoning about scientific phenomena outside of human perception, there is some evidence from the science education literature to suggest that such phenomena are reasoned about using magnitude-based categories, akin to the accounts described above. Patterns of overestimation of relatively smaller magnitudes and underestimation of relatively larger magnitudes are also seen at extreme scales. For example, a majority of high school students overestimate how long ago dinosaurs first appeared on Earth (Libarkin et al., 2007; Petcovic & Ruhf, 2008; Resnick et al., 2012); and underestimate when life first appeared on Earth (Catley & Novick, 2008). Furthermore, estimations can vary by over 2 billion years in both cases. People also use conceptual categories to organize magnitudes at extreme scales (e.g., Swarat et al., 2011; Trend, 2001; Tretter et al., 2006); for example, geologic time is conceptualized as the Geologic Time Scale. These similarities between estimations within and outside of human perception are present for different types of magnitudes, including both temporal (Catley & Novick, 2008) and spatial (Tretter, Jones, & Minogue, 2013b) magnitude estimations.
Research examining novice estimation of scientific phenomena has previously come from science education literature, which has aimed to identify areas of difficulty for student comprehension and common misconceptions. Our research is one of the first to examine the cognitive reasoning employed to make such estimations of scientific phenomena. Here, we assess if reasoning about scientific phenomena outside of human perception involves using conceptual categories, and, if so, how these categories are structured. If extreme magnitudes are reasoned about using categories, much like smaller magnitudes, then different types of extreme magnitudes (e.g., temporal and spatial) should follow the same pattern of overestimation of relatively smaller magnitudes and underestimation of relatively larger magnitudes at unfamiliar scales. In addition, differences in accuracy between different types of extreme magnitudes would suggest content-specific category boundaries independent, at least in part, of abstract numeric magnitude.
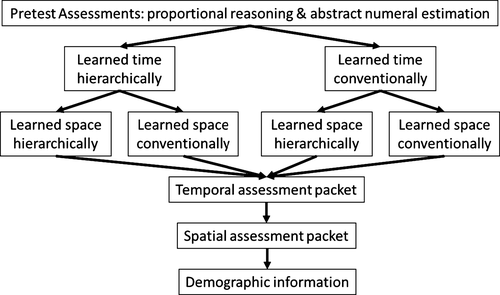
We examine this hypothesis in the context of two training paradigms designed to teach unfamiliar temporal and spatial magnitudes. One training activity, the hierarchical alignment activity, has been shown to support learning about large temporal magnitudes (Resnick et al., 2012; in press) compared to conventional approaches. In this activity, participants mapped increasingly larger scales (e.g., time) to a 1-m space using multiple analogies, locating the relative positions of all previous scales in each analogic step. The hierarchical organization of scale information helps to populate one's mental number line with salient category boundaries. The second training activity, the conventional activity, was developed for this study to be similar to conventional education approaches, which focus on correctly ordering items. Participants were trained on temporal magnitudes and then spatial magnitudes using the hierarchical alignment activity for both, the conventional activity for both, or a combination of both activities (e.g., learn time hierarchically and space conventionally).
If magnitudes outside of human perception are reasoned about using categorical information, the hierarchical alignment activity should be more effective than the conventional activity in developing more accurate estimation of both temporal and spatial magnitudes. A similar pattern of estimation for the different types of magnitudes (temporal and spatial), and comparable effects of the hierarchical alignment training, would suggest that novices use similar conceptual categories to reason about both types of magnitudes. For participants who learned about temporal and spatial magnitude using a combination of activities, transfer effects (i.e., interference or facilitation of learning) from one paradigm to the other may be suggestive of common resources for processing magnitudes. While such a finding is not sufficient to establish that the same neural and conceptual resources are used in reasoning about magnitudes outside of and within human perception, it would, however, be consistent with the mounting evidence suggesting a generalized magnitude system at human scales (e.g., Bueti & Walsh, 2009; Cantlon et al., 2009; Lourenco & Longo, 2011; Walsh, 2003; for a review, see Cohen Kadosh et al., 2008).
2 Methods
2.1 Participants
Eighty individuals (20 male and 60 female), ages 18–29 years old (μ = 21.41, σ = 3.98), participated in this experiment. Participants were recruited from an undergraduate psychology experiment pool at a large urban American university in exchange for course credit. The study sample contained 63% participants identifying as “Caucasian,” 18% identifying as “African-American,” and 19% identifying with another ethnicity (including “Asian,” “Haitian,” “Jamaican,” “Trinidadian,” “Vietnamese,” and bi-racial). Education levels include 19% Freshman, 18% Sophomore, 13% Junior, 23% Senior, and 27% who simply identified themselves as an “undergraduate student.” Fifty-six percent of students had previously taken a geoscience course in high school or college.
2.2 Materials
2.2.1 Hierarchical alignment activity
Participants completed the hierarchical alignment activity developed by Resnick et al. (2012; in press), which is based on the progressive alignment approach to analogical learning (Kotovsky & Gentner, 1996; Thompson & Opfer, 2010). The progressive alignment approach advocates the comparison of two highly similar items. The more commonalities that exist between these items, and if these commonalities are highlighted, the more salient corresponding relations will be. Thus, comparing two very similar items will help extend the analogy to unfamiliar items (Gentner & Namy, 2010). The act of performing comparisons may change original mental representations, increasing the uniformity between the two representations, as well as make higher order relational similarities more salient.
When creating an analogy between two very different items, the progressive alignment approach suggests making as many intermediate analogies as necessary, moving stepwise from a familiar base concept through increasingly unfamiliar concepts to the target concept. Recognition of higher order relational commonalities may promote making the same subsequent higher order connections with these intermediate analogies (Kotovsky & Gentner, 1996). Thus, the progressive alignment of scales may alleviate the conceptual dissimilarity between human scales and extreme scales by providing more structural alignment across smaller increases of scale.
In this study, participants made 10 separate time lines, aligning time to a 1-m line. They began by making a personal time line. A personal time line was chosen as the base concept, because participants should be familiar with their own personal history as well as mapping human temporal scales onto space (i.e., making time lines). The participants then made nine additional time lines; progressively working through different historic and geologic time lines, up to the full Geologic Time Scale (see Table 1). Each time line was chosen for use in the hierarchical alignment activity based on conventionally defined boundaries (e.g., the Archean, Proterozoic, and Cenozoic are all divisions in the Geologic Time Scale) that differ by orders of magnitude. For each time line, students were presented with a partially completed time line (Fig. 1).
| Temporal Scale | Years | Spatial Scale | Miles |
|---|---|---|---|
| Personal | 20 | Troposphere | 11 |
| Human lifespan | 75 | Middle atmosphere | 52 |
| American history | 519 | Exosphere | 400 |
| Recorded history | 5,512 | Inner Van Allen Radiation Belt | 6,000 |
| Human evolution | 6,000,000 | 3753 Cruithne (quasi-satellite) | 8,450,000 |
| Cenozoic | 65,000,000 | Mercury | 57,000,000 |
| Phanerozoic | 542,000,000 | Saturn | 777,000,000 |
| Proterozoic | 2,500,000,000 | Neptune | 2,700,000,000 |
| Archean | 3,800,000,000 | Pluto | 3,580,000,000 |
| Hadean | 4,600,000,000 | Makemake (dwarf planet) | 4,800,000,000 |
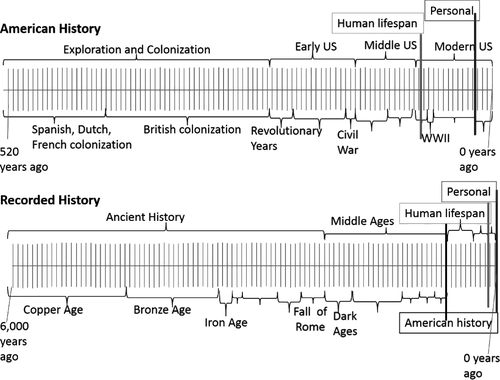
Example of a temporal and spatial number line at the thousands scale in the hierarchical condition.
The three previous temporal/spatial number lines are located relative to the current scale.
The hierarchical alignment approach to analogical reasoning adds an additional step to the progressive alignment of concepts; each intermediate concept is hierarchically organized within the new target concept (Resnick, et al., in press). In this study, participants were required to locate where all previous time lines would begin on the current time line. This hierarchical organization highlights how each temporal scale is related to the others. Hierarchical organization helps to populate each scale with boundary information by providing internal structure of magnitude relations across scales.
To figure out where previous time lines were located, participants were given two mathematical equations: one to determine how many years each centimeter would equal (number of years the time line represents/number of centimeters [always 100]), and another equation to determine how many centimeters were needed to make up previous time lines (number of years previous time line represents/number of years each centimeter represents). Help completing these calculations was provided as needed. After all previous time lines were located, participants were then told information about events on that time line. After the completion of each time line, the completed time line was taken away; so only one time line was visible at a time. While comparison aides in alignment, presentation of a single number line allows for participants to make relevant comparisons within each scale, minimizing distractions, such as looking at another unrelated information on another number line.
This study developed an activity for spatial distances that was analogous to the temporal hierarchical alignment activity (Table 1 and Fig. 1). For the hierarchical alignment of spatial distances, participants align 10 increasingly larger scales of distance to a 1-m line, beginning with a familiar distance. The 10 spatial scales were chosen for use in this study by aligning distances with the temporal orders of magnitude used in the temporal activity. The spatial scales represent the average distance of different celestial objects from Earth's surface. The participants were told that while the distances between Earth and these other celestial objects varies according to where each is in their individual orbits, the information presented is how far on average, or typically how far, each object is from Earth. All participants understood the information presented was the average distance.
While temporal and spatial magnitudes were equated on orders of magnitude, none of the individual magnitudes were the same. For example, the Cenozoic time line and the Mercury distance line are matched on the scale of tens of millions, but the two lines represent different magnitudes (65 and 57 million, respectively). There are two practical reasons why the individual temporal and spatial magnitudes are not the same. For both temporal events and spatial objects, real scientific data were used and rarely are the scientific temporal and spatial magnitude divisions the same. In addition, having the same magnitudes for time and space might draw a participant's attention to the experimental objectives (e.g., thinking about magnitudes), which might change the participants' approach to learning. The new spatial hierarchical alignment condition, like the temporal condition, took approximately 45 min to complete.
2.2.2 Conventional activity
The study sought to contrast the intervention with a realistic training program similar to one that might be used to instruct students in a classroom on these scales. Common pedagogical approaches to teaching geologic time (Libarkin et al., 2007) and astronomical distances (Miller & Brewer, 2010) are to create spatial analogies, such as placing events/objects in the correct sequence. To examine the effects of hierarchical alignment, the experimental (hierarchical) and control (conventional) conditions were matched on the following properties: number of time lines (10), number of times participant interacts with each scale (i.e., the first scale is learned and then located nine times in relation to the other scales, whereas the last scale is learned just once), progressive increase in magnitude, information provided about each event/object, and total length of time on task.
The conventional intervention of correctly ordering the relative magnitude of events or distances was presented in the context of a puzzle. Participants completed 10 separate puzzles, placing the events/objects into the correct sequence. The puzzles were made up of pieces of paper, half containing magnitude information and half with the respective category information. Participants were required to match the magnitude information with the corresponding category information for each scale, and place the scales in the correct sequence. The first puzzle represented the first temporal/spatial scale (see Table 1), with each puzzle representing magnitude at a larger scale. The tenth and final puzzle represented all of geologic time/distance to the dwarf planet Makemake (Fig. 2). Participants were told the same information about the events/objects at each scale as in the hierarchical condition. After the completion of each puzzle, the puzzle was taken away; so that only one puzzle was visible at a time. The conventional condition took approximately 45 min to complete. Thus, the only difference between conditions was the hierarchical alignment of scale information.

2.2.3 Familiarization to vertical scale for spatial magnitude
One potential difference between the temporal and spatial information was identified. Participants are likely to be familiar with thinking about temporal scales extending back hundreds of years ago; learning about recent human history is common. However, participants may not have the same level of familiarity with conceptualizing the vertical nature of the spatial scales. Because it is likely people have more experience traveling parallel to Earth's surface, or “horizontally,” as opposed to traveling vertically away from Earth's surface, we used this horizontal experience as an initial introduction of the vertical scale. As a way to familiarize participants with the vertical scale, a horizontal map was presented for each of the first three scales in both the hierarchical and conventional conditions. The maps showed an 11, 52, and 400 mile radius extending out from the university where the study took place. To engage the participants in grounding this scale to their personal experience, participants were asked if they had been anywhere on that radius or if they were familiar with the area. No map was provided for the remainder of the spatial scales, since these larger spatial scales are likely equally unfamiliar to participants as the matched temporal scales.
2.3 Measures
2.3.1 Magnitude estimation
A series of line estimation tasks were developed to assess participants' estimation of geologic time, astronomical distances, and numeric magnitudes associated with events and distance. All line estimation tasks were presented on a vertical number line 173.5 mm in length, with responses measured to within 0.5 mm. To assess estimation of geologic time, participants were given a blank time line anchored by “present day” and “Earth forms,” and asked to locate the relative positions of the following four events: “life appears,” “dinosaurs appear,” “dinosaurs disappear,” “humans appear.” To assess estimation of astronomical distances, participants were presented with a blank number line anchored by “Earth's surface” and “Makemake,” and asked to locate the relative position of the following four objects, which are at the same scale as the events: “Pluto,” “Mars,” “Mercury,” and “Cruithne.” Celestial objects vary in distance depending on their orbit, and do not all align in one straight line, nevertheless, in this task, participants are asked to map the celestial objects' relative distances to one another using a single number line. To assess estimation of numeric magnitudes associated with events and distance, participants were given a sentence stating when/where an event/object was, and then asked to locate that magnitude on a blank number line (e.g., “Venus is 26 million miles away from Earth. Please draw on the line provided where Venus is located.”). To note, the statements provide the numerical values of the event/object. For these estimations, participants were asked to estimate two event magnitudes and two object magnitudes on a 4.6 billion scale, and two of each on a 542 million scale to assess the use of categories at both scales.
2.3.2 Understanding of scientific phenomena at extreme magnitudes
Twelve multiple choice items on temporal phenomena, and 12 direct analogs for spatial phenomena, were developed to assess understanding. One of the items was developed by Barghaus and Porter (2010) for use with middle school students. The remaining 11 items were developed through collaboration between a cognitive psychologist and a geologist specializing in scientific phenomena that occur at large scales. Importantly, eight of these items require magnitude recall only (e.g., “When did dinosaurs disappear?”); whereas the remaining four items required magnitude recall plus an additional step of reasoning (e.g., “What is the relationship between dinosaurs disappearing and humans appearing?”). In this example, participants are required to recall when dinosaurs disappeared, when humans appeared, and compare the relative durations in between. To assess if people use categorical and numerical information when reasoning about magnitudes outside of human perception four of the eight recall only items include categorical response options (e.g., “A. Triassic…), and four include the equivalent numerical response options (e.g., “A. 65 million years ago…). Note, in this example, the categorical response option “Triassic” is equivalent in magnitude to the numerical response option. While participants answered the same question with both types of response options, repeated questions were presented on separate pages so participants could not compare answers. An additional item from the Geoscience Concept Inventory (Libarkin et al., 2005) was included for only the temporal packet as a thirteenth multiple choice item. See online supplemental material for a list of all multiple choice items.
2.4 Mathematical ability
2.4.1 Experimenter rating of participant's calculation ability
Pilot testing revealed substantial variations in math skill. To keep track of this potential source of variability participants were classified as “poor at calculation,” “average at calculation,” or “strong at calculation” based on their performance during participation. Participants classified as “poor at calculation” had difficulty completing basic mathematical calculations, such as dividing numbers by 100 (e.g., 400/100 = 4). Participants classified as “strong at calculation” demonstrated a mastery over more complex mathematical calculations, such as mentally dividing large numbers quickly. For example, participants who divided numbers like 3.5 billion by 46 million quickly using no paper and pencil were labeled as “strong at calculation.” Participants classified as “average at calculation” were able to complete basic mathematical calculations with minor to no problems, and used paper and pencil for more complex mathematical calculations.
Each participant was classified based on observations made while they completed the math required in the construction of the temporal and/or spatial number lines. Participants who learned both the temporal and spatial information conventionally (TCSC) could not be assigned a classification because they did not perform any mathematical tasks with the experimenter (i.e., the participants in this group did not construct any number lines). As the experimenter worked one-on-one with the participant, inter-coder reliability was not obtained. Thus, interpretations of any findings involving math skill should be considered as preliminary.
2.4.2 Prior proportional reasoning ability
Basic proportional reasoning ability was assessed immediately prior to beginning the training activity. The proportional reasoning measure developed by Park, Park, and Kwon (2010) was used. The measure is composed of common proportional reasoning items (e.g., Hines & McMahon, 2005; Lamon, 1993, 1999) representing the four kinds of proportional reasoning identified by Lamon (1993): part-part-whole, associated sets, well-known measures, and growth. Participants were required to calculate a missing value or identify the correct numerical response option. This measure has an internal reliability of 0.75 (Park et al., 2010).
2.4.3 Prior numeric magnitude estimation
Estimation of numeric magnitudes not associated with any context (i.e., abstract numerals) was assessed immediately prior to beginning the training activity using four number line estimation tasks. Participants were asked to identify where a numeral would be located (e.g., Where is 400 million on this number line). Consistent with the context-based numeric magnitude estimation tasks, two of the number lines represented 542 million and two represented 4.6 billion.
2.5 Procedure
All participants read an information sheet and signed a consent form. Participants completed pretest measures: a hard-copy packet containing questions (fixed order) on proportional reasoning and abstract numeral estimation. Next, individuals learned about temporal magnitude either hierarchically or conventionally (~45 min), and then learned about spatial magnitudes either hierarchically or conventionally (~45 min), resulting in the following four conditions learning: (a) time hierarchically and space hierarchically (THSH), (b) time conventionally and space hierarchically (TCSH), (c) time hierarchically and space conventionally (THSC), and (d) time conventionally and space conventionally (TCSC). There were 20 participants in each condition (80 total). Participants across conditions then completed the same outcome measures. Participants first completed a hard-copy packet of temporal assessment questions, and then a hard-copy packet of spatial assessment questions. At the end of the study, demographic information (e.g., sex, ethnicity, age, etc.) was obtained, including if the participant has previously taken a geoscience course. The entire study took approximately 2 hours to complete. See Fig. 3 for a summary of the experimental protocol.
3 Results
3.1 Accuracy
Participants from the four conditions estimated the location of events, objects, and numerals associated with events and objects on separate number lines, which were matched for scale. Accuracy was calculated by taking the absolute distance (in mm) of a given response from the correct location. Across conditions, participants were more accurate when estimating spatial magnitudes than they were when estimating temporal magnitudes (t(76) = 4.64, p < .001), and were minimally more accurate when estimating numerals associated with objects compared to numerals associated with events (mean μ = 4.11 mm or 2.37% error, SD = 17.83 mm; t(79) = 2.04, p = .05; d = .12). A factorial multivariate analysis of variance (manova) was conducted to assess the influence of condition (THSC, THSH, TCSC, and TCSH) on the three types of magnitude estimations (events, objects, and associated numerals).1 There was a significant effect of condition at the multivariate level (F(3, 76) = 2.35, p = .015, 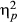 = .09), and at the univariate level for temporal (F(3, 76) = 3.44, p = .021,
= .09), and at the univariate level for temporal (F(3, 76) = 3.44, p = .021, 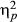 = .12), spatial (F(3, 76) = 5.40, p < .002,
= .12), spatial (F(3, 76) = 5.40, p < .002, 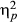 = .176), and associated numeral (F(3, 76) = 3.37, p = .023,
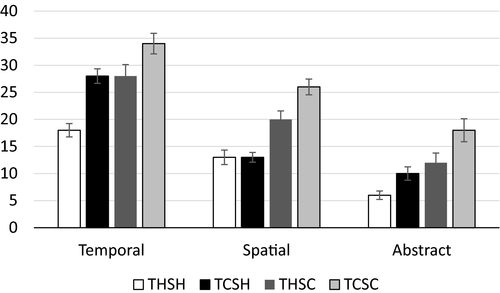
= .176), and associated numeral (F(3, 76) = 3.37, p = .023, 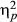 = .117) estimations. Pairwise comparisons were corrected using a Bonferroni adjustment (see Table 2 for test statistics and p values). Participants were more accurate on spatial estimations when they learned about spatial magnitude hierarchically (THSH and TCSH) compared to participants who learned about spatial magnitude conventionally (TCSC and THSC). The same is not true for learning about temporal magnitudes and associated numerals. Participants were only more accurate on temporal magnitude and associated numeral estimations compared with the conventional only condition (TCSC) when they learned about both temporal and spatial magnitudes hierarchically (THSH). No differences emerged on temporal estimations between the THSC condition and the TCSH and TCSC conditions, nor between the TCSC and THSC on spatial estimations. See Fig. 4 for error on temporal, spatial, and numeric magnitude estimations by condition.
= .117) estimations. Pairwise comparisons were corrected using a Bonferroni adjustment (see Table 2 for test statistics and p values). Participants were more accurate on spatial estimations when they learned about spatial magnitude hierarchically (THSH and TCSH) compared to participants who learned about spatial magnitude conventionally (TCSC and THSC). The same is not true for learning about temporal magnitudes and associated numerals. Participants were only more accurate on temporal magnitude and associated numeral estimations compared with the conventional only condition (TCSC) when they learned about both temporal and spatial magnitudes hierarchically (THSH). No differences emerged on temporal estimations between the THSC condition and the TCSH and TCSC conditions, nor between the TCSC and THSC on spatial estimations. See Fig. 4 for error on temporal, spatial, and numeric magnitude estimations by condition.
| Condition | Type of Estimation | THSH | TCSH | THSC | TCSC |
|---|---|---|---|---|---|
| THSH | Temporal | — | −2.09, p = .32 | 1.94, p = .33 | 3.15, p = .01* |
| Spatial | — | 02, p = 1.00 | 1.81, p = . 31 | 3.40, p = .01* | |
| Abstract | — | −.774, p = 1.00 | 1.39, p = 1.00 | 3.056, p = .02* | |
| TCSH | Temporal | — | −.20, p = 1.00 | .98, p = 1.00 | |
| Spatial | — | 1.85, p = .41 | 3.46, p = .01* | ||
| Abstract | — | .616, p = 1.00 | 2.28, p = .15 | ||
| THSC | Temporal | — | −1.22, p = 1.00 | ||
| Spatial | — | −1.63, p = .87 | |||
| Abstract | — | −1.666, p = .60 | |||
| TCSC | Temporal | — | |||
| Spatial | — | ||||
| Abstract | — |
- Note. p-values have been corrected for multiple comparisons using a Bonferroni adjustment; *indicates a significant difference; df = 76.
3.2 Patterns of error in estimation
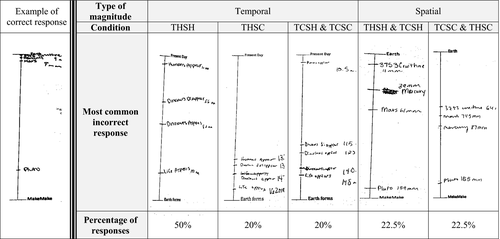
Participants estimated four events and four objects on separate number lines, with each estimation matched for scale. Qualitative examination of responses allows for identification of potential category boundaries. For both the temporal and spatial number lines, participants across conditions were accurate on estimations of the event/object at the 10 million scale (smallest magnitude) and 1 billion scale (largest magnitude). Variation in accuracy was, therefore, driven primarily by the estimation of the second and third magnitudes for both temporal and spatial scales. See Fig. 5 for an example of a correct response along with the distribution of the most common patterns of error, which varied by training activity. While it was common to cluster three or four of the four estimations, events tended to cluster in the bottom third of the number line (closer to when Earth formed), whereas objects tended to cluster in the top third (closer to Earth's surface) or middle third of the number line. For temporal estimations, the second and third estimation (when dinosaurs appeared and disappeared) were frequently placed in the middle of the number line.
3.3 Estimation of numerals associated with events and objects at different scales
This study examined the range of adults' familiarity with scales outside of human perception by separately analyzing accuracy of estimations at the million and billion scales. Participants across conditions were significantly more accurate when estimating magnitudes on the million scale (M (error) = 19.61, SD = 26.40) than on the billion scale (M (error) = 25.21, SD = 31.80) (t(78) = 2.61, p = .01). There were no significant differences between conditions on the estimation of associated numerals on the million scale (p > .05). There was an effect of condition on the billion scale, with participants who learned at least one domain-specific magnitude hierarchically making more accurate estimations than participants who learned temporal and spatial magnitudes conventionally (TCSC) (THSH: t(77) = 2.43, p = .02; TCSH: t(77) = 2.12, p = .04; and THSC: t(77) = 2.48, p = .02). There were no significant differences between the THSH, TCSH, and THSC conditions (p > .05).
3.4 Understanding of Scientific Phenomena at Extreme Magnitudes
There were no significant performance differences on the multiple choice items assessing understanding of temporal and spatial phenomena at extreme scales across the training conditions (ps > .05). Participants had significantly more items correct, on average, for the spatial content items than the temporal content items (t(71) = 8.36, p < .01).
For each multiple choice question (e.g., “When did dinosaurs appear?”), there was a correct response (230 million years ago), and incorrect response options that ranged in difference in magnitude from the correct answer (e.g., 398 million years ago to 3.5 billion years ago). Thus, for each item, responses could be ranked from one (correct) to four (incorrect by the largest amount). Correlations were analyzed between accuracy on temporal and spatial magnitude estimations with the ranked responses to multiple choice items, using Tukey's HSD to correct for multiple comparisons.
There were no significant correlations between performance on temporal and spatial magnitude estimations and performance on multiple choice items requiring recall only. Performance on temporal magnitude estimations was correlated with performance on multiple choice items that required recall plus reasoning (r = .33, p = .01). Performance on spatial magnitude estimations was not correlated with performance on the multiple choice items that required recall plus reasoning (p > .05).
3.5 Use of Categorical and Numerical Information
If people use categorical information when estimating magnitudes outside of human perception when they do not know the precise metric, then participants should be equally or more accurate for multiple choice items that have categorical response options compared to those items that have numerical response options. Indeed, overall there was better recall of categorical facts about events and objects than corresponding numerical facts (t(78) = 2.68, p = .009).
3.6 Role of Mathematical Abilities
Participants were assigned a ranking of “poor at calculation,” “average at calculation,” or “strong at calculation.” Based on performance during the training, 11 participants were categorized as “poor at calculation,” 37 as “average at calculation,” and 12 as “strong at calculation.” The relatively small numbers and unequal sample sizes preclude statistical tests of significance; however, as a preliminary analysis, differences in average error between mathematical skill levels were assessed. Participants categorized as “poor at calculation” had the greatest average error across temporal and spatial magnitudes and associated numerals, participants categorized as “average at calculation” had less error, and those categorized as “strong at calculation” had the least error (see Fig. 6 for mean percent error and standard deviation).
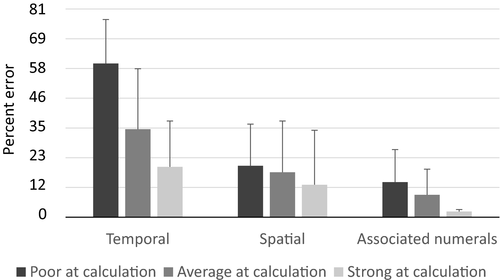
All participants possessed basic proportional reasoning skills, with all participants answering at least 80 percent of the proportional reasoning items correctly. No demographic information (e.g., sex, age, handedness, etc.) was related with performance (p > .05), including previous participation in geoscience courses (p > .05).
Participants estimated abstract numerals (not associated with any context) prior to participating in a training condition. Pretest abstract numeral estimations were all moderately correlated (mean r = .69, ps < .01), and had strong internal reliability (Cronbach's alpha = .93). Mean error for abstract numeral estimation at pretest was not correlated with estimations of temporal or spatial magnitude across conditions (p > .05). Pretest abstract numeral estimation was correlated with the posttest estimations of numeric magnitude associated with events and objects for participants in the TCSC condition only (r = .45, p = .05), and not with any other condition (p > .05).
4 Discussion
In this study, participants learned about geologic time and astronomical distances in the context of the hierarchical alignment activity, which provides salient category boundaries for increasingly larger scales. That the hierarchical alignment activity was successful in fostering greater accuracy in estimations of temporal and spatial magnitude and numeric magnitudes associated with events and objects compared to a conventional approach, suggests that participants are able to use categories in meaningful ways when reasoning about different types of magnitudes at scales outside of human perception. Indeed, our findings are aligned with predictions of the category adjustment model (Huttenlocher et al., 1988), which suggests people use categories to estimate magnitude when the precise metric value is unknown. For example, one prediction is increased accuracy for estimations close to salient category boundaries. In this study, participants across conditions had increased accuracy for the estimations located closest to the ends of the number line for both temporal and spatial magnitudes. Another prediction suggests increased variation biased toward the mean for estimations farther away from salient category boundaries. In this study, a common error was to place the 2nd and 3rd estimations directly in the middle of wherever the 1st and 4th estimations were placed. If the participants knew when life appeared (1st) and humans appeared (4th), but nothing about what happened in between, for example, the middle would represent the mean of these category boundaries, making it the best possible location to minimize possible estimation error for locating when dinosaurs appeared (2nd) and disappeared (3rd). Better overall recall of categorical facts about events and objects compared with corresponding numerical facts on the multiple choice measures suggests that not only is categorical information used to make estimations, it is actually more salient than numerical information.
There were also a number of differences in performance on estimations of temporal and spatial magnitude and associated numerals. Participants across conditions were most accurate when estimating associated numerals, then spatial magnitudes, and least accurate on temporal magnitudes. Participants also exhibited distinct patterns of error for temporal and spatial magnitudes. For example, participants who learned temporal and spatial magnitudes hierarchically (THSH), incorrectly placed “dinosaurs appear” and “dinosaurs disappear” in the middle of the number line, whereas the same participants placed the spatial equivalents “Mars” and “Mercury” in the top third of the number line (closer to Earth). Finally, the hierarchical alignment activity was not equally effective across the different types of magnitude: accuracy in estimating spatial magnitude improved for participants who learned about spatial magnitudes hierarchically (THSH and TCSH); whereas temporal and associated numeral accuracy only improved for participants who learned both temporal and spatial magnitudes hierarchically (THSH).
These observed differences in accuracy and patterns of estimation are consistent with the participants having different categories for temporal and spatial magnitudes and associated numerals. The hierarchical alignment activity provided category boundaries at the same scales for temporal and spatial phenomena. However, geologic time is often neglected in the classroom (Dodick, 2007; Trend, 2001), whereas learning about the solar system is commonplace. Thus, it seems likely participants had more knowledge (and therefore more and more accurate categories) of the solar system than geologic time prior to beginning the study. We predict that the apparent spatial advantage would disappear, or lessen, if an unfamiliar spatial scale were used in the hierarchical alignment activity. For example, learning about an unfamiliar solar system would have a different time-course as well as different celestial objects.
While more research is required to detail the specific categories people may use to estimate magnitude and scientific phenomena outside of human perception, here we speculate about two possible categories. One common pattern of errors was to compress all estimations toward the bottom of the number line, which translate to being further away in time or space. This may suggest all the events and all the objects were grouped into one category of “really long ago” or “really far away,” respectively. Another common response was to correctly locate the first estimation toward the top of the number line (closer in time of space) and the fourth estimation toward the bottom of the number line, and incorrectly place the second and third estimation in the middle of the number line. This pattern of error is consistent with not having any intermediary category boundaries between the first and fourth estimation (as explained by the category adjustment model above).
An alternative explanation for the observed differences in accuracy and estimation patterns is that temporal and spatial magnitudes are reasoned about differently. Research showing asymmetrical relationships in cross-dimensional interference paradigms suggests that different types of magnitudes may be processed using independent cognitive resources (Agrillo, Ranpura, & Butterworth, 2010; Dormal, Andres, & Pesenti, 2008). Here, we also see an asymmetrical relationship, with participants being more accurate, and the hierarchical alignment activity being more effective, for spatial estimations compared to temporal estimations. However, given the similar role of categories in reasoning about both temporal and spatial magnitude, and transfer to reasoning about numeric magnitude associated with events and objects, it seems more likely that magnitudes outside of human perception are reasoned about the same way. That is, with different categories biasing estimations to result in different patterns of estimation. Despite the similar use of categorical information, more research is required to determine if the same cognitive resources are employed when reasoning about scales within and outside of human perception.
4.1 Educational Implications
Findings suggest that having the opportunity to engage in hierarchically aligning magnitudes at different scales is important for learning how to reason about magnitude, and, thus, has programmatic implications for curriculum design. Analogy and visual displays are the most commonly used pedagogical practices when teaching about magnitudes outside of human perception (Libarkin et al., 2007). However, there are a number of potential barriers to alignment, such as unfamiliar base concepts, dissimilar base and target concepts, psychological barriers, and practical constraints of the classroom (Resnick et al., in press). This study illustrates the benefit of hierarchical alignment in addition to progressive alignment in learning magnitude information through analogy. In addition, this study finds transfer from learning domain-specific magnitudes hierarchically to accurate estimations of more abstract magnitudes (e.g., numeric magnitude associated with events and objects). These findings are particularly important for educators across STEM disciplines, as understanding size and scale is predictive of performance on a range of standardized tests in mathematics (Booth & Siegler, 2006; Siegler & Booth, 2004), essential in understanding a range of scientific concepts (e.g., Hawkins, 1978; Peterson & Parker, 1998; Schneider, 1994; Tretter et al., 2006), and has been identified as a fundamental and unifying theme in science education (American Association for the Advancement of Science, 2008; NGSS Lead States, 2013; National Research Council, 2011). We predict that the analogical principles included in the hierarchical alignment activity could build a foundation of scale understanding—to potentially align the vast set of scales across the STEM disciplines.
Acknowledgments
This research was supported by the National Science Foundation Grants SBE-0541957 and SBE-1041707 which support the NSF funded Spatial Intelligence Learning Center, and the Institute of Education Sciences Grant R305B130012 as part of the Postdoctoral Research Training Program in the Education Sciences.




