FDI, defense spending, and economic prosperity
Abstract
The relationship between foreign direct investment (FDI) and military spending in the Middle East and North Africa (MENA) region is complex and multifaceted. High levels of military spending can deter foreign investors, as it creates an uncertain and potentially volatile investment climate. However, countries that invest in their military infrastructure and capabilities may be seen as more stable and secure, which can attract foreign investors. Taking into account several factors that can influence this relationship, including political stability, security concerns, and economic factors, this work analyzes whether military spending attracts foreign capital into the region. Using a dynamic panel data methodology along with other relevant macroeconomic variables, results show that the military expenditure has a positive and significant impact on FDI inflows into the MENA region. The paper highlights the fact that policymakers in the region must carefully balance military spending with investments in other areas of the economy in order to create a stable and favorable investment climate that attracts foreign investors and contributes to long-term economic growth and development achieving both security and welfare.
1 INTRODUCTION
Foreign direct investment (FDI) is a key driver of economic growth for developed and developing economies, mainly by contributing to economic growth through the transfer of financial resources, new technologies and know-how, as well as innovative and improved management techniques. These benefits can help raise productivity, improve competitiveness, create employment opportunities, and enhance the overall economic growth of the host country.1 Given the widely recognized relevance of FDI as a source of economic activity, many developed and developing countries have implemented policy measures aimed at creating a favorable investment climate, such as offering tax incentives, providing investment guarantees, and improving infrastructure and regulatory frameworks. These policy efforts are aimed at promoting a welcoming and stable business environment that can attract foreign investors and encourage them to establish operations in the host country. Among these developing countries, though, the distribution of world FDI inflows is uneven and concentrated in the largest economies and/or oil-exporting countries. Despite the significant increase over the last decade in global FDI,2 the Middle East and North Africa (MENA) region has disappointing performance in attracting FDI compared to developing and emerging countries.3 After experiencing sustained economic growth and increased foreign investment inflows, economies in the MENA region have been, since 2008, exposed to repeated external and internal shocks as a result of the global economic and financial crisis and, more importantly, the “Arab Spring” and resulting social and political turmoil. Host country's stability in combination with financial and fiscal incentives are seen as crucial factors to attract foreign investors. Several countries in the region have implemented economic reforms to attract foreign investment, such as privatization programs, tax incentives, and simplified business registration procedures. Security concerns need, however, to be taken into account when explaining the overall poor performance of the MENA region in attracting FDI.4
FDI flows seem to be strongly influenced by security concerns. This paper seeks to illustrate this potential relationship by empirically testing the effect of defense spending, as a proxy for national security, on FDI inflows in the MENA region. We attempt to investigate ways in which military expenditures could affect private-sector investment decisions. Prior studies argue that there exists a form of geoeconomic favoritism in that the greater a country's military capabilities, the more it attracts private capital seeking safe and secure environment (Norrlof, 2010). Acemoğlu and Robinson (2012), on the other hand, argue that defense spending “crowds out” FDI by revealing a less friendly business environment for investors. All too often, military spending can have negative impacts on a country's economic development and its ability to attract FDI. High military spending can divert resources away from more productive sectors of the economy, such as education, health, and infrastructure, which can ultimately hinder economic growth and development.
The association between FDI and military spending in developing economies is dependent on various factors, including the strategic alignment of military spending with broader development goals, the perceived impact on stability and security, and the overall economic environment of the host country. From an international investor's perspective, developing economies with high levels of military spending may be perceived as more stable and secure (Papaioannou, 2009). The presence of a strong military can also contribute to a stable political environment, reducing the perceived risks for these investors (Beckley, 2012). Drezner and Hite-Rubin (2016) find a positive and significant FDI–military spending relationship for developing countries. Their finding goes out to ascertain that the crowding out hypothesis applies, most likely, to the advanced industrialized economies.
The aim of this paper is to test whether military spending is an attractor for FDI for one of the less FDI attracting regions in the world (i.e., MENA). In fact, despite the significant increase in FDI during the last two decades, the MENA region has disappointing performance in attracting FDI compared to other developing and emerging countries (see Figure 1). Following the World Development Indicators data, out of the $1.26 trillion in global FDI in 2020, MENA region attracted only $65.9 billion, or less than 6% compared, for example, to $144.0 billion in FDI inflows to Latin America and the Caribbean region (see Figure 2 for a comparison).
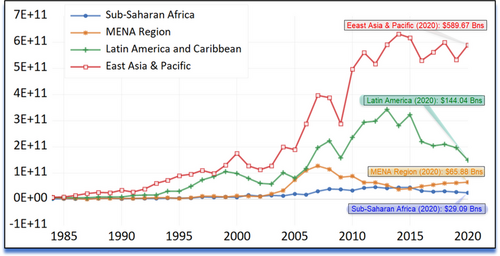
Foreign direct investment (FDI), net inflows (BoP, current US$, log). [Colour figure can be viewed at wileyonlinelibrary.com]
Note: FDI inflows by region for East Asia and Pacific, Middle East and North Africa, and Latin America and Caribbean over the period 1984−2020.
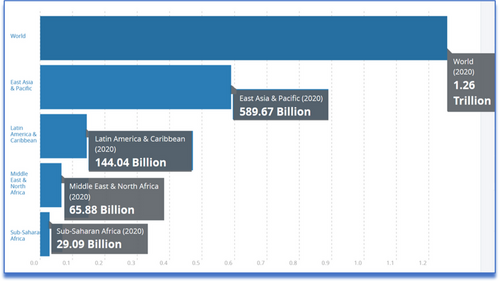
Foreign direct investment (FDI), net inflows (BoP, current US$, log). [Colour figure can be viewed at wileyonlinelibrary.com]
Note: FDI inflows by region for East Asia and Pacific, World, Middle East and North Africa, sub-Saharan Africa, and Latin America and Caribbean in 2020.
FDI flows can play a pivotal role in financing economic activities and development if the host country is politically stable and enjoys sustainable economic growth. Defense spending, if well used, can then work as a positive catalyst to economic growth in the host country, especially, in emerging economies (Smyth & Narayan, 2009). The seminal work by Benoit (1973) was the first to assume a positive relationship between military spending and economic conditions. Since then, the argument is far from being complete. Between studies finding a positive relationship (Fredericksen & Looney, 1983; Smith, 1980; Yildirim et al., 2005, to cite few) and studies that show negative relationship (Deger & Smith, 1983, Dunne et al., 2005; Heo, 2010; Lim, 1983), the long debate is never ending among defense economists.
During the post–Cold War era, the level of global military spending is increasing exponentially. Following the Stockholm International Peace Research Institute (SIPRI) figures, global military spending reached $1.98 trillion in 2020, an increase of 2.6% in real terms from 2019 and more than 9.3% increase compared to 2011 figures. Seven of the 10 countries with the highest military burden (military spending as a ratio of gross domestic product [GDP]) in 2019 are in the MENA region.5 MENA countries considered doubled (113%) their military spending during the period 1990−2020. Trends in other regions such as the sub-Saharan Africa (72% over the same period) and Latin America (54%) are rather muted.6
Norrlof (2010) suggests different causal mechanisms through which military power is hypothesized to lead to positive economic benefits. Investors in seeking the best return will always opt to locate their FDIs where they have the highest potential for profit and least risk.
The intersection between military expenditure and FDI in developing countries has been a subject of growing interest among policymakers and scholars. Smith and Smith (1980) argue that a certain level of military expenditure contributes to a perception of stability, encouraging FDI inflows to the host country. However, the challenge lies in finding the optimal balance between security needs and diverting resources from other sectors of the economy (Jones et al., 1998). Various studies found that military expenditure can have both positive and negative effects on FDI inflows to developing economies, depending on the level of security, macroeconomic stability, and governance in the host country (Ebere et al., 2019; Kishi et al., 2017; Norrlof, 2010; Posma, 2021).
Based on their empirical study using data for the period 1994 to 2017, Ebere et al. (2019) suggest that defense spending has a positive and significant impact on FDI for Nigeria. In contrast, Posma (2021) provided robust evidence revealing that military expenditure reduces private investment and FDI in Indonesia. From a theoretical perspective, Kishi et al. (2017) suggest that the positive relationship between FDI and military spending comes from the “dependency perspective,” that is, a state in which developing economies, in seeking outside financial resources, will always seek military options, rather than engage in economic reforms. In this case, FDI inflows will most likely provide revenues to these developing economies for pursuing military choices, reducing incentives to make concessions. This argument can be of importance when linking military expenditure to infrastructure growth, assuming that military budgets in some developing economies promote or even complement infrastructure development (Alptekin & Levine, 2012). That is, military establishments in some developing countries (including in the MENA region) contribute directly in enhancing or developing infrastructure projects (Dunne, 2000).7 Authors like Looney (1990), Kollias and Paleologou (2011), and Lin et al. (2015), for example, argue that the military expenditure has an indirect effect on enhancing infrastructure projects, through research and development and advanced new technology. Foreign firms and, by extension, foreign investors preferring their host countries to have well-developed logistics and connectivity, will be attracted by such involvement.
The focus of this paper is to see whether military spending is an attractor for FDI in the MENA region. As such, this work contributes to the literature on FDI by focusing exclusively on the relationship between FDI and military spending. This empirical evaluation tests the arguments that military spending yields economic returns (geoeconomic favoritism). This geoeconomic favoritism theory suggests that foreign capital inflows will be attracted if the host country is spending enough resources for military purchases (Norrlof, 2010). Given, however, the context of the MENA region (a region with ongoing conflicts for the whole post–Cold War era), it is hard to assert that international investors can potentially make voluntary resource transfers using military spending as a powerful market signal. To pursue this aim, a dynamic panel approach is applied to the 18 MENA countries over a 37-year time span (from 1984 to 2020). The autoregressive distributed lag technique used enables the assessment of both the short- and long-run dynamics of the relationship. This econometric approach helps also overcome the delicate problem of the order of integration of variables in the model.8
Using the autoregressive distributed lag approach, this paper empirically tests the effect of defense spending on FDI inflows to the MENA region. The results suggest that high levels of investment in military capabilities lead to geoeconomic favoritism in this region. Our main finding is, indeed, that military spending and FDI exhibit a significant positive relationship in the region. Specifically, the estimation results suggest that a 1 percentage point increase in military spending leads to 1.3% increase in FDI Inflows to MENA countries.9 It is worth noting that military spending is strongly associated with FDI inflows in all specifications even when controlling for conflicts in the region and natural resource variables used in our diagnostic check stage. Our results suggest that military spending functions as an attractor for FDI, and that these results hold with alternative regression models controlling for a number of factors affecting social and economic conditions in the region.
The remaining of this paper is divided into three sections. The next section frames the empirical methodology and data sources. The third section provides the main results. The final section summarizes and discusses limitations and future extensions.
2 EMPIRICAL METHODOLOGY
There are ways in which military posture can be hypothesized to attract inward FDI. International investors, for example, might interpret military power as a powerful market signal. Stable security environment is then the most obvious benefit from a country's military strength. A country with sufficient military capabilities is far more likely to attract foreign capital if it is secure from foreign invasion and domestic threats. This security, in turn, can make the country an attractive place for FDI (Beckley, 2012; Norrlof, 2010).
In this section, we start by providing an overview of the data used in this work, before moving to the examination of the empirical relationship between the main variables of interest, FDI inflows, and military expenditures. We do this by first considering a bivariate case net of all control variables. We shall, then, consider multivariate extensions, adding controls in a stepwise fashion.
2.1 Data and panel unit root tests
2.1.1 Data description
Level data are normalized using current US dollars. SIPRI is the main source for military expenditures data while the World Bank economic indicators (WDI) provide data on all economic variables, including FDI inflows. In our robustness check analysis, we utilize WDI natural resources data, while conflict data are obtained from the Uppsala Conflict Data Program (UCDP).10 The International Country Risk Guide (ICRG) variables are retrieved from the subscription-based Political Risk Services (PRS) group,11 which is an online service providing data on foreign investment and country-specific political and economic factors to international investors.
By this transformation, negative and zero values are retained. We also measure FDI inflows in dollars (not in millions), hence adding 1 in the previous equation is equivalent to adding one dollar to gross inflows.
All other macrovariables in the panel are used in their natural logarithmic forms, ICRG risks and education are used in levels. Table 1-A shows the descriptive statistics; namely, mean value, standard deviation, and number of observations of all variables in the panel. As stated by SIPRI,12 military spending is a measure of all costs incurred as a result of current military forces, consisting of expenditure on personnel, operations, and maintenance. SIPRI also highlights the general lack of transparency and accountability regarding military matters in the MENA region.13 Between data availability for some countries and uncertainty due to the lack of detail in public documents (high level of secrecy), military spending data for the region are to be used with a precaution. This issue will not, however, limit researchers from using the available data for economic analysis.
| Variables | Mean | Std. Dev. | Min. | Max. |
|---|---|---|---|---|
| 14.2059 | 13.5247 | −23.0433 | 24.3985 | |
| 21.5360 | 1.2785 | 17.4264 | 25.1913 | |
| 24.5623 | 1.2930 | 19.8263 | 27.4645 | |
| 8.5661 | 1.3142 | 3.1290 | 11.4931 | |
| 2.5335 | 0.8777 | 1 | 5 | |
| 31.6151 | 9.2740 | 0 | 50 | |
| 19.3859 | 18.7072 | 0 | 73 | |
| 5.9521 | 2.3577 | 0 | 10 | |
| s— | 8.0831 | 2.4266 | 0.7917 | 10 |
| 18.2891 | 1.2750 | 15.1309 | 20.8592 | |
| 3.7717 | 1.2711 | 1 | 6 | |
| 2.8379 | 1.4794 | 0 | 5 | |
| 78.9980 | 33.6860 | 0.0210 | 210.161 | |
| 21.6792 | 3.1893 | 12.4526 | 26.6088 | |
| 0.2673 | 0.4429 | 0 | 1 | |
| 0.3919 | 0.4885 | 0 | 1 |
- Note: Our data set includes 18 Middle East and North Africa (MENA) countries over 1984−2020 time period (18 cross-sections by 37 years).
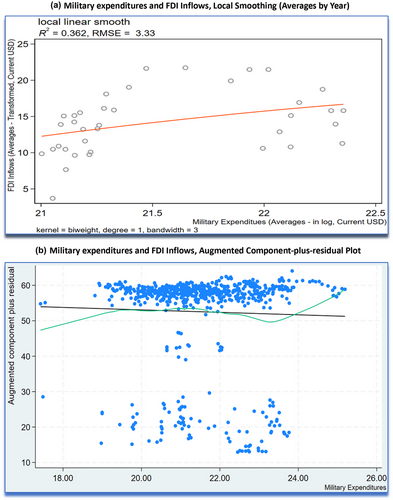
To analyze the relationship between military expenditures and FDI, we start by plotting the average of country-year observations on these two variables for the period 1984 to 2020. Plots in Figure 3 depict the average FDI inflows and the average military expenditures (in log forms) for all countries (averages by country). A closer look at the scatterplot in Figure 3 shows a strong divergence among countries between the average military spending and the attractiveness of foreign capital. Israel is the frontrunner when both military spending and FDI attractiveness are considered. Saudi Arabia is by far the largest military spender in the region and was the world's fifth largest spender in 2020. FDI inflows to Saudi Arabia have, however, followed a downward trend over the last decade, due mainly to political factors and lower oil prices. Iraq, Libya, and Yemen are the only three other countries in the region attracting similar level or less FDI than Saudi Arabia. Overall, the scatterplot in Figure 5a suggests a slightly positive relationship between the two variables. This association is also highlighted in the correlation matrix shown in Table 1-B where FDI inflows is significantly and positively correlated with military spending (in levels). The significant Pearson correlation coefficient value of 0.497 confirms what was apparent from Figure 5a. Table 1-B also reports the correlation coefficients between FDI and military expenditures per capita () and military burden14 (), showing a significant and positive coefficient for and a negative one for A detailed description of the data is provided in the Online Appendix.
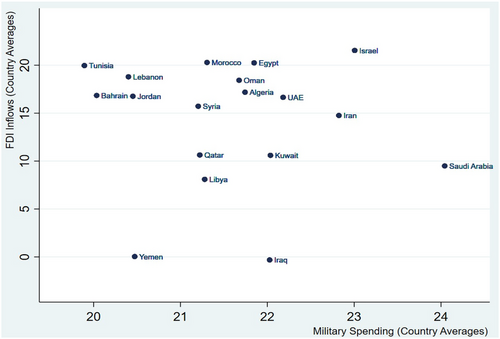
Foreign direct investment (FDI) inflows (log) and military spending (log)—Averages by country. [Colour figure can be viewed at wileyonlinelibrary.com]
Note: The scatterplot depicts average FDI inflows (country average, in transformed form) and average (log) military expenditures per country. Sample period: 1984−2020.
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
|---|---|---|---|---|---|---|---|---|---|
| (1) | 1.000 | ||||||||
| (2) | 0.497*** | 1.000 | |||||||
| (3) | 0.213*** | 0.389*** | 1.000 | ||||||
| (4) | −0.024 | 0.036 | 0.027 | 1.000 | |||||
| (5) | 0.577*** | 0.839*** | 0.258*** | −0.040 | 1.000 | ||||
| (6) | 0.301*** | 0.249*** | 0.652*** | −0.039 | 0.323*** | 1.000 | |||
| (7) | 0.325*** | 0.063* | −0.045 | −0.063* | 0.357*** | 0.147*** | 1.000 | ||
| (8) | 0.041 | 0.089** | 0.196*** | −0.070* | −0.007 | 0.178*** | −0.193*** | 1.000 | |
| (9) | 0.323*** | 0.223*** | 0.297*** | −0.129*** | 0.345*** | 0.556*** | 0.317*** | 0.022 | 1.000 |
| (10) | 0.140*** | 0.200*** | 0.092** | −0.113*** | 0.329*** | 0.050 | 0.187*** | −0.031 | 0.432*** |
| (11) | 0.264*** | 0.156*** | 0.155*** | −0.151*** | 0.298*** | 0.342*** | 0.492*** | −0.208*** | 0.688*** |
| (12) | 0.241*** | 0.152*** | 0.252*** | −0.110*** | 0.183*** | 0.380*** | 0.299*** | 0.181*** | 0.532*** |
| (13) | 0.069* | 0.243*** | 0.188*** | 0.022 | 0.231*** | 0.118*** | 0.145*** | −0.129*** | 0.147*** |
| (14) | 0.176*** | 0.261*** | 0.656*** | −0.029 | 0.236*** | 0.712*** | −0.083** | 0.128*** | 0.479*** |
| (15) | 0.115*** | −0.063* | 0.238*** | −0.108*** | −0.097** | 0.332*** | 0.000 | 0.144*** | 0.340*** |
| (16) | 0.448*** | 0.389*** | 0.399*** | −0.060 | 0.543*** | 0.523*** | 0.418*** | 0.077** | 0.463*** |
| (17) | 0.448*** | 0.785*** | 0.244*** | −0.025 | 0.820*** | 0.273*** | 0.115*** | −0.115*** | 0.358*** |
| (18) | 0.048 | 0.168*** | −0.064* | 0.056 | 0.240*** | −0.057 | 0.134*** | −0.056 | −0.146*** |
| TABLE 1-B. Correlation Matrix—Part 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variables | (10) | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) |
| (1) | |||||||||
| (2) | |||||||||
| (3) | |||||||||
| (4) | |||||||||
| (5) | |||||||||
| (6) | |||||||||
| (7) | |||||||||
| (8) | |||||||||
| (9) | |||||||||
| (10) | 1.000 | ||||||||
| (11) | 0.357*** | 1.000 | |||||||
| (12) | 0.359*** | 0.541*** | 1.000 | ||||||
| (13) | 0.132*** | 0.215*** | 0.035 | 1.000 | |||||
| (14) | 0.246*** | 0.264*** | 0.421*** | 0.205*** | 1.000 | ||||
| (15) | −0.030 | 0.289*** | 0.248*** | −0.006 | 0.458*** | 1.000 | |||
| (16) | −0.220*** | 0.466*** | 0.386*** | 0.327*** | 0.529*** | 0.269*** | 1.000 | ||
| (17) | 0.310*** | 0.256*** | 0.119*** | 0.228*** | 0.299*** | 0.013 | 0.329*** | 1.000 | |
| (18) | −0.059 | −0.060 | −0.249*** | 0.166*** | −0.181*** | −0.209*** | 0.294*** | 0.072* | 1.000 |
- *** p < 0.01,
- ** p < 0.05,
- * p < 0.1.
2.1.2 Panel unit root tests
In the recent literature of dynamic panel data, unit root tests have become commonplace. With data sets including time period, which is fairly long (37 years), it is very likely that some of the macroeconomic variables will follow a unit root process (Nelson & Plosser, 1982). The first generation of these tests includes Harris and Tzavalis (1999), Maddala and Wu (1999), Choi (2001), and Im et al. (2003). These tests relay on the assumption that the individual time series in the panel are cross-sectionally independently distributed. A second generation of these tests is developed around the concerns of the existence of cross-sectional dependencies. Various tests have been proposed including the works of Choi (2002), Ploberger and Phillips (2002), Chang (2002), Pesaran (2003), Phillips and Sul (2003), Moon and Perron (2004), and Bai and Ng (2004).
Nonstationarity is a very important issue, which has been taken into consideration, in this work, by applying selected first-generation tests: Harris and Tzavalis (1999), Maddala and Wu (1999), and Im et al. (2003). Second-generation unit root tests: Pesaran (2007) and Bai and Ng (2004) are also applied. Panel unit root results are shown in Tables 2 and 3. Results report that the series are a mix of I(0) and I(1) and that no series is I(2), allowing us to employ the panel autoregressive distributed lag (ARDL) approach in the estimation stage (Pesaran, 1997; Pesaran et al., 1999).
| First-generation tests | ||||||
|---|---|---|---|---|---|---|
| Harris and Tzavalis (1999) | Maddala and Wu (1999) | Im et al. (2003) | ||||
| HT test () | MW test | () | IPS test | () | ||
| Variables | Level | First difference | Level | First difference | Level | First difference |
| 0.4033*** | −0.4057*** | 247.233*** | 1065.686*** | −8.3833*** | −29.6245*** | |
| 0.9296 | 0.0641*** | 32.330 | 461.380*** | −0.2781 | −17.2035*** | |
| 0.9387 | −0.0475*** | 17.706 | 362.760*** | 0.9915 | −13.2337*** | |
| 0.8861* | −0.0555*** | 27.536 | 377.183*** | 0.0628 | −14.6598*** | |
| 0.9105 | 0.1751*** | 18.603 | 397.362*** | 0.0373 | −16.8656*** | |
| 0.8350*** | −0.0297*** | 15.695 | 453.738 | 3.4749 | −16.7792*** | |
| 1.0011 | 0.3622*** | 10.021 | 272.009*** | 1.6248 | −8.6483*** | |
| 0.9084 | 0.1768*** | 10.926 | 356.136*** | 1.5388 | −15.1269*** | |
| 0.8483*** | −0.2326*** | 44.766 | 642.987*** | 0.5215 | −18.7209*** | |
| 0.9249 | −0.0176*** | 42.537 | 549.528*** | 1.9400 | −14.8773*** | |
| 0.8836** | 0.2470*** | 16.283 | 341.982 | −0.5541 | −14.3696*** | |
| 0.8472*** | 0.0523*** | 29.429 | 478.185*** | −1.9822 | −17.1570*** | |
| 0.8547*** | 0.0025*** | 37.371 | 457.272*** | −0.4311 | −18.0029*** | |
| 0.9981 | 0.4622*** | 19.230 | 231.010*** | 1.2941 | −9.7131*** | |
| 0.9157 | −0.0182*** | 20.678 | 502.621*** | 1.5145 | −18.5113*** | |
| 0.6656*** | −0.2996*** | 102.243*** | 904.278*** | −2.3140** | −26.1022*** | |
- Note: The null and alternative hypotheses are as follows: HT test and MW test, H₀: Panels contain unit roots and H₁: Panels are stationary. MW test assumes cross-section independence. IPS test, H₀: All panels contain unit roots and H₁: Some panels are stationary. Lags are chosen by Akaike information criterion (AIC).
- ***, **, and * denote significant at 1%, 5%, and 10% level, respectively.
| Second-Generation Tests | |||||||
|---|---|---|---|---|---|---|---|
| Pesaran (2007) | Bai and Ng (2004) | ||||||
| CIPS* test | PANIC test | ||||||
| Level | First difference | Level | |||||
| Variables | MQc | MQf | Pa | Pb | PMSB | ||
| −4.679*** | −5.885*** | −35.47*** | −29.142*** | −8.202*** | −4.849*** | −2.318** | |
| −3.143** | −5.142*** | −22.549*** | −25.188*** | 1.400 | 1.811 | 2.320 | |
| −2.539 | −4.569*** | −30.483*** | −20.004*** | −0.099 | −0.098 | −0.078 | |
| −2.547 | −4.570*** | −27.458*** | −28.541*** | 0.071 | 0.072 | 0.086 | |
| −2.171 | −5.171*** | −21.352*** | −15.181*** | −0.508 | −0.483 | −0.400 | |
| −2.511 | −5.309*** | −33.165*** | −12.131*** | −2.553** | −2.037* | −1.493* | |
| −2.296 | −4.513*** | −17.465*** | −21.886*** | 1.262 | 1.540 | 1.861 | |
| −2.196 | −4.549*** | −19.609*** | −16.879*** | −2.674** | −2.119* | −1.547* | |
| −3.538*** | −5.870*** | −36.39*** | −17.821*** | −4.855*** | −3.191*** | −1.823** | |
| −2.427 | −5.267*** | −28.979*** | −13.512*** | 0.725 | 0.804 | 0.898 | |
| −3.795*** | −4.715*** | −30.819*** | −23.421*** | −0.472 | −0.452 | −0.361 | |
| −2.389 | −5.390*** | −19.164*** | −16.282*** | −3.406*** | −2.608*** | −1.847** | |
| −2.693* | −5.764*** | −27.185*** | −19.916*** | −3.276*** | −2.47*** | −1.647** | |
| −1.912 | −4.030*** | −15.35*** | −28.520*** | 0.318 | 0.332 | 0.338 | |
| −3.152*** | −5.557*** | −20.81*** | −23.076*** | −0.009 | −0.009 | 0.052 | |
| −3.646*** | −5.787*** | −35.833*** | −16.228*** | −6.905*** | −3.581*** | −2.327*** | |
- Note: The null and alternative hypotheses are as follows. Cross-sectionally augmented Im-Pesaran-Shin (CIPS)* test, H₀: Panels contain unit roots and H₁: Panels are stationary. CIPS test assumes cross-section dependence is in form of a single unobserved common factor. The null hypotheses for the Panel Analysis of Non-stationarity in Idiosyncratic and Common components (PANIC) test are nonstationarity for the common and idiosyncratic components. MQc and MQf are statistics for the multiple factors; Pa, Pb, and PMSB are for the idiosyncratic term. Overall stationarity of the series is achieved if both components are stationary. All variables are stationary in first difference with the Bai and Ng (2004) panic test (results not shown).
- ***, **, and * denote significant at1%, 5%, and 10% level, respectively;
To analyze the relationship between military expenditures and FDI, we start by plotting the average of country-year observations on these two variables for the period 1984 to 2020.15
2.2 The empirical model
2.2.1 Bivariate analysis
We start our analysis by checking the empirical relationship between FDI inflows () and military expenditures () in a bivariate setup. Bivariate analysis is the empirical analysis of two variables to ascertain if a relationship exists between them. Specifically, this strategy can be used to describe the strength and the direction of the relationship between and The aim is to check whether an association between these two variables exists, without controlling for any other factor. Therefore, and rather than moving forward with the inferential statistics, we first use a bivariate analysis to determine if any potential connection exists between the two variables at the observational level.
FDI inflows and military spending vary widely across the MENA region. As shown in Figure 3, countries like Israel, Egypt, Tunisia, and Morocco have traditionally attracted the most significant FDI in the region. On the other hand, Saudi Arabia is one of the largest military spenders globally, often ranking in the top five. A significant portion of its budget is allocated to defense due to regional security concerns (e.g., the war in Yemen, tensions in the region). FDI inflows are typically low in countries like Iraq, Libya, and Yemen, where conflicts have led to political and economic instability, but military spending remains relatively high due to ongoing conflict.
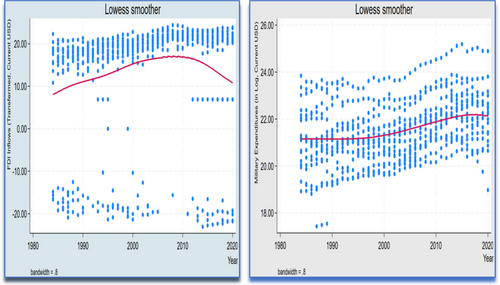
Trends, over the time period of this study (Figure 4), show that both variables increase significantly, with showing a more uneven path, with a setback in 2008 when it reaches a historic level for the MENA region. All lines in this figure show an overall upward trend, which indicates that FDI inflows have appeared to substantially increase while military spending has also increased, suggesting the possibility of a positive relationship between the two variables.
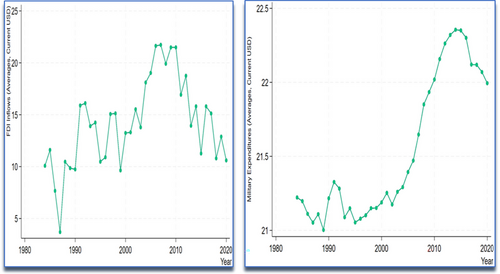
Average foreign direct investment (FDI) inflows and military expenditures in the Middle East and North Africa (MENA) region. [Colour figure can be viewed at wileyonlinelibrary.com]
Note: The line charts show average FDI inflows (in transformed form) and average (log) military expenditures. Sample period: 1984−2020.
Going deeper into the relationship between country-level averages and in order to visualize this association without resorting to trend lines, we rely on a local smoothing technique. Smoothing methods attempt to find functional relationships between different measurements. Essentially this means drawing lines through the data nearest to the independent variable, not from the entire set of points. Figure 5a shows a scatterplot of the data (averages), together with a kernel smooth using the local smoothing technique. The smooth is constructed using the bi-weight kernel and a bandwidth of 3. The smooth fit captures the main trend of the data, showing a positive relationship with an To further check the possibility of a quadratic relationship between the two variables, the augmented component-plus-residual plot is used to detect any possible nonlinearity in the data. As shown in Figure 5b, the low-smoothed line does not appear to deviate too much from the line of best fit (polynomial pattern). Further investigation using a formal test16 is conducted and we conclude that nonlinearity is not an accurate relationship between FDI inflows and military expenditures, pointing toward a monotone relationship between these variables.
A more sophisticated smoothing procedure is also available via the locally estimated scatterplot smoothing technique (LOWESS). The LOWESS smoother uses a regression model with polynomial terms on a local subset of the data (avoiding sensitivity to extreme data points) to estimate a fitted value for each observation (see Cleveland, 1979, and Mallows, 1986, for more details about these techniques). The positive association between the two variables is again put forward by LOWESS, even though post–2008 financial crisis negatively impacted the flow of FDI to the region. The impact on FDI inflows leads to a curved shape albeit very minimal (See Figure 6). As a result, these probably indicate that there may be a (weak) negative relationship between the variables of interest after 2008.
Finally, and in order to summarize, the association between the two variables classified categorically as to whether observations are above the 90th percentile of FDI or military spending, respectively (defined as high observations). Table 4 displays a breakdown of the data by these two categories (high and low, with the later defined as observations below the 90th percentile) along with the Pearson chi-square test. The aim here is to see if high levels of FDI inflows are associated with high level of military expenditure in the MENA region (results shown in Table 4). It is evident, though, that low FDI is associated with low military spending as 95% (567/599) of “low” FDI inflows are associated with “low” military spending. Only 5% (32/599) of low military expenditure observations are linked to high FDI inflows while 52% (35/67) of high military spending coincide with high FDI observations, thus, providing some evidence that high FDI inflows and high military spending are linked together. The Pearson's statistic is significant at all confidence levels with a p-value < 0.000, thus providing ample confidence that the above associations are not due to random chance.
| Military expenditures (log) | |||
|---|---|---|---|
| FDI inflows (log) | Low | High | Total |
| Low | 567 | 32 | 599 |
| High | 32 | 35 | 67 |
| Total | 599 | 67 | 666 |
- Note: Pearson's χ2 (1) = 146.47, p = 0.0000. “High” is defined as above the 90th percentile.
To summarize the bivariate analysis, we can conclude that an empirical observed positive relationship exists between the two variables of interest in this study, FDI inflows, and military expenditures. We will, now, proceed with this association between the two variables in the next section, adding more controls and testing the relationship in a multivariate framework.
2.2.2 Multivariate analysis
This section will introduce control variables into our analysis, in order to test the assertion that a positive association exists between the FDI inflows and military spending, as highlighted in the bivariate case.
Our empirical model fills the gaps in the literature. A panel model on all MENA countries tests the relationship between FDI inflows () and military expenditures (), controlling for institutional, economic, and political factors () over a period of 37 years (1984−2020).
As it is well known in the literature, allowing for the presence of subject-specific unobserved heterogeneity represents one of the key advantages of using panel data. In this context, we deal with this unobserved heterogeneity by using the one-way fixed effects models, or by taking first differences if the second dimension of the panel is a proper time series, that is, dynamic panel. Dynamic panels in which the regressors include the lagged dependent variable are developed around the work of Arellano and Bond (1991), Arellano and Bover (1995), and Blundell and Bond (1998). The resulting generalized method of moments (GMM) approach, and its extension to the “System GMM” context, are, however, estimators designed for situations with, “small , large ” panels, that is, few time periods and many individual units.
The analysis of panel data with both large and becomes increasingly important in the literature. Pesaran and Smith (1995), Pesaran (1997), and Pesaran et al. (1999) present the ARDL in the error correction form allowing both the short-run dynamic, and the long-run equilibrium, relationships between and military expenditures to be separately identified. When both and are sufficiently large, there have been two approaches in the literature to analyzing dynamic panels. The fixed versus random effects estimators, on the one hand, and the mean group (MG) versus the pooled mean group (PMG) estimator on the other hand. The dynamic fixed effects (DFE) being another option used for situations in which it is reasonable to assume that short- and long-run parameters are identical for all individuals in the panel. Choosing among these estimation techniques is based on a Hausman test of the null hypothesis that the difference between the and the (or , assuming a dynamic panel) estimator is zero. The estimator is selected if the null hypothesis is rejected; otherwise, the more efficient pooled estimator is to be preferred. As shown by Pesaran (1997) and Pesaran et al. (1999), these models can be estimated with the variables being I(0) and/or I(1).
Furthermore, in order to assess simultaneously both in the short- and long-run, we also consider the panel ARDL technique. The ARDL approach estimates the effect of a particular variable on military expenditures separating the short-run from the long-run effects (Bentzen & Engsted, 2001). ARDL is based on Pesaran (1997) and Pesaran et al. (2001). The dynamics in these models is incorporated into the error correction term by using lags of the dependent and independent variables. This incorporation allows for rich dynamics in the sense that the dependent variable adapts to changes in the explanatory variables.
The key parameters are defined as Of interest are the parameter , which is the error-correcting speed of adjustment term, and the vector , which contains the long-run relationships between the variables. The error-correcting term is expected to be significantly negative under the prior assumption that the variables show a return to a long-term equilibrium.18 If the coefficient is rather zero, there is no evidence of long-term relationship.
In our empirical work, we utilize a panel regression method for the 18 MENA countries. The analysis covers the period . The length of each time series in the panel is determined by data availability. Our dependent variable is the net FDI inflows into the host country in a given year, measured in current US dollars. We use the World Bank measure of FDI inflows in this analysis. Military expenditure data are produced by the SIPRI and GDP is retrieved from the WDI database. All other control variables are from the PRS group or constructed from the World Bank indicators.
FDI inflows are known to be linked to domestic conditions of the host country. A number of institutional, political, and economic factors are to be considered when dealing with the relationship between military spending and FDI. Following Hite-Rubin (2015) and Drezner and Hite-Rubin (2016), we use the Political Risk Services Group's International Country Risk Guide (PRS-ICRG) risk measures for control variables in our empirical work. The PRS-ICRG is a subscription-based service that provides data on foreign investment and country-specific institutional, political, and economic factors.19 According to the PRS-ICRG methodology, an index is created for each of three main categories, which can be defined as political, economic, and financial risk categories. The political risk index is based on 100 points, financial risk index is based on 50 points, and economic risk index is based on 50 points. Likewise, each category is divided into subfactors where each factor has its own weight.20 Six of these factors are used in our data set. In order to assess the impact of these factors, we include control variables in our model estimation in a stepwise fashion.
Military expenditure, , is the main explanatory variable in this paper. This variable is constructed using military expenditure by country, in millions of US$ at current prices, converted at the exchange rate for the given year (in log form). In the defense economics literature, the choice of the military spending proxy has a long tradition of empirical and theoretical debate before settling on a specific choice. In the military spending–growth literature, whether the level or share is the appropriate measure, military burden (the share of national income going into military expenditure) is usually chosen (see Brauer, 2002, for an excellent discussion and Smith, 2017, for a recent confirmation). In the demand for military expenditures literature, levels are often used (Smith, 2017). Each approach provides different insights into a country's defense capabilities and priorities. On the one side, military spending as a share of GDP offers insights into the economic impact of military expenditures, as it captures the relative burden of this category of spending on a country's overall budget. On another side, military spending (in levels) primarily measures the financial resources allocated by a government to its defense and military capabilities. It provides insight into the extent to which a country invests in its armed forces, military capabilities, defense infrastructure, and security-related activities. This variable is then considered as a good proxy for a nation's commitment to national security. This paper uses the level of military spending (in log form) as a signal and test of the country's attractiveness of the business environment. International investors may interpret this signal as a sign that the country is committed to maintaining stability and security. In contrast, high military spending at the expense of crucial social and economic investments may, also, raise concerns about the government's priorities and its commitment to creating a business-friendly environment, which might discourage foreign investors.22
We test the relationship among our variables controlling for a number of other factors,23 including: income proxied by log of GDP expressed in current US dollars (); log of GDP per capita expressed in current US dollars (); the ICRG's risk points for Corruption (); the ICRG's combined economic risk rating (); a country measure of the number of active Bilateral Investment Treaties in a given year (); as an alternative to , the degree of economic openness of a given country is used to measure the degree to which nondomestic transactions take place and affect the size and growth of a national economy (). Other control variables accounting for country's financial and political risks are: the ICRG's risk points for gross foreign debt expressed as a percentage of GDP (financial risk, ); the ICRG's risk points for exchange rate stability (); the ICRG political risk measure of the strength and impartiality of the legal system as long as an assessment of the observance of law in practice () and the ICRG's risk points for international liquidity (financial risk, ).
The energy consumption is measured in quadrillions British thermal unit (BTU) per capita (in log form, ). Education is measured by the Human Development Index (HDI), mean years of schooling (). In order to account for country-specific banking-sector vulnerabilities or certain types of recessions, a financial dummy variable is constructed
In this equation, we control for most institutional, political, financial, and economic factors that, in our view, have an impact on the FDI inflows into a given country in the MENA region from one year to the next. As stated before, dynamic panel regressions often employ any one of the following three estimators: the DFE, the MG, and the PMG estimator. The choice among the three estimators is determined by the joint Hausman test. In this case, PMG is tested against both MG and DFE as reported in the last panel of Table 5. The Hausman test indicates that PMG is consistent and more efficient when compared to MG and DFE. The PMG technique is known for pooling the long-run parameters, restricted to be homogeneous across countries. This technique avoids, at the same time, the inconsistency problem flowing from the heterogeneous short-run dynamics.24 This is particularly useful where there are reasons to accept that the long-run equilibrium relationship between the variables is similar across countries or at least, a subset of them, which is the case for countries in the MENA region.
| Variables | CD-test | Mean 𝝆 | Mean ABS(𝝆) | p-value |
|---|---|---|---|---|
| 10.456 | 0.14 | 0.22 | 0.0000 | |
| 31.705 | 0.42 | 0.48 | 0.0000 | |
| 59.573 | 0.79 | 0.79 | 0.0000 | |
| 51.036 | 0.68 | 0.71 | 0.0000 | |
| 16.696 | 0.22 | 0.42 | 0.0000 | |
| 47.593 | 0.63 | 0.63 | 0.0000 | |
| 68.591 | 0.91 | 0.91 | 0.0000 | |
| 14.977 | 0.20 | 0.36 | 0.0000 | |
| 12.934 | 0.17 | 0.33 | 0.0000 | |
| 13.704 | 0.18 | 0.42 | 0.0000 | |
| 47.723 | 0.63 | 0.71 | 0.0000 | |
| 63.826 | 0.85 | 0.85 | 0.0000 | |
| 17.21 | 0.23 | 0.35 | 0.0000 | |
| 70.327 | 0.93 | 0.93 | 0.0000 | |
| 47.882 | 0.64 | 0.68 | 0.0000 | |
| 15.978 | 0.21 | 0.36 | 0.0000 |
3 ESTIMATION RESULTS AND FINDING
Over the last few decades, various econometric approaches have been developed, as part of the big data revolution. The main objective is to deal with large cross-country panel data. Developed methods include pooled ordinary least squares (OLS), fixed/random effects, Two Stage Least Squares and Instrumental variables estimation (2SLS/IV), GMM (difference and system), and panel ARDL, to name few of the most popular tools for empirical econometrics. System GMM, for example, can be applied to small T large N panels. If T is large enough, dynamic panel bias becomes insignificant, and a more straightforward fixed/random effects estimator works. Moreover, the GMM is more focused on the short-run dynamics as it does not distinguish between the short- and long-run relationships between variables. Henceforth, the panel autoregressive distributed lag (panel-ARDL) technique is preferred in the context of this work and seems a very successful method for overcoming these drawbacks.
This paper is specifically measuring the long-run impact of military spending on FDI inflows to the MENA region. As reported above and after testing the variables for stationarity, we apply the panel ARDL methodology. Pesaran et al. (1999) suggest two different estimators, PMG and MG estimator. As mentioned before, the main difference between the two estimators being that PMG estimator is consistent under the assumption of long-run slope homogeneity while MG estimator is more consistent under the assumption that both slope and intercepts are allowed to vary across units. An alternative estimator being set up under the assumption of homogeneity slope is DFE, in which slopes are fixed and the intercepts are allowed to vary across countries.
We want to establish a multiple regression model with FDI inflows as the dependent variable and military expenditures as the main independent variable. We also control for other factors, known to impact this relationship, introduced in a stepwise regression to build the model. The variables introduced in the model and their regression coefficients are given in Tables 6-A and 6-B. This table presents the results of the panel-ARDL multivariate regression and discerns that military spending is a significant determinant of FDIs, even after controlling for institutional, economic, and political factors.
| Variables | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 |
|---|---|---|---|---|---|---|
| 2.0825*** | 1.7747*** | 1.7440*** | 1.1172*** | 1.6751*** | 1.2713*** | |
| 4.0286*** | − | 3.9787*** | 4.1681*** | 3.2987*** | 5.5165** | |
| − | 4.4297*** | − | − | − | −2.1309 | |
| −0.0040 | −0.0041 | −0.0813 | 0.2815 | 0.18421 | −0.3045 | |
| 0.1243*** | 0.1254*** | 0.1301*** | 0.1165*** | 0.11221*** | 0.1083*** | |
| −0.0382*** | −0.0441*** | − | −0.0111 | − | − | |
| − | − | −0.0275** | − | −0.0135 | −0.0660*** | |
| − | − | − | −0.3606*** | −0.0665 | −0.1846** | |
| − | − | − | −0.0762 | −0.0454 | −0.3265*** | |
| − | − | − | 1.0501 | −0.1508 | 1.1291** | |
| − | − | − | 0.1073 | 0.0386 | 0.3574*** | |
| − | − | − | −0.0286 | 0.1863 | −0.0592 | |
| − | − | − | −0.3207 | 0.7068*** | 0.5604 | |
| −1962.06 | −1963.15 | −1952.76 | −1845.13 | −1832.84 | −1800.64 |
- Note: The dependent variable is FDI Inflows (). An ARDL(1,1,1,1,1,1,1,1,1,1,1) is estimated for Model 6, optimal lag length is based on the Akaike information criterion (AIC). To ease the presentation, only the first difference of each variable is included in the following chart.
- ***, **, and * denote significant at1%, 5% and 10% level, respectively.
| Variables | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 |
|---|---|---|---|---|---|---|
| CoinEq | −0.7501*** | −0.7465*** | −0.7203*** | −0.7545*** | −0.7386*** | −0.8142*** |
| Δ(lMilex) | 5.6275 | 5.8895 | 5.6630 | 5.6280 | 5.9249 | 4.7602 |
| Δ(lGDP) | 3.0461 | − | 7.5445 | 3.0117 | 6.7906 | 39.0332 |
| Δ(lGDPPC) | − | 3.2272 | − | − | − | −32.4976 |
| Δ(CoRrUp) | −2.5781 | −2.1684 | −3.0691 | 0.1652 | −0.8051 | −2.2522 |
| Δ(eRisk) | 0.3350*** | 0.3172*** | 0.3485*** | 0.3215*** | 0.3408*** | 0.3700*** |
| Δ(BIT) | −0.2732 | −0.2361 | − | −0.5295 | − | − |
| Δ(Open) | − | − | −0.0403 | − | −0.0153 | −0.0057 |
| Δ(FDebt) | − | − | 0.7036 | 0.7285 | 0.6900 | |
| Δ(IntLiq) | − | − | −0.3443 | −0.0629 | −0.0881 | |
| Δ(lEU) | − | − | −2.3125 | −5.1088 | −4.6572 | |
| Δ(LawO) | − | − | −1.5683 | −1.4575 | −1.1379 | |
| Δ(ER) | − | − | 0.5014 | 0.0818 | −0.3273 | |
| Δ(Educ) | − | − | −5.3339 | −3.7058 | 0.6846 | |
| −0.1939*** | −0.1271*** | −0.2192*** | −0.1824*** | −0.3092*** | −0.3163*** | |
| 1.4704 | 1.3937 | 0.9656 | 1.2746 | 0.4502 | −0.0091 | |
| −95.9921*** | −46.0906*** | −84.6737*** | −94.3615*** | −73.7319*** | −122.325*** | |
| Hausman Tests | ||||||
| Pooled mean group (PMG) against mean group (MG) | ||||||
| H-test () | 1.65 | 2.24 | 4.44 | 3.67 | 1.83 | 10.12 |
| p-value | 0.9491 | 0.8961 | 0.6174 | 0.9886 | 0.9996 | 0.6839 |
| PMG against dynamic fixed effects (DFE) | ||||||
| H-test () | 0.48 | 0.40 | 0.67 | 3.59 | 4.93 | 11.39 |
| p-value | 0.9981 | 0.9988 | 0.9951 | 0.9898 | 0.9601 | 0.5781 |
- Note: The cointegration equation coefficient is denoted by ( in the text). The null hypothesis for the Hausman Tests is that the difference between MG and PMG or DFE and PMG estimation is not significant. If the null is rejected, the PMG estimator is recommended since it is efficient.
- ***, **, and * denote significant at 1%, 5%, and 10% level, respectively.
Panels A and B of Table 5 provide the long-run and the short-run coefficients of the respective variables. The value of the error correction term () is significant and negative for all iterations (Model 1 to Model 6), indicating the convergence of the model over a relatively short period of time. A significant error correction term also indicates that we can infer the joint causality of the variables, that is, all variables in the model jointly influence the dependent variable in the long run. The long-run coefficients of the ARDL model indicate a strong positive and significant connection between FDI inflows and military expenditures for Models 1 to 6. Quantitatively and in the long run, the impact of a 1% increase in military spending ranges from 1.12% increase (Model 4) to 2.08% increase in net FDI inflow (Model 1), to an average of 1.62% increase across all six models in Table 6. These results indicate that an increase in military expenditure in the MENA region is positively associated with inward FDI in the long run.
The relationship between the two variables of interest is positive but insignificant in the short run (Models 1 to 6). The short-run insignificant results are likely to be due to country differences in terms of economic attractiveness and/or policy lags between spending on military forces and activities and the relative impact on other variables in the model including on FDI inflows.25
GDP (in levels, ) and the economic risk factor () have the expected positive signs and exert statistically significant effects on the dependent variable. A 1% increase in GDP has a 5.52% corresponding increase in FDI, in the long run, while the same increase in affects FDI by 0.11% in Model 6. In the short run, the relationship between GDP and FDI is positive but not significant. Short-run insignificance of this variable indicates, again, that the effects of national income could not be felt in the short run. As expected, economic risks in the region depict significant estimates in the short run for all iterations, indicating a stronger dynamic interaction between the risk dimensions and FDI inflow. This is in line with other studies that find economic risks to be an important determinant of inward FDI for developing economies (Cavusgil et al., 2020).
Surprisingly, corruption within the political system and exchange rate risks are with mixed signs but not significant for all iterations, both in the short- and long run. Recent studies show that higher levels of corruption as well as other poor institutional quality factors in the host nation might hinder FDI (Huynh et al., 2020). On the other hand, exchange rate risk is known to make uncertainty and reduces foreign investment incentives and particularly reduces inward FDI into developing countries (Bleaney & Greenaway, 2001; Serven, 2002). Our results fail to show these significant connections for the MENA region, over the studied period.
BITs seem to have a negative relationship with FDI inflows. However, the only points where this relationship is statistically significant at above the 5% level are in Model 1 and 2. Previous studies on the impact of BITs on FDI have found mixed results (e.g., Busse et al., 2010; Hallward-Driemeier, 2003; Kerner, 2018). While BIT arrangements are likely designed to reduce risks and boost investor confidence in the host country, their aim is mainly to attract greater inflows of FDI. Empirical results support this view and advance a positive association between BITs and FDI inflows (Busse et al., 2010; Egger & Merlo, 2007, Makoni, 2018). Other studies argue that BITs have little effect, if any, on FDI inflows (Hallward-Driemeier, 2003). Our results are in line with Bae and Keum (2013) and Falvey and Foster-McGregor (2018), in that BITs are negatively related to FDI. One possible explanation is that these bilateral treaties are probably a small encouragement to invest in the MENA region as a whole, but they may influence the final decision for international investors to allocate capital investment in a particular country in the region. This study uses an alternative variable to proxy the economic environment in the region, namely, the economic openness, and found a significant negative relationship between openness to trade and FDI inflows into MENA.26 This is comparable to recent studies findings (Adow & Tahmad, 2018; Cantah et al., 2018; Khan & Hye, 2014). In contrast, Wickramarachchi (2019) found that trade openness had no significant impact on FDI inflows, while other studies found this relationship to be positive (Makoni, 2018; Zaman et al., 2018).
All other risk factors (, and ) show mixed signs, but significance is only seen in Model 6 (and Model 4 for risk points for gross foreign debt). For example, provides a comparative liquidity risk ratio on a scale of 0 to 5, with the risk rating of 0 indicating a very high risk and 5 indicating very low risk. These variables are expected to have positive signs, that is, higher risk points imply lower risk, leading to more FDI into the given country. This is only depicted by LawO, where a one-point increase (lowering the overall risk by 1) in the variable related to the legal system strength and observance of law in practice leads to 0.36% increase in FDI (Model 6). and are negatively related to the dependent variable. This may be explained by the diversity among countries in MENA with regard to foreign reserves. The link between reserve accumulation and the exchange rate may also, at least partly, explain these results. In fact, reserve accumulation/deaccumulation can lead to exchange rate misalignments, which can trigger strong exchange rate depreciation/appreciation and financial crises (Jeanne, 2010), negatively impacting FDI net inflows to the region.
Education and energy use are controls for human capital and size of the economy, respectively. Our results are mixed for these two variables. Education parameter is positive and significant in one model (iteration 5),27 while energy use is only significant in Model 6, with a positive value of 1.13% increase in FDI inflows following a 1% increase in energy consumption. The evidence of the relationship between human capital (proxied by education in our model) and FDI remains mixed in the literature. Authors like Brooks et al. (2010) and Noorbakhsh et al. (2001) found that education is one of the key determinants of FDI. In contrast, Cleeve (2008) and Cleeve al. (2015) did not find any evidence of the importance of human capital for FDI inflows to developing economies. Similar issues are found when linking FDI to energy use in developing economies, with some studies even reporting a bidirectional causality relationship between the two variables (Anwar & Nguyen, 2010; Amri, 2016). Belmokaddem et al. (2014) found, however, no causal relationship between energy consumption and inward FDI.
The above results hold with alternative specifications controlling for both conflicts in the MENA region and natural resources. Systematic evidence from the existing literature points to the risk of conflict being higher in resource-rich countries impacting the stability of the country and its attractiveness to foreign investors. It is also widely acknowledged that conflicts act as a major detractor for international investors exploring investment or business activities in a given country (Barry, 2018). As we have already accounted for a number of economic and political risks, including corruption, strength of institutions, and rule of law, and in the light of extant literature and getting robust estimation results, two other variables are included in the main ARDL model, conflict () and natural resources (). Results in Table 7-A (Models 7 to 10) show positive and highly significant estimates for military expenditures and depict this variable as a significant determinant of FDI inflows. The error correction term is, again, significant and negative for all iterations.
| Variables | Model 7 | Model 8 | Model 9 | Model 10 |
|---|---|---|---|---|
| 1.2491*** | 3.8824*** | 1.0950*** | 1.1284*** | |
| 4.4867*** | −8.0023*** | 4.0390*** | 4.3536*** | |
| 0.2685 | −0.8782*** | 0.1816 | 0.1779 | |
| 0.1176*** | 0.2538*** | 0.1046*** | 0.1035*** | |
| −0.0145 | − | −0.0009 | −0.0029 | |
| − | −0.0213** | − | − | |
| −0.3676*** | −0.2758*** | −0.1842* | −0.2212** | |
| −0.0480 | 0.3928* | 0.0417 | 0.0269 | |
| 0.5220 | 0.1148 | 1.7312** | 1.4224** | |
| 0.1289 | 1.5439*** | −0.0549 | −0.0146 | |
| 0.0484 | 0.9543*** | −0.0477 | −0.0243 | |
| −0.4283 | 5.4274*** | 0.0454 | −0.0691 | |
| 0.4017 | 55.167*** | − | 0.2131 | |
| − | −2.5811*** | − | − | |
| − | − | −0.3186*** | −0.3158*** | |
| −1829.84 | −1788.91 | −1824.78 | −1808.84 |
- ***, **, and * denote significant at 1%, 5%, and 10% level, respectively.
is a measure of the number of conflicts a country is involved in,28 including internal and external conflicts. Data on conflict are obtained from the UCDP data set version 19.1.29 This data set provides information on the dates of start and termination, locations, and the number of deaths caused by all violent events around the world. The hypothesized link between FDI and conflicts is well studied in the literature. A host country's instability due to conflicts (internal or external) could be a significant obstacle to FDI inflows and can damage investors’ perceptions about the future profit to be made (Blair et al., 2022; Driffield et al., 2013). Barry (2018) highlights, however, that “existing evidence does not support the strong, negative relationship between conflict and investment that is typically assumed.” One possible explanation for the “surprising” positive relationship, where higher FDI flows into conflict zones, is the relative insensitivity of resource-seeking FDI (natural resource extraction for instance) to conflict (Witte et al., 2017). Our results are in line with this literature. We observe a statistically insignificant and positive relationship between FDI and conflict in Models 7 and 10. This relationship reverts to a highly significant and positive impact of on FDI, in the long run, once the interaction effects between military spending and conflicts is introduced in Model 8.
is added to the model to control for the abundance of natural resources, particularly natural gas and oil, in the MENA region. This variable is constructed by summing the real rents (in $US) for a giving country from its natural resources (oil, minerals, natural gas, coal, and forests), which is then divided by GDP.30 It is worth noting here that there is no common consensus in the literature over the impact of natural resources on FDI (Asiedu, 2013; Kang, 2018). A plethora of empirical studies on the relationship between the natural resources and FDI have, in fact, found that resource-rich developing countries attract a lower volume of FDI than resource-scarce developing countries (see, for instance, Asiedu & Lien, 2011; Elheddad, 2018; Poelhekke & van der Ploeg, 2013). The phenomenon is often referred to as the resource curse, a paradoxical situation in which a country failed to achieve higher economic performance, including attracting large volume of inward FDI, despite being home to valuable natural resources (Douch & Solomon, 2018). Again, not all MENA countries are rich in oil or natural gas, the main coveted resources in the region. FDI inflows, also, vary across countries, indicating that FDI motives are not homogeneous among all countries.
The negative and significant estimate of in Model 9 enforce the crowding-out effects of FDI studied in the literature (Asiedu & Lien, 2011; Corden & Neary, 1982). These effects are related to the fact that natural resource (mining and extraction) sector, which is characterized by high profits and wages, tends to attract production factors such as capital and labor from other sectors like manufacturing and servicing, leading to a decline in the productivity of those sectors, and to an overall sharp decline of FDI inflows toward the primary sector of the economy (referred to as “Deindustrialization,” Corden & Neary, 1982). Abundance of natural resources could, therefore, be detrimental to FDI spillovers, rather than beneficial.
Short-run estimates are not significant for all variables. Again, FDIs are sources of long-run financing and the impact of military spending, conflicts, natural resource endowments, and all other variables on FDI can only be seen in the long run. The short-run adjustments related to the FDI inflows, reported in Table 7-B, show that all coefficients are, also, statistically significant with a negative sign, confirming a stable long-run relationship between the variables.
| Variables | Model 7 | Model 8 | Model 9 | Model 10 |
|---|---|---|---|---|
| −0.7353*** | −0.6314*** | −0.7693*** | −0.7464*** | |
| 5.2387 | 4.9388 | 4.9028 | 4.6263 | |
| 2.9154 | −1.2638 | 4.9805 | 4.3817 | |
| −0.3341 | −1.5292 | 0.5247 | −0.0084 | |
| 0.3078*** | 0.3644*** | 0.3186*** | 0.3184*** | |
| −0.4247 | − | −0.3844 | −0.2601 | |
| − | −0.0547 | − | − | |
| 0.9100 | 0.9577 | 0.7443 | 0.9057 | |
| −0.3309 | −0.4472 | −0.4976 | −0.4888 | |
| −1.8399 | −14.307 | −3.3841 | −2.1645 | |
| −1.8952 | 1.7782 | −0.2063 | −0.5531 | |
| 0.4158 | −1.1228 | 0.2320 | 0.1654 | |
| −5.6581 | −7.3294 | −4.4424 | −4.9690 | |
| −0.9746 | 155.46 | − | −0.7465 | |
| − | −6.3981 | − | − | |
| − | − | −1.1966 | −0.8734 | |
| −0.2043*** | −0.4327*** | −0.2187*** | −0.2263*** | |
| 0.9140 | −0.6994 | 1.2446 | 0.8673 | |
| −92.1681*** | 51.7563*** | −99.4882*** | −97.7220*** | |
| Hausman Tests | ||||
| Pooled mean group (PMG) against mean group (MG) | ||||
| H-test () | 2.04 | 2.47 | 2.69 | 1.11 |
| p-value | 0.9993 | 0.9993 | 0.9988 | 0.9999 |
| PMG against dynamic fixed effects (DFE) | ||||
| H-test () | 5.25 | 4.44 | 4.66 | 5.56 |
| p-value | 0.9492 | 0.9922 | 0.9820 | 0.9764 |
- Note: The cointegration equation coefficient is denoted by CoinEq.
- ***, **, and * denote significant at1%, 5%, and 10% level, respectively.
To further explore the relationship between FDI inflows and military expenditures and check the robustness of our empirical findings, we re-estimate the model taking into account the possible presence of cross-sectional dependence (CD) in the panel. We note that data used in this study may suffer from CD issue. It is not a secret that all MENA countries not only are sharing the geographical space, but also exchange goods and services and are linked through other socioeconomic activities. Because of these close ties, there is a good chance that the data from these nations will show some cross-sectional interdependence.
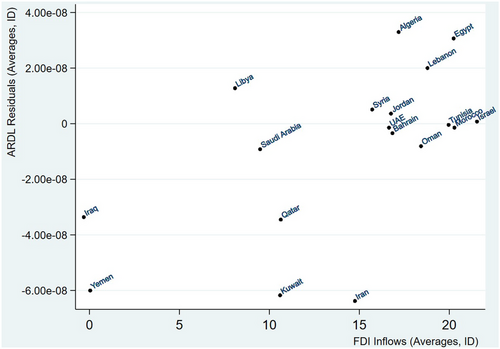
As shown in Table 5, the Pesaran's CD test on all variables fails to reject the null hypothesis of no CD. The error dependence problem has been addressed in the literature showing that a strong form of CD may result in inconsistent parameter estimates (Bai, 2009; Pesaran, 2007; Song, 2013). The full model is then re-estimated using the cross-section augmented autoregressive distributed lag (CS-ARDL) estimation technique, which accounts for CD and cross-country heterogeneity issues. Table 8 presents the long- and short-run analytical results for selected iterations of our model.31 Results for Models 1-B and 4-B show a positive but not significant relationship between FDI and military spending. Model 10-B depicts a positive and significant association between the two variables in the short run. The long-run coefficients are not significant in all cases when considering the CS-ARDL estimator. Figure 7 displays the average residual (from Model 10-B) for each country on the y-axis and the average logged FDI inflows on the x-axis. Each country represents one data point. As highlighted in the plot, the residuals are very small, indicating that these data points fit the model specification well. This means that the estimated model performs well in predicting FDI inflows for all countries in the region.
| Variables | Model 1-B | Model 4-B | Model 10-B |
|---|---|---|---|
| Short-run est. | |||
| Δ(lFDI)t-1 | −0.4080*** | −0.4778*** | −0.5471*** |
| Δ(lMilex)t | 6.5381 | 6.5419 | 1.2640 |
| Δ(lGDP)t | 1.7885 | 9.9254 | −5.3731 |
| Δ(Corrup)t | −1.1664 | −1.7850 | −1.0999 |
| Δ(eRisk)t | 0.2567** | 0.4506 | 0.4373 |
| Δ(BIT)t | −0.8075 | −1.9679* | 0.5430 |
| Δ(FDebt)t | — | 0.1757 | 0.6171 |
| Δ(IntLiq)t | — | −1.6040 | 0.7125 |
| Δ(lEU)t | — | −11.178 | −12.814 |
| Δ(LawO)t | — | 1.2754 | 0.0038 |
| Δ(ER)t | — | −1.1562 | −0.8469 |
| Δ(Confl)t | — | — | −4.8698 |
| Δ(lNatRes)t | — | — | −1.88e-07 |
| Adjustment term (mean group [MG]) | −1.4778*** | −1.5471*** | −1.5471*** |
| Long-run est. | |||
| Lr_lMilex | 5.2588 | 5.1278 | 1.2438 |
| Lr_lGDP | 0.6276 | 6.5102 | −3.6553 |
| Lr_Corrup | −0.6365 | −0.9256 | −0.1579 |
| Lr_eRisk | 0.1764** | 0.2720 | 0.3099 |
| Lr_BIT | −0.6511 | −1.4202* | 0.3654 |
| Lr_FDebt | — | 0.1624 | 0.1615 |
| Lr_IntLiq | — | −1.2243 | 0.3942 |
| Lr_lEU | — | −6.5898 | −7.9912 |
| Lr_LawO | — | 0.6457 | 0.3750 |
| Lr_ER | — | −1.2403 | −0.8467 |
| Lr_Confl | — | — | −4.1011 |
| Lr_lNatRes | — | — | −1.12e-07 |
|
Residuals’ CD Statistic (p-value) |
−1.40 (0.1620) | −0.24 (0.8080) | −1.09 (0.2780) |
- Note: Testing for weak cross-sectional dependence using Pesaran (2015) test for weak cross-sectional dependence. Weighted CD statistics from Juodis and Reese (2021) are used. The null hypothesis for the test is, H0: weak cross-section dependence and the alternative, H1: strong cross-section dependence.
- ***, **, and * denote significant at1%, 5%, and 10% level, respectively.
These results should, however, be interpreted with caution given the number of time periods in our sample and the impact on the degree of freedom of the estimation. As pointed out by Chudik et al. (2013), CS-ARDL approaches suffer from large sampling uncertainty especially with moderate time periods.32 In this case, and with the inclusion of lagged dependent variables in the CS-ARDL regression, a relatively large time dimension is required for satisfactory small sample performance (Chudik et al., 2016).33 The coefficient of adjustment in all models indicates that an unstable process is encountered as it is larger than 1, in absolute value. An adjustment term between −2 and −1 indicates, indeed, an oscillating type of convergence to long-run equilibrium (Narayan & Smyth, 2006). Longer time periods need to be covered in order to test time-series properties, and add more lags to CS-ARDL, to better tackle the cross-sectional dependencies (CSD) issue. We rely on future work to better model this CSD and mitigate the impacts of these dependencies on the relationship between FDI and military spending in the MENA region.
4 CONCLUDING REMARKS
The MENA region is known for its geopolitical importance, natural resources, and strategic location. The region has been attracting significant FDI over the years, with some of the largest investments being made in the energy, construction, and finance sectors. Despite the opportunities, the MENA region faces challenges in attracting and retaining FDI, including corruption, and a lack of transparency in some countries. At the same time, the MENA region has seen a considerable increase in military spending over the years. One of the risks of high level of military expenditure in the region is that, it can create political instability and contribute to conflicts, which can deter foreign investors. High levels of military spending can also divert resources away from other areas, such as education and infrastructure, which are important for economic growth and development.
This study empirically tests the effects of military spending on FDI inflows over the last four decades on all MENA countries. Our results show a strong positive and significant relationship between the two variables of interest, while controlling for a number of institutional, political, and economic factors. Quantitatively speaking, it can be concluded that the military expenditure is positively associated with inward FDI, with impact ranging from 1.10% (Model 9) to 3.88% (Model 8). These findings are in line with previous studies in which military spending is hypothesized to contribute positively to economic prosperity (Brooks et al., 2013; Brooks & Wohlforth, 2008; Drezner, 2013; Ikenberry, 2011; Kagan, 2012; Maass et al., 2014). These results are of importance, especially in the MENA context. On the one hand, FDI plays a vital role in the economic development of the MENA region. The inflow of FDI has been instrumental in financing infrastructure projects, creating jobs, and boosting economic growth. In order to attract more FDI, MENA countries have implemented reforms to increase economic openness, diversification, and private-sector development. These countries have been actively promoting FDI through various measures such as tax incentives, investment protection laws, and streamlined procedures. As a result, the region has seen a significant increase in FDI in recent years.
On the other hand, military spending in the MENA region has also been on the rise. Many countries in the region have been increasing their defense budgets, with some of the highest military spending in the world being recorded in the MENA region. The reasons for this increase in military spending vary from country to country, but some common factors include regional security threats, conflicts, and geopolitical tensions.
The relationship between FDI and military spending in the MENA region is, however, a complex and multifaceted one. There are several factors that can influence this relationship, including political stability, security concerns, and socioeconomic factors. While high levels of military spending can create challenges for foreign investors, there are also examples of countries in the region that have successfully attracted investment despite high levels of military spending.34 Ultimately, an extended research agenda including more facets of the investment climate in the region is needed. Data availability and credibility are other issues in this region. Arms procurement by MENA countries with lower institutional credibility and political stability prevents us from splitting military spending into personnel and weapon purchases and test the validity of our results with these variables,35 a promising, but challenging, agenda for future research.
REFERENCES
- 1 See, for example, Zhang (2001), Hansen and Rand (2006), Gursoy et al. (2013), and Okada and Samreth (2014).
- 2 After a strong rise in 2015, global FDI flows lost growth momentum in 2016 to 2019. FDI Global flows fell by 2% in 2016 to a sharp decrease of 23% in 2017. The year 2018 saw another sharp decline to an estimated $1.34 trillion from $1.64 trillion in 2017, and slight increase to $1.71 trillion 2019, before been severely hit by the COVID-19 pandemic (World Investment Reports, 2023, available at: https://unctad.org/publication/world-investment-report-2023).
- 3 The following countries are typically included in the MENA and considered in this study: Algeria, Bahrain, Egypt, Iran, Iraq, Israel, Jordan, Kuwait, Lebanon, Libya, Morocco, Oman, Qatar, Saudi Arabia, Syria, Tunisia, United Arab Emirates, and Yemen. Due to data availability, this list excludes Djibouti, Ethiopia, Mauritania, Sudan, and Palestinian territories, which are sometimes included in the MENA region.
- 4 According to the World Investment Report 2021 by UNCTAD, FDI inflows to the MENA region increased by 11% in 2020, despite the global pandemic, reaching $29 billion. However, this is still below the peak level of $82 billion in 2008.
- 5 Seven of the highest military burden in the world in 2019 are in the MENA region: Oman (8.8% of its GDP which is the highest level in the world), Saudi Arabia (8.0%), Kuwait (5.6%), Israel (5.3%), Jordan (4.7%), Lebanon (4.2%), and Algeria (6.0%).
- 6 Summary of the 2020 SIPRI report are available online at: https://www.sipri.org/sites/default/files/2021-04/fs_2104_milex_0.pdf
- 7 This aspect of military involvement in infrastructure development is highly criticized in some developing countries, as this may divert resources away from civilian priorities, and there may be concerns about transparency and accountability in project execution. Historically, however, there is a long heritage of military involvement in infrastructure projects going back to ancient history.
- 8 The autoregressive distributed lag can be used upon variables that are I(0) and/or I(1).
- 9 Considering the specification with all variables in Model 6. The impact between the two variables ranges from 1.10% (Model 9 specification) to 3.9% (Model 8. This long-term relationship is positive and highly significant regardless of model specifications.
- 10 For more details about this data set, see: https://ucdp.uu.se/
- 11 Given the high cost of these data sets, our sample is covering the period 1984–2020. More about these ICRG risk variables following this link: http://www.prsgroup.com/CountryData.aspx.
- 12 See the military spending definition used by SIPRI following this link: https://www.sipri.org/commentary/topical-backgrounder/2017/monitoring-military-expenditure.
- 13 More on this from SIPRI: https://www.sipri.org/sites/default/files/SIPRIYB17c03sIII.pdf.
- 14 The military burden is an alternative measure to military spending and is defined as military spending as a share of GDP.
- 15 The time period being dictated by the PRS group data set starting for all covered countries in 1984 and ending in 2020.
- 16 Using Lind and Mehlum (2010) test for a U-shaped relationship, we find that data are not compatible with a model with a quadratic term and conclude that no U-shaped relationship exists between FDI inflows and military expenditures. The quadratic term is also not statistically significant when running a regression with both military expenditures and the square of this variable.
- 17 Results not shown and available upon request.
- 18 The error-correcting term is also expected to be between –1 and 0 to achieve a high speed of adjustment.
- 19 The PRS-ICRG country risk index is one of the most common indexes used by multinational companies, banks, importers, exporters making direct foreign investments, and/or similar organizations or individuals. More information about the Group's data is available at: https://www.prsgroup.com/explore-our-products/international-country-risk-guide/.
- 20 The PRS-ICRG country risk methodology consists of 12 political and social factors included in the political risk category. The economic risk category consists of five factors and again five subfactors are used to assess the financial condition of countries, forming the financial risk category.
- 21 We also include US recession dates (NBER-based Recession Indicators) and banking crisis dummy and country fixed effects. In order to control for the impact of financial and banking crises in the region on FDI inflows, the crisis dummy () is constructed following Nguyen et al. (2022) and NBER dates of US recessions.
- 22 When analyzing military spending as a proxy for national security, researchers often use both the absolute level of military expenditure and the military spending as a share of GDP. Results using military burdens—that is, military expenditure as a share of GDP—are available upon request.
- 23 A detailed description of all explanatory variables is provided in the Online Appendix.
- 24 PMG allows short-run coefficients, including the intercepts, the speed of adjustment to the long-run equilibrium values and error variances to be heterogeneous country by country. PMG imposes, then, long-term homogeneity without implementing the homogeneity of the parameter in the short term (Pesaran et al., 1999).
- 25 The panel ARDL estimation technique is known to be a long-run estimate of the equilibrium analysis, and therefore the long-run coefficients are usually given higher importance.
- 26 Results from Models 3 and 6 shows a significant and negative long-term relationship between economic openness to trade and FDI.
- 27 For Model 5, a one extra year on average schooling leads to 0.71% increase in FDI inflows.
- 28 is a binary variable taking value 1 if a country had experienced or participated in an armed conflict in a given year, and 0 otherwise.
- 29 It should be noted here that UCDP-PRIO only records conflicts that have resulted in at least 25 battle-related deaths in a calendar year. These conflicts are defined as contested incompatibility between two parties, one of which is the government.
- 30 Total natural resource rents are the sum of oil rents, natural gas rents, coal rents (hard and soft), mineral rents, and forest rents. Total natural resource rents (current USD, in log) variable is used in the data set.
- 31 Results for all iterations are available upon request. Using the alternative CS-DL technique did not improve the significance of the results.
- 32 CCE estimators and thus the CS-ARDL estimator require the time dimension and the cross-sectional dimension to be very large. A panel is large if the number of cross-sectional units (or countries) and the number of time periods are going to infinity.
- 33 Yet, data limitations are at play and without a very large time period, techniques such as CS-ARDL or CS-DL are not appropriate in this context. As such, we consider it more appropriate to relay on the results obtained using the panel-ARDL approach.
- 34 For example, countries like Saudi Arabia and the United Arab Emirates have attracted significant levels of investment, even though they are among the world top military spenders.
- 35 For most countries in the region, many of these details are classified and not publicly available. Data availability also prevents us from using other important variables, like wages and remunerations and sectoral FDI into MENA region.




