Bayesian inference of hub nodes across multiple networks
Corresponding Author
Junghi Kim
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorCorresponding Author
Kim-Anh Do
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorCorresponding Author
Min Jin Ha
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorCorresponding Author
Christine B. Peterson
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorCorresponding Author
Junghi Kim
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorCorresponding Author
Kim-Anh Do
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorCorresponding Author
Min Jin Ha
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorCorresponding Author
Christine B. Peterson
Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas, U.S.A.
email: [email protected]
email: [email protected]
email: [email protected]
email: [email protected]
Search for more papers by this authorSummary
Hub nodes within biological networks play a pivotal role in determining phenotypes and disease outcomes. In the multiple network setting, we are interested in understanding network similarities and differences across different experimental conditions or subtypes of disease. The majority of proposed approaches for joint modeling of multiple networks focus on the sharing of edges across graphs. Rather than assuming the network similarities are driven by individual edges, we instead focus on the presence of common hub nodes, which are more likely to be preserved across settings. Specifically, we formulate a Bayesian approach to the problem of multiple network inference which allows direct inference on shared and differential hub nodes. The proposed method not only allows a more intuitive interpretation of the resulting networks and clearer guidance on potential targets for treatment, but also improves power for identifying the edges of highly connected nodes. Through simulations, we demonstrate the utility of our method and compare its performance to current popular methods that do not borrow information regarding hub nodes across networks. We illustrate the applicability of our method to inference of co-expression networks from The Cancer Genome Atlas ovarian carcinoma dataset.
Supporting Information
Additional Supporting Information may be found in the online version of this article.
| Filename | Description |
|---|---|
| biom12958-sup-0001-SuppData-S1.pdf520 KB | Supplementary Data S1. |
| biom12958-sup-0002-SuppDataCode-S1.zip110.8 KB | Supplementary Data Code S1. |
Please note: The publisher is not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing content) should be directed to the corresponding author for the article.
References
- Albert, R. (2005). Scale-free networks in cell biology. Journal of Cell Science 118, 4947–4957.
- Atay-Kayis, A. and Massam, H. (2005). A Monte Carlo method for computing the marginal likelihood in nondecomposable Gaussian graphical models. Biometrika 92, 317–335.
-
Baldwin, R.,
Tran, H., and
Karlan, B.
(2003).
Loss of c-myc repression coincides with ovarian cancer resistance to
transforming growth factor
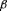 growth arrest independent of transforming
growth factor
growth arrest independent of transforming
growth factor 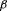 /smad signaling.
Cancer Research
63, 1413–1419.
/smad signaling.
Cancer Research
63, 1413–1419.
- Barabasi, A. and Oltvai, Z. (2004). Network biology: Understanding the cell's functional organization. Nature Reviews Genetics 5, 101–113.
- Barabasi, A. L., Gulbahce, N., and Loscalzo, J. (2011). Network medicine: A network-based approach to human disease. Nature Reviews Genetics 12, 56–68.
- Bryant, C., Rawlinson, R., and Massey, A. (2014). Chk1 inhibition as a novel therapeutic strategy for treating triple-negative breast and ovarian cancers. BMC Cancer 14, 570.
-
Cai, T.,
Kang, J.,
Kemmer, P., and
Guo, Y.
(2011).
A constrained
 1 minimization approach to sparse precision
matrix estimation.
Journal of the American Statistical Association
106,
594–607.
1 minimization approach to sparse precision
matrix estimation.
Journal of the American Statistical Association
106,
594–607.
- Csárdi, G. and Nepusz, T. (2006). The igraph software package for complex network research. InterJournal, Complex Systems 1695, 1–9.
- Danaher, P., Wang, W., and Witten, D. (2014). The joint graphical lasso for inverse covariance estimation across multiple classes. Journal Royal Statistics Society, Series B 76, 373–397.
- DePicciotto, N., Cacheux, W., Roth, A., Chappuis, P., and Labidi-Galy, S. (2016). Ovarian cancer: Status of homologous recombination pathway as a predictor of drug response. Critical Reviews in Oncology Hematology 101, 50–59.
- Dempster, A. P. (1972). Covariance selection. Biometrics 28, 157–175.
- Friedman, J., Hastie, T., and Tibshirani, R. (2007). Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–441.
- Fu, L. and Wang, B. (2013). Investigation of the hub genes and related mechanism in ovarian cancer via bioinformatics analysis. Journal of Ovarian Research 6, 92.
- George, E. and McCulloch, R. (1993). Variable selection via Gibbs sampling. Journal of the American Statistical Association 88, 881–889.
- Ha, M., Baladandayuthapani, V., and Do, K. (2015). Dingo: Differential network analysis in genomics. Bioinformatics 31, 3413–3420.
- Jeong, H., Mason, S. P., Barabási, A.-L., and Oltvai Z. N. (2001). Lethality and centrality in protein networks. Nature 411, 41–42.
- Jonsson, P. and Bates, P. (2006). Global topological features of cancer proteins in the human interactome. Bioinformatics 22, 2291–2297.
- Kanehisa, M., Furumichi, M., Tanabe, M., Sato, Y., and Morishima, K. (2017). KEGG: New perspectives on genomes, pathways, diseases, and drugs. Nucleic Acids Research 45, D353–D361.
- Kim, H., George, E., Ragland, R., Rafail, S., Zhang, R., Krepler, C., et al. (2016). Targeting the ATR/CHK1 axis with PARP inhibition results in tumor regression in BRCA mutant ovarian cancer models. Clinical Cancer Research 23, 3097–3108.
- Kobayashi, H., Shigetomi, H., and Yoshiomoto, C. (2015). Checkpoint kinase 1 inhibitors as targeted molecular agents for clear cell carcinoma of the ovary (review). Oncology Letters 10, 571–576.
- Konstantinopoulos, P. A., Ceccaldi, R., Shapiro, G. I., and D'Andrea, A. D. (2015). Homologous recombination deficiency: Exploiting the fundamental vulnerability of ovarian cancer. European Journal Cancer 5, 1137–1154.
- Lauritzen, S. (1996). Graphical Models. Oxford: Clarendon Press.
- Ledermann, J., Drew, Y., and Kristeleit, R. (2016). Homologous recombination deficiency and ovarian cancer. European Journal Cancer 60, 49–58.
- Mitra, R., Müller, P., and Ji, Y. (2016). Bayesian graphical models for differential pathways. Bayesian Analysis 11, 99–124.
- Mohan, K., London, P., Fazel, M., Witten, D., and Lee, S. (2014). Node-based learning of Gaussian graphical models. Journal of Machine Learning Research 15, 445–488.
- Peterson, C., Stingo, F., and Vannucci, M. (2015). Bayesian inference of multiple Gaussian graphical models. Journal of the American Statistical Association 110, 159–174.
- Roverato, A. (2002). Hyper inverse Wishart distribution for non-decomposable graphs and its application to Bayesian inference for Gaussian graphical models. Scandinavian Journal of Statistics 29, 391–411.
- Stegh, A. (2012). Targeting the p53 signaling pathway in cancer therapy ’ the promises, challenges, and perils. Expert Opinion on Therapeutic 16, 67–83.
- Tan, K., London, P., Mohan, K., Lee, S., Fazel, M., and Witten, D. (2014). Learning graphical models with hubs. Journal of Machine Learning Research 15, 3297–3331.
- The Cancer Genome Atlas Research Network (2011). Integrated genomic analyses of ovarian carcinoma. Nature 474, 609–615.
- Wachi, S., Yoneda, K., and Wu, R. (2005). Interactome- transcriptome analysis reveals the high centrality of genes differentially expressed in lung cancer tissues. Bioinformatics 21, 4205–4208.
- Wang, H. (2012). Bayesian graphical lasso models and efficient posterior computation. Bayesian Analysis 7, 771–790.
- Wang, H. (2015). Scaling it up: Stochastic search structure learning in graphical models. Bayesian Analysis 10, 351–377.
-
Yamada, S.,
Baldwin, R., and
Karlan, B.
(1999).
Ovarian carcinoma cell cultures are resistant to
TGF’
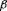 1-mediated growth inhibition despite expression of functional
receptors.
Gynecologic Oncology
75, 72–77.
1-mediated growth inhibition despite expression of functional
receptors.
Gynecologic Oncology
75, 72–77.
-
Yeung, T.,
Leung, C.,
Wong, K.,
Samimi, G.,
Thompson, M.,
Liu, J., et al.
(2013).
TGF’
 modulates ovarian cancer invasion by upregulating
CAF-derived versican in the tumor microenvironment.
Cancer Research
73, 5016–5028.
modulates ovarian cancer invasion by upregulating
CAF-derived versican in the tumor microenvironment.
Cancer Research
73, 5016–5028.
- Zhou, B., Su, L., Hu, S., Hu, W., Yip, M., Wu, J., et al. (2013). A small-molecule blocking ribonucleotide reductase holoenzyme formation inhibits cancer cell growth and overcomes drug resistance. Cancer Research 17, 6484–6493.




