Using virtual microscopy for the development of sampling strategies in quantitative histology and design-based stereology
Abstract
Only a fraction of specimens under study are usually selected for quantification in histology. Multilevel sampling or tissue probes, slides and fields of view (FOVs) in the regions of interest (ROIs) are required. In general, all parts of the organs under study should be given the same probability to be taken into account; that is, the sampling should be unbiased on all levels. The objective of our study was to provide an overview of the use of virtual microscopy in the context of developing sampling strategies of FOVs for stereological quantification. We elaborated this idea on 18 examples from multiple fields of histology, including quantification of extracellular matrix and muscle tissue, quantification of organ and tumour microvessels and tumour-infiltrating lymphocytes, assessing osseointegration of bone implants, healing of intestine anastomoses and osteochondral defects, counting brain neurons, counting nuclei in vitro cell cultures and others. We provided practical implications for the most common situations, such as exhaustive sampling of ROIs, sampling ROIs of different sizes, sampling the same ROIs for multiple histological methods, sampling more ROIs with variable intensities or using various objectives, multistage sampling and virtual sampling. Recommendations were provided for pilot studies on systematic uniform random sampling of FOVs as a part of optimizing the efficiency of histological quantification to prevent over- or undersampling. We critically discussed the pros and cons of using virtual sections for sampling FOVs from whole scanned sections. Our review demonstrated that whole slide scans of histological sections facilitate the design of sampling strategies for quantitative histology.
1 INTRODUCTION
Virtual microscopy or digital microscopy is the digital conversion of light microscopic specimens at full resolution and their presentation over a computer network. The term ‘virtual’ refers to the examination of the specimens without direct contact with the object slide or the light microscope (Smart In Media AG, 2021). Virtual microscopy makes samples accessible to specialists without needing to be present and without needing to have extensive equipment (Saliba et al., 2012). It is discussed intensively in the frame of diagnosis and treatment of different diseases (telepathology, more than 1400 Scopus entries in September 2021) in human as well as in veterinary medicine (e.g. Bertram & Klopfleisch, 2017), resulting in the first guidelines by the respective expert groups (Jahn et al., 2020).
Another huge field of application for virtual microscopy is education and training, fuelled even more by the increased demand for remote learning during the COVID-19 pandemic (for reviews, see, e.g., Bertram & Klopfleisch, 2017; Kuo & Leo, 2019).
In addition, virtual microscopy is also a powerful tool for research. Our review demonstrates how whole slide scans of histological sections facilitate the design of sampling strategies for quantitative histology and how they can be compared to other technical options.
1.1 Design-based stereology
Design-based stereology is a set of tools that allows quantification without making assumptions regarding the shape, size, distribution or orientation of the structures of interest (Howard & Reed, 2005; Mouton, 2002). Strict sampling rules have to be followed to achieve this independence; that is, stereology includes detailed prescriptions of the sampling procedure and guidelines on how to test its quality. Stereology has become the gold standard in morphometry due to its reproducibility and assumption-free design. A number of both general and organ-specific protocols, recommendations and algorithms have been published to facilitate planning and conducting quantitative histology studies (Table 1).
| Research field | Brief characteristics | Reference |
|---|---|---|
| General guidelines for microanatomy | Planning, volumetry and sampling as crucial steps for a successful study in quantitative anatomy |
Tschanz et al., 2014 Vatsos et al., 2021 |
| Cardiovascular microanatomy |
Quantitative 3D morphology in cardiac research Quantification of vascular beds Vascularization of organs 3D characterization of capillary networks Numbers and lengths of brain capillaries |
Mühlfeld et al., 2010 Dockery & Fraher, 2007 Mühlfeld, 2014 Eržen et al., 2011 |
| Neuroanatomy and neurohistology |
Total number of neurons in the subdivisions of the hippocampus Assessment of developmental neurotoxicity Morphometry of brain Morphometry of grey and white matter of spinal cord Morphometry of the pineal gland |
West et al., 1991 Bolon et al., 2011 Selcuk & Tipirdamaz, 2020; Sadeghinezhad et al., 2020 Sadeghinezhad & Nyengaard, 2021; Cakmak & Karadag, 2019 Bolat et al., 2018 |
| Gastrointestinal microanatomy |
Practical stereology of the stomach and intestine. Morphometry of the oesophagus Volumes and numbers in the liver 3D counting of hepatocytes Quantification of hepatic connective tissue Morphometry of intestinal mucosa in nutritional studies |
Nyengaard & Alwasel, 2014 Goodarzi et al., 2019 Marcos et al., 2012; Junatas et al., 2017; Mik et al., 2018 |
| Respiratory system |
Policy Statement of the American Thoracic Society/European Respiratory Society on quantitative assessment of lung structure Quantitative microscopy of the lung Study designs in diseases of the respiratory tract |
Hsia et al., 2010 Ochs & Mühlfeld, 2013; Knudsen et al., 2021 Mühlfeld & Ochs, 2013 |
| Urinary system | Application of stereology in kidney research | Nyengaard, 1999 |
| Genital system | Stereology tools in testicular research |
Noorafshan, 2014 Ferreira et al., 2021 |
| Skeletal system |
Stereology of femoral cartilage Standardized nomenclature for bone histomorphometry Quantification of bone microporosities |
Noorafshan et al., 2016 Dempster et al., 2013, Parfitt et al., 1987 Tonar et al., 2011 |
| Embryology | Stereology of the human placenta | Mayhew, 2014 |
Note
- Papers compatible with design-based stereology are listed.
1.2 Sampling in an integral part of design-based stereology
All the guidelines mentioned in Table 1 refer to sampling strategies on all levels of any reduction of material in histological studies. Only a fraction of specimens under study are usually selected for quantification in histology. This multilevel sampling includes (i) taking tissue probes from large macroscopic organs that cannot be processed completely (i.e. porcine liver, human brain); (ii) selecting histological slides from tissue blocks that undergo exhaustive sectioning (not all slides are selected for further analysis); and (iii) selecting microscopic fields of view (FOVs) that are captured and analysed to represent various regions of interest (ROIs). In general, all parts of the organs under study should have the same probability of being taken into account; that is, the sampling should be unbiased on all levels (Howard & Reed, 2005; Tschanz et al., 2014). One of the advantages of stereological concepts in morphometry is that sampling is inherent to stereology. The attention given to the sampling is comparable to that paid to the analysis of micrographs, as sampling actually is part of any unbiased estimation. If design-based stereology, including sampling, is not used for quantitation in histology, the lack of standardized sampling threatens the repeatability of research. More than 70% of researchers encounter problems when trying to repeat another scientist's experiments (Baker 2016). More than 90 researchers from five continents have recently formulated a strategy to improve the reproducibility of research based on light microscopy (Nelson et al., 2021). We propose that proper sampling of microscopic specimens might be a significant contribution to this issue. Citing the paper by Hsia et al. (2010), “the only effective way to avoid bias and ensure accuracy is via standardization of sampling”.
1.3 Sampling strategies and their benefits with regard to magnification
Sampling is of cardinal importance and a practical necessity in morphometrics (Mayhew & Lucocq, 2015). Depending on the uniformity of the distribution of the item of interest, the sampling intensity would have to be greater (in the case of heterogeneous samples) or smaller (in the case of homogeneous samples). Unfortunately, the biological variability of the microscopic structures on the scale of large organs is mostly unknown in human organs as well as in large animal models. There is ongoing work to map the variability in histopathology to enable researchers to plan the sampling of tissue probes, slides and fields of view efficiently. The theoretical foundations for predicting the efficiency of systematic sampling are quite well known (Gundersen & Jensen, 1987; Gundersen et al., 1999; Gundersen & Osterby, 1981). In the past and in contrast, for example, to biochemistry, standards for sampling in histology seemed to have been neglected; not all authors customarily referred to sampling strategies, numbers of tissue probes, sections, FOVs or any repeatable rules for their selections. Currently, the sampling issue receives more attention as a part of quantitative morphomics that describes the 3D biological structures from gross anatomy to the micro- or even nanomorphome (Mayhew & Lucocq, 2015).
In microscopy, FOV sampling is closely related to the magnification used. When increasing the magnification, the area of the image field decreases quadratically, and the number of FOVs necessary to cover the same original area increases quadratically (Figure S1). Traditionally, it was recommended that the lowest magnification that enables the detection of the structures of interest be used (Howard & Reed, 2005; Mouton, 2002) to maximize the area of the FOVs. Introducing virtual slides into the research might seem to be a ‘game changer’. However, whole slide sampling with automated quantitation still requires validation by humans to ensure that the readouts are correct. Combining the benefits of using slide scanners with a clever sampling strategy might be a very efficient tool in quantitative histology.
The aim of our paper was to provide an overview of the use of virtual microscopy in the context of developing sampling strategies for stereological quantification. We elaborated this idea on a number of examples from multiple fields of histology. We critically discussed the pros and cons of using virtual sections for sampling image fields (FOVs and ROIs) from whole scanned sections in quantitative histological studies.
2 MATERIALS AND METHODS
2.1 Origin of tissue blocks and histological staining
This paper uses examples of virtual slides from a number of studies representing various fields of quantitative histology. All the original illustrations were newly prepared from archive specimens for the purpose of this review. The origin of the specimen and their use for studying biological questions is summarized in Table 2. The staining methods used in the examples presented in this paper are summarized in Table 3.
| Example | Origin | Biological question studied (Reference) |
|---|---|---|
| #1 | Virtually generated standardized image datasets | Testing and calibrating quantification of volumes, surfaces, lengths and object counts (Jiřík et al., 2016, 2018). |
| #2 | Human mesenchymal stem cells (hMSCs) isolated from bone marrow of healthy donors (A) | Metabolic activity assay comparing the ATP production rate and % of glycolysis and oxidative phosphorylation in hMSCs (Tonarova et al., 2021). |
| #S2 | hMSCs isolated from bone marrow of healthy donors (B) | Cell growth assay and metabolic activity assay when studying the effects of different cross-linking conditions on collagen-based nanocomposite scaffolds; an in vitro evaluation using mesenchymal stem cells (Suchý et al., 2015). |
| #S3 | Soft palate of an adult dog fixed in formalin, archive of (C) | Quantitation of connective tissue in the soft palate of the dog; pilot study to assess sampling intensity (unpublished results). This was motivated by assessment of operative outcome of veloplasty (e.g. Arai et al., 2016; Crosse et al., 2015; Dupré & Heidenreich, 2016; Pichetto et al., 2015; Tamburro et al., 2019). |
| #3 | Porcine femurs with titan implants after 6 months of healing, (B) | Assessing osseointegration of titan implants with four different surface composition using quantification of bone-implant contact (BIC) according to Babuska et al. (2016). |
| #S4 | Condylar cartilage and bone of rabbit femur (B) | Estimation of healing of osteochondral defects of condylar cartilage stimulated by three different tissue-engineered scaffolds (unpublished results). |
| #S5 | Brains of female C57B1/6 mice (C) | Tracking the transduction of various viral vectors in neurons after being injected into mice brains (Hlavatý et al., 2017). |
| #4 | Porcine liver (B) | Describe the propagation of the rupture caused by blunt trauma within liver parenchyma with respect to the liver microstructure, namely, the reticular fibres. Does the rupture propagate randomly or does the rupture follow some pattern through the tissue? (Malečková et al., 2021). |
| #S6 | Porcine common carotid arteries (B) | Quantification of type I and type III collagen within tunica intima and media in porcine common carotid artery (Tomášek et al., 2020). |
| #S7 | Archived canine lymph nodes and core biopsies from canine lymph nodes (C) | Quantification of microvessels in canine lymph nodes. Does the density of microvessels correlate with vascular endothelial growth factor expression? (Tonar et al., 2008; Wolfesberger et al., 2008). |
| Patient-derived murine xenografts of mantle cell lymphoma (A) | Histological validation of quantitative in vivo monitoring of hypoxia and vascularization of patient-derived murine xenografts of mantle cell lymphoma using photoacoustic and ultrasound imaging (Keša et al., 2021). | |
| #5 | Small intestine of 12 to 14-week-old pigs used in research on healing of intestinal anastomoses (B) | Histological validation of healing of intestinal anastomosis, quantification of vascularization, inflammatory infiltration, and collagen formation (Rosendorf et al., 2020, 2021a, 2021b). |
| #S8 | Human and ewe perineal body used for mechanical testing and microstructure quantification (D) | Quantification of volume fraction of smooth muscle, skeletal muscle, adipose cells, elastin, and type I collagen of the perineal body. Does the structure differ along the perineal body? (Kochová et al., 2019a, 2019b). Does the structure differ between the pregnant and post-menopausal ewe perineal bodies? (Kochová et al., 2019b) |
| #6 | Resected human liver with hepatocellular carcinoma (E) | Quantification of CD8+ T cells in different regions of interest (tumour centre, inner and outer invasive margin, peritumoural area and non-tumour liver) can reflect the overall reaction of the immune system to tumour growth, penetration of immune cells through tumour border and expression of pro- and antiapoptotic factors by tumour cells and microenvironment (Andryi Trailin, unpublished results). |
| #S9 | Mouse ovaries (B) | Discover the effects of exposure to bisphenol A analogs during breastfeeding on ovarian capacity of offspring. The quantification of primordial, primary, preantral, antral and atretic follicles (Nevoral et al., 2021). |
| #S10 | The cerebellum of 3-month-old mouse model with degeneration of Purkinje cells (B) | Quantitative validation of potential abnormalities in total number of microvessels in the cerebellum layers of adult mice with degeneration of Purkinje cells (Kolinko et al., 2016). |
| #S11 | Samples of human aortae collected during surgery for abdominal aortic aneurysm (AAA) repair (F) | Comparison of the expression of structural proteins, osteoprotegerin, and pentraxin 3 and the presence of immune factors (T and B lymphocytes, neutrophils and macrophages), microvessels and hypoxic cells in AAA and non-aneurysmatic aortic walls and exploration of their relationships (Blassova et al., 2019). |
| #7 | Decellularized porcine liver tissue (B) | Quantitative analysis of morphological preservation of liver extracellular matrix (ECM) after decellularization with the purpose of generation a high-quality biological scaffold for liver tissue engineering (Moulisová et al., 2020) |
| #S12 | 3D collagen scaffolds containing dermal fibroblasts used as an in vitro model of dermis (B) | Development of a new method of total cell count determination in 3D collagen scaffolds in order to quantify cell proliferation (unpublished results). |
Note
- Most examples are based on studies already published, so references are provided for further details on the study design. All in vivo procedures were performed in compliance with the law of the Czech Republic, which is compatible with the legislation of the European Union and, wherever appropriate, were approved by the Ethics Committees in the following institutions where the samples originated: A – First Faculty of Medicine, Charles University; B – Faculty of Medicine in Pilsen, Charles University; C – Institute of Morphology, University of Veterinary Medicine Vienna, Austria; D – Centre for Surgical Technologies, KU Leuven, Leuven, Belgium; E – Department of Pathology, Faculty of Medicine in Pilsen, Czech Republic; and F – Department of Surgery, University Hospital in Pilsen. The examples are numbered according to their appearance in the Results section.
| Example | Staining | Purpose and visualization of tissue components |
|---|---|---|
| #1 | None (computer-generated virtual image). | Virtual sections through three-dimensional objects (spheres and cylinders) mimicking tissue components in X-ray microtomography. |
| #2 | DAPI nuclear staining (Sigma-Aldrich). | Visualization of nuclei. |
| #S2 | DAPI nuclear staining (Sigma-Aldrich, Burlington, MA) and Phalloidin-Alexa Fluor 488 (Life Technologies, Rockford, IL). | Visualization of nuclei and actin microfilaments. |
| #S3 | Aniline blue and nuclear fast red. | Clear distinction of collagen fibres from other tissue components for automated quantitation. |
| #3 | 20% Giemsa's azur eosin methylene blue solution | New bone and connective tissue around titan implants within porcine femur. |
| #S4 | Alcian blue staining and PAS reaction. | Detection of acidic and neutral glycosaminoglycans in newly formed cartilage. |
| #S5 | Immunohistochemistry for enhanced green fluorescent protein (EGFP) (Chemicon International, Temecula, CA), counterstained with haematoxylin. | Identification of cells expressing the EGFP as a reporter gene detecting the cells transduced by a viral vector. |
| #4 | Reticulin kit (BioGnost Ltd, Zagreb, Croatia). | Reticular fibres (collagen III) – component of extracellular matrix of connective tissue located in the interlobular septa and in the delicate network, that separates the hepatic sinusoids and hepatocytes |
| #S6 | Picrosirius red (Direct Red 80, Sigma-Aldrich, Munich, Germany). | Type I collagen (yellow–red colour) and type III collagen (green colour) visualized in polarized light (Rich & Whittaker, 2005). |
| #S7 | Immunohistochemical detection of von Willebrand factor (polyclonal rabbit anti-human antibody, Dako, Glostrup, Denmark) combined with lectin histochemistry (WGA, Vector laboratories, Burlingame, CA). Avidin-biotin-peroxidase complex detection (Vector Laboratories). Counterstaining Mayer's haematoxylin. | Endothelium of blood microvessels within canine lymph nodes. |
| Immunohistochemical detection of CD31 (rabbit anti-mouse CD31 monoclonal IgG, clone SP38, Thermo Fisher Scientific, Rockford, IL). Counterstained with haematoxylin. | Endothelium of blood microvessels within patient-derived murine xenografts of mantle cell lymphoma. | |
| #5 | Immunohistochemical detection of von Willebrand factor (ab6994Abcam, Cambridge, UK). | Endothelium of blood microvessels |
| Immunohistochemical detection of Calprotectin (Monoclonal Antibody—MAC387Invitrogen MA1-81381, Thermo Fisher Scientific). Counterstaining Mayer's haematoxylin. | Granulocytes and tissue macrophages. | |
| Picrosirius Red. | Collagen observed in circularly polarized light. | |
| #S8 | Verhoeff's haematoxylin and green trichrome (Kocová, 1970). | Overall morphology; smooth and skeletal muscle of the perineal body. |
| Orcein (Tanzer's orcein, Bowley Biochemical Inc., Danvers, MA, USA). | Adipose cells and elastin of the perineal body. | |
| . | Picrosirius red (Direct Red 80, Sigma-Aldrich, Munich, Germany) | Type I collagen of perineal body was observed in polarized light. |
| #6 | Immunohistochemical detection of CD8+ T cells (BOND™ Ready-to-Use monoclonal primary anti-CD8 Antibody 4B11, Leica Biosystems Newcastle Ltd, UK). Counterstaining Mayer's haematoxylin. | Tumour-infiltrating cytotoxic T cells as actors of antitumour immunity. |
| #S9 | Haematoxylin and eosin | Primordial, primary, preantral, antral and atretic follicles within mice ovaries. |
| #S10 | Immunohistochemical detection of laminin (polyclonal rabbit anti-laminin antibody, Dako, Glostrup, Denmark), counterstained with haematoxylin. | Detection of microvessels in individual layers of the cerebellar cortex in a mouse model of neurodegeneration. |
| #S11 | Immunohistochemical detection of pentraxin 3 (polyclonal rabbit anti-human pentraxin3 antibody, Thermo Fischer Scientific) and MAC387 (monoclonal mouse anti-human macrophages/monocytes antibody, Thermo Fisher Scientific). Counterstaining Gill's haematoxylin. | Detection of Pentraxin 3, a protein produced in response to inflammatory signals in aortic wall. Detection of macrophages infiltrating the aortic wall in abdominal aortic aneurysms. |
| #7 | Haematoxylin & eosin | Visualization of ECM proteins (stained reddish with eosin) and absence of cell nuclei in decellularized samples (lack of blue haematoxylin stain). |
| #S12 | DAPI nuclear staining (Thermo Fisher Scientific, Rockford, IL) | Staining cell nuclei as countable structures for cell counting. |
2.2 Scanning virtual slides
As the paper focuses mainly on the sampling strategies in the context of various histological studies, the devices and techniques used for acquiring the images in the paper are briefly summarized in Table 4.
| Device and manufacturer | Properties, settings, software | Used in Example #: |
|---|---|---|
| Aperio ScanScope CS2 automatic slide scanner (Leica Biosystems, Vienna, Austria). |
Bright field transmitted light microscope, 20× and 40× lens. Scanning time of 1 cm2 approx. 60 s (20× objective) or 90 s (40× objective) Automatic white balance Autofocus No immersion, no Z-stack tools Scanscope 12.4.3 software. *SVS document format readable with freely downloadable ImageScope software, tiled images universally viewable in browsers. *.SVS can also be opened directly with ImageJ (Schneider et al., 2012) with the Bio-Formats Plugin or with Fiji (Schindelin et al., 2012). |
#S3, #S5 |
| Eclipse Ti-U microscope (Nikon, Tokyo, Japan), XYZ stepper motor focus drives Prior H117E1N4/F and PS3H122R_NB (Prior Scientific Instruments, Fulbourn, UK), Prior ProScan III stepper motor controller, digital camera Nikon DS-Fi2. |
Bright field, polarized light and fluorescence microscopy 2×, 4×, 10×, 20×, 40×, 60× (oil immersion) objectives Scanning time of 1 cm2 approx. 25 min (10× objective) or 3.5 h (20× objective) Scanning and montage controlled by the NIS Elements Ar software (v 5.11.03) *ND2 document format readable with freely downloadable nis-Elements Viewer software Scanning in XY plane and in Z-axis. Export to universal format TIFF images. |
#2, #S2, #S4,#5, #S6, #S9, #S10 |
| Zeiss Axio Scan.Z1 Slide Scanner (Zeiss, Jena, Germany). |
Bright field microscopy 20× and 40× objectives Scanning time of 1 cm2 approx. 5–10 min (20× objective) Scanning controlled by Zeiss Zen Blue software Zeiss ZEN Microscopy free software offers both basic image analysis, as well as export functionality of the scanned images into TIFF or JPG file formats. Native pyramidal*.CZI files readable with FiJi. |
#4, #S8, #S11, #7 |
| Olympus CX41 microscope (Olympus, Tokyo, Japan) with Promicam 3-3CP camera (Promicra, Prague, Czech Republic). |
Bright field and polarized light microscopy 2×, 4×, 10×, 20×, 40×, 60× (oil immersion) objectives Manual stage Scanning time of 1 cm2 takes approx. 30 min (10× objective) of manual work Stitching virtual slides manually using the ImageStithing module of the QuickPhoto Industrial 3.2 software (Promicra, Prague, Czech Republic) Export to TIFF. |
#3, #S6, #S7 |
2.3 Systematic uniform random sampling of microscopic FOVs
Multistage sampling in quantitative microscopy comprises several levels (Mayhew & Lucocq, 2015). During each step, a sample size divided by the whole specimen size represents the sampling fraction. In this paper, two levels will be considered: If, for example, every 10th histological section is selected from an exhaustively sectioned tissue block, and the position of the 1st section was selected randomly, the section sampling fraction (ssf) is 1/10. When considering a single slide, selecting 5 FOVs out of the 50 FOVs covering the whole section would represent an area sampling fraction (asf) of 1/10. The rules for the systematic uniform random sampling (SURS) are simple, regardless of the technical implementation (slide scanners, motorized microscope stages, manual sampling). The position of the first FOV within the ROI is chosen randomly, for example, by multiplying the maximum ranges of XY coordinates of the ROI by randomly generated numbers (RND function in MS Excel). A previously selected pattern, named a sampling interval, determines the positions of the other FOVs (see, e.g., Mayhew & Lucocq, 2015 for review).
2.4 Stereological techniques
The sampling strategies illustrated among the examples that follow were part of histological quantitative studies. All the quantitative morphometric parameters used in the examples presented in this study are explained in Table 5.
| Example | Quantitative parameter abbreviation (units) | Definition, reference area, interpretation | Objective used | Image fields sampled per slide | Typical area sampling fraction |
|---|---|---|---|---|---|
| #1 | VV (objects, section) (−) | The volume fraction of objects within a virtually generated section. | Not applicable | 6 | 6/54 (0.11) |
| #2 | QA (nuclei, well) (mm−2) | Two-dimensional density of cell nuclei per area of the well bottom in an 8-well XPf cell culture miniplate (Agilent, Santa Clara, CA). | 4× | Whole image processed | Whole image processed |
| 40× | 15 | 15/160 (0.093) | |||
| #S2 | QA (nuclei, well) (mm−2) | Two-dimensional density of cell nuclei per area of the well bottom in a 48-well cell culture plate (Thermo Scientific, Waltham, MA). | 10× | Whole image processed | Whole image was processed |
| 40× | 9 | 9/22 (0.41) | |||
| #S3 | AA (connective tissue, palate) (−) | Mean area fraction of connective tissue in whole histological sections of the soft palate of a dog (pilot study). | 20× (whole slide scan) | Analysis of whole slide scan | One whole slide scan analysis 0.003 to 0.005 in relation to one complete palatal half |
| #3 | BIC | Bone-implant contact as the ratio of the profile length of direct contact between the implant profile and bone tissue and the total profile length of the implant surface. | 10× | 15 |
15/70 (0.214) related to the whole scan 15/15 (1.00) related to the bone-implant interface |
| #S4 | VV (cartilage, defect) (−) | The volume fraction of Alcian blue and PAS-positive cartilage within the healing bone defect. | 10× | 22 | 21/22 (0.95) |
| #S5 | N (EGFP-positive neurons, brain) (−) | Absolute number of EGFP-positive neurons in the injected half of mouse brain. | 40× (oil immers) | 45–55 | 1/1 (exhaustive sampling) |
| #4 | P′L (interlobular septa) and PL (interlobular septa) (mm−1) | Real number of intersections of interlobular septa with rupture and predicted number of intersections based on the total length of the interlobular septa | Whole slide scan | Not applicable | Whole slide scan |
| P′L (reticular fibres) and PL (reticular fibres) (mm−1) | Real number of intersections of reticular fibres with rupture and predicted number of intersections based on the total length of the reticular fibres | 40× | 10 | Between 10/40 (0.25) and 10/50 (0.2) | |
| #S6 | AA (type I collagen, int + med) (−) | The area fraction of type I collagen within the tunica intima and media ROI | 40× | 4 | Between 4/23 (0.17) and 4/37 (0.11) |
| AA (type III collagen, int + med) (−) | The area fraction of type III collagen within the tunica intima and media ROI | 40× | 4 | Between 4/23 (0.17) and 4/37 (0.11) | |
| #S7 | QA(vWF and WGA-positive microvessels, lymph node) (mm−2) | The number of profiles of stained microvessels per sectional area of the lymph node. | 40× | 50–70 | Between 50/1800 (0.028) and 70/2500 (0.03) |
| LV (CD31+ microvessels, lymphoma) (mm−2) | The length density of stained microvessels per volume unit of lymphoma | 40× | 10 | Between 10/40 (0.25) and 10/80 (0.125) | |
| #5 | VV (objects, intestinal wall without mucosa located 3 mm proximally and distally from the anastomosis centre) (−) | The volume fraction of vWF positive cells within the ROI | 20× | 5–38 vWF | Between 1/5 (0.20) and 1/3 (0.35) |
| The volume fraction of MAC387-positive cells within the ROI | 20× | 12–53 MAC387 | Approx. 1/2 (0.49) | ||
| The volume fraction of collagen within the ROI | 20× | 8–24 PSR | Between 1/3 (0.33) and 1/5 (0.22) | ||
| #S8 | VV (smooth muscle; skeletal muscle, perineal body) | The volume fraction of smooth muscle and skeletal muscle within the ROI | 10× | 12 | 12/42 (0.3) |
| VV (adipose cells; elastin, perineal body) | The volume fraction of adipose cells and elastin within the ROI | 10× | 12 | 12/42 (0.3) | |
| VV (type I collagen, perineal body) | The volume fraction of type I collagen within the ROI | 10× | 12 | 12/42 (0.3) | |
| #6 | QA(CD8-positive T cells, liver) (mm−2) | The number of profiles of stained CD8+ T cells per sectional area of the ROI of the liver. | 20× | 8 per ROI | 8/133 0.064 in TC and NT ROIs: |
| 40 per slide | 8/25 (0.32) in IL, OL and PT ROIs | ||||
| #S9 | N (different types of follicles) | The number of primordial, primary, preantral, antral and atretic follicles | 20× | 14 | 14/25 (0.56) |
| #S10 | VV (cerebellar layers, cerebellum) (−) | The volume fractions of histological layers of cerebellum. | 20× | 4–7 | 0.33 |
| N (microvessels, cerebellum) (−) | Number of microvessels calculated from the number of branching nodes according to Gundersen et al. (1993). | 60× | 20–40 | 0.33 | |
| #S11 | AA (pentraxin 3, wall) (−) | The area fraction of the pentraxin 3-positive cells within the whole wall reference area | 40× | 4 | Between 4/112 (0.035) and 4/328 (0.012) |
| AA (MAC387, wall) (−) | The area fraction of the MAC387-positive macrophages within the whole wall reference area. | 20× | 4 | Between 4/28 (0.143) and 4/82 (0.049) | |
| #7 | L (skeleton length, liver) (mm) | Length and 2D length density of the ECM within liver lobules. Number of EMC branching nodes per sectional area of liver lobules. Both parameters refer to the quality of network structure of sinusoidal vessel ECM in the decellularized scaffold. | 40× | 10 | Typically 5/100 (0.05) |
| LA (ECM fibres, liver) (mm−2) | |||||
| QA (ECM branches, liver) (mm−2) | |||||
| #S12 | N (nuclei, scaffold) (−) | Total cell number in the whole scaffold estimated from cell number in 1 column. | 10× | 9 columns from the 3D scaffold | 9 × 1.4 µl/200 µl = 0.063 (9 columns per scaffold) |
Note
- The magnification of the microscope objective, which was an approximate equivalent to the sampled image field area used for quantification of each parameter, is provided. The number of image fields that were sampled in each study is shown as well.
- Abbreviations: AA (component, space), Area fraction of the respective components within their reference spaces; BIC, bone-implant contact; LV (component, space), Length density of objects per reference volume; NV (component, space), Numerical density of objects per reference volume; QA (component, space), number of object profiles per section area; VV (component, space), Volume fraction of the respective components within their reference spaces.
2.5 Statistics of sampling density and evaluating the variability of the sampling
The sampling in histology introduces an error into the resulting data. Increasing the sampling frequency reduces the variability of the data but also increases the labour needed to complete the research. Stereologists are used to calculate the variability on each level of the sampling to identify the major source of potential bias and to optimize the sampling procedures in terms of time and material costs, provided that enough precision remains to draw conclusions on a pre-determined level of confidence. Several measures of variability are illustrated for this purpose, such as standard deviations (SD), coefficient of error (CE; standard error of the mean of repeated estimates divided by the mean) and the estimates of CE for spatially correlated objects using the Matheron quadratic approximation method with various smoothness constants (Gundersen & Jensen, 1987; Slomianka & West, 2005). The relative percentage error used for comparing the data based on whole slide analysis vs. various levels of subsampling was calculated as 100 × (measured value-expected value)/expected value.
3 EXAMPLES
A number of combinations of imaging approaches, uses of virtual slides, scanners, or individually sampled micrographs with various magnifications are presented in sequence corresponding to Tables 2, 3 and 5. The examples were tailored to facilitate the solving of biological problems described in Table 2, and the strong and weak points are illustrated. Due to the number of possible combinations, the examples are ordered approximately in increasing complexity.
3.1 Whole slide analysis vs. density of sampling multiple micrographs
Figure 1 (Example #1) demonstrates the effect of the intensity of sampling on the accuracy of the quantitative results. This can be done in virtually generated scenes. Considering the whole slide as the ‘true expected value’, the relative error increases with decreasing sampling intensity. In this case, intermediate sampling would provide results with an acceptable relative error. Similarly, Figure 2 (Example #2) compares automated counting of cell nuclei in a single well of a cell culture miniplate with counting based on 15 image fields. In cases of a more homogeneous distribution (Figure S2, Example #S2), the relative error of the sample is acceptably low. It is worth performing a pilot study of heterogeneous histological samples with multiple tissue components (Figure S3, Example #S3) that shows how the moving average depends on the sampling intensity.
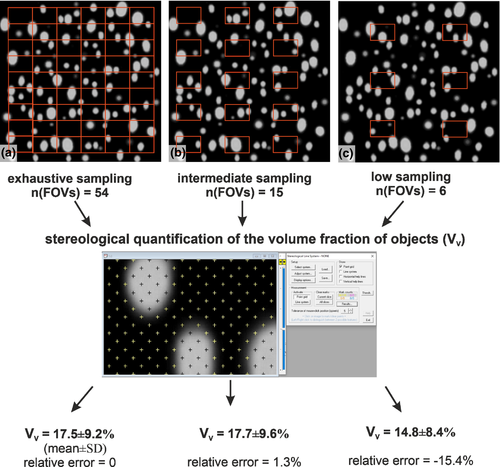

3.2 Slides requiring exhaustive sampling of the ROIs
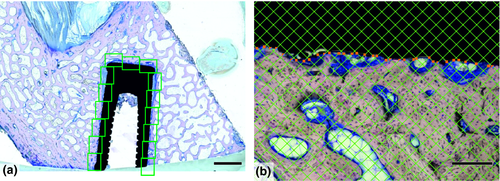
In some studies, it is advisable to evaluate the complete ROI. This strategy prevails when the number of slides available is limited, such as in ground sections of bone implants (Figure 3, Example #3). Similar situations occur when the ROI has small dimensions, for example central regions of experimental bone defects in small animal models (Figure S4, Example #S4). Exhaustive sampling might also be needed in cases with significant biological variability among the study groups when counting every few cells matters, such as in counting virus-transduced neurons in mouse brains (Figure S5, Example #S5).
3.3 Using the same sampling count but in ROIs of different absolute sizes
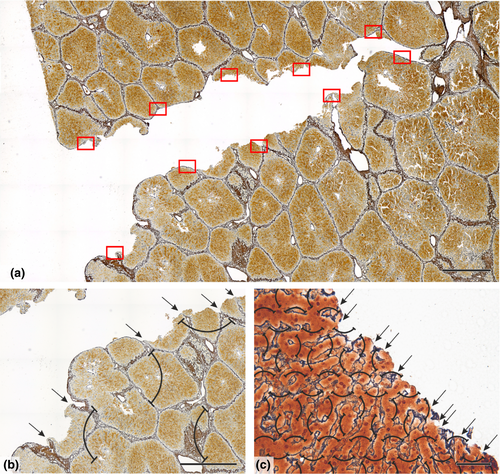
In some study designs without excessive biological variability, it is possible to maintain the same number of FOVs (Figure 4, Example #4). When the size of the specimens and ROI varies, this will result in a variable sampling density (the numerator is the same, the denominator varies), as in samples of proximal vs. distal segments of blood vessels (Figure S6, Example #S6) or large vs. small lymph nodes (Figure S7B, Example #S7). The case presented in Figure S7A (Example #S7) shows a very extensive sampling, the ex post analysis of which identified as an unnecessary and laborious oversampling when compared to Figure S7B.
3.4 Sampling the same ROI for more histological staining methods
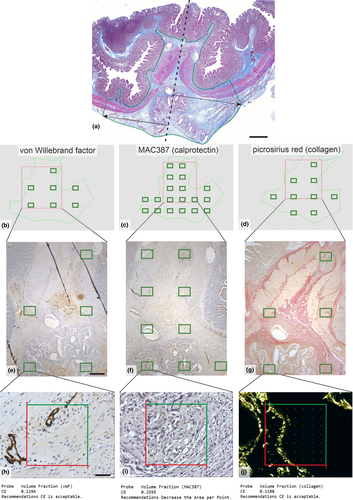
Quantifying the volume fractions of tissue components within the same ROI might require more histological staining. Figure 5 (Example #5) shows three stains within the same ROI and objective. It is of great advantage when the sampling is facilitated by a map that helps adjust the sampling density according to the variability of the structures under study, as provided by the estimates of CE in the Stereologer software (v11.0; SRC Biosciences, Tampa, Florida, USA) (Figure 5H-I). When the CE becomes unacceptably high (Figure 5I), it is recommended to increase the ssf, asf or the density of the stereological grid. Figure S8 (Example #S8) shows a similar design.
3.5 Sampling one or more ROIs with a variable intensity or using various objectives
Figure 6 (Example #6) illustrates a complex sampling problem that would be difficult to solve without planning on virtual slides. There were five ROIs in every slide, representing the tumoural area, three zones of the tumour invasive margin and healthy non-tumorous tissue. In all five ROIs, multiple structures of interest were identified immunohistochemically (CD8+ T lymphocytes shown, CD3+ T lymphocytes only discussed), and their occurrence within these ROIs was very variable and with different biological interpretations. To maintain the feasibility of such a complex task, two sampling densities were chosen, and part of the sampling variability was compensated with more or less dense counting grids (Figure 6B-D). Similarly, Figure S9 (Example #S9) demonstrates that the present settings were suitable for frequently occurring types of ovarian follicles but too low for the rare types. Figure S10 (Example #S10) shows a solution using lower magnification and less intense sampling for the volume fractions of histological layers of cerebellum but a greater magnification and more intense sampling for counting cerebellar microvessels within the layers. Similarly, Figure S11 (Example #S11) shows two magnifications useful for two different components of the aortic wall.

3.6 Multistage sampling of FOVs and virtual sampling
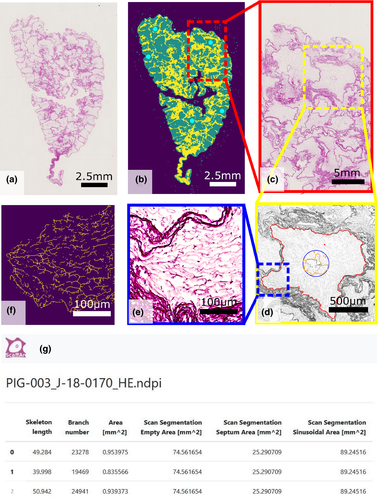
Figure 7 (Example #7) shows a special case of multiscale sampling and analysis performed by a semiautomatic software tool when evaluating the quality and composition of decellularized liver. This demonstrates that tailoring a software tool to a specific problem might increase the efficiency of the whole work significantly, especially when the sampling of FOVs is an integral part of the quantification procedure. Figure S12 (Example #S12) demonstrates virtual sampling when counting fibroblasts within a 3D scaffold in vitro; such an approach requires programming skills, but the users are rewarded by a reasonable mapping of the variability of their results.
4 DISCUSSION
4.1 Sampling FOVs is only a part of a 3D multistage sampling
For any quantification, at least two criteria are to be met: (i) the staining should allow for a clear identification of all the structures under study, and (ii) borders of the reference space are clearly defined, either anatomically or by convention (Howard & Reed, 2005; Mouton, 2002). We would like to point out explicitly that the sampling of FOVs in virtual scanned sections illustrated above represents only a small part of the whole multistage sampling in quantitative histology. Therefore, the variability of results affected by the sampling of FOVs in a single slide represents only a small part of the total variability of data in the whole study. Other levels of sampling should also be emphasized, such as the number of subjects per study group, the sampling of tissue probes from organs, and the sampling of slides. We highly recommend classical papers on this topic (Gundersen & Osterby, 1981; Slomianka & West, 2005).
The importance of proper sampling of sections is elaborated in Figure S3. We found that the tissue composition of the canine soft palate was so heterogeneous that a whole half of the velum had to be sampled using a minimum of 10–15 sections distributed approximately uniformly throughout the complete tissue block to obtain reliable and robust results. Single sections cannot be used as ‘representative’ of this organ. Justifying the number of sections required for a valid quantitative histological study is suggested in Figure S3D-E. However, even when a single slide is available (e.g. in archive material), the repeatability, reliability and correctness, even of simple quantification, might greatly benefit from correct FOV sampling.
4.2 Choosing the FOV sampling intensity and practical implications
In all the examples presented, our effort was to spread the sampling items evenly and widely throughout the ROIs and specimens. This strategy is called systematic uniform random sampling, and it is superior and more efficient than simple (independent) random sampling, as it covers all parts under study uniformly (Mayhew & Lucocq, 2015). The examples illustrated above do not involve all possible situations in 2D sampling of FOVs in quantitative histology but might provide clues to the reader to most of these. We included mostly examples of sampling optimized in pilot studies but also problematic cases. Unnecessary intensive sampling (oversampling), for example in Figure 1A and Figure S7A, makes the work more laborious and expensive without providing new information. In contrast, insufficient sampling (undersampling), for example in Figure 1C and Figure S9C, Figure S10B,C, might compromise the study design and make it difficult to reach a pre-determined level of significance when testing statistical hypotheses, although biological differences might be present in the samples under study.
As the sampling error (introduced by all levels of the sampling procedure), represented by CE estimates, sums up with the biological variance (i.e. the differences between the samples themselves), according to Tschanz et al. (2014), it is always advisable to perform a pilot study on typical samples and groups under research. This allows for calculating a power sample analysis. Mapping both the total variability of our data and its components is an essential step when designing further studies on the same material, which involves calculating the minimum number of samples needed to compare the groups under study. Descriptive statistics of the pilot data (mean and standard deviation) are useful for the power sample analysis (Chow et al., 2008); for example, when planning an experiment and expecting one of the histological quantitative parameters to be increased by 20%, the minimum number of samples required per group would be calculated using the typical test power β = 0.8 (the type II error) and α = 0.05 (type I error).
4.3 Whole slide scanning vs. taking multiple micrographs
Currently, researchers have more technical options for acquiring virtual slides and planning the sampling of FOVs. The pros and cons of whole slide scanning vs. taking multiple individual micrographs are summarized in Table 6. An inexpensive alternative for acquiring virtual slides with large areas but high resolution might be image stitching, supported currently by stitching modules in most of the proprietary camera software solutions (extra costs in Nikon NIS Elements BR; Zeiss Zen Core, Leica LAS). Moreover, free ImageJ (Schneider et al., 2012) and FiJi software can be used as well (Schindelin et al., 2012). However, stitched images do not support the pyramidal file architecture, and they may require more RAM than the optimized file formats of the slide scanners. Stitching algorithm also fail in case of optically empty regions.
| Scanning whole slides | Sampling multiple individual micrographs |
|---|---|
| Histological scanner required. | Can be done even on routine microscopes with motorized or manual stage. |
| The data from the whole slide are always available, so more ROIs can be added when necessary. | Usually, is done once. |
| Can be fast and efficient when automated. However, issues occurring during the automated scanning do not appear until checked. | Usually, takes more time to be done. Any technical issues can be seen and solved immediately. |
| Problems with atypical size of archive slides might occur (Leica Biosystems, 2021). Either the holders are not adapted, or the slides might get stuck within the device. | Can be performed even if archive slides sometimes do not fit the feeding trays or holders of scanners (uniform slide dimensions and thickness required). |
| In some scanners, only bright field illumination technique and a limited choice of objectives are available. The use of immersion oil objectives is rare. | Can be done using any observation technique available of the microscope, for example fluorescence imaging, phase contrast, polarizing microscopy. No issues with using oil immersion easily. |
| Generates large datasets (typically 0.5–2 GB per typical histological slide). The pyramidal architecture of the files is usually optimized for viewing. | No special data infrastructure required. |
| Corresponds to state-of-the art of the whole-mount pathology (Look Hong et al., 2016; Rashid et al., 2019). | Does not permit whole-mount analysis (or this becomes extremely laborious). |
| In some scanners, multiplane (z-stack) scanning is possible to reflect the thickness of the slide. This might depend on the availability of high-aperture oil immersion objectives. Depth of focus problems might occur that cannot be solved automatically by the scanner software. | Optical sections could be captured in stacks using oil immersion objectives with high numerical aperture. Multiplane scanning might be crucial for studies involving confocal microscopy and requiring not only lateral resolution but also 3D information. |
| Using automated image-processing methods, the texture pattern of the whole sampling area can be analysed. | Analysing the whole slide would be very laborious or impossible. Texture patterns that exceed the size of individual micrographs are lost and cannot be analysed. |
5 CONCLUSION
We conclude that combining scanning virtual slides in histology with efficient use of unbiased sampling is fully compatible with the plethora of data from quantitative microscopy, which can be expressed as the ‘Do less well’ rule (Gundersen & Osterby, 1981). Virtual microscopy proved to be extremely helpful to facilitate correct sampling at the level of individual slides. Uniform distribution of FOVs can also be reached using motorized microscope stages. Principles of SURS are beneficial not only for validity, efficiency and ethics of quantitative studies but also for improving accuracy and repeatability in qualitative studies. We suggest that modules supporting the SURS of FOVs with variable settings of ROIs and sampling intensity should be natively supported by all virtual slide scanners intended for scientific use.
ACKNOWLEDGEMENTS
This study was supported by the National Sustainability Program I (NPU I) Nr. LO1503 provided by the Ministry of Education, Youth and Sports of the Czech Republic and by the Charles University Research Fund (Progres Q39). LC, AT, VL, VM and MJ also received support from the Ministry of Education, Youth and Sports under the project FIND No. CZ.02.1.01/0.0/0.0/16_019/0000787 and from the European Regional Development Fund–Project ‘Application of Modern Technologies in Medicine and Industry’ (No. CZ.02.1.01/0.0/0.0/17_048/0007280). JH was supported by the Ministry of Health of the Czech Republic (Grant no: 15–29241A) and by the grant SVV–2020-2022 No. 260 536. MG was supported by the Charles University Grant Agency, project No. 1313420 and SVV 260 536. LC and VL received support from the Charles University grant UNCE/MED/006, and by the grant of Ministry of Health of the Czech Republic – AZV NU20J-08-00009. AT has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement Nº856620. The analysis demonstrated in example O represented a pilot study for the dissertation project of Violeta García-Espín, supervised by Prof. Monika Egerbacher and Prof. Gilles Dupré (all University of Veterinary Medicine Vienna, Austria). The help of Dr. Stephan Handschuh (University of Veterinary Medicine Vienna) with the whole slide image analysis is gratefully acknowledged.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
Primary data supporting the calculations in the examples can be requested from the authors or have been already published in the papers that were cited appropriately.




