Impacts of terrain attributes on economics and the environment: costs of reducing potential nitrogen pollution in wheat production
[Correction added on 8 March 2017, after first online publication: The in-text citation “Steward, 1987”. was removed in consultation with the corresponding author, as it was not included in the References.]
Abstract
The economic cost of achieving desired environmental outcomes from uniform and variable rate fertilizer application technologies depends both on market forces and agronomic properties. Using spatial econometric methods, we analyze the impact of nitrogen fertilizer supply by terrain attribute on the yield and protein content of hard red spring wheat grown in Eastern Washington as well as the impact on residual nitrogen. We find significant association with all three. The economic impact of nitrogen restrictions depends critically on both prices and level of the restriction. Uniform application of nitrogen was found to economically outperform variable rate application, but variable rate application provided positive environmental benefits due to less residual nitrogen.
1. Introduction
Stabilizing and improving environmental quality represents an important goal of several U.S. regulatory agencies as well as a broad societal goal. Actually achieving such goals has become a monumental task because influencing human behavior so that the new behavior is more environmentally friendly has proved particularly challenging (Hahn and Stavins, 1991; Hahn et al., 2003).1 To improve environmental quality, one must first understand the economic forces driving individual decisions as well as the physical and biological processes that convert the collective decisions into environmental consequences.
Market forces, such as prices, have been demonstrated to be among the important factors that drive individual decisions. Physical and biological processes that affect the interface between agricultural production and the environment are primarily agronomic. As a result, both market forces and agronomic relationships must be understood in order to influence agricultural production decisions in environmentally positive ways. The motivation behind this research is to incorporate detailed consideration of market forces and agronomic properties in an analysis of producers’ economic costs of achieving desired environmental outcomes. We focus specifically on potential nitrogen pollution from production of hard red spring wheat (HRSW) production on rolling terrain in Eastern Washington.
Effective nitrogen management is critical for the economic production of crops and the long-term protection of the environment (Lopez-Bellido et al., 2006). Agricultural producers apply nitrogen to increase yields which, in wheat production, also increases protein content. However, removal rates of applied nitrogen in harvested cereal grain are estimated to average only 33%, leaving the remainder potentially subject to loss from the intended agricultural production system (Raun and Johnson, 1999).1 Much of the remaining nitrogen is immobilized (i.e., changed from an inorganic to an organic form) and may be recovered in the future through mineralization (changed from organic to inorganic form). Nevertheless, losses of available nitrogen supplies to the environment (i.e., pollution) can also be very large, as high as 35% (Kumar and Goh, 2000).
Empirical evidence documents that one of the most important motivations that translates market forces and agronomic rules into individual production choices is the goal of maximizing profit. Management of risk and environmental stewardship goals may also be important factors in a farmer's preference hierarchy, and may temper actions aimed at profit maximization. In each case, input and output prices are primary signals of market forces. For example, consider the low-profit scenario where wheat price is low and nitrogen fertilizer price is high. In this scenario, producers typically respond by applying less nitrogen, thereby lowering the probability of nitrogen pollution. The opposite can also be true; high wheat price and low nitrogen price would incentivize higher nitrogen application rates, thereby increasing the probability of nitrogen pollution. Fertilizer (input) and wheat (output) prices matter in determining both the level of environmental quality and the economic impact on producers from maintaining or improving environmental quality.
Technology, particularly site-specific management, may play a large role in maintaining or improving environmental quality while minimizing adverse economic impact on producers. Agricultural producers typically apply nitrogen to their fields at a uniform rate. But fields are seldom uniform in their nitrogen requirements. For fields with different intrafield nitrogen needs, a uniform application of nitrogen results in overapplication for some areas and underapplication for other areas (Fiez et al., 1995; Mamo et al., 2003; Pan et al., 1997). Underapplication reduces yield, revenue, and profit. In addition to adversely affecting profit, overapplication can result in pollution when excess available nitrogen impacts ecosystems by contaminating groundwater, streams, lakes, and oceans. Hence, determination of the intrafield variables that affect potential nitrogen pollution and the resulting economics of reducing nitrogen pollution would be a valuable contribution to achieving desired environmental outcomes from agricultural production and possibly even enhancing profit.
Terrain attributes (i.e., topographic properties) have previously been used to help explain spatial variability of crop yields (Green and Erskine, 2004). Terrain attributes may be linked to differences in yields through a variety of mechanisms. They include both the spatial and topographical features like slope and aspect (direction to which a slope faces). They also include underlying soil properties through their systematic spatial distribution—e.g., adjoining plots can be expected to have similar soil properties, other things equal, and hilltops often have “thinner” soil than bottom lands. Terrain attributes may also help explain potential nitrogen pollution. Therefore, identifying terrain attributes that can lead to higher amounts of nitrogen pollution could be a valuable step toward reducing nitrogen pollution.
Several studies have addressed the impact of spatial variability in yield response to nitrogen. Lambert et al. (2006) found that the spatial variation of crop response to both nitrogen and phosphate is significant. Fiez et al. (1995) identified terrain attributes for which nitrogen fertilizer uptake efficiency was low and nitrogen loss percentages were high. Anselin et al. (2004) found that nitrogen response differs by landscape position and identified conditions under which site-specific application may be profitable.
While there has been considerable economic research based on the yield response of various crops to nitrogen application levels, less has focused on the economic effects of grain protein response to available nitrogen. Further, none has addressed the environmentally important residual nitrogen effects (i.e., the amount of nitrogen unaccounted for after measuring the amount available during the growing season less the amount found at harvest) of alternative nitrogen application levels when terrain attributes vary within a field.
We seek to fill an important gap in the literature by evaluating the economic effect on wheat growers from reducing residual nitrogen through use of variable rate technology on fields with multiple terrain attributes.2 With regard to the effects of nitrogen application, residual nitrogen is treated as a proxy for potential nitrogen pollution.3 Due to complex soil and landscape-scale processes, it is difficult to measure the actual level of nitrogen pollution. To circumvent this problem, we measure the amount of nitrogen that has the highest probability of becoming pollution and label it residual nitrogen. Residual nitrogen represents the amount of nitrogen not accounted for by crop production and soil measurements.
We examine the effect of nitrogen supply and terrain attributes on yield and protein content of HRSW production as well as residual nitrogen levels at a research site in Eastern Washington with rolling terrain. We identify important terrain attributes and determine whether an innovative spatial weights matrix that accounts for elevation results in greater statistical efficiency in parameter estimation. We also assess the economics of uniform and variable rate nitrogen application methods under alternative prices and nitrogen regulations.
The importance of examining the economics of protein as well as yield effects of nitrogen application is due to protein premiums and discounts in HRSW price. A premium is added to the price for each ¼ percentage point above the base of 14%, and a discount is subtracted from the price for each ¼ percentage point below the base. Traditionally, the premium-discount structure has been asymmetric with discounts larger than premiums.
This article proceeds as follows. We first develop the methods used for analysis. The experiment and data used in the estimation are reported in the subsequent section. We present and interpret findings in the results section. Conclusions and discussion of implications occur in the final section.
2. Method of analysis
In this section, we first develop response equations for yield, protein, and residual nitrogen. We then explain the need for using spatial autocorrelation regression methods based on the rolling topography and develop a unique spatial weights matrix to improve statistical efficiency of the estimated model. We also build a constrained optimization model to simulate economic and environmental outcomes.
2.1. Nitrogen response equations
Fertilizer response equations are formulated to evaluate the effect of available nitrogen and terrain attributes on yield, protein, and residual nitrogen. We allow for the possibility that the yield, protein, and residual nitrogen response to nitrogen supply are quadratic. Although there has been much debate about the appropriate functional form for fertilizer response functions (e.g., Berck et al., 2000; Paris, 1992), recent work by Liu et al. (2006) found that the quadratic yield response function for nitrogen fertilizer could not be rejected for corn production in Michigan over the alternatives of von Liebig linear and plateau or von Liebig quadratic and plateau response functions when tested with field-level data.4 Consequently, we employ the quadratic response function because it is both flexible and computationally convenient (Lau, 1986).
Based on previous research that found that corn yield, soil properties, and erosion were strongly related to terrain attributes (e.g., Kaspar et al., 2003), we include terrain attributes. Wheat producers also apply nitrogen to increase or maintain protein level. Because crop yield can vary within a field, it is likely that protein will also vary due to terrain attributes.
If both yield and protein of wheat vary within a field, then it is likely that residual nitrogen also does. Identifying terrain attributes that result in the highest residual nitrogen response to available nitrogen could also identify locations that would achieve greatest environmental benefit from a reduction in applied nitrogen.
We analyze 10 terrain attributes that fully characterize the highly variable terrain in the experiment—global irradiation, planform curvature, profile curvature, tangential curvature, flow direction, specific catchment area, wetness index, slope, elevation, and aspect. Global irradiation measures the amount of annual solar energy a surface receives based on the geometry of the sun, earth, and field; consequently, a north facing slope would have a smaller irradiation measure than a south facing slope.5 Planform (or plan) curvature measures the rate of slope change along the contour (horizontal plane) (Kimberling et al., 2012); it describes whether the flow is converging (concave, negative values) or diverging (convex, positive values) from a point. Profile curvature measures the rate of slope change along the direction of the slope; it describes whether the flow is accelerating (convex, negative value) or decelerating (concave, positive values). Tangential curvature measures the inclined plane perpendicular to the slope.6 Flow direction measures the direction of steepest decent from a point. Specific catchment area measures the size of the contributing area. Wetness index measures the hydrological process at a point by taking into account the size of the upslope contributing area and slope. Slope measures the angle (steepness) of the surface. Elevation measures the vertical height. Aspect measures the direction to which the slope is facing, assigning values in degrees from north.
In addition to terrain attributes, we incorporate time and previous crop as regressors in the response functions. Time dummy variables control for year-to-year weather variations. Previous crop dummy variables control for rotational benefits yet to be realized.
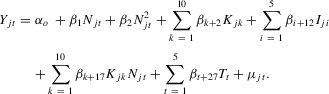 (1)
(1)Contemporaneous correlation is likely to exist among the three equations. Since they include the same regressors, there would be no efficiency gain by estimating them as a seemingly unrelated system. Consequently, each equation is estimated independently. With only two observations for each geo-referenced location and three years between observations (as explained subsequently), we do not use a panel data estimator.7
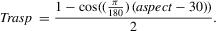 (2)
(2)2.2. Modeling spatial autocorrelation
Considered independently, production units with the same terrain attributes can appear at significant distances from each other. For modelers, this is desirable because standard statistical models generally assume independence among observations or data points. However, in agronomic research data, it is more likely that land parcels with close proximity share common characteristics (e.g., soil properties), which brings the validity of the independence assumption into question (Anselin et al., 2004). Failing to account for valid spatial autocorrelation would result in inefficient parameter estimates that bias the test statistics. Consequently, we appended a spatial component to Eq. 1 to correct for spatial autocorrelation. We used a spatial weights matrix that considered all uphill neighbors with the closest neighbors having more influence on the error term than neighbors farther away.8
Standard spatial autocorrelation techniques assume a two-dimensional spatial effect (i.e., latitude and longitude). With a nonflat surface, like a hill, the two-dimensional assumption is insufficient. While nitrogen can move uphill in limited ways, it generally moves down a slope with water and eventually to a stream or river. Nitrogen deposits at a location in the field can be influenced by locations higher in elevation, thus creating a vertical spatial interdependence. Not accounting for the three-dimensional spatial structure in the spatial econometric methodology can lead to biased variance. In this study, we incorporated a third axis, elevation, into the spatial weights matrix. It effectively models the spatial effect as three dimensional. We determined whether a spatial weights matrix that includes positions higher in elevation results in greater statistical efficiency of parameter estimation than when elevation is not considered.
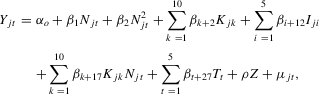 (3)
(3) (4)
(4)The estimation equation 3 represents a spatial lag model where the spatial autocorrelation is restricted to the dependent variable (Anselin, 1988; Anselin et al., 2004). The spatial lag model corrects for nonindependent observations and correlated error terms. The constants in each estimated equation represent observations in 2006 with a previous crop of spring peas. The six previous-year crops were spring peas, winter peas, spring canola, winter canola, spring barley, and winter barley.
The system of equations was estimated via maximum likelihood (Anselin, 1988). We used GAUSS 8.0 to perform the estimation.
In estimating Eq. 3, we encountered high multicollinearity between terrain attributes. It is not entirely surprising that multicollinearity exists between different terrain attributes because they are all in some form measuring landscape. For example, global irradiation and trasp both measure direction and therefore have a high correlation, 84% in this case. Because high multicollinearity inflates the variance and often produces wide swings in parameter estimates with small changes in the data (Greene, 2003), it limits our ability to identify the contribution of specific terrain attributes to yield, protein, or residual nitrogen. We used the variance inflation factor (VIF) magnitudes to identify and remove the most highly collinear terrain attributes.10 We started with 10 terrain attributes. After accounting for high VIFs, defined as a value greater than 40, we were left with four terrain attributes: plan curvature, profile curvature, slope, and trasp. These four terrain attributes measure whether the slope is converging or diverging from the point through plan curvature, whether the slope is accelerating or decelerating through profile curvature, steepness of the terrain through the slope, and direction the slope is facing through trasp.
2.3. Constrained optimization model
For the final objective, we solved a constrained profit-maximization problem based on the regression parameter estimates.11 The optimization model was used to simulate the economic impact on producers from restricting residual nitrogen in the production of HRSW. The economic effects on producers from different scenarios were modeled by considering wheat price, protein premium/discount, nitrogen price, and/or the acceptable amount of residual nitrogen.
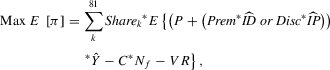 (5)
(5)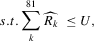
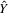 and
and 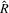 are predicted values of yield and residual nitrogen per acre, respectively, for the kth terrain attribute from Eq. 3;
are predicted values of yield and residual nitrogen per acre, respectively, for the kth terrain attribute from Eq. 3; 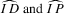 represent the number of predicted quarter percents above or below 14% protein, respectively, for the kth terrain attribute coming from Eq. 3; Prem and Disc represent positive protein premium and negative discount per bushel for quarter percents above or below 14%, respectively; C is the price of nitrogen per pound;
represent the number of predicted quarter percents above or below 14% protein, respectively, for the kth terrain attribute coming from Eq. 3; Prem and Disc represent positive protein premium and negative discount per bushel for quarter percents above or below 14%, respectively; C is the price of nitrogen per pound; 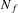 is the amount of applied nitrogen per acre;
is the amount of applied nitrogen per acre; 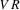 is the per acre incremental cost of variable rate nitrogen application technology; and U is the maximum acceptable amount of residual nitrogen per acre.
is the per acre incremental cost of variable rate nitrogen application technology; and U is the maximum acceptable amount of residual nitrogen per acre.For the constrained optimization, each terrain attribute was divided into three categories: low, average, and high. Means and standard deviations were used to create the three categories. Assuming normality, the average was specified as the mean value, the low value was two standard deviations below the mean, and the high value was two standard deviations above the mean. Data for this analysis came from a six-year (2001–2006) field-level experiment in the rolling Palouse hills north of Pullman, Washington, in a 21 inch rainfall zone. Additional modeling, experiment description, and data details are reported in the Appendix.
3. Results
We first report the results of the statistical analysis. We then present simulation results from the optimization model.
Based on the estimated spatial lag autoregression coefficient (ρ) in Table 1, we found a statistically significant improvement by incorporating the higher elevation spatial weight matrix (significant at the 1% level for yield and protein and at the 10% level for residual nitrogen) over the model with no spatial weighting. Hence, the hypothesis that the higher elevation spatial weights matrix results in no greater statistical efficiency in parameter estimation was rejected. Our finding is consistent with Anselin et al. (2004) who found that incorporating a spatial structure in corn-nitrogen response models considerably improved model fit.
| Equation parameter | Yield | Protein | Residual nitrogen | |||
|---|---|---|---|---|---|---|
| Parameter | Std. error | Parameter | Std. error | Parameter | Std. error | |
| Constant | 28.27*** | 7.08 | 11.86*** | 0.94 | −149.96*** | 37.52 |
| Available nitrogen, N | 0.07** | 0.03 | 0.01*** | 0.004 | 0.75*** | 0.16 |
| N2 | −0.0001* | 0.00003 | −0.00001*** | 0.000004 | 0.0001 | 0.0002 |
| Plan curvature | 2.47 | 6.39 | −1.29 | 0.85 | −17.08 | 33.89 |
| Profile curvature | −3.93 | 6.59 | −0.35 | 0.88 | 89.16** | 35.29 |
| Slope | −0.27 | 0.54 | 0.01 | 0.07 | 7.30** | 2.89 |
| Trasp | −5.73 | 4.33 | 1.27** | 0.58 | −7.82 | 23.00 |
| Spring barley | 0.08 | 1.34 | −0.77*** | 0.18 | 20.84*** | 7.10 |
| Spring canola | 1.89 | 1.32 | −0.47*** | 0.18 | 3.92 | 7.00 |
| Winter canola | 2.26* | 1.35 | −0.09 | 0.18 | −3.66 | 7.16 |
| Winter pea | 2.95** | 1.39 | 0.17 | 0.19 | −5.54 | 7.36 |
| Winter barley | −0.39 | 1.41 | −0.48*** | 0.19 | 22.34*** | 7.46 |
| Plan curvature*N | −0.04** | 0.02 | 0.004* | 0.003 | −0.06 | 0.10 |
| Profile curvature*N | 0.01 | 0.02 | 0.002 | 0.003 | −0.39*** | 0.11 |
| Slope*N | 0.0003 | 0.002 | −0.0002 | 0.0002 | −0.02*** | 0.01 |
| Trasp*N | 0.0038 | 0.01 | −0.002 | 0.002 | 0.02 | 0.07 |
| Year 2005 | 22.92*** | 1.50 | −2.48*** | 0.20 | 30.66*** | 7.96 |
| Year 2004 | 19.67*** | 1.44 | 0.39** | 0.19 | 5.57 | 7.63 |
| Year 2003 | −0.63 | 1.38 | 0.27 | 0.18 | 19.76*** | 7.32 |
| Year 2002 | 25.70*** | 1.44 | −0.76*** | 0.19 | 5.24 | 7.62 |
| Year 2001 | 12.86*** | 1.48 | −1.05*** | 0.20 | 36.12*** | 7.84 |
| ρ | 0.03*** | 0.004 | 0.01*** | 0.002 | 0.003* | 0.002 |
- Notes: Significance level: 10% *, 5% **, and 1% ***. 704 observations. Slope is measured in percent. Plan and profile curvature are measured in degrees per meter.
Yield, protein, and residual nitrogen equation parameter estimates from the spatial model incorporating the higher elevation spatial weights matrix are also reported in Table 1. In both the yield and protein equations, estimated coefficients on both nitrogen supply variables (N and N2) were found to be significant (5% level for N and 10% for N2 in yield and 1% level for both in protein). Thus, both yield and protein content were found to be dependent on nitrogen supply and exhibited diminishing marginal productivity, as reflected by the positive coefficient on the linear terms and the negative coefficient on the quadratic terms. This finding supports previous research in the Pacific Northwest by Baker et al. (2004) who found diminishing marginal productivity for HRSW yield.12 For the residual nitrogen equation, only the coefficient on N was found to be significant (1% level), indicating a positive linear relationship between applied nitrogen and residual nitrogen over the range of our data.
A necessary condition for variable rate application to be a viable technology is a significant response to the interaction of at least one terrain attribute and nitrogen in at least one of the equations. For all three equations, we found at least one significant interaction term, suggesting that at least one dimension of terrain attribute significantly affects yield, protein, and residual nitrogen response to nitrogen supply. For yield and protein, a statistically significant relationship was found for the interaction of plan curvature and nitrogen supply—negative for yield and positive for protein. For the same amount of nitrogen supply, yield was found to decrease and protein increase as flows diverge from the point.13 For residual nitrogen, we found statistically significant negative relationships for the interaction of profile curvature and nitrogen supply and the interaction of slope and nitrogen supply. For the same amount of nitrogen supply, residual nitrogen response to nitrogen supply was found to decrease as the slope increases, indicating that flatter areas, possibly near a waterway, release larger amounts of residual nitrogen than areas with greater slope. Residual nitrogen response from nitrogen supply was found to decrease at higher profile curve values or areas with decelerating flows. In none of the response equations was a statistically significant relation found for the interaction of trasp and nitrogen supply. As a consequence, we did not include trasp in the optimization model with which we conducted the economic simulations. This reduced the number of terrain attribute zones considered from 81 (34) to 27 (33) and thus reduced the dimensions of the optimization problem.
Other factors also contributed significantly to yield, protein, and residual nitrogen, as evident from Table 1. The constant, which represents spring peas in year 2006, was significant and positive in the yield and protein equation and significant and negative in the residual nitrogen equation. Year control variables significantly impacted all three dependent variables. In the yield and protein equations, four of the five year controls were significant; for residual nitrogen, three of the five year controls were significant. Several previous crops were also significant in all three response equations. Of the five previous crop controls, two were significant in the yield and residual nitrogen equations and three in the protein equation.
For a robustness check, we compared results from the higher points spatial model to those obtained from the OLS model. The magnitudes of most estimated parameters were similar in both models. Only one parameter estimate changed sign. The primary differences affected a few parameter estimates on the year dummy variables in the residual nitrogen equation. However, the most notable difference was that the parameter on N2 in the yield equation was insignificant in the OLS model that implies constant marginal productivity over the range of data. Thus, drawing inferences about yield response to nitrogen supply based on our test statistics from OLS could have been seriously misleading.
Table 2 presents the comparative statics of response for all three equations due to the interaction of nitrogen supply and terrain attributes found to be significant in at least one equation. We analyzed three different values of plan curvature, profile curvature, and slope—low, average, and high (as previously defined). All other variables were set at their mean values.
| Terrain attribute | Equation | ||||
|---|---|---|---|---|---|
| Plan curvature | Profile curvature | Slope | Yield (bushels) | Protein (percent) | Residual nitrogen (pounds) |
| Low | Low | Low | 0.087 | 0.009 | 0.988 |
| Low | Average | Low | 0.090 | 0.010 | 0.759 |
| Low | High | Low | 0.093 | 0.011 | 0.529 |
| Average | Low | Low | 0.068 | 0.011 | 0.962 |
| Average | Average | Low | 0.072 | 0.012 | 0.733 |
| Average | High | Low | 0.075 | 0.013 | 0.503 |
| High | Low | Low | 0.050 | 0.013 | 0.936 |
| High | Average | Low | 0.053 | 0.014 | 0.707 |
| High | High | Low | 0.056 | 0.015 | 0.477 |
| Low | Low | Average | 0.089 | 0.008 | 0.853 |
| Low | Average | Average | 0.092 | 0.009 | 0.623 |
| Low | High | Average | 0.095 | 0.011 | 0.394 |
| Average | Low | Average | 0.070 | 0.010 | 0.827 |
| Average | Average | Average | 0.074 | 0.011 | 0.597 |
| Average | High | Average | 0.077 | 0.013 | 0.368 |
| High | Low | Average | 0.052 | 0.012 | 0.801 |
| High | Average | Average | 0.055 | 0.013 | 0.571 |
| High | High | Average | 0.058 | 0.015 | 0.342 |
| Low | Low | High | 0.091 | 0.007 | 0.718 |
| Low | Average | High | 0.094 | 0.009 | 0.488 |
| Low | High | High | 0.097 | 0.010 | 0.258 |
| Average | Low | High | 0.072 | 0.009 | 0.692 |
| Average | Average | High | 0.075 | 0.011 | 0.462 |
| Average | High | High | 0.079 | 0.012 | 0.232 |
| High | Low | High | 0.054 | 0.011 | 0.666 |
| High | Average | High | 0.057 | 0.013 | 0.436 |
| High | High | High | 0.060 | 0.014 | 0.206 |
- Notes: Low and high represent values of two standard deviations to the left and right of the mean, respectively. Average indicates the mean value. Slope is measured in percent. Plan and profile curvature are measured in degrees per meter. All other variables are set at their mean values.
The yield response to a one-pound increase in nitrogen supply ranged from a low of 0.050 to a high of 0.097 bushel increase depending on terrain attributes. Protein response to a one-pound increase in nitrogen supply ranged from a low of 0.007 to a high of 0.015 percentage point increase depending on the terrain attribute. The effect of terrain attribute on residual nitrogen response to a one-pound increase in nitrogen supply ranged from a low of 0.206 to a high of 0.988 pound increase. Hence, terrain attributes were estimated to have the biggest impact on residual nitrogen that varied by 379% from the lowest value. This impact compares to the protein response that varied by 110% from the low value and to yield response that varied by 95%.
For yield and residual nitrogen, points with diverging flows (high plan curvature) decreased response to nitrogen over points with converging flows (low plan curvature). The opposite effect was found for protein. Points with decelerating slope (high profile curvature) increased yield and protein over points with accelerating slope (low profile curvature).14 The opposite effect was found for residual nitrogen. For yield, high slope increased response to nitrogen supply relative to low slope. The opposite effect was found for protein and residual nitrogen, with the difference being greatest for residual nitrogen. Differences in plan curvature had the greatest impact on yield and protein response, and differences in profile curvature had the greatest impact on residual nitrogen response to an increase in nitrogen supply. Because responses were all positive, these comparative static results also make clear that, at mean available nitrogen levels, additional nitrogen increases yield, protein, and residual nitrogen for all terrain attributes.
For the final objective, we used the constrained optimization model to examine the impact on producers from restricting residual nitrogen under two different application methods—uniform and variable rate. Three levels of maximum allowable residual nitrogen from applied nitrogen were considered—maximum of 0 pounds per acre, maximum of 60 pounds per acre, and unconstrained residual nitrogen profit-maximizing level. In order to assess the sensitivity of economic returns, four separate price scenarios were examined for each application method. Three of the scenarios were the highest, average, and lowest ratio of HRSW grain price and of protein price relative to nitrogen price observed during the experimental trial period (2001–2006).15 The fourth scenario used current (Spring 2014) price ratios.
Results from scenarios with applied nitrogen are reported in Table 3 for both application methods. Results are presented on a per-acre basis. In addition to the four scenarios in which additional residual nitrogen was constrained to zero, no nitrogen was applied for the other two scenarios with the low price ratio because the marginal cost was greater than the marginal benefit. Consequently, nitrogen was applied in only 6 of the 12 examined scenarios with either application method. Their results are presented in Table 3. When additional residual nitrogen was constrained to 60 pounds per acre, we found local maxima (i.e., nonbinding constraints) for uniform and variable application with both average and current price ratios. The local maxima were due to the stepped protein premium/discount scales.16 Further, despite very different nominal prices that resulted in substantial differences in profit, the average and current price ratios were sufficiently similar to induce identical levels of applied nitrogen in both scenarios. An identical amount of nitrogen was also applied by variable application in the unconstrained profit maximization scenarios with high and current price ratios.
| Grain/nitrogen and protein/nitrogen price ratios | Maximum allowable additional residual nitrogen | Applied nitrogen | Profit | Additional residual nitrogen | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Uniform | Variable | Difference | Uniform | Variable | Difference | Uniform | Variable | Difference | ||
| Average | Unconstrained | 147.20 | 133.86 | 13.34 | 116.47 | 103.49 | 12.98 | 112.87 | 82.12 | 30.75 |
| 60b | 73.13 | 79.93 | −6.80 | 115.35 | 102.73 | 12.62 | 55.43 | 48.52 | 6.91 | |
| High | Unconstrainedc | 269.73 | 230.41 | 39.32 | 160.90 | 146.65 | 14.25 | 210.79 | 144.02 | 66.77 |
| 60 | 79.10 | 98.48 | −19.38 | 135.00 | 123.92 | 11.08 | 60.00 | 60.00 | 0.00 | |
| Current | Unconstrainedc | 203.89 | 230.41 | −26.52 | 206.13 | 192.27 | 13.86 | 157.73 | 144.02 | 13.71 |
| 60b | 73.13 | 79.93 | −6.80 | 188.64 | 176.69 | 11.95 | 55.43 | 48.52 | 6.91 | |
- Notes:
- a Nitrogen units are in pounds per acre; profit is in dollars per acre. Average and High represent mean and highest price ratios during the study period, and Current represents spring 2014 price ratios. When the maximum allowable additional residual nitrogen was constrained to zero and also at low price ratios, no nitrogen was applied.
- b The residual nitrogen constraint was not binding in either of these scenarios because of the stepped protein premium/discount scales. The constraints were binding when the protein premiums and discounts were ignored. Despite very different prices, the price ratios were sufficiently similar to induce the same levels of applied nitrogen in both scenarios.
- c Despite different prices, the same level of nitrogen was applied with variable rate application in both scenarios.
In all six scenarios with positive applied nitrogen, producer profit was greater under uniform application than under variable rate application. In each of these cases, the benefits of variable rate application were less than the cost of its application. This finding indicates that there was not enough spatial variability response to nitrogen (even with the statistically significant interaction of the plan curvature terrain attribute and nitrogen in yield and protein response equations) for the economic benefits of variable rate application to cover the additional costs.
Except for the unconstrained profit maximization scenarios with average and high price ratios, the variable rate application also used more nitrogen than did uniform application. However, variable rate application reduced residual nitrogen when compared to uniform rate application in five of the six scenarios in which nitrogen was applied, and it was the same in the other scenario. Thus, we find evidence that variable rate application provides positive environmental benefits although not positive producer economic benefits.
Constraining the amount of residual nitrogen generally reduced producer profit, as it logically must if the constraint is binding. The effects differed noticeably between low, average, high, and current price ratios but were similar for both application methods. When additional residual nitrogen was constrained to 60 pounds per acre, profit was reduced by $23–$26 per acre (for a 16% reduction) under the high price ratio, $16–$17 per acre (8%) under current prices, and $1 per acre (1%) under average prices.
The impact on per-acre profit and residual nitrogen of limiting additional residual nitrogen from the profit maximization level to zero is reported in Table 4. To gauge the impact of prices, we consider four distinct price cases over the data period: high grain/nitrogen price ratio and protein/nitrogen price ratio, high grain/nitrogen price ratio with average protein/nitrogen price ratio, high protein/nitrogen price ratio with average grain/nitrogen price ratio, and average grain/nitrogen price ratio and protein/nitrogen price ratio. When any of these price ratios is high, there is a substantial impact on both profit and residual nitrogen from the full restriction on residual nitrogen. For example, with high grain/nitrogen and high protein/nitrogen price ratios, limiting residual nitrogen from the profit-maximization level to zero resulted in a profit reduction of $42–44 per acre and residual nitrogen reduction of 144–211 pounds per acre. The reduction in profit from full restriction was less with only the grain/nitrogen or protein/nitrogen price ratio at the high value, and the reduction in residual nitrogen was less in these cases under uniform application. In each case, the reduction in profit was similar for both application methods. There was more variability in residual nitrogen reduction, and the greater reduction occurred with uniform application.
| Price ratio | |||||
|---|---|---|---|---|---|
| Application method | Measure | High grain/nitrogen and high protein/nitrogen | High grain/nitrogen and average protein/nitrogen | High protein/nitrogen and average grain/nitrogen | Average grain/nitrogen and average protein/nitrogen |
| Uniform | Profit | −44.27 | −26.38 | −32.79 | −5.56 |
| Residual nitrogen | −210.79 | −182.97 | −182.97 | −112.87 | |
| Variable | Profit | −42.45 | −26.80 | −31.74 | −5.01 |
| Residual nitrogen | −144.02 | −143.61 | −143.61 | −82.12 | |
- Notes: Profit is in dollars per acre. Residual nitrogen is in pounds per acre.
With all price ratios at their averages, profit dropped by $5–$6 and residual nitrogen by 82–112 pounds per acre. The drop was greater for residual nitrogen with uniform application. Thus, imposing full restrictions on residual nitrogen had little effect on profit at average prices but substantially reduced residual nitrogen.
As already noted, no nitrogen was applied when both output prices were low relative to nitrogen price. In addition, when one output price was low relative to nitrogen price and the other output price was average relative to nitrogen price, no nitrogen was applied under unconstrained profit maximization. These results were the same for both application methods. Thus, there was no effect on residual nitrogen or profit in any of these scenarios. Consequently, low price ratios during the experimental period would have done as much for the environment as quantity restrictions on residual nitrogen.
4. Conclusions
Using spatial econometric methods, we have analyzed the impact of nitrogen fertilizer supply by terrain attribute on the yield and protein content of HRSW grown in Eastern Washington as well as the impact on residual nitrogen. We also examined potential impacts on producer profit from requirements to reduce residual nitrogen and from using variable rate fertilizer application methods. Understanding the environmental connections of agricultural production helps to identify market conditions and technology that policymakers can use to design policies to minimize the economic cost of reducing environmental degradation.
We found that including a three-dimensional (longitude, latitude, and elevation), spatial weights matrix in the econometric estimation improved statistical efficiency in parameter estimation over standard econometric estimation. Spatial econometric methods provided better model fit by accounting for soil and topographic spatial dependence, thereby improving model accuracy and, more importantly, facilitating more precise economic inference.
With the spatial model controlling for local soil and topographic spatial dependence, we identified statistically significant impacts of nitrogen supply by terrain attribute on yield, protein, and residual nitrogen. We found that yield response to nitrogen supply was the greatest with high slope and high profile curvature (i.e., accelerating slope) and small plan curvature (converging flow). We also found that residual nitrogen response to nitrogen supply was greatest under the opposite extreme in slope, plan curvature, and profile curvature. Consequently, to reduce residual nitrogen and have the least impact on yield, greater attention should be paid to reducing nitrogen supply in the flatter areas. In these areas, nitrogen has a higher probability of becoming pollution since the only way to exit the field is into plants, surface or ground water, or the atmosphere and not by passing the nitrogen to lower elevations.
The economic effect on producer profit from restricting residual nitrogen was examined by simulating 12 price scenarios with a constrained optimization, mixed integer nonlinear programming model. The results of these simulations suggest ways that policymakers might induce producers to reduce residual nitrogen. If required to minimize residual nitrogen, producers could lose up to $44 per acre at high grain/nitrogen and high protein/nitrogen price ratios but only $5–6 per acre at average price ratios. Yet, the reduction of residual nitrogen would be more than half as great at average price ratios as at high price ratios. Thus, inducement to reduce residual nitrogen and consequently applied nitrogen could be accomplished with trivial cost to the farmer at average grain and protein relative to nitrogen price ratios, but the same standard could impose substantial costs at high price ratios. The economic burden of environmental policy associated with nitrogen fertilizer could thus be greatly reduced by implementing a price-dependent partial restriction policy.
Despite the significant effect of terrain attributes on yield and protein content of wheat and on residual nitrogen, uniform application of nitrogen was found to economically outperform variable rate application because of the higher cost of variable rate application. However, variable rate application provided positive environmental benefits over uniform application by leaving less residual nitrogen. Nevertheless, while incentivizing producers to adopt variable rate application is a goal policymakers concerned with environmental quality might consider, it does not exhibit the same impact potential as a price-dependent partial restriction policy.




