Water access, farm productivity, and farm household income: Sri Lanka's Kirindi Oya irrigation system
Abstract
Income differences attributed to differential access to water in irrigation systems are common. Prior studies of farm-level water use in developing areas have typically been limited to using number of irrigations as a proxy for water use. We develop a volumetric measure in Sri Lanka's Kirindi Oya Irrigation System through recent farmer recall and use it in production function estimation and welfare analysis. Findings indicate substantial differences in water use by farms across seasons and across subareas of the irrigation district. Alternative plans for allocating additional water among seasons and subareas to elevate net rice revenues are examined. The recommended plan predicts higher net returns from rice and greater equality in the distribution of household income than would be generated if the additional water were allocated based on the current allocation criteria. Concurrent application of fertilizer at recommended levels would further increase net revenues and reduce income inequality.
1. Introduction
Irrigation contributes to agricultural development through improving land productivity and reducing risk of crop failure. Improved irrigation facilities and introduction of new seed and fertilizer technology have played major roles in improving land productivity throughout the world (Kikuchi and Hayami, 1978). For example, irrigation developments coupled with introduction of high yielding wheat and rice varieties during the 1960s led to a fivefold increase in world grain production between 1960 and 1990 (IWMI, 2002). Irrigated area worldwide grew from 139 million hectares in 1961 to 312 million hectares in 2010 (FAO, 2012). For countries in Monsoon Asia, which have been historically dependent on wet rice cultivation, improved irrigation systems have had both direct and indirect impacts on crop yields because systematic irrigation also encourages farmer application of fertilizer. The combination of timely irrigation and fertilizer application significantly reduces the risk of crop failure.
However, water is a multipurpose resource. Agriculture is only one of its many uses. Irrigation management institutions throughout the world are facing a multitude of challenges arising both from increased water demand and from changing social and economic environments, including concerns about water pollution and water demand for environmental purposes. As availability of water for agriculture decreases, methods have evolved to address the problem. Water rotation, diversification with low water-use crops, implementation of water-conserving techniques, and augmentation of existing supply through trans-basin diversions are examples of methods used to address water shortages in irrigation systems.
Irrigation system developments have contributed to increased food production, income of farm households, and livelihood security. When rainfall is limited during the growing season, the quantity of irrigation water applied and its timing largely determine the farm's crop output. Therefore, differences in water availability inevitably lead to differences in household income.
The geographic focus for the study is the Kirindi Oya Irrigation and Settlement Project (KOISP), a major surface gravity irrigation system situated in southeastern Sri Lanka, a small country with more than a half million hectares under irrigation. This system serves two subareas—the Old Irrigation Area (OIA) and the New Irrigation Area (NIA). Both of these subareas use irrigation water primarily to produce rice, but they have very different access to water and very different socioeconomic status of farm households. Smallholder farmers in OIA receive water from five ancient reservoirs plus a 35-year-old main reservoir. The main reservoir also provides water to smallholder farmers in NIA.
Since construction, water inflow to the main reservoir has declined, while demand by other sectors for water from the reservoir has increased sufficiently that the entire system has been facing water scarcity (Marikar, 1999). In response, a project (the Veheragala Reservoir Project) was constructed to increase water available to farmers in the irrigation system through trans-basin diversions. This project is important and unique in three respects: (a) the additional irrigation water will be used to increase productivity on existing irrigated land rather than expanding the area irrigated, (b) water diverted for irrigation will be carefully monitored for environmental impacts because it will reduce the water supply to the Yala Protected Area Complex (a nationally and globally important wildlife refuge), and (c) water resource use in the source river basin is less developed than in the target river basin. Thus, the project not only competes for water with important nonagricultural uses but also has the potential to significantly alter income distribution in southeastern Sri Lanka. New water diversions had not begun by the study period. Neither had a water distribution policy been established between the two subareas for the new water diversions.
Although water is one of the most important inputs in irrigated agriculture, the water input is seldom carefully quantified at the farm level in developing countries. Water used at the farm level can be best determined by measuring water inflow to a given field with meters or measurement structures. However, these monitoring procedures are cumbersome, expensive, and require a high level of commitment in measuring and reporting. Alternatives to such real-time measures that have been used for economic analysis include the number of irrigations (Hussain and Young, 1985; Young, 2005) and an index of water availability (Wijayaratne, 1986). As competition for water from other uses increases, understanding the quantitative relationships between farm-level water use and agricultural output becomes more important. Water can be used more efficiently, and available water at the system level can be allocated among farmers in ways that enhance aggregate economic welfare and/or greater equality of its distribution. It is therefore important to quantify and record the irrigation water input at the farm level more precisely.
We conceptualize and empirically estimate the relationship between water use, irrigated rice production, and household income at the farm level within this irrigation system. Specific objectives of the study are to: (a) use structured surveys to obtain farmers’ recall of recent use of water and other inputs at the farm level as a means of more accurately determining quantities used by individual farms, (b) estimate the production function for rice, (c) use the estimated production function and price data to determine the effect of differential access to water on household income, and (d) predict changes in aggregate and distribution of farmer household income under alternative water allocation policy scenarios.
2. Method of analysis
The conceptual foundation of the analysis is production by a semisubsistence household firm (Strauss, 1984). Profit-maximizing behavior of farmers in Sri Lanka has been examined by Herath et al. (1983) and Jegasothy et al. (1990). Rice production in the country is dominated by smallholders, and well-developed factor and product markets exist. We therefore treat the household model as separable between production and consumption decisions. We model production decisions subject to the behavioral objective of maximizing profit without regard to possible interactions with utility-maximizing consumption decisions. We also expect farmers to operate as perfect competitors in output and variable input markets.
Farm household income is related to access to water as an input in agricultural production and also through its life-supporting domestic uses. Water also generates utility through indirect means such as recreation and scenic value. In this study, we confine our analysis to aggregate income effects generated by water through production of rice. We hypothesize that the marginal product of water is positive and that the value of the marginal product exceeds the user cost. If correct, higher applied water quantities would lead to greater rice production, and the greater production would lead to increased net income from rice. Increased net rice income is expected to lead to higher net farm income and potentially to higher household income.
To assess the connection between water access differentials and economic welfare of farmers in the two subareas, we collect water quantity and other input data through structured, recent recall surveys, and then econometrically estimate a rice production function to document the relationship between rice yield and water application. We use farm budgeting techniques to calculate net farm incomes and conduct simulations of alternative policy scenarios using the estimated production function.
2.1. Production function
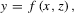 (1)
(1)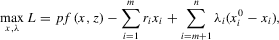 (2)
(2)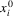 is the level of a constrained input, and λi is a Lagrange multiplier. This leads to first-order conditions:
is the level of a constrained input, and λi is a Lagrange multiplier. This leads to first-order conditions:
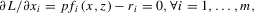
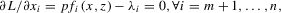
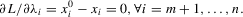 (3)
(3)Choice of functional form for production analysis is a particularly important consideration. Previous researchers have used a wide variety of functional forms. For example, agricultural production functions related to rice farming in other irrigation systems in the Sri Lankan Dry Zone were previously estimated by Abeygunawardena (1986) using a linear functional form and by Wijayaratne (1986) and Jegasothy et al. (1990) using a quadratic functional form. The Cobb–Douglas is the most widely used functional form in agricultural production and has been used in a variety of applications ranging from farm level (Bakhshoodeh and Thompson, 2001) to international comparisons (Barker et al., 1985). It continues to be widely used (e.g., Crost et al., 2007; DiFalco et al., 2008; Ferreira et al., 2007; Wei, 2007). This functional form imposes the strong assumptions that a constant percentage change in inputs leads to a constant percentage change in output at all levels of inputs and that the elasticity of substitution between inputs is 1. Less restrictive alternatives to the Cobb–Douglas, such as the translog and quadratic, could provide a more accurate description of production technology. Yet, the Cobb–Douglas functional form has several advantages over these more “flexible” functional forms, including parsimony of parameters, convenience for inference, and perhaps more importantly, it tends to be globally well behaved (Antle and Pingali, 1995). This last property is particularly important in simulating production at different levels of inputs, which is an important objective of our study. Since the translog nests the Cobb–Douglas functional form, we estimated the translog functional form to model rice yield and tested for the Cobb–Douglas as a special case.
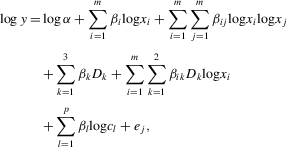 (4)
(4)We estimate the translog production function using pooled ordinary least squares (OLS) with time fixed effects. We use this model to conduct the nested test for the Cobb–Douglas functional form that we find is not rejected. We then estimate the Cobb–Douglas functional form using the same estimator and perform robustness checks with this functional form using the random effects panel data estimator with time fixed effects and an OLS estimator for each season's production function estimated independently. Lacking firm-level price data, we are unable to account explicitly for the endogeneity of the input choices. Thus, the possibility of bias in the reported estimates due to regressor endogeneity remains.1
2.2. Economic welfare indicators
Following Just et al. (2004), we consider two widely used economic welfare indices for producers—profit and producer surplus. In the long run, producer surplus for the industry is equal to the sum of producer profits. Consequently, profit, defined as gross revenue minus total costs, is an obvious candidate as a measure of producer economic welfare for the firm seeking to maximize profit. However, profit serves as an appropriate measure only in certain cases. An alternative to profit as an economic welfare measure is producer's net revenue, defined as the excess of total revenue over variable costs, which is short-run producer surplus. This measure, also known as quasi-rent (R), is generally considered to be more appropriate in the context of smallholders who have difficulty valuing fixed costs, especially land.
We compute net revenue from rice farming for each cultivation season through farm budgeting. We define farm income as net revenue generated from activities within the family farm. To obtain household income, we also include nonfarm income. We conduct a series of simulations on alternative water allocation policies based on these budgets and the estimated parameters of the production function.
3. Data
Farm households were selected from the KOISP area through two-stage probability-proportionate-to-size sampling. In the first stage, 10 and 9 farmer organizations were randomly selected from NIA and OIA, respectively. Ten farmers were then randomly selected from each selected farmer organization using membership lists.
Data for two consecutive cultivation seasons, the wet season (Maha) in 2006/2007 and the dry season (Yala) in 2007, were collected in two sets of interviews in July and December 2007 using a pre-structured survey schedule. Enumerators had a farming background and were high school graduates. They visited households during principal operators’ leisure time to collect data. A separate interview was scheduled following each cultivation season to minimize recollection errors and also to avoid long interview times. Consistency of data was verified through cross-checking by the senior author and review with field-level officers from the Sri Lanka Department of Agriculture.
A total of 190 interviews were conducted in the first season. However, due to respondent attrition between the two interviews, only 360 questionnaires were available for data analysis.
In the study area and period of observation, farmers in both subareas followed the same irrigation water use practices during land preparation and the early vegetative phase of the rice crop. Continuous irrigation water was available system-wide until 30 days after the agreed date for crop establishment. Water was not used as a means of weed control. Minimal wetting of the field occurred three times during the first 10 days after the crop was established. Water flows in NIA during the late vegetative phase and maturity phase in both seasons were restricted to a few days every week. In contrast, OIA had continuous water availability throughout the season. Based on these observations, farmers were expected to use constant volumes of water per hectare during land preparation and the early vegetative phase. Access-induced differential use would then have occurred only during the latter two phases, i.e., late vegetative and maturity, of the rice crop. Consequently, data on water use were collected only for the latter two phases.
The data collection procedure gathered farmers’ recall data through structured survey instruments. Data collected for each production season included duration of an average irrigation, average height of the irrigation water, and number of irrigations after the early vegetative phase; the quantity of rice grown, quantity sold, quantity retained for consumption, and farm-gate price for rice sold; quantities used and prices paid for seed, fertilizer, hired labor, and farm machinery; quantity used of family labor; and cost of chemicals used. Information was also collected on land tenure and rental rates; distance to the water distribution canal; the household head's education and experience in farming; share of rice income in farm income; and share of farm income in household income.
4. Results
4.1. Input use patterns and production relationships
Per hectare means, standard deviations, minima, and maxima of farm size as well as variables used in the production function estimation are reported in Table 1 for each cultivation season and subarea. Also reported in the table are mean differences of the variables between subareas and between seasons and results of t-tests for comparison of their differences. t-tests indicate significant interseasonal and inter-subarea differences in means of rice yields, water quantities applied, and machinery used per hectare. They also show significant inter-subarea differences in means of seed and labor used and significant interseasonal differences in means of chemicals used per hectare. Mean quantity of irrigation water applied per hectare is higher in the Maha season than in the Yala Season for both subareas and is higher in the OIA subarea than in the NIA subarea in both seasons. Farmers in both subareas use higher levels of chemicals during the Maha season. This is due to preventive measures taken due to the higher incidence of pests and diseases during the wetter Maha season. OIA farmers use less labor and more rice seed and machinery than NIA farmers during both seasons indicating substitution of machinery and seed for labor in both seasons. Further, correlation analysis of the farm-level data indicates a strong negative relationship (−0.531 and −0.526 for Maha and Yala seasons, respectively) between quantities of labor and machinery.
| OIA | NIA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variableb | Mean | Std. dev. | Minimum | Maximum | Mean | Std. dev. | Minimum | Maximum | Mean difference between subareas | |
| Farm size (ha)c | 0.94 | 0.5 | 0.2 | 2.0 | 0.88 | 0.2 | 0.1 | 1.6 | 0.05 | (0.1) |
| Education (years) | 9.0 | 2.5 | 4 | 16 | 8.1 | 2.2 | 3 | 16 | 0.9** | (0.4) |
| Schooling dummy | 0.5 | 0.5 | 0 | 1 | 0.3 | 0.5 | 0 | 1 | 0.2*** | (0.1) |
| Experience (years) | 25.1 | 10.4 | 9 | 54 | 18.4 | 5.8 | 2 | 37 | 6.7*** | (1.2) |
| Distance to canal (m) | 338 | 324 | 2 | 1,000 | 536 | 340 | 25 | 1,000 | −198*** | (50.9) |
| Maha season | ||||||||||
| Rice yield (kg/ha) | 7,157 | 578 | 5,583 | 8,750 | 6,275 | 815 | 4,800 | 8,438 | 882*** | (105) |
| Water (m3/ha) | 10,783 | 1,832 | 6,500 | 15,000 | 9,425 | 1,410 | 6,500 | 14,000 | 1,358*** | (243.6) |
| Fertilizer(kg/ha) | 421 | 36 | 312 | 450 | 415 | 37 | 325 | 450 | 5.5 | (5.4) |
| Labor(days/ha) | 36 | 11 | 20 | 83 | 49 | 17 | 23 | 100 | −13.0*** | (2.2) |
| Machinery(SLR/ha) | 26,511 | 4,624 | 8,120 | 34,792 | 24,286 | 5,104 | 14,100 | 36,438 | 2,225*** | (725.9) |
| Chemicals(SLR/ha) | 3,959 | 1,356 | 825 | 7,125 | 3,908 | 1,230 | 894 | 7,250 | 51 | (192.9) |
| Seed (kg/ha) | 204 | 31 | 150 | 250 | 187 | 40 | 100 | 250 | 16.9*** | (5.2) |
| Yala season | ||||||||||
| Rice yield (kg/ha) | 6,722 | 606 | 5,250 | 8,250 | 5,894 | 776 | 4,500 | 7,875 | 828*** | (104) |
| Water (m3/ha) | 10,303 | 1,388 | 7,500 | 13,500 | 8,667 | 1,448 | 5,000 | 11,250 | 1,638*** | (211.4) |
| Fertilizer (kg/ha) | 419 | 26 | 362 | 450 | 414 | 39 | 328 | 450 | 5.8 | (3.3) |
| Labor (days/ha) | 34 | 14 | 11 | 71 | 46 | 15 | 14 | 78 | −11.8*** | (2.1) |
| Machinery (SLR/ha) | 28,362 | 3,499 | 13,895 | 34,500 | 25,823 | 4,968 | 14,950 | 33,480 | 2,539*** | (640.4) |
| Chemicals (SLR/ha) | 3,550 | 1,058 | 488 | 6,500 | 3,321 | 1,098 | 1,000 | 6,000 | 229 | (160.7) |
| Seed (kg/ha) | 201 | 23 | 150 | 250 | 193 | 30 | 125 | 250 | 7.7* | (4.0) |
| Mean difference between seasons | ||||||||||
| Rice yield (kg/ha) | 435*** | (88) | 381*** | (119) | ||||||
| Water (m3/ha) | 481** | (242.3) | 758*** | (213.0) | ||||||
| Fertilizer (kg/ha) | 1.4 | (4.7) | 1.7 | (4.8) | ||||||
| Labor (days/ha) | 1.7 | (1.9) | 2.9 | (2.4) | ||||||
| Machinery (SLR/ha) | −1,851*** | (611.2) | −1,537** | (750.7) | ||||||
| Chemicals (SLR/ha) | 409*** | (181.3) | 587*** | (173.7) | ||||||
| Seed (kg/ha) | 3.2 | (4.1) | −6.0 | (5.3) | ||||||
Notes
- a Numbers in parentheses are standard errors for mean differences. Std. dev. is standard deviation. Significance codes: *P < 0.10, **P < 0.05, ***P < 0.01.
- b SLR is Sri Lanka Rupees. Official exchange rate during the survey period was SLR 108.89 per US$1.
- c Farm sizes did not change between seasons.
These data were analyzed to determine relationships between input intensities and rice production per hectare. The initial model was formulated as a Cobb–Douglas production function and estimated with all observations using pooled OLS. Variance inflation factors were calculated as multicollinearity diagnostics. High multicollinearity was evident in the data. Three variables with highest variance inflation factors (each in excess of 1,000) that were not statistically significant were deleted. They were the season dummy, subarea dummy × log of fertilizer, and season dummy × log of fertilizer variables. The parameter estimates for the model estimated with the remaining variables are reported in the first column of Table 2.
| Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Pooled OLS | Random effects panel data | OLS Maha season | OLS Yala season | |||||
| Variable | Parameter | Std. error | Parameter | Std. errora | Parameter | Std. error | Parameter | Std. error |
| Subarea dummy (OIA = 1) | 2.2948 | 0.6931*** | 1.0456 | 0.4245** | 3.2348 | 0.9101*** | 0.7710 | 0.2568*** |
| Subarea X season (Maha = 1) | 0.0412 | 0.0188** | 0.0160 | 0.0063** | ||||
| Log of water | 0.4041 | 0.0414*** | 0.1557 | 0.0279*** | 0.3615 | 0.0541*** | 0.4002 | 0.0384*** |
| Log of fertilizer | 0.1527 | 0.0453*** | 0.0105 | 0.0207 | 0.2646 | 0.0607*** | 0.0505 | 0.0684 |
| Log of labor | 0.0896 | 0.0233*** | 0.0331 | 0.0112*** | 0.1509 | 0.0276*** | 0.0806 | 0.0267*** |
| Log of machinery | 0.0752 | 0.0378** | 0.0152 | 0.0156 | 0.1605 | 0.0451*** | 0.0448 | 0.0371 |
| Log of chemicals | 0.0301 | 0.0183 | 0.0065 | 0.0067 | −0.0085 | 0.0210 | 0.0440 | 0.0220** |
| Log of seed | 0.0669 | 0.0429 | −0.0030 | 0.0134 | 0.0157 | 0.0335 | 0.0785 | 0.0420* |
| Subarea × log of water | −0.0708 | 0.0518 | −0.0533 | 0.0376 | −0.1211 | 0.0698* | ||
| Subarea × log of labor | −0.0747 | 0.0263*** | −0.0048 | 0.0153 | −0.1127 | 0.0392*** | −0.0594 | 0.0326* |
| Subarea × log of machinery | −0.1004 | 0.0456** | −0.0255 | 0.0190 | −0.1665 | 0.0581*** | ||
| Subarea × log of chemicals | −0.0425 | 0.0204** | −0.0156 | 0.0071** | −0.0083 | 0.0292 | −0.0630 | 0.0288** |
| Subarea × log of seed | 0.0081 | 0.0497 | −0.0121 | 0.0205 | 0.0259 | 0.0593 | ||
| Season × log of water | −0.0458 | 0.0429 | −0.0428 | 0.0147*** | ||||
| Season × log of labor | 0.0477 | 0.0237** | 0.0124 | 0.0079 | ||||
| Season × log of machinery | 0.0640 | 0.0342* | 0.0232 | 0.0114** | ||||
| Season × log of chemicals | −0.0202 | 0.0201 | 0.0095 | 0.0075 | ||||
| Season × log of seed | −0.0420 | 0.0473 | 0.0151 | 0.0174 | ||||
| Log of education | 0.0098 | 0.0196 | 0.0497 | 0.0389 | 0.0293 | 0.0264 | −0.0101 | 0.0290 |
| Completed schooling dummy | 0.0674 | 0.0119*** | 0.0671 | 0.0213*** | 0.0536 | 0.0163*** | 0.0768 | 0.0174*** |
| Lof of farming experience | 0.0335 | 0.0099*** | 0.0495 | 0.0147*** | 0.0373 | 0.0133*** | 0.0297 | 0.0142** |
| Log of distance to D canal | −0.0002 | 0.0032 | 0.0009 | 0.0048 | −0.0003 | 0.0043 | −0.0009 | 0.0046 |
| Intercept | 2.2669 | 0.5293*** | 6.6161 | 0.3562*** | 1.4499 | 0.7373* | 3.1395 | 0.6609*** |
| Observations | 360 | 360 | 180 | 180 | ||||
| R2 | 0.7182 | 0.5992 | 0.7233 | 0.7020 | ||||
| Adjusted R2 | 0.6998 | 0.6961 | 0.6786 | |||||
| White's test for heteroskedasticity | ||||||||
| Null hypothesis: heteroskedasticity not present | ||||||||
| Test statistic: LM | 185.73 | 123.85 | 90.84 | |||||
| P-value | 0.49 | 0.27 | 0.57 | |||||
| Ramsey RESET test for specification | ||||||||
| Null hypothesis: specification adequate | ||||||||
| Test statistic: F | 1.92 | 0.66 | 0.62 | |||||
| P-value | 0.13 | 0.58 | 0.61 | |||||
Notes
- a Standard errors are heteroskedasticity-consistent robust standard errors.
- Significance codes: *P < 0.10, **P < 0.05, ***P < 0.01.
Thirteen of the 22 independent variables were statistically significant at the 0.10 level. All of the inputs except chemicals and seed had a statistically significant positive impact on yield. The estimated production function exhibited diminishing returns to scale with a scale elasticity of 0.82. The area dummy (OIA) was statistically significant as were most of its interaction terms. It had a significant interaction effect with labor, machinery, and chemicals. In each of these cases, the OIA had a lower partial elasticity of production than did the NIA. The season dummy (Maha) was significant as an interaction term with area, labor, and machinery. All three had positive impacts indicating that the partial elasticities of production were higher for both labor and machinery in the Maha (wet) season than in the Yala (dry) season. The significantly positive coefficients on farming experience and the completed schooling dummy variable indicate that yields increased with farming experience and with attainment of 10 years of education. Only seed and the indirect variables of years of education and distance to the distributor canal had no significant impact on yields.
We conducted statistical tests for heteroskedasticity and the current Cobb–Douglas specification with the three deleted variables. The test statistics are reported in Table 2. We found no evidence of heteroskedasticity nor of model misspecification based on these tests. Neither null hypothesis was rejected.
We also estimated the production function using the translog functional form. This form was the second-order Taylor expansion for which the Cobb–Douglas was the first-order expansion. It included the same variables as in the Cobb–Douglas production function plus the 21 quadratic terms on input quantities. An F-test was conducted to determine whether all 21 coefficients on the quadratic terms were jointly zero. With a test statistic of 1.29, the P-value was 0.18, and the hypothesis that the true functional form was Cobb–Douglas was not rejected against the alternative that it was translog.
As robustness checks on our pooled OLS estimation of the Cobb–Douglas production function, we include three additional models. They included the same specification estimated with a random effects panel data estimator and separate OLS estimates for each season.
The production function was reestimated using panel data procedures because the data set included observations for the same producers in two seasons. Based both on the Hausman test and our interest in determining whether there were systematic differences in the production function for the two subareas, we used the random effects estimator. The fixed effects estimator prevented our keeping the group cross-sectional dummy variables in the specification. The parameter estimates for this model are reported in the second set of columns in Table 2. To allow for the possibility of heteroskedastic errors, robust standard errors were computed. Fewer parameters were statistically significant, and the parameter estimates were very different from the OLS estimates. For example, the scale elasticity for the panel data estimates was 0.22, little more than a quarter of that from the OLS estimates and much lower than most agricultural production function estimates in which all inputs are treated as variable. Therefore, the panel data estimates are not considered reliable and will not be used to draw economic inferences.2
A separate production function was estimated by OLS for each season. They differed from the model estimated by pooled OLS in deleting all season interaction variables and only using observations from one season. The same procedures were followed as in the pooled OLS estimation. Multicollinearity diagnostics were calculated first and variables deleted with the highest variance inflation factors that were not statistically significant. That resulted in deletion of the subarea dummy × log of fertilizer from both models as well as subarea dummy × log of water, subarea dummy × log of machinery, and subarea dummy × log of seed from the Yala Season model. Ten of 16 variables were statistically significant at the 0.10 level in the Maha season model and nine of 13 variables were significant in the Yala model. Returns to scale was estimated to be 0.96 in the Maha season and 0.70 in the Yala season, thus bracketing the pooled OLS estimate and being much higher than the panel data estimate. The subarea dummy was statistically significant in both seasons. The only input variables that were statistically significant in both seasons were water, labor, and Subarea dummy × log of labor. In all models, the estimated partial production elasticity was greatest for water. As in the other models, completed schooling and the log of farming experience were statistically significant in these models. These model estimates will be used as robustness checks to the pooled OLS production function estimates for selected economic implications.
4.2. Marginal value productivities of inputs
The marginal productivity of each input was calculated at the data means for each subarea and cultivation season using the pooled OLS estimates and the individual season OLS estimates of the production function. All calculated marginal products were positive. Each was also declining with increasing level of input use. Thus, our estimated production function was consistent with the theory of price-taking profit-maximizing firms.
Marginal value products (MVPs) were obtained by multiplying marginal products by average product prices. They are presented in Table 3 together with their respective opportunity costs (OCs) for the potentially constrained inputs of water and labor and the subsidized input of fertilizer. We used the current value of net benefits realized by inland capture fishery when reservoir water is not released for irrigation as the OC of water. Wage rates for hired labor and the subsidized price of fertilizer were used as the OCs of labor and fertilizer, respectively.
| Opportunity | MVP (SLR/unit) | Ratio of MVP to OC | |||
|---|---|---|---|---|---|
| Input, season | cost (OC)b | Pooled | Individual | Pooled | Individual |
| and subarea | (SLR/unit) | OLS | season OLS | OLS | season OLS |
| Water | |||||
| OIA-Maha | 1.07 | 3.16 | 2.65 | 2.96 | 2.47 |
| OIA -Yala | 1.07 | 3.60 | 4.33 | 3.37 | 4.05 |
| NIA-Maha | 1.07 | 3.98 | 4.03 | 3.73 | 3.77 |
| NIA -Yala | 1.07 | 4.59 | 4.56 | 4.30 | 4.26 |
| Fertilizer | |||||
| OIA-Maha | 7.00 | 88.87 | 153.98 | 12.70 | 22.00 |
| OIA -Yala | 7.00 | 84.71 | 28.02 | 12.10 | 4.00 |
| NIA-Maha | 7.00 | 85.77 | 148.61 | 12.25 | 21.23 |
| NIA -Yala | 7.00 | 78.05 | 25.81 | 11.15 | 3.69 |
| Labor | |||||
| OIA-Maha | 583.89 | 206.37 | 126.21 | 0.35 | 0.22 |
| OIA -Yala | 561.11 | 48.79 | 69.35 | 0.09 | 0.12 |
| NIA-Maha | 562.22 | 294.31 | 323.60 | 0.52 | 0.58 |
| NIA -Yala | 535.00 | 192.17 | 172.82 | 0.36 | 0.32 |
Notes
- a Average subarea product prices are used in the calculations: 16.59 SLR/kg for OIA and 16.74 SLR/kg for NIA for both seasons.
- b The opportunity cost of water is the value of freshwater artisan fishery if water is not released for irrigation. Values were updated using current prices and technical information from Renwick (2001). The opportunity cost of fertilizer is the current subsidized price for fertilizer under the Government of Sri Lanka's Rice Fertilizer Subsidy Scheme (Central Bank of Sri Lanka, 2008). For labor, it is the current market wage rate.
The ratio of MVPs and OCs are much larger than unity for water and fertilizer, suggesting that an additional unit of water or fertilizer in rice production will generate additional revenues higher than the OC of the respective resource. In contrast, the MVP/OC ratio for labor is less than unity in all four cases, indicating that the true OC for additional labor is much less than the wage rate.
This information provides important policy insight for allocation of inputs. Since there is no established market price for water, the calculated MVP for water can be used as an estimate of the true value of water at the prevailing market price for rice.
The MVP/OC ratio for fertilizer calculated from the pooled OLS parameter estimates is very large, with all estimates greater than 10. Farmers currently pay a subsidized price for the allocated fertilizer. It can be inferred that farmers are likely to apply more fertilizer (until MVP equals OC) even if they are not subsidized. The agronomically maximum realizable farm level yield for the irrigation district is considered to be about 10.0 metric tons per hectare. The mean yield on sample farms in each subarea and season is less than 75% of this expected yield plateau. Thus, there appears to be considerable opportunity to increase yield and net returns from rice through economic application of more fertilizer.
As goodness of fit and statistical tests are satisfactory, the pooled OLS estimate of the production function is judged suitable to predict output due to changes in input combinations within the range of our data. We use this estimated model to simulate the effects of applying different quantities of water on rice yields.
The same qualitative implications about marginal value productivities and their relationship to input OCs were obtained from the individual season production functions, the results of which are also reported in Table 3. The estimated MVPs for water and labor were similar to those from the pooled OLS estimates. The estimates for fertilizer showed greater difference between the two seasons.
4.3. Economic welfare implications of differential access to water
Farm budgeting techniques were used to compute gross revenue, net revenue, and profit from rice for representative farms at the data means. Their averages and standard deviations by subarea and season are reported in Table 4.
| OIA | NIA | |||
|---|---|---|---|---|
| Economic measures per hectare | Maha season | Yala season | Maha season | Yala season |
| Rice gross | 118,738 | 111,563 | 105,103 | 98,737 |
| revenueb | (12,501) | (12,879) | (18,927) | (179,640) |
| Rice net revenuec | 66,050 | 54,811 | 48,913 | 39,832 |
| (13,663) | (14,177) | (18,167) | (17,825) | |
| Rice profitd | 34,901 | 26,233 | 23,593 | 16,397 |
| (12,865) | (13,520) | (16,380) | (15,810) | |
| Household economic measures | OIA | NIA | Mean difference | t-Ratio |
| (1) Annual net net | 114,271 | 73,899 | 40,372 | 5.47*** |
| revenue from | (63,250) | (30,007) | (7,379) | |
| rice (SLR/Household) | ||||
| (2) Annual net | 159,453 | 120,397 | 39,056 | 3.00*** |
| farm income(SLR/Household) | (100,008) | (71,876) | (12,982) | |
| (3) Annual | 261,903 | 194,043 | 67,860 | 2.88*** |
| household | (190,351) | (116,973) | (23,550) | |
| income(SLR/Household) | ||||
Notes
- a Numbers in parentheses are standard deviations for means and standard errors for mean differences. Significance codes: **P < 0.05, ***P < 0.01. Average subarea product prices were used in the calculations: 16.59 SLR/kg for OIA and 16.74 SLR/kg for NIA for both seasons.
- b Gross revenue = average yield × average subarea product price.
- c Net revenue = gross revenue minus average subarea cash costs.
- d Profit = net revenue minus sum of imputed costs for family labor, returns to management, and land rent.
In preparing rice budgets, household-owned inputs were valued at market rental/sales values for the respective season and area, and the OC of capital per season was considered to be 4.5% of all cash costs, to reflect the ongoing short-term market borrowing rate of about 18% per annum. Family labor was imputed at the wage rate incurred by the household during the respective season. Based on the convention used in standard farm budgeting, 5% of net revenue was imputed as returns to management. Land rental practices varied greatly within and across subareas. Precise land rental rates were difficult to assess. Based on information from farmer leaders, land rental values per hectare per season were imputed at SLR 20,000 for OIA and 15,000 for NIA.
Representative farm annual household incomes were calculated for each subarea using the calculated rice net revenue, the mean share of rice income in farm income for the sample in each subarea, the mean share of farm income in household income for the sample in each subarea, and the mean farm size. Calculated means and standard deviations of household annual net revenue from rice, net farm income, and household income are also reported in Table 4. Each of these indicators of economic welfare is considerably higher in OIA than in NIA, and statistical tests based on the farm-level data indicate that they are significantly higher.
The survey revealed important differences in the distribution of household income in each subarea between rice, farm, and nonfarm income. Shares of rice income in annual household income varied from 10% to 100% and its average was greater in the more established farming subarea, OIA (44%), than in NIA (38%). However, it is in the skewness of the distribution of rice to household income that the greatest differences in income composition between subareas are evident. The distribution of OIA households is slightly skewed to lower percentages of household income from rice, while the distribution of NIA households is strongly skewed toward higher percentages.
As evidenced from the survey and household budgeting, water availability and rice income was associated. This finding was corroborated by our production function estimates that revealed large positive impacts of additional water. Using the pooled OLS estimates of the production function, the effect of water use on net rice income was simulated per hectare for each individual farm for both seasons by changing water quantities applied while holding all other input quantities at current levels. We first simulated net revenues from rice for all farms while holding water quantities applied at the current OIA mean. Water quantities were then decreased to the current NIA mean, while all other input levels were kept at current levels (see Table 5). A paired sample t-test indicated that net rice revenues are higher when water levels are set at the OIA mean, and the differences are highly significant. It is anticipated that annual household income will also be increased if the quantity of water applied per hectare is increased. In the next section, we examine the effects on farm household income of alternative interventions to allocate additional water.
| OIA | NIA | |||
|---|---|---|---|---|
| Water level | Maha | Yala | Maha | Yala |
| OIA mean | 65,749 | 54,273 | 53,828 | 47,698 |
| (9,040) | (8,228) | (9,136) | (9,597) | |
| NIA mean | 61,235 | 48,030 | 48,652 | 40,563 |
| (8,896) | (8,132) | (8,938) | (9,331) | |
| Difference | 4,515 | 6,243 | 5,176 | 7,134 |
| (21) | (25) | (33) | (43) | |
| t-Ratiob | 210.6*** | 245.6*** | 156.5*** | 165.8*** |
Notes
- a Standard deviations from the means and standard errors for the test of differences are in parentheses. Significance code: ***P < 0.01. Simulated net revenue = predicted yield × product price – total cash costs. Yields were predicted using parameters of the estimated production function (Table 2) and actual quantities of inputs.
- b Based on paired sample t-test on mean differences at two water levels.
4.4. Economic implications of alternative augmented water allocation plans
The Veheragala Reservoir Project, a project under construction during the survey period to increase water available through trans-basin diversions, did not anticipate increasing the irrigated area in the KOISP. Therefore, additional water would be available for distribution only among existing farms.
Our simulated interventions target farms that currently use quantities of water less than the minimum level defined by alternative allocation criteria, each of which is described in Table 6. The simulations focus only on the distribution of additional water supplied by the new project and do not consider reallocation of initial water rights. Therefore, water quantities applied and thus yields on farms that currently use higher quantities of water than implied by the allocation criteria remain unchanged.
| Allocation criteria | Objective | Procedure | Notes |
|---|---|---|---|
| Economic criterion | Maximize system-wide net benefits from new water | Progressively increase the water available to farms beginning with the user with the highest MVP for water until the MVP for each user receiving additional water is equal | This is the sole criterion in Allocation Plan A. It is a supplementary criterion in Plans B and C |
| Agronomic criterion | Ensure that all farms receive the minimum water quantity required for evapotrans-piration and percolation losses | Allocate water to ensure at least 10,250 m3/ha irrigation water to each farm in the Maha season and 10,750 m3/ha in the Maha season | First criterion in Plan B and second criterion in Plan C |
| Fertilizer criterion | Ensure that all farms receive the minimum fertilizer quantity recommended by the Sri Lanka Department of Agriculture | Increase fertilizer quantity to recommended levels before allocating additional water | First criterion in Plan C |
| Status quo | Allocate new water in same proportion as current water allocation | Allocate new water among subareas and seasons following the current allocation plan | Used in Plan D |
Note
- a All allocation plans address the use of additional water being made available through the Veheragala Reservoir Project. In none of the allocation plans is current water supply taken away from any farm.
When water is allocated based on economic criteria, water quantity is allocated among subarea–season strata so that their mean MVPs for water are the same when all available water is exhausted. The agronomic criterion used in other plans ensures that all farms receive sufficient water to meet minimum agronomic requirements and then additional water, if any, is allocated according to the economic criterion.
The pooled OLS estimated production function is used to predict yields at new water levels for each farm assuming that quantities of other inputs, except fertilizer in one simulation, remained at current levels. Water is allocated to each farm until all farms in the respective subarea receive the minimum water quantities as defined above.
We consider four alternative water allocation plans. All plans are constrained by the availability of 50 million cubic meters (MCM) of additional water at the reservoir (or 35 MCM at the farm level).
In Plan A, the allocation of additional water is based solely on the economic criterion of equalizing MVP of water in all receiving subarea–season combinations. This criterion generates maximum economic value from the additional water as a Pareto optimum. Water quantity is defined as the level of water at which MVPs for receiving additional water are equated when the total additional water is exhausted.
Plan B deviates from Plan A as the latter ensures that all farms receive sufficient water to meet minimum agronomic requirements for crop evapotranspiration (ET) and percolation losses. This criterion is applied to all farms even if a subarea–season stratum has a sufficiently low mean MVP that it does not receive additional allocations based on the economic criterion. Based on Dimantha and de Alwis (1985) and Guerra et al. (1998), we define the minimum water levels as 10,250 and 10,750 m3/ha, respectively, for the Maha and Yala seasons. After the minimum water requirement is met for each farm, any additional water available is allocated based on the economic principle of Plan A.
In addition to these two basic water allocation plans, we consider two additional plans to highlight policy implications. Plan C represents a water allocation plan based on Plan B criteria with farmers applying fertilizer at rates recommended by the Sri Lanka Department of Agriculture. It supports the government's objective of increasing crop productivity by promoting fertilizer application. Plan D is a “business as usual” plan to compare net benefits if KOISP managers allocate additional water in the same proportions by subarea and season as the current allocation. All of the plans maintain the (strong) assumption that, with more water available, households do not change any other production decision, other than changing fertilizer rates in Plan C. Thus, we assume that households do not reallocate labor away from nonfarm jobs, hire more labor, or increase seed, chemical, or machinery input use when they receive additional water. Thus, our estimates of income effects are lower bound estimates since these inputs are not permitted to adjust to their optimal levels.
The pooled OLS estimated production function was used to predict yields at new water levels for each farm. Yields for farms that receive additional water allocations would increase. Yields for other farms would remain unchanged. Consequently, the marginal product of water for the subarea–season combinations receiving water will decrease. With constant output price, decreasing marginal productivity implies that MVP also decreases as the quantity of an input increases. Compared to current water quantities and yields, the incremental water quantities and resulting yield increases from each of the four alternative water allocation plans are presented in Table 7.
| Season and subarea | Current | Plan A | Plan B | Plan Ca | Plan D |
|---|---|---|---|---|---|
| Water volume (m3) per hectareb | Mean water increase (m3) per hectareb | ||||
| OIA-Maha | 10,783 (3.16) | 0 (3.16) | 461 (3.07) | 461 (3.11) | 2,353 (2.75) |
| OIA-Yala | 10,303 (3.60) | 567 (3.48) | 797 (3.43) | 797 (3.47) | 2,250 (3.16) |
| NIA-Maha | 9,425 (3.98) | 2,220 (3.48) | 1,969 (3.53) | 1,962 (3.57) | 2,058 (3. 51) |
| NIA-Yala | 8,667 (4.59) | 5,181 (3.48) | 4,841 (3.53) | 4,848 (3.57) | 1,892 (4.09) |
| Aggregate water (m3 × 106) | Aggregate water increase (m3 × 106) | ||||
| OIA-Maha | 40.9 | 0.0 | 1.8 | 1.8 | 8.9 |
| OIA-Yala | 39.1 | 2.2 | 3.0 | 3.0 | 8.5 |
| NIA-Maha | 41.8 | 9.9 | 8.7 | 8.7 | 9.1 |
| NIA-Yala | 38.5 | 23.0 | 21.5 | 21.5 | 8.4 |
| Maha season | 82.8 | 9.9 | 10.5 | 10.5 | 18.1 |
| Yala season | 77.6 | 25.1 | 24.5 | 24.5 | 16.9 |
| OIA | 80.1 | 2.2 | 4.8 | 4.8 | 17.5 |
| NIA | 80.3 | 32.8 | 30.2 | 30.2 | 17.5 |
| KOISP | 160.4 | 35.0 | 35.0 | 35.0 | 35.0 |
| At reservoirc | 229.1 | 50.0 | 50.0 | 50.0 | 50.0 |
| Yield (kg/ha) | Mean yield increase with additional water (kg/ha)d | ||||
| OIA-Maha | 7,157 | 0 | 98 | 175 (75) | 438 |
| OIA-Yala | 6,261 | 130 | 179 | 255 (74) | 469 |
| NIA-Maha | 6,696 | 501 | 449 | 533 (79) | 467 |
| NIA-Yala | 5,892 | 1,240 | 1,169 | 1,265 (76) | 501 |
Notes
- a All water volumes reported are for vegetative and maturity phases of rice. Total irrigated areas are 3,796 and 4,438 ha for OIA and NIA, respectively.
- b MVP of water is in parentheses (SLR/m3).
- c Conveyance efficiency of 0.7 was assumed in calculating water volumes at the reservoir.
- d Numbers in parentheses for Plan C are increments over Plan B due to additional fertilizer applied.
Under the current water allocation, mean water use per hectare shows notable differences between subareas and between seasons (left column, top panel). Per hectare water use in the highest water using subarea–season stratum (OIA-Maha) is a quarter higher than in the lowest water using stratum (NIA-Yala). However, annual total water used by both subareas is almost equal (middle panel) because there are more irrigated hectares in NIA.
When the economic criterion is used to allocate additional water (Plan A), OIA would receive just a little more than 6% of the additional water available. Further, it would not receive any additional water during the Maha season because the available water quantity is exhausted before reaching the current low MVP of farms in that stratum. In Plan B, OIA receives additional water during both seasons, but only to meet the minimum agronomic requirements on each farm. In Plan C with rice fertilized at Department of Agriculture recommended rates, the allocation to OIA is the same as in Plan B but there is minor redistribution in NIA between seasons. In both Plans B and C, the OIA receives about 14% of the additional water available. Under Plan D, the allocations of additional water are proportional by subarea and season to the current allocation, so each subarea receives approximately the same amount.
MVPs of water in each subarea and season are also reported in Table 7 (within parentheses in the top panel). When the mean water quantity increases, the MVP of water decreases because the marginal product decreases. MVPs of water are equated in Plan A for all subarea–season strata receiving additional water and in Plan B for both NIA seasons. The agronomic constraint provides sufficient additional water for OIA that the MVP in both seasons is less than for NIA. Because of the additional fertilizer applied in Plan C, the MVPs in all subareas and seasons increase over Plan B.
Mean current yields and predicted yield increases for each stratum are shown in the bottom panel of the table. Except when fertilizer is also increased (Plan C), highest incremental yields in NIA for both seasons occur with Plan A (for which the economic criterion is used). In all other plans, a part of the water is reallocated based on other criteria, and incremental yields for NIA are less.
The average physical and value productivities (APP and AVP) of water can be computed from the information presented in Table 7. The APPs range from 0.61 kg/m3 for OIA in the Yala season to 0.71 kg/m3 for NIA in the Maha season. These estimates are in the middle of the range of 0.2–1.2 kg/m3 reported by Bouman et al. (2007) based on agronomic trial data from China, India, Malaysia, and the Philippines. They are also within the range of 0.2–0.9 kg/m3 reported by Murray-Rust et al. (1999) for subsystems of the Sri Lanka GalOya Irrigation System. They are slightly higher than the range of global average water productivity estimates for rice of 0.15–0.60 kg/m3 and those for China and Southeast Asian countries of 0.4–0.6 kg/m3 reported by Rosegrant et al. (2002).
Using average prices for rice (see Table 3), the U.S. exchange rate (see Table 1) during the survey period, and the India average exchange rate during 2007 (2.689 SR/Indian rupee), our AVP estimates range from $0.09 to $0.11/m3 (3.7–4.4 Indian rupees/m3). These estimates are on the low end of the range of $0.10–$0.74/m3 reported by Hussain et al. (2007) for South Asia and Africa and a little lower than the range of 4.5–7.8 Indian rupees/m3 reported by Kumar et al. (2008) for the Western Punjab and Eastern Uttar Pradesh regions of India. Thus, although our OLS estimates of the production function exceed our panel data estimates, they provide physical and value productivity estimates that are well within the range of other relevant literature.
The predicted yield increases are used to compute predicted aggregate increases in net revenue from each plan. The predicted aggregate increases in net revenue and the percentage share of the increases are reported by subarea–season stratum, season, and subarea in Table 8.
| Aggregate increase in net revenue (SLR million) | Percentage share of increased net revenue | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Plan C | |||||||||
| Plan A | Plan B | From fertilizerb | Total | Plan D | Plan A | Plan B | Plan C | Plan D | |
| By season and subarea | |||||||||
| OIA-Maha | 0.0 | 6.2 | 4.0 (29) | 10.3 | 27.6 | 0 | 5 | 7 | 21 |
| OIA-Yala | 8.2 | 11.3 | 3.9 (31) | 15.3 | 29.5 | 6 | 8 | 10 | 23 |
| NIA-Maha | 37.3 | 33.3 | 4.8 (35) | 38.5 | 34.7 | 27 | 24 | 25 | 27 |
| NIA-Yala | 92.1 | 86.8 | 4.7 (36) | 92.6 | 37.3 | 67 | 63 | 58 | 29 |
| By season | |||||||||
| Maha | 8.2 | 17.5 | 7.8 | 25.5 | 57.1 | 6 | 29 | 32 | 48 |
| Yala | 129.4 | 120.2 | 9.5 | 131.4 | 72.0 | 94 | 71 | 68 | 52 |
| By area | |||||||||
| OIA | 37.3 | 39.5 | 8.8 | 48.8 | 62.3 | 6 | 13 | 17 | 44 |
| NIA | 100.3 | 98.1 | 8.6 | 108.1 | 66.8 | 94 | 87 | 83 | 56 |
| KOISP | 137.6 | 137.6 | 17.4 | 156.9 | 129.1 | 100 | 100 | 100 | 100 |
Notes
- a Net revenue estimates are based on mean yield increases reported in Table 7.
- b Numbers in parentheses are additional fertilizer applied (kg/ha) by following the recommendations of the Sri Lanka Department of Agriculture.
The distribution of increased net revenue among subareas and among seasons differs the most with Plan A. The share of increases in aggregate net revenue accruing to the NIA subarea and to the Yala season is also highest with Plan A.
Without increasing use of any input other than water, total annual increase in net revenue for the water system (KOISP row) is highest under both Plans A and B. A difference is evident only at the second decimal place. Net benefits are expected to increase an additional 14% by adding fertilizer in addition to water. Comparing Plans B and C, we find that nearly 9/10 of the increased net revenue in OIA accrues because of increased fertilizer use and one-tenth because of the higher MVP of water when fertilizer is increased. However, the magnitude of net revenue increases due to application of more fertilizer is higher in NIA for both seasons because initial yields are lower and incremental fertilizer quantities are higher. Increases in net revenue are somewhat more equally distributed among subareas and seasons in Plan C, and therefore, if implemented will contribute to a continuation of current income disparities between subareas.
Plan D (status quo) generates a lower increase in annual net revenue than any of the alternatives. Increases in net revenue are 7% higher under Plans A and B and 22% higher under Plan C than under Plan D, all of which demonstrate that the current water allocation criterion is suboptimal at the margin. Its distribution of additional water is also much more favorable to OIA and thus would contribute to a continuation of initial income disparities.
We report the distributional effects of additional water on household income for each plan in Table 9 using both the pooled OLS and individual season estimates of the production function. Distributional effects are noted by measuring the average additional household income for households grouped into five income quintiles prior to the intervention. Income group 1 represents the quintile of households with the lowest initial income.
| Plan A | Plan B | Plan C | Plan D | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Income quintile | Before | After | Increase | Percent increase | After | Increase | Percent increase | After | Increase | Percent increase | After | Increase | Percent increase |
| Based on pooled OLS production function | |||||||||||||
| 1 | 90,989 | 103,603 | 12,614 | 14 | 103,789 | 12,800 | 14 | 105,580 | 14,591 | 16 | 105,015 | 14,026 | 15 |
| 2 | 133,020 | 151,990 | 18,970 | 14 | 151,952 | 18,932 | 14 | 154,601 | 21,581 | 16 | 147,313 | 14,293 | 11 |
| 3 | 178,170 | 189,159 | 10,989 | 6 | 190,020 | 11,850 | 7 | 191,427 | 13,257 | 7 | 189,482 | 11,312 | 6 |
| 4 | 248,330 | 262,075 | 13,745 | 6 | 261,911 | 13,581 | 5 | 264,458 | 16,128 | 6 | 262,862 | 14,532 | 6 |
| 5 | 489,350 | 503,267 | 13,917 | 3 | 503,275 | 13,925 | 3 | 505,441 | 16,091 | 3 | 506,385 | 17,035 | 3 |
| Based on individual season production functions | |||||||||||||
| 1 | 90,989 | 104,651 | 13,662 | 15 | 103,845 | 12,856 | 14 | 105,705 | 14,716 | 16 | 102,191 | 11,202 | 12 |
| 2 | 133,020 | 148,556 | 15,536 | 12 | 147,410 | 14,390 | 11 | 149,290 | 16,270 | 12 | 146,221 | 13,201 | 10 |
| 3 | 178,170 | 194,767 | 16,597 | 9 | 194,316 | 16,146 | 9 | 196,135 | 17,965 | 10 | 193,435 | 15,265 | 9 |
| 4 | 248,330 | 263,036 | 14,706 | 6 | 262,328 | 13,998 | 6 | 265,116 | 16,786 | 7 | 266,449 | 18,119 | 7 |
| 5 | 489,350 | 506,793 | 17,443 | 4 | 507,290 | 17,940 | 4 | 509,865 | 20,515 | 4 | 509,726 | 20,376 | 4 |
Note
- a Income quintiles are based on ranking of household income before the intervention. Income quintile 1 includes the 20% of households with lowest initial income.
Under each of the intervention plans, the additional water will have considerably higher relative impact on households with lower incomes and thus is expected to have a positive impact in reducing income inequality. In fact, the order of increases by income groups is exactly the opposite of the ordering of initial income. This finding is robust both across plans and across production function estimators. Both production function estimators suggest that Plan C benefits the lowest income quintile the most and Plan D benefits it the least. With some ties, the same finding applies to the next lowest and the middle income quintiles. The highest income quintile is unaffected by plan selection. Consequently, not only would the status quo Plan D provide the smallest aggregate benefit from the additional water, it would also have least impact on reducing income inequality.
5. Conclusions
This article has focused on the economic effects of alternative allocation policies for distributing new water among existing farmers in the Kirindi Oya Irrigation and Settlement Project (KOISP) in Sri Lanka. We collected data from farmers using a recent recall method designed to increase the accuracy of water measurement over alternative viable methods in developing countries. We estimated a production function for rice, the main crop user of the irrigation water, and simulated the effects of alternative policies on aggregate household income and its distribution.
The estimated production functions supported the hypothesis that at the margin, rice yields increase with quantity of water applied. That same hypothesis was also supported for each of the inputs. We also found that the marginal product of each input was declining. As a consequence, we conclude that there exists a positive but declining relationship between input quantities applied to rice and net income from rice. The same conclusion applies to total household income.
The economic effects of an additional 50 MCM of water allocated to farmers in the KOISP were examined under alternative allocation policies. The plan that maximized total system-wide income by equalizing MVPs of water across seasons and production subareas receiving new water provided aggregate increases in household income 7% higher than the status quo (historical) allocation plan. It also distributed that additional income among households in a way that decreased initial income inequality more than continuing the current allocation plan. However, it provided only slightly larger aggregate benefits and income equality than an alternative plan that first ensured that each farm received sufficient water for minimum agronomic requirements.
If, in addition to the application of more water, fertilizer were applied at agronomically recommended levels, household income would increase by another 15% and result in an even greater reduction of income inequality. These findings of increased benefits of fertilizer application with additional water should be applicable to other irrigation systems in Sri Lanka as well.
In our study area, the greatest incremental benefits from additional water, with or without additional fertilizer, were gained by applying the water in the less developed subarea and in the drier season. Each of the alternative allocation plans is feasible but will introduce new challenges to KOISP managers compared to the historical allocation plan. It will require a higher level of managerial attention to store more water in the reservoir during the wetter season and change the allocation when releasing it to subareas during the drier season.
Acknowledgments
The authors gratefully acknowledge the significant contributions of Jonathan Yoder and the anonymous reviewers to the quality of this article. The research was supported by the PhD Fellowship Program of the International Water Management Institute, by the Washington Agricultural Research Center and by the USDA National Institute of Food and Agriculture, Hatch grant WPN000275.




