Economic crisis and determinants of solvency in the insurance sector: new evidence from Spain
Abstract
This paper analyses the factors that determine the solvency of insurance companies operating in Spain. The selected time span, from 2008 to 2015, encompasses a period of economic instability characterised by record low interest rates and low or even negative economic growth. Using a dynamic panel data model, we conclude that actual solvency margins are positively related to profitability, underwriting risk and a mutual-type organisation but inversely related to size, reinsurance use, longer-tailed business and life insurance specialisation. We also find that less concentrated markets and the context of an economic crisis decrease solvency margins.
1 Introduction
Given their crucial role in the financial system, insurers have received increasing attention from researchers and regulators since the financial crisis of 2008 (Dhaene et al., 2017). Similar to the banking system, the insurance industry mobilises savings and invests part of them in nonfinancial sectors of the economy, making it an important provider of the investments needed for economic growth. In fact, in 2016, European insurers generated total premium income of €1189 billion (31.1 percent of the global market share) with €10 112 billion invested in the economy, making this industry the largest institutional investor in this area (Insurance Europe, 2018b). Moreover, the insurance sector plays a relevant role in terms of financial stability by acting as a conduit for households and firms to transfer risks to entities that are better suited to handle them.
Traditionally, insurance companies have been regarded as posing potentially lower systemic risks than the banking sector because they are less exposed to liquidity risk, that the average maturity of insurer liabilities is longer than that of their assets makes insurance companies much less vulnerable to ‘runs’. In addition, insurers are not as strongly interconnected through the interbank market and payment systems as banks are (Trichet, 2005). However, from the perspective of financial stability, the increasing interactions among the insurance sector, financial markets and other financial intermediaries call into question the traditional approach that considers insurance an activity with low systemic risk. Billio et al. (2012) find that hedge funds, banks, broker/dealers and insurance companies have become closely interrelated, likely increasing the level of systemic risk in the finance and insurance industries through a complex and time-varying network of relationships.1
Insurer capitalisation is an important element to consider regarding the stability of the financial system. The European Union (EU) is aware of this element and has established a new regulation on solvency for insurance companies, known as Solvency II. This regulation has replaced 28 national regimes with a single set of risk-based capital requirements and advanced risk management principles.2 However, although adequate capital requirements are necessary to protect customers, excessive solvency margins could increase the costs of some products (e.g., guaranteed savings products) and may even restrict the ability of insurers to allocate capital to long-term investments (Insurance Europe, 2018a).3 As stated by Cummins et al. (1999), the accuracy of the solvency regulation system is essential not only to avoid insolvencies but also to reduce unnecessary regulatory costs on financially sound insurers.
This paper aims to contribute to the ongoing debate surrounding insurer solvency in Europe by analysing the factors (firm-specific and macro) that determine the actual solvency margin of insurance companies operating in Spain during 2008–2015. To conduct this analysis, we use a comprehensive dataset of 202 firms (1537 observations) that represents approximately 94 percent of the premiums in the Spanish insurance sector. Because social benefit institutions and reinsurance specialists have singular characteristics that may affect solvency, we limit our analysis to stock and mutual insurers. The selected timespan, from 2008 to 2015, encompasses a period of economic instability with a prolonged situation of record low interest rates and low or even negative economic growth.
We focus on Spain as an interesting case study: Spain is among the top ten European countries by asset volume and gross premiums written (EIOPA, 2017). Some additional background information is required to better understand the Spanish insurance sector. By the end of 2017, insurance penetration, i.e., the relationship between premiums and gross domestic product (GDP), was 5.45 percent. Total investment by insurance companies amounted to €292.064 billion, representing a 1.4 percent increase over 2016. The return on equity (ROE) in the industry maintained the upward trend initiated in 2015, with an ROE of 12.03 percent or 1.3 percentage points higher than in 2016. Likewise, profitability measured in terms of return on assets (ROA) showed a slight increase to 1.6 percent (MAPFRE Economic Research, 2018). The Spanish insurance industry is mainly governed by rules originated in the EU, particularly the Solvency II Directive, whereas supervision is carried out by the Directorate General of Insurance and Pension Funds (Dirección General de Seguros y Fondos de Pensiones) (DGSFP), an administrative body within the Ministry of Economy and Business.4,5
Our results show that actual solvency margins in Spain are directly and significantly related to profitability, underwriting risk and a mutual-type organisation. However, company size, the use of reinsurance, a longer-tailed business and life specialisation seem to reduce insurers’ capitalisation. We also find that less concentrated markets and the context of an economic crisis (with a declining GDP) decrease solvency margins. Portfolio risk and interest rates are found not to be significant in our model. Because the European Commission has expressed its intention to review the methods, assumptions and standard parameters used in Solvency II, those findings may have broad implications for supervisors concerned about benchmarking and validating this new regulatory framework. These implications are even stronger if we consider that approximately 90 percent of insurers operating in Spain had capital buffers of up to 50 percent higher than the minimum requirements, which brings to light the fact that regulators could have been requiring far less capital than demanded by the market under the former supervisory regime (i.e., Solvency I).
Our analysis complements the literature along different dimensions. First, there is little empirical evidence on the determinants of insurers’ solvency in the context of an economic crisis. Although the insurance sector has shown stronger resistance to the recent financial crisis than the banking sector, the volatility of the financial markets, a prolonged situation of record low interest rates and a scenario of low or even negative economic growth (with high unemployment rates) have had widespread effects in most countries, especially those in the euro area. Second, by using actual solvency margins (roughly defined as available capital divided by total assets) instead of solvency ratios (actual solvency margins divided by required solvency margins) as the main proxy of insurer solvency, our findings would not be affected by regulatory requirements.6 Finally, we use the system-generalised method of moments (system-GMM) estimator developed by Arellano and Bover (1995) and Blundell and Bond (1998) for dynamic panel data models. Only very few papers on the determinants of solvency in the insurance industry have used this new methodology that allows us to control for endogeneity and for unobserved heterogeneity (Rubio-Misas and Fernández-Moreno, 2017).7
This paper is structured as follows. Section 22 reviews the most significant studies and presents our research hypotheses. Section 2.13 describes the data and methodology employed in the empirical research. Section 2.24 presents and discusses the results obtained. Section 2.35 summarises the results and draws conclusions.
2 Theoretical background and hypotheses
Indicators of insurer solvency are mostly defined in terms of capitalisation: as previously mentioned, we use as a proxy for the insurer's solvency the actual solvency margin, which is calculated as available capital divided by total assets.8 Therefore, we adopt capital structure theories as a starting point to formulate most of our hypotheses. Two main theories may influence the capital structure of insurers.9 Trade-off theory states that the main benefit of holding a capital buffer is that it may help the insurer avoid the cost of financial distress when there are relevant losses in the portfolio, whereas the main advantage of using financial debt is a reduction in taxes.10 Moreover, financial debt may be pitted against technical provisions in the different trade-offs that define the capital structure of insurance companies (Dhaene et al., 2017). Reducing financial debt to increase provisions when keeping all else fixed has the benefit of creating more insurance business for the same investment in the securities portfolio. In addition, the extra provisions are usually tax deductible (Bradford and Logue, 1999). Jensen and Meckling (1976) introduce ‘agency costs’ as another potential source of costs and benefits to consider when firms are choosing the optimal capital structure. Insurers are subject to two main sources of agency costs: owner–policyholder and owner–manager conflicts of interest. Based on this, the optimal capital structure of an insurance company may depend on the dominant type of conflict, whereas lower capitalisation mitigates the owner–manager conflict and higher capitalisation reduces the owner–policyholder conflict (De Haan and Kakes, 2010). In contrast, the pecking order theory of financing (Myers and Majluf, 1984) states that information asymmetries between managers and investors make external financing costlier than internal financing. As a result, firms may prefer financing through internal funds and debt rather than issuing new equity.11 We should, however, consider some particular issues in insurance companies. First, insurers mainly invest in financial securities because they are not required to finance important amounts of inventories or accounting receivables; therefore, we might expect fewer financial deficits than in industrial firms, other things being equal (Dhaene et al., 2017). Second, because insurers are subject to asymmetric information in liabilities (Zhang et al., 2009), and financial debt is subordinated to policyholder claims, this debt may be considered risky by investors. Consequently, the pecking order theory in insurance companies also predicts little use of financial debt, making these firms highly dependent on internal funds.
Factors influencing insurer capitalisation can be classified into two main groups. The first group includes determinants specific to each insurance company, such as size, profitability, reinsurance use, risk profile of the asset portfolio, underwriting risk, long-tailed business, organisational form and specialisation. Most of these determinants are a result of decisions made by managers. The second group of determinants comprises factors relating insurers’ capital to the industry structure and to the macroeconomic environment, such as industry concentration, interest rates and economic growth.
2.1 Size
Sharpe and Stadnik (2007) find that financially distressed insurers are typically small in size. Because the average losses for a larger pool of policyholders may be more easily predictable, larger insurance firms may have lower default probabilities with the same amount of capital (De Haan and Kakes, 2010). Additionally, larger insurers may need less capital than smaller firms because they normally benefit from economies of scale and scope and have lower financing costs (Bouzouita and Young, 1998; Adams et al., 2003; Caporale et al., 2017). Previous studies by Cummins and Nini (2002), Carayannopoulos and Kelly (2004), De Haan and Kakes (2010) and Cheng and Weiss (2013), among others, find that size is negatively and significantly related to insurer capitalisation.
Consequently, we formulate the following hypothesis:
- H1 There is a negative relationship between size and actual solvency margin.
We use the natural logarithm of total assets to account for the effect of size on the insurer's actual solvency margin.
2.2 Profitability
The empirical literature on insurance firms concludes that higher profitability contributes to higher levels of capitalisation and lower probabilities of insolvency (Sharpe and Stadnik, 2007; Kleffner and Lee, 2009; Shim, 2010; Rauch and Wende, 2015; Caporale et al., 2017; among others). Shim (2010) finds that, consistent with the pecking order theory, profitability plays a significant role in determining an insurer's ability to increase capital (i.e., insurers seem to rely heavily on retained earnings due to costly external financing caused by asymmetric information). Rauch and Wende (2015) state that an insurer's profitability positively influences the company's equity and solvency because premium and investment income exceeds claims and other expenses. In the same vein, Caporale et al. (2017) report that highly profitable insurers are less likely to become insolvent because they manage expenses effectively and can set competitive premium rates.
Therefore, we test the following relationship:
- H2 There is a positive relationship between profitability and actual solvency margin.
We divide profits after tax by total assets to examine the influence of profitability on the margin.
2.3 Reinsurance
According to the renting capital hypothesis, reinsurance serves as a substitute for equity because the cost of renting capital from reinsurers may be lower than the cost of issuing extra equity (Shiu, 2011; Dhaene et al., 2017).12 That reinsurance allows insurers to transfer part of its risk to third parties results in more predictable future losses and, consequently, a reduction in its capital reserves (Caporale et al., 2017). Moreover, reinsurance enables primary insurers to have sufficient risk capacity for planning and pricing new business lines (Upreti and Adams, 2015). Nevertheless, although reinsurance is widely used by insurance firms to reduce capital requirements, it exposes them to counterparty risk (Caporale et al., 2017), potentially resulting in insurers with higher probabilities of default. Nevertheless, most of the empirical evidence shows an inverse relationship between the use of reinsurance and the insurer's capitalisation (Cummins and Nini, 2002; Carayannopoulos and Kelly, 2004; Shiu, 2011; Cheng and Weiss, 2013; Mankaï and Belgacem, 2016; among others).13
We formulate the following hypothesis to be tested:
- H3 There is a negative relationship between the use of reinsurance by the insurer and its actual solvency margin.
We use the ratio of reinsurance premiums paid to total premiums earned to analyse the effect of reinsurance on the solvency margin.
2.4 Risk profile of the asset portfolio
Most studies report a positive relationship between the risk of the asset portfolio and capitalisation for insurance companies (Cummins and Sommer, 1996; Baranoff and Sager, 2002; Cummins and Nini, 2002; Mankaï and Belgacem, 2016; Rauch and Wende, 2015; among others). Cheng and Weiss (2013) provide several reasons to explain this positive relationship. First, higher capital may help insurers prevent financial distress costs. Second, insurers will raise capital to offset policyholders’ awareness of insolvency when increasing risk taking. Third, agency costs also lead to a positive relationship between risk and capital if managers compensate for increases in risk by holding higher capital buffers.
We therefore derive the following hypothesis:
- H4 There is a positive relationship between portfolio risk and actual solvency margin.
We choose the share of equity securities in total assets to measure the effect of investment risk on insurer solvency.14
2.5 Underwriting risk
Underwriting risk captures the risk on the insurance portfolio (De Haan and Kakes, 2010), reflecting the amount and types of business that the insurer underwrites each year (Cheng and Weiss, 2013). Therefore, although asset risk mainly accounts for the risk of bond defaults and stock price fluctuations (i.e., the investment portfolio), underwriting risk refers to the risk that loss payments will be greater than the expected losses allowed for in the premiums charged to policyholders (Cummins and Sommer, 1996). Following a similar reasoning to the line applied in the asset risk hypothesis, we might again expect a positive relationship between underwriting risk and insurer capitalisation. Empirical literature corroborates this positive association (Cheng and Weiss, 2013; Hu and Yu, 2014; among others).
Consequently, we formulate the following testable hypothesis:
- H5 There is a positive relationship between underwriting risk and actual solvency margin.
Similar to De Haan and Kakes (2010), we proxy underwriting risk by the standard deviation over the sample period of the loss ratio, defined as incurred losses divided by premiums earned net of reinsurance.
2.6 Long-tailed business
Long-tail lines of insurance (i.e., with a higher time lag between the policy issuance and the payment of the claims) may have a negative effect on insurer solvency because they tend to generate less income from underwriting than shorter-tail lines (De Haan and Kakes, 2010). In addition, a longer-tailed business implies that managers control policyholder funds for longer periods, which gives these managers higher chances of squandering these funds (Carayannopoulos and Kelly, 2004). Consequently, owner–manager conflicts may be more severe in these firms, resulting in higher agency costs. Owners could mitigate this type of conflict by reducing capital and increasing leverage (Cummins and Nini, 2002).
Therefore, we hypothesise a negative effect of long-tailed business on solvency.
- H6 There is a negative relationship between long-tailed businesses and actual solvency margins.
Following Cummins and Nini (2002), we use the ratio of technical provisions (i.e., loss reserves) over incurred losses to test the effect of the time lag between the issuance and payment of claims. Higher ratios indicate a longer-tailed business.
2.7 Organisational form
Ownership structure is another possible determinant of an insurer's solvency margins. Based on agency costs, we might expect that mutual insurance companies will hold less capital than stock companies because mutual firms control owner–policyholder conflicts (Carayannopoulos and Kelly, 2004).15 However, mutual insurers are likely to find it more difficult to raise capital; therefore, pecking order theory predicts that they will have a stronger tendency to accumulate capital (De Haan and Kakes, 2010).16 The empirical literature mostly finds evidence that the existence of a mutual organisation contributes to higher capital ratios and, thus, higher actual solvency margins (Cummins and Sommer, 1996; Cummins and Nini, 2002; Harrington and Niehaus, 2002; De Haan and Kakes, 2010; Cheng and Weiss, 2013; Rauch and Wende, 2015).
Considering this, we test the following hypothesis:
- H7 Mutual insurers have higher actual solvency margins than stock companies.
We account for the ownership structure of the firm using a dummy variable that takes the value of 1 for mutual insurers and 0 for stock companies.
2.8 Specialisation
Investment activities, operations and liabilities’ maturities notably differ between life and non-life segments of the insurance industry (Rubio-Misas and Fernández-Moreno, 2017). Although life insurance companies function as financial intermediaries, non-life insurers operate as ‘risk takers’ (Chen and Wong, 2004). Non-life insurers are considered riskier than life insurance companies, not only because of the uncertainty of claim payments but also on account of the difficulty in predicting threats (Gründl et al., 2016).
Since we might expect that insurers involved in less risky lines of business hold less capital, we establish the following hypothesis:
- H8 Life specialised insurers have lower actual solvency margins than non-life specialised insurers.
We test the effect of the line of business on the actual solvency margin using a dummy variable that takes the value of 1 if the written premiums of the company during that year are 50 percent or higher in the life insurance sector and 0 otherwise.
2.9 Industry concentration
Most of the literature analysing the relationship between concentration and financial stability has focused on the banking industry, reporting two contrary hypotheses (Baselga-Pascual et al., 2015). The ‘concentration-stability’ view states that a concentrated industry with few large firms is more stable because large firms are likely to earn more profits due to market power. These profitable firms have the ability to increase capital, thus increasing their solvency. However, the ‘concentration-fragility’ view asserts that a more concentrated industry is more vulnerable to financial fragility because the ‘too-big-to-fail’ protective mechanism may lead to excessive risk-taking by managers, thus negatively affecting the solvency of companies. Only a few recent studies analyse this relationship in the insurance sector, also with contradictory results. Although Cummins et al. (2017) report a positive relationship between concentration and soundness in European life insurance firms, Altuntas and Rauch (2017) and Shim (2017) conclude that higher market concentration is associated with lower financial stability in the insurance sector, providing empirical support for the ‘concentration-fragility view’.
Thus, we propose the following contradictory hypotheses:17
- H9a There is a positive relationship between industry concentration and actual solvency margin.
- H9b There is a negative relationship between industry concentration and actual solvency margin.
We measure industry concentration using a Herfindahl–Hirschman index calculated as the sum of the squares of all insurers’ market shares in terms of total assets (in percentage). An index greater than 1800 suggests a highly concentrated market whereas an index lower than 1000 indicates an unconcentrated market.
2.10 Interest rates
The extant literature on the impact of interest rates on insurer solvency is also ambiguous (Cheng and Weiss, 2012; Shim, 2017; among others). These contradictory findings could be due to two opposing effects of interest rates. Higher interest rates increase the yields of insurer account portfolios and thus may have a positive impact on its solvency but also may negatively affect insurer capitalisation due to the decreasing market value of fixed-income assets (Rubio-Misas and Fernández-Moreno, 2017).
Again, we formulate two testable hypotheses:
- H10a There is a positive relationship between interest rates and actual solvency margin.
- H10b There is a negative relationship between interest rates and actual solvency margin.
We use the interest rate of the main refinancing operations (MRO) of the European Central Bank (ECB) as our proxy for interest rates. This rate is one of the main instruments of monetary policy in the euro area.
2.11 Economic growth
Previous studies on banking solvency have demonstrated the positive influence of economic growth on capital. Banks use an expansionary macroeconomic environment to accumulate capital (Laeven and Majnoni, 2003; Schaeck and Cihák, 2012). Moreover, defaults on bank loans during recessions increase and generate higher losses that are charged against bank capital (Brewer et al., 2008). Nevertheless, some of the banking literature also concludes that certain institutions may behave in an excessively lax manner during upturns because they do not properly consider the cyclical nature of output and, therefore, tend to underestimate risks. (Ayuso et al. (2004) find that capital buffers were countercyclical in Spain during 1986–2000.) Although the literature on the effect of economic growth on insurer solvency is still scarce, it seems obvious that general economic conditions are also likely to affect insurer capitalisation because raising capital may be easier in a relatively strong economy (Cummins and Sommer, 1996).
Consequently, we formulate the following hypothesis:
- H11 There is a positive relationship between economic growth and the actual solvency margin.
We use the growth rate of the Spanish GDP to examine this relationship.
Table 1 summarises the hypotheses and variables considered in the current study. Data are mainly obtained from the database maintained by the Spanish regulatory authority, the DGSFP.18
| Hypotheses and expected signs | Variables | Definition | Data source |
|---|---|---|---|
| Actual solvency margin | Solvency margin (according to Spanish legislation) divided by total assets | Authors’ calculation using DGSFP data | |
| H1 (−) | Size | Natural log of total assets | Authors’ calculation using DGSFP data |
| H2 (+) | Profitability | Profits after tax divided by total assets | Authors’ calculation using DGSFP data |
| H3 (−) | Reinsurance | Reinsurance premiums paid divided by total premiums earned | Authors’ calculation using DGSFP data |
| H4 (+) | Portfolio risk | Equity securities in the asset portfolio divided by total assets | Authors’ calculation using DGSFP data |
| H5 (+) | Underwriting risk | Standard deviation over sample period of loss ratio, defined as incurred losses divided by premiums earned net of reinsurance | Authors’ calculation using DGSFP data |
| H6 (−) | Long-tailed business | Technical provisions (loss reserves) divided by incurred losses | Authors’ calculation using DGSFP data |
| H7 (+) | Mutual | Dummy variable that takes the value of 1 for mutual companies and 0 otherwise | Authors’ calculation using DGSFP data |
| H8 (−) | Life insurance | Dummy variable that takes value of 1 if the written premiums of the company in that year are 50 percent or higher in the life insurance sector and 0 otherwise | Authors’ calculation using DGSFP data |
| H9a (+), H9b (−) | Industry concentration | Herfindahl–Hirschman index calculated as the sum of the squares of all insurance companies’ market shares in terms of premiums written (in percentage) | Authors’ calculation using DGSFP data |
| H10a (+), H10b (−) | Interest | Interest rate on the MRO of the ECB | ECB |
| H11 (+) | Economic growth | Annual real GDP growth rate | Eurostat |
3 Empirical tests
3.1 Sample selection
Our sample consists of 202 insurance companies operating in Spain during 2008–2015. As previously stated, we limit our analysis to stock and mutual insurers because social benefit institutions and reinsurance specialists have singular characteristics that may affect solvency. We only chose those companies in the DGSFP database that have information for all of the variables analysed over at least five consecutive years during the period considered. This is a required condition for the implementation of the system-GMM estimator (to test for the absence of second-order serial correlation). We use unconsolidated financial statements, thereby reducing the possibility of introducing aggregation bias in the results. Merged insurers are also considered separate firms before the merger and a single company afterwards. Finally, to ensure that the analysis is not affected by potential measurement errors and misreporting, we remove from the sample those firms that present abnormal ratios or extreme values. After completing this filtering, we obtain a final dataset consisting of an unbalanced panel with 1537 observations (see Table 2).
| Year | Mutual insurers | Stock insurers | Total |
|---|---|---|---|
| 2008 | 29 | 159 | 188 |
| 2009 | 29 | 163 | 192 |
| 2010 | 30 | 168 | 198 |
| 2011 | 30 | 172 | 202 |
| 2012 | 30 | 172 | 202 |
| 2013 | 30 | 166 | 196 |
| 2014 | 29 | 158 | 187 |
| 2015 | 29 | 143 | 172 |
| Total | 236 | 1301 | 1537 |
3.2 Methodology
The firm-specific factors that influence insurer solvency may be endogenous. For instance, insurers with a higher capital ratio could have incentives to invest more in shares (De Haan and Kakes, 2010). In the same vein, the insurer's current capital structure may affect the utilisation of reinsurance (Shiu, 2011). Furthermore, not all the factors that may influence solvency margins are easy to measure or identify in an equation (e.g., managerial ability). If the influence of the so-called unobserved heterogeneity is not considered, one could observe correlations between some of the coefficients of the explanatory variables and the error terms that bias these coefficients. Finally, the persistence of capital ratios has been previously documented in the literature (Rubio-Misas and Fernández-Moreno, 2017).
To address all these concerns, we use the system-GMM estimator developed by Arellano and Bover (1995) and Blundell and Bond (1998) for dynamic panel data models. As proposed by Windmeijer (2005), we employ the two-step estimation procedure with finite-sample corrected standard errors, which provides less biased coefficient estimates and more accurate standard errors. We treat insurer characteristics (except their organisational form) as endogenous variables by using suitable instruments for both the equation in levels and the equation in differences. Industry concentration and macroeconomic variables are considered as strictly exogenous. We verify the validity of the instruments by using the Hansen J-test of overidentifying restrictions.
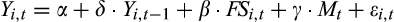 (1)
(1)4 Results
4.1 Determinants of actual solvency margins in Spain
Table 3 sets out an initial outline of the Spanish insurance industry from 2008 to 2015. The actual solvency margin decreased by 8 percent from 2008 to 2013, when it reached a minimum value. Although the solvency margin increased from then up to 2015, probably caused by the start of the economic recovery in Spain and/or the necessary adjustments before the entry into force of Solvency II in 2016, it did not recuperate its value from 2008. Nevertheless, the mean value of the actual solvency margin for the full period is in line with that reported by De Haan and Kakes (2010), who examined the Dutch insurance industry in a pre-crisis period (1995–2005). Mean size values decreased steadily during the sample timespan. Insurers’ profitability remained mostly unchanged, with slight signs of improvement following 2012. The use of reinsurance was stable, although with a mean value of only 11.5 percent during the period analysed. Competitive markets and low investment returns have forced insurers to retain more risk on their balance sheets as they became increasingly price-sensitive and developed their risk management capabilities over time (EIOPA, 2016). Portfolio risk accounted for less than 7 percent and increased in the last 3 years, especially in 2014 and 2015. Although the Spanish insurance sector's investment portfolio is mostly made up of fixed-income investments, the decline in interest rates may be pushing insurers to invest in riskier assets in search of higher returns. Moreover, the transition to the Solvency II regulatory framework might have been driving this reallocation of investments. Underwriting risk mean values are also similar to those found in other European countries (De Haan and Kakes, 2010). In contrast, technical provisions are approximately three times the amount of the incurred losses, with the time lag between issuance and payment of claims remaining stable. The dummy variables show that ~15 percent of the sample are mutual insurers (85 percent stock companies) and ~30 percent of the sample observations correspond to life-specialised insurers (70 percent non-life-specialised companies). Regarding industry and macroeconomic variables, Table 3 reports an increase in the concentration of the Spanish insurance sector according to the evolution of company size over the sample period. Finally, macroeconomic variables show a deterioration of the economic situation in Spain after the 2007–2008 global financial crisis, with negative economic growth and a low interest rate environment.
| Actual solvency margin | Firm-specific variables | Industry and macroeconomic variables | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size | Profitability | Reinsurance | Portfolio risk | Underwriting risk | Long-tailed business | Mutual | Life insurance | Industry concentration | Interest | Economic growth | ||
| 2008 | ||||||||||||
| Mean | 0.409 | 18.608 | 0.023 | 0.116 | 0.056 | 0.873 | 3.036 | 0.154 | 0.282 | 291.656 | 0.025 | 0.011 |
| SD | (0.433) | (2.337) | (0.058) | (0.186) | (0.101) | (0.553) | (5.823) | (0.362) | (0.451) | |||
| 2009 | ||||||||||||
| Mean | 0.406 | 18.660 | 0.023 | 0.119 | 0.066 | 0.838 | 2.877 | 0.151 | 0.292 | 272.936 | 0.010 | -0.036 |
| SD | (0.403) | (2.328) | (0.050) | (0.194) | (0.123) | (0.545) | (2.660) | (0.359) | (0.456) | |||
| 2010 | ||||||||||||
| Mean | 0.395 | 18.670 | 0.021 | 0.116 | 0.054 | 0.795 | 2.890 | 0.152 | 0.293 | 271.408 | 0.010 | 0.000 |
| SD | (0.374) | (2.295) | (0.057) | (0.194) | (0.092) | (0.466) | (2.899) | (0.359) | (0.456) | |||
| 2011 | ||||||||||||
| Mean | 0.384 | 18.713 | 0.023 | 0.110 | 0.047 | 0.802 | 2.970 | 0.149 | 0.297 | 296.040 | 0.010 | -0.010 |
| SD | (0.341) | (2.270) | (0.068) | (0.184) | (0.076) | (0.613) | (3.141) | (0.356) | (0.458) | |||
| 2012 | ||||||||||||
| Mean | 0.387 | 18.764 | 0.023 | 0.103 | 0.053 | 0.883 | 2.935 | 0.149 | 0.297 | 313.130 | 0.008 | -0.029 |
| SD | (0.327) | (2.265) | (0.064) | (0.176) | (0.088) | (0.804) | (2.970) | (0.356) | (0.458) | |||
| 2013 | ||||||||||||
| Mean | 0.376 | 18.845 | 0.026 | 0.114 | 0.067 | 0.964 | 3.056 | 0.153 | 0.301 | 329.115 | 0.003 | -0.017 |
| SD | (0.292) | (2.250) | (0.052) | (0.204) | (0.109) | (0.869) | (3.037) | (0.361) | (0.460) | |||
| 2014 | ||||||||||||
| Mean | 0.383 | 18.917 | 0.027 | 0.123 | 0.090 | 1.089 | 3.061 | 0.155 | 0.294 | 330.835 | 0.001 | 0.014 |
| SD | (0.291) | (2.277) | (0.040) | (0.217) | (0.143) | (1.953) | (2.845) | (0.363) | (0.457) | |||
| 2015 | ||||||||||||
| Mean | 0.390 | 19.013 | 0.027 | 0.118 | 0.097 | 0.952 | 3.214 | 0.169 | 0.279 | 422.944 | 0.001 | 0.034 |
| SD | (0.288) | (2.281) | (0.044) | (0.194) | (0.146) | (0.874) | (2.978) | (0.375) | (0.450) | |||
| 2008–2015 | ||||||||||||
| Mean | 0.391 | 18.770 | 0.024 | 0.115 | 0.066 | 0.897 | 3.387 | 0.154 | 0.292 | 314.343 | 0.008 | -0.005 |
| SD | (0.347) | (2.286) | (0.055) | (0.193) | (0.112) | (0.942) | (3.091) | (0.361) | (0.455) | (44.055) | (0.007) | (0.022) |
| Median | 0.308 | 18.620 | 0.020 | 0.033 | 0.023 | 0.754 | 2.110 | 0.000 | 0.000 | 296.040 | 0.010 | -0.010 |
| No. of obs. | 1537 | 1537 | 1537 | 1537 | 1537 | 1537 | 1537 | 1537 | 1537 | 1537 | 1537 | 1537 |
- This table reports the main descriptive statistics for the variables used in the study during the period analysed (2008–2015) and the evolution of the mean and standard deviation (SD) values (in parentheses) from 2008 to 2015. The sample comprises 202 insurance companies (1537 observations). See Table 1 for a description of the variables.
Table 4 reports the results of the empirical estimation of Equation 1) using the system-GMM estimator proposed by Arellano and Bover (1995) and Blundell and Bond (1998). The dynamic character of the model specification is confirmed by the high levels of significance of the lagged dependent variables. The higher values of δ indicate strong persistence, i.e., that the adjustment of the actual solvency margin is very slow.
| Variables | (1) | (2) |
|---|---|---|
| Actual solvency margin | Actual solvency margin | |
| Lagged dependent | 0.802*** | 0.812*** |
| (0.039) | (0.038) | |
| Size | −0.037*** | −0.035*** |
| (0.013) | (0.013) | |
| Profitability | 0.862*** | 0.908*** |
| (0.204) | (0.203) | |
| Reinsurance | −0.129* | −0.129* |
| (0.077) | (0.077) | |
| Portfolio risk | −0.033 | −0.030 |
| (0.070) | (0.077) | |
| Underwriting risk | 0.038*** | 0.038*** |
| (0.011) | (0.010) | |
| Long-tailed business | −0.000** | −0.000** |
| (0.000) | (0.000) | |
| Mutual | 0.065** | 0.055** |
| (0.027) | (0.027) | |
| Life insurance | −0.290*** | −0.277*** |
| (0.081) | (0.081) | |
| Industry concentration | 0.001*** | 0.000*** |
| (0.000) | (0.000) | |
| Interest | 1.384 | |
| (1.931) | ||
| Economic growth | 1.369*** | |
| (0.365) | ||
| Constant | 0.263 | 0.279 |
| (0.214) | (0.208) | |
| Year dummies | No | Yes |
| z 1 | 178.28 (10, 201) | 151.39 (8, 201) |
| z 2 | 9.11 (2, 201) | 6.00 (7, 201) |
| m 1 | −4.90 | −4.85 |
| m 2 | −0.57 | −0.61 |
| Hansen | 190.42 (206) | 193.65 (209) |
| No. of obs. | 1537 | 1537 |
| No. of firms | 202 | 202 |
- This table presents the determinants of the actual solvency margin in the Spanish insurance sector during the period 2008–2015 using the system-GMM estimator developed by Arellano and Bover (1995) and Blundell and Bond (1998). See Table 1 for a description of the variables. The dependent variable is included in logarithmic form. The model in column (2) includes year dummies instead of macroeconomic variables. Except for Mutual, Industry concentration, Interest, Economic growth and Year dummies, all variables are considered endogenous in our model. We report heteroskedasticity-consistent asymptotic standard errors in parentheses, and significance levels are indicated as follows: ***significance at the 1 percent level; **significance at the 5 percent level; and *significance at the 10 percent level. z1 and z2 are Wald tests of the joint significance of the reported coefficients for the non-dummy and the dummy explanatory variables, respectively, asymptotically distributed as F under the null hypothesis of no significance, with degrees of freedom in parentheses. mi is a serial correlation test of order i using residuals in first differences, asymptotically distributed as N(0,1) under the null hypothesis of no serial correlation. Hansen is a test of the overidentifying restrictions, asymptotically distributed as χ2 under the null hypothesis of no correlation between the instruments and the error term, with degrees of freedom in parentheses.
We validate our first hypothesis (H1), in which we anticipated a positive relationship between the insurer's size and its actual solvency margin based on the literature, and found that larger insurance firms require relatively less capital due to more predictable losses and because they benefit from economies of scale and scope as well as lower financing costs (Bouzouita and Young, 1998; Adams et al., 2003; De Haan and Kakes, 2010; Caporale et al., 2017). According to previous studies (Shim, 2010), a positive relationship between profitability and capitalisation may be expected, consistent with pecking order theory. Our results corroborate this hypothesis (H2): the higher the profitability, the higher the capitalisation. This finding indicates that insurers seem to rely on retained earnings due to costly external financing caused by asymmetric information. We also report that greater use of reinsurance may negatively affect insurers’ capitalisation, i.e., higher levels of reinsurance result in lower actual solvency margins (H3). By transferring part of their risk to third parties, reinsurance allows primary insurers to reduce their capital reserves, acting thus as contingent capital. Reinsurance use also mitigates solvency risk and enables companies to increase their capacity to underwrite new businesses (Mankaï and Belgacem, 2016). Portfolio risk is statistically insignificant in both specifications (H4). However, we find a positive relationship between underwriting risk and actual solvency margins, supported by the high levels of significance for the standard deviation of the loss ratio in the equation. This result confirms our hypothesis that insurers facing higher risk in their insurance portfolio tend to be relatively more capitalised (H5), a statement broadly agreed on in the literature (Cheng and Weiss, 2013). Similarly, a longer time lag between policy issuance and claims payment is shown to reduce actual solvency margins (H6). As previously stated, long-tail lines of insurance may have a negative effect on insurer solvency because they tend to generate less income from underwriting than shorter-tail lines (De Haan and Kakes, 2010). Moreover, based on agency costs, long-tailed businesses may be more levered to discourage managers from taking actions that are contrary to the interests of policyholders (Cummins and Nini, 2002). Mutual insurers appear to be more capitalised compared with stock companies (H7), in agreement with other authors (Cheng and Weiss, 2013). This finding may be explained in accordance with the pecking order theory, which predicts that mutual insurers are likely to find it more difficult to raise capital and, therefore, have a stronger tendency to accumulate capital. The insurer's specialisation is another possible determinant of solvency margins (H8). As we expected, life-specialised insurers would hold less capital than non-life-specialised insurance companies because the latter are considered riskier given the uncertainty of claim payments and the difficulty of predicting threats (Gründl et al., 2016).
Industry concentration has a positive relationship with solvency, corroborating H9a, which states that a more concentrated sector is associated with higher insurer capitalisation. Concentrated markets may enhance profits due to market power, thus increasing actual solvency margins. This finding coincides with the recent empirical evidence provided by Cummins et al. (2017), who report higher financial soundness of European life insurance firms in more concentrated markets. Among the macroeconomic variables, interest rates are found not to be significant in our model (H10). Thus, the low interest rate environment in Spain during the sample period might not have affected the capitalisation of the insurance sector. However, we find that actual solvency margins are positively related to economic growth (H11), exhibiting a clear cyclical behaviour. During recessions, lower profits are charged against capital. Moreover, raising capital may be more difficult in a relatively weak economy (Cummins and Sommer, 1996).
4.2 Robustness checks
We subject our findings to a number of robustness tests. First, following Altuntas et al. (2015) and Rubio-Misas and Fernández-Moreno (2017), among others, all quantitative firm-specific variables are winsorised at the 1 percent and 99 percent level to minimise the influence of potential outliers. As expected, the results do not differ from those previously obtained.20
Second, in Table 5, we re-estimate our equation by changing some of the variables used as regressors. The model in column (1) includes the square of the logarithm of total assets to address a potential nonlinear relationship between size and solvency. Both linear and quadratic terms significantly enter the regression, which suggests an exponential relationship between insurer size and capitalisation. The model in column (2) considers ROE instead of ROA as our profitability measure. Both sign and statistical significance are not affected, corroborating a positive relationship between profitability and actual solvency margin. We also consider the fixed-income investments to total assets ratio as the portfolio risk measure (model in column (3)), although, as previously reported for the equity securities to total assets ratio, this variable is not found to be significant. Finally, because unemployment has been recognised as an important factor in the recent economic crisis in Spain, in the model in column (4), we replace the GDP growth rate with the unemployment rate as a proxy for economic growth. As expected, higher unemployment rates imply lower solvency margins, thus confirming a cyclical behaviour of the insurance industry.
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Actual solvency margin | Actual solvency margin | Actual solvency margin | Actual solvency margin | |
| Lagged dependent | 0.778*** | 0.812*** | 0.803*** | 0.798*** |
| (0.038) | (0.037) | (0.039) | (0.039) | |
| Size | −0.318** | −0.041*** | −0.031*** | −0.037*** |
| (0.138) | (0.013) | (0.013) | (0.013) | |
| Size 2 | 0.007** | |||
| (0.004) | ||||
| Profitability | 0.817*** | 0.221*** | 0.923*** | 0.911*** |
| (0.192) | (0.084) | (0.212) | (0.219) | |
| Reinsurance | −0.141* | −0.155** | −0.120* | −0.135* |
| (0.079) | (0.078) | (0.071) | (0.080) | |
| Portfolio risk | −0.003 | −0.031 | 0.149 | −0.021 |
| (0.069) | (0.076) | (0.093) | (0.077) | |
| Underwriting risk | 0.039*** | 0.040*** | 0.037*** | 0.039*** |
| (0.011) | (0.012) | (0.010) | (0.011) | |
| Long-tailed business | −0.000** | −0.000** | −0.000** | −0.000* |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| Mutual | 0.071** | 0.059** | 0.059** | 0.067** |
| (0.034) | (0.028) | (0.027) | (0.028) | |
| Life insurance | −0.304*** | −0.308*** | −0.271*** | −0.296*** |
| (0.076) | (0.077) | (0.082) | (0.082) | |
| Industry concentration | 0.001*** | 0.001*** | 0.001*** | 0.001** |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| Interest | 1.608 | 1.848 | 1.419 | 1.454 |
| (1.970) | (1.957) | (1.880) | (2.367) | |
| Economic growth | 1.393*** | 1.415*** | 1.419*** | −0.411** |
| (0.348) | (0.355) | (0.358) | (0.203) | |
| Constant | 2.822** | 0.346 | 0.144 | 0.255 |
| (1.301) | (0.224) | (0.204) | (0.210) | |
| Year dummies | No | No | No | No |
| z 1 | 175.29 (11, 201) | 190.90 (10, 201) | 160.35 (10, 201) | 165.15 (10, 201) |
| z 2 | 10.53 (2, 201) | 9.59 (2, 201) | 7.36 (2, 201) | 9.08 (2, 201) |
| m 1 | −4.90 | −4.90 | −4.90 | −4.85 |
| m 2 | −0.60 | −0.58 | −0.51 | −0.79 |
| Hansen | 196.06 (233) | 192.12 (206) | 197.23 (206) | 192.92 (206) |
| No. of obs. | 1537 | 1537 | 1537 | 1537 |
| No. of firms | 202 | 202 | 202 | 202 |
- This table presents the results for our baseline equation after changing some of the explanatory variables. The model in column (1) includes Size2 (the square of Size). The model in column (2) considers ROE in place of ROA as a proxy for Profitability. The model in column (3) considers fixed-income investments divided by total assets in place of the equity securities to total assets ratio as a proxy for Portfolio risk. The model in column (4) considers the unemployment rate in place of the GDP growth rate as a proxy for Economic growth. Regressions use the system-GMM estimator developed by Arellano and Bover (1995) and Blundell and Bond (1998). See Table 1 for a description of the variables. The dependent variable is included in logarithmic form. Except for Mutual, Industry concentration, Interest and Economic growth, all variables are considered endogenous in our model. We report heteroskedasticity-consistent asymptotic standard errors in parentheses, and significance levels are indicated as follows: ***significance at the 1 percent level; **significance at the 5 percent level; and *significance at the 10 percent level. z1 and z2 are Wald tests of the joint significance of the reported coefficients for the non-dummy and the dummy explanatory variables, respectively, asymptotically distributed as F under the null hypothesis of no significance, with degrees of freedom in parentheses. mi is a serial correlation test of order i using residuals in first differences, asymptotically distributed as N(0,1) under the null hypothesis of no serial correlation. Hansen is a test of the overidentifying restrictions, asymptotically distributed as χ2 under the null hypothesis of no correlation between the instruments and the error term, with degrees of freedom in parentheses.
Third, because factors that influence insurer solvency may be affected by their specialisation (life versus non-life), we now remove from the baseline sample insurers who specialise in the life segment.21 Table 6 shows that the results obtained when the sample includes only non-life-specialised insurers do not differ substantially from those obtained previously for the entire sample.
| Variables | (1) | (2) |
|---|---|---|
| Actual solvency margin | Actual solvency margin | |
| Lagged dependent | 0.793*** | 0.796*** |
| (0.043) | (0.042) | |
| Size | −0.043*** | −0.044*** |
| (0.013) | (0.013) | |
| Profitability | 0.409*** | 0.420*** |
| (0.151) | (0.146) | |
| Reinsurance | −0.240*** | −0.225*** |
| (0.091) | (0.085) | |
| Portfolio risk | −0.040 | −0.052 |
| (0.065) | (0.063) | |
| Underwriting risk | 0.073** | 0.066** |
| (0.029) | (0.030) | |
| Long-tailed business | −0.000** | −0.000* |
| (0.000) | (0.000) | |
| Mutual | 0.095*** | 0.091*** |
| (0.031) | (0.031) | |
| Industry concentration | 0.000* | 0.001*** |
| (0.000) | (0.000) | |
| Interest | −3.010 | |
| (1.914) | ||
| Economic growth | 0.660* | |
| (0.369) | ||
| Constant | 0.560 | 0.490 |
| (0.211) | (0.199) | |
| Year dummies | No | Yes |
| z 1 | 578.60 (9, 144) | 396.70 (8, 144) |
| z 2 | 9.05 (1, 144) | 2.84 (6, 144) |
| m 1 | −4.26 | −4.28 |
| m 2 | 0.27 | 0.33 |
| Hansen | 139.00 (188) | 137.02 (191) |
| No. of obs. | 1088 | 1088 |
| No. of firms | 145 | 145 |
- This table presents the determinants of the actual solvency margin for non-life specialised insurers operating in Spain during 2008–2015. We consider that an insurer is specialised in the non-life segment when the written premiums of the company are higher than 50 percent in this sector for that year. See Table 1 for a description of the variables. The dependent variable is included in logarithmic form. We use the system-GMM estimator developed by Arellano and Bover (1995) and Blundell and Bond (1998). The model in column (2) includes year dummies instead of macroeconomic variables. Except for Mutual, Industry concentration, Interest, Economic growth and Year dummies, all variables are considered endogenous in our model. We report heteroskedasticity-consistent asymptotic standard errors in parentheses, and significance levels are indicated as follows: ***significance at the 1 percent level; **significance at the 5 percent level; and *significance at the 10 percent level. z1 and z2 are Wald tests of the joint significance of the reported coefficients for the non-dummy and the dummy explanatory variables, respectively, asymptotically distributed as F under the null hypothesis of no significance, with degrees of freedom in parentheses. mi is a serial correlation test of order i using residuals in first differences, asymptotically distributed as N(0,1) under the null hypothesis of no serial correlation. Hansen is a test of the overidentifying restrictions, asymptotically distributed as χ2 under the null hypothesis of no correlation between the instruments and the error term, with degrees of freedom in parentheses.
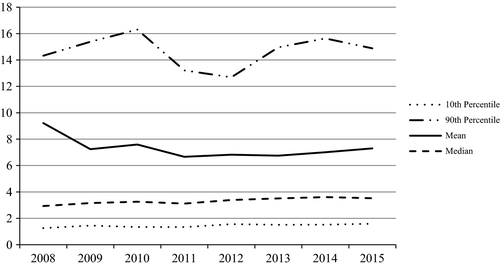
Finally, we consider an alternative measure of solvency. Table 7 reports the results of our empirical estimation when the solvency ratio and not the actual solvency margin is used as the dependent variable. Although different measures of capitalisation are often used in the literature as indicators of the financial soundness of the company (Baranoff and Sager, 2002; Cummins and Nini, 2002; Carayannopoulos and Kelly, 2004; Shim, 2010; Mankaï and Belgacem, 2016; among others), some studies recently use the solvency ratio as an alternative measure of insurer financial strength (Berry-Stölze et al., 2010; Rauch and Wende, 2015; Rubio-Misas and Fernández-Moreno, 2017). The solvency ratio, defined as the ratio of the actual solvency margin to the required solvency margin, must be equal to or >1.22 Therefore, this measure compares the insurer's capital reserves with its regulatory capital requirements, allowing for the identification of potentially weak capital positions that could require intervention by supervisors (Rubio-Misas and Fernández-Moreno, 2017). Solvency ratios are usually substantially higher than 1 because insurers maintain large capital buffers to reduce their risk of insolvency.23 Figure 1 shows the distribution of the solvency ratio for insurers operating in Spain from 2008 to 2015. The median takes values slightly higher than 3, indicating that approximately 50 percent of the insurers have more than three times the amount of capital required for the period analysed. Moreover, the 10th percentile line shows that ~90 percent of companies have capital buffers up to 50 percent higher than the minimum requirements. These ratios, which are in line with those found in other European countries (De Haan and Kakes (2010) for Dutch companies and Rauch and Wende (2015) for the German insurance sector), bring to light the fact that supervisors could have been requiring far less capital than demanded by some stakeholders (ratings agencies, investment analysts, shareholders, policyholders and others). Table 7 shows that the results obtained for the solvency ratio do not differ substantially from those obtained previously for the actual solvency margin; most of the explanatory variables retain both their signs and statistical significance. The high levels of significance for the lagged variables also indicate strong persistence in the solvency ratios, confirming the dynamic character of the model specification. Solvency ratios are positively related to insurers’ profitability and underwriting risk, whereas long-tail lines of insurance may have a negative effect on the ratio. However, size and reinsurance use both lose their statistical significance. This result suggests that, although these variables may affect insurer capitalisation, they might not be related to higher capital buffers (possibly because they also influence minimum regulatory capital requirements). In line with the previously reported results for the actual solvency margin, portfolio risk is not found to be significant. Mutual insurers have larger solvency ratios compared with stock companies, in agreement with other authors (Rauch and Wende, 2015). However, we now find that an insurer's specialisation is not a determinant of the solvency ratio (recall that the required solvency margin is different for life and non-life insurance segments). As previously reported in the actual solvency margin equation, industry concentration shows a positive relationship with the solvency ratio. We also find that solvency ratios exhibit cyclical behaviour that is positively related to economic growth. Finally, although the low interest rate environment in Spain during the sample period may not have affected the capitalisation of the insurance sector, it could have negatively affected solvency ratios.
| Variables | (1) | (2) |
|---|---|---|
| Solvency ratio | Solvency ratio | |
| Lagged dependent | 0.727*** | 0.739*** |
| (0.062) | (0.059) | |
| Size | −0.001 | −0.001 |
| (0.016) | (0.015) | |
| Profitability | 1.273** | 1.320** |
| (0.536) | (0.517) | |
| Reinsurance | 0.073 | 0.076 |
| (0.155) | (0.154) | |
| Portfolio risk | 0.131 | 0.131 |
| (0.162) | (0.163) | |
| Underwriting risk | 0.034** | 0.034** |
| (0.013) | (0.013) | |
| Long-tailed business | −0.000** | −0.000** |
| (0.000) | (0.000) | |
| Mutual | 0.212*** | 0.198*** |
| (0.067) | (0.064) | |
| Life insurance | −0.107 | −0.099 |
| (0.071) | (0.073) | |
| Industry concentration | 0.000* | 0.000** |
| (0.000) | (0.000) | |
| Interest | 7.962*** | |
| (3.029) | ||
| Economic growth | 1.905*** | |
| (0.458) | ||
| Constant | 0.201 | 0.096 |
| (0.340) | (0.292) | |
| Year dummies | No | Yes |
| z 1 | 136.71 (10, 201) | 163.10 (8, 201) |
| z 2 | 6.00 (2, 201) | 8.24 (7, 201) |
| m 1 | −2.88 | −2.87 |
| m 2 | 0.52 | 0.42 |
| Hansen | 196.33 (206) | 198.45 (209) |
| No. of obs. | 1537 | 1537 |
| No. of firms | 202 | 202 |
- This table presents the determinants of the solvency ratio (defined as the actual solvency margin divided by the required solvency margin) in the Spanish insurance sector during the period 2008–2015 using the system-GMM estimator developed by Arellano and Bover (1995) and Blundell and Bond (1998). See Table 1 for a description of the variables. The dependent variable is included in logarithmic form. The model in column (2) includes year dummies instead of macroeconomic variables. Except for Mutual, Industry concentration, Interest, Economic growth and Year dummies, all variables are considered endogenous in our model. We report heteroskedasticity-consistent asymptotic standard errors in parentheses, and significance levels are indicated as follows: ***significance at the 1 percent level; **significance at the 5 percent level; and *significance at the 10 percent level. z1 and z2 are Wald tests of the joint significance of the reported coefficients for the non-dummy and the dummy explanatory variables, respectively, asymptotically distributed as F under the null hypothesis of no significance, with degrees of freedom in parentheses. mi is a serial correlation test of order i using residuals in first differences, asymptotically distributed as N(0,1) under the null hypothesis of no serial correlation. Hansen is a test of overidentifying restrictions, asymptotically distributed as χ2 under the null hypothesis of no correlation between the instruments and the error term, with degrees of freedom in parentheses.
5 Summary and conclusions
This paper contributes to the debate about insurer solvency in Europe by analysing the factors (firm-specific and macro) that determine the actual solvency margin of a large sample of insurance companies operating in Spain. The selected timespan, from 2008 to 2015, encompasses a period of economic instability characterised by record low interest rates and low or even negative economic growth. The applied methodology relies on the system-GMM estimator, developed by Arellano and Bover (1995) and Blundell and Bond (1998), which has only recently been used in a few studies on the determinants of insurer solvency (Rubio-Misas and Fernández-Moreno, 2017).
Policymakers and supervisors may benefit from our findings since the European Commission has recently expressed its intention to review methods, assumptions and parameters used in Solvency II. We report that actual solvency margins are directly and significantly related to profitability, underwriting risk and a mutual-type organisation. However, insurers’ size, the use of reinsurance, a longer-tailed business and a life specialisation seem to reduce their capitalisation. We also find that less concentrated markets and a context of economic crisis (with a falling GDP) decrease solvency margins. Portfolio risk and interest rates are found not to be significant in our model. We apply different robustness tests, first by minimising the influence of potential outliers by winsorising all quantitative firm-specific variables. Furthermore, we re-estimate the baseline equation using alternative regressors. We also use a reduced sample that only includes insurers specialised in the non-life segment. All these tests yield results that are consistent with those reported in the baseline model, thus proving their robustness. As a final robustness check, we consider the solvency ratio as an alternative measure of insurer financial strength. We report that ~90 percent of insurers operating in Spain have capital buffers of up to 50 percent higher than the minimum requirements, which brings to light the fact that supervisors could have been requiring far less capital than demanded by the market under the former supervisory regime (i.e., Solvency I). Both size and reinsurance use lose their statistical significance, suggesting that although these variables may affect insurer capitalisation, they might not be related to higher capital buffers. We also show that insurers’ specialisation is not a determinant of solvency ratios. Finally, although the low interest rate environment in Spain during the sample period might not have affected the capitalisation of the insurance sector, it could have negatively affected solvency ratios.




