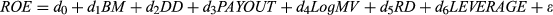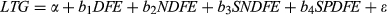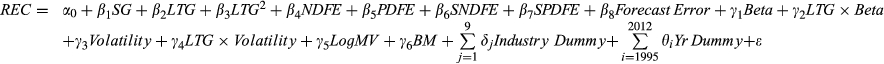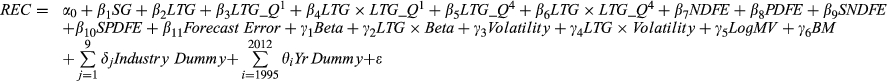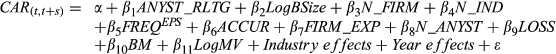Analysts’ stock recommendations, earnings growth and risk
We thank the editor, Anne Wyatt, and the anonymous reviewer for their detailed comments and suggestions. We also thank Steve Young, Herb Hunt and seminar participants at Lancaster University Management School, the University of Amsterdam and the 2009 American Accounting Association Western Regional Meeting for their helpful comments. The usual disclaimer applies.
Abstract
A key output of sell-side analysts is their recommendations to investors as to whether they should, buy, hold or sell a company's shares. However, relatively little is known regarding the determinants of those recommendations. This study considers this question, presenting results that suggest that recommendations are dependent on analysts’ short-term and long-term earnings growth forecasts, as well as on proxies for the analysts’ unobservable views on earnings growth in the more distant future and risk. Furthermore, analysts who appear to incorporate earnings growth beyond the long-term growth forecast horizons and risk into their recommendation decisions make more profitable stock recommendations.
1 Introduction
Sell-side analysts are important information intermediaries in the capital market. Over the past four decades, a staggering number of published academic studies – more than 500 to date – have examined the properties of analysts’ earnings per share forecasts (for useful reviews, see, Brown, 2000; Ramnath et al., 2008a,b; M. T. Bradshaw, unpubl. data, 2011). However, Schipper (1991) notes that earnings forecasts are just one output of sell-side research; she calls for more study of how analysts reach their final judgments, expressed in the form of buy–sell–hold stock recommendations.
Some limited progress has been made in the two decades that have passed since Schipper (1991) reached this conclusion (Ramnath et al., 2008a; M. T. Bradshaw, unpubl. data, 2011; Brown et al., 2015). However, much still remains to be done. One difficulty that researchers face is that the work analysts perform is unobservable. Nevertheless, as M. T. Bradshaw, unpubl. data (2011) notes, we have reached a point where some penetration of the ‘black box’ is required to develop deeper insights. He suggests that a potentially useful approach would be to simultaneously examine analysts’ multiple summary outputs. This is the focus of this study.
We build on the prior literature within the context of a valuation framework. This provides a structured approach to think about the linkages between the forecasts and stock recommendations carried out by analysts. We predict that analysts’ stock recommendations are positively associated with their forecasts of earnings growth in the short term and in the medium term. We also predict that analysts’ stock recommendations will be positively influenced by their expectations of earnings growth in the more distant future, and be negatively associated with their views on risk, neither of which can be directly conveyed by analysts to investors in simple but credible metrics. To test these predictions, we examine the relationships between analysts’ stock recommendations and (i) their short-term earnings growth and long-term growth forecasts, (ii) proxies designed to capture their expectations about earnings growth beyond their long-term growth forecast horizons and (iii) risk metrics employed to proxy for analysts’ risk assessments. Our study uses US data covering the 1995–2012 period.
We believe this study is among the first to provide empirical evidence that analysts’ long-term growth forecasts appear to incorporate the tendency of profitability to revert to the mean over time. We find that, all else being equal, firms with higher short-term earnings growth forecasts receive more favourable stock recommendations. Consistent with Bradshaw (2004), we show that the relationship between stock recommendations and long-term growth forecasts is positive, but in addition we show that the relationship is nonlinear and declining, reflecting the valuation implication of profitability being mean reverting. We also show that above-mean (below-mean) profitability has positive (negative) but diminishing effects on stock recommendations. We find that stock price volatility is negatively associated with stock recommendations. In contrast, market beta appears to enter analysts’ recommendation decisions primarily through its adverse mediating effect on the sensitivity of recommendations to long-term growth forecasts.
Bradshaw (2004) suggests that the relationship between analysts’ long-term growth forecasts and recommendations has a negative impact on the value of their stock recommendations.1 This conclusion is based on Bradshaw's (2004) evidence that long-term growth forecasts are negatively associated with future stock returns. In contrast, Jung et al. (2012) show that the market appears to view long-term growth forecasts as informative, and reacts more strongly to recommendation revisions that are accompanied by long-term growth forecasts. Motivated by this line of inquiry, we also investigate whether analysts’ incorporation of expectations about earnings growth beyond their long-term growth forecast horizons and their incorporation of risk is associated with the profitability of their stock recommendations. Our empirical analysis suggests that analysts who are employed by large brokerage firms and who follow less industries and have higher forecast accuracy and more firm-specific experience are more likely to incorporate earnings growth beyond long-term growth forecast horizons in making recommendations. We find that abnormal returns of stock recommendations issued by analysts who appear to take into account earnings growth beyond their long-term growth forecast horizons and risk are significantly higher than those of other analysts. Additional empirical analyses also suggest that our proxies for analysts’ expectations about earnings growth beyond their long-term growth forecast horizons predict the realised actual earnings growth rates in the next 10 years and that the stock market appears to price the proxies in a way that is consistent with how they are linked to analyst recommendations.
This study contributes to the literature in several ways. First, it extends and complements previous studies that attempt to explain analysts’ recommendation decisions (Block, 1999; Bradshaw, 2002, 2004; Brown et al., 2015). Bradshaw (2004) documents a positive relationship between analysts’ stock recommendations and long-term growth forecasts using a parsimonious empirical specification as a first pass to look at the issue. We build on this work by presenting results that suggest that stock recommendations are also dependent on analysts’ short-term earnings growth forecasts and their expectations about earnings growth in the more distant future, as well as of their views about risk. Second, this study contributes proxies for constructs that are already in the models of analysts’ decisions but cannot be conveyed by analysts to investors in a simple and credible metric. Third, we extend previous studies (Ertimur et al., 2007; Jung et al., 2012) that examine the relationship between analyst earnings and long-term growth forecasts and the economic value of their recommendations. We present results that suggest that analysts’ incorporation of risk and expectations about earnings growth beyond long-term growth forecast horizons is associated with their providing more profitable recommendations. Not only do these findings enhance our understanding of analysts’ recommendation decisions, they also have the potential to assist investors in identifying which recommendations are likely to signal positive returns and which will not.
The remainder of this study is organised as follows. Section 2 develops our theoretical framework and predictions, and describes our research design. Section 3 outlines our sampling procedure and data, and provides descriptive statistics. Section 4 reports results and presents our investigation of the effect of incorporation of risk and long-run earnings growth on recommendation profitability, while Section 5 summarises and concludes.
2 Theoretical framework and research design
2.1 Outputs of sell-side analysts
Sell-side analysts are important information intermediaries in the capital market. In addition to providing detailed comments and discussions of the prospects of companies and industries they follow, analysts generally provide three summary outputs of their work: (1) a short-term earnings per share (EPS) forecast; (2) a forecast of growth in expected EPS, typically over a 3- to 5-year horizon; and (3) a recommendation to investors to buy, hold or sell the stock.2 While the first one has been extensively studied by accounting researchers, the last two have received much less attention.
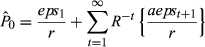(1a)
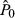can be thought of as the analyst's view of how much the stock is really worth (which may differ from the current share price, P0); r is the cost of capital and R = 1 + r; and 
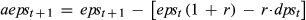is the abnormal earnings growth, defined as the change in EPS adjusted for the cost of capital and dividends (dpst). To relate Equation (1a) to the earnings forecasts reported by analysts, it is helpful to break the stream of future pay-offs into three sets, as follows:
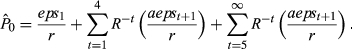(1b)
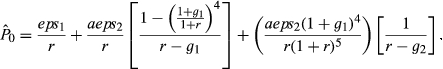(2)The analyst provides two measures of future earnings: a forecast of 1-year-ahead earnings per share, eps1, and a forecast of what is conventionally but somewhat misleadingly referred to as ‘long-term’ (really medium term) growth in earnings, LTG, where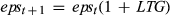 
, t = 1, 2, …, 4. From this, we could infer that the rate of growth, g1, in abnormal earnings over this interval (together with the discount rate, r) will enable the analyst to arrive at an estimate of the second term on the right-hand side of Equation (1b). If a firm pays out all its medium-term earnings as dividends, abnormal earnings growth during this period will be reduced to aepst + 1 = epst + 1 − epst, and g1 = LTG. However, to complete the valuation exercise represented by Equation 2, the investor must also estimate g2, the growth rate of aeps in the more distant future, and this cannot be discerned from the analyst's published outputs. In what follows, we follow conventional market practices here and define what is really medium-term earnings growth as long-term growth (LTG), and define the unobservable ‘really long-term growth’ in eps as g2 = RLTG.
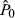as a representation of the (unobservable) view the analyst has of how much the stock is worth, and the analyst's recommendation (REC) as a function of the difference between this unobservable amount and the stock's current price 
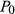. We can also treat 
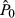as dependent on (i) the analyst's observable forecasts of eps1 and LTG, (ii) the unobservable RLTG and (iii) the discount rate for the stock, the principal determinant of which is the analyst's (also unobservable) views on risk (RISK). Putting these together, we get:
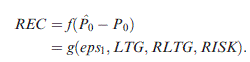(3)Logically, analysts ought to make a buy recommendation when intrinsic value is sufficiently larger than current price to justify the transaction costs involved (i.e.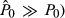 
, and vice versa when the reverse condition holds 
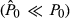. Being dependent on 
REC therefore ought to depend on the extent to which analysts think their beliefs, regarding eps1, LTG, RLTG and RISK, are at variance with those embedded in current prices.
However, analysts’ views are not observable. Hence, we formulate the reduced form of 3 in terms of the analysts’ beliefs concerning the levels of these variables, that is as REC = g (eps1, LTG, RLTG, RISK). We use this framework to explore the relationship between analysts’ stock recommendations and their forecasts of earnings (eps1 and LTG), and how these relationships can be affected by their beliefs about RLTG and RISK. Because we are unable to identify the direction or extent to which our observable measures eps1, LTG, RISK and our proxies for RLTG differ from current market beliefs, classification errors will result. This will reduce the power of our tests to detect relationships between REC and these measures.3
A starting point for our investigation is Bradshaw (2004) who examines how analysts use their earnings forecasts to generate stock recommendations. The author analyses the associations between stock recommendations and value estimates derived from the residual income model and practical valuation heuristics using analysts’ earnings forecasts. He finds that LTG better explains the cross-sectional variation in analysts’ stock recommendations compared to residual income value estimates.
Bradshaw's (2004) empirical specification is parsimonious in that it involves regressing REC on LTG alone, and does not consider eps1. However, our framework, and the huge amount of attention given to eps1 in the financial press (Brown, 1993), suggests it is an important additional analyst output, and one therefore likely to be an important determinant of their recommendations. Bradshaw's (2004) empirical specification implicitly assumes that LTG will persist indefinitely, and thus, no account need be taken of RLTG (i.e. of the analysts’ unobservable views of the more distant future), or of RISK (their assessments of how risk should affect share valuations). Previous studies (La Porta, 1996; Dechow and Sloan, 1997) that examine the relationship between earnings expectations and stock returns have also used analysts’ LTG forecasts to proxy for investors’ expectations about earnings growth in all future years without explicitly considering the likely declining persistence of LTG.
To advance our understanding of the role of analysts’ earnings growth expectations in their stock recommendation decisions, we analyse the effects of the short-term earnings growth rate (i.e. the proportionate increase in forecast eps1 over the reported earnings per share of the previous fiscal year, eps0), LTG, and proxies designed to capture the extent to which the latent variable RLTG differs from LTG.
- REC is a positive but diminishing function of LTG: ∂REC/∂LTG > 0 and ∂2REC/∂LTG2 < 0.
- Above-mean (below-mean) past profitability will have a positive (negative) but diminishing effect on REC.
The first prediction reflects the attenuating effect the unobservable latent variable RLTG is expected to have on the analyst's estimation of intrinsic value,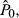 
and hence on REC. In our design, RLTG plays the role of a correlated omitted variable. We address this problem in our experimental design in two ways: by modifying our expectations concerning the relationship between REC and LTG, and by incorporating profitability mean reversion into the design.
If we hold all else equal, economic theory predicts that the risk aversion of investors will result in high-risk companies having lower equity prices than low-risk ones. Not only will high predicted earnings growth attract competition, it will often be dependent on high-risk investments in R&D and other intangibles. We therefore predict that REC will be a negative function of RISK: ∂REC/∂RISK < 0.
2.2 Research design
We use a quadratic model of LTG, REC = g(LTG, LTG2…) to test for the predicted attenuating effect of the correlated omitted variable RLTG on the analyst's estimation of intrinsic value,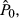 
and hence on REC. We predict REC will be positively associated with LTG and negatively associated with LTG2, because the higher LTG is, the greater the potential deviation between RLTG and LTG and the less weight the analysts will place on LTG in estimating 
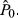To reflect the possibility that analysts respond differently to the mean reversion of losses and profits, we also use an alternative model including two interaction variables between LTG and indicator variables representing the bottom and top LTG quartiles, respectively, to examine the relationship between LTG and recommendations.
We allow for the previously documented fact that the reversion of profitability to its mean can take a very long time (Fairfield et al., 2009). The extent to which profitability deviates from its mean signals expected changes in profitability and earnings growth in the long run. Hence, we use this deviation to construct proxies for the latent variable, RLTG. We follow Fama and French (2000) both in our estimation of the mean of profitability and in how profitability reverts to its mean. We then examine the effects of the latent variable RLTG on stock recommendations using measures representing both the magnitude and direction of the deviations of profitability from its mean. We predict that analysts are likely to think favourably of firms with high past profitability, and their recommendations are likely affected by their expectations about how profitability will change in the long run. We predict above-mean (below-mean) past profitability will have a positive (negative) but diminishing effect on REC.
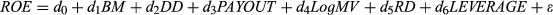(4)For each firm-month observation, we compute the deviation of past ROE from its expected value (hereafter, DFE) by taking the difference between ROE in the previous year and its expected value, E(ROE): DFEt = ROEt−1 − E(ROEt−1). Let NDFE denote DFEt < 0 and PDFE denote DFEt > 0. Fama and French (2000) find that the speed of mean reversion is faster when return on assets is below its expected value, and when it is further from the expected value in either direction. They use the squared values of NDFE and PDFE to measure the magnitude to which profitability is below and above its expected value, respectively. For the purpose of modelling, the diminishing effect of above-mean (below-mean) past profitability on REC, the squared values of NDFE and PDFE are computed and denoted as SNDFE and SPDFE, respectively. We predict REC will be positively associated with PDFE, NDFE and SNDFE, and negatively associated with SPDFE.
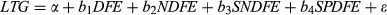(5)Existing evidence on how analysts make allowances for risk is scarce. One possibility is that analysts adjust for the risk of equity by discounting future pay-offs using a discount factor based on the Capital Asset Pricing Model (CAPM; Sharpe, 1964; Lintner, 1965), an approach emphasised in standard valuation textbooks. Prior research, however, suggests that analysts tend to mainly rely on valuation multiples instead of present value models and that they are concerned about risk in a firm-specific sense rather than in terms of its marginal impact on a well-diversified portfolio (Barker, 1999; Block, 1999). This raises the possibility that analysts do not adjust for risk using a discount factor based on a formal pricing model such as the CAPM. Consistent with A. Kecskes, R. Michaely, and K. Womack, unpubl. data (2009), our own reading of brokers’ reports suggests that risk is generally defined by reference to firm-specific operational and business risks, and uncertainties concerning macroeconomic factors that potentially affect a firm's future earnings. It is difficult, if not impossible, to construct a quantitative measure of analysts’ risk assessments by codifying such qualitative discussions. At any rate, no such metric is currently available. Moreover, to our best knowledge, few brokerage houses generate quantitative risk forecasts, and no such data are available from any data vendor. Hence, instead of examining how analysts’ (unobservable) risk assessments affect their stock recommendations, we step back and ask a different question: To what extent do analysts take into account traditional risk measures in making stock recommendations?
We mainly consider two traditional risk measures, market beta and stock price volatility. The CAPM assumes that only systematic risk (market beta) is priced. However, it has been demonstrated theoretically that in a market with incomplete information and transaction costs, rational investors price idiosyncratic risk (Merton, 1987) and there is evidence that idiosyncratic risk does indeed play a role in explaining the cross-section of average stock returns (Malkiel and Xu, 1997; B. Malkiel, and Y. Xu, unpubl. data, 2006). Furthermore, sell-side analysts specialise by industry and usually follow a limited number of stocks (Boni and Womack, 2006), suggesting that they might not take full account of the big (diversification) picture when recommending individual stocks.
Fama and French (1992) argue that the risk of a stock is also a function of firm size and book-to-market. Behavioural studies (La Porta, 1996; Dechow and Sloan, 1997) argue that the book-to-market factor in returns is the result of market participants systematically overestimating (underestimating) the growth prospects of growth (value) firms. We do not address why size and book-to-market may affect returns, but simply include them as controls.
We also examine the potential interactions between risk and growth. The future earnings of high beta firms are likely to be more sensitive to changes in the overall economy. We predict that analysts are able to capture this earnings implication of market beta and discount the LTG forecasts of high beta firms when making recommendations. Meanwhile, for a firm with high growth but also a high degree of risk, analysts are likely to issue a less favourable recommendation. We allow for such possible interaction between LTG and market beta and stock price volatility in our empirical analysis.
We compute the analyst's short-term earnings growth forecast (hereafter, SG) using the formula: SG = (EPS1 − EPS0)/EPS0. EPS1 is 1-year-ahead consensus earnings per share forecast, and EPS0 is the last reported earnings per share. Because it is difficult to make economic sense of SG when EPS0 < 0, we follow Bradshaw and Sloan (2002) by computing the short-term growth forecast only for observations with positive EPS0. We predict SG to be positively associated with stock recommendations.
Prior research has shown that analysts’ earnings forecasts are optimistically biased, possibly due to analysts’ incentives to generate trading, to cultivate management and to maintain good relationships with underwriting clients of their brokerage firms (Francis and Philbrick, 1993; Lin and McNichols, 1998; Jackson, 2005; Brown et al., 2015). However, it is possible that the analysts may take into account the optimistic bias in their earnings forecasts when making stock recommendations. We include the signed forecast error of EPS1 (Forecast Error) in our empirical specifications to capture this possible element in analysts’ recommendation decisions. We predict the coefficient on Forecast Error to be negative, reflecting the analysts’ effort to discount the optimistic bias in their earnings forecasts.
We primarily use an ordinary least-squares (OLS) regression analysis to test our predictions. Following Bradshaw (2004), Barniv et al. (2009) and He et al. (2013), we use the monthly consensus (mean) stock recommendation as the dependent variable. We use consensus (i.e. average) data, both to facilitate comparison with key prior studies and because there are strong reasons to believe that average measures are likely to better reflect the price setting process in the market. In addition, we also examine our predictions using multinomial ordered logit regression analysis, in which the dependent variable is the quintile ranking of monthly consensus stock recommendation, a 5-point scale discrete variable.
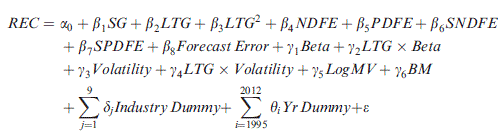(6a)Forecast Error is measured by dividing the difference between EPS1 and the actual earnings per share (EPSa) by the absolute value of EPSa. Beta is calculated monthly using 5 years’ monthly stock and market returns; Volatility represents the 3-month stock price volatility; LTG × Beta and LTG × Volatility represent the interaction variables between LTG and Beta and Volatility, respectively; LogMV represents size as measured by market capitalisation; and BM is the book-to-market ratio. We predict the coefficients on Beta, Volatility, BM and LTG × Beta to be negative and the coefficient on LogMV to be positive. We make no prediction with regard to the sign of LTG × Volatility. The model controls for both year and industry effects by including year indicator variables (Yr Dummy) and industry indicator variables (Industry Dummy) formed based on the first-level Global Industry Classification Standard (GICS) industry classification.
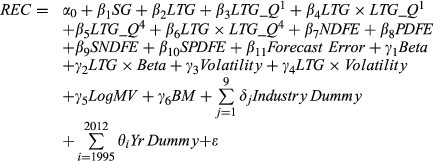(6b)3 Sample selection, data and descriptive statistics
Our sample selection procedures are summarised in Table 1. The analyst data are from the Institutional Brokers’ Estimate System (I/B/E/S). Our sample covers the period January 1995–December 2012. We obtain monthly consensus analyst forecasts including stock recommendations (mean), long-term growth (median) and 1-year-ahead earnings per share (EPS1) for all US firms listed on the NYSE, the AMEX and on NASDAQ. I/B/E/S enters reported earnings on the same basis as analysts’ forecasts. To ensure comparability, we use the actual earnings per share (EPS0) from the I/B/E/S detailed actual file for the estimation of SG and ROE. During the sample period, I/B/E/S analysts provide both recommendations and EPS1 forecasts for 16,877 US firms. LTG forecasts are available for approximately 79 percent of these firms. We eliminate duplicated monthly observations.
| Sample period: January 1995–December 2012 | ||||
|---|---|---|---|---|
| Procedures | Observations | Firms | Remaining | |
| Observations | Firms | |||
| Step1: Collect consensus monthly forecasts from I/B/E/S | ||||
| Stock recommendations | 1 073 545 | 17 987 | ||
| EPS 1 | 1 028 291 | 17 733 | ||
| Long-term growth forecasts (LTG) | 754 144 | 13 325 | ||
| Merge recommendations, LTG and EPS1; eliminate duplicate monthly data points | 744 274 | 13 181 | ||
| Step2: Collect accounting data from Compustat | ||||
| Estimate book-to-market, LogMV, the dividiend indicator variable, payout ratio, leverage and R&D ratio | ||||
| Merge Compustat and I/B/E/S data | ||||
| No. of firm–month observations with explanatory variables for estimating Equation 4 | 429 698 | 7437 | ||
| Step 3: Calculate ROE, SG, earnings forecast error and other variables | ||||
| Collect the last reported EPS (EPS0) from I/B/E/S for firm-year units with I/B/E/S data | 68 677 | 12 240 | ||
| Calculate ROE for observations with positive book value | 530 952 | 8480 | ||
| Remaining observations for estimating Equations 4 and 5 | 401 451 | 7023 | ||
| Calculate SG for firm–month units with positive EPS0 | 594 079 | 10 624 | ||
| Step 4: Estimate risk variables using CRSP data | ||||
| Calculate the 5-year market beta for firm–month units | 444 192 | 6973 | ||
| Calculate the annualized 3-month stock price volatility | 607 576 | 9790 | ||
| Merge CRSP, Compustat and I/B/E/S data | ||||
| Eliminate the 1% of the lowest and highest tails of all variables except for REC | ||||
| Remaining observations with all data items for estimating Equation (6a) | 284 655 | 4946 | ||
- This table describes our sample selection. The first two numeric columns report the number of firm-month (firm-year, in the case of accounting data) observations and firms. The next two columns report the number of firm-month observations and firms remained after each of the data merging and elimination procedures. At the first step, monthly consensus stock recommendations, long-term growth forecasts and EPS1 are collected from I/B/E/S. The three data items are merged based on the estimation dates of I/B/E/S consensus forecasts (the third Thursday). At the second step, accounting data are collected from COMPUSTAT to estimate the variables in Equation 4. Accounting data are merged with I/B/E/S forecasts. At step 3, ROE and SG are estimated using the last reported earnings per share (EPS0) collected from the detailed actual file of the I/B/E/S. At step 4, for each observation with I/B/E/S analyst data, the 5-year market beta and the annualised 3-month stock price volatility are estimated using the CRSP return data. CRSP data are merged with I/B/E/S and COMPUSTAT data. To mitigate the potential influence of outliers, we trim the 1 percent of the lowest and highest tails of all variables except for stock recommendations.
We merge I/B/E/S data with COMPUSTAT data used for the calculation of accounting variables. We require firm–month observations to have positive EPS0 and book value per share for the estimation of SG and ROE, respectively. We estimate risk variables for firm–month units using firm and stock return data from the Center for Research in Security Prices (CRSP) database. Beta is estimated each month by regressing monthly returns of the stock on monthly market returns over a 5-year period. Volatility4 is measured using the annualised standard deviation of daily returns 3 months preceding the consensus recommendation dates. Definitions of variables used in empirical analysis are detailed in Table 2.
| Panel A: Descriptive statistics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Mean | Standard deviation | Minimum | Q1 | Median | Q3 | Maximum | N |
| REC | 3.782 | 0.617 | 1.000 | 3.350 | 3.800 | 4.200 | 5.000 | 744 323 |
| LTG | 0.170 | 0.098 | 0.010 | 0.100 | 0.150 | 0.200 | 0.600 | 730 230 |
| SG | 0.192 | 0.703 | −2.713 | −0.021 | 0.129 | 0.295 | 6.136 | 582 168 |
| ROE | 0.086 | 0.155 | −1.222 | 0.045 | 0.093 | 0.147 | 0.681 | 520 543 |
| DFE | −0.002 | 0.070 | −0.134 | −0.049 | −0.010 | 0.032 | 0.300 | 405 172 |
| NDFE | −0.027 | 0.034 | −0.134 | −0.049 | −0.010 | 0.000 | 0.000 | 409 313 |
| PDFE | 0.025 | 0.047 | 0.000 | 0.000 | 0.000 | 0.032 | 0.300 | 409 299 |
| Beta | 1.085 | 0.677 | −0.127 | 0.592 | 0.973 | 1.454 | 3.537 | 435 305 |
| Volatility | 0.476 | 0.263 | 0.128 | 0.286 | 0.409 | 0.594 | 1.620 | 595 425 |
| LogMV | 6.741 | 1.720 | 3.074 | 5.475 | 6.605 | 7.865 | 11.379 | 551 248 |
| BM | 0.535 | 0.355 | 0.044 | 0.283 | 0.460 | 0.693 | 2.374 | 538 406 |
| R&D | 0.042 | 0.090 | 0.000 | 0.000 | 0.000 | 0.040 | 0.794 | 567 196 |
| LEVERAGE | 0.538 | 0.245 | 0.066 | 0.344 | 0.540 | 0.717 | 1.189 | 563 717 |
| DD | 0.462 | 0.499 | 0.000 | 0.000 | 0.000 | 1.000 | 1.000 | 573 631 |
| PAYOUT | 0.240 | 0.422 | 0.000 | 0.000 | 0.047 | 0.339 | 4.013 | 463 221 |
| Forecast Error | 0.227 | 0.820 | −1.167 | −0.057 | 0.000 | 0.167 | 8.000 | 687 327 |
| Panel B: Pearson correlation (significance levels are in parentheses) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| REC | LTG | SG | ROE | DFE | Beta | Volatility | LogMV | BM | R&D | LEVERAGE | DD | PAYOUT | |
| REC | — | 0.296 (0.001) | 0.155 (0.001) | 0.030 (0.001) | −0.038 (0.001) | 0.069 (0.001) | 0.051 (0.001) | −0.091 (0.001) | −0.174 (0.001) | 0.032 (0.001) | −0.120 (0.001) | −0.167 (0.001) | −0.178 (0.001) |
| LTG | — | 0.158 (0.001) | −0.221 (0.001) | −0.111 (0.001) | 0.303 (0.001) | 0.416 (0.001) | −0.221 (0.001) | −0.269 (0.001) | 0.369 (0.001) | −0.384 (0.001) | −0.449 (0.001) | −0.306 (0.001) | |
| SG | — | −0.193 (0.001) | −0.243 (0.001) | 0.039 (0.001) | −0.022 (0.001) | −0.027 (0.001) | −0.066 (0.001) | 0.038 (0.001) | −0.025 (0.001) | −0.066 (0.001) | 0.021 (0.001) | ||
| ROE | — | 0.878 (0.001) | −0.151 (0.001) | −0.253 (0.001) | 0.265 (0.001) | −0.205 (0.001) | −0.253 (0.001) | 0.110 (0.001) | 0.207 (0.001) | 0.004 (0.007) | |||
| DFE | — | 0.037 (0.001) | 0.060 (0.001) | −0.012 (0.001) | 0.036 (0.001) | 0.017 (0.001) | −0.028 (0.001) | −0.010 (0.001) | −0.013 (0.001) | ||||
| Beta | — | 0.332 (0.001) | −0.036 (0.001) | −0.009 (0.001) | 0.311 (0.001) | −0.228 (0.001) | −0.347 (0.001) | −0.233 (0.001) | |||||
| Volatility | — | −0.323 (0.001) | 0.029 (0.001) | 0.272 (0.001) | −0.218 (0.001) | −0.38 (0.001) | −0.201 (0.001) | ||||||
| LogMV | — | −0.277 (0.001) | −0.081 (0.001) | 0.159 (0.001) | 0.373 (0.001) | 0.170 (0.001) | |||||||
| BM | — | −0.171 (0.001) | 0.134 (0.001) | 0.041 (0.001) | 0.057 (0.001) | ||||||||
| R&D | — | −0.36 (0.001) | −0.304 (0.001) | −0.163 (0.001) | |||||||||
| LEVERAGE | — | 0.344 (0.001) | 0.218 (0.001) | ||||||||||
| DD | — | 0.545 (0.001) | |||||||||||
| PAYOUT | — | ||||||||||||
- Panel A of the table describes the main variables used in empirical analysis. Panel B of the table presents Pearson correlation analysis of the main variables used in empirical analysis. Variable Definitions: REC = monthly analysts’ consensus (mean) stock recommendation from the I/B/E/S database; LTG = monthly analysts’ consensus (median) long-term growth forecast from I/B/E/S; SG = analyst forecast of short-term earnings growth rate, measured as the difference between analyst consensus 1-year-ahead earnings per share forecast and the last reported earnings per share (both from I/B/E/S) divided by the last reported earnings per share, that is (EPS1 − EPS0)/EPS0, when EPS0 > 0; ROE = return on equity as of the prior fiscal year, measured as the last reported earnings per share before extraordinary items divided by book value per share; DFE = deviation of return on equity from its mean, measured as the difference between return on equity as of the prior fiscal year (ROE) and its expected value, E(ROE), the fitted value from a cross-sectional regression; NDFE = negative deviations of ROE from its mean, equal to DFE when DFE is negative and 0 otherwise; PDFE = positive deviations of ROE from its mean, equal to DFE when DFE is positive and 0 otherwise; Beta = 5-year market beta, estimated using CRSP monthly firm and market returns over a 5-year period based on the CAPM, that is reti = α + βMKTret + ɛ; Volatility = 3-month stock price volatility, estimated as annualised 3-month standard deviation of daily stock returns from CRSP; BM = book-to-market ratio as of the prior fiscal year, measured as book value divided by market value; LogMV = natural logarithm of market value, which is estimated as the number of shares outstanding multiplied by stock price at the end of the fiscal year; DD = indicator variable taking the value of 1 if the firm issues common dividends in year t, and 0 otherwise; PAYOUT = dividend payout ratio, measured as total common dividends divided by earnings before extraordinary items if earnings before extraordinary items >0 or measured as total common dividends divided by (0.08*common equity) if earnings before extraordinary items < 0; R&D = research and development expense divided by net sales; LEVERAGE = total liabilities divided by total assets; and Forecast Error = signed analyst EPS1 forecast error, measured as the difference between EPS1 and the actual earnings per share (EPSa) scaled by the absolute value of EPSa.
To mitigate the potential influence of outliers, we eliminate 1 percent of the lowest and highest tails of all variables except the consensus monthly stock recommendations. The sample we use to analyse whether analysts’ LTG forecasts incorporate the mean reversion in profitability comprises 401,451 firm–month observations, representing 7023 distinct firms. The sample used for the estimation of the full model of Equation (6a) includes 284,655 firm–month observations and 4946 distinct firms. Following prior literature, the coding of recommendations is inverted to be 1 = strong sell, 2 = sell, 3 = hold, 4 = buy and 5 = strong buy.
Panel A in Table 2 presents descriptive statistics for the main variables that will be used in the subsequent analysis. Both the mean and the median of consensus recommendation are close to a buy rating (3.782; 3.800), revealing analysts’ optimism that has been widely documented in prior literature. The mean and median of LTG are 0.170 and 0.150, respectively. The mean of SG is 0.192, higher than mean LTG. The average ROE of the sample firms is 8.6 percent. The mean and median of DFE, deviation of ROE from its expected value, are −0.002 and −0.010, respectively; the mean of negative deviations is −0.027 and that of positive deviations is 0.025. The mean (median) of market beta and stock price volatility are 1.085 (0.973) and 0.476 (0.409), respectively.
Panel B in Table 2 presents the results of Pearson correlation analysis of the main variables used in the subsequent empirical analysis. Stock recommendations are positively correlated with both the short-term and the medium-term earnings growth forecasts and with ROE but are negatively correlated with DFE. Both Beta and Volatility are positively correlated with recommendations. Note that the positive correlation between recommendations and Volatility possibly is caused by year effects (price volatility was extremely high during the two most recent stock market crashes). LTG is negatively correlated with past ROE and its deviation from its expected value DFE. SG is also negatively associated with both ROE and DFE. The moderate correlation between Beta and Volatility (0.332) indicates that the information content of the two risk measures is to some degree overlapping; Volatility and Beta are both manifestations of risk. This necessitates the control of each of the pair in the regression tests. The mean of DD was 0.462, indicating that in less than half of the sample firm-years were dividends paid.
Our OLS regression analyses use panel data pooled across firms and multiple periods (months). When the residuals are correlated across observations, OLS standard errors can be biased and the inferences about the coefficient estimates will be inaccurate. Following Petersen (2009), we therefore adjust the standard errors of the regression slopes in our regression tests for the possible dependence in residuals by clustering standard errors on firm and month dimensions.
Our sample covers three subperiods marked by dramatic shifts in the economic conditions in the USA as well as important regulatory changes. The first subperiod is 1995–2000, which covers the dot-com bubble period, during which time analysts and investors were highly optimistic about the growth prospects of high-tech stocks. The second subperiod follows the introduction of Regulation Fair Disclosure (RegFD) and ends in 2006, a period often referred to as ‘the great moderation’. RegFD was promulgated by the SEC in August 2000, after which analysts lost their privileged access to corporate management. RegFD changed the information environment and to some extent the incentives analysts face (Jung et al., 2012). The final subperiod from 2007 to 2012 covers the years of the financial crisis and its aftermath. Our empirical analyses are based on the sample covering the 1995–2012 period. We repeat the empirical analysis for each of the above subperiods, but for space reasons report without tabulating the results.
4 Empirical results
4.1 Relationship between analysts’ LTG forecasts and profitability mean reversion
Panel A of Table 3 presents the results of the first-stage cross-sectional regression that is used to construct a proxy for the mean of ROE.5 PAYOUT, BM and R&D are negatively associated with ROE, while DD, LogMV and LEVERAGE are positively associated with it. Panel B reports estimates of Equation 5 that analyses the associations between LTG and the mean reversion variables of ROE. Model 1 shows that LTG is negatively associated with the deviation of ROE from its mean, suggesting that analysts expect firms with higher levels of DFE to have lower earnings growth rates over the next 3–5 years. In Model 2, the coefficient on DFE is positive, while that on NDFE is negative, suggesting that, while analysts appear to consider high past ROE to be associated with high medium-term earnings growth, they predict earnings of firms with below-mean past ROE will grow at a faster pace in the following years. As predicted, the coefficient on SNDFE is positive and statistically significant, suggesting that analysts expect earnings growth of firms with extreme below-mean profitability to revert at a faster pace. SPDFE has the predicted negative sign, suggesting that analysts expect earnings growth of firms with extreme above-mean profitability to slow more rapidly over the next 3–5 years as their high profitability fades. It appears that the negative relationship between LTG and DFE in Model 1 is mainly attributable to the anticipated reversals of negative deviations and extremely negative and positive deviations of ROE from its mean. The results presented in Model 3 show that LTG is negatively associated with the level of previous year ROE. This suggests that analysts expect firms with higher past profitability to have lower earnings growth in the next 3–5 years, and vice versa.
Panel A: Regression to explain the level of ROE
 ((4)) |
||||
|---|---|---|---|---|
| Model | Predicted sign | 1 | ||
| Intercept | ? | 0.122 (0.001) | ||
| BM | − | −0.106 (0.001) | ||
| DD | + | 0.002 (0.001) | ||
| PAYOUT | − | −0.009 (0.001) | ||
| LogMV | + | 0.005 (0.001) | ||
| R&D | +/− | −0.063 (0.001) | ||
| LEVERAGE | + | 0.052 (0.001) | ||
| n | 401 451 | |||
| Adjusted R2 | 0.172 | |||
Panel B: Relationship between LTG and profitability mean reversion variables
 (5) |
||||
|---|---|---|---|---|
| Model | Predicted sign | 1 | 2 | 3 |
| Intercept | ? | 0.155 (0.001) | 0.144 (0.001) | 0.176 (0.001) |
| DFE | − | −0.128 (0.001) | 0.065 (0.001) | |
| NDFE | − | −0.228 (0.001) | ||
| SNDFE | + | 2.720 (0.001) | ||
| SPDFE | − | −0.147 (0.001) | ||
| ROE | − | −0.132 (0.001) | ||
| n | 401 451 | 401 451 | 512 837 | |
| Adjusted R2 | 0.012 | 0.030 | 0.049 | |
- Panel A of the table reports the coefficient estimates and p-values (in parentheses) of the regression explaining the level of return on equity. Panel B of the table reports the results of regression tests that analyse the associations between LTG and measures of the mean reversion of profitability. The dependent variable, LTG, represents monthly (median) long-term growth forecasts. We adjust the standard errors of the regression slopes in the regression tests for the possible dependence in residuals by clustering standard errors on firm and month dimensions. SNDFE, the square of DFE when DFE is negative and 0 otherwise; SPDFE, the square of DFE when DFE is positive and 0 otherwise. See also Table 2 for variable definitions.
These findings suggest that analysts understand the mean reversion property of earnings, and they appear to exploit it when issuing LTG forecasts. As a sensitivity check, we run the regression tests in panel B of Table 3 for the subperiods 1995–2000, 2001–2006 and 2007–2012. The results (untabulated) are consistent with those reported in panel B of Table 3. The only exception is that SPDFE has the predicted sign but is not statistically significant in Model 2 for the 2007–2012 period.
4.2 Relationships between stock recommendation and the short-term growth forecast, LTG, RLTG and RISK
The results of regression tests of our main predictions are presented in Table 4. The coefficient estimates of Equation (6a) are reported in panel A. Models 1–10 in the panel report OLS regression tests in which monthly consensus stock recommendation serves as the dependent variable. As predicted, in all the models, the coefficient on the short-term earnings growth forecast SG is positive and significant at the 1 percent confidence level. The results for Model 2 confirm the positive relationship between stock recommendation and LTG documented in Bradshaw (2004) and Jegadeesh et al. (2004). When LTG2 is added to the regression in Models 3–4 and 7–10, the relationship between stock recommendation and LTG increases markedly and, as predicted, the LTG2 coefficient is always negative and significant, indicating that the relationship between stock recommendation and LTG is positive but diminishing.
Panel A:
 (6 a) |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dependent variable | OLS estimates (consensus stock recommendation) | Ordered multinomial logit regression estimates (LTG quintile ranking) | |||||||||||
| Model | Predicted sign | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| Estimate | Odds ratio | ||||||||||||
| Intercept | + | 3.756 (0.001) | 3.469 (0.001) | 3.207 (0.001) | 3.177 (0.001) | 3.732 (0.001) | 3.721 (0.001) | 3.141 (0.001) | 3.113 (0.001) | 3.373 (0.001) | 3.320 (0.001) | ||
| SG | + | 0.131 (0.001) | 0.091 (0.001) | 0.153 (0.001) | 0.117 (0.001) | 0.105 (0.001) | 0.101 (0.001) | 0.103 (0.001) | 0.379 (0.001) | 1.461 | |||
| LTG | + | 1.848 (0.001) | 4.766 (0.001) | 5.158 (0.001) | 5.571 (0.001) | 5.730 (0.001) | 5.413 (0.001) | 5.638 (0.001) | 2.003 (0.001) | 7.411 | |||
| LTG 2 | − | −6.073 (0.001) | −6.934 (0.001) | −7.816 (0.001) | −8.241 (0.001) | −7.147 (0.001) | −7.139 (0.001) | −0.521 (0.001) | 0.594 | ||||
| NDFE | + | −0.109 (0.248) | 0.439 (0.001) | 0.634 (0.001) | 0.471 (0.001) | 0.560 (0.001) | 0.252 (0.01) | 1.238 (0.001) | 3.449 | ||||
| PDFE | + | 1.061 (0.001) | 1.293 (0.001) | 1.055 (0.001) | 0.977 (0.001) | 1.008 (0.001) | 0.656 (0.001) | 3.999 (0.001) | 54.544 | ||||
| SNDFE | + | 15.584 (0.001) | 14.564 (0.001) | 7.941 (0.001) | 7.186 (0.001) | 8.257 (0.001) | 1.970 (0.035) | 31.918 (0.001) | 7.E + 13 | ||||
| SPDFE | − | −4.129 (0.001) | −4.929 (0.001) | −4.034 (0.001) | −4.217 (0.001) | −4.661 (0.001) | −3.376 (0.001) | −18.555 (0.001) | 0.000 | ||||
| Forecast error | − | −0.049 (0.001) | −0.049 (0.001) | −0.050 (0.001) | −0.169 (0.001) | 0.845 | |||||||
| Beta | ? | 0.006 (0.001) | 0.114 (0.001) | 0.132 (0.001) | 0.335 (0.001) | 1.398 | |||||||
| LTG × Beta | − | −0.681 (0.001) | −0.645 (0.001) | −1.945 (0.001) | 0.143 | ||||||||
| Volatility | − | −0.017 (0.002) | −0.171 (0.001) | −0.251 (0.001) | −1.142 (0.001) | 0.319 | |||||||
| LTG × Volatility | ? | 0.972 (0.001) | 0.388 (0.001) | 7.665 (0.001) | 2.E + 03 | ||||||||
| LogMV | + | −0.025 (0.001) | −0.026 (0.001) | −0.027 (0.001) | −0.087 (0.001) | 0.917 | |||||||
| BM | − | −0.098 (0.001) | −0.104 (0.001) | −0.128 (0.001) | −0.385 (0.001) | 0.680 | |||||||
| Industry effects | No | No | No | No | No | No | No | No | No | Yes | Yes | ||
| Year effects | No | No | No | No | No | No | No | No | No | Yes | Yes | ||
| n | 582 168 | 730 230 | 730 230 | 575 727 | 405 160 | 396 934 | 370 801 | 284 655 | 284 655 | 284 655 | 282 063 | ||
| Adjusted R2/Pseudo R2 | 0.018 | 0.088 | 0.110 | 0.136 | 0.012 | 0.033 | 0.146 | 0.152 | 0.154 | 0.196 | 0.019 | ||
Panel B:
 (6b) |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dependent variable: Consensus stock recommendation | |||||||||||||
| Model | Predicted sign | Full sample period: 1995–2012 | Period: 1995–2006 | Period: 2007–2012 | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||
| Intercept | + | 3.319 (0.001) | 3.497 (0.001) | 3.319 (0.001) | 3.289 (0.001) | 3.587 (0.001) | 3.166 (0.001) | 3.426 (0.001) | 3.335 (0.001) | 3.459 (0.001) | |||
| SG | + | 0.091 (0.001) | 0.106 (0.001) | 0.092 (0.001) | 0.118 (0.001) | 0.107 (0.001) | 0.104 (0.001) | 0.101 (0.001) | 0.109 (0.001) | 0.117 (0.001) | |||
| LTG | + | 3.217 (0.001) | 3.420 (0.001) | 3.216 (0.001) | 3.447 (0.001) | 3.134 (0.001) | 4.246 (0.001) | 4.254 (0.001) | 2.850 (0.001) | 2.941 (0.001) | |||
| LTG_Q 1 | − | −0.023 (0.001) | −0.042 (0.001) | −0.136 (0.001) | −0.110 (0.001) | −0.230 (0.001) | −0.083 (0.001) | −0.068 (0.001) | 0.081 (0.001) | 0.092 (0.001) | |||
| LTG_Q1 × POSTY06 | ? | 0.261 (0.001) | 0.254 (0.001) | 0.306 (0.001) | |||||||||
| LTG × LTG_Q 1 | + | −0.496 (0.001) | −0.291 (0.001) | 0.668 (0.001) | 0.360 (0.001) | 1.169 (0.001) | 0.976 (0.001) | 0.819 (0.001) | −1.838 (0.001) | −1.726 (0.001) | |||
| LTG × LTG_Q 1 × POSTY06 | ? | −2.706 (0.001) | −2.669 (0.001) | −2.081 (0.001) | |||||||||
| LTG_Q 4 | + | 0.614 (0.001) | 0.595 (0.001) | 0.614 (0.001) | 0.699 (0.001) | 0.565 (0.001) | 0.663 (0.001) | 0.580 (0.001) | 0.521 (0.001) | 0.452 (0.001) | |||
| LTG × LTG_Q 4 | − | −2.848 (0.001) | −2.811 (0.001) | −2.848 (0.001) | −3.258 (0.001) | −2.618 (0.001) | −3.565 (0.001) | −3.159 (0.001) | −2.810 (0.001) | −2.434 (0.001) | |||
| NDFE | + | 0.241 (0.001) | 0.588 (0.001) | 0.439 (0.001) | −0.316 (0.009) | 2.037 (0.001) | |||||||
| PDFE | + | 0.703 (0.001) | 1.018 (0.001) | 0.752 (0.001) | 1.289 (0.001) | 0.472 (0.001) | |||||||
| SNDFE | + | 1.959 (0.001) | 7.718 (0.001) | 3.050 (0.001) | 2.225 (0.001) | 10.284 (0.001) | |||||||
| SPDFE | − | −3.525 (0.001) | −3.960 (0.001) | −3.567 (0.001) | −5.775 (0.001) | −2.926 (0.001) | |||||||
| Forecast error | − | −0.003 (0.001) | −0.045 (0.001) | −0.053 (0.001) | −0.054 (0.001) | −0.041 (0.001) | |||||||
| Beta | ? | 0.110 (0.001) | 0.113 (0.001) | 0.049 (0.001) | 0.139 (0.001) | ||||||||
| LTG × Beta | − | −0.555 (0.001) | −0.543 (0.001) | −0.431 (0.001) | −0.627 (0.001) | ||||||||
| Volatility | − | −0.292 (0.001) | −0.278 (0.001) | −0.007 (0.001) | −0.230 (0.001) | ||||||||
| LTG × Volatility | ? | 0.552 (0.001) | 0.680 (0.001) | 0.226 (0.001) | 1.178 (0.001) | ||||||||
| LogMV | + | −0.026 (0.001) | −0.025 (0.001) | −0.030 (0.001) | −0.013 (0.001) | ||||||||
| BM | ? | −0.136 (0.001) | −0.104 (0.001) | −0.139 (0.001) | −0.048 (0.001) | ||||||||
| Industry effects | No | Yes | No | No | Yes | No | No | ||||||
| Year effects | No | Yes | No | No | Yes | No | No | ||||||
| n | 575 727 | 291 834 | 575 727 | 370 909 | 284 655 | 188 677 | 186 482 | 96 687 | 95 581 | ||||
| Adjusted R2 | 0.137 | 0.194 | 0.138 | 0.156 | 0.197 | 0.168 | 0.179 | 0.097 | 0.116 | ||||
- Panel A of the table presents the coefficient estimates and p-values (in parentheses) of Equation (6a). The sample period is January 1995–December 2012. Models 1–10 of the panel report the results of the OLS regression tests that employ monthly consensus stock recommendation as the dependent variable. REC can be any value between 1 and 5, with the favourableness increasing from ‘strong sell’ to ‘strong buy’. Model 11 reports the estimates of the ordered multinomial regression analysis that employs the quintile ranking of consensus stock recommendation as the dependent variable. Panel B of the table presents the coefficient estimates and p-values (in parentheses) of Equation (6b). Following Petersen (2009), we adjust the standard errors of the regression slopes in the regression tests of the table for the possible dependence in residuals by clustering standard errors on firm and month dimensions. LTG2, square value of LTG; SNDFE, the square of DFE when DFE is negative and 0 otherwise; SPDFE, the square of DFE when DFE is positive and 0 otherwise; LTG_Q1, indicator variable taking the value of 1 when the LTG forecast falls into the 1st (low) quartile of LTG, and 0 otherwise; LTG_Q4, indicator variable taking the value of 1 when the LTG forecast falls into the 4th (high) quartile of LTG, and 0 otherwise; LTG × LTG_Q1, interaction variable between LTG and the indicator variable LTG_Q1; LTG × LTG_Q4, interaction variable between LTG and the indicator variable LTG_Q4; Industry effects, vector of industry indicator variables based on the GICS level-1 classification; Year effects, vector of calendar year indicator variables. POSTY06, indicator variable taking the value of 1 when the consensus recommendation is estimated after December 2006, and 0 otherwise. LTG × LTG_Q1 × POSTY06, interaction variable between LTG × LTG_Q1 and POSTY06. See also Table 2 for variable definitions.
Models 5–7 analyse the relationships between stock recommendations and the mean reversion variables (NDFE, PDFE, SNDFE and SPDFE) that are intended to serve as proxies to capture analysts’ expectations about earnings growth beyond the 3- to 5-year LTG forecast horizons, and hence also serve as a proxy for the latent variable RLTG. The coefficients on the mean reversion variables are largely consistent with predictions, suggesting that analysts do take account of this longer run aspect of profitability. The relationship of recommendations to the mean reversion variables is little affected by the addition of various controls that reflect relevant aspects of uncertainty (forecast error, book-to-market, firm size), and the relationships between the risk variables and recommendations are largely consistent with predictions except for Size. In particular, Volatility is significant and negative in Models 8–10, suggesting that firms with volatile stock prices tend to receive less favourable stock recommendations. The coefficient on Beta is positive in all models. However, the coefficient on LTG × Beta is significant and negative in Models 9 and 10. A possible explanation for this result is that analysts tend to be cautious about firms whose future earnings have a high degree of covariance with the overall economy (Fama and French, 1995) and consequently award them with less favourable recommendations. From this we infer that Beta enters analysts’ stock rating decision-making primarily through its adverse mediating effect on the LTG sensitivity of stock recommendation.
Stock recommendations are measured on an ordinal scale. This raises the question of whether the LTG2 variable is capturing a truncation effect caused by the upper bound on the ratings scale. To assess the sensitivity of our results to this feature, we use an Ordered Multinomial Logit regression (Model 11) to test the nonlinear relationship between LTG and stock recommendations, measured as the quintile ranking of consensus stock recommendations (a 5-point scale discrete variable). Consistent with the OLS regressions, the results for Model 11 show that the likelihood of obtaining more favourable recommendations still decreases with LTG2. This finding suggests that the OLS results cannot simply be attributed to the way recommendations have been scaled. We run all regression tests in panel A of Table 4 for the subperiods 1995–2000, 2001–2006 and 2007–2012. Untabulated results reveal that these results hold for all three subperiods exception that SNDFE has the wrong sign for the period 1995–2000.
Panel B of Table 4 reports results from estimating Equation (6b), a model that allows LTG to vary depending on whether the observation falls in the lowest quartile or not. Models 1–5 report the regressions based on the full 1995–2012 sample period. Contrary to prediction, the coefficient on LTG × LTG_Q1 is negative in both Model 1 and Model 2, the latter model including the mean reversion variables, risks and control variables. However, when allowance is made in Models 3–5 for whether the observation is in the pre- or post-financial crisis period by the inclusion of the interaction variable LTG × LTG_Q1 × POSTY06, it is apparent that the explanation can be found in the changed economic conditions. This can be seen most clearly by comparing the results for Models 2 and 5 that include all explanatory variables in Equation (6b). The coefficient on LTG × LTG_Q1 in Model 5 is positive as predicted, suggesting that firm–months in the bottom quartile of LTG forecasts receive more favourable stock recommendations prior to the financial crisis. However, the coefficient on LTG × LTG_Q1 × POSTY06 is negative, indicating that the predicted relationship broke down after the crisis. This finding is consistent with the interpretation that, prior to the financial crisis, analysts expect future earnings of firms in the bottom quartile of LTG forecasts to grow at an increased rate over longer horizons due to the reversals in profitability, and they issue more favourable recommendations accordingly, but their beliefs that mean reversion would apply were punctured by the crisis. These results are confirmed in the separate regressions based on the subperiods 1995–2006 and 2007–2012 (Models 6–9). The reasons are unclear, but may be due to how much analyst recommendations changed after the crisis. The relationships between recommendations and SG, the nonlinear mean reversion variables and the risk measures are qualitatively the same as those reported in panel A.
Our theoretical framework suggests that LTG is an important determinant of stock recommendations. It may also be a function of stock recommendations. If LTG and recommendations are jointly determined, OLS parameter estimates could be biased and inconsistent. To investigate the potential endogeneity between recommendations and LTG, and its potential influence on the coefficient estimates of our regression analyses, we use simultaneous equations methods to explore our main predictions. The results of a Hausman (1983) specification error test confirm that LTG and stock recommendations are endogenous. We therefore use a two-stage least-squares (2SLS) regression analysis to rerun the main regression tests in Table 4. The untabulated results of the simultaneous-equation specification are consistent with those reported in previous sections. Hence, we conclude that the findings and inferences reported in previous sections hold after the endogeneity bias between REC and LTG is taken into account.
4.3 Relationship between profitability of stock recommendations and analysts’ consideration of really long-term growth and risk
In this section, we empirically explore whether analysts’ incorporation of RLTG into their recommendation decisions positively affects the profitability of those recommendations. Risk analysis is undoubtedly an important part of securities appraisal. We also analyse how analysts’ risk analysis can impact the profitability of their stock recommendations. Specifically, we seek to answer two questions: (i) Do analysts who consider the really long-term growth make more profitable stock recommendations than those who do not? (ii) Do analysts who consider both really long-term growth and risk make more profitable stock recommendations? We use individual analyst recommendations and earnings forecasts along with LTG for this empirical analysis.
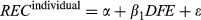(7)
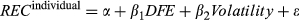(8)We examine the returns of stock recommendations issued by the 1262 analysts for whom we have the necessary data. We calculate accumulative abnormal returns from event date t (the announcement day of the recommendation) to t + s. We examine three return periods: a short 3-day event window (t − 1 to t + 1), a 1-month window (t + 30) and a 12-month window (t + 365). Following previous studies (Womack, 1996; Bradshaw, 2004), we calculate the size-adjusted abnormal return for a given firm's recommendation by subtracting the appropriate CRSP market capitalisation decile returns from the firm's raw return given on the appropriate CRSP NYSE/AMEX/NASDAQ index data file. We also calculate standard deviation-adjusted abnormal returns by subtracting the appropriate CRSP standard deviation decile portfolio returns from the raw return of the sample firm given on the CRSP NYSE/AMEX or NASDAQ index file. We follow Ertimur et al. (2007) by notionally investing $1 in the stock for ‘buy’ and ‘strong buy’ recommendations, and going short $1 for ‘hold’, ‘sell’ and ‘strong sell’ recommendations.
We use a multivariate regression analysis to examine the relationship between abnormal returns of recommendations and indicator variables ANYST_RLTG and ANYST_RLTGVOL, which measure analyst incorporation of RLTG and risk. We include the following characteristic variables at the brokerage firm, analyst, and firm level in our regressions to control for factors that could affect recommendation profitability. We include the natural logarithm of the number of analysts employed by a brokerage firm (LogBSIZE) to control for brokerage firm size because analysts at large brokerage firms have access to more resources, can benefit from their firms’ stronger marketing abilities and they appear to issue more profitable stock recommendations (Stickel, 1995; Clement, 1999; Ertimur et al., 2007). As proxies for analyst time constraints, the number of firms and industries covered by an analyst are expected to negatively impact forecast accuracy and recommendation profitability (Clement, 1999; Ertimur et al., 2007). We therefore include the number of firms an analyst covers in a given year (N_FIRM), as well as the number of industries covered by the analyst in a given year (N_IND). We include the number of EPS1 forecasts issued by an analyst for a firm in a given year (FREQEPS) to proxy for analyst effort (Clement, 1999; Jung et al., 2012). We use the number of years an analyst has issued recommendations for a firm (FIRM_EXP), which is a firm-specific measure of experience, to control for analyst experience (Clement, 1999). Ertimur et al. (2007) show that earnings forecast accuracy is positively associated with recommendation profitability. We measure analyst forecast accuracy (ACCUR), as the absolute value of the difference between the actual earnings of a given fiscal year and the analyst's last EPS1 forecast for that year, deflated by the absolute value of actual earnings. Firms with a high level of analyst following have better information environments, and therefore, stock reactions to recommendations of these firms are expected to be relatively weaker (Stickel, 1995). We use the number of analysts following a firm in a given year (N_ANYST) to capture this effect. We include the natural logarithm of the market value of the last fiscal year (LogMV) because market reactions to stock recommendations of small firms with poorer information environments tend to be stronger (Stickel, 1995). We include in the regression model the book-to-market ratio of the last fiscal year (BM) and an indicator variable of loss-making (LOSS) that is equal to 1 if the earnings before extraordinary items of the firm in a given year is negative, and 0 otherwise.
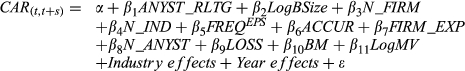(9a)
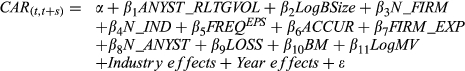(9b)We collect individual analyst stock recommendations, as well as EPS1, and LTG forecasts from I/B/E/S for the 1995–2012 sample period. Accounting data come from COMPUSTAT, and stock return data come from CRSP. Among the 1262 analysts in our sample, we find that 782 consider or are likely to consider RLTG when making recommendations (ANYST_RLTG = 1), and the remaining 480 do not or are not likely to incorporate RLTG or earnings changes over time (ANYST_RLTG = 0). The two groups issued a total of 240 366 stock recommendations during the sample period.
We perform univariate tests of mean and median differences of abnormal returns, and the control variables between the two analyst groups and the untabulated findings are as follows. The recommendations issued by the ANYST_RLTG = 1 group analysts tend to be more favourable. The means of the size-adjusted abnormal returns on the recommendations issued by analysts who tend to consider RLTG are statistically significantly higher than those of the recommendations issued by analysts who do not take account of RLTG. Furthermore, for all three return periods, the means and the medians of the standard deviation-adjusted returns of the ANYST_RLTG = 1 group are both statistically higher than those of the ANYST_RLTG = 0 group. Analysts who tend to take account of RLTG are generally employed by larger brokerage firms, and they appear to follow fewer industries and have more firm-specific experience than those who do not capture RLTG. They also appear to issue earnings forecasts more frequently and with lower forecast errors than those who do not incorporate RLTG. Finally, analysts who tend to take RLTG into account generally cover smaller firms with relatively lower analyst followings.
The results for Equation (9a) are reported in panel A of Table 5. The R2s of the regressions are low, indicating (unsurprisingly) that stock returns are affected by many sources of news in addition to analysts’ forecasts. The resultant coefficient estimates are unbiased but therefore lack precision. With that caveat in mind, the results reveal that the ANYST_RLTG coefficient is statistically significant at least at the 10 percent confidence level for all return periods, suggesting that analysts who consider earnings growth beyond the next 3–5 years are able to provide more profitable stock recommendations to investors. The direction of the effect of the control variables is broadly as expected. The results for Equation (9b) are reported in panel B of Table 5. Overall, the results for ANYST_RLTGVOL are weaker than for ANYST_RLTG, but they tend to suggest that analysts who take account of both RLTG and risk generate higher abnormal returns. The results of control variables are similar to those in panel A of Table 5.
Panel A: RLTG and stock recommendation profitability
 (9a) |
||||||
|---|---|---|---|---|---|---|
| Dependent variable | Size-adjusted abnormal returns | Standard deviation-adjusted abnormal returns | ||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 |
| 3-day | 1-month | 12-month | 3-day | 1-month | 12-month | |
| Intercept | 0.033 (<0.001) | 0.049 (<0.001) | 0.129 (<0.001) | 0.040 (<0.001) | 0.054 (<0.001) | 0.043 (0.015) |
| ANYST_RLTG | 0.002 (0.001) | 0.002 (0.004) | 0.007 (0.078) | 0.002 (0.001) | 0.003 (0.006) | 0.006 (0.100) |
| LogBSIZE | 0.000 (0.161) | 0.000 (0.542) | −0.005 (0.001) | 0.000 (0.099) | 0.000 (0.386) | 0.002 (0.319) |
| N_FIRM | 0.000 (0.014) | 0.000 (0.865) | 0.000 (0.820) | 0.000 (0.034) | 0.000 (0.833) | 0.000 (0.141) |
| N_IND | −0.001 (<0.001) | −0.001 (0.001) | −0.002 (0.072) | −0.001 (<0.001) | −0.001 (<0.001) | −0.003 (0.001) |
| FREQ EPS | 0.001 (<0.001) | 0.001 (<0.001) | 0.001 (0.079) | 0.001 (<0.001) | 0.001 (<0.001) | 0.002 (0.001) |
| ACCUR | 0.003 (<0.001) | 0.004 (0.004) | −0.016 (0.029) | 0.007 (<0.001) | 0.005 (0.001) | 0.008 (0.221) |
| FIRM_EXP | 0.000 (<0.001) | 0.000 (<0.001) | 0.002 (<0.001) | 0.000 (0.006) | 0.000 (<0.001) | 0.001 (<0.001) |
| N_ANYST | 0.000 (0.129) | 0.000 (0.578) | 0.000 (0.322) | 0.000 (0.006) | 0.000 (0.492) | 0.001 (0.026) |
| LOSS | 0.001 (0.106) | 0.003 (0.003) | −0.022 (0.002) | 0.002 (0.004) | 0.004 (0.002) | −0.003 (0.666) |
| BM | 0.000 (0.748) | 0.002 (0.124) | 0.017 (0.011) | −0.001 (0.279) | 0.003 (0.059) | 0.039 (<0.001) |
| LOGMV | −0.004 (<0.001) | −0.006 (<0.001) | −0.013 (<0.001) | −0.005 (<0.001) | −0.006 (<0.001) | −0.011 (<0.001) |
| Year effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Industry effects | Yes | Yes | Yes | Yes | Yes | Yes |
| n | 141 473 | 146 984 | 147 540 | 149 569 | 151 116 | 149 350 |
| Adjusted R2 | 0.023 | 0.011 | 0.005 | 0.020 | 0.010 | 0.005 |
Panel B: RLTG, risk and stock recommendation profitability
 (9b) |
||||||
| Dependent variable | Size-adjusted abnormal returns | Standard deviation-adjusted abnormal returns | ||||
| Model | 1 | 2 | 3 | 4 | 5 | 6 |
| 3-day | 1-month | 12-month | 3-day | 1-month | 12-month | |
| Intercept | 0.034 (<0.001) | 0.050 (<0.001) | 0.112 (<0.001) | 0.043 (<0.001) | 0.050 (<0.001) | 0.044 (0.012) |
| ANYST_RLTGVOL | 0.001 (0.071) | 0.001 (0.146) | 0.002 (0.545) | 0.001 (0.078) | 0.001 (0.103) | 0.007 (0.044) |
| LogBSIZE | 0.000 (0.103) | 0.000 (0.423) | 0.000 (0.886) | 0.001 (0.091) | 0.000 (0.175) | 0.002 (0.280) |
| N_FIRM | 0.000 (0.009) | 0.000 (0.900) | 0.000 (0.421) | 0.000 (0.032) | 0.000 (0.863) | 0.000 (0.122) |
| N_IND | −0.001 (<0.001) | −0.001 (0.001) | −0.002 (0.024) | −0.001 (<0.001) | −0.001 (<0.001) | −0.003 (0.001) |
| FREQ EPS | 0.001 (<0.001) | 0.001 (<0.001) | 0.002 (<0.001) | 0.001 (<0.001) | 0.001 (<0.001) | 0.002 (0.001) |
| ACCUR | 0.003 (<0.001) | 0.000 (0.646) | 0.001 (0.093) | 0.000 (0.194) | 0.000 (0.412) | 0.008 (0.222) |
| FIRM_EXP | 0.000 (<0.001) | 0.000 (<0.001) | 0.002 (<0.001) | 0.000 (0.017) | 0.000 (<0.001) | 0.001 (<0.001) |
| N_ANYST | 0.000 (0.143) | 0.000 (0.577) | 0.001 (0.001) | 0.000 (0.006) | 0.000 (0.303) | 0.001 (0.026) |
| LOSS | 0.001 (0.101) | 0.004 (0.004) | 0.005 (0.204) | 0.003 (0.003) | 0.005 (<0.001) | −0.003 (0.667) |
| BM | 0.000 (0.739) | 0.002 (0.114) | 0.022 (<0.001) | −0.001 (0.560) | 0.002 (0.077) | 0.039 (<0.001) |
| LOGMV | −0.004 (<0.001) | −0.006 (<0.001) | −0.015 (<0.001) | −0.005 (<0.001) | −0.006 (<0.001) | −0.011 (<0.001) |
| Year effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Industry effects | Yes | Yes | Yes | Yes | Yes | Yes |
| n | 141 473 | 148 193 | 144 856 | 150 850 | 149 775 | 149 350 |
| Adjusted R2 | 0.023 | 0.011 | 0.007 | 0.019 | 0.011 | 0.006 |
-
This table reports the regression results of the relationships between the profitability of recommendations and analyst incorporation of RLTG and risk. Panel A reports the results of estimating Equation (9a). Panel B reports the results of estimating Equation (9b). ANYST_RLTG, 1 if the estimate of DFE in Equation 8 for an analyst is negative, and 0 otherwise; ANYST_RLTGVOL, 1 if the estimates of DFE and Volatility in Equation (9) for an analyst are both negative, and 0 otherwise; RECindividual, stock recommendations issued by individual analysts on the I/B/E/S database;
, size-adjusted cumulative abnormal stock return over the three trading days beginning on the day prior to the stock recommendation announcement day t. We calculate the size-adjusted returns by subtracting the appropriate CRSP market capitalisation decile returns from the stock's raw returns;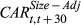 
, size-adjusted cumulative abnormal stock return over the 30 days following the stock recommendation announcement day t; 
, size-adjusted cumulative abnormal stock return over the 12 months following the recommendation announcement day t; 
, standard deviation decile-adjusted cumulative abnormal stock return over the 3 days beginning on the trading day prior to the stock recommendation announcement day t. We calculate the standard deviation decile-adjusted abnormal returns by subtracting the appropriate CRSP standard deviation decile returns from the stock's raw returns;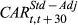 
, standard deviation decile-adjusted cumulative abnormal stock return over the 30 days following the stock recommendation announcement day t; 
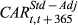, standard deviation decile-adjusted cumulative abnormal stock return over the 12 months following the stock recommendation announcement day t; N_FIRM, number of firms covered by an analyst in a given year; N_IND, number of industries covered by an analyst in a given year; LogBSIZE, nature log of the number of analysts employed by a brokerage firm in a given year; BM, book-to-market ratio; LogMV, nature log of the market capitalisation of the last fiscal year; LOSS, 1 if the firm's earnings before extraordinary items is negative in the previous year, and 0 otherwise; N_ANYST, number of analysts following a specific firm in a given year; FIRM_EXP, number of years the analyst issues stock recommendation for a specific firm; FREQEPS, number of 1-year-ahead earnings per share forecasts issued by an analyst for a given firm in a given year; ACCUR, accuracy of the analyst's earnings forecast, measured as the absolute value of the difference between the actual earnings and the analyst's last earnings forecast, deflated by the absolute value of the actual earnings.
Our analysis uses DFE to proxy for RLTG. As a test of the reliability of this measure, we calculate the realised actual earnings growth rate over the next year, 5 years and 6–10 years8 in order to shed light on the extent to which DFE predicts actual earnings growth rates in the future. Untabulated results reveal that DFE is negatively associated with the realised actual earnings growth rates in the subsequent 10 years. We interpret this as suggesting that above (below) mean profitability is associated with declines (rises) in the realised actual earnings growth rates, which suggests that DFE is indeed a reasonable proxy for very-long-run profitability. In addition, we perform regressions to examine the relationship between firms’ raw returns and DFE. The untabulated results show that DFE is negatively associated with both 1- and 12-month returns, thereby suggesting that the stock market prices the change in the earnings growth rate over time correctly and in a way that is consistent with how it is related to analyst recommendations.
5 Summary and concluding remarks
Our study aims to enhance the understanding of analysts’ stock recommendation decisions. We present a valuation framework that provides a way of thinking about the linkages between analyst recommendations and their expectations about earnings growth over the short-term, medium-term and the really long-term future. We present results suggesting that while positive, the effect of LTG on stock recommendations declines the greater is LTG, which we attribute to the attenuating effect of earnings growth beyond the LTG forecast horizons (RLTG) on the analysts’ value estimates for the stock, and hence on their stock recommendations. For the first time in the literature, we employ profitability mean reversion variables from prior empirical literature to proxy for analysts’ unobservable expectations about earnings growth beyond the LTG forecast horizons. We show how RLTG is associated with analysts’ stock recommendations and that the effort analysts exert to study earnings growth beyond the LTG forecast horizons and risk enhances recommendation profitability.
To summarise, our study provides insights into analysts’ stock recommendation decisions. Our findings suggest that it is important for empirical studies to explicitly recognise the really long-term growth factor when examining the relationship between stock returns and firms’ future earnings and growth. Our proxy for the really long-term growth predicts the realised actual earnings growth rates over the next 10 years, and thus could potentially act as a proxy for this latent variable. Furthermore, our study provides additional evidence that analysts’ fundamental analyses, such as investigations into firms’ growth prospects and risk, promote the efficient allocation of financial resources in the capital market.
Notes
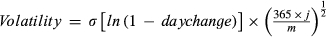, where σ is standard deviation; j represents the number of business days in the period; and m represents the number of days in the period.
