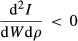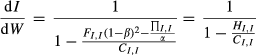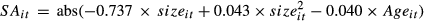Investment–cash flow sensitivity measures investment thirst, but not financial constraint
Abstract
Literature streams disagree about the capacity of investment–cash flow sensitivity (ICFS) to measure both investment thirst and financial constraint. We argue that ICFS measures the former but not the latter. Therefore, we use Fazzari et al.'s study (1988) to develop a model to test the relationship between ICFS and financial constraint, but extend that model using Kornai (1979) to include investment thirst. We demonstrate: because the ICFS–financial constraint relationship varies, ICFS cannot measure financial constraint. Conversely, using a natural experiment of China's Four Trillion Stimulus policy, we show ICFS significantly and positively correlates with investment thirst after controlling for financial constraint.
1 Introduction
The concept of soft budget constraint and investment thirst was first introduced by Kornai (1979, 1980, 1986). The two concepts are closely linked with investment–cash flow sensitivity (ICFS). Kornai suggests that investment thirst leads to overinvestment, and this overinvestment syndrome is prominent in economies characterised by soft budget constraint. According to the previous literature, a positive relationship between ICFS and overinvestment can be pinned down.1 Thus, in this paper, we hypothesise a positive relationship between ICFS and investment thirst. We focus on the intuition and then develop a theory model to prove this positive relationship. Lastly, we test this model empirically using a sample of firms in the Chinese economy that are characterised by soft budget constraint.
ICFS was originally proposed as a measure of financial constraint in the seminal work of Fazzari et al. (1988).2 Their suggestion of a positive relationship between ICFS and investment has been supported by empirical evidence such as D'Espallier and López-Iturriaga (2009). The positive relationship, however, has been challenged by increasing evidence suggesting that less financially constrained firms are associated with greater ICFS (see Hoshi et al., 1991; Kaplan and Zingales, 1997; Beatty et al., 2007). Moreover, some recent studies based on time series evidence in the U.S. markets have found declining and disappearing trends in ICFS (see Allayannis and Mozumdar, 2004; Agca and Mozumdar, 2008; Brown and Petersen, 2009; Chen and Chen, 2012).3 These authors hence conclude that ICFS cannot be a good measure of financial constraint.
Therefore, we disentangle the relationship between ICFS, investment thirst and financial constraint under the framework of Fazzari et al. (1988) by extending that model using Kornai (1979) so as to include investment thirst. In Section 3, we show that the ICFS–financial constraint relationship varies. The varying relationship supports the finding in recent studies that ICFS cannot be a good measure of financial constraint. To ascertain the relationship between ICFS and investment thirst, we develop in Section 4 a model and prove that a hypothesised positive relation exists between them theoretically. In Section 5, we design an empirical test using a natural experiment setting of China's Four Trillion Stimulus policy announced in 2008;4 this finds a significantly positive relationship between ICFS and investment thirst after we control for financial constraint (see Section 6). Further robustness tests such as subperiod regression, using GMM estimation method instead of OLS presented in Section 7, suggest our results are robust. By taking these steps theoretically and empirically, we show that ICFS is a good firm-level measure of investment thirst.
2 Background and literature review
2.1 Soft budget constraint
According to Kornai (1979, 1980, 1986), investment thirst is driven by soft budget constraint. A soft budget constraint can occur for three reasons: first, when investors lack the wherewithal to ensure an enterprise stays on budget; second, when the investment plans proposed by the manager are ex-ante efficient; and third, when the manager overinvests at his or her own volition. The issue therefore with soft budget constraint is that it may motivate managers to follow irresponsible incentives and thus risk enterprise finance without adequate surveillance (Dewatripont and Maskin, 1995; Qian and Roland, 1998). The soft budget-constraint problem is especially prominent in transitional economies. Qian and Roland (1998) model the relationship between soft budget constraint and federalism tailored for the China economy to show that soft budget constraint significantly characterises Chinese firms. This is also why we chose Chinese markets to test the relationship.
2.2 Investment thirst, free cash flow and overinvestment
Investment thirst, therefore, arises from two particular investment approaches: first, when firms characterised by soft budget-constraint overinvest, and second, from managers’ investment impulsion for short-term gains. The often-researched relationship between overinvestment and cash flows is derived from Jensen (1986) theory paper on free cash flows (FCFs). FCFs are considered cash flows beyond those required to fund all projects with positive net-present values. Lang and Litzenberger (1989) find a significantly positive relationship between the extent of managerial overinvestment and market reaction. They conclude that overinvestment denotes that the situation firms possessing high FCFs are investing in unprofitable projects.
Furthermore, Richardson (2006) creates a measure of overinvestment to provide direct empirical evidence of a significantly positive relationship between FCFs and overinvestment. Therefore, the positive relationship between FCF and overinvestment is valid both theoretically and empirically. Vogt (1994) investigates the over- and underinvestment effects of ICFS to find that, for large firms of low dividends, ICFS signifies overinvestment, while ICFS in small firms of low dividends, it indicates financial constraint. Such evidence suggests a positive relationship between ICFS and overinvestment.
Although both streams of theories indicate a positive relationship between ICFS and overinvestment, these theories vary in three ways: (i) the investment thirst theory introduced by Kornai (1979, 1980, 1986) stresses the necessity of soft budget constraint and expansion impulsion, while Jensen (1986) FCF theory does not. Instead, Jensen attributes the main reason to the agency problem induced by free cash flows. (ii) Soft budget constraint in a firm refer to the situation whereby the manager violates his or her promises to investors about using investment cash flows previously budgeted for (e.g. the original investment plan would have been considered efficient by investors, while the investment in violation ex post is not). This occurs because of a lack of surveillance received by managers, whereas FCF is linked to investments after the investment plan promised by the manager has been executed. (iii) While we predict that investment thirst is closely related to ICFS, this is not necessarily the case for FCFs. Investment thirst induces a firm to invest eagerly, resulting in a higher level of ICFS. In contrast, FCFs without monitoring relax the direction of investments and hence do not necessarily change the sensitivity of investment–cash flows. Therefore, the point is that overinvestment caused by investment thirst is closely related to ICFS, while overinvestment caused by FCF may not be.
Our study differs from the existing literature in three significant ways. First, almost all the existing finance studies explain the overinvestment problem within the framework of the FCF theory developed by Jensen (1986).5 However, we find the investment thirst theory from the macroeconomics work of Kornai (1979, 1980, 1986) better explains the overinvestment phenomenon in transitional economies such as China.
Second, we discover that ICFS validly measures investment thirst at the firm level. In existing macroeconomics studies (see Lee et al., 2012), the ratio of incremental capital to output is commonly used to measure investment thirst at the country level. However, no analogous index at the firm or industry level has been offered. We propose that investment–cash flow sensitivity (hereafter ‘ICFS’) is a good firm-level measure of investment thirst.
Third, we find that the ICFS index combines the effects of financial constraint and investment thirst on investment, whereas many of the existing studies do not discern these two effects.6 In this paper, our empirical tests are designed in a way such that the effects of investment thirst and financial constraint on ICFS can be separated, and therefore, the relationship between investment thirst and ICFS can be directly tested.
Correspondingly, our findings enrich the literature in three main ways. First, we show the connection between ICFS and investment thirst theoretically. For example, we propose that ICFS is more closely related to investment thirst than financial constraint. Second, we present evidence to demonstrate that in a transitional economy like China, in which firms face severe financial constraint and exhibit it concurrently with investment thirst, ICFS measures investment thirst after financial constraint is controlled for. Third, using the natural experiment setting we have chosen for this research offers two benefits: it makes our empirical results less prone to endogeneity problems;7 second, the empirical findings support our conjecture that ICFS is a good measure of investment thirst.
3 The relationship between ICFS, investment thirst and financial constraint
According to Kornai (1979, 1980, 1986), investment thirst is driven by two factors: the behaviour of short-term expansion in firms and soft budget constraint. The former is related to the risk-seeking preference of managers, while the latter relates to the misuse of investment funds by managers provoked by a lack of surveillance from investors. For example, the manager may be directing budgeted funds to unplanned investments that violate his/her ex-ante promises to shareholders.
In this section, we illustrate the relationship between ICFS and investment thirst figuratively, followed by a model in the next section to identify their relationship in theory. We propose that a higher level of ICFS found in a firm at least relates to one of the four following factors: (i) a manager with a higher risk-seeking preference, (ii) more severe levels of agency problems caused by soft budget constraint, (iii) more investment opportunities or (ii) higher levels of financial constraint.
Following Fazzari et al. (1988), Figure 1a depicts the relationship between the marginal cost of investment financing and the total amount of investment financing. The difference between marginal cost of internal financing and marginal cost of external financing, that is, the slope of the dashed line CI, indicates the level of financial constraint. The solid line HI represents the demand line of investment financing (as well as the marginal benefit from investment for a firm). The ratio of ΔI/ΔW hence conveys ICFS, according to Fazzari et al. (1988).

Figure 1b plots the effect of financial constraint on ICFS. When the firm encounters a higher level of financial constraint, the line CI moves rightward to C’I and becomes steeper. Moreover, if the HI line remains at the same position, the ratio ΔI/ΔW (indicating ICFS) will rise, as discussed in Fazzari et al. (1988).
However, in most situations, line HI would change with line CI rather than maintaining its original position. In reality, higher levels of financial constraint result in not only a higher valued slope of CI, but also higher uncertainty in CI. Therefore, the increase in financial constraint is not just closely related to rising external financing costs, but also shows that an increase in investment risk would change the demand line, HI. Specifically, when managers encounter higher levels of financial constraint, they will also change investment demand, which makes HI steeper and move to the left; H’I is so depicted in Figure 1c. Consequently, the ratio of ΔI/ΔW would shrink and thus not change given the level of financial constraint.
To sum up, the value of ICFS depends on the comparative slope of HI to CI. The slope of CI depends on the level of financial constraint, while the slope of HI depends on three other factors besides financial constraint, notably: (i) the short-term expansion behaviour determined by the risk preference of managers: as indicated in Figure 1c, the higher the risk-seeking preference of a manager, the flatter the HI line will be and will thus move further to the rightward position; (ii) soft budget constraint can cause investor infringement: soft budget constraint by nature occurs as a type of agency problem between investors of a firm and the firm manager. Therefore, higher levels of soft budget constraint correspond to a flatter and more rightward position of HI;8 and (iii) investment opportunities: more investment opportunities push HI further to the right-hand side and flatten it. Because previous works on ICFS emphasise the impact of financial constraint and investment opportunities but overlook the role of soft budget constraint and managers’ risk-seeking preferences, this paper approaches this research accordingly.
Soft budget constraint in a firm and the risk-seeking preference of its manager are related to the characteristics of investment thirst (Kornai, 1979, 1980, 1986). As previous studies on ICFS focus mainly on investment opportunities and financial constraint in explaining the level of ICFS, little attention has been allocated to soft budget constraint and risk-seeking preferences of a manager. In particular, research into soft budget constraint after controlling for investment opportunities with measures, such as Tobin's Q and sales growth rates, has led those involved to debate the relationship between ICFS and financial constraint acrimoniously.9 From what is shown above, financial constraint, affects the slope of HI and CI simultaneously, thus suggesting that the relationship between ICFS and financial constraint is unclear. On the other hand, soft budget constraint and managers’ risk-seeking preferences only affect HI, but not CI. Consequently, ICFS changes in the same direction as investment thirst. Furthermore, even if financial constraint can affect ICFS after controlling for the effect using reliable financial constraint measures documented in the literature – we use the SA index and the WW index to control for financial constraint in the regression model used in Section 4 – the effect of investment thirst on ICFS can be separated out and tested directly.
4 The theory model
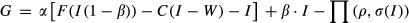 (1)
(1)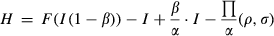 (2)
(2)α denotes the incentive payment from investment returns for the manager. I stands for the amount of investment. β (0 < β < 1) represents the level of soft budget constraint and the agency problem between the manager and investors. β·I denotes the private benefits to the manager exploited from investment I which result from the problem of soft budget constraint in a firm. W denotes the level of internal investment and operating cash flow, with I-W reflecting external investment. C (·) is the cost of investment, which is determined by external funding (I-W). ρ defines the level of risk-aversion of the manager. σ (·) denotes the risk of investment, which is a monotone increasing function of I, 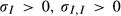 . Π(·) represents the utility loss accounting for risk, which involves a monotone increasing function of ρ and σ.
. Π(·) represents the utility loss accounting for risk, which involves a monotone increasing function of ρ and σ.
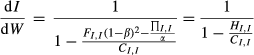 (3)
(3)Consistent with the above figures, Equation 3 depicts that the value of ICFS depends on the slopes of HI and CI. In detail, it is related to four factors: (i) risk preference of the manager denoted by ΠI,I, (ii) level of soft budget constraint denoted by β, (iii) investment opportunities denoted by FI,I and (iv) financial constraint denoted by CI,I. As the increase in CI,I usually enhances HI,Iby increasing σ (·), it is difficult to detect the level of financial constraint using ICFS.
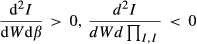 (4)
(4)Combining Equations 4 and 5, we have therefore shown that ICFS arises from investment thirst, rather than financial constraint. ICFS can then be used to detect investment thirst if the effect of financial constraint can be controlled for.12 In the next two sections, we build our regression model and test this theoretical hypothesis.
5 Empirical tests
5.1 The regression model
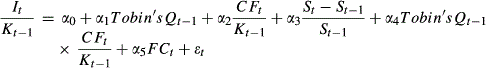 (6)
(6)Where It/Kt−1 represents the firm's capital expenditure It scaled by beginning-of-period total asset, Kt−1; Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1×CFt/Kt−1 here according to Vogt (1994), of which the sign of the coefficient represents the characteristics of ICFS.13 In detail, if the sign is negative, we can deduce that ICFS rises while investment opportunities decline, and that ICFS should be correlated with soft budget constraint, firm risk-seeking behaviour and overinvestment.14 Hence, introducing the interaction term here can help identify the relationship between ICFS and investment thirst. We also include year- and industry-fixed effects.
5.2 Data and sample selection
To determine the relationship between ICFS and investment thirst, we select a sample of Chinese publicly listed firms for a number of reasons. First, according to Kornai (1979, 1980, 1986) and Qian and Roland (1998), the problem of investment thirst usually arises from transitional economies characterised by soft budget constraint. Indeed, China is the largest emerging and transitional economy in the world. Second, Chinese firms might be facing severe investment thirst and financial constraint problems at the same time, which could provide benefits in testing wherein ICFS can be a good proxy for investment thirst. For example, an International Monetary Fund (IMF) report entitled ‘Is China Over-Investing and Does it Matter?’ suggests that China has experienced prominent overinvestment problems over the last decade; this conclusion draws on the evidence of comparing the incremental capital–output ratio among a large numbers of countries (Lee et al., 2012). Meanwhile, according to a series of surveys conducted by the Development Research Center of State Council in China, 2007 to 2012, more than 90 percentage of managers in Chinese firms believe they are facing serious financial constraint.15 These two pieces of evidence indicate that financial constraint and investment thirst co-exist in Chinese firms.
Although the sample for our research was set to be derived over 2001 to 2012, the regression model was narrowed to a sample period of 11 years from 2002 to 2012, after we took into account that some variables are 1-year lagged. We also eliminated observations from the finance industries as well as those missing values in the variables used in the study. Our final sample hence consists of 15,576 firm-year observations from 2297 firms in 30 provinces of China. We obtained all accounting data from the China Stock Market and the Accounting Research (CSMAR) database, which is widely used in China-related research.
5.3 Summary statistics
We split the sample into four groups according to the quartile values of financial constraint in each year. In Panels A and B of Table 1, we present summary statistics of each subsample based on the WW index of Whited and Wu (2006) and the SA index developed by Hadlock and Pierce (2010) to denote the degree of financial constraint for each.16 The two studies suggest that the WW index is supposed to be positively related to the level of financial constraint, whereas the SA index has a reverse relation to financial constraint. In Panel A, while we observe Tobin's Qt−1 increases with a rising value in WW index and financial constraint, Sizet and (St−St−1)/St−1 decrease with the augment of the WW index, It/Kt−1 and CFt/Kt−1 do not show any obvious relationship with the WW index. In Panel B, we observe that the coefficient of Tobin's Qt−1 is decreasing with the value of SA index goes up (and augment of financial constraint), and It/Kt−1, Sizet, CFt/Kt−1, and (St−St−1)/St−1 increase when the value in SA index goes up (and decreasing financial constraint). The results on the SA index are more persistent than those of using the WW index, which indicate the SA index provides a better measure of financial constraint than the WW index in this study. Moreover, in Panel B of Table 1, the value of Tobin's Qt−1 in groups with less financial constraint (Groups 3 and 4) is lower than 1, which coincides with the definition of ‘bad firms’ in Lang and Stulz (1994) and the definition of ‘overinvestment companies’ in Lang and Litzenberger (1989).
| Panel A: four portfolios sorted on Whited and Wu (2006)'s WW index | ||||
|---|---|---|---|---|
| ← Smallest WW (Least FC) | Biggest WW (Largest FC)→ | |||
| Group 1 | Group 2 | Group 3 | Group 4 | |
| Tobin'sQ t−1 | 1.535 | 1.675 | 1.761 | 1.755 |
| I t /K t−1 | 0.056 | 0.069 | 0.065 | 0.062 |
| CF t /K t−1 | 0.059 | 0.041 | 0.043 | 0.045 |
| (S t −S t−1 )/S t−1 | 4.207 | 1.451 | 0.601 | 0.539 |
| Size t | 22.174 | 21.422 | 21.225 | 21.401 |
| SA index | 4.540 | 3.673 | 3.433 | 3.619 |
| WW index | −16.365 | −13.485 | −11.607 | −7.057 |
| Obs. | 3893 | 3897 | 3897 | 3889 |
| Panel B: four portfolios sorted on Hadlock and Pierce (2010)'s SA index | ||||
|---|---|---|---|---|
| ← Smallest SA (Largest FC) | Biggest SA (Least FC)→ | |||
| Group 1 | Group 2 | Group 3 | Group 4 | |
| Tobin'sQ t−1 | 2.343 | 1.660 | 0.064 | 0.060 |
| I t /K t−1 | 0.051 | 0.062 | 0.064 | 0.074 |
| CF t /K t−1 | 0.036 | 0.047 | 0.047 | 0.058 |
| (S t −S t−1 )/S t−1 | 0.648 | 0.254 | 1.341 | 4.566 |
| Size t | 20.274 | 21.098 | 21.766 | 23.074 |
| SA index | 2.358 | 3.289 | 4.007 | 5.570 |
| WW index | −11.516 | −11.708 | −12.185 | −13.096 |
| Obs. | 3893 | 3896 | 3898 | 3883 |
- This table presents the means of the main variables in this paper in quartile groups on behalf of different levels of financial constraint (WW index or SA index). The WW index is calculated following Whited and Wu (2006), Lin et al. (2011), and Zeng and Lin (2014); the SA index is computed as in Hadlock and Pierce (2010). More detail on both indexes is given in Appendix II. Tobin's Qt−1 is defined as the previous year's Tobin's Q. It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total assets, Kt−1 (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total assets, Kt−1. sizet indicates the log of inflation-adjusted total book-assets.
- The inflation rate is obtained from the website of China's National Bureau of Statistics (http://www.stats.gov.cn/).
We hereby identify the relationship between ICFS and investment thirst in three steps: first, we need to disentangle the relationship between ICFS, financial constraint and overinvestment. By doing this, we can show that ICFS is more closely related to overinvestment than to financial constraint. Second, we offer direct evidence of the positive relationship between ICFS and a firm's risk-seeking preferences. Third, we present empirical results to show that the value of ICFS is related to soft budget -constraint and investor infringements. In particular, using the exogenous setting of a natural experiment of the ‘Four Trillion Stimulus’ policy in China, we provide valid evidence on the explanatory power of ICFS on investment thirst.
6 Empirical results
6.1 ICFS, financial constraint and overinvestment
We first divide the sample into four groups according to their degree of financial constraint (the WW index and the SA index, see Table 1). Group 1 consists of firms with the least financial constraint, while Group 4 consists of firms with the most financial constraint. In Panel A of Table 2, the sample is sorted by the value of the WW index using the regression model without the interaction term Tobin's Qt−1 × CFt/Kt−1 and the WW index (results displayed in the left-hand side of Panel A of Table 2).17 No definite pattern is observed in the relationship between the financial constraint and the coefficient of CFt/Kt−1. Nevertheless, after introducing the interaction term Tobin's Qt−1 × CFt/Kt−1 and the WW index term, we observe that the coefficients of CFt/Kt−1 in Groups 1 and 2 are larger than those in Groups 3 and 4 (results displayed in the right-hand side of Panel A of Table 2) showing that all the coefficient estimates are significant at a 1 percentage level.
| Group 1 (Least FC) | Group 2 | Group 3 | Group 4 (Largest FC) | Group 1 (Least FC) | Group 2 | Group 3 | Group 4 (Largest FC) | |
| Panel A: four portfolios sorted by Whited and Wu (2006)'s WW index | ||||||||
| Tobin's Q t−1 | −0.0026** (0.001) | −0.0007* (0.000) | −0.0035*** (0.001) | −0.0026*** (0.001) | 0.0002 (0.002) | −0.0003 (0.000) | −0.0031** (0.001) | −0.0027*** (0.001) |
| CF t /K t−1 | 0.1169*** (0.014) | 0.1324*** (0.014) | 0.1066*** (0.014) | 0.1185*** (0.015) | 0.1555*** (0.022) | 0.1499*** (0.016) | 0.1236*** (0.023) | 0.1328*** (0.018) |
| (S t −S t−1 )/S t−1 | 0.0018 (0.002) | 0.0061*** (0.002) | 0.0025 (0.002) | 0.0089*** (0.002) | 0.0017 (0.002) | 0.0061*** (0.002) | 0.0026 (0.002) | 0.0090*** (0.002) |
| Tobin's Q t−1 × CF t /K t−1 | −0.0234** (0.010) | −0.0086** (0.004) | −0.0084 (0.010) | −0.0075 (0.006) | ||||
| WW index t | 0.0001 (0.000) | 0.0078** (0.003) | −0.0038*** (0.001) | −0.0003 (0.001) | ||||
| Obs. | 3837 | 3833 | 3830 | 3813 | 3837 | 3833 | 3830 | 3813 |
| R 2 | 0.1412 | 0.1075 | 0.1026 | 0.1043 | 0.1430 | 0.1104 | 0.1060 | 0.1047 |
| Panel B: four portfolios sorted on Hadlock and Pierce (2010)'s SA index | ||||||||
| Tobin's Q t−1 | −0.0005 (0.001) | 0.0013 (0.001) | 0.0029* (0.002) | −0.0009* (0.000) | 0.0002 (0.001) | 0.0054*** (0.002) | 0.0034* (0.002) | −0.0002 (0.000) |
| CF t /K t−1 | 0.1419*** (0.018) | 0.1148*** (0.014) | 0.0427*** (0.012) | 0.0806*** (0.012) | 0.1488*** (0.024) | 0.1810*** (0.022) | 0.1400*** (0.029) | 0.0845*** (0.013) |
| (S t −S t−1 )/S t−1 | −0.0008 (0.002) | 0.0029 (0.002) | 0.0074*** (0.002) | 0.0041*** (0.002) | −0.0011 (0.002) | 0.0025 (0.002) | 0.0087*** (0.002) | 0.0042*** (0.002) |
| Tobin's Q t−1 × CF t /K t−1 | −0.0061 (0.011) | −0.0416*** (0.010) | −0.0269* (0.016) | −0.0050* (0.003) | ||||
| SA index t | 0.0025* (0.001) | 0.0065 (0.004) | −0.0003 (0.005) | 0.0161*** (0.002) | ||||
| Obs. | 3814 | 3829 | 3842 | 3822 | 3814 | 3829 | 3842 | 3822 |
| R 2 | 0.1657 | 0.1051 | 0.0694 | 0.1675 | 0.1087 | 0.0884 | 0.0895 | |
-
This table presents ICFS in quartile groups on behalf of different levels of financial constraint (WW index or SA index). The ICFS are calculated from the OLS estimators of the model:
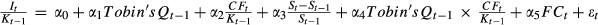 . It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt, deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. The WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); the SA index is computed as Hadlock and Pierce (2010); both are shown in Appendix II in more detail. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries with the exception of the financial industry in the CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
. It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt, deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. The WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); the SA index is computed as Hadlock and Pierce (2010); both are shown in Appendix II in more detail. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries with the exception of the financial industry in the CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
Panel B of Table 2 shows the regression results of the sample sorted on the value of the SA index. In the regression model without the interaction term Tobin's Qt−1 × CFt/Kt−1 and the SA index term, the coefficients of CFt/Kt−1 in Groups 1 and 2 are larger than those in Groups 3 and 4. After introducing the interaction term Tobin's Qt−1 × CFt/Kt−1 and the SA index term, the results only change slightly. Notably, in Panels A and B of Table 2, a significantly positive coefficient of CFt/Kt−1 is accompanied by a negative coefficient of Tobin's Qt−1 × CFt/Kt−1,18 which implies that, in China, ICFS is significantly correlated with soft budget constraint and investor infringements.
Panel A of Table 2 shows that most of the coefficients of Tobin's Qt−1 are negative and that the pattern does not change even after introducing the WW index term. On the contrary, Panel B of Table 2 shows that, after introducing the SA index term, the coefficients of Tobin's Qt−1 become larger and most become positive. Thus, we hereby argue that the ability of the SA index in discerning the effect of financial constraint and the effect of investment opportunities (e.g. Tobin's Q) is greater than that of the WW index in our sample.
Following Richardson (2006), we next sort our firms based on the quartile values of overinvestment each year.19 Each sample firm falls into one of the four exclusive groups: Groups 1 and 2 represent firms of underinvestment, while Groups 3 and 4 represent firms of overinvestment. Table 3 shows ICFS levels in each of these four groups. In Panel A of Table 3, with the sample sorted on the value of the WW index using the regression model without the interaction term Tobin's Qt−1 × CFt/Kt−1 and the WW index, we observe a significantly positive relationship between the level of investment and CFt/Kt−1. Furthermore, after introducing the interaction term Tobin's Qt−1 × CFt/Kt−1, the significant positive relationship between the level of investment and CFt/Kt−1 is unchanged. This consistency implies that ICFS is closely related to overinvestment. Furthermore, the largest coefficient of CFt/Kt−1 in Group 4 is accompanied by a significantly negative coefficient of CFt/Kt−1.
| Underinvestment | Overinvestment | Underinvestment | Overinvestment | |||||
|---|---|---|---|---|---|---|---|---|
| Group 1 | Group 2 | Group 3 | Group 4 | Group 1 | Group 2 | Group 3 | Group 4 | |
| Panel A: without the financial constraint index term | ||||||||
| Tobin's Q t−1 | −0.0015*** (0.000) | −0.0008 (0.001) | −0.0028*** (0.001) | −0.0002 (0.001) | −0.0016*** (0.000) | −0.0009* (0.001) | −0.0029*** (0.001) | 0.0010 (0.001) |
| CF t /K t−1 | 0.0621*** (0.007) | 0.0650*** (0.006) | 0.0752*** (0.008) | 0.0964*** (0.016) | 0.0582*** (0.010) | 0.0584*** (0.008) | 0.0730*** (0.013) | 0.1423*** (0.024) |
| (S t −S t−1 )/S t−1 | 0.0043*** (0.001) | 0.0010 (0.001) | 0.0001 (0.001) | 0.0037 (0.003) | 0.0043*** (0.001) | 0.0010 (0.001) | 0.0001 (0.001) | 0.0039 (0.003) |
| Tobin's Q t−1 × CF t /K t−1 | 0.0020 (0.004) | 0.0036 (0.003) | 0.0012 (0.005) | −0.0235*** (0.009) | ||||
| Obs. | 3196 | 3198 | 3199 | 3192 | 3196 | 3198 | 3199 | 3192 |
| R 2 | 0.0658 | 0.0829 | 0.1219 | 0.0523 | 0.0659 | 0.0833 | 0.1220 | 0.0545 |
| Panel B: introducing the financial constraint index | ||||||||
| Tobin's Q t−1 | −0.0017*** (0.000) | −0.0009* (0.001) | −0.0029*** (0.001) | 0.0010 (0.001) | −0.0001 (0.000) | 0.0020*** (0.001) | 0.0026*** (0.001) | 0.0042*** (0.001) |
| CF t /K t−1 | 0.0578*** (0.010) | 0.0579*** (0.008) | 0.0731*** (0.013) | 0.1422*** (0.024) | 0.0579*** (0.010) | 0.0529*** (0.008) | 0.0713*** (0.013) | 0.1247*** (0.025) |
| (S t −S t−1 )/S t−1 | 0.0043*** (0.001) | 0.0010 (0.001) | 0.0001 (0.001) | 0.0039 (0.003) | 0.0029*** (0.001) | −0.0009 (0.001) | −0.0020** (0.001) | 0.0022 (0.003) |
| Tobin's Qt−1 × CFt/K −1 | 0.0025 (0.004) | 0.0038 (0.003) | 0.0012 (0.005) | −0.0235*** (0.009) | −0.0002 (0.004) | 0.0033 (0.003) | −0.0079 (0.006) | −0.0233** (0.010) |
| WW index t | 0.0003* (0.000) | 0.0001** (0.000) | 0.0000 (0.000) | −0.0000 (0.000) | ||||
| SA indext | 0.0037*** (0.001) | 0.0059*** (0.001) | 0.0084*** (0.001) | 0.0070*** (0.001) | ||||
| Obs. | 3196 | 3198 | 3199 | 3192 | 3196 | 3198 | 3199 | 3192 |
| R 2 | 0.0680 | 0.0845 | 0.1220 | 0.0545 | 0.0885 | 0.1506 | 0.2120 | 0.0778 |
-
This table presents ICFS in quartile groups on different levels of investment. The four portfolios are sorted using Richardson (2006)'s method of measuring levels of investment. The ICFS are calculated from the OLS estimators of the model:
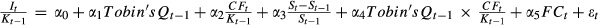 . It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), CFt is deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. The WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); SA index is computed as in Hadlock and Pierce (2010); both are shown in more detail in Appendix II. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries with the exception of the financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
. It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), CFt is deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. The WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); SA index is computed as in Hadlock and Pierce (2010); both are shown in more detail in Appendix II. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries with the exception of the financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
Panel B of Table 3 shows more evidence of the relationship between ICFS and overinvestment after adding the interaction term Tobin's Qt−1 × CFt/Kt−1 and the financial constraint index term. When using the WW index as the proxy for financial constraint, the regression results are almost the same as for the results in the right-hand side of Panel A of Table 3. The coefficient of Tobin's Qt−1 remains negative, and most coefficients of the WW index are positive, both of which illustrate that, using the WW index, it is hard to separate the effect of financial constraint and that of Tobin's Q in our sample. However, when the SA index instead of the WW index is used as the proxy for financial constraint, the regression results are different to those in Panel A of Table 3. Most of the coefficients of Tobin's Qt−1 become positive, and the coefficients of the SA index are significantly positive. Therefore, this again demonstrates that the capability of the SA index to discern both the effect of financial constraint and the effect of Tobin's Q on investment is better than the WW index for our sample.
6.2 ICFS and risk-seeking preferences
In the second step, we discuss the relationship between ICFS and risk-seeking preferences. We sort our firms based on the quartile values of relative idiosyncratic risk in each year20 and clarify all observations into four groups from the lowest risk (Group 1) to the highest risk (Group 4).21
However, it is difficult to determine the effect of risk-seeking preference on ICFS by computing ICFS directly in each group, because of its close association with soft budget constraint and investor-infringement effects. To account for the possible confounding effects, we have to manage our sample more carefully. Therefore, we construct a sample consisting of observations with low soft budget constraint only. We examine our results in Table 3 and find that the coefficient of Tobin's Qt−1 × CFt/Kt−1 in Group 2 is the largest; this suggests that firms in this group could, on average, afford the lowest soft budget constraint. However, even when we include firms in Group 2 of Table 3 in the sample, we cannot rule out the effect that firms with high soft budget constraint tend to have lower levels of soft budget constraint together, which can also lead to a high coefficient of Tobin's Qt−1 × CFt/Kt−1. To mitigate such effects as much as possible, we further examine the results in Table 2 and identify that the coefficient of Tobin's Qt−1 × CFt/Kt−1 in Group 4 is the largest. Consequently, we select the observations existing in both Group 4 of Table 2 and Group 2 of Table 3 simultaneously and divide them into four groups by their quartile values of relative idiosyncratic risk.
Table 4 presents the results of the relationship between ICFS and risk. We find the coefficients of CFt/Kt−1 in Groups 3 and 4 are commonly larger than those in Groups 1 and 2. However, as this is an obviously exceptional case, the largest coefficient of CFt/Kt−1 emerges in Column 1 of Panel B, although, at the same time, the only significant negative coefficients of CFt/Kt−1 are also shown here. Therefore, the abnormal coefficient of CFt/Kt−1 in Column 1 of Panel B not only represents the effect of risk-seeking preference, but also includes the effect of soft budget constraint and investor infringements. In short, our evidence shows a positive relationship between ICFS and risk-seeking preferences, although it is difficult to remove the effect of soft budget constraint from that of risk seeking.
| Financial constraint denoted by Whited and Wu (2006)'s WW index | Financial constraint denoted by Hadlock and Pierce (2010)'s SA index | |||||||
|---|---|---|---|---|---|---|---|---|
| Risk-lowest | Risk- 2 | Risk-3 | Risk-largest | Risk-lowest | Risk- 2 | Risk-3 | Risk-largest | |
| Panel A: three-factors model | ||||||||
| Tobin's Q t−1 | −0.0039*** (0.001) | −0.0050 (0.003) | −0.0013** (0.001) | −0.0020 (0.002) | −0.0036** (0.002) | −0.0019 (0.002) | −0.0010 (0.001) | −0.0002 (0.001) |
| CF t /K t−1 | 0.0432* (0.023) | 0.0421* (0.024) | 0.0561*** (0.019) | 0.0568* (0.029) | 0.0283 (0.017) | 0.0292 (0.019) | 0.0527*** (0.016) | 0.0316** (0.015) |
| (S t −S t−1 )/S t−1 | −0.0036 (0.004) | 0.0070* (0.004) | −0.0007 (0.002) | 0.0057 (0.004) | 0.0045 (0.004) | −0.0001 (0.004) | 0.0005 (0.002) | 0.0010 (0.003) |
| Obs. | 228 | 176 | 191 | 206 | 230 | 201 | 178 | 211 |
| R 2 | 0.2115 | 0.2151 | 0.3310 | 0.2818 | 0.1728 | 0.1391 | 0.2080 | 0.2111 |
| Panel B: five factors model | ||||||||
| Tobin's Q t−1 | −0.0038** (0.002) | −0.0053 (0.003) | −0.0025 (0.002) | −0.0033** (0.001) | −0.0017 (0.002) | 0.0008 (0.001) | 0.0016 (0.002) | 0.0015 (0.001) |
| CF t /K t−1 | 0.0843** (0.033) | 0.0156 (0.070) | 0.0680*** (0.024) | −0.0109 (0.054) | 0.0115 (0.026) | 0.0004 (0.026) | 0.0386 (0.025) | 0.0613* (0.033) |
| (S t −S t−1 )/S t−1 | −0.0036 (0.004) | 0.0073* (0.004) | −0.0008 (0.002) | 0.0053 (0.004) | 0.0032 (0.003) | 0.0001 (0.003) | 0.0001 (0.003) | −0.0000 (0.003) |
| Tobin's Q t−1 × CF t /K t−1 | −0.0262* (0.014) | 0.0178 (0.049) | −0.0067 (0.009) | 0.0337 (0.027) | 0.0105 (0.013) | 0.0136** (0.007) | 0.0066 (0.010) | −0.0130 (0.010) |
| WW index t | 0.0001 (0.001) | −0.0000 (0.001) | −0.0000 (0.001) | −0.0006 (0.001) | ||||
| SA indext | 0.0099*** (0.003) | 0.0169*** (0.004) | 0.0103*** (0.003) | 0.0103*** (0.002) | ||||
| Obs. | 228 | 176 | 191 | 206 | 230 | 201 | 178 | 211 |
| R 2 | 0.2180 | 0.2161 | 0.3327 | 0.2945 | 0.2201 | 0.2361 | 0.2503 | 0.2836 |
-
This table presents ICFS in quartile groups at different levels of relative idiosyncratic risk. The ICFS are calculated from the OLS estimators of the model:
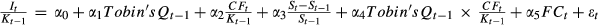 . It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. The WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); the SA index is computed as in Hadlock and Pierce (2010); and both are shown in Appendix II in more detail. Industry and year fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. We select the observations existing in both Group 4 of Table 2 and Group 2 of Table 3 simultaneously, and divide them into four groups by their quartile value of relative idiosyncratic risk. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
. It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. The WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); the SA index is computed as in Hadlock and Pierce (2010); and both are shown in Appendix II in more detail. Industry and year fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. We select the observations existing in both Group 4 of Table 2 and Group 2 of Table 3 simultaneously, and divide them into four groups by their quartile value of relative idiosyncratic risk. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
Similar to Table 3, when using the WW index to denote financial constraint in Table 4, we still observe the coefficient estimate of Tobin's Qt−1 being negative, whereas most of the coefficient estimates of the WW index are positive. This means that, with the WW index, separating the effect of financial constraint and that of Tobin's Q in our sample is again difficult. Additionally, when we use the SA index as the proxy for financial constraint, the sign of Tobin's Qt−1 in most cases becomes positive, and the coefficients of the SA index are significantly positive. Again, we find the ability of the SA index in discerning the financially constrained effect and Tobin's Q effect on investment is better than the WW index in our sample.
6.3 ICFS, soft budget constraint and Investor infringements
Table 5 presents the regression results of ICFS in each year from 2002 to 2012. Panel A shows both the results for ICFS from the regression model without the interaction term of Tobin's Qt−1 × CFt/Kt−1 and the financial constraint proxy. We do not find any obvious pattern in the value of ICFS coefficient estimates. After introducing the interaction term Tobin's Qt−1 × CFt/Kt−1, we find that the coefficients of CFt/Kt−1 are significant and increasing in the three periods of 2002–2004, 2007–2008 and 2009–2012. We note that they are insignificant in 2005 and 2006 based on the results shown in Panel B of Table 5. Furthermore, most of the significant coefficient estimates on CFt/Kt−1 are accompanied by negative coefficient estimates on Tobin's Qt−1 × CFt/Kt−1, which implies ICFS, soft budgets and investor infringements are closely correlated.
| Variables | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: three-factors model | |||||||||||
| Tobin's Q t−1 | −0.0000 (0.003) | −0.0037 (0.004) | −0.0027 (0.005) | 0.0104 (0.007) | 0.0058 (0.007) | −0.0015 (0.001) | −0.0019 (0.001) | 0.0032 (0.002) | −0.0044*** (0.001) | −0.0036*** (0.001) | −0.0004 (0.000) |
| CF t /K t−1 | 0.1645***(0.024) | 0.1179*** (0.023) | 0.1878*** (0.022) | 0.1600*** (0.023) | 0.1536*** (0.022) | 0.1150*** (0.019) | 0.1312*** (0.019) | 0.0481*** (0.017) | 0.0911*** (0.017) | 0.0890*** (0.019) | 0.1001*** (0.017) |
| (S t −S t−1 )/S t−1 | 0.0058* (0.003) | 0.0050 (0.003) | 0.0006 (0.003) | 0.0074* (0.004) | 0.0051 (0.003) | 0.0021 (0.002) | 0.0096*** (0.003) | 0.0031 (0.003) | 0.0051** (0.003) | 0.0103*** (0.003) | 0.0031 (0.002) |
| Obs. | 1081 | 1135 | 1183 | 1246 | 1240 | 1316 | 1431 | 1461 | 1514 | 1720 | 1989 |
| R 2 | 0.1023 | 0.1012 | 0.1405 | 0.1437 | 0.1234 | 0.1099 | 0.1238 | 0.1000 | 0.1125 | 0.1023 | 0.0869 |
| Panel B: four factor model (including interaction term) | |||||||||||
| Tobin's Q t−1 | −0.0002 (0.004) | −0.0021 (0.005) | −0.0025 (0.005) | 0.0058 (0.009) | 0.0048 (0.009) | −0.0016 (0.005) | −0.0010 (0.001) | 0.0048** (0.002) | −0.0043*** (0.001) | −0.0036*** (0.001) | 0.0002 (0.000) |
| CF t /K t−1 | 0.1582** (0.067) | 0.1636** (0.067) | 0.1926*** (0.067) | 0.0842 (0.099) | 0.1332 (0.105) | 0.1145*** (0.030) | 0.1846*** (0.032) | 0.0937*** (0.029) | 0.0991*** (0.028) | 0.1138*** (0.026) | 0.1506*** (0.029) |
| (S t −S t−1 )/S t−1 | 0.0058* (0.003) | 0.0049 (0.004) | 0.0006 (0.003) | 0.0072* (0.004) | 0.0051 (0.003) | 0.0021 (0.002) | 0.0099*** (0.003) | 0.0032 (0.003) | 0.0052** (0.003) | 0.0104*** (0.003) | 0.0031 (0.002) |
| Tobin's Qt−1 × CFt/K −1 | 0.0037 (0.036) | −0.0301 (0.042) | −0.0036 (0.048) | 0.0642 (0.081) | 0.0183 (0.092) | 0.0004 (0.018) | −0.0205** (0.010) | −0.0286** (0.015) | −0.0031 (0.009) | −0.0081 (0.006) | −0.0253** (0.012) |
| Obs. | 1081 | 1135 | 1183 | 1246 | 1240 | 1316 | 1431 | 1461 | 1514 | 1720 | 1989 |
| R 2 | 0.1023 | 0.1016 | 0.1405 | 0.1441 | 0.1234 | 0.1099 | 0.1265 | 0.1024 | 0.1126 | 0.1033 | 0.0889 |
| Panel C: five factors model (financial constraint denoted by Whited and Wu (2006)'s WW index) | |||||||||||
| Tobin's Q t−1 | −0.0008 (0.004) | −0.0036 0.005) | −0.0026 (0.005) | 0.0060 (0.009) | 0.0046 (0.009) | −0.0018 (0.005) | −0.0009 (0.001) | 0.0048** (0.002) | −0.0043*** (0.001) | −0.0041*** (0.001) | 0.0002 (0.000) |
| CF t /K t−1 | 0.1603** (0.067) | 0.1609** (0.067) | 0.1931*** (0.067) | 0.0832 (0.099) | 0.1327 (0.106) | 0.1136*** (0.030) | 0.1845*** (0.032) | 0.0937*** (0.029) | 0.0994*** (0.028) | 0.1043*** (0.025) | 0.1505*** (0.029) |
| (S t −S t−1 )/S t−1 | 0.0059* (0.003) | 0.0047 (0.003) | 0.0006 (0.003) | 0.0072* (0.004) | 0.0051 (0.003) | 0.0021 (0.002) | 0.0097*** (0.003) | 0.0033 (0.003) | 0.0052** (0.003) | 0.0095*** (0.003) | 0.0031 (0.002) |
| Tobin's Q t−1 × CF t /K t−1 | 0.0041 (0.036) | −0.0270 (0.042) | −0.0037 (0.048) | 0.0646 (0.082) | 0.0194 (0.092) | 0.0009 (0.018) | −0.0210** (0.010) | −0.0285* (0.015) | −0.0032 (0.009) | −0.0068 (0.006) | −0.0253** (0.012) |
| WW index t | 0.0014 (0.002) | 0.0011* (0.001) | 0.0001 (0.001) | −0.0001 (0.000) | 0.0002 (0.000) | −0.0008* (0.000) | −0.0006 (0.000) | 0.0001 (0.000) | −0.0001 (0.000) | 0.0015*** (0.000) | −0.0000 (0.000) |
| Obs. | 1081 | 1135 | 1183 | 1246 | 1240 | 1316 | 1431 | 1461 | 1514 | 1720 | 1989 |
| R 2 | 0.1026 | 0.1043 | 0.1405 | 0.1442 | 0.1235 | 0.1122 | 0.1277 | 0.1024 | 0.1126 | 0.1218 | 0.0889 |
| Panel D: five factors model (financial constraint denoted by Hadlock and Pierce (2010)'s SA index) | |||||||||||
| Tobin's Q t−1 | 0.0078* (0.004) | 0.0056 (0.005) | 0.0148*** (0.006) | 0.0336*** (0.009) | 0.0267*** (0.009) | 0.0063 (0.005) | 0.0021 (0.001) | 0.0098*** (0.002) | −0.0034*** (0.001) | −0.0035*** (0.001) | 0.0002 (0.000) |
| CF t /K t−1 | 0.1203* (0.068) | 0.1367** (0.068) | 0.0956 (0.066) | 0.0679 (0.096) | 0.0793 (0.104) | 0.1439*** (0.029) | 0.1757*** (0.031) | 0.0954*** (0.028) | 0.0993*** (0.028) | 0.1130*** (0.026) | 0.1505*** (0.029) |
| (S t −S t−1 )/S t−1 | 0.0052 (0.003) | 0.0035 (0.004) | −0.0007 (0.003) | 0.0039 (0.004) | 0.0020 (0.003) | −0.0001 (0.002) | 0.0060* (0.003) | 0.0019 (0.003) | 0.0043 (0.003) | 0.0101*** (0.003) | 0.0031 (0.002) |
| Tobin's Q t−1 × CF t /K t−1 | 0.0191 (0.036) | −0.0203 (0.042) | 0.0493 (0.047) | 0.0526 (0.079) | 0.0452 (0.091) | −0.0269 (0.018) | −0.0220** (0.010) | −0.0325** (0.014) | −0.0039 (0.009) | −0.0081 (0.006) | −0.0253** (0.012) |
| SA index t | 0.0080*** (0.002) | 0.0067*** (0.002) | 0.0141*** (0.002) | 0.0137*** (0.002) | 0.0108*** (0.001) | 0.0091*** (0.001) | 0.0089*** (0.001) | 0.0069*** (0.001) | 0.0024** (0.001) | 0.0006 (0.001) | 0.0000 (0.001) |
| Obs. | 1081 | 1135 | 1183 | 1246 | 1240 | 1316 | 1431 | 1461 | 1514 | 1720 | 1989 |
| R 2 | 0.1112 | 0.1091 | 0.1817 | 0.1892 | 0.1596 | 0.1456 | 0.1602 | 0.1289 | 0.1157 | 0.1035 | 0.0889 |
-
The table presents coefficients from the OLS estimators of investment for 2002 to 2012 from the model as:
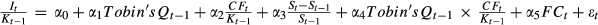 . It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin(2014), the SA index is computed following Hadlock and Pierce (2010), and both are shown in more detail in Appendix II. Industry-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries with the exception of the financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
. It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. WW index is calculated as in Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin(2014), the SA index is computed following Hadlock and Pierce (2010), and both are shown in more detail in Appendix II. Industry-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries with the exception of the financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
To separate the effect of financial constraint on ICFS from that of investment thirst, Panels C and D introduce the WW index and SA index, respectively. Similar to Tables 3 and 4, in which we used the WW index to denote financial constraint, in Panel C of Table 5, we still observe that the signs of coefficient estimates on Tobin's Qt−1 are negative in most cases. Nevertheless, these signs are positive in the WW index coefficient estimates in most cases, both indicating that, for the WW index, it is hard to separate the effect of financial constraint and that of Tobin's Q.
Next, we use the SA index (instead of the WW index) as the proxy for financial constraint, which shows that most of the coefficients of Tobin's Qt−1 become positive, and a number of the coefficients of the SA index are significantly positive. The result of this comparison again shows the ability of the SA index to discern the effect of financial constraint and the effect of Tobin's Q on investment, as well as its relative efficiency compared to the WW index. Consequently, the results in Panel C are almost identical to those in Panel B, while the results in Panel D differ somewhat. In particular, the coefficient estimates of CFt/Kt−1 are significant in that they increase in the three periods of 2002 to 2003, 2007 to 2008 and 2009 to 2012, while being insignificant between 2004 and 2006.
6.4 ICFS and incremental capital–output ratio
In this section, we discuss the third step used in our empirical work and test the explanatory power of ICFS on investment thirst. Existing studies in macroeconomics typically employ the incremental capital-to-output ratio to detect investment thirst and overinvestment in China (e.g. Lee et al., 2012).22 If ICFS is a good measure of investment thirst as we suggest, it should coincide with the incremental capital-to-output ratio.
In a typical transitional environment such as China, where investment thirst tends to connect with government policy (Kornai, 1980; Stiglitz, 1996), we test the effect of ICFS on investment thirst using a natural experiment of a typical government policy that occurred during the sample period. The Four Trillion Stimulus investment policy, announced in December 2008, is regarded as the most important policy adopted by the Chinese government. Thus, we use this event to analyse the relationship between ICFS and investment thirst as follows.
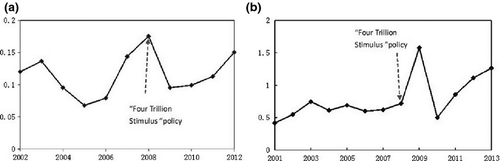
Figure 2a,b compare the changing trends of ICFS with that of incremental capital-to-output ratios from 2002 to 2012. The values of ICFS in Figure 2a are sourced from Panel D of Table 5, and the values of incremental capital-to-output ratios in Figure 2b are calculated using the data from investment on fixed assets and gross domestic product (GDP) during 2000 to 2013.23 We observe that the changes in ICFS (firm-level measure of investment thirst) accurately mirror the changes in incremental capital-to-output ratios (country-level measure of investment thirst) changes over the sample period.
-
Note:
The figures plot the changing trend of ICFS and that of incremental capital-to-output ratios from 2002 to 2012. In (a), We calculate the coefficients from the OLS estimators of investment using the model:
It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), CFt, deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin’ s Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of coefficient represents the characteristic of investor infringement of ICFS. FCt represents the level of financial constraint, denoted by SA index computed as Hadlock and Pierce (2010). The values of incremental capital-to-output in (a and b) are calculated by two datasets from 2001 to 2013 downloaded from the website of China's national bureau of statistics (http://www.stats.gov.cn/), including the investment on fixed asset, and gross domestic products (GDP). The 4 sub-sample periods are given based on (a and b). Industry and year fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries but financial industry in CSMAR from 2002 to 2012.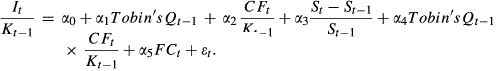
7 Further robustness tests
In this section, we show both that ICFS coincides with incremental capital–output ratios in different economic cycles, and that the GMM estimate of ICFS is also correlated to investment thirst.
7.1 Subperiod regressions
We find similar trends in both ICFS over time and the incremental capital-to-output ratios, which further confirms the significant relationship between ICFS and investment thirst. Moreover, the ICFS captures the effect of the Four Trillion Stimulus investment policy of 2008 accurately, whereas the incremental capital-to-output ratios exhibit a 1-year lag. Indeed, while the policy was announced in 2008, most of the investment activities occurred in 2009, which explains the 1-year-lagged macrodata. This difference also suggests that ICFS is more efficient than incremental capital-to-output ratios in detecting investment thirst.
We further split the sample period into four subperiods according to the trends of incremental capital-to-output ratios in Figure 2b, so as to present the ICFS of each subperiod displayed in Table 6. The results of ICFS are 0.1112, 0.0529, 0.1186 and 0.1061 in the using the data from 2002 to 2006 (considering 1-year lag, we are left with 4 years panel), respectively. A similar pattern is observed in the changes of the incremental capital-to-output ratios. Again, we show that the changes in firm-level investment thirst measure (ICFS) are consistent with the county-level measure results.
| Variables | 2002–2003 | 2004–2006 | 2007–2009 | 2010–2012 |
|---|---|---|---|---|
| Tobin's Q t−1 | 0.0063* (0.003) | 0.0202*** (0.004) | 0.0035*** (0.001) | −0.0009 (0.001) |
| CF t /K t−1 | 0.1112* (0.057) | 0.0529 (0.049) | 0.1186*** (0.014) | 0.1061*** (0.016) |
| (S t −S t−1 )/S t−1 | 0.0045* (0.002) | 0.0014 (0.002) | 0.0023 (0.002) | 0.0047** (0.002) |
| Tobin's Q t−1 ×CF t /K t−1 | 0.0091 (0.035) | 0.0728* (0.040) | −0.0167*** (0.005) | −0.0073 (0.005) |
| SA index | 0.0074*** (0.002) | 0.0125*** (0.001) | 0.0081*** (0.001) | 0.0015** (0.001) |
| Obs. | 2216 | 3669 | 4208 | 5223 |
| R 2 | 0.1053 | 0.1724 | 0.1400 | 0.0944 |
-
The table presents coefficients from the OLS estimators of investment on the model:
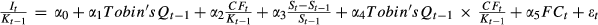 . It/Kt−1 represents the firm's capital expenditure. It deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), CFt, deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994) – of which the negative sign of coefficient represents the characteristic of investor infringement of ICFS. FCt represents the level of financial constraint, denoted by WW index or SA index. WW index is calculated as Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); SA index is computed as Hadlock and Pierce (2010); both are shown in Appendix II in detail. The four subsample periods are given based on the Figure 2a. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries but financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
. It/Kt−1 represents the firm's capital expenditure. It deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), CFt, deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994) – of which the negative sign of coefficient represents the characteristic of investor infringement of ICFS. FCt represents the level of financial constraint, denoted by WW index or SA index. WW index is calculated as Whited and Wu (2006), Lin et al. (2011) and Zeng and Lin (2014); SA index is computed as Hadlock and Pierce (2010); both are shown in Appendix II in detail. The four subsample periods are given based on the Figure 2a. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. The sample includes firms of all industries but financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
7.2 GMM results
To address the concern that the measurement errors in Tobin's Q might contaminate the OLS regression results in Section 5, we use high-order moment estimators of Erickson and Whited (2000). Based on the overidentification J-test results, we use the third up to the six order moments in our regression.24 Following EW, we first partial out the perfectly measured regressors (all other regressors except Tobin's q, it is assumed that Tobin's q is the only mismeasured variable and EW's approach is specifically used to address the measurement problem of Tobin's q.)



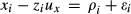
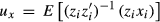
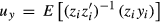
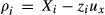
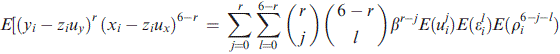
Table 7 presents the test results implementing the EW's GMM method. Given that our previous tests showed that the SA index is found to be better than the WW index in measuring financial constraint, we therefore use the SA index to proxy for financial constraint. The same concern of measurement errors can apply to the interaction term used in the models, as exemplified by the interaction terms containing Tobin's Q. To address this problem, we introduce a dummy variable to replace Tobin's Q and create a new interaction term, I-Dummyt × CFt/Kt−1, to detect investor infringement. The dummy variable I-Dummy is defined in the condition: if the sustainable growth rate is larger than the real growth rate, (St−St−1)/St−1, then I-Dummy equals to 1, otherwise 0. In general, if the sustainable growth rate is larger than the real growth rate, managers would invest more, causing an increase in ICFS. If the sustainable growth rate is below the real growth rate, investment detriments can be found and a negative sign of the coefficient of I-Dummyt × CFt/Kt−1 is expected.
| Variables | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tobin's Q t−1 | −0.2403** (0.093) | −0.5236** (0.236) | 0.0031 (0.026) | 0.4411*** (0.151) | 0.6088*** (0.220) | 0.0001*** (0.000) | 0.0009 (0.000) | 0.0253*** (0.002) | 0.0036** (0.001) | 0.0027*** (0.003) | 0.0000 (0.000) |
| CF t /K t−1 | 0.1854*** (0.066) | 0.2552*** (0.097) | 0.2440*** (0.029) | −0.0385 (0.094) | −0.0289 (0.1196) | 0.2188*** (0.031) | 0.2561*** (0.031) | 0.0768** (0.034) | 0.1195*** (0.020) | 0.1281*** (0.025) | 0.1154*** (0.028) |
| (S t −S t−1 )/S t−1 | 0.0222* (0.012) | 0.0618* (0.032) | −0.0019 (0.003) | −0.0123 (0.010) | −0.0345 (0.022) | −0.0010 (0.003) | 0.0041 (0.003) | −0.0035 (0.003) | 0.0030 (0.004) | 0.0010 (0.004) | 0.0010 (0.003) |
| I-Dummy t × CF t /K t−1 | −0.1010 (0.091) | 0.0792 (0.195) | −0.1620*** (0.043) | 0.1427 (0.110) | 0.0521 (0.104) | −0.1369*** (0.036) | −0.1437*** (0.035) | −0.0339 (0.036) | −0.0441 (0.030) | −0.0802** (0.036) | −0.0064 (0.032) |
| SA index | −0.0765** (0.032) | −0.1249** (0.059) | 0.0123*** (0.004) | 0.0563*** (0.015) | 0.0549*** (0.016) | 0.0091*** (0.001) | 0.0088*** (0.001) | 0.0106*** (0.001) | 0.0057*** (0.001) | 0.0032*** (0.001) | −0.0002 (0.001) |
| Obs. | 1989 | 1135 | 1183 | 1246 | 1240 | 1316 | 1431 | 1461 | 1514 | 1720 | 1989 |
-
The table presents the coefficients from the Erickson and Whited (2000) GMM6 (utilising the third up to the six moments) estimators of investment on the model:
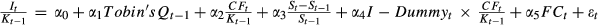 . It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), CFt is deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term I-Dummyt × CFt/Kt−1 here, of which the negative sign of coefficient represents the characteristic of investor infringement of ICFS. If the sustainable growth rate is larger than real growth rate, (St−St−1)/St−1, the dummy variable I-Dummy equal to 1, otherwise it equals to 0. FCt represents the level of financial constraint, denoted by SA index, computed as in Hadlock and Pierce (2010); details about constructing the SA index are shown in Appendix II. Industry-fixed effects are included but unreported. The sample includes firms of all industries with the exception of the financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the level of 1%, 5%, and 10% level, respectively.
. It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), CFt is deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term I-Dummyt × CFt/Kt−1 here, of which the negative sign of coefficient represents the characteristic of investor infringement of ICFS. If the sustainable growth rate is larger than real growth rate, (St−St−1)/St−1, the dummy variable I-Dummy equal to 1, otherwise it equals to 0. FCt represents the level of financial constraint, denoted by SA index, computed as in Hadlock and Pierce (2010); details about constructing the SA index are shown in Appendix II. Industry-fixed effects are included but unreported. The sample includes firms of all industries with the exception of the financial industry in CSMAR from 2002 to 2012. ***, **, and * denote significance at the level of 1%, 5%, and 10% level, respectively.
Table 7 reports the GMM estimation results showing that the trend in the ICFS GMM estimators is similar to its OLS estimators in Table 5. We conclude that ICFS is a good measure of investment thirst and thus that our results in Section 5 are robust.
7.3 Relative idiosyncratic risk calculated through CAPM
Table 8 presents some robust tests for the results of the relationship between ICFS and risk. Here, we use the CAPM model instead of Fama and French (1992) method to compute idiosyncratic risk. We find that the coefficients of CFt/Kt−1 in Groups 3 and 4 are commonly larger than those in Groups 1 and 2, which is similar to the results in Table 4. Therefore, our evidence in Table 8 also implies a positive relationship between ICFS and risk-seeking preferences.
| Risk-lowest | Risk-2 | Risk-3 | Risk-largest | |
|---|---|---|---|---|
| Tobin's Q t−1 | −0.0014 (0.002) | 0.0021* (0.001) | −0.0024* (0.001) | 0.0020* (0.001) |
| CF t /K t−1 | −0.0070 (0.027) | 0.0304* (0.016) | 0.0363 (0.027) | 0.0380 (0.030) |
| (S t −S t−1 )/S t−1 | 0.0148** (0.006) | −0.0013 (0.002) | 0.0036 (0.003) | −0.0002 (0.002) |
| Tobin's Q t−1 × CF t /K t−1 | 0.0307*** (0.010) | 0.0053 (0.005) | −0.0095 (0.010) | −0.0088 (0.009) |
| SA indext | 0.0150*** (0.003) | 0.0124*** (0.003) | 0.0083*** (0.002) | 0.0071*** (0.002) |
| Obs. | 206 | 242 | 211 | 163 |
| R 2 | 0.2744 | 0.2423 | 0.2088 | 0.3295 |
-
This table presents ICFS in quartile groups at different levels of relative idiosyncratic risk. The ICFS are calculated from the OLS estimators of the model:
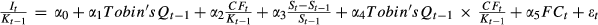 . It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. the SA index is computed as in Hadlock and Pierce (2010); and both are shown in Appendix II in more detail. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. We select the observations existing in both Group 4 of Table 2 and Group 2 of Table 3 simultaneously, and divide them into four groups by their quartile value of relative idiosyncratic risk. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
. It/Kt−1 represents the firm's capital expenditure. It is deflated by its beginning-of-period total asset, Kt−1. Tobin's Qt−1 is defined as the previous year's Tobin's Q. (St−St−1)/St−1 is the sales growth rate. CFt/Kt−1 is the firm's internal cash flow (net operating cash flow), with CFt deflated by its beginning-of-period total asset, Kt−1. We also introduce the interaction term Tobin's Qt−1 × CFt/Kt−1 here according to Vogt (1994), of which the negative sign of the coefficient represents the characteristic of investor infringement of ICFS. FCt is the level of financial constraint, denoted by the WW index or SA index. the SA index is computed as in Hadlock and Pierce (2010); and both are shown in Appendix II in more detail. Industry- and year-fixed effects are included but unreported. Standard errors are heteroskedasticity consistent and clustered at the firm level. We select the observations existing in both Group 4 of Table 2 and Group 2 of Table 3 simultaneously, and divide them into four groups by their quartile value of relative idiosyncratic risk. ***, **, and * denote significance at the 1%, 5%, and 10% level, respectively.
8 Conclusion
In the existing theories of ICFS, doubts have arisen as to whether ICFS serves as a valid measure of financial constraint in a firm. Indeed, it is not clear what ICFS truly captures, particular after conflicting the literature's evidence on the relationship between ICFS, financial constraint and overinvestment, which brings the research about ICFS to be even more challenging.
To address these doubts, we extend the framework of Fazzari et al. (1988) to find that the ICFS level is determined by managers’ risk preferences and overinvestments owing to soft budget constraint, investment opportunities and financial constraint. When the first two factors are combined, the result coincides with the concept ‘investment thirst’ introduced by Kornai (1979, 1980, 1986), while the latter two are correspond with the work of Fazzari et al. (1988). After controlling for the effects of investment opportunity and financial constraint, we show that ICFS measures the level of investment thirst in a firm.
We use a sample of China's listed firms from 2002 to 2012 to determine the capacity of ICFS to measure investment thirst, because investment thirst and financial constraint may co-exist insofar as China is a transitional economy. After using reliable proxies [e.g. we use the WW index of Whited and Wu (2006) and the SA index Hadlock and Pierce (2010)] to control for financial constraint, we find that the ICFS can be used to detect investment thirst. This finding about ICFS at the firm level is highly consistent with that using country-level measures (e.g. the index of incremental capital–output ratios). In addition, using a natural experiment of China's Four Trillion Stimulus policy announced in December 2008, we provide robust evidence showing that ICFS is a good measure of investment thirst at the firm level.
While our results are consistent with most of the existing literature, it newly explains some anomalies about ICFS as well. For example, Vogt (1994) argues that, in firms of large size and low dividends, ICFS might denote overinvestment, while ICFS can also proxy for financial constraint in firms of small size and low dividends. Our evidence, however, shows that, if we do not control for the effect of financial constraint, the ‘financial constraint’ effect and ‘investment thirst’ effect on ICFS can exist in the same firm. Moreover, in firms of small size and low dividends, the effect of financial constraint dominates the effect of investment thirst, while for large, low-dividends firms, the opposite is found.
Notes
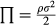 , followed by
, followed by  , and
, and 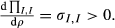
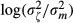 , where
, where 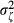 denotes the absolute idiosyncratic risk, and
denotes the absolute idiosyncratic risk, and  denotes the systematic idiosyncratic risk. A number of studies show that
denotes the systematic idiosyncratic risk. A number of studies show that 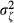 has a closely positive relation with
has a closely positive relation with  (such as Chun et al., 2008; Han and Lesmond, 2011; Panousi and Papanikolaou, 2012), thus we use relative idiosyncratic risk here instead of absolute idiosyncratic risk. For robustness, we also present similar results in Section 6.3 (Table 8) based on the relative idiosyncratic risk estimated through CAPM.
(such as Chun et al., 2008; Han and Lesmond, 2011; Panousi and Papanikolaou, 2012), thus we use relative idiosyncratic risk here instead of absolute idiosyncratic risk. For robustness, we also present similar results in Section 6.3 (Table 8) based on the relative idiosyncratic risk estimated through CAPM.Appendix I
Proof of Equation 3
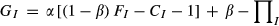
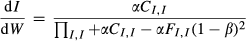
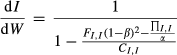 ()
()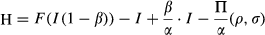
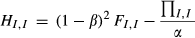 ()
()Q.E.D.
Appendix II
Calculating financial constraint indices
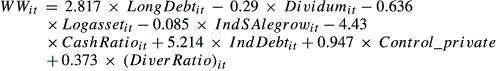
- LongDebt: long-term debt, scaled by total assets.
- Logasset: log value of total assets.
- IndSAlegrow: average sales growth ratio of each industry, calculated by the asset-weighted average value of each firm's sales growth ratio in one industry. The industries are categorised by the SIC criterion of China's Securities Regulatory Commission (two digits).
- Cash Ratio: cash-holding ratio, defined as cash plus short-term investment, scaled by total assets.
- IndDebt:industrial mean long-term debt ratio weighted by firm total assets.
- Control_private: an indicator equalling to 1 for firms ultimately controlled by private firms and 0 otherwise.
- Diver Ratio: control-ownership wedge, defined as the difference between control rights and cash-flow rights for the ultimate controlling shareholder.
Control rights and cash flow rights for the ultimate controlling shareholder are both defined following La Porta et al. (1999). The WW index is positively related to financial constraint, that is, the larger the index is associated with a higher degree of financial constraint.
Where size indicates the log of inflation-adjusted total-book-assets, and Age is the number between the current year and the listed year of the firm. According to Hadlock and Pierce, 2010, the SA index is a reverse index of financial constraint, that is, the larger the index, the lower degree of financial constraint.
For robustness, in our unreported results, we have replaced the value of size with the total-book-assets without inflation-adjustment. These results are similar with the reported results in this paper.
Appendix III
Definition of the level of investment
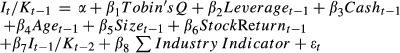
- I/K: the firm's capital expenditure, I is deflated by its beginning-of -period total asset, K.
- Tobin's Q: a normal measure of growth opportunities.
- Leverage: the sum of the book value of debt deflated by the sum of the book value of assets.
- Cash: the balance of cash and short term investments deflated by total assets measured at the start of the year.
- Age: the log of the number of years the firm has been listed on China's Stock Market.
- Size: the log of the book value of total assets.
- Stock Return: the stock return for the year prior to the investment year. It is measured as the change in market value of the firm over that prior year.
- Industry Indicators: a vector of indicator variables to capture industry fixed effects. Note that there are 13 industry indicator variables (one digit SIC) in this regression.
As a result, we obtain ε for each firm in every year, and divide the sample into four groups according their value of ε. The observations in Groups 3 and 4, with larger values, are defined as firms of overinvestment, while the observations in Groups 1 and 2, with smaller values, are defined as firms of under-investment.



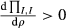 ,
,