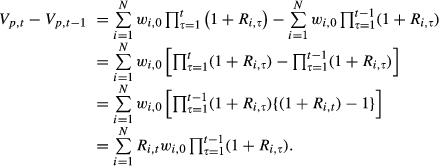Stock weighting and nontrading bias in estimated portfolio returns
Abstract
Liu and Strong (2008) note that researchers often employ a simple (but incorrect) averaging approach that induces significant error into estimated buy-and-hold portfolio returns. This study explores the additional challenges that arise when stocks are subject to nontrading. We develop a decomposition of the total bias in estimated return into the components attributable to the stock weighting approach and the treatment of nontrading. While the latter is shown to be negligible, the former can approach 150 basis points per month. Our empirical analysis of Australian equities shows that the simple averaging approach tends to overstate the size and book-to-market effects, and understate the momentum effect.
1. Introduction
Empirical research in accounting, finance and capital markets often sorts stocks into portfolios. There are many sound reasons for this. First and foremost, it is a natural and convenient way to summarise the characteristics of a large number of individual stocks. Second, dating back to Blume (1970) and Black et al. (1972), researchers have utilised portfolios of stocks to diversify estimation error. More recently, Fama and French (2008) highlight the ability of the portfolio approach to accommodate nonlinearities in the relationship between returns and stock characteristics.
Examples of the portfolio approach abound, especially in the market efficiency and stock market anomalies literature. Stocks have been sorted into portfolios by market capitalisation (Banz, 1981), price (Bhardwaj and Brooks, 1992), book-to-market ratio (Rosenberg et al., 1985), long-horizon returns (De Bondt and Thaler, 1985), short-horizon returns (Jegadeesh and Titman, 1993), accruals (Sloan, 1996), asset growth (Cooper et al., 2008), earnings surprise (Bernard and Thomas, 1990), to name but a few applications of the portfolio approach.
In some contexts, researchers are interested in the portfolio return over a specified holding period. For example, De Bondt and Thaler (1985) report the cumulative return to portfolios of past winners and losers over the 3 years post portfolio formation. However, it is more common to calculate a time series of monthly portfolio returns. Having formed portfolios sorted on the characteristic of interest (size, BM, momentum, etc.), researchers look for a monotonic pattern in average returns across portfolios, and examine the significance of a long–short investment in the extreme portfolios. To adjust for risk factors, the intercept in a time series regression of monthly portfolio returns on established risk factors (for example, using the Fama-French three-factor or Carhart four-factor models) is estimated. Further, when anomalous returns are identified, the time series of portfolio returns may be utilised to propose new risk factors.1
Given the prevalence of portfolio sorts in empirical work, it is paramount that researchers calculate monthly portfolio returns correctly. In a recent study, Liu and Strong (2008) document that researchers often employ a simple averaging approach to calculating monthly portfolio returns that has a number of undesirable consequences: (i) it generates monthly portfolio returns that do not accurately capture the wealth effects to an investor holding the portfolio, (ii) it reflects a trading strategy that transaction costs would preclude in practice, because it implies that the portfolio is rebalanced to initial weights each month, and (iii) it can result in misleading inferences about the existence of anomalies. After demonstrating how to correctly calculate monthly portfolio returns, Liu and Strong (2008) show that the averaging approach tends to overstate the well-known size effect, but understate the profitability of momentum trading.
The current study contributes to this literature from both methodological and empirical perspectives. First, building on Liu and Strong (2008), we explore the additional challenges that arise when stocks are subject to nontrading and missing returns. When a stock does not trade in 1 (or more) months during the holding period, an ad hoc assumption is necessary to estimate periodic portfolio returns. We consider alternate treatments of missing returns and demonstrate the impact of the chosen assumption on estimated portfolio returns. A methodological contribution of the current study is to develop an approach to approximating returns in the presence of nontrading, in the spirit of Liu and Strong (2008).
Second, we compare portfolio returns estimated using the approach of Liu and Strong (2008) to the simple averaging approach, thereby documenting the bias induced by the latter. In effect, this is the total bias resulting from two methodological choices. Levering on our proposed treatment of missing returns, we are able to partition the total bias into components arising from (i) the method of averaging stock returns into the portfolio, and (ii) the method chosen to accommodate nontrading. The relative importance of each component of bias is then quantified both empirically and via simulation experiments.
The empirical analysis is conducted within the context of three well-known anomalies (size, momentum and book-to-market). For several reasons, the Australian equity market is ideal for our study of methodological issues surrounding the estimation of portfolio returns. Liu and Strong (2008) provide an analytic representation of the bias induced by the simple averaging approach and show how it is related to stock price. As the Australian stock market is characterised not only by a large number of small-cap low-priced stocks, but also nontrivial frequencies of nontrading, the potential impact of methodological choices on empirical findings are brought to the fore.2
The findings confirm that the simple averaging approach systematically over (under) states returns to portfolios comprising low (high)-price stocks. When low-price stocks cluster in a given portfolio (as occurs when studying the size anomaly), the stock weighting bias approaches 150 basis point per month. When a portfolios's constituent stocks have more heterogeneous market caps, this bias is less severe but nonetheless significant. Empirically, the nontrading bias is an order of magnitude smaller than the stock weighting bias. This finding suggests that relatively crude treatments of nontrading may suffice in common empirical settings.
The discussion in and findings of this study have implications for a broad and ongoing capital markets literature. For any empirical study where portfolios are formed on the basis of firm characteristics, this study serves a warning that great care must be taken with respect to how stock returns are weighted into portfolios and, to a lesser extent, how nontrading is treated. Further, our partitioning of the total bias in portfolio return into components highlights the ranges of market cap, share price and nontrading for which empirical findings are most vulnerable to methodological choices. Accordingly, we stress the importance of understanding the characteristics of a portfolio's constituent stocks, in particular the extreme portfolios on which a long–short strategy is based.
The remainder of this study proceeds as follows. Section 2. articulates the two central issues examined in this study using two stylised examples. First, several drawbacks of the popular averaging approach to estimating portfolio returns are demonstrated, along with the difficulties induced by nontrading. Next, we develop a way of augmenting the approach of Liu and Strong (2008) such that it continues to correctly estimate monthly portfolio returns even in the presence of nontrading. Section 3. conducts empirical studies of the size, momentum and book-to-market effects in Australian equity returns. Each anomaly is studied using both the popular (but incorrect) averaging approach and the augmented Liu and Strong approach, with the total bias in portfolio returns partitioned into components attributable to stock weighting and nontrading. Particular interest is taken in the firm-size, share price and nontrading characteristics of the constituent stocks of key portfolios to better understand how the chosen methodology influences findings. In a more general setting, Section 3. also conducts a brief simulation experiment to demonstrate how the return bias (and its components) vary with share price and market cap. Finally, levering on the insights into Sections 3. and 4. rounds off this study by reconsidering whether the anomalies are truly ‘investable’. Our objective is to mitigate the factors that give rise to ambiguity in results, thereby enhancing the reliability of findings. Section 5. concludes the study.
2. Stylised examples
2.1. Base case
The central issues in this study can be easily conveyed with two simple numerical examples. Assume that, at time 0, stock A and stock B are combined into an equally weighted portfolio, which is held without rebalancing until the end of month 4 (i.e. it is a buy-and-hold portfolio). For ease of exposition, and without loss of generality, assume that neither stock experiences a dividend or capitalisation adjustment over the holding period.
Table 1 shows the monthly prices and returns for this base case.3 Liu and Strong (2008) document that it is common practice in empirical research to simply average the monthly returns on the stocks in the portfolio. For example, by averaging month-1 returns to stock A (25 per cent) and stock B (−4 per cent), the portfolio return is 10.50 per cent. Following the same approach in each month gives the time series of portfolio returns. Taking the product of the portfolio price relatives, the estimated 4-month holding-period return is shown as 3.06 per cent.4
| Time | Prices | Price relatives | Portfolio | Dollar investment | Portfolio | ||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | A | B | Average | A (25 sh) | B (10 sh) | Value | Return | |
| 0 | 2.00 | 5.00 | $50.00 | $50.00 | $100.00 | ||||
| 1 | 2.50 | 4.80 | 1.2500 | 0.9600 | 1.1050 | $62.50 | $48.00 | $110.50 | 1.1050 |
| 2 | 2.20 | 5.40 | 0.8800 | 1.1250 | 1.0025 | $55.00 | $54.00 | $109.00 | 0.9864 |
| 3 | 2.40 | 5.10 | 1.0909 | 0.9444 | 1.0177 | $60.00 | $51.00 | $111.00 | 1.0183 |
| 4 | 1.80 | 5.50 | 0.7500 | 1.0784 | 0.9142 | $45.00 | $55.00 | $100.00 | 0.9009 |
| Estimated holding-period return | 3.06% | 0.00% | |||||||
- The numerical example assumes that Stock A and Stock B are formed into an equally weighted portfolio at time 0. This buy-and-hold portfolio is held until time 4. Stock returns are shown in ‘price relative’ format, where the price relative is equal to the simple stock return plus unity.
In reality, the true holding-period return on the portfolio is zero. Assume an initial budget of $100. Formation of an equally weighted portfolio requires the purchase of 25 shares in stock A and 10 shares of stock B (hence, a $50 investment in each stock). After 1 month, this portfolio is worth $110.50 (25 shares in A worth $2.50 and 10 shares in B worth $4.80). Consequently, the true portfolio return in month 1 is 10.50 per cent ($110.50/$100 −1). While this month-1 portfolio return is identical to the return calculated above by averaging the returns on each stock, this is where the similarities end. At the end of month 2, the portfolio is worth $109, so the portfolio return is −1.36 per cent ($109/$110.50 −1). In contrast, the averaging approach erroneously suggests that the portfolio has a positive return in month 2 (0.25 per cent). Similarly, the averaging approach generates portfolio returns in months 3 and 4 that differ from the true returns.
By tracking dollar investments in each stock, Table 1 clearly demonstrates that the averaging approach generates an incorrect time series of monthly portfolio returns and therefore a spurious holding-period return of 3.06 per cent.5 Clearly, the portfolio value is $100 at both month 0 and month 4; hence, the return over the holding period is zero. An examination of the dollar investments columns in Table 1 shows why the two approaches differ. At time 0, the portfolio is indeed equally weighted with $50 invested in each stock (this is why the averaging and dollar approaches agree in the first month). However, the month-1 stock returns tilt the portfolio away from equal weights. At the end of month 1, stock A contributes 56.56 per cent ($62.50/$110.50) and stock B contributes 43.44 per cent ($48/$110.50). These are the correct (updated) weights for calculating the month-2 portfolio return. Similarly, the correct month-3 weights are the initial time-0 weights, updated to reflect each stock's cumulative returns over the first 2 months.
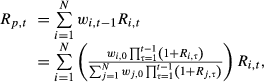 (1)
(1)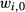 is the initial portfolio weight for stock i,
is the initial portfolio weight for stock i, 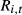 is the month-t simple return on stock i, and there are N stocks in the portfolio. With reference to Table 1, the numerator of (1) measures the ‘dollar investment’ in each stock at the beginning of month t, while the denominator captures the ‘portfolio value’. The key take away from (1) is that the correct weights to apply in calculating month-t portfolio return are a time-varying function of each stock's cumulative returns from the commencement of the holding period up to the beginning of month t. Hereinafter, we refer to this as the updated weights approach.
is the month-t simple return on stock i, and there are N stocks in the portfolio. With reference to Table 1, the numerator of (1) measures the ‘dollar investment’ in each stock at the beginning of month t, while the denominator captures the ‘portfolio value’. The key take away from (1) is that the correct weights to apply in calculating month-t portfolio return are a time-varying function of each stock's cumulative returns from the commencement of the holding period up to the beginning of month t. Hereinafter, we refer to this as the updated weights approach.In contrast, the averaging approach uses the same initial vector of stock weights to calculate portfolio return in every holding-period month. By averaging the monthly stock returns, the implicit assumption is that the portfolio is rebalanced to the initial equal weights each month (from this point on, we refer to this as constant weights approach). This assumption is therefore inconsistent with the buy-and-hold position that is intended in many empirical applications, and clearly, transaction costs would prohibit monthly rebalancing of portfolios containing a large number of stocks.6
While these are important issues, they are not new. Blume (1974), Roll (1983), Blume and Stambaugh (1983), Conrad and Kaul (1993) and Dissanaike (1994) have all highlighted potential methodological traps in averaging stock returns into portfolios and estimating multiperiod returns. We revisit this issue in Section 2.3. and propose a number of possible reasons why researchers continue to utilise constant-initial weights to calculate portfolio returns.
One final comment pertains to the implementation of the correctly updated weights approach to estimating portfolio returns. While Equation 1 serves to illustrate why and how the initial stock weights must be updated to reflect returns on a genuine buy-and-hold portfolio, it is notationally cumbersome and arguably lacking in intuition. A simple and more intuitive exposition of the calculation of portfolio returns follows from utilising the dollar value of the portfolio along the lines of the far right columns in Table 2.7 The Appendix provides details of this approach and shows that it is equivalent to Liu and Strong's (2008) approach.
| Time | Prices | Price relatives | Portfolio | Dollar investment | Portfolio | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | Average | A (16.67 sh) | B (6.67 sh) | C (3.33 sh) | Value | Return | |
| 0 | 2.00 | 5.00 | 10.00 | $33.33 | $33.33 | $33.33 | $100.00 | |||||
| 1 | 2.50 | 4.80 | 5.00 | 1.2500 | 0.9600 | 0.50000 | 0.9033 | $41.67 | $32.00 | $16.67 | $90.33 | 0.9033 |
| 2 | 2.20 | 5.40 | n/a | 0.8800 | 1.1250 | −9 | 1.0017 | $36.67 | $36.00 | $16.67 | $89.33 | 0.9889 |
| 3 | 2.40 | 5.10 | 8.00 | 1.0909 | 0.9444 | −99 | 1.0118 | $40.00 | $34.00 | $26.67 | $100.67 | 1.1269 |
| 4 | 1.80 | 5.50 | 10.00 | 0.7500 | 1.0784 | 1.2500 | 1.0261 | $30.00 | $36.67 | $33.33 | $100.00 | 0.9934 |
| Estimated holding-period return | −6.06% | 0.00% | ||||||||||
- The numerical example assumes that Stock A, Stock B and Stock C are formed into an equally weighted portfolio at time 0. This buy-and-hold portfolio is held until time 4. Stock returns are shown in ‘price relative’ format, where the price relative is equal to the simple stock return plus unity. Price relatives flagged −9/−99 indicate a return cannot be calculated due to nontrading.
2.2. Nontrading and missing returns
The base case illustrates the main issue: rather than averaging the monthly returns of constituent stocks, true portfolio returns follow from updating initial weights to reflect each stock's cumulative return since the beginning of the holding period. While calculating correctly updated weights was straightforward in the stylised example, complications arise when constituent stocks have missing returns. Even in highly developed markets like the UK and Australia, the incidence of nontrading is nontrivial. It is instructive, therefore, to carefully consider the alternative treatments of missing returns available to researchers. This allows a better understanding of why researchers adopt certain empirical methodologies and an assessment of the likely influence of the chosen approach on estimated returns.
Table 2 extends the example by considering an equally weighted portfolio of three stocks. The data for stocks A and B are identical to the previous example. Stock C does not trade in month 2; hence, no return can be calculated in months 2 and 3.8 Under the constant weights approach, a convenient ‘solution’ to missing returns is to simply calculate the portfolio return as the average over stocks with a valid return. While this is trivial for equal-weighted portfolios, it is unclear how to proceed for value-weighted portfolios.9 An alternative treatment of missing returns is to ‘fill the gaps’ by inserting a price relative of unity (i.e. zero return). This approach allows easy calculation of the monthly portfolio return under the constant weights approach, irrespective of whether stocks are equal or value weighted. In Table 2, the portfolio returns in month 2 (0.17 per cent) and month 3 (1.18 per cent) are calculated by replacing the missing price relatives with unity, then taking the average across the three stocks. Having filled the gaps created by missing returns, the estimated 4-month holding-period return on the portfolio is −6.06 per cent.
Under the updated weights approach, the first point to note is that the true 4-month portfolio holding-period return is again zero (by construction). If each constituent stock trades at the beginning and end of the holding period (as is the case here), calculating the portfolio dollar investments and holding-period return is straight forward. On a month-to-month basis, difficulties arise when stocks do not trade. For example, stock C's nontrading in month 2 makes it difficult to calculate the dollar investment in stock C, and therefore the month-2 portfolio return. As was the case with the constant weights approach, where two ad hoc fixes were considered, the updated weights approach also requires some creative thinking.
Our suggested way forward follows from considering the perspective of the investor. An investor asked what her portfolio is worth at the end of month 2 might reply: my investments in stocks A and B are currently worth $36.67 and $36, respectively, and although stock C did not trade this month, the last time it did trade, it was worth $16.67. Arguably, the investor's best guess as to the portfolio worth is $89.33. Accordingly, the month-2 portfolio return can be estimated (−1.11 per cent).10 Stock C trades in month 3, therefore allowing an update to it's true dollar investment ($26.67).
The suggested approach to handling missing returns under the updated weights method is ad hoc and clearly imperfect. In month 2, it uses current prices for stocks A and B and a stale price for stock C (the alternate treatment discussed above has the same implication). Further, the variance of portfolio returns may be overstated, because zero returns in nontrading months may be followed by a potentially large return when the stock next trades. For example, in Table 2, Stock C records a zero return in month 2 followed by a 60 per cent return in month 3. As such, the approach we advocate to handle missing returns has implications for the estimated portfolio variance. Of course, so too does the alternate treatment of turning a blind eye to missing returns and simply inserting zeros to fill the gaps.11 Nonetheless, the suggested approach has merit. In particular, it generates portfolio returns that cumulate to the correct holding-period return (0 per cent in this case). There is no look-ahead bias in the suggested ‘fix’.12 At the very least, it is no more ad hoc than the constant weights approaches that either ignore missing returns or insert a price relative of unity.
Finally, two important issues must be noted. First, while inserting price relatives of unity to fill gaps under the constant weights approach may be computationally convenient, doing so masks a potentially serious drawback. Specifically, the fact that Stock C moved from $5 in month 1 to $8 by the end of month 3 is totally missed. This ignorance drives the erroneous 4-month holding-period return (−6.06 per cent). In contrast, the updated weights approach captures this capital gain in month 3, thereby ensuring that the 4-month holding-period portfolio return is accurate.
 (2)
(2)2.3. Discussion
The stylised examples demonstrate several important flaws in the approach commonly used to estimate portfolio returns. As highlighted by Liu and Strong (2008), the constant weights approach implies that stock holdings are rebalanced to initial weights each month during the holding period. In addition to being practically infeasible, the implication is inconsistent with the buy-and-hold perspective intended in many empirical studies. As a consequence, monthly portfolio returns are mis-estimated and holding-period returns do not reflect the wealth effects to a buy-and-hold investor.
Further, the stylised examples extend the analysis of Liu and Strong (2008) to highlight the potentially important impact of nontrading. In the presence of nontrading, an ad hoc assumption is necessary to estimate monthly portfolio returns. Assumptions that are commonly employed in conjunction with the constant weights approach (e.g. replacing missing price relatives with unity) induce further error into the estimation of returns. The susceptibility of characteristic-sorted portfolios to these nontrading problems is a feature of the empirical analysis in the remainder of this study.
One caveat is necessary. Sections 2.1. and 2.2. demonstrate biases in estimated portfolio returns that are attributable to the method of averaging stock returns and the treatment of nontrading, respectively. Clearly, the stylised examples use somewhat extreme numbers for the purpose of illustrating the key points. Ultimately, the magnitude and direction of any bias is an empirical issue. The major contribution of this study is to empirically document the importance of each component of the bias in common research settings and demonstrate how to diagnose potential methodological problems with reference to stock characteristics.
Given the numerous flaws in the constant weights approach, we can only conjecture why its use remains prevalent. One possible explanation is careless adherence to the textbook definition that the time-t return on a portfolio of N stocks is 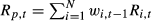 . This formula is correct, if and only if the vector of weights
. This formula is correct, if and only if the vector of weights 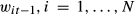 are the correctly updated weights at the beginning of period t as shown in (1). An alternate motivation is programming simplicity – updating stock weights each month as per (1) and (2) is considerably more difficult than simply inserting unity and averaging.
are the correctly updated weights at the beginning of period t as shown in (1). An alternate motivation is programming simplicity – updating stock weights each month as per (1) and (2) is considerably more difficult than simply inserting unity and averaging.
3. Empirical analysis
The empirical analysis re-examines several well-known anomalies (size, momentum, book-to-market) utilising data from the Australian equity market. Several factors make this an ideal scenario within which to study the potential influence of key methodological choices in estimating portfolio returns. The population of ASX-listed stocks is characterised by a large number of small-cap stocks.14 As such, the bias in estimated returns shown analytically by Liu and Strong (2008) is likely to be exacerbated. This provides strong motivation to re-examine the anomalies using correctly updated stock weights to estimate returns to the various characteristic-sorted portfolios. Further, the prevalence of nontrading amongst ASX stocks also allows an assessment of the importance of methodological choices made in relation to missing returns.
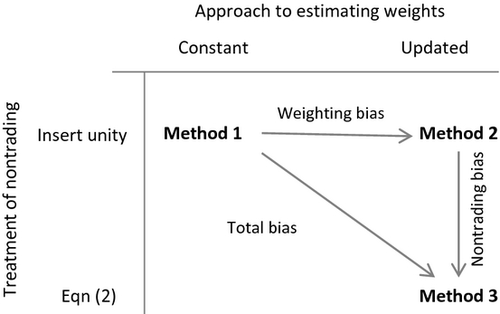
In effect, we decompose the total bias in portfolio returns into components induced by two key methodological choices. For each portfolio of interest, we estimate monthly returns under three approaches. First, portfolio returns are calculated using constant stock weights and after inserting a price relative of unity to fill the gaps caused by nontrading. Figure 1 denotes this approach ‘Method 1’. Second, portfolio returns are estimated using correctly updated weights as per (1) while still inserting unity to cover nontrading (‘Method 2’). The difference between average returns under Method 1 and Method 2 isolates the bias induced using constant weights instead of the correctly updating weights required for a genuine buy-and-hold position. Third, portfolio returns are estimated using correctly updated weights as per (1) and employing (2) to accommodate nontrading (‘Method 3’). The difference between Method 2 and Method 3 isolates the bias induced by an incorrect treatment of nontrading. Finally, the total bias is simply the addition of the individual biases (or equivalently Method 1 - Method 3).
Data for the empirical work are drawn from two sources. The AGSM CRIF database contains monthly data for all ASX-listed stocks from December 1973 to December 2010. The key fields utilised in this study are returns, prices, market capitalisation and industry codes. All analysis is restricted to stocks with ‘ordinary’ share type. To facilitate comparison with prior book-to-market studies, property trusts and investment funds are excluded.
Accounting data are drawn from the Aspect Huntley database from 1989 to 2009. Book value of equity is estimated as total shareholder equity less outside equity interests, preference shares and future tax benefits. As 81 per cent of our sample companies have June balance dates, we form BM portfolios each December. To allow a minimum 6 months between year end and portfolio formation, year t BM utilises year t book value for companies with balance dates in June or earlier, and year t−1 book value otherwise. From the initial sample of 26,385 firm-year records, further exclusions are as follows: 100 records with zero book value, 996 records with negative book value and 108 records with BM exceeding 10.
3.1. Size effects
The size effect is one of the most-heavily researched anomalies. Brown et al. (1983), Beedles et al. (1988), Gaunt et al. (2000), Durand et al. (2007), O'Brien (2008) and Gharghori et al. (2009) have all studied the size effect in Australian equities. At face value, the weight of evidence suggests that there is a distinct small firm premium. Notably, each of these studies reports incredulously high average returns to the smallest size portfolio (ranging from 5 to 10 per cent per month).
In a recent study, Gaunt (2011) explores the legitimacy of such large apparent returns to small-stock portfolios by adopting a methodology that strives to estimate the returns that could realistically be achieved. To mitigate market-microstructure return bias and illiquidity concerns, his portfolio-formation procedure excludes stocks with price below 20 cents. In brief, Gaunt (2011) finds no evidence of a size premium given these methodological choices. The disturbingly high average returns to small stocks reported in prior work are absent, and there is no statistically significant difference in average returns across size deciles.
Our study of the size effect proceeds as follows. Starting in December 1973, all stocks are ranked by market capitalisation and sorted into decile portfolios. Buy-and-hold positions in the constituent stocks are maintained for 12 months, after which the ranking and portfolio-formation procedure is repeated. Over the 37-year sample period (444 months), 970 stocks on average per annum are assigned to decile size portfolios.
Table 3 reports the empirical findings. When returns to size portfolios are estimated under the constant weights approach, there is evidence of a substantial size effect. Irrespective of whether stocks are equal-weighted (Panel A) or value-weighted (Panel B) into portfolios, the magnitude of the size premium (as measured by the spread portfolio) exceeds 4 per cent per month and is highly statistically significant.15 These findings under the constant weights approach are highly consistent with prior research. However, a material proportion of the apparent size premium reflects bias induced by this methodology. Table 3 quantifies the total bias in portfolio returns and facilitates its decomposition into stock weighting and nontrading components.
| Small | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Big | Spread | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Equally weighted portfolios | ||||||||||||
| Constant weights | 5.72 | 3.35 | 2.32 | 1.56 | 1.38 | 0.88 | 1.05 | 0.96 | 1.07 | 1.14 | 4.58 | (p < 0.001) |
| Updated weights | 4.34 | 2.48 | 1.59 | 1.26 | 1.30 | 0.94 | 1.12 | 1.16 | 1.20 | 1.20 | 3.14 | (p < 0.001) |
| Total bias | 1.38 |
0.87 |
0.73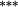 |
0.30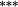 |
0.08 | −0.06 | −0.07 | −0.20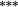 |
−0.13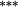 |
−0.06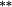 |
1.44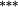 |
|
| Weighting bias | 1.54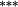 |
0.87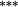 |
0.65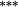 |
0.29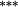 |
0.05 | −0.09 |
−0.09 |
−0.20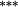 |
−0.15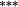 |
−0.07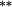 |
1.61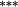 |
|
| Nontrading bias | −0.16 | 0.00 | 0.08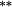 |
0.01 | 0.03 |
0.03 |
0.02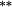 |
0.00 | 0.02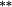 |
0.01 | −0.17 | |
| Panel B: Value-weighted portfolios | ||||||||||||
| Constant weights | 5.11 | 3.21 | 2.21 | 1.48 | 1.32 | 0.85 | 0.99 | 0.95 | 1.06 | 1.09 | 4.02 | (p < 0.001) |
| Updated weights | 3.90 | 2.42 | 1.54 | 1.24 | 1.27 | 0.93 | 1.11 | 1.16 | 1.19 | 1.13 | 2.77 | (p < 0.001) |
| Total bias | 1.21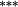 |
0.79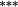 |
0.67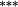 |
0.24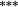 |
0.05 | −0.08 | −0.12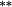 |
−0.21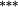 |
−0.13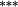 |
−0.04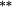 |
1.25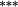 |
|
| Weighting bias | 1.31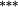 |
0.78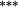 |
0.59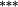 |
0.23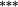 |
0.01 | −0.11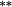 |
−0.14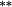 |
−0.21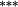 |
−0.15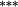 |
−0.04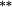 |
1.35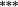 |
|
| Nontrading bias | −0.10 | 0.01 | 0.08 |
0.01 | 0.04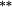 |
0.03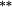 |
0.02 |
0.00 | 0.02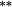 |
0.00 | −0.10 | |
| Panel C: Summary statistics | ||||||||||||
| Mkt Cap ($m): mean | 1 | 3 | 5 | 7 | 11 | 19 | 33 | 67 | 181 | 2600 | ||
| Mkt Cap ($m): median | 1 | 3 | 5 | 7 | 11 | 18 | 32 | 65 | 164 | 1036 | ||
| Price ($): mean | 0.23 | 0.31 | 0.44 | 0.55 | 0.71 | 0.93 | 1.22 | 1.81 | 2.57 | 6.18 | ||
| Price ($): median | 0.12 | 0.19 | 0.27 | 0.37 | 0.48 | 0.65 | 0.90 | 1.36 | 1.90 | 3.88 | ||
| Missing prels (%) | 20.45 | 12.97 | 9.84 | 8.74 | 7.75 | 6.81 | 6.41 | 5.51 | 4.64 | 3.58 | ||
- The initial sample comprises all stocks listed in the AGSM CRIF database from 1973 to 2010. Stocks that have nonordinary shares and/or are classified as real estate, property trusts, investment and financial services are excluded. Starting in December 1973, stocks are ranked annually by market capitalisation and sorted into decile portfolios. The table reports average monthly portfolio returns calculated under the constant and updated weights approaches. Panel A (Panel B) reports average monthly portfolio returns when stocks are equal (value) weighted. The statistical significance of return bias is shown, with ***, ** and * indicating significance at 1, 5 and 10 per cent levels, respectively. Panel C summary statistics are the time series average of annual cross-sectional means and medians.
Holding the treatment of nontrading constant, the stock weighting bias isolates the error induced by applying constant-initial weights to monthly stock returns. Liu and Strong (2008) provide an analytic representation of the bias induced by the constant weights method and suggest that it will over (under) state returns to portfolios comprising low (high)-price stocks. The empirical results in Table 3 are highly consistent with this conjecture. Summary statistics in Panel C demonstrate that share prices are lowest in the smaller deciles, and it is these deciles where the stock weighting bias is greatest (Method 1 – Method 2 ≈ 130–155 basis points per month for the smallest portfolio). Similarly, the constant weights approach results in a modest understatement of average returns for the larger size portfolios, where share prices are highest. In terms of the size premium (far right column labelled ‘spread’), using constant stock weights overstates the average spread return by 161 (135) basis points per month for equal (value) weighted portfolios.
A second pertinent aspect of Table 3 is the influence of nontrading bias. Holding constant the method of weighting stocks into portfolios, the nontrading bias quantifies the return differential resulting from using approach (2), compared to simply inserting a price relative of unity to cover nontrading. Panel C documents a high incidence of nontrading clustered in the small-stock portfolio. Over the 12 months following portfolio formation, stocks in the smallest size portfolio do not trade in 20.45 per cent of these months on average (this is nearly six times higher than the frequency of nontrading for large stocks). A priori, estimated returns for this portfolio are expected to be most sensitive to methodological choices regarding the treatment of nontrading. Somewhat surprisingly, average returns to the smallest size portfolio exhibit a very modest bias (Method 2 – Method 3 ≈ negative 10–16 basis points per month), which is statistically insignificant. This preliminary finding suggests that the approach taken to handle missing returns is less important than the approach to weighting stock returns into the portfolio.
After aggregating the two sources of bias, the nontrading bias partially offsets the stock weighting bias, yet a significant upward bias to the size premium remains. Specifically, when genuine buy-and-hold portfolio returns are calculated under the updated weights approach (1), and after applying (2) to accommodate nontrading, the size premium decreases by 144 (125) basis points per month under equal (value) weighting. This total bias in the size premium is almost entirely attributable to the stock weighting bias in the small-stock portfolio. To summarise, while there is still evidence of a size effect in Australian equity returns, Table 3 suggests that its magnitude is grossly overstated by popular methodologies.
Throughout this study, we repeatedly stress the importance of examining the share price and nontrading characteristics of portfolios. As demonstrated in Table 3 in the context of size-sorted portfolios, the low-price characteristics of stocks in small size portfolios makes them acutely vulnerable to the bias induced by the constant weights approach to estimating portfolio returns. Similarly, the prevalence of nontrading amongst small stocks signals that assumptions made over missing returns may be influential. In such circumstances, a careful study of portfolio characteristics may guide key methodological choices.
A final point to note is that the average returns to smaller size deciles in Table 3 are notably larger than reported in Gaunt (2011). The summary statistics in Table 3 allow us to reconcile the findings. Panel C suggests that the difference is primarily attributable to Gaunt's (2011) exclusion of stocks with sub-20c share price as at portfolio-formation date. Examining the mean and median share prices, many of the stocks in our smallest 3–4 size portfolios would be excluded by a sub-20c filter. In fact, when we repeat our analysis with a similar exclusion, our results almost precisely match Gaunt (2011). While Gaunt's motivation for a sub-20c filter is to mitigate the market-microstructure issues with low-price stocks, inadvertently, it also alleviates problems raised in the current study arising from stock weighting bias in portfolio returns.
3.2. Momentum profits
In the jargon of Jegadeesh and Titman (1993), our momentum study is a 6/6 strategy. Starting in June 1974, prior 6-month momentum is calculated for all stocks with valid prices in December 1973 and June 1974. The momentum metric includes both capital gains/losses and dividends. Stocks are ranked by their prior momentum and sorted into decile portfolios. Buy-and-hold positions in the constituent stocks are maintained for 6 months, after which the ranking and portfolio-formation procedure is repeated. Over the sample period, this generates 72 nonoverlapping 6-month test periods (hence 432 months), encompassing 899 stocks on average.16
As noted above, one of the aims of this study is to demonstrate the importance of carefully considering the characteristics of stocks assigned to various portfolios, with an eye towards how this may combine with the chosen research methodology to influence estimated portfolio returns. Accordingly, before examining the empirical evidence on momentum profitability, we take a brief look at the summary statistics in Table 4 Panel C.
| Losers | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Winners | Spread | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Equally weighted portfolios | ||||||||||||
| Constant weights | 3.17 | 1.88 | 1.51 | 1.66 | 1.50 | 1.69 | 1.58 | 1.98 | 2.07 | 2.16 | −1.01 | (p = 0.135) |
| Updated weights | 2.75 | 1.58 | 1.35 | 1.46 | 1.40 | 1.66 | 1.51 | 1.96 | 2.06 | 2.02 | −0.73 | (p = 0.294) |
| Total bias | 0.42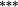 |
0.30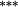 |
0.16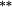 |
0.20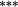 |
0.10 | 0.03 | 0.07 | 0.02 | 0.01 | 0.14 |
−0.28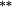 |
|
| Weighting bias | 0.56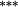 |
0.28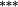 |
0.16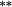 |
0.20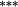 |
0.09 |
0.02 | 0.06 | 0.05 | 0.05 | 0.14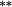 |
−0.42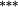 |
|
| Nontrading bias | −0.14 | 0.02 | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | −0.03 | −0.04 | 0.00 | 0.14 | |
| Panel B: Value-weighted portfolios | ||||||||||||
| Constant weights | 0.40 | −0.15 | 0.79 | 0.81 | 1.11 | 1.34 | 0.95 | 1.47 | 1.43 | 1.90 | 1.50 | (p = 0.019) |
| Updated weights | 0.24 | −0.16 | 0.87 | 0.83 | 1.14 | 1.35 | 1.00 | 1.50 | 1.46 | 2.01 | 1.77 | (p = 0.005) |
| Total bias | 0.16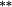 |
0.01 | −0.08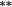 |
−0.02 | −0.03 | −0.01 | −0.05 |
−0.03 |
−0.03 | −0.11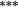 |
−0.27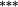 |
|
| Weighting bias | 0.16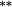 |
−0.02 | −0.09 |
−0.01 | −0.04 | −0.02 | −0.06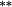 |
−0.02 | −0.03 | −0.12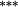 |
−0.28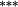 |
|
| Nontrading bias | 0.00 | 0.03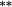 |
0.01 |
−0.01 | 0.01 | 0.01 | 0.01 | −0.01 | 0.00 | 0.01 | 0.01 | |
| Panel C: Summary statistics | ||||||||||||
| Mkt Cap ($m): mean | 34 | 115 | 212 | 294 | 464 | 526 | 518 | 497 | 383 | 164 | ||
| Mkt Cap ($m): median | 5 | 9 | 14 | 25 | 29 | 32 | 32 | 32 | 29 | 18 | ||
| Price ($): mean | 0.38 | 0.78 | 1.18 | 1.50 | 1.88 | 2.02 | 2.13 | 2.15 | 2.05 | 1.46 | ||
| Price ($): median | 0.19 | 0.37 | 0.54 | 0.71 | 0.86 | 0.98 | 1.04 | 1.06 | 0.99 | 0.60 | ||
| Missing prels (%) | 8.34 | 5.87 | 5.49 | 5.54 | 4.92 | 5.16 | 5.39 | 5.33 | 6.33 | 7.48 | ||
- The sample comprises all stocks listed in the AGSM CRIF database over the period 1973 to 2010. Stocks that have nonordinary shares and/or are classified as real estate, property trusts, investment and financial services are excluded. Starting in June 1974, stocks are ranked by their prior 6-month momentum and sorted into decile portfolios. The composition of the portfolios remain fixed for 6 months, after which the ranking and portfolio-formation procedure is repeated. The table reports average monthly portfolio returns calculated under the constant and updated weights approaches. Panel A (Panel B) reports average monthly portfolio returns when stocks are equal (value) weighted. The statistical significance of return bias is shown, with ***, ** and * indicating significance at 1, 5 and 10 per cent levels, respectively. Summary statistics are the time series average of annual cross-sectional means and medians.
As pre-empted in footnote,15 portfolios sorted according to momentum are more heterogeneous in terms of market capitalisation and share price than size-sorted portfolios. With greater dispersion of market caps within a portfolio, we expect to see a larger difference between equal- and value-weighted portfolio returns. Further, low-price stocks are more evenly distributed across decile portfolios (not necessarily evenly, but more so than with size-sorted portfolios). As such, the stock weighting bias in portfolio returns is likely to be less extreme than observed with size-sorted portfolios. With respect to nontrading, Panel C shows that the occurrence of nontrading is both less clustered in specific portfolios and less prevalent than observed for size portfolios.17 These characteristics should to some extent mitigate the nontrading bias. Each of these conjectures is confirmed in Table 4.
In Panel A, average returns to equal-weighted momentum-sorted portfolios show no evidence of momentum profits. In fact, recent losers outperform recent winners, although the spread portfolio is statistically insignificant. As was the case with the size effect, the stock weighting bias is greatest for the portfolio comprising the lowest-priced stocks (Losers in this case).
In Panel B, average portfolio returns are notably lower when stocks are value-weighted into portfolios (compared with Panel A equal-weighted portfolios). This occurs when small stocks have higher returns, and there is heterogeneity in market caps within each portfolio. The nontrading bias is virtually nonexistent, suggesting that nontrading within portfolios is confined to small-cap stocks that carry relatively little weight.18 Importantly, the stock weighting bias shows that the constant weights approach overstates (understates) returns to the Loser (Winner) portfolio. As such, there is a double whammy effect that increases momentum profits when genuine buy-and-hold returns are calculated using correctly updated stock weights. Providing further support for the notion that the constant weights approach understates the momentum effect, average returns to the momentum spread strategy are approximately 30–40 basis points per month higher after correcting the stock weighting bias.19
With reference to the extant Australian momentum literature, the results in Table 4 warrant two final comments. First, the current findings shed light on prior Australian momentum findings, which have been inconclusive. Using all ASX-listed stocks, Durand et al. (2006) find no evidence of momentum profits. While they do not articulate how stocks are weighted into their portfolios, the findings in Table 4 Panel A suggest that equal weighting is likely. Second, 4 replicates the dramatic reversal in momentum findings under equal- and value-weighted momentum portfolios previously reported in Brailsford and O'Brien (2008). In Section 4., we show that momentum effects are unduly affected by small stocks under equal-weighted portfolios. When the analysis is restricted to the Top 500 stocks, a clear momentum effect is apparent regardless of how stocks are weighted into portfolios.
3.3. Book-to-market effects
Early Australian research into the book-to-market (BM) effect was severely hampered by the limited availability of financial-statement data required to calculate book value. Utilising modest subsets of the population of stocks, early studies by Halliwell et al. (1999) and Gaunt (2004) provide cautious evidence of a significant value premium. With the benefit of an extended time series of accounting data (1981–2005) and near-complete cross-sectional coverage, O'Brien (2008) finds evidence of a value premium only for equal-weighted BM-sorted decile portfolios. Gharghori et al. (2009) report a significant value premium to six value-weighted BM portfolios over the period 1993–2005. Gharghori et al. (2013) document a positive relationship between BM and average returns to BM-sorted decile portfolios spanning 1993–2009. Recently, Dou et al. (2012) show that the value premium in the population is driven by micro-cap stocks, with little evidence amongst large caps.
Our study of the BM effect proceeds as follows. Using financial-statement data sourced from Aspect Huntley, book value of equity is calculated as described in Section 3.. Starting in December 1989, stocks are ranked by BM and sorted into decile portfolios. Buy-and-hold positions in the constituent stocks are maintained for 12 months, after which the ranking and portfolio-formation procedure is repeated each year through to December 2009. Over the 21-year period (252 months), 946 stocks per annum are assigned to decile BM portfolios on average.
The results in Table 5 cast further doubt over the existence of a BM effect in Australian equity returns. Under the constant weights approach, there is apparent evidence of a statistically significant value premium regardless of how the stocks are weighted into portfolios (2.07 and 1.41 per cent under equal- and value-weighting, respectively). These findings are highly consistent with prior results. O'Brien (2008) reports an average value premium of 1.87 per cent per month for equal-weighted portfolios. Gharghori et al. (2009) report an average value premium of 1.28 per cent per month for value-weighted portfolios.
| Growth | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Value | Spread | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Equally weighted portfolios | ||||||||||||
| Constant weights | 0.80 | 1.06 | 1.41 | 1.36 | 1.54 | 1.71 | 1.91 | 2.05 | 2.47 | 2.87 | 2.07 | (p = 0.003) |
| Updated weights | 0.78 | 1.00 | 1.51 | 1.32 | 1.65 | 1.73 | 1.64 | 2.00 | 2.11 | 2.38 | 1.60 | (p = 0.024) |
| Total bias | 0.02 | 0.06 | −0.10 | 0.04 | −0.11 | −0.02 | 0.27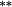 |
0.05 | 0.36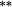 |
0.49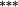 |
0.47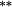 |
|
| Weighting bias | 0.16 | 0.01 | 0.01 | −0.02 | −0.03 | 0.10 | 0.19 |
0.18 | 0.50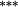 |
0.62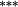 |
0.46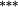 |
|
| Nontrading bias | −0.14 | 0.05 |
−0.11 | 0.06 |
−0.08 | −0.12 |
0.08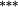 |
−0.13 | −0.14 |
−0.13 |
0.01 | |
| Panel B: Value-weighted portfolios | ||||||||||||
| Constant weights | 0.14 | 0.45 | 0.90 | 0.89 | 0.98 | 0.79 | 1.18 | 1.26 | 1.01 | 1.55 | 1.41 | (p = 0.019) |
| Updated weights | 0.37 | 0.52 | 0.98 | 0.91 | 0.98 | 0.83 | 1.20 | 1.36 | 1.11 | 1.33 | 0.96 | (p = 0.096) |
| Total bias | −0.23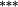 |
−0.07 | −0.08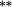 |
−0.02 | 0.00 | −0.02 | −0.02 | −0.10 |
−0.10 | −0.22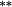 |
0.45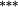 |
|
| Weighting bias | −0.23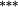 |
−0.07 | −0.09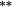 |
−0.02 | 0.00 | −0.04 | −0.02 | −0.11 |
−0.10 | 0.17 | 0.40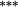 |
|
| Nontrading bias | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.02 | 0.00 | 0.01 | 0.00 | 0.05 | 0.05 | |
| Panel C: Summary statistics | ||||||||||||
| Mkt Cap ($m): mean | 415 | 711 | 920 | 932 | 754 | 623 | 365 | 221 | 95 | 36 | ||
| Mkt Cap ($m): median | 36 | 40 | 43 | 38 | 31 | 27 | 23 | 14 | 10 | 6 | ||
| Price ($): mean | 2.10 | 2.35 | 2.59 | 2.29 | 1.84 | 1.71 | 1.31 | 0.98 | 0.66 | 0.38 | ||
| Price ($): median | 0.48 | 0.63 | 0.75 | 0.63 | 0.57 | 0.53 | 0.44 | 0.33 | 0.24 | 0.13 | ||
| BM ($): mean | 0.12 | 0.28 | 0.40 | 0.52 | 0.65 | 0.80 | 0.99 | 1.26 | 1.70 | 3.26 | ||
| BM ($): median | 0.13 | 0.28 | 0.40 | 0.52 | 0.65 | 0.80 | 0.99 | 1.25 | 1.68 | 2.77 | ||
| Missing prels (%) | 7.39 | 5.35 | 5.25 | 5.38 | 6.77 | 6.43 | 7.36 | 8.38 | 9.93 | 13.56 | ||
- The initial sample comprises all stocks listed in the Aspect Huntley database from 1989 to 2009. Stocks that have nonordinary shares and/or are classified as real estate, property trusts, investment and financial services are excluded. The book value of stocks is calculated as the total value of equity, less outside equity interests, less preferences shares, less future tax benefits. Market value is drawn from AGSM CRIF as at December of the portfolio-formation year. Starting December 1989, stocks are ranked annually by BM and sorted into decile portfolios. The table reports average monthly portfolio returns calculated under the constant and updated weights approaches. Panel A (Panel B) reports average monthly portfolio returns when stocks are equal (value) weighted. The statistical significance of return bias is shown, with ***, ** and * indicating significance at 1, 5 and 10 per cent levels respectively. Summary statistics are the time series average of annual cross-sectional means and medians.
However, when the procedure of (1) and (2) is applied to estimate genuine buy-and-hold returns, the evidence in favour of a book-to-market effect is less compelling. The magnitude of the value premium is reduced by 47 (45) basis points per month under equal (value)-weighted portfolios. Statistical support for a value premium exists for equally weighted portfolios (p = 0.024), but is weak for value-weighted portfolios (p = 0.096).
Again, the share price and nontrading statistics are the key to understanding how bias is induced. Focusing on value-weighted portfolios in Panel B, the Value portfolio (high BM) comprises low-price stocks, for which the constant weights approach overstates average returns (17 basis points). Similarly, the Growth portfolio comprises higher-priced stocks, for which the constant weights approach understates average returns (23 basis points). This results in the value premium being overstated by 40 basis points per month under the constant weights approach. Note also that the constituents of the value portfolio are small-cap stocks, with high nontrading frequencies thereby inducing a modest bias (5 basis points).
3.4. Simulation evidence
Several points emerge from our empirical exploration of size, momentum and book-to-market anomalies. When a buy-and-hold investment strategy is intended, estimating portfolio returns using the constant weights approach can induce a significant bias. Depending on the characteristics of stocks involved, this bias can approach 150 basis points per month. While the treatment of nontrading induces an additional bias, its magnitude is modest and virtually negligible for value-weighted portfolios. Nonetheless, taken together, the stock weighting and nontrading biases combine for individual portfolios and flow through to hedge portfolio, potentially influencing empirical findings. As such, examining the size, price and nontrading characteristics of a portfolio's constituent stocks is a useful starting point in understanding the direction and magnitude of the bias.
Arguably, these insights are limited in the sense that they derive from our empirical analysis in very specific settings (the study of size, momentum and book-to-market effects). With an eye towards providing a more general analysis, we conduct a simple simulation experiment. A random month is chosen between December 1973 and December 2009. The population of stocks at that point is filtered using either share price or market capitalisation (as indicated below). From the resulting subset of stocks, 100 stocks are randomly selected and formed into a buy-and-hold portfolio. Monthly portfolio returns are estimated over the subsequent 12 months using the approach of Method 1, Method 2 and Method 3 described above. The total bias in average monthly portfolio returns is decomposed into stock weighting and nontrading bias. This simulation procedure is repeated 5000 times, with average bias reported.
Table 6 provides an insight into the complexity of the bias induced by methodological choices. In each case, the reported bias is basis points per month. A positive (negative) bias indicates that an ‘inferior’ methodological combination over (under) states average portfolio returns relative to a ‘superior’ approach. Consistent with Liu and Strong's (2008) analytic representation, Table 6 documents positive (negative) bias for low (high) priced stocks. Similarly, as there is a strong correlation between share price and market capitalisation, the constant weights approach under (over) estimates monthly returns to big (small) firms. Curiously, however, the bias is not a monotonic function of price or firm-size. For example, as we move from Top 200 stocks to those ranked 201 to 500, the understatement of returns increases. However, for partitions outside the Top 500, the constant weights approach overstates monthly returns.20
| Components of Bias | Components of Bias | % Missing | |||||
|---|---|---|---|---|---|---|---|
| Weighting | Nontrading | Total | Weighting | Nontrading | Total | Returns | |
| Equal-weighted portfolios | Value-weighted portfolios | ||||||
| P≥$2 | −8.05 | −0.90 | −8.95 | −3.40 | −0.74 | −4.14 | 6.59 |
| $1≤P < $2 | −16.02 | −0.27 | −16.29 | −15.14 | 0.04 | −15.10 | 7.58 |
| 50c≤P < $1 | −14.07 | 1.66 | −12.41 | −20.85 | 1.01 | −19.84 | 8.41 |
| 20c≤P < 50c | 12.16 | 1.96 | 14.12 | −9.96 | 1.22 | −8.74 | 8.60 |
| P < 20c | 99.19 | −5.26 | 93.93 | 41.31 | 1.47 | 42.78 | 9.97 |
| Top 200 | −8.99 | −0.22 | −9.21 | −3.66 | −0.54 | −4.20 | 3.96 |
| 200−500 | −10.87 | 1.04 | −9.83 | −17.87 | 0.89 | −16.98 | 6.80 |
| 500−1000 | 58.63 | −7.53 | 51.10 | 32.55 | −2.22 | 30.33 | 12.03 |
| 1000+ | 105.22 | 3.96 | 109.18 | 93.35 | 5.32 | 98.67 | 11.81 |
- A random month is chosen during the period December 1973 through December 2009. The population of stocks is filtered as indicated below (using share price or market capitalisation). From this subset of stocks, 100 randomly chosen stocks are formed into a portfolio (either equal- or value-weighted). Monthly portfolio returns for the following 12 months are estimated using the Method 1, Method 2 and Method 3 approaches. The total bias in average monthly portfolio returns is decomposed into stock weighting bias (Method 1 - Method 2) and nontrading bias (Method 2 - Method 3). The reported bias is basis points per month. A positive (negative) bias indicates that an ‘inferior’ methodological combination over (under) states average portfolio returns relative to a ‘superior’ approach. This simulation procedure is repeated 5,000 times.
In terms of the relative importance of each bias component, Table 6 documents that the nontrading bias is less problematic than the stock weighting bias. With the exception of stocks outside the top 1000, the nontrading bias is negligible. The stock weighting bias, however, has the potential to be empirically significant. For stocks with share price below 20 cents or outside the top 1000, using the constant weights approach generates an overstatement of average monthly returns in the vicinity of 100 basis points per month. To some extent, value-weighting stocks into the portfolio reduces the severity of the stock weighting bias in extreme cases. Nonetheless, the total remaining bias can be material. To grasp the potential influence of this bias, one simply needs to note that there were 2045 stocks in the AGSM database as at December 2010. Hence, at least half the population lies outside the Top 1000. Further, just over 900 of these stocks have share price below 20 cents. Clearly, there is enormous potential for empirical studies to be affected when portfolios are formed under the constant weights approach.
4. Investable anomalies
While the discussion and analysis in this study inevitably raises concerns over the reliability of evidence for well-known anomalies, academics and practitioners are nonetheless likely to remain acutely interested in the topic. Therefore, notwithstanding the intention of this study is to explore methodological issues surrounding the estimation of portfolio returns, we conclude with a brief re-examination of the size, momentum and BM anomalies. Our objective is to mitigate the factors that give rise to ambiguity in interpretation of results; in short, we consider whether these are ‘investable’ anomalies.
The empirical approach is identical to Section 3., with the exception that the analysis is restricted to the Top 500 stocks by market capitalisation as at each portfolio-formation point. There are several obvious motivations for this restriction. Table 6 shows that the occurence of nontrading is modest within the Top 500, thereby mitigating inaccuracies induced by ad hoc assumptions over the treatment of missing returns. Given the correlation between market cap and share price, focusing on large-cap stocks also mitigates the bid-ask bias in returns (Blume and Stambaugh, 1983). Perhaps most importantly, investment professionals rarely consider stocks outside the subset of stocks included in major indices.21
With regards to the size effect, recall from Table 3 that the apparent size effect was driven by incredulously high returns to a small-stock portfolio populated with micro-cap, low-priced stocks with high nontrading frequencies. In contrast, Table 7 reports no evidence of a size effect in the Top 500 stocks. In fact, there is very little difference between average returns estimated under constant and updated weights approaches (the bias in the spread portfolio is statistically insignificant). The size premium is a modest 20–30 basis points per month, and statistically insignificant. Restricting the analysis to the Top 500 stocks appears to have much the same effect on the size premium as Gaunt's (2011) exclusion of sub-20c stocks to mitigate bid-ask bias. The inferences from Table 7 are also highly consistent with Dou et al. (2012). Similar to Table 3, Dou et al. (2012) report a significant size effect in the population of stocks. However, they find no evidence of an investable size premium after restricting the analysis to the Top 300 stocks (approximately).
| Small | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Big | Spread | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Equally weighted portfolios | ||||||||||||
| Constant weights | 1.43 | 1.13 | 1.01 | 1.06 | 0.96 | 1.05 | 1.14 | 1.14 | 1.07 | 1.20 | 0.23 | (p = 0.583) |
| Updated weights | 1.41 | 1.08 | 1.14 | 1.15 | 1.14 | 1.16 | 1.26 | 1.26 | 1.18 | 1.21 | 0.20 | (p = 0.623) |
| Total bias | 0.02 | 0.05 | −0.13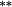 |
−0.09 | −0.18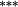 |
−0.11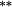 |
−0.12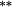 |
−0.12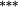 |
−0.11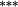 |
−0.01 | 0.03 | |
| Weighting bias | 0.01 | 0.01 | −0.15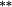 |
−0.13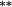 |
−0.20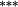 |
−0.13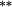 |
−0.11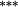 |
−0.13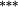 |
−0.12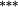 |
−0.01 | 0.02 | |
| Nontrading bias | 0.01 | 0.04 |
0.02 | 0.04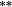 |
0.02 |
0.02 | −0.01 | 0.01 | 0.01 | 0.00 | 0.01 | |
| Panel B: Value−weighted portfolios | ||||||||||||
| Constant weights | 1.37 | 1.10 | 0.96 | 1.04 | 0.92 | 1.02 | 1.14 | 1.14 | 1.02 | 1.10 | 0.27 | (p = 0.503) |
| Updated weights | 1.41 | 1.08 | 1.15 | 1.16 | 1.13 | 1.14 | 1.27 | 1.26 | 1.15 | 1.13 | 0. 28 | (p = 0.500) |
| Total bias | −0.04 | 0.02 | −0.19 |
−0.12 |
−0.21 |
−0.12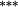 |
−0.13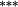 |
−0.12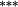 |
−0.13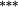 |
−0.03 | −0.01 | |
| Weighting bias | −0.05 | −0.02 | −0.21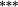 |
−0.16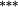 |
−0.23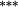 |
−0.13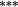 |
−0.12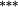 |
−0.14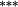 |
−0.14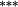 |
−0.02 | −0.03 | |
| Nontrading bias | 0.01 | 0.04 |
0.02 | 0.04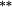 |
0.02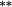 |
0.01 | −0.01 | 0.02 | 0.01 | −0.01 | 0.02 | |
| Panel C: Summary statistics | ||||||||||||
| Mkt Cap ($m): mean | 21 | 26 | 35 | 46 | 64 | 94 | 150 | 289 | 705 | 5214 | ||
| Mkt Cap ($m): median | 22 | 26 | 35 | 46 | 63 | 94 | 147 | 278 | 657 | 2919 | ||
| Price ($): mean | 0.78 | 0.88 | 1.11 | 1.26 | 1.62 | 1.99 | 2.31 | 3.06 | 4.40 | 8.76 | ||
| Price ($): median | 0.52 | 0.63 | 0.79 | 0.96 | 1.18 | 1.48 | 1.80 | 2.35 | 3.20 | 5.82 | ||
| Missing prels (%) | 7.81 | 7.64 | 6.42 | 7.00 | 5.80 | 6.27 | 5.49 | 4.20 | 3.90 | 3.10 | ||
- The initial sample comprises all stocks listed in the AGSM CRIF database from 1973 to 2010. Stocks that have nonordinary shares and/or are classified as real estate, property trusts, investment and financial services are excluded. Starting in December 1973, the Top 500 stocks by market capitalisation are sorted annually into decile portfolios. The table reports average monthly portfolio returns calculated under the constant and updated weights approaches. Panel A (Panel B) reports average monthly portfolio returns when stocks are equal (value) weighted. The statistical significance of return bias is shown, with ***, ** and * indicating significance at 1, 5 and 10 per cent levels, respectively. Summary statistics are the time series average of annual cross-sectional means and medians.
Table 8 shows that a distinct momentum effect resides in the Top 500 stocks. Irrespective of how portfolio returns are estimated, prior winners outperform prior losers by around 200 basis points per month, which is highly statistically significant. The disconcerting reversal of findings reported in Table 4 as we moved from equal- to value-weighted portfolios does not recur, suggesting small stocks outside the Top 500 were to blame. Note also that, even within the Top 500, the constant weights approach results in a statistically significant understatement of the momentum effect (14–17 basis points). On the whole, the results in Table 8 strongly suggest that momentum is an investable anomaly.
| Losers | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Winners | Spread | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Equally weighted portfolios | ||||||||||||
| Constant weights | 0.02 | 0.27 | 0.75 | 0.96 | 1.19 | 1.27 | 1.44 | 1.60 | 1.81 | 1.82 | 1.80 | (p = 0.002) |
| Updated weights | −0.05 | 0.25 | 0.80 | 0.99 | 1.21 | 1.34 | 1.50 | 1.64 | 1.87 | 1.89 | 1.94 | (p < 0.001) |
| Total bias | 0.07 | 0.02 | −0.05 | −0.03 | −0.02 | −0.07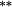 |
−0.06 |
−0.04 | −0.06 | −0.07 | −0.14 |
|
| Weighting bias | 0.05 | −0.01 | −0.06 | −0.03 |
−0.04 | −0.08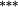 |
−0.06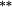 |
−0.04 | −0.06 | −0.09 |
−0.14 |
|
| Nontrading bias | 0.02 | 0.03 |
0.01 | 0.00 | 0.02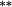 |
0.01 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | |
| Panel B: Value-weighted portfolios | ||||||||||||
| Constant weights | 0.07 | 0.47 | 1.01 | 1.10 | 1.31 | 0.89 | 1.32 | 1.24 | 1.62 | 1.98 | 1.91 | (p < 0.001) |
| Updated weights | 0.03 | 0.50 | 1.03 | 1.16 | 1.33 | 0.89 | 1.37 | 1.27 | 1.67 | 2.11 | 2.08 | (p < 0.001) |
| Total bias | 0.04 | −0.03 | −0.02 | −0.06 |
−0.02 | 0.00 | −0.05 |
−0.03 | −0.05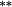 |
−0.13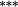 |
−0.17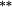 |
|
| Weighting bias | 0.02 | −0.04 | −0.02 | −0.05 | −0.03 | −0.01 | −0.06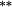 |
−0.03 | −0.04 |
−0.14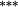 |
−0.16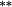 |
|
| Nontrading bias | 0.02 | 0.01 | 0.00 | −0.01 | 0.01 | 0.01 | 0.01 | 0.00 | −0.01 | 0.01 | −0.01 | |
| Panel C: Summary statistics | ||||||||||||
| Mkt Cap ($m): mean | 109 | 431 | 688 | 855 | 899 | 981 | 925 | 723 | 578 | 277 | ||
| Mkt Cap ($m): median | 42 | 71 | 88 | 99 | 109 | 112 | 114 | 97 | 87 | 65 | ||
| Price ($): mean | 1.06 | 1.89 | 2.53 | 2.80 | 2.95 | 3.10 | 3.26 | 3.01 | 2.87 | 2.20 | ||
| Price ($): median | 0.60 | 1.04 | 1.38 | 1.55 | 1.76 | 1.87 | 1.84 | 1.80 | 1.59 | 1.14 | ||
| Missing prels (%) | 3.44 | 2.88 | 3.19 | 3.33 | 3.37 | 3.50 | 3.61 | 4.74 | 5.05 | 5.76 | ||
- The sample comprises all stocks listed in the AGSM CRIF database over the period 1973–2010. Stocks that have nonordinary shares and/or are classified as real estate, property trusts, investment and financial services are excluded. Starting in June 1974, the Top 500 stocks by market capitalisation are ranked by their prior 6-month momentum and sorted into decile portfolios. The composition of the portfolios remain fixed for 6 months, after which the ranking and portfolio-formation procedure is repeated. The table reports average monthly portfolio returns calculated under the constant and updated weights approaches. Panel A (Panel B) reports average monthly portfolio returns when stocks are equal (value) weighted. The statistical significance of return bias is shown, with ***, ** and * indicating significance at 1, 5 and 10 per cent levels, respectively. Summary statistics are the time series average of annual cross-sectional means and medians.
Finally, Table 9 sheds further light on the existence of a BM effect. In Table 5, the evidence of a BM effect under the correctly updated weights approach was luke warm. The monthly value premium was 160 basis points (p = 0.024) and 96 basis points (p = 0.096) using equal and value weights, respectively. Confidence in the former was tempered by the presence of small-cap stocks in the value (high BM) portfolio. Restricting the analysis to the Top 500 stocks, support for a value premium strengthens. In particular, for value-weighted portfolios, the average monthly value premium increases to 114 basis points and approaches statistical significance at the 5 per cent level. Should a researcher employ the constant weights approach, however, evidence of a value premium would be overstated (27–37 basis points).
| Growth | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Value | Spread | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Equally weighted portfolios | ||||||||||||
| Constant weights | 0.27 | 0.67 | 0.78 | 0.90 | 0.84 | 1.22 | 1.25 | 1.17 | 1.22 | 1.70 | 1.43 | (p = 0.024) |
| Updated weights | 0.45 | 0.83 | 0.86 | 1.02 | 1.06 | 1.30 | 1.25 | 1.24 | 1.21 | 1.51 | 1.06 | (p = 0.093) |
| Total bias | −0.18 | −0.16 |
−0.08 | −0.12 | −0.22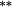 |
−0.08 | 0.00 | −0.07 | 0.01 | 0.19 |
0.37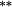 |
|
| Weighting bias | −0.11 | −0.16 |
−0.11 | −0.14 |
−0.23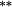 |
−0.07 | −0.05 | −0.13 | 0.02 | 0.19 |
0.30 |
|
| Nontrading bias | −0.07 | 0.00 | 0.03 | 0.02 |
0.01 | −0.01 | 0.05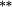 |
0.06 | −0.01 | 0.00 | 0.07 | |
| Panel B: Value-weighted portfolios | ||||||||||||
| Constant weights | 0.09 | 0.35 | 0.71 | 0.89 | 0.92 | 1.06 | 1.09 | 1.01 | 0.79 | 1.50 | 1.41 | (p = 0.017) |
| Updated weights | 0.33 | 0.44 | 0.75 | 0.95 | 0.96 | 1.06 | 1.10 | 1.03 | 0.82 | 1.47 | 1.14 | (p = 0.051) |
| Total bias | −0.24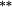 |
−0.09 |
−0.04 | −0.06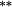 |
−0.04 | 0.00 | −0.01 | −0.02 | −0.03 | 0.03 | 0.27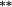 |
|
| Weighting bias | −0.25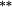 |
−0.09 |
−0.04 | −0.06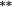 |
−0.03 | −0.02 | −0.01 | −0.03 | −0.04 | −0.03 | 0.22 |
|
| Nontrading bias | 0.01 | 0.00 | 0.00 |
0.00 | −0.01 | 0.02 | 0.00 | 0.01 | 0.01 | 0.06 | 0.05 | |
| Panel C: Summary statistics | ||||||||||||
| Mkt Cap ($m): mean | 659 | 905 | 1516 | 1209 | 1736 | 1424 | 1304 | 894 | 504 | 256 | ||
| Mkt Cap ($m): median | 121 | 119 | 132 | 143 | 143 | 140 | 121 | 103 | 93 | 67 | ||
| Price ($): mean | 3.30 | 3.17 | 4.03 | 3.77 | 3.47 | 3.10 | 2.72 | 2.45 | 1.87 | 1.03 | ||
| Price ($): median | 1.23 | 1.35 | 1.59 | 1.80 | 1.72 | 1.56 | 1.43 | 1.17 | 1.06 | 0.63 | ||
| BM ($): mean | 0.12 | 0.25 | 0.35 | 0.45 | 0.55 | 0.67 | 0.81 | 1.01 | 1.34 | 2.37 | ||
| BM ($): median | 0.12 | 0.25 | 0.35 | 0.45 | 0.55 | 0.67 | 0.81 | 1.01 | 1.32 | 2.07 | ||
| Missing prels(%) | 7.39 | 5.35 | 5.25 | 5.38 | 6.77 | 6.43 | 7.36 | 8.38 | 9.93 | 13.56 | ||
- The initial sample comprises all stocks listed in the Aspect Huntley database from 1989 to 2009. Stocks that have nonordinary shares and/or are classified as real estate, property trusts, investment and financial services are excluded. The book value of stocks is calculated as the total value of equity, less outside equity interests, less preferences shares, less future tax benefits. Market value is drawn from AGSM CRIF as at December of the portfolio-formation year. Starting December 1989, the Top 500 stocks by market capitalisation are ranked by BM and sorted annually into decile portfolios. The table reports average monthly portfolio returns calculated under the constant and updated weights approaches. Panel A (Panel B) reports average monthly portfolio returns when stocks are equal (value) weighted. The statistical significance of return bias is shown, with ***, ** and * indicating significance at 1, 5 and 10 per cent levels, respectively. Summary statistics are the time series average of annual cross-sectional means and medians.
To summarise, restricting the analysis to the Top 500 stocks alleviates many of the concerns that surround small-cap stocks (e.g. bid-ask bias, nontrading, treatment of missing returns, susceptibility to outliers, illiquidity). The results suggest that momentum and BM are investable anomalies, while size is not. Nonetheless, the ‘smaller’ stocks within the Top 500 may still be influential. By partitioning stocks into size groupings, Dou et al. (2012) show that BM and momentum effects exist in stocks ranked (approximately) 100–300 but are absent from the Top 100 stocks. Taken together, the practical importance of these anomalies appears to require sufficient liquidity amongst Top 500 stocks ranked outside the Top 100.
5. Conclusions
Sorting stocks into portfolios based on characteristics is a widely used methodology for empirical work in finance, accounting and capital markets. The resulting time series of monthly returns to portfolios is the foundation on which many empirical questions are examined. Are there patterns between average returns and stock characteristics? Do these relationships give rise to profitable long–short investment strategies? Can the anomalies be explained after adjusting for known risk factors? Do the stock characteristics suggest new risk factors and asset-pricing models? Accordingly, it is imperative that monthly portfolio returns are accurately estimated.
Recently, Liu and Strong (2008) highlight that researchers often employ a simplified approach to estimating monthly portfolio returns that has a number of undesirable consequences. The constant weights approach unrealistically implies that portfolios are rebalanced to initial weights each month and induces estimation error, such that estimated returns do not capture the wealth effects to an investor holding the portfolio. In a US context, they show that the estimation error is sufficient to generate incorrect statistical inferences in relation to popular anomalies.
This study contributes to the literature from both methodological and empirical perspectives. First, we build on Liu and Strong (2008) by exploring the additional complexity that arises when stocks are subject to nontrading. After considering several alternate treatments of missing returns, we develop an approach to approximating returns in the presence of nontrading. The second methodological contribution is to demonstrate how to partition the total bias in estimated returns into the unique components arising from (i) the method of averaging stocks returns into the portfolio, and (ii) the method chosen to accommodate nontrading. Finally, the empirical importance of each bias component is explored within the context of three well-known capital market anomalies. The market cap, share price and nontrading characteristics of Australian stocks make them particularly susceptible to these methodological issues, and hence provide an ideal setting for our study of return bias.
The empirical analysis provides clear implications for capital markets research that requires sorting of stocks into portfolios. When a buy-and-hold investment is intended, estimating portfolios using the popular constant weight approach can induce a significant bias into estimated returns. Depending on the characteristics of stocks involved, this bias can approach 150 basis points per month. The methodological choice relating to how a portfolio's constituent stocks are weighted to obtain portfolio returns is far more important than the treatment of missing returns. The stock weighting bias is economically and statistically important. This is true both when anomalies are examined using the population of stocks (as is common practice), and even when analysis is restricted to a more ‘investable’ set of large-cap stocks.
Finally, this study emphasises the need to carefully examine the characteristics of a portfolio's constituent stocks. Identifying the share price, firm-size and nontrading characteristics of stocks facilitates a better understanding of the susceptibility of empirical ‘findings’ to the chosen methodology. The constant weights approach systematically over (under) states returns to portfolios containing low (high) price stocks. While the nontrading bias is modest, care must be taken when stocks with high incidence of nontrading cluster in one of the extreme portfolios involved in the spread return. In summary, the issues considered in this study surrounding stock returns, portfolio weights and nontrading are likely to be relevant to researchers in many empirical settings.
Appendix
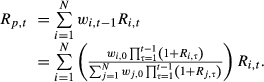 (A1)
(A1)The bracketed term shows how to calculate the correctly updated weight for stock i to be applied to 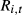 . Summing over N stocks gives the month-t portfolio return
. Summing over N stocks gives the month-t portfolio return 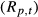 . While (A1) serves to illustrate why and how the initial stock weights
. While (A1) serves to illustrate why and how the initial stock weights  must be updated to reflect returns on a genuine buy-and-hold portfolio, it is notationally cumbersome and arguably lacking in intuition. A more intuitive exposition of the calculation of portfolio returns follows from utilising the dollar value of the portfolio.22
must be updated to reflect returns on a genuine buy-and-hold portfolio, it is notationally cumbersome and arguably lacking in intuition. A more intuitive exposition of the calculation of portfolio returns follows from utilising the dollar value of the portfolio.22
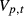 denote the dollar value of the portfolio at the end of month t. Without loss of generality, assume that the initial portfolio investment at month 0 is $1. In the same way that monthly portfolio returns in Tables 1 and 2 were calculated using the ‘portfolio value’ column, the month-t return on the portfolio is simply:
denote the dollar value of the portfolio at the end of month t. Without loss of generality, assume that the initial portfolio investment at month 0 is $1. In the same way that monthly portfolio returns in Tables 1 and 2 were calculated using the ‘portfolio value’ column, the month-t return on the portfolio is simply:
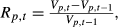 (A2)
(A2)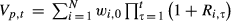 ; or in words, the time-t dollar value of the portfolio is the summation of the time-t dollar value of the N stocks in the portfolio.
; or in words, the time-t dollar value of the portfolio is the summation of the time-t dollar value of the N stocks in the portfolio.


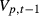 . Second, we simply need to show that the numerator in
. Second, we simply need to show that the numerator in 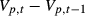 :
: