Significance Testing: We Can Do Better
Abstract
This paper advocates abandoning null hypothesis statistical tests (NHST) in favour of reporting confidence intervals. The case against NHST, which has been made repeatedly in multiple disciplines and is growing in awareness and acceptance, is introduced and discussed. Accounting as an empirical research discipline appears to be the last of the research communities to face up to the inherent problems of significance test use and abuse. The paper encourages adoption of a meta-analysis approach which allows for the inclusion of replication studies in the assessment of evidence. This approach requires abandoning the typical NHST process and its reliance on p-values. However, given that NHST has deep roots and wide ‘social acceptance’ in the empirical testing community, modifications to NHST are suggested so as to partly counter the weakness of this statistical testing method.
Publishing in a top accounting journal requires a massive effort by the author(s). A working paper, once crafted, is typically read and re-read multiple times, presented to multiple audiences, and then subjected to a rigorous review and revision process. This investment, even if successful, can take years to achieve publication. Yet, even after publication, the author(s) and readers are likely to ask, ‘What has been accomplished?’ or ‘What has been learned at the level of true science?’ Is more known of importance about the research issue now than before? Is the conclusion reliable or merely the result of a publication game or ritual?
In this paper, I suggest that our near-exclusive use of ‘null hypothesis statistical tests’, or NHST, undermines the true value of the effort expended in the research effort. Researchers typically address a question about which they have some previously acquired knowledge. If it can be maintained that science is essentially concerned with belief in this or that hypothesis, then it is fair to assert that degrees of belief are probabilities or the odds of belief. The research issue is then framed in terms of hypotheses and degrees of evidence or belief. Data are gathered and refined; we hope with great care and honesty, before being used to adjust our belief as to the hypothesis in question.
In this quest, the discovery process changes our beliefs but does not result in completely abandoning what was believed prior to the testing process. Instead, we continuously modify our understanding by taking what we previously knew (or assumed), modifying it for what is learned from the present study, and proceeding to update our previous revised beliefs. The learning process rarely, if ever, discards previous knowledge and replaces it with something completely different. Our information processing is then ‘Bayesian’. The Bayesian approach, which is assumed in economics of all rational inference and choice, is consistent with adjusting our statistical analysis to better align with the way our natural mental processing tends to update and incorporate new information.
In this paper, I suggest adopting a meta-analysis (i.e., a quantitative survey of an empirical literature on a single parameter) approach to test regression betas. Meta-analysis was introduced to economics from medicine by Jerrell and Stanley (1990). I borrow from Doucouliagos and Paldam (2015) and Cumming (2012, 2014) by focusing on interval estimation of an observed effect's economic significance. The methodology provides, indeed depends on, replication studies. The approach involves moving away from the traditional NHST process and its reliance on p-values favoured by frequentists. However, given NHST has very deep roots in the testing community, this paper suggests modifications to the traditional NHST when used for reported results. The paper also argues that NHST has inbuilt logical flaws that alone render it generally unacceptable in regression analysis and elsewhere.
The most important task before us in developing statistical science is to demolish the p-value culture, which has taken root to a frightening extent in many areas of both pure and applied science, and technology.
Because I will be referring to both researchers using NHST (frequentist) and researchers favouring Bayesian testing, a brief summary (presented in Table 1) of several important differences between the two approaches, adapted from Basturk et al. (2014), seems appropriate. At this point it is important to keep in mind that the frequentist–Bayesian disagreement on the appropriate testing logic is ongoing, as documented by Cox and Mayo (2010) who stress the ‘the difficulty [faced by Bayesians] of selecting subjective priors and … the reluctance among frequentists to allow subjective beliefs to be conflated with the information provided by data’ (p. 277; see also Cox, 2014; Mayo and Cox, 2006, 2011; Owhadi et al., 2015.)
| Frequentist | Bayesian | |
|---|---|---|
| Statisticians | Karl Pearson, Fisher, Neyman, Egon Pearson | Raiffa, Schlaifer, Barnard, Savage, de Finetti, Lindley |
| Concept of probability | Fraction of occurrences | Strength of belief |
| Process parameters | Fixed constant β, unknown | Unknown variable, subject of prior belief distribution f(β) |
| Data X provides for | Parameter estimation and tests of whether or not β = 0, intervals that include true β in given fraction of repetitions | Posterior belief distribution f(β|X), confidence intervals about β based on posterior beliefs |
Why the Frequentist Approach Should Be Abandoned in Favour of a Bayesian Approach
Frequentist Approach
The frequentist NHST relies on rejecting a null hypothesis of no effect or relationship based on the probability, or ‘p-level’, of observing a specific sample result X equal to or more extreme than the actual observation X₀, conditional on the null hypothesis H₀ being true. In symbols, this calculation yields a p-level = Pr(X ≥ X₀|H₀), where ≥ signifies ‘as or more discrepant with H₀ than X₀’. The origin of the approach is generally credited to Karl Pearson (1900), who introduced it in his χ2-test (Pearson actually called it the P, χ2-test). However, it was Sir Ronald Fisher who is credited with naming and popularizing statistical significance testing and p-values as promulgated in the many editions of his classic books Statistical Methods for Research Workers and The Design of Experiments (see Spielman, 1974; Seidenfeld, 1979; Johnstone, 1986; Berger, 2003; and Howson and Urbach, 2006 on the ideas and development of modern hypothesis tests (NHST)).
The Bayesian Approach
Under the Bayesian approach, probabilities rely on informed beliefs rather than physical quantities. They represent informed reasoned guesses. In the Bayesian approach, the objective is the posterior (post-sample) belief concerning where a parameter, β in our case, is possibly located. Bayes' theorem allows us to use the sample data to update our prior beliefs about the value of the parameter of interest. The revised (posterior) distribution represents the new belief based on the prior and the statistical method (the model) applied, and calculated using Bayes theorem. Prior beliefs play an important role in the Bayesian process. In fact, no data can be interpreted without prior beliefs (‘data cannot speak for themselves’).
Bayesians emphasize the unavoidably subjective nature of the research process. The decision to select a model and specific prior or family of priors is necessarily subjective, and the sample data are seldom obtained objectively (Basturk et al., 2014). Indeed, data quality has become a major problem with the advent of ‘big data’ and with the recognition that the rewards for publication tend to induce gamesmanship and even fraud in the data selected for the study.
When the investigator experiences difficulty and uncertainty in specifying a specific prior distribution, the use of a diffuse or ‘uninformative’ prior is typically adopted. The idea is to impose no strong prior belief on the analysis and hence allow the data to have a bigger part in the final conclusions. Ultimately, enough data will ‘swamp’ any prior distribution, but in reality, where systems are not stationary and no models are known to be ‘true’, there is always subjectivity and room for revision in Bayesian posterior beliefs.
The Bayesian viewpoint is that this is a fact of research life and needs to be faced and treated formally in the analysis. Objectivity is not possible, so there is no gain from pretending that it is. Formal Bayesian methods for coping with subjectivity are easy to understand. For example, one approach is to ask how robust the posterior distribution of belief about β is to different possible prior distributions. If we can say that we come to essentially the same qualitative belief over all feasible models and prior distributions, or across the different priors that different people hold, then that is perhaps the most objective that a statistical conclusion can claim.
Bayesian inference recognizes that research is properly concerned with the substantive (e.g., economic) importance of the conclusion, rather than its ‘statistical significance’. Statistical significance of itself implies very little. This has been a Bayesian criticism of frequentist NHST since the Bayesian textbook of Jeffreys (1939), but can be shown even within the conventional frequentist school of thought. A good way to see this is by looking at the results presented in Table 1 based on a similar argument in Johnstone (1997).
| Sample size n | Sample mean
 |
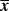p-level (2-sided) | 95% CI (2-sided)
 |
|---|---|---|---|
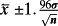| 10 | 0.6198 | 0.05 | (0, 1.240) |
| 30 | 0.3578 | 0.05 | (0, 0.7157) |
| 100 | 0.1960 | 0.05 | (0, 0.3920) |
| 1,000 | 0.0620 | 0.05 | (0, 0.1240) |
| 10,000 | 0.0196 | 0.05 | (0, 0.0392) |
The results in Table 1 are interpreted as follows. Consider a standard test of the null hypothesis H0 : μ = 0 that a normally distributed population with known variance σ2 = 1 has a population mean equal to zero. The table shows results that each has the same two-sided p-level equal to 5%. The only difference between these results is the assumed sample size and the resulting 95% (two-sided) confidence interval. The stark result is that as n gets larger the confidence interval associated with a fixed p-level of 5% shrinks and converges asymptotically to a point, μ = 0.
When n is very large the confidence interval that results from a statistically significant rejection of H₀ suggests that the true parameter is different from zero by only a miniscule amount. This result is nonetheless statistically significant at 5%, which is often understood as sufficient, or at least a pre-requisite, for a publishable result.
Consider now which of the results in Table 1 seems more promising in terms of establishing an economically or practically significant finding. The result with n = 10,000 seems to offer conclusive evidence that there is no practical effect. If this is contested, we can continue with the calculations using larger sample sizes until it is conclusive.
On the other hand, the result with n = 10 is consistent with a much larger possible effect. If this were a pilot study, the researcher would hope that with a larger sample size the observed sample mean would stay at or above
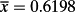, in which case the evidence would become stronger that there is in fact a truly ‘significant’ effect. This is just simple statistical reasoning obeying common sense, and also Bayesian logic, yet the irony is that the result with n = 10 would likely be deemed unpublishable for reasons of its small sample size.
This critique of the phrase ‘significant at 5%’ says essentially that the phrase is meaningless or at least highly ambiguous without knowing the sample size or magnitude of the observed effect, since a result that is depicted merely as ‘significant at 5%’ can suggest very strongly that there is no significant observed effect whatsoever. This very point is explored in greater depth from a Bayesian perspective by Johnstone and Lindley (1995).
The results in Table 1 show why a p-level of 5% means less and less as n gets larger. The confidence interval attached to a fixed p-level is not fixed as n changes, but instead shrinks and begins to look like a point at the null value of the unknown parameter. There is no need, therefore, to adopt an explicit Bayesian view to see how n makes a difference to the interpretation or meaning of a given p-level (here 5%, but equally for any other fixed p-level). The Bayesian demonstration of this same point is often described under the heading ‘Lindley's Paradox’, and is discussed later in this paper.
The Limitations of Nhst
Hubbard and Lindsay (2008, p. 71) point out that the basic methodological question remains: ‘Does the p-value, in fact, provide an objective, useful and unambiguous measure of evidence in hypothesis testing?’ 1 The present paper adopts an identical position drawing, in addition, on the recent efforts of researchers in other fields, particularly statistics and psychology. This paper will urge accounting researchers to consider a methodological approach suggested by the work of Paldam (2015) and Cumming (2012, 2014).
Cumming (2014, p. 4) observes that rarely can a single research study reach a definitive conclusion. Thus, Cumming and others advise researchers to avoid dichotomous logic and conclusions—such as whether a test result is significant or not, or a hypothesis is rejected or not—and instead advocate reliance on statistical thinking in terms of parameter estimation.
The prevailing yes-no decision at the magic 0.05 level from a single research is a far cry from the use of informed judgment. Science does not work that way. A successful piece of research doesn't settle an issue; it just makes some theoretical position more [or less] likely. (Cohen, 1990)
Regardless of whether our interest is in theory construction, treatment comparisons, or determining the practical importance of a result, parameter estimation (and its interval) is the primary statistic of interest; statistical significance is ancillary. (Lindsay, 1995).
This discussion raises the issue of what a p-value has to say about the probability distribution of the parameter β. The strict frequentist's answer is ‘nothing’ because frequentists never calculate or even acknowledge the existence of a probability distribution of a parameter. Rather, parameters are seen as unknown constants rather than as random (i.e., uncertain) variables. 2
Although the strict frequentist position is that testing does not lead to any probability statement or degree of belief about the null hypothesis, researchers do use tests that way. Fisher's (1925) approach tended to encourage this interpretation. His logic, repeated in some textbooks, is as follows. The researcher finds the probability of a result as contrary to the null hypothesis as the result actually observed, Pr(X ≥ X₀|H₀), as if the null hypothesis were true. The researcher then works backwards and concludes that either the null hypothesis is false or a result with that probability has occurred. Finally, in a step where the logic becomes only sketchy, the researcher reasons that in cases where the calculated probability, also known after Fisher as the ‘p-level’, is very low, the natural conclusion is that the null hypothesis is false, since the only alternative is a very low probability event. This roundabout logic, in one form or another, is why researchers tend to see a low p-level as grounds for disbelief in the null hypothesis, contrary to those strict interpretations in other textbooks that specifically deny any such interpretation. 3
Ultimately, the natural leap for many researchers is to interpret a p-level, such as 5%, as if it represents not Pr(X ≥ X₀|H₀) but Pr(H₀|X ≥ X₀). This common and somewhat natural mistake is often raised by critics of NHST, but tends to occur in empirical research communities anyway, perhaps because journal discussion usually takes significance testing as ‘assumed knowledge’ or as self-evident or well enough understood to not warrant any caveat or tutorial.
What is the probability of obtaining a dead person (D) given that the person was hanged (H); that is, in symbol form, what is Pr(D|H)? This probability will be very high, perhaps 0.97 or higher. Now, reverse the question: What is the probability that a person has been hanged (H) given that the person is dead (D); that is, what is Pr(H|D)? This time the probability will undoubtedly be very low, perhaps 0.0001 or lower. No one would be likely to make the mistake of substituting the first estimate (0.97) for the second (0.0001); that is, to accept 0.97 as the probability that a person has been hanged given that the person is dead. Even though this seems to be an unlikely mistake, it is exactly the kind of mistake that is made with the interpretation of statistical significance testing—by analogy, calculated estimates of Pr(H|D) are interpreted as if they were estimates of Pr(D|H), when they are certainly not the same.
Consider, further, the following example adapted from Oakes (1986) of how NHST results fall short of what is desired. Suppose, for example, that 5% of a firm's balance sheet accounts are in error and the auditor elects to examine 400 accounts selected at random. Assume that the auditor's test has a ‘Type II’ error probability of Pr(reject|no error) = 0.05 and also a ‘Type I’ error probability of Pr(accept|error) = 0.05. This test would be acceptable and powerful by frequentist standards. Now suppose the audit test examines 400 random accounts, the auditor's test is set to reject 400(0.95)(0.05) = 19 correct accounts and accept 400(0.05)(1–0.05) = 19 incorrect accounts. So the probability that an account that has been rejected is actually in error is only 19/(19 + 19) = 0.5. Hence, ‘rejection’ using a frequentist test with good error frequencies can give a false impression of the strength of the implied evidence. In this example, the fact that the auditor rejects a balance still leaves that balance with a 50% probability of being correct.
A Bayesian interpretation of this result is that rejection has raised the probability of the account in question being in error from a prior of 5% to a posterior of 50%. The mistake of interpreting ‘rejection’ in the NHST as rejection in a substantive sense is that the NHST does not allow for prior probabilities. Another way to say this is that if users of NHST want to interpret results in a pseudo-Bayesian way, as is almost always the case, then there will inevitably be logical mistakes if prior knowledge is ignored. Conclusions expressed in roughly Bayesian forms, such as ‘the null hypothesis is discredited and appears false’, require that the test result is merged with prior beliefs according to the weights afforded to them under the Bayes theorem.
To avoid any call upon the Bayes theorem and prior knowledge, the strictest advocates of NHST have opted away from any evidential interpretation at all. Their alternative test interpretation gets very strained and is often set up for deserved mockery. For example, strict NHST users will say that a test with critical significance level α = 0.05 rejects true null hypotheses only 5% of the time in repeated use, but will not make any statement to the effect that within this hypothetically infinite population of test repetitions a particular null hypothesis that has been rejected has only a 5% probability of being true. 4 When empiricists using NHST do in fact make such a natural leap, that step is regarded as an abuse typical of inexpert users rather than as any innate problem in the methods themselves.
While a p-level in a NHST is a random variable, α-levels or ‘critical’ levels are not, because they are chosen by the researcher, and are meant in the strict practice of frequentist NHST to be preset rather than being chosen after the test is run. Generally α is set to 0.05 although 0.10 and 0.01 are also common. Authors typically give no reason for their specific choice of α other than implicitly relying on the choices of previous researchers or tradition. Indeed, researchers often report only the smallest level of the three commonly reported α-levels larger than the calculated value of p. When reporting α-levels post-test, the consequent ‘power’ of the test or importance of a ‘Type II’ error (a failure to reject the null hypothesis when it is false) is implicitly ignored.
The most common concern with NHST results from equating statistical significance with basic importance. Ziliak and McCloskey (2008) in a review of the journals across a number of fields, found that nine out of 10 published articles make this critical error. In less than 2% of accounting papers surveyed and reported by Dyckman and Zeff (2014) did the author team attempt to estimate the cost or benefit implications of their results. Most researchers, if asked, would simply assert that to do so is simply not feasible, helpful, or even necessary and move on. Indeed, this criticism might do more harm than good since it leaves researchers with the view that there is nothing too much wrong with NHST, or nothing wrong in principle; rather it is merely an issue to do with some peoples' over-interpretation. The example discussed previously in regard to p-levels and the importance of the sample size should convince the reader that in fact there are much deeper issues than mere misuse, albeit that such misuse is common if not accepted.
Nhst from a Bayesian Viewpoint
Under a Bayesian approach, the questionable logic of NHST finds itself on even less stable ground. Using a Bayesian significance test for a normal mean, Sellke et al. (2001) point out that p-values of 0.20, 0.10, 0.05, 0.01, 0.005, and 0.001 correspond respectively to error probabilities in rejecting H of at least 0.465, 0.385, 0.289, 0.111, 0.067, and 0.018. These substantial differences further suggest p-values do not provide useful measures of evidence concerning H. In addition, they demonstrate (Sellke et al., 1987) that data yielding a p-value of 0.05 when testing a normal mean nevertheless results in a posterior probability of the null hypothesis of at least 0.30 for any possible symmetric prior with equal prior weight given to H and H. Recent research by Johnson (2013) indicates that if NHST with alpha set equal to 0.05 is used, the researcher can assume that one half of the possible alternative hypotheses should yield a positive result, suggesting that between ‘17% and 25% of marginally significant results are false’. The implications for those using NHST are immediate.
Johnstone (1986, p. 494; italics added) summarizes the results of Lindley (1957), who further references Jeffreys, 1939) as demonstrating ‘that for any prior probability Pr(H₀) other than zero and any level of significance p, no matter how small, there is always a sample size such that the posterior probability of the null hypothesis equals 1p. Thus depending on the sample size, the null hypothesis H₀ might be strongly supported by Bayes Theorem, yet irrevocably discredited by [a frequentist's significance test]’.
Hence, a null hypothesis that is soundly rejected at, say, the 0.05 level by a frequentist's significance test can nevertheless show 95% support from a Bayesian viewpoint. The rationale behind this, perhaps surprising, result, Johnstone (1986, p. 494) explains, is that regardless of how small the given fixed p-value of observation Xo, the likelihood ratio Pr(Xo|H₀)/Pr(Xo|Hₐ), where Hₐ is any given point alternative to H₀, approaches infinity as the sample size increases without limit. Consequently, for large n, a small p-value can actually be interpreted as evidence in favour of H₀ rather than against it (Hubbard and Lindsay, 2008, p. 76). Put another way, as the sample gets larger without limit, p can be made as small as desired while the posterior probability of the null being true approaches one.
An additional insight here, helping to explain how NHST and Bayesian testing diverge, is that Bayesian methods treat the data X = X₀ as exactly that, whereas NHST redefines X = X₀ as an unspecified observation X equal to or greater than X₀, that is, X ≥ X₀. This prompted Jeffreys (1939) to make something of a joke along the lines that a NHST rejection is where H₀ is rejected because results more inconsistent than X₀ with H₀ did not occur. In a Bayesian hypothesis test, the relevant measure of the evidence contained in the sample observation X = X₀ is the ratio of the two probability ordinates, f(X₀|H₀)/f(X₀|Ha), called the likelihood ratio, which has different ingredients and a different structure to a p-level, Pr(X ≥ X₀|H₀). See the excellent discussions on Bayesian testing logic in Berger (1985), Kadane (2011), O'Hagen (1994), Robert (2007), and a growing number of widely adopted Bayesian textbooks.
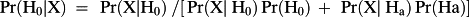
Without any obvious unique alternate hypothesis, such as Ha: θ = θa, the researcher judges some probability distribution over all of the a priori possible values of the unknown parameter. 5 The need to consider alternative possible values of the unknown parameter, and their prior probabilities, is often held as a weakness of Bayesian methods. There are several important points in response to this claim. The first is that there is no logical alternative, because if we wish to reason consistently with the laws of probability, evidence cannot be found against one hypothesis unless it can be shown to be in favour of at least one possible alternative. Put another way, probability logic (i.e., Bayesian logic) requires that there must be a better alternative explanation for what has been observed, in the sense that some other hypothesis better explains the data than the null hypothesis being tested.
A second response, not discussed in detail here but still very important, was made by statistical theorists Berger and Sellke in a series of papers (e.g., 1987). They set about testing the strength of evidence offered by p-levels by testing the maximum strength of rejection of H₀ that could be drawn from them when we try every prior distribution in an extremely broad class of distributions. For example, suppose that the test is two-sided. We might then use the class of all symmetric prior distributions. The idea is to give significance tests their most generous possible Bayesian interpretation. The general result is that even on this interpretation, significant results often provide only weak rejection of the null hypothesis.
This response is a twist on the older argument that two Bayesian users with quite different prior beliefs will come to the same posterior conclusion given enough data. Berger and Sellke (1987) argue in effect that if we cannot find any reasonable prior on which the data provide strong evidence against the null, then it can't be said logically to be a ‘rejection’ or to discredit the null in any rational sense of evidence, that is, there is no rational user who would see it that way, despite their possibly very different starting beliefs.
- It is not meaningful to calculate a p-value without considering an alternative hypothesis in the calculation of that measure. By definition the p-value of a given observation Xo with respect to any given hypothesis H₀ is the same no matter what possible alternatives exist or rate a mention, no matter how plausible these might seem a priori. The method of p-values tests H0 in isolation, as if the meaning of the data is unaffected by the range or prior plausibility of alternatives, or by how they could have occurred.
- A ‘point’ null hypothesis like H₀: μ = 1 is a straw man, and can be rejected even when the evidence favours it more than any reasonable or plausible alternative. 6 Indeed any—no effect—hypothesis is always false in the social sciences.
- A point null hypothesis can be rejected even when the evidence favours it relative to any materially different hypothesis. For example, suppose we observe
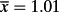in a sample of n = 200. With a known population variance of 1, that evidence must tend to support H0: μ = 1 relative to even close alternative hypotheses like Ha: μ = 1.05, especially given that the sample size seems reasonably large. However, with σ = 1, the (two-sided) p-level Pr(X ≥ 1.01|μ = 1) = 0.046 is low enough to allow a rejection of H₀: μ = 1 ( ‘≥’ denotes ‘as or more discrepant with H0’).
7 This example illustrates how reasoning mechanically by p-levels can contradict common sense. While the evidence might appear to provide strong evidence against the null, the common sense and Bayesian interpretation of that result is that it shows strong evidence in favour of the null being either precisely true or as good as true. Lindley (1957) was first to highlight this point. - When interpreting a sample observation X, it is not logically defensible to ignore the exact observation X, which is a point, and instead treat it as an interval X ≥ Xo. Doing so hides or ignores information and is therefore not good science.
- The logical measure of evidence in a probability theory sense is to summarize data not by a p-level P(X ≥ Xo|H₀), but by the ‘likelihood ratio’ λ = Pr(X|H₀)/Pr(X|Hₐ). Any evidence X that has a likelihood ratio λ > 1 adds evidential support for H₀ relative to Hₐ. A likelihood ratio λ < 1 supports the alternate hypothesis, Hₐ relative to H₀. Thus, the likelihood ratio summarizes the direction and strength of the sample evidence (and is then combined with prior beliefs). This simple rule is implied by Bayes' theorem and is known to Bayesians as the likelihood principle (see Edwards et al., 1963; Berger, 1985; Berger and Wolpert, 1988; Royall, 1997; Lindley, 2014; and Kadane, 2011).
A large number of researchers, yet hardly any in accounting, have come to the conclusion that NHST should be replaced with a Bayesian approach. Following are notable examples from other fields. Lindley (1999, p. 75) writes, ‘My personal view is that p-values should be relegated to the scrap heap by those who wish to think and act coherently’. Berger and Sellke (1987) opine, ‘The overall conclusion is that p-values can be highly misleading measures of the evidence provided by the data against the null hypothesis’. Berger is a past president of the Institute of Mathematical Statistics, so he cannot be seen as just another of the long list of applied statisticians who have come to such a conclusion. Ioannidis (2005), a professor of statistics and a medical doctor at Stanford University, advises abandonment of NHST in medicine, suggesting that ‘false findings may be the majority or even the vast majority of published research claims’. Because the research in the medical field is subject to more effective experimental control than is attainable in the behavioural sciences, accountants and others are on more slippery turf when attempting to determine statistically justified conclusions. It is noted that Goodman (1999) has challenged Ioannidis' results but concludes ‘[T]here are more false claims made in the medical literature than anyone appreciates’. Harvey et al. (2014) come to the same conclusion based on a review of 296 finance papers. Kline (2004) concludes that the criticisms in over 400 papers support the minimization or elimination of NHST in the behavioural sciences. Johnson (2013) reaches a similar conclusion.
Cumming (2014), who has written extensively on the limitations of NHST, concludes that NHST should not be used. He argues (2014, p. 1) why the ‘formulation of research questions in estimation terms, has no place for NHST …’. Additional papers that discredit NHST are included in the references to this paper and in Hubbard and Lindsay (2008), among others. In accounting, Johnstone (1995, 1997) argues against using NHST in statistical sampling in auditing, where unlike a great deal of empirical research there can be actions or decisions based on the results. Similarly rare papers on significance tests in accounting are Lindsay (1994, 1995).
A Meta-Analysis Approach
Paldam (2015, p. 3) reports that the meta-analysis methodology has been used on half a dozen simulation studies, where the true value of parameter β is known (also see Leamer, 1983 for an early example in economics). This approach, he maintains, has built trust in the tools, and it allows the researcher to claim that the resulting meta-average is much closer to the true value than is the sample mean. The author concludes that the difference between the two averages is an estimate of publication bias, a systematic difference between the published results and the true value, not just white noise. He adds that the difference could also be affected by work rejected for publication, control issues, and systematic errors. Paldam (2015, pp. 4–5) describes and illustrates (Figure. 1, p. 5) the results of using meta-analysis ‘based on data-samples with up to 1,000 observations … and a ‘literature reporting N = 366 estimates’ with results that are consistent with the advantage claimed for the meta-average approach.
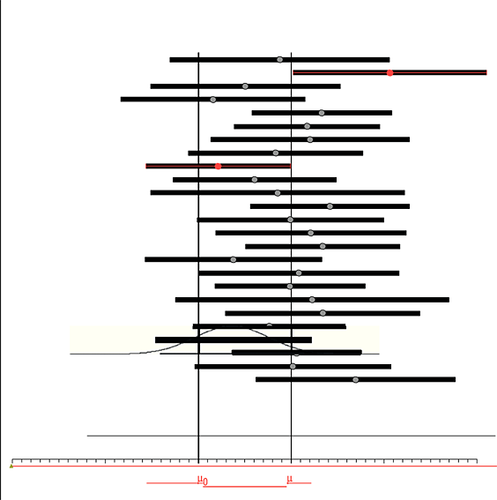
It is unlikely in the near future that accounting will encounter the opportunity to consider a sufficiently large set of papers to permit a similar study. Therefore, an intermediate approach suggested by Cumming (2014) in which confidence intervals (CIs) play the key role suggests that a sample used to calculate the p-value so often reported and uniformly relied on by researchers, can instead be used to calculate the first step (the first confidence interval) in his approach to establishing a more reliable confidence level.
The process illustrated in Figure. 1 (Cumming, 2014, p. 12, simplified), is based on successive samples from a single distribution with a known mean and variance. More generally, additional intervals would result from replication studies of the effect in question. As the number of replications increases, it becomes possible to compute a refined confidence interval with a specified probability level in which the value of parameter β would be inferred to lie. In social science research, the individual intervals would be based on replication studies that would not be considered as being drawn from precisely the same underlying distribution.
Advantages of Interval Reporting
One advantage of this meta-analysis is that it provides more information through CI statements than is possible with only p-values. CIs are also more in tune with a Bayesian approach in estimating the posterior odds of the parameter's location. This is because, unlike p-values, they account for the sample size and show not only an estimated interval for the unknown parameter, but also a measure of confidence attached to that interval, which is dependent on the sample size. (Thus, sensibly, the confidence for any given interval increases with the sample size.) Bayesian confidence intervals are often identical to frequentist confidence intervals, especially in the case of diffuse priors, so the two schools of thought can tend to merge once frequentists report CIs rather than the more obscure p-levels.
The main point shown by this analysis is that the mean confidence interval over the 25 simulations is a much better estimator of the true parameter than virtually every single study or confidence interval. Similar results are known throughout statistics, where averages tend to outperform their constituents. (In Figure 1, CIs 2 and 9, from the top, do not include the mean.)
In an editorial statement, Eich (2014, p. 5), the Editor of Psychological Science, strongly urges authors to avoid NHST that focus on dichotomous (significant/non-significant) thinking and to instead rely on effect sizes, CIs, and meta-analysis similar to Cumming's approach. Cumming's CI example for the parameter μ, illustrated in Figure 1, provides the type of information on which such increased reliance could be justified. Cumming (2014, p. 23) points out, for the case above, that if only the observations in the example for which p < 0.05 are considered, the resulting confidence interval would be too large. Further, of relevance to frequentist's interpretation, if the null value for μ (here μ = 0) is not contained in this interval, the null is rejected at the complement of the interval's calculated probability (0.95, for α = 0.05).
Replications become critical to the success of this approach. The objective of the process, as Lindsay (1995, p. 35), in one of few papers critical of NHST in the accounting literature states, is to establish ‘whether the same model holds over the many sets of data and not what model fits best for one particular data set’. Replication provides the confirmation that the findings are robust to different conditions, thereby supporting generalization as the ultimate criterion of success.
Unfortunately, while replications contribute to a result's validity, the practice has seldom been attempted in accounting and would be difficult to do properly. In economic studies, considerably more replications would be required to justify credibility. In addition, identical conditions and performance (including identical computer protocols and the problem of time invariance) create differences from one replication to another. Therefore, on these criteria alone, it would be prudent to be cautious of the results. Cumming (2014) recognizes these concerns. He emphasizes that it is necessary for the author(s) to explain precisely how the inputs to the calculation were determined and how the additional trials reflected in the final result were conducted. Replication attempts require this information.
In addition, any attempt to replicate a previous finding requires the investigator(s) to assure the statistical validity of the model. To do so requires satisfying the necessary probabilistic assumptions regarding normality, linearity, heteroskedasticity, independence, and time invariance. The last of these requirements is particularly difficult to assure. Of the papers reviewed for this research, not one addressed the full range of these requirements. Most of the papers appear to expect the reader to assume the author(s) have attended properly to all these matters. Claims such as the automatic adjustment for homoskedasticity are made but rarely, if ever, documented.
Furthermore, the data generating process (DGP) specified in one study is not likely to match either the DGP in other studies or the unknown true DGP. In fact, the implicit DGP of any study inevitably contains fewer explanatory variables than the true DGP. ‘In this common situation, the strategy of adding variables may increase both the bias and the variance of the OLS estimators. The consequences of adding or omitting variables are ambiguous’ (Deluca et al., 2015). See also Clark (2005).
Cumming also councils that a thorough approach would require the researcher to justify inclusion (or exclusion) of each replication. (Inclusion of only ‘significant’ results would give the biased result mention above.) There is also the substantial difficulty of identifying relevant research that has either not been submitted for review or was rejected for publication (perhaps for an insignificant p-value). Fortunately, the presence of the SSRN and other networks provide the opportunity for additional, otherwise unpublished, studies to be considered. Yet, unfortunately these studies too will generally not be subject to the editorial review process and provide only a partial solution. While the proper review process is messy and frustrating, it remains essential to the quest for reliable scientific findings.
The information contained in unpublished studies, if well done but ignored, contributes to the inaccuracy of any CI resulting from published studies. Poorly crafted or possibly even manipulated (cherry-picked) regressions yet accepted work would also affect the final CI. 8 These two concerns contribute to the necessity for researchers to consider results with full knowledge of how the study was conducted and in light of their own experience. ‘Any single study [or set of studies] is most likely contributing rather than determining. Each analysis needs to be considered alongside any comparable past studies and with the assumption that future studies will build on its contribution (Cumming, 2014, p. 24; brackets added).
Each CI in the set leading up to the final collective interval is a random variable as would be the final reported interval. For good reason, most frequentists are not comfortable concluding categorically that θ is in the interval or it is not. Yet that is all that can be concluded according to strict frequentist dogma, which does not allow any probability to be attached to the stated interval. Frequentist's CIs are explicitly not probability statements about the hypothesis or parameter in question, despite the fact that we tend to interpret them that way. By emphasizing the estimation process and giving it a different rationale, the Bayesian is justified in saying far more, often in regard to the very same interval. This is why empiricists are actually more Bayesian than they often know, and why Bayesian statistics has so much to offer empirical research. 9
Interval Data Gathering Issues
There are several additional considerations that need to be addressed as they relate to the interval-gathering approach as described above. The first of these considerations occurs because the raw data are rarely usable for analysis as gathered. The reader needs to be confident that the necessary preparatory data work (Mimno, 2014 refers to this activity as ‘data carpentry’) has been done. Seldom in accounting studies is this issue addressed explicitly or adequately. Changing conditions over time or location can also seriously hamper the analysis often in ways that defy the required statistical test properties of the analysis. Readers are implicitly asked to trust the author(s) and this is simply not appropriate or convincing.
Another concern also discussed by Cumming and others relates to stopping strategies. While the approach of multiple preset stopping intervals mitigates convenience stopping as well as other forms of processing truncation, it does not resolve the matter. Indeed, one particular form of truncation is particularly troublesome. This truncation occurs when well-done studies with p-values that do not meet apparent publication requirements result in a decision not to submit the work, or in its ultimate rejection by reviewers for that or other reasons.
The typical stopping problem for frequentists can occur when sampling is expensive and time is sensitive. For convenience, consider the situation where a limited sample size is selected. Assume, for example, the researcher decides on a sample of size 100 but continues sampling beyond 100 when no result with a p-value less that 0.05 is observed. At some later point a p-value less than 0.05 is observed. A frequentist would conclude that an association has been found. But any such p-value is misleading, because if the test had not provided a p-value less than 0.05, the sampling process would simply be continued. In so doing, the ex ante probability increases of finding an association, even when one is not present. Bayesian methods lead to results that avoid the above problems associated with convenience stopping. 10
Data are gathered from what Kass (2011) refers to as the ‘real world’, while the statistical analysis takes place in the much more tightly organized ‘theoretical world’. In the theoretical world, it is important not to underestimate the extent and importance of the assumptions made by the statistical analysis concerning the more complex real world. This is a critical place for incorporating the researcher's knowledge of the data space in relation to the statistical analysis space. Ultimately, as Kass (2011, p. 6) points out in his conclusions, the researcher makes inferences that are necessarily subjective because they represent ‘what would be inferred if our assumptions were to hold’.
An example is the fundamental concept of a random sample. A truly random sample would require that each element in the sample space has an identical chance of selection. Furthermore, the DGP would need to be identical and unchanging. Such samples can be possible with carefully planned games of chance but they are basically impossible in the social sciences. Instead, we implicitly rely subjectively on the belief that ‘a test of significance is legitimate, regardless of whether the sample was drawn at random, if the reference set includes no recognizable (given current knowledge) relevant subset containing that sample’ (see Johnstone, 1988, p. 324, relying on Kyberg, 1976 and the writings of R. A. Fisher). This is essentially the Bayesian notion of randomness or ‘exchangeability’.
The objective, physical, or frequentist randomness necessary to exclude all selectivity and which requires any unknown differences to be distributed in identical proportions across the population is essentially impossible. Authors must be alert to the difficulties imposed and inform the reader of the same. After all, who is most likely to know of the studies' limitations if not the authors?
Sample size plays an important role in statistical testing, specifically in the computation of the CI. The CI calculation depends on the estimated standard deviation, which is an inverse function of the square root of the sample size. Empirical researchers have known for some time, but have only acknowledged quite recently, that if the sample is sufficiently large, essentially any null hypothesis can be rejected (Marden, 2000). Large samples are not always easy to obtain in many disciplines. In accounting, however, this is not the case with the large majority of published empirical regression papers.
For many of the empirical regression studies reviewed, the existence today of very large databases coupled with computer power has made it possible to acquire large samples using sources such as CRSP, Compustat, I/B/E/S, and others. Therefore, the null hypothesis is more easily rejected with the conventional confidence probability levels used in NHST. In the empirical regression studies reviewed here, only a very few sample sizes were less than 100 and only about 17% were less than 500. On the other hand, 70% of samples exceeded 1,000 and about 9% exceeded 100,000. The traditional frequentist's tests based on p-values were developed before such large samples were readily available. Hence, the effects of large samples were not generally appreciated. 11
Despite, or rather precisely because of, the limitations researchers encounter in attempting to replicate previous results, meta-analysis is recommended as the favoured approach to adopt.
Informational Considerations
There are several informational factors that favour the approach proposed here. The first centres on the importance of informing the reader of the research finding's importance and, where appropriate, a measure of its magnitude. The finding of a ‘statistically significant’ result is very different from locating an important result and estimating its magnitude, a fact apparently not observed by many authors in accounting. Confidence interval reporting also provides an indication of the range of possible outcomes. Indeed, Sterne and Smith (2001) suggest that the CIs based on 90% may be preferred to 95% to focus on the range of values included in the interval (remembering that the width of an interval is not linearly related to its confidence percentage).
Recognition of Economic Significance
Dyckman and Zeff (2014) examined 55 analytical regression articles of the 90 papers published in JAR and TAR during the period 2013–14. The economic importance of the work was explicitly addressed by only a quarter of the regression papers and less than 2% considered the economic significance sufficiently important to include an estimate of its magnitude in their conclusions section. The typical and inappropriate justification for alleging economic significance was that the research ‘indicated statistical significance’. This mistaken conclusion is not limited to just accounting authors. Ziliak and McCloskey (2004) found that this error was present in 82% of the 137 articles in the American Economic Review during the 1990s, and had actually increased from 70% of 182 articles examined during the 1980s. Fidler et al. (2004, p. 619) provide evidence that the problem also exists in psychology.
The major accounting journals (JAR, TAR, JAE) have not been altogether welcoming to papers that could be classified as replications. These journals stress the application of new methods and essentially require empirical research to report statistically significant results in order to be considered acceptable for publication. Indeed, it is nearly impossible to publish insignificant findings. This situation has been described as the ‘market for significance’. Fortunately, online means of distribution are plentiful but, typically, these papers will not have been subjected to an appropriate review process as they would have been in the more highly respected journals. And the requirement for a review, while important and essential, does not assure the accuracy of the results. It is not a surprise then that the current publication process in accounting has created a near empty set of replications. 12 This situation alone makes all the more important, if difficult to construct, the confidence interval suggested by a meta-analysis approach. 13
An additional change that would help is to re-model the journal review process. Doing so would involve a more complete submission of the steps in data collection and analysis, including explanations for truncated, rejected, and spliced data, and disclosure of their effects on results. The statistical research analysis, including all tests run regardless of the results, can be submitted and retained centrally, and made available on demand to researchers. Additionally, authors should be willing to accept and review replications. If the work passes the review, the journal should publish at least a brief synopsis of the paper while making the full project available on request. This may sound like an impractical level of extra work for everyone concerned, but what is impractical and unnecessary is a mark of whether the work is worth doing and valuable enough to warrant a serious effort towards rigour, disclosure, and honesty. Less important work will be seen as such when the publication requirements are set more scientifically, or with more focus on obtaining repeatable results rather than merely new results, and hence more effort and transparency. Furthermore, professional recognition, including promotions and salary, might well be enhanced if it also reflected serious proposals reviewed, grants, and books containing provocative ideas or leading to important new knowledge.
Authors need to be alert to the opportunities that open the door to moral hazard. Robustness tests and out-of-sample predictions can easily be completed during the exploratory phase of the research effort. Further, once the data are loaded into the computer, multiple model designs can be run, leaving the author to select ex-post the one(s) to be reported, and leaving readers none the wiser about what results might have been made public. Such behaviours also include data mining for patterns, made all the easier to find when only ‘statistically significant’ relationships are required. Rather than repeated sampling or holdout samples, hypotheses are sometimes tested using the same data that suggested them. Similarly, using all the available data encourages over-fitting without there being further data to reveal that mistake.
Searching specifically for observations to include or exclude (cherry picking) and adopting rigid rules that automatically exclude certain data values (e.g., winsorizing, a common approach in accounting noted in one-third of the papers in Dyckman and Zeff, 2014) leads also to doubts as to whether results are real or contrived. 14 When it is deemed essential and appropriate to ignore certain data (or insert new data sets), a complete enumeration and explanation of each such instance needs to be included and justified in the submission of the research. The simultaneous analysis of any sub-groups, particularly in observational studies, must also be carefully done to avoid confounding and selection bias (see Smith and Phillips, 1992)
Finally, researchers should acknowledge all assumptions that are being made in conducting the research. Doing so should be required and include the computer program(s), commands, and statistical codes used in the research. This information is universally omitted from the papers in the accounting studies I reviewed. It is also the case that different statistical computer packages can produce different results based on the numerical methods included in the program that determines the numeric results. Blattman (2014) reports that in a study of 24 QJPS empirical papers using computer statistical codes, only four required no modifications in review. One set of 13 would not execute and another set of 13 reported results in the paper that differed from those generated by the author's own code. The computer-related information should be submitted perhaps in separate documents and made available on demand.
An Interim Suggestion When Authors Elect to Report Nhst Results
Despite the logical arguments behind avoiding NHST, this approach is likely to be with us for some time, in part because of the familiarity of the method to researchers and because not all research issues across disciplines are easily resolved with a Bayesian approach. In these situations, the researcher(s) should report the appropriate CI based on the sample result and the sample size. The p-value, however indicated, would be better left unmentioned as the effect of reporting creates no additional information or value and is likely to even mislead the reader.
A makeshift solution to the issue of p-levels that often, if not generally, represents weaker evidence than would appear—recommended by van der Pass (2010) and others—is to rely on smaller critical α-values (equivalent to higher ‘critical’ t-values). An alternative fix is discussed in papers by Berger and co-authors, starting with Berger and Sellke (1987). They attempt to find translation factors between p-values and Bayesian posterior odds or Bayes factors, so as to establish some rules of thumb for interpreting just how strong the frequentist evidence is from a Bayesian perspective, relative to the sample size and various wide (and hence more ‘objective’) classes of possible prior distribution.
Ultimately, however, although the work by Berger and others is highly revealing to a Bayesian, and a bridge between dissenting camps, the arbitrary resetting of critical α-levels relative to the sample size and a class of possible priors is a half-way house that is not likely to appeal to the more committed non-Bayesian frequentists, nor is it likely to satisfy committed Bayesians who advocate a wholesale shift in philosophy.
A more palatable solution, at least to researchers who wish to hide or avoid any explicit reference to prior distributions, is simply to express frequentist inference by a confidence interval rather than by a p-value. For decades, Bayesians have explained the relative attraction of confidence intervals over p-values. It was noted that there are numerous common models in which frequentist confidence intervals coincide exactly with Bayesian intervals under diffuse, or locally diffuse, prior distributions.
Conclusions and Recommendations
There are several key takeaways that I hope readers will find important. First, NHST should be avoided where possible. In estimating regression parameters, p-values should be replaced with interval measures of the effect (slope coefficient) investigated together with the sample size. Ideally, the interval should be based on, and adjusted for, replication studies, of the effect where each interval is itself a random variable. By this I mean that the empirical literature should be seen as repeated estimates of a given parameter and these should be assimilated to the extent that common experimental conditions allow. Where formal meta-analysis is impossible, informal assimilation based on intuition is of course still a rational guide to what has been learned in total.
Meta-analysis provides an excellent platform to facilitate the study of regression phenomena. Unfortunately, it is limited by the lack of replication studies, the difficulties of their execution, and the current journal policies toward such work. There is reason to hope that the prospects for replication studies may be improving based on the process being considered for the 2017 University of Chicago's Empirical Research Conference associated with the JAR (see Bloomfield et al., 2015). There is also now a replication network (http://replicationnetwork.com/).
As a matter of basic science, as relevant in empirical accounting research as in other empirical sciences, the reporting of all aspects of the data gathering process and justification of the statistical model including all tests conducted with results, data omissions, and splicing of sources noted, and all aspects of the computer programing including commands and packages made available to the publishing journal where they are retained indefinitely for the access and audit of future investigations, is absolutely essential.
Research findings should address the importance—economic, behavioural, or otherwise—of the research, including an estimate of the magnitude of the effect whenever possible. The impact of the work is more likely to have an impact when authorship involves the expertise of a related discipline to the topic such as psychology, statistics, or economics, etc.
The latent impact of the sample size on the meaning of p-levels, particularly in relation to the large data sets often available to accounting researchers, should be explicitly recognized. Big data come with their own limitations (Cox, 2014). It has been suggested that the pre-set critical value α should be a decreasing (nonlinear) function of the sample size. The point widely unappreciated is that just because the sample size n is used in the calculation of a p-level or test result (accept/reject at α), interpretation of that result cannot go through without further reference to n. Unfortunately, however, there is no formal rule or equation by which to discount a given p-level for the sample size used to obtain it.
We can acknowledge that the debate continues as to whether frequentists or Bayesians have Kipling's elephant properly identified; however, the first step for accounting, as a discipline which prides itself on its empiricist credentials, is to follow psychology, econometrics, finance, forensic science, and essentially every other branch of applied statistics, by admitting that all is not right with NHST, or with the conventional and mechanical ways by which these are used by both researchers and the journals themselves.
References
- 1 It is beyond the scope of this paper to list all such critiques. Typical of the diverse authors and papers bringing forward the problems with a culture of NHST are Hunter (1997), Hubbard et al. (1997), and Hauer (2004). See also the series of papers in psychology by Schmidt (1992, 1996a, 1996b) and jointly by Schmidt and Hunter (1995, 1997). A casual web search reveals literally hundreds of such critical papers over the last 30 to 40 years across all fields of research. See, for example, the website by David Parkhust at Indiana University (http://www.indiana.edu/~stigtsts/quotsagn.html), which lists many authors' specific quotes against the logic of NHST and the common use thereof. Similarly, see http://lesswrong.com/lw/g13/against_nhst/ and a vast array of similar critiques surfacing over many empirical fields. Another useful list is http://warnercnr.colostate.edu/~anderson/thompson1.html, compiled by Bill Thompson.
- 2 Bayesians see unknown parameters as simply uncertain amounts, and hence as subjects for probability distributions like any other subject of uncertainty (e.g., whether it will rain or how much).
- 3 The strict NHST interpretation follows Neyman rather than Fisher.
- 4 That is why NHST methods are often described by the term ‘frequentist’.
- 5 Because a unique specification of the prior is generally impossible, an obvious practical choice, avoiding any strong prior belief, would be a uniform, reasonably flat, or symmetric distribution over the parameter space.
- 6 There is a general mathematical result, similar to one in gambling where a player who plays forever will sooner or later be ahead of the casino, virtually no matter what her playing strategy, suggesting that any point null hypothesis will eventually be rejected if the researcher continues sampling long enough.
- 7 At the same time, another possible null H₀: μ = 2 is rejected with a two-sided p-level Pr(X ≥ Xo|μ = 1) ≅ 0. Thus, it becomes almost a matter of choice as to which hypothesis is set up for rejection. Furthermore, when doing so, the probability of the same result on any other possible hypothesis is not considered.
- 8 Several papers that have recently been retracted by leading accounting journals for faked data.
- 9 Bayesians have made this point repeatedly over many years—applied researchers tend to behave like Bayesians to the extent at least that their training and the rules of the journals allow. Indeed the religious fervour that many Bayesians exude, usually off-putting to those whose training is non-Bayesian or even anti-Bayesian, is attributed by many ‘converts’ to the delight of seeing methods that make sense and that can be interpreted in ways that users need (e.g., if you were a consultant and you were engaged by a business to estimate a production parameter, would you enjoy explaining to the customer that she can't interpret the reported 95% confidence interval as what she understands naturally as an interval warranting under its assumptions much confidence?).
- 10 The ‘stopping rule problem’ afflicts frequentist statistics in serious ways and led the famous statistician-philosopher I. J. Good (1983) to make fun of frequentist logic by saying that if the experimenter left town, the data would need to be tossed out, since no one would know the stopping rule.
- 11 Johnstone (email communication) notes that, interestingly, the medical researcher Berkson (1938) commented long ago that large samples always seemed to produce significant results.
- 12 Replications in the accounting literature do get published but rarely. See Bamber et al. (2000) for an excellent example of a published replication. Replications such as in Mareno et al. (1987) are more likely to be included in research papers if they are incorporated in a larger study reporting significant results. A recent paper (Li et al., 2014) includes work that suggests promise for replications in interval estimation. A study by van der Pass (2010) replicates Ioannidis (2005), but I am unaware as to whether it has been published. Additional hope is to be found in The Replication Network recently available at http://replicationnetwork.com/
- 13 Have accounting researchers adopted statistical significance as the appropriate choice after thorough investigation or simply because it was the choice of previous authors? If the former is the case, future researchers can build on the findings in their study. If the latter, the solution to improved analysis relies on changing the reviewing/acceptance process and the reward structure. The latter, unfortunately, does not seem likely. This situation reflects badly on the field and may help explain why, of all the applied disciplines, accounting appears to be near last to question its trust in significance tests. A tempting alternative hypothesis is that the fields most concerned about potential failings in their experimental methods are those where users depend on them and where findings have the most substantive significance. Accounting research has been criticized for the fact that other disciplines and related professionals apparently pay it little or no attention. See similar criticism in Basu (2013) and other papers in the same issue of Accounting Horizons. Also see Basu (2015).
- 14 Such implicit manufacturing of results is natural. Imagine that a researcher implementing the common practice of winsorizing her data finds that results are then ‘better’ or ‘more significant’. The obvious tendency is to regard them as also more reliable, largely because the tactic is commonly relied on in accounting research as a means of cleaning the data of observations that appear to be unreasonable. But the possibility of manipulation is ever present. Unfortunately, the justification of each deletion is never revealed.
