Equity Value as a Function of (eps1, eps2, dps1, bvps, beta): Concepts and Realities
Abstract
This paper examines three basic equity valuation concepts: (1) residual income valuation (RIV); (2) in the spirit of Miller-Modigliani, the irrelevance of a firm's dividend payout policy; (3) betas/CAPM, to quantify risk and capitalization factors. As a first cut, results show that RIV, concept (1), lacks empirical support while in contrast concepts (2) and (3) hold up reasonably well. To address (2) and (3) we develop a model where earnings and earnings growth determine value. This model supplants RIV because of its greater intuitive appeal and empirical support. A linear function of eps1, eps2, dps1 maps into stock prices and theory specifies the coefficients’ admissible magnitudes. Both the concepts of dividend payout irrelevance and risk (cost-of-equity per CAPM) restrict the coefficients. Bvps is value-irrelevant, in both the analytical and empirical analyses. The latter can be viewed as a case study; it considers S&P500 firms at two points in time, and the data was hand-collected in real time from a public website (Yahoo!Finance). This scheme ensures perfectly synchronized data and it usefully provides not only consensus forecasts but also real time betas. Overall, the paper contributes by developing valuation concepts and by showing how these can be evaluated empirically.
Business school academics occasionally suggest that research influences practice. If this is true, then textbooks should reflect new ideas and findings. And so they tend to do. The resulting changes can be quite substantial, as has been the case in financial statement analysis (FSA) and related accounting-based equity valuation. This points toward a tangible record of intellectual progress. The problem, of course, is that informed people can disagree as to whether the suggested advances actually help or are even valid. Students generally find it too difficult to make such assessments and many experienced academics feel the same. The latter suggests that researchers can benefit from revisiting basics to ask if the concepts taught make empirical sense. In this paper we study three such concepts, all related to accounting-based equity valuation, found in most FSA textbooks. 1
First, consider the formulae that use financial forecasts as input to derive equity value estimates. Textbooks spell out several possibilities, including the Gordon-Williams dividend-growth model and the FCF model. In contrast to these models, residual income valuation (RIV) appeals because it reconciles earnings and book values with dividends—and earnings ought to be relevant. Students, however, are often puzzled because RIV actually focuses on residual earnings rather than on plain earnings. And RIV's starting point, the so-called valuation anchor, current bvps, does not align with practice in the minds of most professionals. Investment practice refers to price-to-earnings (P/E) (and price-to-cash flow) ratios more often than to market-to-book ratios and residual earnings (or profitability); accordingly, gut reactions to RIV can be quite negative. 2It leads to the question: does RIV help us explain observed stock prices?
Second, with or without RIV, at some point textbooks must move away from forecasts of dividends and turn their attention to accounting variables, in particular future eps, FCF and (in RIV) bvps. But this requires some reference to dividend-policy irrelevance. 3This concept involves a number of subtleties, including borrowing/lending as a zero net present value (NPV) activity. It can also be perused on a more concrete level by noting that many firms pay no dividends though they have a solid financial position. Nonetheless, dividends’ status as ‘yes, dividends are fundamental in valuation, but as a practical matter we do not really focus on forecasting them’, means that PVED fades into the background and yet future dividends cannot simply be dismissed. One can reasonably ask: do stock prices reflect dividend-policy irrelevance?
Third, as a baseline, textbooks put in place the idea that discount rates derive from CAPM. Students and teachers alike have long felt queasy about this approach, but it has proven durable in the absence of a better choice; after all, something must be taught. Teachers can fall back on the wide awareness, and even use, of betas in investment practice. It leads to the question: do stock prices reflect discount factors as inferred from betas?
We address the above questions using a restricted data set, much like a case study. The data set is based on S&P500 firms and was hand-collected from Yahoo!Finance in real time, at two particular dates, 13 April 2013 and 11 March 2014. The scheme implies perfect synchronization ‘without errors’—and the data, which include betas, can be used as is and without any other sources. High quality data generally eliminates any need for statistical tools like data trimming and winsorization; all the data points enter the analyses on an equal basis. In a similar spirit, we do not experiment with specifications to check what seems to work the best. That said, because of our limited data set, the reader must judge whether results would change for smaller firms or in an alternative macro-economic environment.
For all three questions, the empirical analyses follow two distinct stages. The first stage poses a valuation model and the second stage measures the model's goodness-of-fit, or ‘success’ in explaining stocks’ prices. Main metrics are: (a) the rank-correlation between actual and model-implied values; and, most important, (b) the median absolute percentage error between actual and model-implied values. To compare the relative success of any two models of implied values, the models’ scores provide the required information.
Out of the five variables in the paper's title, the two eps numbers will, of course, be central when one tries to explain prices. The eps numbers define STG (short term growth), (eps2–eps1)/eps1, a key metric of a firm's expected performance in investment practice. LTG has been left out due to its commonly perceived low quality and extreme upward bias. 4Instead, we view STG as an all-purpose measure of growth, applicable when the data set comprises large and mature firms. As to the remaining three variables, dps1 is needed to assess dividend policy irrelevance, and bvps to apply RIV. Betas are used to evaluate the risk hypothesis, that is, whether value increases as betas decrease, keeping the financial inputs constant.
Our evaluation of RIV, the first question, considers the extent to which the values implied by the model explain prices. A key test compares RIV-derived values to values based on a benchmark model using eps2 by itself. In addition, the empirical analysis sorts out the RIV-implied values' dependence on the various inputs. Inputs may, of course, differ in their relative importance. The objective here is to get a sense of the reasons for RIV's (in-)ability to explain actual stock prices. Results do not impress. 5RIV performs about the same as the benchmark model based on eps2 alone, and, further, eps2 alone explains most of RIV's implied value. Eps1 and bvps are remarkably unimportant in the scheme of things.
RIV's inability to explain stock prices better than the eps2-based benchmark model suggests the need for a fresh approach. Our proposed model deviates from RIV by assigning an explicit role for STG and how it relates to the two forward-P/E ratios, P/eps1 and P/eps2. 6 The analysis introduces a subtlety because it is STG's relation to P/eps2—not P/eps1—that yields the key insights. These ideas can be sketched out without difficulty to identify conditions for STG to influence values consistent with investment practice. An appendix formalizes the underlying PVED-based valuation model; it can then be shown in precise terms how the two P/E ratios increase as STG increases or risk decreases. 7
Empirical analyses based on these ideas initially consider how the four accounting variables explain prices, leaving out beta. In this model bvps adds little empirically, so only eps1, eps2, and dps1 remain on the right hand side (RHS). We refer to this as the earnings and earnings growth model, expressed as P = k1*eps1 + k2*eps2 + k3*dps1, where k1 < 0, k2 > 0, k3 > 0. Given this model without bvps, the subsequent theoretical and empirical analyses show how the three coefficients depend on betas.
With respect to the second issue, about dividend-policy irrelevance, the answer depends on the estimated values of k2 and k3. The concept we evaluate presumes that dps1 has an effect on eps2 because dps1—the end of the forthcoming year's expected distribution of wealth—reduces the subsequent year's earnings via reduced (net) investment. The estimated coefficients should therefore satisfy k3/k2 = earnings rate on dividends, had they been retained. A 5–10% range would seem reasonable. Our estimates of the ratio tend to exceed this range, roughly in the 10–15% range.
Finally, the question whether betas act as risk measures when one explains prices. In a simple and direct approach, we split the data into two (approximately) equal-sized groups, based on whether a firm's beta exceeds one or not. We then estimate the earnings and earnings growth model separately for each group and compare the results to the model with the two groups pooled. The split improves the goodness-of-fit materially. The results also show that given a fixed set of forecasts, low-beta firms’ prices exceed those of high-beta firms.
Our conclusions depend on specific implementations. RIV requires the two parameters g and r, and our particulars can be questioned. But the comment applies no less to our methodology dealing with betas and dividend-payout irrelevance. How to interpret tables can also be a challenging task. While the narrative tries to reflect these ambiguities, they can easily be under-appreciated. The final section accordingly discusses nuances and qualifications related to the findings summarized above.
The Data and Elementary Valuation Concepts
Because the data set pertains to only two points in time and has few variables, the statistical summary of the data will be unusually straightforward. The reader will find it helpful to internalize this information; it anticipates the subsequent, more elaborate, statistical analyses and ideas. Table 1 shows the medians and spreads of the four accounting-based variables (normalized by price), plus STG and beta.
| eps1/p | eps2/p | dps1/p | bvps/p | stg | beta | |
|---|---|---|---|---|---|---|
| 2013 | ||||||
| 25th percentile | 5.21% | 5.88% | 0.83% | 21.93% | 8.22% | 0.70 |
| 50th percentile | 6.39% | 7.21% | 1.84% | 36.13% | 12.34% | 1.07 |
| 75th percentile | 7.87% | 9.11% | 2.81% | 57.02% | 16.49% | 1.50 |
| 2014 | ||||||
| 25th percentile | 4.88% | 5.65% | 1.09% | 20.19% | 8.21% | 0.70 |
| 50th percentile | 5.91% | 6.73% | 1.81% | 31.36% | 11.80% | 1.06 |
| 75th percentile | 7.28% | 8.08% | 2.69% | 51.45% | 15.79% | 1.50 |
For all columns of Table 1, differences between the 2013 and 2014 distributions are minor. With respect to the first four variables, the medians have decreased somewhat though the spreads have changed little. The STG and beta distributions are very similar for the two years. That said, it should be noted that any individual firm can change materially from one year to the next. For example, the inter-temporal E/P correlations are about 0.8; low eps-yield stocks tend to remain low yield, but there is ample room for a change, either due to a change in the numerator or the denominator, or both.
In terms of the two forward-E/P ratios, stocks were less expensive in 2013 compared to 2014. This finding confirms the market's increase in excess of 20% from the first date to the second. This increase also shows up in the bvps/p and dps1/p ratios. Turning to the median STG, at both dates it is approximately 12%, a substantial number. By comparison, the median growth in expected sales (not tabulated) is about 7% (and expected GNP growth is even less). These magnitudes do not surprise insofar that analysts’ (consensus) eps2 forecasts are, as is well-known, too optimistic in general. The median STGs certainly exceed any reasonable estimate of the average firm's cost-of-equity, a natural reference point.
Figure 1 shows the distribution of two key variables, forward E/P (eps1/P) and STG, for the year 2013 (the 2014 graphs have been left out; they differ little from the 2013 graphs).
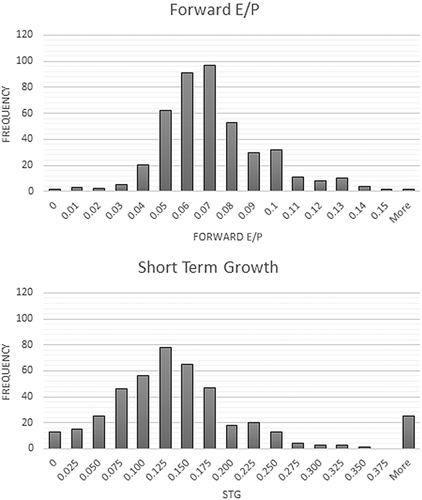
The distributions are fat-tailed, especially the right side of STG. This aspect most likely reflects the way the world works, as opposed to how the data has been prepared by Yahoo!Finance or retrieved by us. In the absence of information suggesting that there are problems, to trim or winsorize the data would be unfounded. To the contrary, the extremes may be quite helpful when one tries to understand real-world equity valuation.
Like STG, eps1/P varies materially; a yield outside the 5–9% range is by no means uncommon. The distribution can be compared to that of eps2/P (unreported); the latter looks similar but is slightly tighter.
We next examine the rank-correlations between the five ratios and beta.
The two panels of Table 2 differ little. None of the signs (+/−) of the correlations change over the two dates. It suggests robustness not only here but also in subsequent analyses.
| eps1/p | eps2/p | dps1/p | bvps/p | stg | beta | |
|---|---|---|---|---|---|---|
| 2013 | ||||||
| eps1/p | 1 | |||||
| eps2/p | 0.94 | 1 | ||||
| dps1/p | 0.18 | 0.08 | 1 | |||
| bvps/p | 0.44 | 0.49 | 0.13 | 1 | ||
| stg | −0.43 | −0.23 | −0.43 | −0.24 | 1 | |
| beta | 0.30 | 0.43 | −0.25 | 0.25 | 0.27 | 1 |
| 2014 | ||||||
|---|---|---|---|---|---|---|
| eps1/p | 1 | |||||
| eps2/p | 0.97 | 1 | ||||
| dps1/p | 0.29 | 0.21 | 1 | |||
| bvps/p | 0.50 | 0.49 | 0.21 | 1 | ||
| stg | −0.43 | −0.26 | −0.50 | −0.24 | 1 | |
| beta | 0.21 | 0.30 | −0.27 | 0.19 | 0.29 | 1 |
The two forward E/P ratios, eps1/P and eps2/P, correlate strikingly (0.94 and 0.97). The large correlations pick up on the close connection between eps1 and eps2, and the relatively large cross-sectional variations in the two eps/P ratios.
All of the four price-normalized accounting variables correlate positively. In other words, if one of the ratios suggests that a stock looks inexpensive then it is likely to look inexpensive on the other ratios too. The point must be qualified insofar that the correlations are marginal when it comes to dps1/P.
STG correlates negatively with the four accounting ratios. This finding supports a central hypothesis in practical equity valuation: price picks up on growth and STG acts as a valid growth measure. Our subsequent analysis revisits this issue.
Beta satisfies the property of a risk measure. That is, beta correlates positively with the three non-dividend accounting-based ratios to reflect a lower price as risk increases. It is also the case that beta and STG correlate positively. Consistent with elementary equilibrium concepts, the ‘bad’—risk—comes with the ‘good’—STG—at least on average.
Though not part of Table 2, next we note that one can correlate betas and PEGs to get a preliminary read on the validity of beta as a risk indicator. Research on implied cost-of-capital (ICC) exploits this idea. Under reasonable assumptions, PEG and r relate negatively (in a square root formula). 8PEG and beta should, therefore, also correlate negatively if CAPM holds. In our sample, the (rank-)correlation is −0.33 for both years, which indeed supports CAPM as a model of risk. 9
The descriptive statistics align with ideas about what determines a stock's value. There are aspects of a stock that are liked and other aspects that are disliked, and in equilibrium the good typically comes with the bad. To bridge the gap between these basic points and valuation models, a more formal analysis helps.
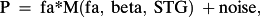
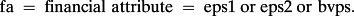
M = a multiplier that depends on the financial attribute, in addition to STG and risk.
We leave out dps1 because of Miller-Modigliani concepts and the fact that it often equals zero. So that leaves the two eps ratios and bvps as desirable financial attributes.
The M function satisfies M > 0, and M increases as STG increases and beta decreases. These properties appeal intuitively, and the data support. But the expression also requires a noise term because none of the attributes suffice as a valuation statistic. This raises the possibility of using multiple attributes in the valuation to explain prices better, without losing any of the key properties. A formal valuation model, like RIV, can now potentially come in handy. But before moving in this direction it is worth noting that the valuation game changes radically, for two reasons. First, the sign of the price response to a change in one attribute can now depend on what other attributes have been held fixed. Unlike the single-variable framework, more is no longer necessarily better than less. Second, while a multiple-attribute model might well reduce the noise term (that is, added information should help if handled in a reasonable way), a more poignant reality must be faced: the noise term in a multi-attribute formal valuation model may, in fact, increase compared to a simple benchmark model. Both of these issues arise in our examination of RIV.
Explaining Share Prices: An Evaluation of riv
While FSA textbooks describe how RIV can be applied to estimate a firm's equity value, they typically do not provide any evidence of whether RIV meshes with the real world. Does RIV explain equity values for the data set retrieved in this paper? The issue here is not the extent to which the model helps to identify over- or underpriced stocks. 10Rather, the question at hand addresses whether one can apply RIV and show that the values implied by the model achieve some success in explaining actual prices. This leads to the related question: as compared to what alternative scheme? We deal with this issue later; before that we present the goodness-of-fit metrics. Suffice to say here, we compare the implied RIV values to (i) a benchmark model based solely on eps2, and (ii), later in the paper, a model of earnings and earnings growth.
Implementation of RIV requires two firm-specific model parameters: the post-horizon growth rate (g) and the discount factor (r). There is no common agreement on how one should quantify these, which is precarious since the ‘success’ of RIV in explaining actual values may depend on these model inputs. However, we argue later that the issue is less important than one might think.
We specify g and r as follows. For the parameter r, we use the CAPM with the intercept and risk premium both equal to 4%. In the spirit of the Fed-model, we assume that g and r on average offset each other so that r–g is constant. We put the constant equal to 0.065, which approximates the typical forward earnings yield ratio (eps1/P). This approach is indeed subjective and somewhat arbitrary. But, as noted earlier, we will argue that the issue is not all that critical. The results are sufficiently compelling to suggest that trying out alternative (r, g) specification schemes is unnecessary.
Three metrics are employed to assess the degree of success in connecting implied model values (V) to actual values (P). The first two are (i) the rank-correlation between V and P, and (ii) the rank-correlation between the percentage change in implied values (going from 2013 to 2014) and the percentage change in actual values; thus we correlate ΔV/V and ΔP/P (a model return and market return correlation, setting aside dividends paid). Metric (iii) is the often-used median absolute percentage model error, denoted median ABS[log(V/P)]. All of the metrics provide descriptive content, though, as was noted earlier, the scores should be used to compare models or results from the prior literature; the magnitudes do not tell us much otherwise. Consistent with the literature, the metric of most interest is (iii), a model's typical absolute percentage error.
The metrics are not beyond reproach. Using rank correlations has the disadvantage that the metric depends on the cross-sectional distribution of the price per share; had firms’ shares outstanding been different, then the correlation would also have been different. 11Rank correlations can only be used for comparative purposes. Though the other two metrics avoid this shares-outstanding problem, they raise other issues. The third metric depends on the overall bias in the (non-absolute) value of the valuation errors. In other words, if the unsigned median log(V/P) deviates materially from zero, the final metric will do so too. As to the second metric, it can be viewed as a too radical shift away from explaining values; changes in values are not uninteresting, but as a metric in our context it seems the least relevant. Overall, though, the three metrics will be reasonably mutually supportive.
Table 3 provides the results showing RIV's goodness-of-fit metrics.
| Rank correlation (V, P) | Rank correlation (ΔV/V, ΔP/P) | Median Abs[log(V/P)] | |
|---|---|---|---|
| 2013 | 0.87 | N/A | 19.11% |
| 2014 | 0.86 | 0.51 | 21.49% |
Taken at face value the results may perhaps appeal. The rank-correlation between V and P (column 1) appears to be high and robust. The return-correlation (column 2) is much larger than the classical returns on earnings correlations, which typically show correlations of about .33 (or R2 of about 10%). In other words, forward earnings are more informative than reported earnings, as should be expected. Our column 2 result is in the approximate range of Liu and Thomas (2000) who use a similar approach. As to column 3, a 20% median percentage valuation error may seem reasonable enough. Liu et al. (2002) obtain roughly the same result (though their sample is very different, of course).
Assessing RIV's degree of success as a valuation model requires a benchmark comparison. Table 1 provides four alternatives on which to base such a benchmark model: eps1, eps2, dps1, and bvps. The best choice minimizes the median-normalized range, sometimes referred to as the quartile range of dispersion (QRD = [Q3 – Q1]/Q2). Based on an average for the two years, eps2 has the smallest QRD. Using the median (P/eps2) as a multiple implies the benchmark model V = eps2*median(P/eps2). Table 4 provides its goodness-of-fit scores.
| Rank correlation (V, P) | Rank correlation (ΔV/V, ΔP/P) | Median Abs[log(V/P)] | |
|---|---|---|---|
| 2013 | 0.84 | N/A | 21.32% |
| 2014 | 0.87 | 0.59 | 18.09% |
As one compares Table 3 to Table 4 it becomes clear that RIV valuations reflect the actual values no better than the simple benchmark model. All metrics support this claim, though one can perhaps argue that the (V, P) rank-correlation is marginally larger for RIV. The return metric is unambiguous and the percentage valuation error metric in the third column drives home the point: RIV averages 20.5% as opposed to 19.7% for the benchmark model. Moreover, note that the first two metrics in Table 4 do not depend on the choice of benchmark multiple, median(P/eps2). For the third metric, a benchmark model based on eps1 performs only slightly worse than the one based on eps2. (When using bvps, the median error exceeds 40% for both years—bvps is evidently a poor starting point to estimate actual values.) One can conclude that RIV and the eps2-based benchmark model perform about the same, a disappointing outcome insofar that RIV builds in a certain sophistication that seems to have added nothing.
A different specification approach to the two parameters (r, g) could potentially improve RIV's performance. But rough calculations combined with common sense suggest that improvements at best will be minor. Calibrating the risk measurement is unlikely to be an issue here since the discount factor has only a small effect on V in a short-horizon framework. And we are not quite sure what to do with g to make RIV perform better. As noted earlier, the prior literature does not provide much hope that there exists a ‘clever’ way of specifying r and g (Liu et al., 2002).
To appreciate RIV's limits it helps to connect inputs and the implied model value. Estimations with V as the dependent variable and the four inputs on the RHS can inform about the relative importance of these inputs. This estimation leaves out r and g because the parameters enter non-linearly in RIV. The approach seems reasonable enough as a first cut to get a sense of how RIV converts inputs to an implied value. Table 5 shows the results; it also includes a cross-check in which the sample has been winsorized at the 2% level.
| OLS | OLS (winsorized) | |||
|---|---|---|---|---|
| Coefficient | t-value | Coefficient | t-value | |
| 2013 | ||||
| eps1 | −2.13 | −2.01 | −4.35 | −4.40 |
| eps2 | 16.62 | 17.24 | 17.69 | 18.44 |
| bvps | −0.52 | −18.19 | −0.41 | −11.23 |
| dps1 | 6.44 | 11.21 | 6.29 | 11.34 |
| adj R2 | 0.98 | 0.98 | ||
| 2014 | ||||
|---|---|---|---|---|
| eps1 | 0.88 | 0.46 | 0.65 | 0.33 |
| eps2 | 14.09 | 8.78 | 14.24 | 8.43 |
| bvps | −0.54 | −12.64 | −0.44 | −10.61 |
| dps1 | 4.51 | 6.12 | 3.45 | 4.79 |
| adj R2 | 0.98 | 0.97 | ||
The two years do not differ enough to affect key conclusions. The main finding is that eps1 seems irrelevant. In turn, this means that STG is no less irrelevant. Some elementary mathematics of the RIV formula reveal that the finding should not surprise; V's response to a change in eps1 is very small. This point is often overlooked in textbooks and research. It is also clear that the sign of the bvps coefficient is negative, and it comes with a double-digit t-statistic. Again there is no reason to be surprised. The property that V increases as bvps decreases, keeping the remaining inputs fixed can be deduced from the RIV formula: RIV implies a valuation premium for profitability as measured by roe2 = eps2/bvps and roe1 = eps1/bvps. In some ways this is a property that makes RIV interesting. We note next that eps2 contributes materially to the regression with t-statistics about the same as for bvps. As for dps1, it contributes as expected but with a lower t-statistic.
The t-statistics may suggest that bvps is at least as relevant as eps2. However, this is actually not true. Eps1 and eps2 correlate strongly, and this reduces the eps2 t-statistic. A regression of V on eps2 and bvps alone, with results presented in Table 6, shows this aspect.
Note that the estimated coefficients do not change much, but the t-statistics change materially for eps2 (the t-statistic for bvps is roughly the same as in Table 5). Going back to Table 1, the median eps2 is about 20% of the median bvps, but Table 6 shows that the coefficient ratio of eps2 to bvps is about 35. The impact of eps2 on RIV values is thus about seven times larger than that of bvps—a great differential in materiality. And if one deletes book value in the model the R2 drops by less than one percentage point (from 98% to 97%). Finally note that the four R2s in Table 6 have effectively not changed compared to the starting point, Table 5. When everything is said and done, it is clear that eps2 alone pretty much explains V per RIV.
| OLS | OLS (winsorized) | |||
|---|---|---|---|---|
| Coefficient | t-value | Coefficient | t-value | |
| 2013 | ||||
| eps2 | 15.41 | 100.53 | 15.43 | 68.12 |
| bvps | −0.44 | −13.74 | −0.42 | −9.78 |
| adj R2 | 0.98 | 0.97 | ||
| 2014 | ||||
|---|---|---|---|---|
| eps2 | 15.31 | 89.72 | 15.6 | 62.73 |
| bvps | −0.43 | −11.61 | −0.42 | −9.19 |
| adj R2 | 0.98 | 0.97 | ||
Conceptually, RIV does have some appeal because a firm's profitability, as measured by eps2/bvps, adds to its value (holding the other inputs fixed). A negative loading on bvps (though relatively small) may therefore seem reasonable. But investment practice does not usually refer to the idea of a profitability premium. Even more relevant is the effective absence of eps1 and STG in explaining RIV's V. It denies the practical principle that STG should have an impact on value. RIV places the burden to capture growth on g, the post-horizon residual earnings growth. This is an elusive parameter; there appears to be little agreement on how one should measure g given the forecasting that actually takes place in the real world. RIV's handling of growth via g lacks robust empirical and conceptual support, which makes it problematic to teach and apply.
In light of the negatives associated with RIV, the question arises as to how to proceed. One crude approach would be to simply estimate a model with eps1, eps2, dps1 and bvps on the RHS. Such estimation may improve our goodness-of-fit metrics, compared to RIV and the eps2-based benchmark model. A more refined inquiry recognizes that the central organizing principle in investment practice starts from forward earnings and forward earnings growth—eps1 and STG—and that dps1 can modify STG. Such an approach ought to provide some guidance about firm valuation. Note that bvps has no role here except that it may have influenced the forecasting of eps1 and STG (which is an interesting topic by itself but of course outside this paper's scope).
The next section discusses the valuation principle focusing on earnings and earnings growth. It leads to an analysis of the two forward P/E ratios' dependence on STG, including orders of magnitude of the associated coefficients. Following that, the first-order empirical question is addressed, that is, whether this earnings and earnings growth valuation approach improves the goodness-of-fit compared to the benchmark model based on eps2 alone (reported in Table 4). These empirics then set the stage for an analysis of whether incorporating beta-risk in the analyses enhances the goodness-of-fit metrics.
Value: The Principle of Earnings and Earnings Growth
This section probes what can be said when eps1 and eps2 suffice to determine value. In this context bvps is irrelevant. As to dps1, it is relevant but put equal to zero initially to keep matters simple. Generalizations that incorporate dps1 (and risk) come later in the section.
 (1)
(1)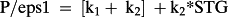 ()
()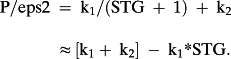 ()
()The approximation uses that 1/(1 + x) ≈ 1 – x, x close to zero. It follows that k1 < 0 and k2 > 0 if and only if the two forward P/E ratios increase as STG increases.
The boundary case k1 = 0 is necessary and sufficient for eps2 alone to determine value (as in our benchmark model). But the fact that eps2 provides all the value-relevant information—and STG is wholly irrelevant—nonetheless allows the P/eps1 ratio, as opposed to P/eps2, to vary with STG (as long as k2 > 0). That is, one cannot infer that P depends on STG just because P/eps1 and STG correlate; the positive correlation illustrates the potential of a specious correlation when two variables have the same denominator. 12The overall message here is that this analysis provides the statistically necessary and sufficient condition for STG to have an effect on P: it must correlate with P/eps2. This corresponds to the equivalent takeaway that k1 < 0—not k2 > 0—ensures that the valuation picks up on growth: given eps2, the firm's value increases as STG increases.
Going back to Table 1, combined with elementary calculations one can derive rough estimates of the coefficients k1 and k2. Two points of (P/eps1, STG) suffice to solve for the two coefficients. Suppose first that the median STG corresponds to the median P/eps1. From Table 1 (for the year 2013) one obtains the point (P/eps1 = 16, STG = 0.12). Second, a close look at the data shows that firms with approximately zero STG on average have a P/eps1 ratio of about 10. Hence (P/eps1 = 10, STG = 0) provides the second point needed to solve the two-by-two equation system. The solution equals k1 = −40 and k2 = 50. For future reference, note that the sum equals 10. The numbers illustrate that one should expect the coefficients to be relatively large (in absolute value terms) and that there is an offsetting effect so that –k1/k2 is reasonably close to one (.8 in the example above) and the sum is quite a bit less than the (absolute values) of the components.
Equations (2a) and (2b), when linearized, have the same intercept, k1 + k2 (10 in the numerical example). Consider next the two slopes, −k1 and k2: (2b), the more important equation when one assesses the role of growth, has the smaller slope –k1 < k2. We therefore expect the correlation (P/eps2, STG) to be less than the correlation (P/eps1, STG). Going back to Table 2, one can see that this is indeed the case.
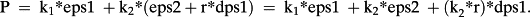
In other words, k3 = k2*r under the assumption of foregone earnings. In the previous example with k2 = 50, a foregone-earnings rate of 10% implies k3 = 5. However, the foregone-earnings rate on dps1 does not have to equal the cost-of-equity since dividends may reduce financial income rather than the foregone earnings due to a cancelled risky operating activity. The framework here will be applied in a somewhat open-ended way to investigate the dividend-payout irrelevance. We judge an estimated k3/k2 in the range of 5–10% as consistent with the dividend-irrelevance concept. A greater ratio supports the so-called bird-in-hand hypothesis—the market rewards an expectation of generous dividend payouts.
The next issue concerns the first two coefficients' dependence on risk (cost-of-equity). Intuition suggests that as r decreases the coefficient k2 increases; less risk should increase the stock's price via enhanced earnings capitalization. What about (the negative of) k1? Given the expression for P/eps2 in (2b), intuition suggests that –k1 should also increase as r decreases. This relation follows if one thinks about STG as being more valuable for low-risk firms. In other words, both –k1 and k2 can be thought of as capitalization factors that satisfy standard properties—the lower the r, the better. It means in effect that –k1 and k2 both increase as r decreases (k3 also increases as r decreases if one fixes the earnings rate). But there is one more condition needed to ensure that P increases as r decreases, namely that the sum of k1 and k2—the intercept in the two equations—does not depend on r. In other words, −k1 and k2 must increase by the same amount, as r decreases.
With the above ideas in place one can ask whether the model of earnings and earnings growth can be formalized. Such a model must be PVED consistent, so the theoretical setup requires subtle Miller-Modigliani-type economics that distinguish between the creation and distribution of wealth. The appendix develops the theory on the basis of three main ingredients: PVED, reduced-form valuation, and the dynamics of the forecasted earnings. The three coefficients (the kis) derive from three exogenous parameters (risk and parameters specifying the growth dynamics). The approach generalizes Ohlson and Juettner-Nauroth (2005), yet sharpens this model in crucial aspects.
While not essential, the reader may want to review this appendix before turning to the next section that evaluates empirically the concepts developed in this section. The appendix should help the reader to appreciate how the coefficients depend on risk as well as growth persistence and the ‘typical’ P/eps1 ratio.
Estimations: The Earnings and Earnings Growth Model
This section reports on results related to the earnings and earnings growth model: estimates of the coefficients and the three goodness-of-fit metrics. The initial analysis includes bvps, which implies four independent variables, eps1, eps2, dps1, and bvps, in the linear model that explains P. Though bvps is not part of the core model, checking on the sign and magnitude of k4 is an interesting issue because bvps serves as RIV's valuation anchor. If not zero, the coefficient per RIV should be negative. The next model estimated excludes bvps; thus one obtains the core model with RHS variables eps1, eps2, and dps1. All coefficients should be relevant with signs negative, positive, positive. We also evaluate a parsimonious third model with only eps1 and eps2 on the RHS, which is only slightly more complicated than the previously examined benchmark model, which relies solely on eps2. We assess the goodness-of-fit at each stage of the above sequence. The procedures followed are such that one cannot presume that ‘more variables are better than fewer’, because the estimations are not tied to any of the goodness-of-fit-metrics.
Firms’ risk (betas in case of CAPM) influences the coefficients, as was noted earlier. The current section, however, disregards this aspect; it will be dealt with in the section that follows. This one-step-at-a-time approach allows us to investigate the extent to which betas/CAPM actually helps when one tries to explain values.
The models put forward have properties that suggest that OLS ought not to be used. The data include outliers, but there are no logical reasons why these should be dealt with via trimming or winsorization. A second issue pertains to heteroscedasticity. Standard procedures usually address this problem via scaling of variables. But there are too many scaling choices (at a minimum, eps1, eps2, or bvps can scale the equations) and it is unclear which one should be picked. Trying out a number of these scaling choices introduces the uncomfortable topic of ‘picking the scalar that gives us the results that we like’. Instead of OLS, we use an estimation method due to Theil and Sen (TS for short). Wilcox (2010) provides a textbook treatment. 13Ohlson and Kim (2015) discuss the TS method and show its efficiency advantages over OLS in a number of valuation settings similar to the ones considered here. The TS method satisfies the useful property that scaling of variables is unnecessary; the estimated coefficients would be identical if the RHS and LHS were rescaled. 14TS also handle outliers effectively.
Table 7 shows the estimation results for the three different models that centre on the earnings and earnings growth model. Results differ little for the two years, suggesting that the coefficient estimates are robust. (By contrast, untabulated results show that OLS estimates can differ materially for the two years, including a change of sign.)
| V estimated as a function of (eps1, eps2, dps1, bvps) | ||||
|---|---|---|---|---|
| eps1 | eps2 | dps1 | bvps | |
| 2013 | −22.71 | 33.70 | 6.20 | −0.10 |
| 2014 | −27.06 | 38.52 | 4.77 | −0.11 |
| V estimated as a function of (eps1, eps2, dps1) | ||||
| eps1 | eps2 | dps1 | ||
| 2013 | −24.73 | 33.74 | 6.99 | |
| 2014 | −29.27 | 38.46 | 5.22 | |
| V estimated as a function of (eps1, eps2) | ||||
| eps1 | eps2 | |||
| 2013 | −15.35 | 27.31 | ||
| 2014 | −20.57 | 33.02 | ||
Comparison of goodness-of-fit scores determines the extent to which variables contribute to explaining P. Thus Table 7 provides no p-values, because such numbers do not bear directly on a variable's contribution (but we note that OLS-based standard errors combined with the estimated coefficients imply small p-values for all variables in all cases).
With regard to bvps, its coefficients of roughly −0.1 are arguably too small to be economically relevant. To appreciate this point, the relative magnitude of bvps compared to P is in the order of 30% (Table 1), which in turn implies that k4*bvps constitutes about 3% of price. The sign of k4 makes sense though. As in RIV, it reflects a (small) profitability premium. That is, a firm's profitability adds to value, holding eps1, eps2, and dps1 fixed.
Dps1 loads in the 4.8–7 range, and this magnitude is indeed material (as well as statistically significant—OLS standard errors are consistently less than 1.8). Table 1 shows that dps1 is about 2% of P. Given a coefficient of 5 it follows that dps1 typically contributes about 10% of value—a plausible, modest magnitude that cannot be easily dismissed. In any event, from a theory perspective k3/k2 should roughly approximate the foregone earnings rate on dps1. Table 7 shows that the ratio equals 21% and 13% (for 2013 and 2014 respectively). So if one uses 5–10% as a reference point, then the coefficient on dps1 meets the hurdle—by a non-trivial margin. The evidence can be read as suggesting that dps1 loads excessively, that is, much more than any reasonable guesstimate of implied foregone eps2. It may suggest that the dividend-policy irrelevance hypothesis should be rejected in favour of the idea that investors pay a premium for firms with ‘generous’ dividend policies. But at this point one needs to keep in mind that dps1 tends to correlate negatively with risk, so the high estimate of k3 can potentially pick up on an omitted variable, namely beta. This aspect is addressed in the next section.
Now consider the most prominent coefficients, those related to eps1 and eps2. Overall, the estimates align with the discussion in the previous section, which generated k1 = −40 and k2 = 50 via rough calculations. The sum equalled 10, which corresponded to P/eps1 when STG = 0. This sum of 10 roughly holds up in all of the relevant tables, for both the years. The results also support that the two forward P/E ratios increase as STG increases—and it is no less true for P/eps2 than for P/eps1. But k1 must be materially different from zero, since otherwise eps2 would act as an approximately sufficient statistic (setting aside dps1). To assess such materiality is a delicate matter. While the P/eps2 ratio does indeed depend on STG, since k1 is far from zero, the elasticity is modest. Consider a coefficient of k1 = −29 and k1 + k2 = 9 (see Table 7). To assess P's sensitivity to STG, consider an increase in STG from, say, 12% to 13%. In percentage terms (using the approximation (2b) with k1 = −29) P increases by about (29*0.13 + 9)/(29*0.12 + 9) ≈ 0.25%. Similarly, a six percentage point difference in STG (15% vs. 9%, say) implies a difference in P of about 11%. So there is P/eps2 sensitivity to STG, but it needs to be put in perspective. The results are robust since the estimates of k1 and k2 are stable (and the null can be rejected in both years). It serves as a reminder that variables may indeed come with non-zero coefficients yet materiality can be modest.
To what extent do the estimated models improve on explaining actual values as compared to the benchmark model? Table 8 provides the various goodness-of-fit metrics. Before looking at the numbers, note that the deletion of a variable (even if statistically significant) could potentially improve the goodness-of-fit (and symmetrically, the addition of a variable can potentially make things worse). The key here is simply that the estimation has not been trained to optimize the goodness-of-fit metrics. (To be sure, the sample size plays no role in this context.)
| V estimated as a function of (eps1, eps2, dps1, bvps) | |||
|---|---|---|---|
| Rank correlation (V, P) | Rank correlation (ΔV/V, ΔP/P) | Median Abs[log(V/P)] | |
| 2013 | 0.85 | N/A | 18.12% |
| 2014 | 0.88 | 0.55 | 17.23% |
| V estimated as a function of (eps1, eps2, dps1) | |||
|---|---|---|---|
| Rank correlation (V, P) | Rank correlation (ΔV/V, ΔP/P) | Median Abs[log(V/P)] | |
| 2013 | 0.85 | N/A | 18.11% |
| 2014 | 0.88 | 0.53 | 18.83% |
| V estimated as a function of (eps1, eps2) | |||
| Rank correlation (V, P) | Rank correlation (ΔV/V, ΔP/P) | Median Abs[log(V/P)] | |
| 2013 | 0.84 | N/A | 21.79% |
| 2014 | 0.84 | 0.57 | 17.75% |
| RELATIVE ACCURACY SCORE | |||
|---|---|---|---|
| V4 vs. benchmark | V3 vs. benchmark | V2 vs. benchmark | |
| 2013 | 58.19% | 59.34% | 52.55% |
| 2014 | 55.11% | 52.63% | 49.68% |
The three models differ only marginally, in terms of goodness-of-fit. Deleting bvps makes virtually no difference. With respect to dps1, its deletion reduces the rank-correlation in both years. Thus dps1 seems to improve goodness-of-fit. The average valuation error is also larger when the model excludes dps1. The metric using returns lends no support to the more elaborate models in panels A and B. Going back to Table 4, next consider the extent of improvement in goodness-of-fit relative to the benchmark model with only one variable (which derives from a univariate TS estimation). The benchmark model seems to be ‘competitive’ at the very least. Still, for both years the rank correlations and the percentage errors are worse compared to the earnings and earnings growth model. Not by much, perhaps, but, in our view, enough to make an impression. On the other hand, if one considers the estimated models' success in explaining returns, then the evidence points to the benchmark model performing the best; the rank correlation (ΔV/V, ΔP/P) = 0.59, which, of course, non-trivially dominates the 0.55, 0.53, and 0.57 obtained for the three versions of the earnings and earnings growth model (and, as a reminder, RIV's humble 0.50 score).
Do the differences in performance meet hurdles of statistical significance? To assess this we employ a relative accuracy scoring (RAS) test. This robust, non-parametric, binomial method works as follows: given two models A and B, count the number of cases in which the implied value per model A is closer to the actual value as compared to model B. In our implementation, let A denote the benchmark model and race it against model B, in turn V4 (eps1, eps2, dps1, bvps), V3 (eps1, eps2, dps1), and V2 (eps1, eps2). Table 8, continued, provides the winning scores for the three growth models.
Given 445 observations, a one-sided 5% test requires a sample statistic of about 53.5% to reject the null. Only V4 passes the hurdle for both years, but V3 comes close. Aside from V2, the results have a positive flavour and support that STG help explain values.
Earlier rough calculations showed that the materiality of eps1 and STG could be questioned and thus so could also the statistical significance. Looking at Table 8 (continued), V2 is the ‘worst’ model of the three because of its low RAS score, and thus one might question the relevance of eps1 (and STG). One can hypothesize that eps1 (or STG) does not add anything beyond eps2. However, even as a first cut, the claim seems too severe if one combines the results for the two years. The average RAS score should count for something. In any event, to allow the reader to make his or her own assessment we provide the following scatter plots. Figure 2 plots the two forward P/E ratios against STG (Table 2 provided the rank correlations).
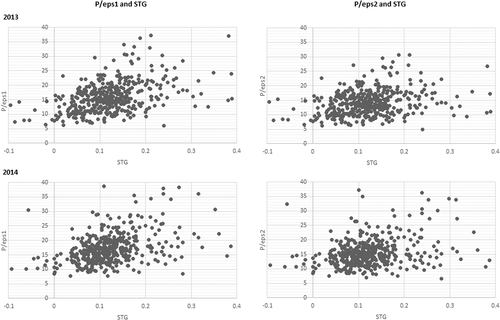
The four correlations are present. One needs to keep in mind though that the plots with the P/eps1 ratio (to the left) are irrelevant for understanding the relative competitive performance of the benchmark model. For P/eps1, a positive correlation with STG should be expected even if eps1 had the characteristic of random numbers with no economic content. We noted this earlier. The focus should instead be on the two plots to the right, with P/eps2 on the y-axis. The positive correlations remain in place: the correlations (STG, P/eps2) equal .22 and .26 (see Table 2). Consistent with implications of equations (2a) and (2b), these P/eps2 correlations are distinctly smaller than the ones related to P/eps1 but they are nonetheless present. One can also note that the slope related to P/eps2 is smaller than the slope related to P/eps1. Thus the plots are solidly consistent with all previous results: STG does influence price via the P/eps2 ratio but at the same time the data clearly shows that the elasticity is as modest as is the underlying correlation.
The kis should per theory depend on risk, but the estimated kis above do not take this into consideration. They are crude averages across firms with different risk levels. Our empirical analysis so far may have prevented the earnings and earnings growth model from showing its strength and disguised that betas can connect with earnings capitalization factors.
Earnings and Earnings Growth Valuation: Recognizing Betas
The appendix develops in detail the coefficients' dependence on the discount factor, r. The intuition comes from elementary capitalization precepts. That is, a value-multiplier should increase as risk decreases. Formal analysis in the appendix shows that as r increases –k1, k2, and k3 decrease. The derivation is technical and depends on a number of subtleties (including the use of ceteris paribus). The theory also implies that k1 + k2 should be independent of risk and, though of lesser importance, this aspect can be looked at too. But one can also set aside formal modelling and simply note that standard investment practice suggests that forward P/Es get marked down as risk increases, as long as one controls for growth. That is, regardless of any formal theory, it is of interest to check if high beta stocks have lower value than low beta stocks after having fixed eps1, eps2, and dps1, eps2 > eps1. It is an appealing and straightforward hypothesis.
Results comprise two parts, as was the case in previous sections. Tables first report on (i) the estimates, so that one can assess the extent to which these depend on betas in accordance with theory, and next (ii), whether the beta-based estimation improves on the goodness-of-fit metrics reported on earlier. As before, the 20% median absolute error rate for the eps2-based benchmark model serves as a reference score.
We use a very straightforward approach to check on betas’ relevance: the sample of 455 firms is split into two halves, depending on whether firms' betas are above one—‘high beta firms’—or below one—‘low beta firms’. This approach involves no additional research design decisions and the results can be compared to previous results because they differ only in one respect, the splitting of our sample into two halves based on beta. The basic hypothesis, per appendix theory as well as investment practice, requires the high beta stocks to be worth less after having fixed eps1, eps2, and dps1 (with eps2 > eps1) That is, the estimates of –k1, k2, and k3 should all be larger for low beta stocks. There is no direct reference in this section to the analytics in the appendix, though it spells out in detail how the kis depends on r and other factors (like the risk-premium on the market portfolio). It is simply not necessary and we do want to keep issues as simple as possible, at least as a first cut (though this might lead to ‘false negatives’).
Table 9 provides the estimates of the three coefficients for the two groups of firms. Results are similar for the two years, suggesting that the estimates are based on a reasonably robust method. Next note that, consistent with theory to a remarkable degree, k1 + k2 differs only marginally for the two sets of firms. Further, all coefficients have the right signs and order of magnitudes. The two panels confirm the hypothesis that relates betas to coefficients: the magnitudes of all three coefficients for high beta firms are distinctly smaller than for the low beta firms. To reinforce this point, for all three coefficients, the maximum magnitude for high beta firms is less than the minimum for low beta firms. The evidence accordingly implies that betas correlate in the right direction with earnings capitalization, consistent with CAPM. No spurious correlation lurks in the background; estimates shown in Table 9 are independent of betas, aside from the sample splitting. One can also easily check numerically that, given any forecasts and year, the high-beta firms are priced lower than low-beta firms. Nonetheless, the evidence should not be over-read; other measures of risk (like Fama-French factors) may yield similar, or even better, results. We have not looked into this possible extension, though it in principle poses few problems.
| eps1 | eps2 | dps1 | |
|---|---|---|---|
| Low Beta | |||
| 2013 | −40.57 | 49.77 | 6.64 |
| 2014 | −49.10 | 58.30 | 4.83 |
| High Beta | |||
| 2013 | −17.15 | 26.33 | 4.63 |
| 2014 | −21.78 | 31.73 | 4.27 |
To compare goodness-of-fit we focus on the median absolute percentage error in Table 10 because the score has the more informative texture. To address the core issue related to the split we compare the results in Table 10 to earlier tables. We, of course, also look at the difference between high- and low-beta firms.
| V estimated as a function of (eps1, eps2, dps1) | |||
|---|---|---|---|
| Rank correlation (V, P) | Rank correlation (ΔV/V, ΔP/P) | Median ABS[log(V/P)] | |
| Low Beta | |||
| 2013 | 0.88 | N/A | 14.46% |
| 2014 | 0.90 | 0.65 | 15.20% |
| High Beta | |||
| 2013 | 0.86 | N/A | 18.78% |
| 2014 | 0.87 | 0.43 | 19.59% |
Results are quite striking: there is a distinct improvement in goodness-of-fit, but only for the group of low beta firms. Findings are robust across the three metrics, though the far right column stands out with 14.5% and 15.2% for low beta firms compared to the 20% benchmark. For the high beta firms compared to the benchmark model results in Table 4, there is no real improvement in any of the metrics. It appears, therefore, that earnings and earnings growth valuation becomes more problematic when stocks are risky. Exactly why this is the case is something that perhaps can be worked out, but at this point we can only offer the mundane statement that ‘high risk introduces a multiplier effect by making the valuation itself risky’.
Using the relative accuracy score, one can check directly whether the last model does better than the non-split model, again based on eps1, eps2, and dps1. There is of course no concern that statistical over-fitting takes place since the metric is totally independent of all prior statistical decisions. The RAS score in favour of splitting is 56.9% (2013) and 53.3%. And, as a reminder, the non-split earnings and earnings growth model beats the eps2-based benchmark model. Taken together, the evidence seems to suggest, in a quite compelling manner, that the use of betas adds to our ability to explain the dependent variable, P.
One can hypothesize that the material difference in goodness-of-fit is more apparent than real because it has been caused by the estimation method, TS. Perhaps the TS estimation distorts the goodness-of-fit comparative evaluations because the cross-sectional distributions of the independent variables differ materially for the two groups. This would suggest that there is room for trying out a variety of alternative estimating schemes (OLS, OLS with winsorized data, LAD, and so on). But such multiplicity of approaches is awkward because it leads to an overflow of potentially contradictory information.
A more direct way of checking on estimation-method sensitivity is to optimize the goodness-of-fit metric itself. Hence we minimize the median absolute percentage model errors separately for each of the two groups of firms (high beta firms and low beta firms, respectively). Under ideal circumstances the coefficients resulting from this optimization exercise should be more or less the same as the ones we obtained using TS estimation. A relatively small difference would suggest robust findings. Table 11, juxtaposed to 10, provides the results.
| V estimated as a function of (eps1, eps2, dps1) | |||||
|---|---|---|---|---|---|
| eps1 | eps2 | dps1 | Median ABS[log(V/P)] | Rank correlation (V, P) | |
| Low Beta | |||||
| 2013 | −34.02 | 43.89 | 7.33 | 12.49% | 0.88 |
| 2014 | −48.11 | 57.79 | 4.91 | 13.70% | 0.90 |
| High Beta | |||||
| 2013 | −22.49 | 31.04 | 5.39 | 17.82% | 0.86 |
| 2014 | −15.82 | 27.21 | 4.10 | 17.17% | 0.88 |
Table 11 shows an even greater improvement due to the split of firms into high and low beta groups. The results are particularly impressive for low beta firms, with a median absolute error of about 13%. But the improvement has to be put in perspective since it is a response to an optimization of the metric. If one shifts the focus to the correlations, the TS results in Table 10 are effectively the same as those in Table 11. Also, the estimated coefficients in the first three columns of Table 11 differ little from the TS coefficients. Overall, the finding that high beta stocks are priced lower than low beta stocks seems robust.
The results allow for a second evaluation of the Miller-Modigliani dividend-irrelevance concept. The optimized coefficient ratios k3/k2 do not change much compared to our previous findings and thus they broadly support the irrelevance hypothesis. But they are still on the high side—in excess of 10%—with an exception for low-risk firms in one year.
The analysis of beta-risk as it impacts the pricing has been based on the simplest possible first-cut method: splitting the sample into two groups. One can, of course, then hypothesize that a more refined approach might lead to better goodness-of-fit results. The model in the appendix considers a refined estimation, with coefficients depending on model parameters, including risk, and risk in turn depending on beta. This refined model can also be evaluated by maximizing goodness-of-fit, similar to the approach above. The resulting absolute valuation errors end up averaging about 16%, which is close to the average error in Table 11. Thus the formal model in the appendix reinforces previous results and confirms that the splitting-on-beta method does a reasonable job in tying the pricing of stocks to STG and betas. Conversely, it also reinforces that models of value can only help us so much: we suspect that no matter how clever the modelling, a valuation error of, say, 15%, will be hard to beat.
Concluding Remarks
As a summary of the three questions asked and answered we have: on RIV's validity (negative answer), on the dividend-payout irrelevance (positive answer, but negative insofar as the bird-in-the-hand hypothesis can also be supported), and on whether betas can help explain capitalization multiples (positive answer). Conclusions hinge on viewing P as a linear function of (eps1, eps2, dps1, bvps) with coefficients depending on betas. This broad framework, combined with the more detailed modelling in the appendix that resulted in the earnings and earnings growth model, has been used to interpret the data.
- While RIV seemingly lacks power when we try to explain the cross-section of prices, such an enterprise is likely to be humbling no matter the formal valuation framework. The totality of the evidence suggests that the earnings and earnings growth model, in our view at least, dominates RIV in terms of explaining prices, but reasonable people can perhaps argue that the improvement is only marginal. It is also well to note that any application of RIV depends on the details, and these can be viewed as quite subjective.
- The benchmark model that relies only on eps2 turns out to be hard to beat whenever one uses a ‘free-standing’ goodness-of-fit metric. This aspect ought not to be overshadowed by the more compelling evidence that the complementary variables eps1 and dps1 also load on the RHS, as per theory.
- While the data at least to some extent support dividend-policy irrelevance as per theory, the findings can also be read as suggesting that dps1 loads materially, in excess of what is implied by strict Miller-Modigliani precepts. In other words, maybe investors do pay a premium for stocks that distribute dividends (as measured in our context by dps1).
- The last two tables show a distinct asymmetry between high and low beta stocks. It raises concerns that betas lack validity as risk measures, at least for the high beta stocks. One can hypothesize that low betas correlate with a much better (unknown) measure of risk, but the correlation ceases for high betas. It also raises concern that the earnings and earnings growth model lacks power when one tries to explain the pricing of risky stocks. In turn, one can further argue that some kind of measure of LTG will now be far more important than STG.
- As to bvps, the tables suggest that the variable can be dismissed (given eps1, eps2, and dps1); the materiality hurdle has not been met. Still, for both years the coefficients are virtually the same, and negative. One can read this result as being consistent with RIV concepts: there is something to be said for the idea that profitable firms trade at a P/E premium, after having fixed STG and dps1. While the effect of bvps on P may be minor, it is arguably not all that different from dps1. Moreover, one can further argue that the profitability premium is potentially material in the case of stocks with a high book-to-market ratio.
Fundamental investment analysis centres on earnings and earnings growth. And within this framework the forward P/E ratio increases as growth increases and it decreases as risk increases. We view these two sentences as capturing a basic truth about how the world works. Accordingly, this has driven everything that has been said in this paper and it has led to the questions addressed. In particular, an investment principle based on earnings and earnings growth differs from RIV in its very essence, which points to the need to evaluate what RIV is all about. It is also clear that the role of dps1 needs to be resolved, because the investment principle ought not to refute PVED. And given the traditional prominence of CAPM, the question whether betas influence equity valuation would also seem to be inevitable. The difficulty, however, has been to wrap all of these ideas into a unified analytical framework. We have interpreted our findings with the help of modelling to get the advantage of formalism. It has served the useful purpose of guiding the interpretation of estimated coefficients to assess the extent to which these align with investment practice.
Appendix: A Model That Explains the Forward p/e Ratio in Terms of stg and Risk
A. Theory
- P(t) = PVED with discount factor R = 1 + r > 1
- P(t) = m*eps(t + 1) + k* [m*eps(t + 2) + dps(t + 1) – R*m*eps(t + 1)]
- Diff(t + 2) = G*Diff(t + 1),
Any two of the three statements imply the third.
- The model depends on the three exogenous, t-independent, parameters, G, R, and m, where 0 < G < R > 1 and m > 0. A proof of the proposition relies on routine calculations. The elements required can also be found in prior work—Ohlson and Juettner-Nauroth (2005) being the closest. Expressions in the proposition have a one-to-one relation with expressions in OJ and RIV analyses. In the OJ model m equals 1/r. The standard RIV model with T = 1 horizon follows by replacing m*eps(t + 1) with bv(t) for all t. (In the proposition, since t defines the current date, more precise notation would be eps(t + 1) = eps(t + 1;t) and eps(t + 2) = eps(t + 2;t) etc.; the two forthcoming expected eps forecasts depend on inherently stochastic information available at date t. Expectations and the law of iterated expectations are implicit in the dynamics.)
- The inter-temporal constant m can be thought of as a ‘long-run’ or ‘typical’ forward P/E ratio. (m = 15 provides a sense of magnitude.) Given such a conceptualization of m, m exceeds 1/r because m picks up on growth as well as r. Hence, m*eps1 provides a first-cut estimate of P which will be modified by a second term. The complementary term equals k*Diff(t), which equals zero in the long run (in expectation), provided that G < 1 restricts the model. G determines the speed of contraction towards zero; the smaller G is the faster the complementary term approaches zero (the restriction G < 1 is empirical; the proposition requires a weaker condition, G < R.)
- The forward P/E ratio equals an intercept, m, and a term picking up on ‘adjusted’ STG in eps after having deducted r. The adjustment to STG pertains to the dividend term:
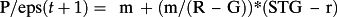
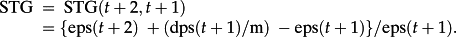
The normalization of the dividend term by m captures the foregone next-period earnings due to dividends. The dps1/m term allows for Miller-Modigliani concepts. It requires eps2 + (dps1/m) to be independent of changes in dps1; that is, changes in dps1 causes changes in eps2 with 1/m measuring the foregone earnings rate.
The forward P/E ratio exceeds the so-called typical forward P/E—picked up by the parameter m—if and only if STG exceeds r. Thus, one interprets m as the forward P/E when the (adjusted) STG equals cost-of-equity.
The multiplier (m/(R – G)) attached to the spread (STG – r) picks up the rate of duration of the superior (or inferior) growth rate. A small G, given r and m, means the P/E ratio will return to its ‘typical’ value relatively quickly (in expectation).
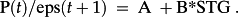
Where A = m*(1 – G)/(R – G) and B = m/(R – G).
- In the long run, high growth comes with high risk (and conversely). Assume a full payout dividend policy, dps1 = eps1 for all future periods; it follows that as T goes to infinity [eps2(T)—eps1(T)]/eps1(T) = r – 1/m. The claim that growth in the long run requires risk follows. (To be sure, the fact that G < 1 in no way suggests that eps or dps1 are expected to grow negatively.)
- G = 1, the boundary case, leads to an exceptionally simple expression connecting r and PEG. Using (3):
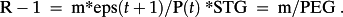
- The term Diff(t + 1)/m equals
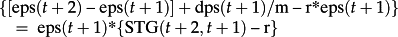
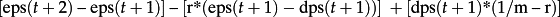
- Perhaps the most intuitive way to think about the valuation identifies m*eps(t + 1) and [m*eps(t + 2) + dps(t + 1)]/R as two rough estimates of today's value, P(t). Let Est(1;t) and Est(2;t) denote the two estimates of value. A weighted average of the two estimates determines value:
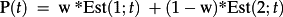
- A reduced form expression of value equals
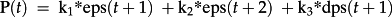
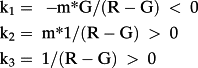
- The model above relies on three parameters; these have a one-to-one relation with the coefficients:
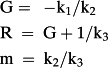
B. Expanding the Theory: G as a Function of R
Whereas r must be firm-specific, the constant m can be thought of as a quantity holding for all stocks. What about G? How should it be interpreted? If firm-specific, should it then connect with r? In other words, can we say something that goes beyond G serving as a statistical/empirical ‘contraction parameter’?
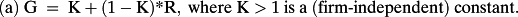
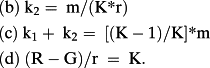
The model thus rests on two firm-independent parameters, m and K, and one firm-specific, R. But since R and G are one-to-one given the broad parameters m and K, the triplet (m, K, R) is one-to-one with (m, K, G), where the more precise notation G(j), R(j) is implicit.
Expression (d) is perhaps the most intuitive. Because the spread R – G reflects risk, one can hypothesize that a risk-normalization, dividing by r, implies a constant ratio, K. From the above it follows that k2 relates directly to classical capitalization concepts, as long as one keeps in mind that r must be scaled by (K/m). Alternatively, given two firms, i and j, k3(i)/k3(j) = (1/r(i))/(1/r(j)). Moreover, the sum k1 + k2 does not depend on the firm's risk, in sharp contrast to the two components. Expression (c) validates this firm-independence. Next consider the ratio –k1/k2: it increases as risk decreases (as do –k1 and k2). Though these are strong statements about the valuation, they can be evaluated empirically (see part C below).
What should K roughly equal? An answer can be derived from equation (3). Estimates supplied earlier suggested that the sum is roughly 10. Putting m = 15 implies K = 3. A lower m leads to a larger K, for example m = 13.3 corresponds to K = 4 so the potential ‘plausible’ range is considerable.
C. The Expanded Model: Estimation and Goodness-of-Fit Evaluation
The two parameters m and K can be estimated provided that r has been dealt with. Suppose that CAPM holds with r(f) = 4%; then r = 0.04 + beta*q2. The model in A and B now has three general—and ‘unknown’—parameters: m, K, and q2. (To make r(f) an additional free parameter leads to an identification problem.) Because the model rules out linear estimation, we obtain estimates of the three parameters by minimizing the median of the absolute value of the model error, that is, for each year we solve for min(median(ABS{log(V(G, K, q2)/P)})) and where the min(…) operator is taken over m, K, q2, none of which, to be sure, is firm-specific.
Results would seem to be reasonable. For starters, the percentage errors are much smaller than earlier, now 17% and 15% respectively. The values for m, K and q2 would also seem reasonable, though perhaps somewhat on the low side. Taken together, the results suggest that the theory and assumptions of this appendix help to explain a stock's price.
One can argue that the results over exploit the data and that they do not hold up outside the data sets that estimate the parameters. But this issue can in fact be addressed. The goodness-of-fit metric changes only slightly if one uses the optimal solution for 2013 on 2014 data and conversely. The goodness-of-fit scores are, of course, worse, but it is a modest change: 18.6% for 2013 data (2014 parameters) and 16.3% for 2014 data (2013 parameters). The relatively large worsening for 2013 can be attributed to an upward bias of 10.4% (measured as the median percentage error, without absolute value) which is indeed quite large. Using the estimates for 2013 and applying them to 2014 yields a bias of −3.9%. We also checked for robustness by fixing m = 15 and q2 = 0.04 and solve for K (9.00 and 5.9 respectively), to find that the optimal solution, which is very close to the Table 12 solution; the two numbers are now 17.3% and 15.6%.
| Panel 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| K | m | q2 | Medianlog (V/P) | Median ABS[log(V/P)] | |||||
| 2013 | 5.40 | 13.50 | 0.04 | 0.02 | 0.17 | ||||
| 2014 | 4.90 | 14.20 | 0.03 | 0.04 | 0.15 | ||||
| Panel 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | k1 | k2 | k3 | k1 | k2 | k3 | |
| (beta = 0.75) | (beta = 0.75) | (beta = 0.75) | (beta = 1) | (beta = 1) | (beta = 1) | (beta = 1.3) | (beta = 1.3) | (beta = 1.3) | |
| 2013 | −26.31 | 37.31 | 2.76 | −21.89 | 32.89 | 2.44 | −17.80 | 28.80 | 2.13 |
| 2014 | −34.52 | 45.82 | 3.23 | −29.51 | 40.82 | 2.87 | −24.79 | 36.09 | 2.54 |
The ultimate test for robustness again relies on data from one year and parameters from the other. The approach follows two steps and can be described as follows. First, define x1 = k1*eps(t+1) where k1 derives from the optimal model reported on in the last table (still implying firm-specific k1 because of its dependence on betas). Consider two cases: use 2013 data but parameters estimated based on 2014; the second case switches the procedure. Repeat the scheme for the second and third variables to calculate x2 and x3 across all firms for each of the two cases (2013 data and 2014 parameters or conversely). Now to the second step: for each of the two years, apply TS to estimate the parameters a1, a2, a3 in the model P = a1*x1 + a2*x2 + a3*x3. Under ideal circumstances the estimated coefficients should all equal 1. Results are (0.92, 1.00, 1.04) and (0.70, 0.75, 1.25) for 2014 data and 2013 data respectively. The relatively low values in the second case can be attributed to the previously mentioned upward model bias if one uses 2013 data but 2014 parameters. Critically though, the two major parameters, related to eps1 and eps2 satisfy the model condition that a1/a2 is approximately one. It seems to us that, overall, one can conclude: given the restriction on valuation inputs, concepts and realities support each other.
References
- 1 Textbooks like Penman (2012), Easton et al. (2013), and Wahlen et al. (2010) all spend considerable space to cover accounting-based valuation.
- 2 It is of course no easy matter to assess the ‘acceptance’ of RIV in practice, but we believe that one can safely say that relatively few investors prefer to rely on market-to-book ratios as opposed to forward P/Es and P to various measures of cash flows, forecasted or not.
- 3 There are numerous studies (too numerous for us to cite) evaluating the Miller-Modigliani dividend-policy irrelevance hypothesis. And the reasons for rejecting the hypothesis are endless, including taxes, signalling, information asymmetry, liquidity, agency considerations, financing constraints, debt market considerations, etc. We are unaware of any study during the past 40 years that has accepted the null hypothesis.
- 4 LTG has a ‘low quality’ reputation partially because of its extreme optimism. It is unclear how, or whether at all, investors make use of these numbers beyond STG. See, for example, Sharpe (2005).
- 5 We do not view this finding as novel: see in particular Liu (2007). Our study tries to contribute by providing the reasons for RIV's lack of success. It should be noted, though, that there are studies that suggest that RIV picks up on valuation realities, including the literature on implied cost-of-capital (ICC), for example, Gebhardt et al. (2001) and Frankel and Lee (1998). But one can reasonably hypothesize that many academics, more so in finance than accounting, view RIV with great scepticism.
- 6 A vast literature explains forward P/Es (and forward E/Ps) and some of what shows up in this paper was anticipated. However, the critical contribution in this paper is the distinguishing of the different roles played by P/eps1 and P/eps2. It should further be noted that the literature, from what we can tell, focuses on explaining P/E rather than P—and in our minds this aspect introduces all sorts of subtleties, conceptual and empirical. A very helpful paper dealing with the subject matter is He and Yu-Thompson (2014). They deal with the P/eps1 ratio as it relates to both growth and risk. Many findings in their paper relate to points made in this paper. Aside from our conceptual focus on P/eps2, we also deal with betas.
- 7 The model in the appendix generalizes the model due to Ohlson and Juettner-Nauroth (2005). Ohlson and Gao (2006) provide an extensive discussion of the latter.
- 8 The formula in question says that r = sqrt{(eps1/P)*STG} = sqrt {1/PEG}; the model is a special case of the model developed in Ohlson and Juettner-Nauroth (2005).
- 9 A substantial literature on ICC deals with how risk relates to various attributes of the firm, such as whether beta correlates with ICC measures. Examples of such papers are Botosan and Plumlee (2005), Easton (2009), Easton and Monahan (2005), Gebhardt et al. (2001).
- 10 Frankel and Lee (1998) pursue the idea that RIV can serve as a stock-picking tool.
- 11 In principle one could visualize that all firms, by engaging in stock splits and reverse stock splits, traded at the same stock price. Now the rank correlation between V and P would be zero.
- 12 The common denominator spurious correlation between P/eps1 and STG is similar to the ‘insight’ associated with Tobin's Q (that MV/BV correlates with the expected ROE).
- 13 See also Wilcox (2004, 2013).
- 14 TS estimation also ensures that the number of shares outstanding has no effect.




