The Starling Principle states that fluid movements between blood and tissues are determined by differences in hydrostatic and colloid osmotic (oncotic) pressures between plasma inside microvessels and fluid outside them. The Revised Starling Principle recognizes that, because microvessels are permeable to macromolecules, a balance of pressures cannot halt fluid exchange. In most tissues, steady oncotic pressure differences between plasma and interstitial fluid depend on low levels of steady filtration from plasma to tissues for which the Revised Principle provides the theory. Plasma volume is normally maintained by fluid losses from filtration being matched by fluid gains from lymph. Steady state fluid uptake into plasma only occurs in tissues such as intestinal mucosa and renal peri-tubular capillaries where a protein-free secretion of adjacent epithelia contributes significantly to interstitial fluid volume and keeps interstitial oncotic pressure low. Steady filtration rates in different tissues are disturbed locally by reflex changes in capillary pressure and perfusion. The rapid overall decline in capillary pressure after acute blood loss initiates rapid fluid uptake from tissue to plasma, that is, autotransfusion. Fluid uptake is transient, being rapid at first then attenuating but low levels may continue for more than an hour. The Revised Principle highlights the role of oncotic pressure of small volumes of interstitial fluid within a sub-compartment surrounding the microvessels rather than the tissue's mean interstitial fluid oncotic pressure. This maximizes oncotic pressure differences when capillary pressure are high and enhances initial absorption rates when pressures are low, accelerating short-term regulation of plasma volume.

Editorial Comment

In this special article, which is one of a pair of invited narrative reviews, the author group focuses on review and reassessment of the model for fluid movement between capillary plasma and tissue, including recent developments in thinking.

1 INTRODUCTION

When Woodcock and Woodcock¹ suggested that more recent work on the physiology of blood-tissue fluid exchange might be relevant in the management of intravenous fluids in clinical situations, they referred to the newer work as the “Revised Starling Principle.” Here they were merely adopting the phrase used by Levick & Michel,² originated by others³ to describe these ideas. The name “Revised Starling Principle” or RSP might imply that the original version of the Starling Principle was wrong and required revision. It should be emphasized that Starling's fundamental idea, that movements of fluid between the circulating plasma and the tissues are determined by the differences between hydrostatic pressures and colloid osmotic (or oncotic) pressures across microvascular walls, remains the central idea of the RSP. This essential point seems to have been overlooked by some who may have been confused by the word “Revised” in the title.^{4, 5}

To emphasize that the RSP builds on and extends Starling's original proposal,⁶ we first summarize its key elements, which describe how the oncotic pressures of the plasma proteins oppose hydrostatic pressure driven filtration of fluid from blood to tissues, when microvascular walls have low but finite permeabilities to plasma protein. We then briefly review the train of logic on which these developments of Starling's classical principle are based.

2 OVERVIEW

Far from challenging the traditional Starling Equation⁴ the RSP uses it as a starting point and consequently as a keystone of its structure. The equation describes both transient and steady state of fluid exchange. The RSP, however, points out that because microvascular walls are permeable to plasma proteins, there is never a true Starling equilibrium. An equilibrium would mean that fluid exchange could be halted by a balance of the opposing forces. While hydrostatic and oncotic pressures might balance momentarily, the leakage of protein from plasma to interstitial fluid (ISF) will reduce oncotic pressure differences across microvascular walls creating an imbalance. In tissues where ISF is generated entirely as capillary filtrate, a low level of filtration is necessary to maintain a steady difference in oncotic pressure across microvascular walls. This has been widely recognized in the past as an excess of filtration over absorption to account for lymph flow. The RSP shows how its magnitude can be calculated from the permeability properties of the microvascular walls.

A second development emphasizes that differences in oncotic pressure across microvascular walls in a tissue can exceed that between plasma and mean ISF oncotic pressure of that tissue. This is even possible in steady states because macromolecules are effectively restricted to a “large pore” pathway through endothelia and are nearly all excluded for the route taken by most of the fluid and small solutes. The ultrafilter of microvascular walls is recognized as the glycocalyx on the luminal surface of the endothelia and it is across the glycocalyx that the oncotic pressure difference is exerted.

A third point is the importance of local hydrostatic pressure differences across microvascular walls, ΔP. Autonomic reflexes can rapidly alter pre-capillary and post-capillary resistances of the microcirculation, which determine ΔP. Unfortunately, there is no way of estimating ΔP at present. This is not a new development but is often forgotten.

3 The Starling equation

Starling never expressed his idea as an equation. The earliest form of the equation was written by Landis⁷ to describe the correlation between his measurements of hydrostatic pressure in single frog mesenteric capillaries and the rates of fluid filtration and absorption through the capillary walls. These measurements were compelling evidence for Starling's hypothesis. Plasma proteins are present in ISF and as ingenious indirect methods of estimating the mean capillary pressure in perfused tissues and organs were developed,^8-10 net fluid movements between the plasma and the tissues were described by equations of the general form:

$urn:x-wiley:00015172:media:aas13603:aas13603-math-0001$ ()

where the symbol J_V is the fluid flow rate through unit area of microvascular walls. J_V is positive when flow is from plasma to tissue and negative value when flows are from tissues to plasma. K is a constant combining the hydraulic permeability of microvascular walls and the area through which fluid is exchanged; P_c and P_i are the hydrostatic pressures in microvessels and ISF respectively and Π_p and Π_i the oncotic pressures of the plasma and ISF. ΔP and ΔΠ are the differences in hydrostatic and oncotic pressures across microvascular walls. For other symbols see Table 1

Table 1. List of P (0 ) Micrvas cular pres s ure when J = 0P Venous pressure

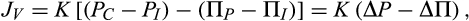ISF	Interstitial fluid.
J_V	Fluid filtration (+) or absorption (−) rates per unit area through microvascular walls.
K	Microvascular filtration coefficient: product of hydraulic permeability and microvascular surface area
P	Hydrostatic pressure.
P_C	Microvascular hydrostatic pressure.
P_C(0)	Microvascular pressure when J_V = 0
P_I	Interstitial fluid hydrostatic pressure.
P_V	Venous pressure
Π	Oncotic pressure (colloid osmotic pressure)
Π_P	Microvascular plasma oncotic pressure.
Π_I	Interstitial fluid oncotic pressure.
Π_G	Interstitial fluid oncotic pressure on tissue side of endothelial glycocalyx.
ΔP, ΔΠ	Hydrostatic and oncotic pressure differences across microvascular walls.
RSP	Revised Starling Principle.
σ	Membrane or osmotic reflection coefficient to a solute.

Equation 1 would be correct if microvascular walls were impermeable to plasma proteins. When a membrane is permeable to the solute responsible for its osmotic pressure, the osmotic pressure difference of that solute's solution across that membrane is less than the value exerted by the same osmotic pressure difference across a membrane, permeable to water but impermeable to the solute.¹¹ The fraction of the osmotic pressure difference that can be measured across a leaky membrane is known as the reflection coefficient of the membrane to that solute and indicated by the symbol, σ, which for water-soluble solutes has values between 0 and 1.0.¹¹ Addition of σ to the Starling equation leads to:

$urn:x-wiley:00015172:media:aas13603:aas13603-math-0002$ ()

with σ ≥ 0.9 for most plasma proteins in the microvessels of most tissues. Equation 2 has been the accepted form of the Starling equation for the past 50 years¹² provided it is recognized that the interstitial hydrostatic and oncotic pressures are those present in the peri-capillary ISF, which change most rapidly with J_V and may differ considerably from their mean values in the ISF. Equation 2 is the most useful expression for describing the rate of fluid movements between the circulating plasma and the ISF.

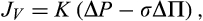4 TRANSIENT AND STEADY STATE FLUID EXCHANGE

Starling⁶ believed that a constant plasma volume reflected an equilibrium between the opposing hydrostatic and oncotic pressures when J_V would be zero. We have already noted that because microvascular walls are finitely permeable to proteins, a true equilibrium cannot be achieved, ΔP cannot equal σΔΠ (in Equation 2) for more than a fraction of a second. A steady state, however, can be reached where, at constant ΔP, and constant values of ΔΠ are maintained by low and constant filtration rates. Transients of J_V change ΔΠ to new steady state values.

The molecular ultrafilter of microvascular walls is the glycocalyx on the luminal surface of the endothelial cells. Steady state concentration differences of macromolecules across the glycocalyx, resulting from ultrafiltration, involve a race between the few macromolecules carried through the endothelial luminal glycocalyx with the filtered fluid and the majority of macromolecules attempting to catch them up by diffusion. Because the reflection coefficients of the glycocalyx to most plasma proteins is high (σ ≥ 0.9) and its diffusional permeability to these macromolecules is low, steady state concentration differences can be maintained by very low rates of filtration. The steady state concentration of macromolecules in the ultrafiltrate can be calculated and in those few microvessels where all permeability coefficients have been estimated, it has been possible to confirm predictions of the steady state theory.^{13, 14}

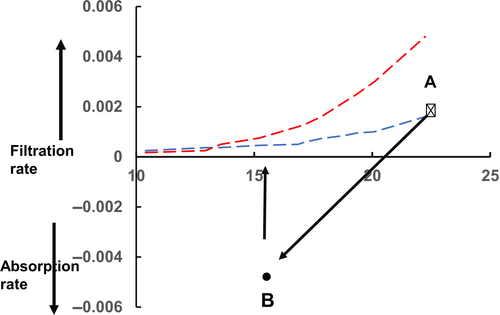
Figure 1 shows the relationship between steady state values of the filtration rate per unit area of microvascular wall (J_V) to ΔP (blue curve). Also shown as a dashed linear relation are the transient changes in J_V with changes in ΔP when initially ΔP lies on the steady state curve with a value which approximates that of Π_C. However, the transient relations show how J_V varies linearly with ΔP at constant σΔΠ, the hockey stick shaped curve represents the steady state relations where σΔΠ is determined by J_V at a given value of ΔP. Woodcock & Woodcock¹ called the hockey stick curve the “J curve”. The differences between the transient and steady state values of J_V are increasingly large as ΔP falls below Π_p. By contrast, transient and steady state relations approach each other more and more closely as ΔP exceeds σΔΠ with high values of J_V.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Transient and steady-state relations between the rate of fluid filtration through unit area of microvascular walls and the hydrostatic pressure difference across them. The dashed linear relation indicates the transient relations between net fluid exchange rate per unit area (*J_V*) and hydrostatic pressure difference (ΔP) when plasma and peri-capillary oncotic pressures are constant and *ΔP_C* has an initial value of 22.5 mmHg; positive values of *J_V* indicate filtration from plasma to tissues and negative values fluid uptake into plasma. The steady state relation for the same plasma oncotic pressure is shown as the solid curvi-linear relation. The point at which the two lines intersect is the steady state condition when ΔP has a value of 22.5 mm Hg. [Colour figure can be viewed at wileyonlinelibrary.com]

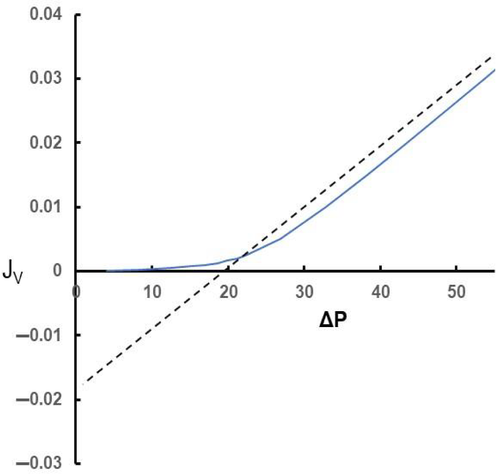
If ΔP is lowered by pre-capillary vasoconstriction in a tissue and held at its low value, fluid moves briskly from tissue into plasma (Equation 2). Even though ΔP is constant, fluid uptake falls with time as J_V approaches its new steady state value. This is shown in Figure 2. Also shown here are the transient responses of J_V when ΔP is restored to its initial value. These changes are typical of those in a tissue where a period of vasoconstriction is followed by vasodilatation with negligible changes in plasma volume and consequently Π_P.

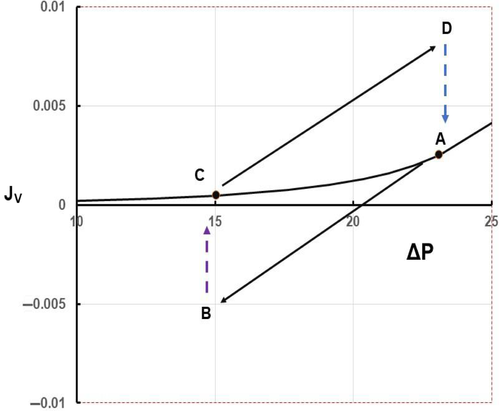
More generalized vasoconstriction after haemorrhage involves a reduction in Π_C and a shift of the steady state curve (see Figure 3).

4.1 Steady state fluid uptake into the microcirculation

The steady state relations shown in Figures 1-3 apply in the tissues, which make up most of the body mass (eg, muscle, skin, connective tissues etc) where the great majority of microvessels have continuous (non-fenestrated) endothelia and the ISF is generated entirely by filtration from the microvessels.

In some tissues (kidney, gastro-intestinal mucosae), the ISF receives a major contribution of protein-free fluid secreted by adjacent epithelial cells. Here steady state fluid uptake into the fenestrated microvessels can be sustained if the rate of fluid uptake into the plasma does not exceed the rate of secretion of protein-free fluid into the ISF. If the epithelial secretion ceases, however, fluid uptake diminishes as Π_I increases and J_V reverts to a steady state of low filtration.

5 ISF volumes and sub-compartments in fluid exchange

In 1969 Lunde & Waaler,¹⁵ reported that, in isolated perfused rabbit lungs, small but sustained increases and decreases in the P_C led to small gains and losses in tissue fluid volume which rapidly attenuated. They suggested a small compartment of ISF was present immediately outside pulmonary capillaries so that the addition or subtraction of small fluid volumes rapidly altered its Π and hence σΔΠ. This hypothesis was consistent with Chinard's demonstration¹⁶ that during a single transit through the lung capillaries, small highly diffusible molecules and ions are distributed in a volume only slightly greater than that of the plasma.

A similar phenomenon was observed during experiments on perfused mesenteric capillaries.¹³ Following a step fall in ΔP, fluid absorption attenuated rapidly to its new steady state value. Since the macromolecular concentration of the solutions perfusing the vessels and ΔP were constant, it suggested that the oncotic pressure of fluid immediately outside the vessel must have risen sufficiently to bring σΔΠ close to ΔP. The rate of attenuation indicated that the volume of ISF in which Π had changed was a small fraction of the ISF in the surrounding tissue.

It seems likely that in the lung, rapid attenuation of fluid filtration is also related to changes in P_I in addition to ΔΠ¹⁷ but the close correlation between the inflexion point of the steady state relation and Π_P indicates that changes in ΔΠ are also important.¹⁸ Changes in ΔP, however, cannot account for the rapid attenuation of J_V in exposed super-fused mesenteries where P_I is independent of varying J_V.¹⁹ These observations emphasize that the ΔΠ term in Equation 2 is ΔΠ across microvascular walls and not the difference between Π_P and the mean value of Π_I for the tissue's ISF.

5.1 Levick's paradox of Starling pressures and lymph flow

The importance of distinguishing between Π_I on the tissue side of the glycocalyx from the mean value of Π_I of tissues resolves an important discrepancy reported by Levick.²⁰ In a review of the blood-tissue fluid exchange and the Starling pressures, Levick²⁰ collected data from 15 studies on 14 organs or tissues from a range of mammals (including humans) where measurements of Π_P, Π_I and P_I had been made along with direct determinations of the venular or venous pressure, P_V. From these data, he calculated the value of P_C when J_V = 0 from a rearrangement of Equation 2, ie,:

$urn:x-wiley:00015172:media:aas13603:aas13603-math-0003$ ()

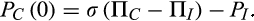Assuming that σ = 1, Levick compared his estimates of P_C(0) with the values of P_V. In 11 out of the 14 tissues, P_C(0) lay between 2 and 10 mm Hg below direct measurements of P_V. Three tissues that were exceptions were the post-glomerular tissue of the renal cortex and medulla and intestinal mucosa during fluid uptake by the gut where P_C(0) exceeded P_V by 6-10 mmHg. Interestingly, P_V rose to 4 mmHg above P_C(0) in the mucosal capillaries when the intestine was not absorbing fluid, consistent with steady state fluid uptake being dependent on protein-free secretions into its ISF. In the 11 tissues, where P_V was greater than P_C(0), microvascular filtration was the only source of the ISF and their values suggested that lymph flows were many times greater than the highest measured values. To resolve the paradox, a hypothesis was suggested based on known differences between the permeability pathways for macromolecules and those for water and small solutes.

5.2 Microvascular permeability pathways for water and macromolecules

Macromolecules cross microvascular walls by a separate route from the main pathway for water and small solutes. Grotte²¹ first proposed these separate pathways to account for the transport of dextran polymers from plasma to lymph. Whereas, transport of smaller polymers (molecular radii < 4 nm) was strongly dependent upon molecular size, the much lower transport rates of larger polymers were only slightly size dependent. He proposed two populations of pores through microvascular walls: large numbers of small pores (radii ~ 4 nm) per unit area for water and small hydrophilic molecules; and a few large pores (radii ~ 10 to 20 nm) for macromolecules. Grotte's experimental findings have been widely confirmed^22-24 and his description of the two pathways as small pores and large pores is generally accepted, though whether the “large pores” are fluid conducting pores or represent cellular mechanisms (eg, transcytosis) has been vigorously debated.²⁴

The small pores are now believed to be the interstices of the endothelial glycocalyx.^{25, 26} To account for Levick's lymph paradox, Michel²⁷ argued that if the ultrafiltrate emerging through the glycocalyx did not immediately mix with macromolecules, a larger difference in oncotic pressure could be sustained across it. All the vessels exhibiting the lymph paradox have continuous endothelia where the ultrafiltrate leaving the glycocalyx then crosses through intercellular clefts. Because the area of the entrances to the clefts are less than 1% of the endothelial surface and between 90% and 99% of the clefts are closed by the tight junctions, the velocity of fluid flow through the breaks in the tight junctions is 10³-10⁴ times greater than its average velocity through unit area of microvascular wall. These velocities are driven by pressure differences as little as 1-2 mm Hg. Protein molecules arriving in the ISF by a different route would have to diffuse against an increasing fluid velocity in the outer regions of the clefts to reach the fluid on the downstream side of the glycocalyx. Michel²⁷ calculated this high fluid velocity would act as a barrier to diffusion of protein molecules. Consequently, the oncotic pressure of the ultrafiltrate, identified² as Π_G, would be considerably less than the mean value for ISF, and ΔΠ across the glycocalyx would be considerably more than the values used in Levick's calculations. Quite independently, Weinbaum²⁸ reached a similar conclusion and followed this up with a comprehensive mathematical model.³

Meanwhile, Curry had suggested how the theory might be tested. Curry, Weinbaum, and their colleagues^{14, 29} collaborated to show that even when Π_I in contact with the outer surface of mesenteric venules equaled Π_C within the vessel, fluid filtration through the vessel walls was dominated by P_C and Π_P. These workers also proposed that a sub-compartment of the interstitial space of the mesentery was formed between microvessels’ basement membranes and a close-fitting sleeve of pericytes.³⁰

A more detailed review of this work is given by Levick and Michel² and Michel et al.³¹

6 GENERAL CONCLUSIONS

The Revised Starling Principle does not challenge⁴ but arises from the meaning of the traditional Starling equation for microvessels with low permeabilities to plasma proteins. It does not say that Π_P is less important than previously thought⁴ nor that there is no osmotic gradient between plasma and ISF.⁵It recognizes that Equation 2 describes both transients and steady states of fluid exchange. It emphasizes that the oncotic pressure difference (ΔΠ in Equation 2) is that between plasma and ISF on the tissue side of the endothelial ultrafilter (Π_G)which may be considerably less than the mean value of Π_I. In many tissues, Π_G behaves as if in an ISF sub-compartment.

Because microvascular walls are permeable to plasma proteins, there are no true Starling equilibria but steady states are maintained by low levels of filtration in most tissues. Steady state fluid uptake occurs only to specialized tissues when a sizeable fraction of ISF volume is contributed by a protein-free epithelial secretion. Steady state fluid uptake here is dependent on epithelial secretion rates keeping interstitial Π_G low.

In most tissues, however, where the ISF is entirely generated from the capillary filtrate, steady states require low levels of filtration to maintain a constant σΔΠ across microvascular walls. This steady flow of ultrafiltrate entering the tissue equals the lymph flow leaving it.

That filtration is necessary to maintain steady states in most tissues has been widely misunderstood. It is, however, implicit in the traditional picture as an excess of filtration over reabsorption to account for lymph flow and the steady state theory indicates how this is achieved throughout the microvascular bed.

While confirmation of the predictions of RSP has come from experiments on single mesenteric microvessels where all variables can be measured, the steady state theory was first used in a review of microvascular fluid exchange¹² and found to account for many of the discrepancies between traditional thinking and observations (eg, in lungs and human limbs). It is in this context that the RSP should be judged as a guide in new scenarios.

As noted earlier “The Revised Starling Principle” may be too grandiose and misleading a title for these newer concepts of blood-tissue fluid exchange. The ideas are really a development of earlier concepts and might be more appropriately described as “The Extension of Starling's Principle”.

CONFLICT OF INTEREST

None.

REFERENCES

1Woodcock TE, Woodcock TM. Revised Starling equation and the glycocalyx model of transvascular fluid exchange: an improved paradigm for prescribing intravenous fluid therapy. Br J Anaesth. 2012; 108: 384-394.
10.1093/bja/aer515
CAS PubMed Web of Science® Google Scholar
2Levick JR, Michel CC. Microvascular fluid exchange and revised Starling principle. Cardiovascular Res. 2010; 87: 198-210.
10.1093/cvr/cvq062
CAS PubMed Web of Science® Google Scholar
3Hu X, Weinbaum S. A new view of Starling's hypothesis at the microstructural level. Microvascular Res. 1999; 58: 281-304.
10.1006/mvre.1999.2177
CAS PubMed Web of Science® Google Scholar
4Zdolsek M, Hahn RG, Zdolsek JH. Recruitment of extravascular fluid by hypertonic albumin. Acta Anaesthesiol. Scand. 2018; 62: 1255-1260.
10.1111/aas.13150
CAS PubMed Web of Science® Google Scholar
5Hasselgren E, Zdolsek M, Zdolsek JH, et al. Long intravascular persistence of 20% albumin in post-operative patients. Anest Analg. 2019; 129(5): 1232–1239.
10.1213/ANE.0000000000004047
PubMed Web of Science® Google Scholar
6Starling EH. On the absorption of fluids from connective tissue spaces. J Physiol. 1896; 19: 312-326.
10.1113/jphysiol.1896.sp000596
CAS PubMed Google Scholar
7Landis EM. Microinjection studies of capillary permeability. II. The relation between capillary pressure and the rate of which fluid passes through the walls of single capillaries. Am J Physiol. 1927; 82(2): 217-238.
10.1152/ajplegacy.1927.82.2.217
Google Scholar
8Pappenheimer JR, Soto-Rivera A. Effective osmotic pressure of the plasma proteins and other quantities associated with the capillary circulation in the hind limbs of cats and dogs. Am J Physiol. 1948; 152: 471-491.
10.1152/ajplegacy.1948.152.3.471
CAS PubMed Web of Science® Google Scholar
9Johnson PC. Effect of venous pressure on mean capillary pressure and venous resistance of the intestine. Circ Res. 1965; 16: 294-300.
10.1161/01.RES.16.3.294
CAS PubMed Web of Science® Google Scholar
10Johnson PC, Hanson KM. Capillary filtration in the small intestine of the dog. Circ Res. 1966; 19: 766-773.
10.1161/01.RES.19.4.766
CAS PubMed Web of Science® Google Scholar
11Staverman AJ. The theory of measurement of osmotic pressure. Recl. Trav. Chim Pays-Bas. 1951; 70: 344-352.
10.1002/recl.19510700409
CAS Web of Science® Google Scholar
12Michel CC. Fluid movements through capillary walls. In: EM Renkin, CC Michel eds. Handbook of Physiology. The Cardiovascular System, vol 4, Microcirculation, part 1. Bethesda, Maryland, USA: American Physiological Society; 1984: 375–409.
Google Scholar
13Michel CC, Phillips ME. Steady state fluid filtration at different capillary pressures in perfused frog mesenteric capillaries. J Physiol. 1987; 388: 421-435.
10.1113/jphysiol.1987.sp016622
CAS PubMed Web of Science® Google Scholar
14Adamson RH, Lenz JF, Zhang X, Adamson GN, Weinbaum S, Curry FE. Oncotic pressures opposing filtration across non-fenestrated rat microvessels. J Physiol. 2004; 557: 889-907.
10.1113/jphysiol.2003.058255
CAS PubMed Web of Science® Google Scholar
15Lunde PKM, Waaler BA. Transvascular fluid balance in the lung. J. Physiol. 1969; 205: 1-18.
10.1113/jphysiol.1969.sp008947
CAS PubMed Web of Science® Google Scholar
16Chinard FP, Enns T. Trans-capillary pulmonary exchange of water in the dog. Am J. Physiol. 1954; 178: 197-202.
10.1152/ajplegacy.1954.178.2.197
CAS PubMed Web of Science® Google Scholar
17Guyton AC, Taylor AE, Drake RE, Parker JC. Dynamics of sub-atmospheric pressure in the pulmonary interstitial fluid. Ciba Found Symp. 1976; 38: 77-96.
PubMed Google Scholar
18Drake RE, Smith JH, Gabel JC. Estimation of filtration coefficient in intact dog lungs. Am J Physiol. 1980; 238: H430-H438.
CAS PubMed Web of Science® Google Scholar
19Kajimura M, Wiig H, Reed RK, Michel CC. Interstitial fluid pressure surrounding rat mesenteric venules during changes in fluid filtration. Experimental Physiol. 2001; 86: 33-38.
10.1113/eph8602106
CAS PubMed Web of Science® Google Scholar
20Levick JR. Capillary filtration-absorption balance reconsidered in the light of extravascular factors. Exp Physiol. 1991; 76: 825-857.
10.1113/expphysiol.1991.sp003549
CAS PubMed Web of Science® Google Scholar
21Grotte G. Passage of dextran molecules across the blood-lymph barrier. Acta Chir Scand Suppl. 1956; 211: 1-84.
CAS PubMed Google Scholar
22Taylor AE, Granger DN. Exchange of macromolecules across the microcirculation. In: EM Renkin, CC Michel eds. Handbook of Physiology. The Cardiovascular System, vol 4, Microcirculation, part 1. Bethesda, Maryland, USA: American Physiological Society; 1984: 467–520.
Google Scholar
23Rippe B, Haraldsen B. Transport of macromolecules across microvascular walls: the two-pore theory. Physiol Rev. 1994; 74: 163-213.
10.1152/physrev.1994.74.1.163
CAS PubMed Web of Science® Google Scholar
24Michel CC, Curry FE. Microvascular permeability. Physiol Rev. 1999; 79: 703-761.
10.1152/physrev.1999.79.3.703
CAS PubMed Web of Science® Google Scholar
25Curry FE, Michel CC. A fiber matrix model of capillary permeability. Microvascular Res. 1980; 20: 96-99.
10.1016/0026-2862(80)90024-2
CAS PubMed Web of Science® Google Scholar
26Vink H, Duling BR. Identification of distinct luminal domains for macromolecules, erythrocytes and leukocytes within mammalian capillaries. Circulation Res. 1996; 79: 581-589.
10.1161/01.RES.79.3.581
CAS PubMed Web of Science® Google Scholar
27Michel CC. Starling: the formulation of his hypothesis of microvascular fluid exchange and its significance after 100 years. Exp Physiol. 1997; 82(1): 1-30.
10.1113/expphysiol.1997.sp004000
CAS PubMed Web of Science® Google Scholar
28Weinbaum S. Distinguished Lecture. Models to solve the mysteries of biomechanics at cellular level. A new view of fiber-matrix layers. Ann. Biomed Eng. 1998; 26: 627-643.
10.1114/1.134
CAS PubMed Web of Science® Google Scholar
29Hu X, Adamson RH, Lui B, Curry FE, Weinbaum S. Starling forces that oppose filtration after tissue oncotic pressure is increased. Am J Physiol. 2000; 279: H1724-H1736.
10.1152/ajpheart.2000.279.4.H1724
CAS PubMed Web of Science® Google Scholar
30Zhang X, Adamson RH, Curry FE, Weinbaum S. Transient regulation of transport by pericytes in venular microvessels via trapped microdomains. Proc Natl Acad Sci USA. 2008; 105: 1374-1379.
10.1073/pnas.0710986105
CAS PubMed Web of Science® Google Scholar
31Michel CC, Arkill KP, Curry FE. The revised Starling Principle and its relevance to post-operative fluid therapy.In: E Farag, A Kurz eds. Perioperative Fluid Management. Chap. 2 6330. Cham Switz: Springer Nature; 2016: 31–74.
Google Scholar

Citing Literature

Volume64, Issue8

September 2020

Pages 1032-1037

Understanding and extending the Starling principle

Abstract

Editorial Comment

1 INTRODUCTION

2 OVERVIEW

3 The Starling equation

4 TRANSIENT AND STEADY STATE FLUID EXCHANGE

4.1 Steady state fluid uptake into the microcirculation

5 ISF volumes and sub-compartments in fluid exchange

5.1 Levick's paradox of Starling pressures and lymph flow

5.2 Microvascular permeability pathways for water and macromolecules

6 GENERAL CONCLUSIONS

CONFLICT OF INTEREST

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Understanding and extending the Starling principle

Abstract

Editorial Comment

1 INTRODUCTION

2 OVERVIEW

3 The Starling equation

4 TRANSIENT AND STEADY STATE FLUID EXCHANGE

4.1 Steady state fluid uptake into the microcirculation

5 ISF volumes and sub-compartments in fluid exchange

5.1 Levick's paradox of Starling pressures and lymph flow

5.2 Microvascular permeability pathways for water and macromolecules

6 GENERAL CONCLUSIONS

CONFLICT OF INTEREST

REFERENCES

Citing Literature

Figures

References

Related

Information