The Impact of Technical Efficiency on Productivity Growth: Evidence from the Korean Pharmaceutical Industry*
This article benefitted from constructive discussion by participants at the Australian Conference of Economists, 2024 held at Adelaide University, July 10–12. Any remaining errors remain with the author. This work was supported by The Catholic University of Korea Research Fund Year 2023.
Abstract
This study examines the effects of technological capability, technological spillovers, and technological gap on firm-level productivity growth in the Korean pharmaceutical industry over the period 2000-2023. Utilizing the generalized true random effects (GTRE) stochastic frontier analysis, this article estimates technical efficiency to serve as a proxy for the technological gap. The results indicate that technological divergence is the primary driver of inter-firm productivity polarization, with limited evidence of technological spillovers from frontier firms to laggards. These findings support the low technological capability hypothesis over the Schumpeterian catch-up hypothesis, which posits convergence through innovation diffusion. The study further highlights that, even at the frontier, intra-firm technological diffusion can be sluggish under conditions of rapid technological change. It underscores the importance of intra-firm diffusion, characterized by distinct mechanisms from inter-firm diffusion, as a key determinant of productivity growth alongside inter-firm technological divergence.
I Introduction
Since the mid-2000s, many countries have experienced declining productivity growth despite rapid technological advancements, such as AI, the Internet of things, and robotics. This phenomenon is reminiscent of the earlier productivity paradox observed during the 1970s and the 1980s. A defining feature of this ‘new productivity paradox’ is the growing productivity polarization between frontier and laggard firms (Andrews et al., 2015, 2016). Several explanations have been proposed for this divergence, including winner-takes-all dynamics driven by information technology and globalization (Chevalier et al., 2012; Choi et al., 2018), misallocation of resources (Cette et al., 2018), and reduced technology diffusion due to rising market entry barriers and strategic patenting (Andrews et al., 2016; Akcigit & Ates, 2023). Yun and Cho (2022) further identify a ‘low technological capability trap’, in which initial differences in technological capability persist or widen over time due to economies of scale in technological learning and adoption.
This study investigates these issues by examining the impact of technological capability, technological spillovers and technological gap on firm-level productivity growth in the Korean pharmaceutical industry. The study adopts a stochastic frontier analysis (SFA) to estimate firm-level technical efficiency, which serves as a proxy for the technological gap. The study then tests convergence dynamics within a Schumpeterian framework, evaluating whether firms are catching up to or diverging from the frontier.
The findings suggest that technical divergence is the main driver of inter-firm productivity polarization, with limited technological spillovers from the frontier to laggard firms. However, unlike other OECD countries where frontier firms sustain strong innovation despite a decline in diffusion, the Korean pharmaceutical industry shows signs of stagnation even at the frontier. Under rapid technological change, intra-firm diffusion at the frontier is sluggish, while at the same time, the laggard firms fall further behind, reinforcing existing gaps due to economies of scale in technological learning and adoption.
The Korean pharmaceutical industry presents a compelling case for study. Despite major scientific advances, the sector seems to suffer from declining productivity (Cockburn, 2007; Laerman-Nguyen & Backfisch, 2021), and long-standing inter-firm disparities (Sakong & Kim, 2015). The growing role of AI – characterized by winner-takes-all effects – may also have exacerbated the gap between leading and lagging firms, with adoption costs favouring larger players and potentially slowing overall technology diffusion. So far, little attempt has been made to understand the interplay between firm performance and technological dynamics for the Korean pharmaceutical industry.
This article attempts to fill this gap, making both theoretical and empirical contributions. Theoretically, it links the technical efficiency literature with broader theories of technical change. This article also identifies intra-firm technology diffusion, with characteristics distinct from inter-firm technology diffusion to be an important factor affecting productivity growth, the impact of which is understudied. Empirically, it extends the application of the SFA by taking heteroscedasticity and endogeneity into account, reflecting recent methodological advancements. Most of all, the study makes an in-depth study of the Korean pharmaceutical industry, which is rapidly growing but for which academic analysis of technical change has been scarce.
The remainder of this article is structured as follows. Section II reviews the relevant prior literature. Section III first provides a brief description of the Korean pharmaceutical industry and then estimates relative technical efficiency as a measure of the technological gap among firms. Section (iv) explores the impact of technological capability, technological spillovers and technological gap on productivity growth. Section V concludes with a summary of the findings, limitations and suggestions for future research.
II Literature Review
(i) Theoretical Foundations: Technological Capability Trap or Catch-Up?
This article draws from two key strands of literature: the productivity convergence literature grounded in Schumpeterian endogenous growth theory, and the technological capability school within development economics. The Schumpeterian framework posits that cross-country productivity convergence occurs through technological diffusion or spillovers. According to this view, countries or firms further away from the frontier will grow faster because they have more opportunities to adopt existing, proven technologies at lower costs than incurred by frontier innovators (Nelson & Phelps, 1966; Grossman and Helpman, 1991; Aghion & Howitt, 1998; Howitt, 2000; Acemoglu et al., 2006).1 The larger the gap, the greater the potential for productivity gains through marginal improvements. Although countries that do not innovate fall behind, the growing gap eventually increases their opportunities to catch up to the growth rate of the leading country or firm as technology diffuses from the frontier. As countries or firms approach the frontier, returns to imitation diminish, and innovation becomes the main engine of growth. I refer to this mechanism as the catch-up hypothesis. The theory implies technological convergence, assuming sufficient spillovers, with a positive correlation between the technological gap and productivity growth: the wider the gap, the faster the expected growth.
The Schumpeterian endogenous growth theory provides microeconomic foundations for empirical productivity convergence studies. For example, Griffith et al. (2006) apply this framework in analysing UK firms from 1980 to 2000, showing that firms further from the frontier grew faster to catch up to the frontier, consistent with the catch-up hypothesis. More recent studies show declining technological convergence. Andrews et al. (2015), for instance, argue that falling productivity in OECD countries stems from reduced technology diffusion, as evidenced by widening technological gap between frontier and laggard firms. Choi et al. (2018) reach similar conclusions for the Korean manufacturing sector, attributing the weakening of convergence to globalization and digitalization. Other studies highlight institutional and structural barriers: Andrews et al. (2016) and Akcigit and Ates (2023) point to rising entry barriers, decreased market contestability, increasing concentration and the strategic use of patents as factors limiting the diffusion of frontier technologies.
Yun and Cho (2022) also report declining total factor productivity convergence among Korean manufacturing firms after 2010. They find that what convergence did occur was largely due to resource reallocation and other non-technical improvements rather than genuine technological catch up. The more dominant force was polarization due to a low technological capability trap.
This notion of a technological capability trap originates in the development literature on technological change. In the development literature, technological capability is defined as ‘the information and skill – technical, managerial, and institutional – that allow productive enterprises to utilize equipment and technology efficiently’ (Lall, 1992). Technological capability is hence viewed as something broader than just the ability to innovate, explicitly acknowledging the presence of technical inefficiency. Technology transfer is not automatic: firms must adapt and internalize external knowledge to use frontier technology with full efficiency. This is because technological knowledge is inherently complex and tacit, meaning it cannot be fully codified or transferred. Consequently, a firm's ability to absorb such knowledge varies, depending on their capability. The uncertain mastery of new technology is shaped by firm-specific technological efforts such as skill development, organizational learning and R&D investment. In this sense, technical efforts build technological capability, which in turn determines technical efficiency.
The firm-specific and path-dependent learning process echoes Stiglitz (1987)'s idea of ‘learning to learn’. Learning by doing is not enough, and a prior, deliberate learning stage to accumulate a critical level of technological capability is necessary before firms can begin to innovate. The learning process typically requires sustained investments in human capital and R&D. It is hence costly and may involve scale economies, implying that smaller firms can become trapped if they fail to reach a critical capability threshold. In the context of rapid technological change, increasing returns and complementarities can amplify initial differences in technological capabilities and generate long-term productivity divergence (Kwon, 2008; Kwon & Ha, 2008; Yun, 2021). From this perspective, the increasing inter-firm productivity polarization that is characteristic of the new productivity paradox is symptomatic of a structural problem where a low technological capability trap prevents firms below critical levels of technological capability to catch up and close the gap. Kwon (2008), for instance, finds that 33 per cent of 1,659 sample of manufacturing firms in Korea between 2002 and 2004, were likely stuck in a low technological capability trap.
This article empirically tests the Schumpeterian catch-up hypothesis against the low technological capability trap hypothesis using firm-level data. A key step in this analysis is accurately measuring the distance to the frontier. A novel feature of this article is the use of relative technical efficiency as a measure of the technological gap between frontier and laggard firms. Technical efficiency is estimated using SFA. The next section elaborates on this measurement approach and addresses key issues surrounding the SFA methodology.
(ii) Technical Efficiency as a Measure of Technological Gap: An SFA Approach
The SFA evaluates a firm's technical efficiency relative to the maximum potential output achieved by the most efficient producer – that is, the technological frontier. Since technical efficiency results from accumulated technological capability, it can serve as a measure of technological capability. A great advantage of this measure is that it only requires firm-level financial data, which is generally more readily available than micro data on technological aspects of a firm. Furthermore, as technical efficiency measures technological capability relative to the technological frontier, it can also be interpreted as an indicator of the technological gap between the frontier and the laggards. More precisely, consider a stochastic frontier production function given by where is technical inefficiency. Then, technical efficiency can be defined as =, where is the actual output, and is the maximum potential output.
The presence of technically inefficient firms can help explain both delayed productivity improvement and deepening polarization among firms in the face of rapid technological progress. Technical inefficiency hampers the diffusion of new technologies and slows down average industry productivity growth. Traditional productivity studies focused on growth accounting or total factor productivity estimation do not explicitly acknowledge the presence of technical inefficiency. Consequently, these approaches cannot effectively explain stagnant productivity growth if it stems primarily from firm-specific technical inefficiency.
Firstly, traditional approaches do not clearly differentiate between technological progress – disembodied technological change that expands the production function – from changes in technical efficiencies, which involve increased output through more efficient use of existing technology. Total technological change is then given by technological progress plus technical efficiency change, and if technical inefficiencies exist, firm-specific technological capability will determine the rate of technological change among individual firms, assuming new technology is accessible to all firms. However, traditional approaches are unable to accurately measure these dynamics. Second, measuring the technological change by total factor productivity conflates productivity gains due to technical efficiency with changes driven by non-technical factors such as returns to scale and allocative efficiencies. This further obscures the accurate measurement of technical efficiency.
Unlike traditional methods, the SFA provides a way to separate technical inefficiency from the residual term in production function estimation. The stochastic frontier approach also enables distinguishing between disembodied technical progress and firm-specific technical efficiency change. Moreover, recent developments in the stochastic frontier production framework provide ways to decompose technical inefficiency into persistent and transient components. This distinction is crucial, as the two types of inefficiency may have different implications for productivity. According to Kumbhakar et al. (2015), persistent technical inefficiency refers to that component of technical inefficiency which varies across firms but not across time – at least in the short term. It is linked to time-invariant firm-specific characteristics (e.g., ownership, organizational structure, location), or other unobserved characteristics that do not change unless some structural change beyond firm's control that affects its technical efficiency occurs (e.g., changes in government policy, change in technological paradigm).
In contrast, transient technical inefficiency refers to that component of firm-specific technical inefficiency that do vary over time, as firms accumulate technological knowledge or as they adjust to changes in the external technological environment. Small, non-innovative generic-oriented pharmaceutical firms characterized by low technological capability may struggle to improve technical efficiency, perpetuating persistent productivity polarization. Then, identifying and distinguishing between persistent and transient inefficiency is vital, as the appropriate managerial and policy response to the two types of technical inefficiencies may differ.
Since persistent productivity polarization is of particular concern in this study, it adopts a stochastic frontier approach that allows decomposing technical inefficiency into persistent and transient ones. The standard four-component stochastic frontier model that distinguishes the error term into random firm effects, persistent technical inefficiency, transient technical inefficiency and random error term, is originally developed by Colombi et al. (2014), Kumbhakar et al. (2014) and Tsionas and Kumbhakar (2014). This model is often referred to as the ‘generalized true random effects (GTRE)’ model in the literature. Kumbhakar et al. (2015) argue that the three-component models such as Green (2005)'s true random-effects model may underestimate technical inefficiency by confounding persistent technical inefficiency with heterogeneous firm effects. The original GTRE model however, overlooks endogeneity and heteroscedasticity issues, potentially leading to biased estimates. To address these limitations, Lien et al. (2018) propose a four-component model that accounts for both endogeneity and heteroscedasticity. This article closely follows their methodology to separately estimate persistent and transient technical inefficiency.
A contemporaneous article by Belotti and Ilardi (2018) proposes two alternative methods for estimating technical inefficiency: the marginal maximum simulated likelihood estimation (MMSLE) and the pairwise difference estimator (PDE). These methods aim to improve upon consistency in Green (2005)'s TRE model, and to allow for persistence of inefficiency when it is due to first-order autoregressive process. For robustness, this article conducts the MMSL and TRE estimations to compare their results with those from the GTRE approach.2
The fundamental difference between the approaches of Lien et al. (2018) and Belotti and Ilardi (2018) is that the latter does not disentangle persistent technical inefficiency from time-invariant unobserved heterogeneity, which is one of the main objectives of this article. As Belotti and Ilardi (2018) note, there is a ‘philosophical debate’ in the stochastic frontier literature about whether persistent inefficiency should be separated from firm effects, and this debate remains unresolved. As this article focuses on the application of SFA rather than its methodological foundations, it does not engage in this debate. The more pressing concern here is that Belotti and Ilardi (2018) do not address endogeneity, which is a critical issue in productivity analysis. For these reasons, this article adopts the GTRE model of Lien et al. (2018) as its baseline specification in Section III.
III Estimation of Technical Efficiency
(i) Background: The Korean Pharmaceutical Industry
The Korean pharmaceutical market grew at an average annual rate of 7.1 per cent between 2017 and 2021, reaching USD 23.6 billion in 2021. It is the 12th largest pharmaceutical market globally, accounting for 1.69 per cent of the global market. As of 2021, the pharmaceutical industry constitutes 1.2 per cent of Korea's total GDP and 4.8 per cent of its manufacturing GDP as of 2021 (Jeung et al., 2023:2). Final drug product, as opposed to active pharmaceutical ingredient, takes up 88 per cent of total pharmaceutical production in terms of value. The industry is highly segmented: it consists of an intensely competitive generics sector, composed largely of SMEs, and a more innovative sector, led by a few large pharmaceutical firms. However, in recent years, a growing number of smaller but R&D-intensive biotechnology firms – some focused on AI-drug development – have emerged. The top 10 firms contribute over 30 per cent of total production as of 2021 (see Table 1). Polarization is evident even among the R&D focused biotech firms. According to media reports, top 10 listed biotechs are valued at five times more than the bottom 10, and attract the majority of the new investment flows (Money Today, 2024).
| 2017 | 2018 | 2019 | 2020 | 2021 | |
|---|---|---|---|---|---|
| Production Value: Final Product | 175,510 | 185,438 | 198,425 | 210,236 | 224,451 |
| Active Ingredient | 28,070 | 25,616 | 24,706 | 35,428 | 30,455 |
| Total | 203,590 | 211,054 | 223,132 | 245,662 | 254,906 |
| Top-10 firm share | 29.5 | 29.5 | 28.5 | 30.3 | 30.2 |
| Number of firms | 577 | 531 | 558 | 617 | 609 |
| Number of products | 26,293 | 26,239 | 28,363 | 28,197 | 27,395 |
- Note: Unit: 100 million won, %.
The pharmaceutical industry is heavily R&D-intensive, and industry literature often highlights declining R&D productivity, defined as the ratio of innovation output (new drugs approved) to innovation input (R&D expenditure), as an indication of a productivity crisis in the industry since the mid-1990s. Although this is a crude measure of innovative activity, changes over time can offer insights into how efficiently R&D expenditure is deployed in the industry. Figure 1 compares R&D productivity trends in the US and Korea for the more recent period. For the US, productivity is measured as the number of new molecular entities approved per billion dollars spent. For Korea, it is measured as the number of new drugs introduced to the market per million dollars. Based on a three-year moving average, R&D productivity in Korea declined from 2005 to the early 2010s but has since rebounded, showing a steady upward trend for a whole decade. In the United States, often considered to be the world frontier, it appears to have overcome the R&D crisis by the early 2010s, with productivity generally increasing between 2008 and 2021. These trends suggest that the outlook for pharmaceutical R&D productivity is not as bleak as earlier literature has depicted.
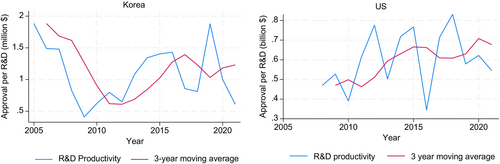
Source: Drug approvals data from Ministry of Food and Drug Safety Drug Information Portal (https://nedrug.mfds.go.kr/pbp/CCBEF04) for Korea and Centre for Drug Evaluation and Research (https://www.fda.gov/drugs/drug-approvals-and-databases) for the US. R&D expenses data are from the OECD
.Nevertheless, the global frontier continues to advance rapidly, leaving the Korean pharmaceutical industry struggling to keep pace. Moreover, as noted above, productivity polarization within the domestic industry remains unresolved. Two prior SFA provide markedly different estimates of overall technical efficiency (OTE) in the Korean pharmaceutical industry. Sakong and Kim (2015), based on Battese and Coelli (1995)'s methodology, report an efficiency level of 85 per cent for the 2006–2012 period, while Yun (2023), employing the four-component methodology of Kumbhakar et al. (2014) reports an overall efficiency level of 42 per cent for the 2000–2019 period. However, neither study examines technological divergence among pharmaceutical firms or its impact on productivity.
A notable advancement in the pharmaceutical industry is the application of AI to drug discovery, which is expected to significantly reduce development time and costs while expanding the market through introduction of novel therapies (Stanley, 2022; Rodriguez et al., 2023). In Korea, AI-driven drug discovery began with Syntekabio in 2009, lagging roughly 20 years behind the global frontier. Since 2015, the number of Korean AI-drug startups has grown, peaking in 2018, with 30–52 firms active and 71 molecules under development by 2023. From the perspective of this article, a key concern regarding AI technology is its ‘winner-takes-all’ dynamic, which may exacerbate firm-level polarization. However, current patterns of competition and collaboration across differentiated therapeutic areas suggest the presence of mitigating forces. While this article does not directly measure AI's impact on technical efficiency due to the lack of systematic data, any effects may be partially captured in the estimates of technological progress and technical efficiency. The impact and implications of the technological paradigm shift remain uncertain for now and warrant further investigation.
(ii) Methodology
Finally, using the Jondrow et al. (1982) procedure, inefficiencies and can be obtained from estimating Equations (9) and (10), and from these estimations, persistent and transient technical efficiencies defined as and can be obtained.
(iii) Data and Variables
The estimation is undertaken on an unbalanced panel of 237 firms for the period 2000–2023, yielding a total observation of 2,844 firm-years. A novel characteristic of this sample is the inclusion of R&D-intensive pharmaceutical startups, including those applying AI to drug development. The conventional categorization of the pharmaceutical industry excludes these firms. They account for 7.55 per cent of the total number of firms in the sample in 2015, increasing to 16.98 per cent by 2023. Table 2 provides summary statistics for the variables used in the estimations. The output variable is value added (VA), and the input variables are labour (L) and capital (K). Labour is measured by the number of full-time employees. Although hours worked would provide a more accurate measure of the contribution of labour, these data are not available at the firm level. Hours worked are only reported at the industry level. Since this is a single industry study, multiplying the industry average and the number of employees would merely be a scaling exercise. OECD (2001) notes that hours worked are not free of measurement issues, and full-time employees can provide a reasonable alternative.
| Variables | Label | No. of Obs. | Mean | SD | Min. | Max. |
|---|---|---|---|---|---|---|
| lny (output) | Value added depreciated by producer price index | 2,150 | 11.982 | 1.456 | 4.234 | 16.547 |
| lnx1 (labour) | Number of full-time employees | 2,768 | 5.230 | 1.094 | 2.303 | 8.419 |
| lnx2 (capital) | Total fixed asset depreciated by capital price index | 2,834 | 17.000 | 1.450 | 10.498 | 22.833 |
| t (year) | Time trend | 2,844 | 9.48 | 6.51 | 1 | 24 |
| Determinants of technical inefficiency | ||||||
| z1 = sales | Sales depreciated by producer price index | 2,844 | 0.68 | 0.47 | 0 | 1 |
| z2 = TCI | Technological Capability Index: (Technology-related expenses)/(SGA&E) | 2,788 | 0.20 | 0.21 | 0 | 0.95 |
Capital is measured by total fixed asset. Real data are used, with VA deflated by producer price index for pharmaceuticals and total fixed asset deflated by capital price index for chemicals, using 2020 as the base year. The capital price index is available only up to year 2021, and predicted values from regressing capital price index on year are used for the years 2022 and 2023. The financial data are acquired from the Korea Listed Companies Association, while producer and capital price index are acquired from the Bank of Korea. Input and output variables are normalized by the number of employees to yield and in Equation (2). Therefore, in this article, Equation (2) in fact estimates labour productivity (value added per employee) as a function of capital per labour.
Economies of scale and technological capability (more accurately, technological efforts) are introduced as determinants of technical inefficiency. These variables are chosen based on prior literature which finds that the larger and the more innovative firms tend to be more technically efficient (e.g., Sakong & Kim, 2015), as well as the discussion in Section II on the process of technology diffusion. The technological capability literature argues that technological efforts build technological capability, which in turn determines technical efficiency. It also emphasizes that if economies of scale exist in the learning process, small firms may fall into a low technological capability trap. In contrast, the proponents of the Schumpeterian catch-up hypothesis argue that it is not the firm size or the absolute level of technological capability per se, but rather the differences in capability levels that determine the rate of catch up through imitation.
Economies of scale is measured by sales deflated by the producer price index for the pharmaceutical industry. In 2000, 77.8 per cent of the sample firms were SMEs, but this falls to 61.79 per cent in 2023. Overall, the proportion of SMEs in the sample remains at around the 60–80 per cent range throughout the 24 years under study.5 Technological capability is measured by a unique index constructed for this study. While technological capability is typically measured by micro-level data such as time or expenditure spent on training or R&D personnel embodying tacit information and skills, such data are generally unavailable from financial statements. To address this limitation, a Technological Capability Index (TCI) is constructed using financial data to approximate the broad concept of technological capability as accurately as possible. It is defined as the ratio of technology-related expenses and gains – available in financial statements and reflective of a firm's technological effort – to total expenses. Technological effort is measured by the sum of the following components: training cost, IT expenses, depreciation related to intangible assets, R&D expenses, technology development reserves, royalties paid and received on patent rights, and amortization on development costs. This procedure does not follow any specific accounting standard but is based on the assumption that greater technological efforts translate into greater technological capability. Training costs and IT expenses capture human-embodied tacit knowledge and the diffusion of IT technology. Royalties paid reflect the extent of technical networking with outside expertise, while royalties received reflect the extent of technical output. Amortization and depreciation related to intangible assets account for the technical groundwork laid in previous periods, reflecting the cumulative nature of technological learning. Total expenses are measured by sales and general administrative expenses (SGA&E). The resulting index ranges from 0 to 1. Since both sales and TCI vary by time, both variables are included as determinants of transient technical inefficiency.
Figure 2 shows movements in the variables over time by top, middle, and bottom quartiles. It is notable that there is a substantial gap between the bottom quartile and the others. For the top quartile, financial indicators, such as VA, total fixed assets, sales, number of employees, and VA per employee generally show an upward trend over the 24-year period. In contrast, the middle two quartiles exhibit little change over time, while the bottom quartile suffers greater volatility and a general downward trend. In particular, the bottom quartile experiences a secular decline in sales throughout the entire period, clearly indicating rising market concentration and polarization within the industry. Unlike the financial indicators, TCI reveals a different pattern. The gap in TCI is significant between the top quartile and the rest, with the bottom two quartiles showing little change over time. The top quartile displays large fluctuations in TCI between 2000 and 2015, followed by a consistently increasing trend thereafter. Conversely, the bottom quartile shows an overall decline in TCI, suggesting a widening technological gap, although the rate of decline slows after the mid-2010s.
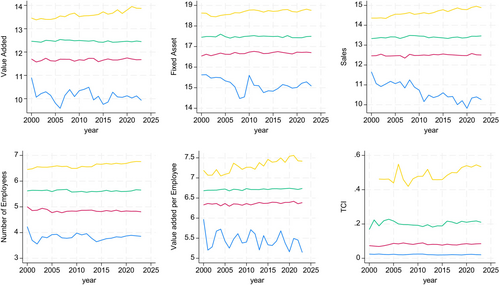
Note: Movements in variables are plotted for quartiles. Log scale used for financial data. TCI, Technological Capability Index [Correction added on 14 July 2025, after first online publication: the first sentence in ‘Note’ has been added]
.(iv) Empirical Analysis
| Variables | Fixed effects | Random effects |
|---|---|---|
| (capital per worker) | 0.103*** (0.033) | 0.120*** (0.030) |
| t (time trend) | 0.017*** (0.003) | 0.015*** (0.003) |
| Constant | 5.092*** (0.380) | 4.926*** (0.355) |
| Statistics | R2 (within) = 0.0363 F(2,1945) = 36.64*** N = 2,132 |
R2 (overall) = 0.0239 Wald Chi2 (3) = 73.55*** N = 2,132 |
- Notes: *** Significant at 1 per cent. Figures in () are standard errors. Chi-square statistic for Hausman test = 7.43, which is significant at 5 per cent, leading to the rejection of the null that the random-effects model is more appropriate.
| Variables | Random effects |
|---|---|
| (capital per worker) | 0.108*** (0.028) |
| t (time trend) | 0.0003 (0.002) |
| Constant | 0.049 (0.048) |
| Statistics | Log likelihood = −2246.774 LR Chi2 (2) = 15.16*** N = 2,088 |
- Notes: *** significant at 1 per cent. Figures in () are standard errors.
The results from these estimations are reported in Table 5. Model 1 estimates derived from fitting the homoscedastic four-component model without allowing for endogeneity. All the coefficients are significant, with the variance of technical inefficiency and firm effects bearing negative signs. Predicted persistent technical efficiency (PTE) based on this estimation gives 61.7 per cent, similar to 66.4 per cent reported in Yun (2023). In Model 2, , estimated from the production function allowing for endogeneity, is used to predict PTE. Both the constant term in the frontier and variance of persistent technical inefficiency are shown to be negative but insignificant, while that of the firm effect was shown to be negative and significant. A likelihood ratio test does not reject the null hypothesis of = 0.8 That is, once endogeneity is taken into account, persistent technical inefficiency becomes very small and insignificant, if it is present at all. Indeed, the average PTE computed based on estimated persistent technical inefficiency was 99.67 per cent, with a standard deviation of 1.26 × 10−5, indicating that almost all the firms are near the frontier on average.
| Model 1 (y = ) | Model 2 (y = ) | Model 3 (y = ) | Model 4 (y = ) | |||
|---|---|---|---|---|---|---|
| Frontier | ||||||
| Constant | 0.510*** (0.036) | −0.041 (0.025) | 0.576*** (0.019) | 0.535*** (0.020) | ||
| −0.888*** (0.137) | −10.964 (85.097) | −0.572*** (0.062) | −1.750*** (0.055) | |||
| −1.399*** (0.079) | −1.395*** (0.031) | −1.735*** (0.056) | Effects on the variance | |||
| Statistics | λ = 1.291 Log likelihood = −2028.499 Wald Chi2 (1) = 196.16 Prob > Chi2 = 0.000 N = 2,132 |
λ = 0.008 Log likelihood = −1506.015 Wald Chi2 (1) = 0.08 Prob > Chi2 = 0.771 N = 2,088 |
λ =1.789 Log likelihood = −1,959.014 Wald Chi2 (1) = 887.11 Prob > Chi2 = 0.000 N = 2,132 |
Sales | −1.21 × 10−7*** (2.51 × 10−8) | |
| TCI | 1.086*** (0.267) | |||||
| Cons | −1.750*** (0.055) | |||||
Log likelihood = −1,845.825 Wald Chi2 (1) = 729.01 Prob > Chi2 = 0.000 N = 2,088 |
||||||
- Notes: *** significant at 1 per cent. Figures in () are standard errors.
Most of the variation in technical inefficiency among firms seems to come from firm-specific, time-variant transient technical inefficiency. In Model 3, , estimated from the production function not allowing for endogeneity under the homoscedasticity assumption, is used to predict transient technical inefficiency. The frontier term coefficient is significant. The coefficients for the variances are also both negative and statistically significant. The predicted transient technical efficiency (TTE) based on this estimation is 59.1 per cent, which is slightly lower than 62.2 per cent reported by Yun (2023), which also does not account for endogeneity or heteroscedasticity.
In Model 4, , estimated from the production function free of endogeneity problems under the heteroscedastic assumption, is used to predict transient technical inefficiency. Two determinants of technical inefficiency, sales, and technological capability are introduced. Economies of scale represented by sales have a decreasing effect on the variance of transient technical inefficiency as expected, but the effect is quite small. However, the effect of technological capability has an unexpected increasing effect on the variance of transient technical inefficiency. It is possible that when adoption of new technology is massive or rapid, firms find it difficult to absorb the new technology internally as technological learning becomes more complex and takes time. Structural shifts such as organizational changes and corporate governance over technical activities to support the technological changes need to be made. The average TTE predicted based on this estimation is 61.3 per cent, which is slightly higher than the value given by Model 3, and comparable to that of Yun (2023).
For robustness and comparison, two different three-component models are estimated additionally. The results from estimating the Belotti and Ilardi (2018)'s MMSLE model and Green (2005)'s TRE model are presented in Table 6. In all models, heteroscedasticity is assumed, using sales and TCI as determinants of technical inefficiency. When the MMSLE is performed on the production function allowing for endogeneity (Model 5), the frontier term is not significant, though positive. Time trend, representing technical progress is 1.2 per cent per year, somewhat lower than the value estimated via Equation (11). However, the effects of sales and technological capability on transient inefficiency shows the same patterns as the GTRE model. Results for Model 6, where MMSLE is performed on the production function not allowing for endogeneity seems to be more reliable. All frontier variables are positive and significant at 1 per cent. The effects of sales and technological capability again show much the same pattern as the GTRE model. The TRE model results are generally similar to that of the MMSLE models.
| Variables | Model 5 (MMSLE) | Model 6 (MMSLE) | Model 7 (TRE) | Model 8(TRE) |
|---|---|---|---|---|
| (No. of employees) | 0.541*** (0.040) | 0.558*** (0.0333) | ||
| (Total fixed asset) | 0.077*** (0.026) | 0.057** (0.023) | ||
| (Total fixed asset/employee) | 0.038 (0.028) | 0.023 (0.025) | ||
| t (Time trend) | 0.012***(0.002) | 0.017***(0.002) | 0.011***(0.002) | 0.016***(0.002) |
| Constant | 6.872*** (0.293) | |||
| Effects on the variance | ||||
| Sales | −0.423*** (0.021) | −0.482*** (0.023) | −1.14 × 10−6*** (1.35 × 10−7) | −1.65 × 10−6*** (1.12 × 10−7) |
| TCI | 0.145*** (0.021) | 0.122*** (0.019) | 2.146*** (0.288) | 2.473*** (0.292) |
| Constant | 5.595 *** (0.264) | 6.309*** (0.285) | 0.191** (0.083) | 0.492 (0.079) |
| Statistics | Log simulated likelihood = −1804.776 No. of Halton Sequences = 62,190 N = 2,073 |
Log simulated likelihood = −1,719.412 No. of Halton sequences = 62,190 N = 2,073 |
Log simulated likelihood = −2014.468 Wald Chi2 (2) = 39.57 Prob > Chi2 = 0.000 N = 2,132 |
Log simulated likelihood = −1874.685 Wald Chi2 (3) = 1103.54 Prob > Chi2 = 0.000 N = 2,132 |
- Notes: *** significant at 1 per cent, ** significant at 5 per cent. Figures in () are standard errors.
Table 7 compares the OTE values predicted by different models. The homoscedastic GTRE model that does not consider endogeneity nor heteroscedasticity yields the lowest OTE (Column 1: 0.365). This is the Kumbhakar et al. (2014) model specification. Column 2 shows the OTE estimated from the GTRE model under the heteroscedastic assumption, but not accounting for endogeneity. There is little change in the OTE from introducing heteroscedasticity. Column 3 shows the OTE estimated by the GTRE model under homoscedastic assumption while accounting for endogeneity. The OTE increases markedly due to the increase in the PTE. This value is similar to the OTE estimated from the GTRE model where both endogeneity and heteroscedasticity are accounted for (Column 4: 61.1). This is the Lien et al. (2018) model specification. Apparently, accounting for endogeneity makes a greater difference than introducing heterogeneity. The OTE estimated from this model yields a value comparable to estimates from the MMSLE and TRE models that incorporate heteroscedasticity, whether or not endogeneity is considered (Columns 5–8: 60–60.8 per cent). In other words, accounting for endogeneity appears to matter within the GTRE model, but not within the three-components models, whose results align closely with the GTRE model specification that eliminates endogeneity problems. The remainder of the discussion is based on the GTRE estimates from the Lien et al. (2018) model.
| 1 | 2 | 3† | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| Model Specification | GTRE: homoscedastic, assume no endogeneity | GTRE heteroscedastic, assume no endogeneity | GTRE: homoscedastic, allowing endogeneity | GTRE: Heteroscedastic, allowing endogeneity | MMSLE: heteroscedastic, allowing endogeneity | MMSLE: heteroscedastic, assume no endogeneity | TRE: heteroscedastic, allowing endogeneity | TRE: heteroscedastic, assume no endogeneity |
| PTE | 0.617 | 0.617 | 0.997 | 0.997 | – | – | – | – |
| TTE | 0.591 | 0.623 | 0.591 | 0.613 | – | – | – | – |
| OTE | 0.365 | 0.384 | 0.589 | 0.611 | 0.601 | 0.600 | 0.607 | 0.608 |
- Note: Efficiency are sample averages. OTE is mean of [].
- † Results for this estimation are not reported in the interest of space. Results are available upon request.
A more detailed examination of estimated technical efficiency leads to some interesting observations. The average OTE of around 60 per cent, which is not very high, shows little improvement over time. Figure 3 (the left panel) shows that OTE falls between 2000 and 2015, with a sharp decline in the mid-2000s, and then rises thereafter. This amounts to a negative average annual growth in technical efficiency of −0.24 per cent throughout the entire period under study, though it turns positive, recording 0.11 per cent for the sub-period of 2011–2023.9 The MMSLE estimate of technical efficiency, though generally lower, exhibits a similar pattern of change, albeit with greater volatility. The right panel in Figure 3 shows OTE by quartiles of firms. There is a significant gap between the three top quartiles and the bottom quartile. The average OTE for the top quartile group is 75.6 per cent. The performance over time even at the top is not very impressive, with a negative annual average growth rate for the period as a whole, though turning positive after 2010.10 The middle two quartiles seem to show little change over time. The bottom quartile experiences the greatest volatility and shows an overall decline, with an annual average growth rate of −0.70 per cent. The average OTE for this group never rises beyond the 48 per cent level for the entire 24-year period, suggestive of a low technological capability trap. All of this indicates significant technical divergence between the frontier and the laggard firms, despite the unimpressive performance by the frontier group.
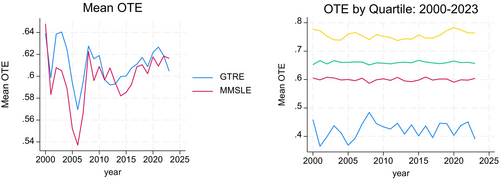
Table 8 compares firm size and technical capability of top 10 per cent OTE firms with the bottom 10 per cent. As expected, the top 10 per cent firms are significantly larger: they generate five times more VA, hold nearly three times more fixed asset, and invest almost twice as much in absolute R&D terms. Their sales volumes are double those of the bottom 10 per cent, and their OTE levels are roughly three times higher. Surprisingly, however, their R&D intensity is only 88.5 per cent of that of the bottom 10 per cent, and their average TCI value is also lower. This seems to suggest that firm size and technical efficiency do not always correspond to higher technological capability.
| Indicators (average values) | Top decile (A) | Bottom decile (B) | A/B |
|---|---|---|---|
| Value Added (million won) | 785,219 | 157,043 | 5.000 |
| Fixed Asset (1,000 won) | 134,000,000 | 53,800,000 | 2.491 |
| Sales (1,000 won) | 1,717,595 | 765,477 | 2.244 |
| R&D (1,000 won) | 9,250,279 | 5,463,993 | 1.693 |
| R&D Intensity (R&D/Sales) | 0.084 | 0.095 | 0.885 |
| TCI | 0.194 | 0.199 | 0.979 |
| OTE | 0.814 | 0.293 | 2.799 |
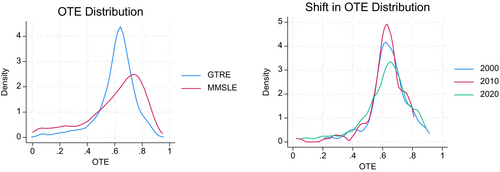
Figure 4 shows the overall distribution of OTE (the left panel) and its change over time (the right panel). There is a thick left-hand tail, showing a concentration of firms below OTE of around 40 per cent, indicating the polarization between a substantial group of laggards and the frontier. At the same time, the shift in the distribution over time shows increasing dispersion, indicating widening polarization between the frontier and the laggards. Dispersion seems to have decreased from 2000 to 2010, but then significantly increases from 2010 to 2020, with the tails being more spread out, and the average falling.
- Taking endogeneity into account seems to make a difference in estimating technical efficiency. In this particular case, once endogeneity is taken into account, persistent technical inefficiency becomes insignificant, resulting in a very high average PTE. The heteroscedastic GTRE model allowing for endogeneity, predicts similar levels of OTE as the heteroscedastic three-component models, whether or not endogeneity is taken into account.
- Korean pharmaceutical firms have a rather low overall level of technical efficiency of around 60 per cent. Technical efficiency falls from 2000 to 2010, and rises thereafter until 2022. For the period under study as a whole, however, it shows a negative annual average growth. Even the improvement of technical efficiency by the top 10 per cent OTE firms is not very impressive. This might explain the generally high level of PTE. The frontier may not be so different from the laggards with respect to PTE. The variation in technical efficiency originates mostly from TTE, leading to the bottom 10 per cent being stuck at an overall efficiency level below 48 per cent throughout the entire study period. Dispersion in technical efficiency increases over time, suggesting that there is a long-term technological divergence among firms, especially due to the decline of the laggards rather than rapid advance of the frontier.
- Economies of scale measured by sales seems to reduce the variance of technical inefficiency but the effect is small. Technological capability measured by TCI seems to increase the variance of technical inefficiency. It is possible that firms that are actively involved in technological efforts have a hard time catching up with itself, unable to rapidly diffuse new technology internally. Indeed, firms in the bottom decile in terms of technical efficiency have smaller firm size but higher TCI levels.
While it seems that inter-firm polarization in technical efficiency has increased, R&D intensity and other technological efforts seem to be negatively correlated with technical efficiency. How does this interaction affect a firm's productivity? Is there likely to be a low technological capability trap or catch-up? The next section delves into these questions in more detail.
IV The Impact of Technical Efficiency on Productivity: Trap or Catch-Up?
(i) Methodology
In this section, a reduced form empirical model is set up to test the Schumpeterian catch-up hypothesis against the low technological capability trap hypothesis. The former posits that the greater the technological gap between the frontier and the laggards, the faster the laggards will grow and catch up. This is because imitation cost is lower than the cost of innovation. According to this view, productivity convergence among firms is expected in the absence of barriers to technology diffusion and if imitation costs are not prohibitive. In contrast, the low technological capability trap hypothesis argues that economies of scale in the diffusion process make technology adoption more advantageous for larger firms, thereby exacerbating productivity polarization. Two types of scale economies may operate. First, implementing innovation requires complementary investments – such as building new facilities or installing advanced equipment – which are more accessible to larger firms with greater sales revenue and deeper pockets. Second, the tacit nature of technology means that firms need a minimum level of technological capability to absorb new knowledge and skills which must be built through sustained technological efforts – such as worker training, information seeking, external collaboration, and supportive internal organizational changes. These efforts are costly, and firms that fall below a certain threshold may be unable to catch up, ultimately falling into a low technological capability trap, deepening the gap between them and the frontier.
Technological capability is measured by the Technological Capability Index constructed in Section III. The technological capability of the frontier firm is measured by the mean value of the TCI for the top 10 per cent of the firms for each year. Estimation is performed on the sample excluding the top 10 per cent TCI firms, so that a positive effect of the frontier firm's technological capability on productivity growth is a measure of technological spillovers from the top 10 per cent TCI firms to the rest. The technological gap is measured by the OTE estimated in Section III, and it implies that the lower the technical efficiency, the greater the distance to the frontier. As an alternative measure of technological gap, the MMSLE estimate of technical efficiency, the difference between the TCI of a firm and that of the frontier group, and the change in technical efficiency are used.
Table 9 provides a summary of the variables and predictions of their effects on labour productivity. The trap hypothesis predicts that firms that are initially more technologically capable will grow faster so that , while the reverse is predicted under the catch-up hypothesis. High technological spillovers facilitate technology diffusion and translate into productivity catch-up so that under the catch-up hypothesis, while the trap hypothesis, which assumes the learning process to be costly, predicts a smaller or negative . The catch-up hypothesis predicts that firms that are further from the frontier will grow faster, so it is expected that lower the OTE, the faster the growth (). The reverse would be true under the trap hypothesis which predicts that large technological gap would inhibit productivity growth of the laggards. A positive coefficient for sales indicates that there are economies of scale, giving larger firms advantage in terms of productivity growth.
| Variables | Explanation | Prediction |
|---|---|---|
| Initial level of technological capability measured by TCI at the first year for each firm's own time series | Catch up hypothesis: Trap hypothesis: |
|
Change in the technological capability of the frontier firm: First differenced mean of frontier group's TCI Frontier group = Top decile TCI firms |
Catch up hypothesis: Trap hypothesis: smaller or negative |
|
Technological gap measured by GTRE estimate of technical efficiency, OTE Alternative variables for ; (1) MMSLE estimate of technical efficiency; (2) differences in TCI; (3) change in OTE |
Trap hypothesis: Catch up hypothesis: |
|
| Sales depreciated by producer price index at the current level | If economies of scale is present: > 0 |
(ii) Empirical Analysis
Estimation results are presented in Table 10. The random effects estimation in Model 1 performed on the sample excluding the frontier firms shows that initial technological capability level has a significant positive effect on labour productivity, supporting the trap hypothesis of divergence. The technological spillover effect is positive but not statistically significant, further reinforcing the trap hypothesis. Technical efficiency is also positive and significant, implying that firms closer to the frontier experience faster productivity growth and therefore again supporting the trap hypothesis of divergence. Sales have a significant positive effect as expected, but is not statistically significant. Model 2, a fixed-effects estimation using 1 year lagged TCI values in place of initial TCI level, yields similar results, except that the lagged TCI variable turns insignificant though still remaining positive, while the scale variable becomes significant.
| Y = | Model 1 (RE) | Model 2† (FE) | Model 3 (Full sample) | Alternative specification for technological gap | ||
|---|---|---|---|---|---|---|
| Model 4 (MMSLE) | Model 5 (TCI gap) | Model 6 () | ||||
| 0.189** (0.096) | 0.245 (0.220) | 0.213** (0.111) | 0.901*** (0.219) | 0.081 (0.185) | 0.039 (0.038) | |
| 0.370 (0.484) | 0.320 (0.397) | 0.277 (0.482) | 0.429 (0.500) | 0.661 (0.634) | 0.115 (0.137) | |
| 2.730*** (0.277) | 2.759*** (0.108) | 2.774*** (0.275) | 2.749*** (0.236) | 0.029 (0.145) | 4.414*** (0.124) | |
| 0.003 (0.021) | 0.061** (0.025) | −0.001 (0.029) | −0.298*** (0.033) | 0.036** (0.018) | −0.0002 (0.006) | |
| Constant | −1.784** (0.250) | −2.596*** (0.347) | −1.746*** (0.355) | 2.183*** (0.340) | −0.600** (0.271) | 0.010 (0.085) |
| Statistic | Overall R2 = 0.293 Wald Chi2 (4) = 135.34 P-value = 0.000 N = 1,710 |
Within R2 = 0.299 F(5, 1,567) = 167.51 P-value = 0.000 N = 1,726 |
Overall R2 = 0.299 Wald Chi2 (4) = 136.66 P-value = 0.000 N = 1,745 |
Overall R2 = 0.240 Wald Chi2 (4) = 138.15 P-value = 0.000 N = 1,712 |
Overall R2 = 0.003 Wald Chi2 (4) = 6.43 P-value = 0.169 N = 1,752 |
Overall R2 = 0.906 Wald Chi2 (4) = 11449.74 P-value = 0.000 N = 1,700 |
- Notes: *** significant at 1 per cent, ** significant at 5 per cent. Figures in () are standard errors.
- † One-year lagged TCI is used for initial TCI values in Model 2.
In Model 3, the random-effects model is performed on the full sample. There is no qualitative difference from the results of Model 1. In Models 4–6, alternative variables are used in place of the GTRE estimate of technical efficiency to measure the technological gap. In Model 4, when the MMSLE estimate of technical efficiency is used, the results are similar to those of Model 1. However, the scale variable turns negative and significant. When the TCI gap is used as the technological gap in Model 5, none of the variables are statistically significant except for sales, which is now shown to have a positive effect. Although initial technological capability and technological gap variables are not significant, their coefficients are still positive, supporting the low technological capability trap hypothesis. Model 6 uses the change in technical efficiency to measure the technological gap, applying a difference-in-difference strategy. This makes initial technological capability insignificant, although it remains positive. The change in technical efficiency is positive and significant, indicating that an increase in technical efficiency (which means a decrease in the technological gap) has a significant positive effect on productivity growth. Sales are shown to be positive but insignificant. Technological spillovers are consistently positive but insignificant across all models.
Overall, these results support the trap hypothesis of divergence over the catch-up hypothesis, and remain robust across different specifications. Firms with higher initial levels of technological capability tend to grow faster, though its effect is not always significant. Larger technological gap levels, and increase in the technological gap both inhibit productivity growth. This is the most robust result that supports the trap hypothesis. The spillover effect does not appear to be significant enough to enable lagging firms to catch up. These findings suggest that the observed productivity polarization has its roots in technological divergence between firms. Technological gap translates into productivity divergence, with labour productivity of top quartile firms growing at 0.13 per cent while the bottom quartile firms de-growing at −0.39 per cent. Results for scale economies is not quite as robust. One possible explanation for this is that, while economies of scale may positively affect productivity growth, their effect is partly reflected through improvements in technical efficiency, already captured by the technological gap variable. It could also be the presence of research-oriented startups with high levels of technological capability but as yet low sales revenue that is obscuring the scale effect. However, excluding them from the regressions do not make any qualitative changes to the results.11
V Conclusion
This study estimates the technical efficiency of Korean pharmaceutical firms for the period 2000–2023 employing the GTRE stochastic frontier model, accounting for both input endogeneity and heteroscedasticity. Further, using the estimated technical efficiency as a measure of the technological gap, it analyses the impact of technological capability, technological spillovers, and the technological gap to explain the deepening inter-firm productivity polarization in the context of rapid technological progress. The findings support the low technological capability trap hypothesis of inter-firm divergence over the catch-up hypothesis of technological convergence. At the heart of this result lies the insignificance of technological spillovers – indicating slow technology diffusion from frontier to the rest. This suggests that productivity polarization has its roots in technological divergence among firms.
The analysis reveals that the nature of polarization among Korean pharmaceutical firms differs from that experienced in other OECD countries, where technological advancement and productivity growth in frontier firms are robust despite a decline in technology diffusion. The average technical efficiency estimated for the Korean pharmaceutical firms is quite low at around 60 per cent, and the improvement in technical efficiency of even frontier firms over time is sluggish. Technological efforts seem to have a surprisingly negative effect on technical efficiency, which in turn, inhibits productivity growth. This implies that massive or rapid technological change raises uncertainties and firms have difficulty in undertaking internal structural reform in keeping with the rapid technological changes. That is, not only is inter-firm technological diffusion important, but intra-firm technological diffusion is also vital for productivity growth.
Prior literature indicates that intra-firm diffusion tends to occur later and more slowly than inter-firm diffusion, implying a distinct underlying dynamics. However, empirical studies on intra-firm diffusion remain limited (Battisti & Stoneman, 2003; Battisti et al., 2009; Stoneman & Battisti, 2010).12 The policy implication from this line of research is different from those arising from studies focusing on inter-firm diffusion, putting greater emphasis on prioritizing direct assistance to enhance firm's own abilities to collect and use information more efficiently rather than attempting to influence other firm's behaviour, for example, through competition policy. Findings from this article suggest that policies focusing solely on inter-firm relations or simple R&D subsidies in the narrow sense would not be effective for firms caught in a low technological capability trap or with low technical efficiency. Policies affecting internal firm capabilities, such as institutional reforms affecting researcher remuneration or developing criteria for regulatory benefits to encourage technical efficiency, could be more helpful, even for the firms at the frontier.
Detailed case studies of firms showing both high levels of technological capability and technical efficiency may help to identify conditions for improving intra-firm technological diffusion. While this article focused only on economies of scale and technological capability as determinants of technical efficiency, intra-firm focus may also help to better identify determinants of technical efficiency. This opens a promising avenue for future research with the potential to yield new insights. It seems to be a natural extension of the technological capability approach, which emphasizes firm-specific technological learning. Such a research direction would be particularly important at times of rapid technological paradigm shift, such as the changes driven by artificial intelligence.
Despite limitations, the major contribution of this article is that it has successfully linked the technical efficiency literature with the more general theories of technological change such as the technological capability and Schumpeterian approaches, showing that technical efficiency estimated using financial data can be a viable option for a measure of technological capability and technological gap when detailed micro-level technological data is unavailable. On the empirical side, the study extends the application of the stochastic frontier approach by introducing heteroscedasticity in the context of the four-component GTRE model and taking endogeneity into account, which is rare in stochastic frontier literature but is standard in general productivity studies. Most of all, this article provides an in-depth study of technical efficiency and catch-up dynamics in the Korean pharmaceutical industry, which is rapidly growing but for which academic analysis of technological change has been scarce.
Conflict of Interest
The author declares no conflicts of interest.
Open Research
Data Availability Statement
Research data are not shared.
References
- 1 Some scholars (e.g., Romer, 1994) refer to the Schumpeterian endogenous growth theory as “neo-Schumpeterian.” This may cause confusion with a distinct strand of literature known as neo-Schumpeterian economics, which is closely related to the evolutionary economics of Nelson and Winter (1982). However, the overall research program of neo-Schumpeterian economics is broad enough to encompass endogenous growth theories incorporating Schumpeter's idea of creative destruction. For an example of the dialogue between these two strands, see Aghion and Festre (2017). For a review of neo-Schumpeterian economics, see Hanusch and Pyka (2007), and for an account of how this literature is evolving, see Callegari (2022).
- 2 I would like to thank the Editor for directing me to these new developments in stochastic frontier analysis. Unfortunately, I could not test for persistence arising from first order autocorrelation using the PDE method due to convergence problems. The MMSLE was conducted by using the “sftfe” command in STATA, written and kindly made available by Belotti and Ilardi. I do not discuss this methodology in detail here. The major references are Belotti and Ilardi (2018) and Chen et al. (2014).
- 3 Assuming a single output, maximizing (py/w'x) where y is output, p is output price, w is input price vector and x is vector of input variables, the first-order conditions are .This is equal to for a Cobb Douglas production function. From this, it follows that input ratios are independent of the error term. Although are correlated with the error term, the input ratios are independent of the error term because all the inputs are affected by it in the same way. For detail, see Lien et al. (2018:55).
- 4 For other approaches that consider endogeneity in stochastic frontier analysis, see Shee and Stefanou (2014), and for a more general discussion of endogeneity issues in stochastic frontier analysis, see Lai and Kumbhakar (2023). For a discussion on the general problem of input endogeneity in estimating production functions, see Levinsohn and Petrin (2003).
- 5 SMEs are here defined as firms with a turnover of <80 billion won, using the sales criteria of the “Small and Medium Enterprises Basic Law (2017).”
- 6 The Chi2 (2) statistic = 17.194 is significant at 1 percent, using the mixed table of Kodde and Palm (1986).
- 7 Conditional expectation is estimated by the non-parametric method, using the “npregress” command in STATA with the kernel option, given the two exogenous determinants of inefficiency, scale, and technological capability.
- 8 The likelihood ratio statistic was −3.35 × 10−5. At P-value of 1 percent, the critical Chi2 (1) from the Kodde and Palm (1986)'s table of mixed distribution is 5.412.
- 9 The average annual growth rate for the previous 10 years (2000–2010) is −0.32 percent.
- 10 Average annual growth rate is −0.07 percent for the period 2000–2023, and 0.18 percent for the period 2011–2023.
- 11 Regression results from these estimations are not reported in the interest of space. Results are available upon request.
- 12 For recent empirical works, see Hollenstein (2022) and Khalifa (2022).




